Abstract
In this paper, we study the bifurcations of periodic solutions from an equilibrium point of a differential equation whose linearization has two pairs of simple pure imaginary complex conjugate eigenvalues which are in 1:2 ratio. This corresponds to a Hopf-Hopf mode interaction with 1:2 resonance, as occurs in the context of dissipative mechanical systems. Using an approach based on Liapunov-Schmidt reduction and singularity theory, we give a framework in which to study these problems and their perturbations in two cases: no distinguished parameter, and one distinguished (bifurcation) parameter. We give a complete classification of the generic cases and their unfoldings.
Similar content being viewed by others
References
Alligood, K. T, &Yorke, J. A., Hopf bifurcation: the appearance of virtual periods in cases of resonance,J. Diff. Eqs. 64 (1986), 375–394.
Arnold, V. I., On matrices depending on parameters. InSingularity Theory: Selected Papers, London Mathematical Society Lecture Note Series,53 (1981), 46–60, Cambridge University Press.
Arnold, V. I.,Geometrical Methods in the Theory of Ordinary Differential Equations. (1983) Springer-Verlag, New York.
Ashkenazi, M. &Chow, S. N., A Hopf's bifurcation theorem for nonsimple eigenvalues,Adv. Appl. Math.,1 (1980), 360–372.
Atadan, A. S. &Huseyin, K., Analysis of dynamical bifurcations in the case of nonsimple eigenvalues,IEEE Proc. Int. Symp. on Circuits and Systems,2 (1985), 871–872.
Bajaj, A. K. &Sethna, P. R., Bifurcation in three-dimensional motions of articulated tubes, I and II,J. Appl. Mech.,49 (1982), 606–611, 612–618.
Bélair, J. &Campbell, S. A., Stability and bifurcations of equilibria in a multiple-delayed differential equation,SIAM J. Appl. Math.,54 (1994), 1402–1424.
Caprino, S., Maffei, C. &Negrini, P., Hopf bifurcation at 1:1 resonance,Nonlin. Anal. Theor. Meth. Appl.,8 (1984), 1011–1032.
Chossat, P. &Dias, F., The 1:2 resonance withO(2) symmetry and its applications to hydrodynamics,J. Nonlin. Sc.,5 (1995), 105–129.
Chossat, P., Golubitsky, M. &Keyfitz, B. L., Hopf-Hopf mode interactions withO(2) symmetry,Dyn. Stab. Sys.,1 (1987), 255–292.
Damon, J., The unfolding and determinacy theorems for subgroups of
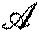 and
and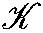 ,Memoirs Amer. Math. Soc.,306 (1984).
,Memoirs Amer. Math. Soc.,306 (1984).Furter, J. E., Hopf bifurcation at non-semisimple eigenvalues: a singularity theory approach. InInternational Series of Numerical Mathematics,104,E. Allgower,K. Böhme &M. Golubitsky (eds.) (1992), 135–145, Birkhäuser, Basel.
van Gils, S. A., Krupa, M. &Langford, W. F., Hopf bifurcation with non-semisimple 1:1 resonance,Nonlinearity,3 (1990), 825–850.
Golnaraghi, M. F., Tuer, K. &Wang, D., Regulation of a lumped parameter cantilever beam via internal resonance using nonlinear coupling enhancement,Dynamics and Control,4 (1994), 73–96.
Golubitsky, M. &Langford, W. F., Classification and unfoldings of degenerate Hopf bifurcations,J. Diff. Eqs.,41 (1981), 375–415.
Golubitsky, M., Marsden, J. E., Stewart, I. &Dellnitz, M., The constrained Liapunov-Schmidt procedure and periodic orbits,Normal Forms and Homoclinic Chaos.W. F. Langford &W. K. Nagata (eds.), Fields Institute Communications.4 Amer. Math. Soc., Providence, RI (1995).
Golubitsky, M. &Schaeffer, D. G.,Singularities and Groups in Bifurcation Theory. Vol. 1. (1985), Springer-Verlag, New York.
Golubitsky, M., Stewart, I. &Schaeffer, D. G.,Singularities and Groups in Bifurcation Theory. Vol 2. (1988), Springer-Verlag, New York.
Guckenheimer, J., On a codimension two bifurcation. InDynamical Systems and Turbulence.D. A. Rand &L. S. Young (eds.), Springer Lecture Notes in Mathematics,898 (1981), 99–142, New York.
Guckenheimer, J. &Holmes, P. J.,Nonlinear Oscillations, Dynamical Systems and Bifurcations of Vector Fields. (1982), Springer-Verlag, New York.
Hale, J.,Functional Differential Equations (1977), Springer-Verlag, New York.
He, Y. Q.,Normal Form Analysis of Strongly Resonant Hopf Bifurcation, M. Math. thesis (1992), University of Waterloo, Canada.
Henry, D.,Geometric Theory of Semilinear Parabolic Equations. Springer Lecture Notes in Mathematics840 (1981), New York.
Hill, A. &Stewart, I., Hopf-steady state mode interactions withO(2) symmetry,Dyn. Stab. Sys.,6 (1991), 149–171.
Holmes, P. J., Unfolding a degenerate nonlinear oscillator: a codimension two bifurcation. InNonlinear Dynamics.R. H. G. Helleman (ed.), (1980), 473–488, New York Academy of Sciences, New York.
Hungerford, T. W.,Algebra. (1974), Springer-Verlag, New York.
Iooss, G., Direct bifurcation of a steady solution of the Navier-Stokes equations into an invariant torus, SpringerLecture Notes in Mathematics,565, (1975), 69–84, New York.
Iooss, G. &Langford, W. F., Conjectures on the routes to turbulence via bifurcation. InNonlinear Dynamics.R. H. G. Helleman (ed.), (1980), 489–505, New York Academy of Sciences, New York.
Keener, J. P., Secondary bifurcation in nonlinear diffusion reaction equations,Stud. Appl. Math.,55 (1976), 187–211.
Keener, J. P., Infinite period bifurcation and global bifurcation branches,SIAM J. Appl. Math.,41 (1981), 127–144.
Knobloch, E. &Proctor, M. R. E., The double Hopf bifurcation with 2:1 resonance,Proc. R. Soc. Lond. A.,415 (1988), 61–90.
Krupa, M.,On 1:1 Resonant Hopf Bifurcation, M.Sc. thesis (1986), University of Waterloo, Canada.
Langford, W. F., Periodic and steady-state mode interactions lead to tori,SIAM J. Appl. Math.,37 (1979), 22–48.
LeBlanc, V. G.,On the 1:2 Resonant Hopf Bifurcation, Ph.D. thesis (1995), University of Waterloo, Canada.
LeBlanc, V. G., Period doubling and tripling in strongly resonant Hopf-Hopf interactions (1995), preprint.
LeBlanc, V. G. &Langford, W. F., Bifurcation of periodic orbits in 1:2 resonance: a singularity theory approach. InDynamics, Bifurcation and Symmetry.P. Chossat (ed.) (1994), 205–219, Kluwer.
Margolis, S. B. &Matkowsky, B. J., Flame propagation in channels: secondary bifurcation to quasi-periodic pulsations,SIAM J. Appl. Math.,45 (1985), 93–129.
Marsden, J. E. &McCracken, M.,The Hopf Bifurcation and its Applications. (1976), Springer-Verlag, New York.
Meyer, K. R., Normal forms for the general equilibrium,Funkcialaj Ekvacioj,27 (1984), 261–271.
Schmidt, D. S., Hopf's bifurcation theorem and the center theorem of Liapunov with resonance cases,J. Math. Anal. Appl.,63 (1978), 354–370.
Schwarz, G., Smooth functions invariant under the action of a compact Lie group,Topology,14 (1975), 63–68.
Stech, H. W., Generic Hopf bifurcation in a class of integro-differential equations,J. Integral Eqs. Appl.,3 (1991), 175–193.
Steen, P. &Davis, S. H., Quasi-periodic bifurcation in nonlinearly coupled oscillators near a point of strong resonance,SIAM J. Appl. Math.,42 (1982), 1345–1368.
Takens, F., Applications of global analysis I,Communications of the Mathematical Institute, Rijksuniversiteit Utrecht (1973).
Vanderbauwhede, A., Hopf bifurcation at non-semisimple eigenvalues. InMultiparameter Bifurcation Theory.M. Golubitsky &J. Guckenheimer (eds.),Contemp. Math.,56 (1986), 343–353,Amer. Math. Soc., Providence, RI.
Yu, P. &Huseyin, K., On phase-locked motions associated with strong resonance,Quart. Appl. Math.,51 (1993), 91–100.
Author information
Authors and Affiliations
Additional information
Communicated byM. Golubitsky
Rights and permissions
About this article
Cite this article
LeBlanc, V.G., Langford, W.F. Classification and unfoldings of 1:2 resonant Hopf Bifurcation. Arch. Rational Mech. Anal. 136, 305–357 (1996). https://doi.org/10.1007/BF02206623
Accepted:
Issue Date:
DOI: https://doi.org/10.1007/BF02206623




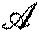 and
and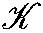 ,Memoirs Amer. Math. Soc.,306 (1984).
,Memoirs Amer. Math. Soc.,306 (1984).