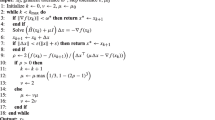Abstract
We describe a new algorithm for the computation of recursion coefficients of monic polynomials {p j } =0/n j that are orthogonal with respect to a discrete bilinear form (f, g) := Σ =1/m k f(x k )g(x k )w k ,m ≥n, with real distinct nodesx k and real nonvanishing weightsw k . The algorithm proceeds by applying a judiciously chosen sequence of real or complex Givens rotations to the diagonal matrix diag[x 1,x 2, ...,x m ] in order to determine an orthogonally similar complex symmetric tridiagonal matrixT, from whose entries the recursion coefficients of the monic orthogonal polynomials can easily be computed. Fourier coefficients of given functions can conveniently be computed simultaneously with the recursion coefficients. Our scheme generalizes methods by Elhay et al. [6] based on Givens rotations for updating and downdating polynomials that are orthogonal with respect to a discrete inner product. Our scheme also extends an algorithm for the solution of an inverse eigenvalue problem for real symmetric tridiagonal matrices proposed by Rutishauser [20], Gragg and Harrod [17], and a method for generating orthogonal polynomials based theoron [18]. Computed examples that compare our algorithm with the Stieltjes procedure show the former to generally yield higher accuracy except whenn ≪m. Ifn is sufficiently much smaller thanm, then both the Stieltjes procedure and our algorithm yield accurate results.
Similar content being viewed by others
References
S.T. Alexander, C.T. Pan and R.J. Plemmons, Analysis of a recursive least squares hyperbolic rotation algorithm for signal processing, Lin. Alg. Appl. 98(1988)3–40.
D.L. Boley, S. Elhay, G.H. Golub and M.H. Gutknecht, Nonsymmetric Lanczos and finding orthogonal polynomials associated with indefinite weights, Numer. Algor. 1(1991)21–43.
D. Boley and G.H. Golub, A survey of matrix inverse eigenvalue problems, Inverse Problems 3(1987)595–622.
C. de Boor and G.H. Golub, The numerically stable reconstruction of a Jacobi matrix from spectral data, Lin. Alg. Appl. 21(1978)245–260.
J. Cullum and R.A. Willoughby, A practical procedure for computing eigenvalues of large sparse nonsymmetric matrices, in:Large-Scale Eigenvalue Problems, ed. J. Cullum and R.A. Willoughby (Elsevier, New York, 1986) pp. 193–240.
S. Elhay, G.H. Golub and J. Kautsky, Updating and downdating of orthogonal polynomials with data-fitting applications, SIAM J. Matrix Anal. Appl. 12(1991)327–353.
Ö. Egecioglu and Ç.K. Koç, A fast algorithm for rational interpolation via orthogonal polynomials, Math. Comput. 53(1989)249–264.
G.E. Forsythe, Generation and use of orthogonal polynomials for data-fitting with a digital computer, J. Soc. Ind. Appl. Math. 5(1957)74–88.
W. Gautschi, On generating orthogonal polynomials, SIAM J. Sci. Stat. Comput. 3(1982)289–317.
W. Gautschi, Orthogonal polynomials — constructive theory and applications, J. Comput. Appl. Math. 12 and 13(1985)61–76.
W. Gautschi, Orthogonality — conventional and unconventional — in numerical analysis, in:Computation and Control, ed. K. Bowers and J. Lund (Birkhäuser, Boston, 1989) pp. 63–95.
W. Gautschi, Computational aspects of orthogonal polynomials, in:Orthogonal Polynomials; Theory and Practice, ed. P. Nevai (Kluwer, Dordrecht, 1990) pp. 181–216.
G.H. Golub, Matrix decompositions and statistical calculations, in:Statistical Computation, ed. R.C. Milton and J.A. Nelder (Academic Press, New York, 1969) pp. 365–395.
G.H. Golub and M.H. Gutknecht, Modified moments for indefinite weight functions, Numer. Math. 57(1990)607–624.
G.H. Golub and C.F. Van Loan,Matrix Computations, 2nd Ed. (Johns Hopkins, Baltimore, 1989).
W.B. Gragg, Matrix interpretations and applications of the continued fraction algorithm, Rocky Mountain J. Math. 4(1974)213–225.
W.B. Gragg and W.J. Harrod, The numerically stable reconstruction of Jacobi matrices from spectral data, Numer. Math. 44(1984)317–335.
L. Reichel, Fast QR decomposition of Vandermonde-like matrices and polynomial least squares approximation, SIAM J. Matrix Anal. Appl. 12(1991)552–564.
L. Reichel, G.S. Ammar and W.B. Gragg, Discrete least squares approximation by trigomometric polynomials, Math. Comput. 57(1991)273–289.
H. Rutishauser, On Jacobi rotation patterns, in:Experimental Arithmetic, High-Speed Computing and Mathematics, Proc. Symp. Appl. Math. 15 (Amer. Math. Soc., Providence, 1963) pp. 219–239.
L. Schrage, A more portableFortran random number generator, ACM Trans. Math. Software 5(1979)132–138.
G. Struble, Orthogonal polynomials: Variable-signed weight functions, Numer. Math. 5(1963)88–94.
Author information
Authors and Affiliations
Additional information
Research supported in part by the Center for Research on Parallel Computation at Rice University and NSF Grant No. DMS-9002884.
Rights and permissions
About this article
Cite this article
Reichel, L. Construction of polynomials that are orthogonal with respect to a discrete bilinear form. Adv Comput Math 1, 241–258 (1993). https://doi.org/10.1007/BF02071388
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF02071388