Abstract
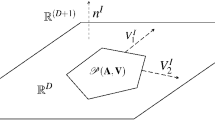
In this paper the principle that the boundary of a boundary is identically zero (∂○∂≡0) is applied to a skeleton geometry. It is shown that the left-hand side of the Regge equation may be interpreted geometrically as the sum of the moments of rotation associated with the faces of a polyhedral domain. Here the polyhedron, warped though it may be, is located in a lattice dual to the original skeleton manifold. This sum is related to the amount of energy-momentum (E-p) associated to the edge in question. In the establishment of this equation the ordinary Bianchi identity is rederived by applying the principle that the (∂○∂≡0) in its (1–2–3)-dimensional formulation to polyhedral domain. Steps toward the derivation of the contracted Bianchi identity using this principle in its (2–3–4)-dimensional form are discussed. Preliminary results in this direction indicate that there should be one vector identity per vertex of the skeleton geometry.
“Space acts on matter, telling it how to move. In turn, matter reacts back on space, telling it how to curve.”—Ref. 3, Chap. 1.
Similar content being viewed by others
References
J. A. Wheeler, “Physics and Austerity: Law Without Law,” A Working Paper, The University of Texas, (1982), pp. 61–83; published in Chinese as “Physics and Austerity,” Anhui, Science and Technology Publication, China August 1982.
J. A. Wheeler, “Particles and Geometry,” inUnified Theories of Elementary Particles, P. Breithenlohner and H. Durr, eds. (Springer-Verlag, New York, 1982), pp. 189–217.
C. W. Misner, K. S. Thorne, and J. A. Wheeler, “Bianchi Identities and the Boundary of a Boundary Is Zero,” inGravitation (W. H. Freeman, San Francisco, 1973), Chap. 16.
É. Cartan, 1928 and 1946,Leçons sur la Géométrie des Espaces de Riemann (Gauthier-Villars, Paris, France); English translation by Robert Hermann (Mathematical Sciences Press, Brookline, Massachusetts, 1983), Chap. 8.
W. A. Miller and J. A. Wheeler, “4-Geodesy,” paper presented at the Congress “Galactic and Extragalactic Dark Matter,” Rome, 28–30 June 1983; to appear inNuovo Cimento (1985).
A. Kheyfets, “The Boundary of a Boundary Principle: A Unified Approach,” to appear,Found. Phys. (1986).
T. Regge, “General Relativity without Coordinates,”Nuovo Cimento 19, 558–571 (1961).
I. Ciufolini, “On a Generalized Geodesic Deviation Equation,” Chap. 2 of dissertation, “Theory and Experiments in General Relativity and Other Metric Theories of Gravity,” The University of Texas (1984).
R. M. Williams and G. F. R. Ellis, “Regge Calculus and Observations. I. Formalism and Applications to Radial Motion and Circular Orbits,”Gen. Relativ. Gravit. 13, 361 (1981).
J. R. Munkres,Elements of Algebraic Topology (Addison-Wesley, Menlo Park, California, 1984), pp. 26–32.
H. Bacry,Lectures on Group Theory and Particle Physics (Gordon and Breach, New York, 1977), Chap. 7.
A. Brøndsted,An Introduction to Convex Polytopes (Springer-Verlag, New York, 1983), p. 64.
B. Grünbaum,Convex Polytopes (Wiley, New York, 1967), pp. 46, 137, 243, and 285.
H. S. M. Coxeter,Regular Polytopes (Dover, New York, 1973), 3rd. edn., pp. 6 and 60.
J. Cheeger, W. Müller, and R. Schrader, “On the Curvature of Piecewise Flat Spaces,”Commun. Math. Phys. 92, 405 (1984).
T. D. Lee, “Time as a Dynamical Variable,” a talk given at the Shelter Island II Conference, June 2, 1983, Columbia University Preprint CU-TP-266 (1983), p. 18.
C. W. F. Everitt,James Clark Maxwell (Charles Scribners, New York, 1975), Chap. 10.
John A. Wheeler, private communication.
W. A. Miller, “Null-Strut Geometrodynamics and the Inchworm Algorithm,” inDynamical Spacetimes and Numerical Relativity, J. Centrella, ed. (Cambridge Univ. Press, 1986), in press.
Author information
Authors and Affiliations
Additional information
Submitted in honor of John Archibald Wheeler's 75th birthday. Original version submitted to Prof. Wheeler's Spring 1985 PHY393T course on Foundations of Physics taught at The University of Texas at Austin. Publication assisted by this Center and by NSF Grants PHY 8503890 and PHY 8205717.
Rights and permissions
About this article
Cite this article
Miller, W.A. The geometrodynamic content of the Regge equations as illuminated by the boundary of a boundary principle. Found Phys 16, 143–169 (1986). https://doi.org/10.1007/BF01889378
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF01889378