Skip to main content
SpringerLink
Log in

Generalized resolution for 0–1 linear inequalities

  • Published:
Annals of Mathematics and Artificial Intelligence Aims and scope Submit manuscript

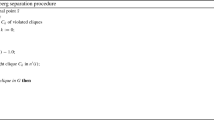
Abstract

We show how the resolution method of theorem proving can be extended to obtain a procedure for solving a fundamental problem of integer programming, that of finding all valid cuts of a set of linear inequalities in 0-1 variables. Resolution generalizes to two cutting plane operations that, when applied repeatedly, generate all strongest possible or “prime” cuts (analogous to prime implications in logic). Every valid cut is then dominated by at least one of the prime cuts. The algorithm is practical when restricted to classes of inequalities within which one can easily tell when one inequality dominates another. We specialize the algorithm to several such classes, including inequalities representing logical clauses, for which it reduces to classical resolution.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. V.J. Bowman, Constraint classification on the unit hypercube, Management Sciences Research Report No. 287, Graduate School of Industrial Administration, Carnegie Mellon University, Pittsburgh, PA 15213 (Revised July 1972).

    Google Scholar 

  2. G.H. Bradley, P.L. Hammer and L.A. Wolsey, Coefficient reduction for inequalities in 0-1 variables, Math. Progr. 7 (1975) 263–282.

    Google Scholar 

  3. V. Chvátal, Edmonds polytopes and a hierarchy of combinatorial problems, Discr. Math. 4 (1973) 305–337.

    Google Scholar 

  4. S.A. Cook, The complexity of theorem-proving procedures,Proc. 3rd Annual ACM Symp. on the Theory of Computing (1971) pp. 151–158.

  5. M.R. Genesereth and N.J. Nilsson,Logical Foundations of Artificial Intelligence (Morgan Kaufmann, 1987).

  6. M. Guinard and K. Spielberg, Logical reduction methods in 0-1 programming (minimal preferred variables), Oper. Res. 29 (1981) 49–74.

    Google Scholar 

  7. A. Haken, The intractability of resolution, Theor. Comp. Sci. 39 (1985) 297–308.

    Google Scholar 

  8. J.N. Hooker, Generalized resolution and cutting planes, Ann. Oper. Res. 12 (1988) 217–239.

    Google Scholar 

  9. J.N. Hooker, A quantitative approach to logical inference, Decision Support Systems 4 (1988) 45–69.

    Google Scholar 

  10. J.N. Hooker, Input proofs and rank one cutting planes, ORSA J. Comput. 1 (1989) 137–145.

    Google Scholar 

  11. E.L. Johnson, M.M. Kostreva and U.H. Suhl, Solving 0-1 integer programming problems arising from large scale planning models, Oper. Res. 33 (1985) 803–819.

    Google Scholar 

  12. W.V. Quine, The problem of simplifying truth functions, Amer. Math. Monthly 59 (1952) 521–531.

    Google Scholar 

  13. W.V. Quine, A way to simplify truth functions, Amer. Math. Monthly 62 (1955) 627–631.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Graduate School of Industrial Administration, Carnegie Mellon University, 15213, Pittsburgh, PA, USA

    J. N. Hooker

Authors
  1. J. N. Hooker
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Supported in part by Air Force Office of Scientific Research, Grant number AFOSR-87-0292.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Hooker, J.N. Generalized resolution for 0–1 linear inequalities. Ann Math Artif Intell 6, 271–286 (1992). https://doi.org/10.1007/BF01531033

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF01531033

Keywords

Search

Navigation