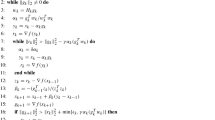Abstract
In this note we discuss Newton's method in a setting somewhat more restrictive than customary. In this setting, however, we claim to have proved superlinear convergence of the Newton process without assuming twice differentiability or Lipschitz continuity of the first derivative of the operator. A further feature is that the iteration to be discussed is not initially but is eventually the Newton process. With this feature global rather than local convergence is achieved.
Similar content being viewed by others
References
Kantorovich, L. V.: Functional analysis and applied mathematics. Uspekhi Mathematicheskikh Nauk3, No. 6, 89–185 (1948). Also NBS Report 1509, edited byG. E. Forsythe.
Schröder, J.: Über das Newtonsche Verfahren. Archive for Rational Mechanics and Analysis1, 154–180 (1957).
Kerner, M.: Die Differentiale in der allgemeinen Analysis. Ann. of Math.34, 546–572 (1933). See also [4].
Vainberg, M. M.: Variational methods for the study of nonlinear operators. Holden Day, San Francisco, 1964.
Author information
Authors and Affiliations
Additional information
This research was supported by the Boeing Scientific Research Laboratories and by Grant AF-AFOSR 937-65.
Rights and permissions
About this article
Cite this article
Goldstein, A.A. On Newton's method. Numer. Math. 7, 391–393 (1965). https://doi.org/10.1007/BF01436251
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF01436251