Skip to main content
SpringerLink
Log in

A posteriori error estimators for the Stokes equations

  • Published:
Numerische Mathematik Aims and scope Submit manuscript

Summary

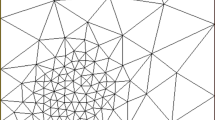
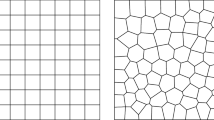
We present two a posteriori error estimators for the mini-element discretization of the Stokes equations. One is based on a suitable evaluation of the residual of the finite element solution. The other one is based on the solution of suitable local Stokes problems involving the residual of the finite element solution. Both estimators are globally upper and locally lower bounds for the error of the finite element discretization. Numerical examples show their efficiency both in estimating the error and in controlling an automatic, self-adaptive mesh-refinement process. The methods presented here can easily be generalized to the Navier-Stokes equations and to other discretization schemes.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Abdalass, E.M.: Resolution performance du probléme de Stokes par mini-éléments, maillages auto-adaptifs et méthodes multigrilles-applications. Thése de 3me cycle, Ecole Centrale de Lyon 1987

  2. Arnold, D.N., Brezzi, F., Fortin, M.: A stable finite element for the Stokes equations. Calcolo21, 337–344 (1984)

    Google Scholar 

  3. Babuska, I.: The finite element method with Lagrange multipliers. Numer. Math.20, 179–192 (1973)

    Google Scholar 

  4. Babuska, I., Rheinboldt, W.C.: A posteriori error estimates for the finite element method. Int. J. Numer. Methods Eng.12, 1597–1615 (1978)

    Google Scholar 

  5. Babuska, I., Rheinboldt, W.C.: Error estimates for adaptive finite element computations. SIAM J. Numer. Anal.15, 736–754 (1978)

    Google Scholar 

  6. Bank, R.E., Dupont, T., Yserentant, H.: The hierarchical basis multigrid method. Konrad Zuse Zentrum, Berlin, Preprint SC-87-2 (1987)

    Google Scholar 

  7. Bank, R.E., Weiser, A.: Some a posteriori error estimators for elliptic partial differential equations. Math. Comput.44, 283–301 (1985)

    Google Scholar 

  8. Brezzi, F.: On the existence, uniqueness, and approximation of saddle-point problems arising from Lagrangian multipliers. RAIRO Anal. Numér.8, 129–151 (1974)

    Google Scholar 

  9. Buckley, A., Lenir, A.:QN-like variable storage conjugate gradients. Math. Program.27, 155–175 (1983)

    Google Scholar 

  10. Ciarlet, P.G.: The finite element method for elliptic problems, 2nd Ed. Amsterdam: North Holland 1978

    Google Scholar 

  11. Girault, V., Raviart, P.A.: Finite element approximation of the Navier-Stokes equations. Series in Computational Mathematics. Berlin Heidelberg New York: Springer 1986

    Google Scholar 

  12. Verfürth, R.: A combined conjugate gradient — multi-grid algorithm for the numerical solution of the Stokes problem. IMA J. Numer. Anal.4, 441–455 (1984)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institut für Angewandte Mathematik, Universität Zürich, Rämistrasse 74, CH-8001, Zürich, Switzerland

    R. Verfürth

Authors
  1. R. Verfürth
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

This work was accomplished at the Universität Heidelberg with the support of the Deutsche Forschungsgemeinschaft

Rights and permissions

Reprints and permissions

About this article

Cite this article

Verfürth, R. A posteriori error estimators for the Stokes equations. Numer. Math. 55, 309–325 (1989). https://doi.org/10.1007/BF01390056

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF01390056

Subject Classifications

Search

Navigation