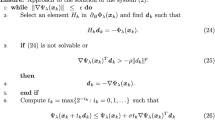Skip to main content
SpringerLink
Log in

Solution of symmetric linear complementarity problems by iterative methods

  • Contributed Papers
  • Published:
Journal of Optimization Theory and Applications Aims and scope Submit manuscript

Abstract

A unified treatment is given for iterative algorithms for the solution of the symmetric linear complementarity problem:

$$Mx + q \geqslant 0, x \geqslant 0, x^T (Mx + q) = 0$$

, whereM is a givenn×n symmetric real matrix andq is a givenn×1 vector. A general algorithm is proposed in which relaxation may be performed both before and after projection on the nonnegative orthant. The algorithm includes, as special cases, extensions of the Jacobi, Gauss-Seidel, and nonsymmetric and symmetric successive over-relaxation methods for solving the symmetric linear complementarity problem. It is shown first that any accumulation point of the iterates generated by the general algorithm solves the linear complementarity problem. It is then shown that a class of matrices, for which the existence of an accumulation point that solves the linear complementarity problem is guaranteed, includes symmetric copositive plus matrices which satisfy a qualification of the type:

$$Mx + q > 0 for some x in R^n $$

. Also included are symmetric positive-semidefinite matrices satisfying this qualification, symmetric, strictly copositive matrices, and symmetric positive matrices. Furthermore, whenM is symmetric, copositive plus, and has nonzero principal subdeterminants, it is shown that the entire sequence of iterates converges to a solution of the linear complementarity problem.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Lemke, C. E.,On Complementary Pivot Theory, Mathematics of the Decision Sciences, Part 1, Edited by G. B. Dantzig and A. F. Veinott, American Mathematical Society, Providence, Rhode Island, pp. 95–114, 1968.

    Google Scholar 

  2. Cottle, R. W., andDantzig, G. B.,Complementary Pivot Theory of Mathematical Programming, Linear Algebra and Its Applications, Vol. 1, pp. 103–125, 1968.

    Google Scholar 

  3. Murty, K. G.,On the Number of Solutions to the Complementarity Problem and Spanning Properties of Complementary Cones, Linear Algebra and Its Applications, Vol. 5, pp. 65–108, 1972.

    Google Scholar 

  4. Mangasarian, O. L.,Linear Complementarity Problems Solvable by a Single Linear Program, Mathematical Programming, Vol. 10, pp. 263–270, 1976.

    Google Scholar 

  5. Mangasarian, O. L.,Solution of Linear Complementary Problems by Linear Programming, Numerical Analysis Dundee 1975, Edited by G. W. Watson, Springer-Verlag, Berlin, Germany, pp. 166–175, 1976.

    Google Scholar 

  6. Mangasarian, O. L.,Characterization of Linear Complementarity Problems as Linear Programs, University of Wisconsin, Madison, Wisconsin, Computer Sciences Report No. 271, 1976.

    Google Scholar 

  7. Cryer, C. W.,The Method of Christopherson for Solving Free Boundary Problems for Infinite Journal Bearings by Means of Finite Differences, Mathematics of Computation, Vol. 25, pp. 435–443, 1971.

    Google Scholar 

  8. Eckhardt, U.,Quadratic Programming by Successive Overrelaxation, Kernforschungsanlage Jülich, Technical Report No. Jül-1064-MA, 1974.

  9. Raimondi, A. A., andBoyd, J.,A Solution for the Finite Journal Bearing and Its Application to Analysis and Design, III, Transactions of the American Society of Lubrication Engineers, Vol. 1, pp. 194–209, 1958.

    Google Scholar 

  10. Fridman, V. M., andChernina, V. S.,An Iteration Process for the Solution of the Finite-Dimensional Contact Problem, USSR Computational Mathematics and Mathematical Physics, Vol. 8, pp. 210–214, 1967.

    Google Scholar 

  11. Ortega, J. M.,Numerical Analysis, A Second Course, Academic Press, New York, New York, 1972.

    Google Scholar 

  12. Gnanadoss, A. A., andOsborne, M. R.,The Numerical Solution of Reynolds' Equation for a Journal Bearing, Quarterly Journal of Mechanics and Applied Mathematics, Vol. 17, pp. 241–246, 1964.

    Google Scholar 

  13. Martinet, B.,Convergence de Certaines Méthodes de Relaxation en Programmation Convexe, Comptes Rendus de L'Académie des Sciences, Paris, France, Vol. 265, Series A, pp. 210–212, 1967.

    Google Scholar 

  14. Cryer, C. W.,The Solution of a Quadratic Programming Problem Using Systematic Overrelaxation, SIAM Journal on Control, Vol. 9, pp. 385–392, 1971.

    Google Scholar 

  15. Glowinski, R.,Sur la Minimisation, par Surrelaxation avec Projection, de Functionnelles, Quadratiques dans les Espaces d'Hilbert, Comptes Rendus de L'Académie des Sciences, Paris, France, Vol. 276, Series A, pp. 1421–1423, 1973.

    Google Scholar 

  16. Martinet, B., andAuslender, A.,Methodes de Decomposition pour la Minimisation d'une Fonction sur une Espace Produit, SIAM Journal on Control, Vol. 12, pp. 635–642, 1974.

    Google Scholar 

  17. Cottle, R. W., Golub, G. H., andSacher, R. S.,On the Solution of Large Structured Linear Complementarity Problems, III, Stanford University, Stanford, California, Operations Research Report No. 73-8, 1973.

    Google Scholar 

  18. Young, D. M.,Iterative Solution of Large Linear Systems, Academic Press, New York, New York, 1971.

    Google Scholar 

  19. Fiedler, M., andPták, V.,On Matrices with Non-Positive Off-Diagnonal Elements and Positive Principal Minors, Czechoslovak Mathematics Journal, Vol. 12, pp. 382–400, 1962.

  20. Varga, R. S.,Matrix Iterative Analysis, Prentice-Hall, Englewood Cliffs, New Jersey, 1962.

    Google Scholar 

  21. Varga, R. C.,On Recurring Theorems on Diagonal Dominance, Linear Algebra and Its Applications, Vol. 13, pp. 1–9, 1976.

    Google Scholar 

  22. Levitin, E. S., andPoljak, B. T.,Constrained Minimization Methods, USSR Computational Mathematics and Mathematical Physics, Vol. 6, pp. 1–50, 1966.

    Google Scholar 

  23. Mangasarian, O. L.,Nonlinear Programming, McGraw-Hill, New York, New York, 1969.

    Google Scholar 

  24. Ostrowski, A. M.,Solution of Equations and Systems of Equations, Second Edition, Academic Press, New York, New York, 1966.

    Google Scholar 

  25. Daniel, J. W.,The Approximate Minimization of Functionals, Prentice-Hall, Englewood Cliffs, New Jersey, 1971.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Computer Sciences Department, University of Wisconsin, Madison, Wisconsin

    O. L. Mangasarian (Professor)

Authors
  1. O. L. Mangasarian
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

This research was supported by the Science Research Council, Grant No. B/RG/4079.7, by the National Science Foundation, Grant No. DCR-74-20584, and by the Wisconsin Alumni Research Foundation.

The author is indebted to C. Elliott for stimulating discussions on the subject of this paper and to R. R. Meyer for suggestions for improving the paper and, in particular, for suggesting the use of an arbitrary constantc, instead of zero, in Lemma 2.3.

This paper was written while the author was a Senior Research Fellow, Oxford University Computing Laboratory, Oxford, England.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Mangasarian, O.L. Solution of symmetric linear complementarity problems by iterative methods. J Optim Theory Appl 22, 465–485 (1977). https://doi.org/10.1007/BF01268170

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF01268170

Key Words

Search

Navigation