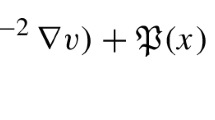Abstract
Certain generalizations of one of the classical Boussinesq-type equations,
are considered. It is shown that the initial-value problem for this type of equation is always locally well posed. It is also determined that the special, solitary-wave solutions of these equations are nonlinearly stable for a range of their phase speeds. These two facts lead to the conclusion that initial data lying relatively close to a stable solitary wave evolves into a global solution of these equations. This contrasts with the results of blow-up obtained recently by Kalantarov and Ladyzhenskaya for the same type of equation, and casts additional light upon the results for the original version (*) of this class of equations obtained via inverse-scattering theory by Deift, Tomei and Trubowitz.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Albert, J., Bona, J. L., Henry, D.: Sufficient conditions for stability of solitary-wave solutions of model equations for long waves. Physica24D, 343–366 (1987)
Benjamin, T. B.: The stability of solitary waves. Proc. Roy. Soc. Lond.A328, 153–183 (1972)
Bennett, D. P., Bona, J. L., Brown, S. E., Stansfield, D. D., Stroughair. J. D.: The stability of internal solitary waves. Math. Proc. Camb. Phil. Soc.94, 351–379 (1983)
Berryman, J.: Stability of solitary waves in shallow water. Phys. Fluids19, 771–777 (1976)
Bona, J. L.: On the stability theory of solitary waves. Proc. Roy. Soc. Lond.A344, 363–374 (1975)
Bona, J. L., Smith, R.: A model for the two-way propagation of water waves in a channel. Math. Proc. Camb. Phil. Soc.79, 167–182 (1976)
Bona, J. L., Souganidis, P., Strauss, W.: Stability and instability of solitary waves of KdV type. Proc. Roy. Soc. Lond.A411, 395–412 (1987)
Boussinesq, J.: Théorie des ondes et de remous qui se propagent....J. Math. Pures Appl., Sect. 2,17, 55–108 (1872)
Boussinesq, J.: Essai sur la théorie des eaux courantes. Mem. prés. div. Sav. Acad. Sci. Inst. Fr.23, 1–680 (1877)
Courant, R., Hilbert, D.: Methods of mathematical physics Vol. 1. New York: Interscience 1953
Deift, P., Tomei, C., Trubowitz, E.: Inverse scattering and the Boussinesq equation. Commun. Pure Appl. Math.35, 567–628 (1982)
Grillakis, J., Shatah, J., Strauss, W. A.: Stability theory of solitary waves in the presence of symmetry I. J. Funct. Anal.74, 160–197 (1987).
Kalantarov, V.K., Ladyzhenskaya, O.A.: The occurrence of collapse for quasilinear equations of parabolic and hyperbolic types. J. Sov. Math.10, 53–70 (1978)
Kato, T.: Quasilinear equations of evolution, with applications to partial differential equations. Lecture Notes in Mathematics Vol.448, pp. 25–70. Berlin, Heidelberg, New York: Springer 1974
Kato, T.: On the Cauchy problem for the (generalized) Korteweg-de-Vries equation. Studies in Applied Mathematics. Ad. Math. Suppl. Stud.8, 93–128 (1983)
Lions, J.-L., Magenes, E.: Problèmes aux limites non homogènes et applications, Vol. I. Paris: Dunod 1968
Weinstein, M.: Lyapunov stability of ground states of nonlinear dispersive evolution equations. Commun. Pure Appl. Math.39, 51–68 (1986)
Zakharov, V. E.: On the stochastization of one-dimensional chains of nonlinear oscillators. Sov. Phys. JETP38, 108–110 (1974)
Author information
Authors and Affiliations
Additional information
Communicated by C. H. Taubes
Work partially supported by the National Science Foundation
Rights and permissions
About this article
Cite this article
Bona, J.L., Sachs, R.L. Global existence of smooth solutions and stability of solitary waves for a generalized Boussinesq equation. Commun.Math. Phys. 118, 15–29 (1988). https://doi.org/10.1007/BF01218475
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF01218475