Abstract
Two-dimensional unsteady free convection and mass transfer, flow of an incompressible viscous dissipative and electrically conducting fluid, past an infinite, vertical porous plate, is considered, when the flow, is subjected in the action of uniform transverse magnetic field. The magnetic Reynolds number is taken to be small enough so that the induced magnetic field is negligible. The solution of the problem is obtained in the form of power series of Eckert numberE, which is very small for incompressible fluids. Analytical expressions for the velocity field and temperature field are given, as well as for the skin friction and the rate of heat transfer for the case of the mean steady flow and for the unsteady one. The influence of the magnetic parameter,M, modified Grashof numberG c , Schmidt numberS c and frequency ω, on the flow field, is discussed with the help of graphs, when the plate is being cooled, by the free convection currents (G r ,E>0), or heated (G r ,E<0). A comparative study with hydrodynamic case (M=0) and the hydromagnetic one (M≠0) is also made whenever necessary.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
Abbreviations
- B0 :
-
applied magnetic field
- |B|:
-
amplitude of the skin friction
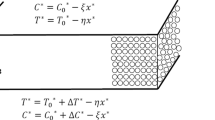
- C′ :
-
concentration inside the boundary layer
- C ′ ∞ :
-
concentration in the free stream
- C ′ w :
-
concentration at the porous plate
- C p :
-
specific heat at constant pressure
- D :
-
diffusion coefficient
- E :
-
Eckert number
- g x :
-
acceleration due to gravity
- G c :
-
modified Grashof number
- G r :
-
Grashof number
- M :
-
magnetic parameter
- N u :
-
Nusselt number
- P :
-
Prandtl number
- |Q|:
-
amplitude of the rate of heat transfer
- S c :
-
Schmidt number
- T′ :
-
temperature of the fluid
- T ′ w :
-
temperature of the plate
- T ′ ∞ :
-
temperature of the fluid in the free stream
- T r ,T i :
-
fluctuating parts of the temperature profile
- u′, v′ :
-
velocity components in thex′, y′ directions
- u :
-
dimensionless velocity in thex direction
- u 0 :
-
mean steady velocity
- u 1 :
-
unsteady part of the velocity
- u r ,u i :
-
fluctuating parts of the velocity profile
- U′ :
-
dimensionless free stream volocity
- U 0 :
-
mean free stream velocity
- v 0 :
-
suction velocity
- x′, y′ :
-
co-rodinate system
- α:
-
phase angle of the skin-friction
- β:
-
coefficient of volume expansion
- β* :
-
coefficient of expansion with concentration
- γ:
-
phase angle of the rate of heat transfer
- η:
-
dimensionless co-ordinate normal to the plate
- θ:
-
dimensionless temperature
- θ0 :
-
mean steady temperature
- θ1 :
-
unsteady part of temperature
- k :
-
thermal conductivity
- v :
-
kinematic viscocity
- ρ′:
-
density of fluid in the boundary layer
- ρ ′∞ :
-
density of fluid in the free stream
- σ:
-
electrical conductivity of the fluid
- τ:
-
skin friction
- τ0 :
-
mean skin friction
- ω′:
-
frequency
- ω:
-
dimensionless frequency
References
Gephart, B. and Pera, L. 1971,In. J. Heat Mass Transfer 14, 2025.
Lighthill, M. J.: 1954,Proc. Roy. Soc. A 224 1–23.
Soundalgekar, V. M.: 1976,Proc. Indian Acad. Sci. 84A, No 5, 194–203.
Soundalgekar, V. M.: 1975,ZAMM,55 257–268.
Sparrow, E. M., Minkowycz, J. J. and Eckert, E. R. G.: 1964,J. Heat Trans. ASME 86c, 508.
Stuart, J. T.: 1955,Proc. R. Soc. A 231, 116–130.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Georgantopoulos, G.A., Koullias, J., Goudas, C.L. et al. Free convection and mass transfer effects on the hydro-magnetic oscillatory flow past an infinite vertical porous plate. Astrophys Space Sci 74, 357–389 (1981). https://doi.org/10.1007/BF00656444
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF00656444