Mathematical quantum theory I: Random ultrafilters as hidden variables

Abstract

The basic purpose of this essay, the first of an intended pair, is to interpret standard von Neumann quantum theory in a framework of iterated measure algebraic ‘truth’ for mathematical (and thus mathematical-physical) assertions — a framework, that is, in which the ‘truth-values’ for such assertions are elements of iterated boolean measure-algebras $\mathbb{A}$ (cf. Sections 2.2.9, 5.2.1–5.2.6 and 5.3 below).

The essay itself employs constructions of Takeuti's boolean-valued analysis (whose origins lay in work of Scott, Solovay, Krauss and others) to provide a metamathematical interpretation of ideas sometimes considered disparate, ‘heuristic’, or simply ill-defined: the ‘collapse of the wave function’, for example; Everett's many worlds'-construal of quantum measurement; and a ‘natural’ product space of contextual (nonlocal) ‘hidden variables’.

More precisely, these constructions permit us to write down a category-theoretically natural correlation between ‘ideal outcomes’ of quantum measurements u of a ‘universal wave function’, and possible ‘worlds’ of an Everett-Wheeler-like many-worlds-theory.

The ‘universal wave function’, first, is simply a pure state of the Hilbert space (L ₂([0, 1])^M in a model M an appropriate mathematical-physical theory T, where T includes enough set-theory to derive all the analysis needed for von Neumann-algebraic formulations of quantum theory.

The ‘worlds’ of this framework can then be given a genuine model-theoretic construal: they are ‘random’ models M(u) determined by M-random elements u of the unit interval [0, 1], where M is again a fixed model of T.

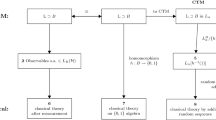
Each choice of a fixed basis for a Hilbert space H in a model of M of T then assigns ‘ideal’ spectral values for observables A on H (random ultrafilters on the range $\mathbb{A}$ of A regarded as a projection-valued measure) to such M-random reals u. If $\mathbb{L}$ is the ‘universal’ Lebesgue measure-algebra on [0, 1], these assignments are interrelated by the spectral functional calculus with value 1 in the boolean extension (V($\mathbb{L}$))^M, and therefore in each M(u).

Finally, each such M-random u also generates a corresponding extension M(u) of M, in which ‘ideal outcomes’ of measurements of all observables A in states are determined by the assignments just mentioned from the random spectral values u for the ‘universal’ ‘position’-observable on L ₂([0, 1]) in M.

At the suggestion of the essay's referee, I plan to draw on its ideas in the projected sequel to examine more recent ‘modal’ and ‘decoherence’-interpretations of quantum theory, as well as Schrödinger's traditional construal of time-evolution. A preliminary account of the latter — an obvious prerequisite for any serious ‘many-worlds’-theory, given that Everett's original intention was to integrate time-evolution and wave-function collapse — is sketched briefly in Section 5.3. The basic idea is to apply results from the theory of iterated measure-algebras to reinterpret time-ordered processes of measurements (determined, for example, by a given Hamiltonian observable H in M) as individual measurements in somewhat more complexly defined extensions M(u) of M.

In plainer English: if one takes a little care to distinguish boolean- from measure-algebraic tensor-products of the ‘universal’ measure-algebra L, one can reinterpret formal time-evolution so that it becomes ‘internal’ to the ‘universal’ random models M(u).