Noise-induced neural impulses

Abstract

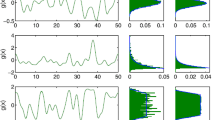
The firing pattern of neural pulses often show the following features: the shapes of individual pulses are nearly identical and frequency independent; the firing frequency can vary over a broad range; the time period between pulses shows a stochastic scatter. This behaviour cannot be understood on the basis of a deterministic non-linear dynamic process, e.g. the Bonhoeffer-van der Pol model. We demonstrate in this paper that a noise term added to the Bonhoeffer-van der Pol model can reproduce the firing patterns of neurons very well. For this purpose we have considered the Fokker-Planck equation corresponding to the stochastic Bonhoeffer-van der Pol model. This equation has been solved by a new Monte Carlo algorithm. We demonstrate that the ensuing distribution functions represent only the global characteristics of the underlying force field: lines of zero slope which attract nearby trajectories prove to be the regions of phase space where the distributions concentrate their amplitude. Since there are two such lines the distributions are bimodal representing repeated fluctuations between two lines of zero slope. Even in cases where the deterministic Bonhoeffer-van der Pol model does not show limit cycle behaviour the stochastic system produces a limit cycle. This cycle can be identified with the firing of neural pulses.