Skip to main content
SpringerLink
Log in

Non-integrability of the problem of motion around an oblate planet

  • Published:
Celestial Mechanics and Dynamical Astronomy Aims and scope Submit manuscript

Abstract

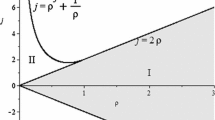
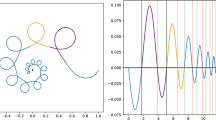
We provide a result of non-analytic integrability of the so-called J 2-problem. Precisely by using the Lerman theorem we are able to prove the existence of a region of the phase space, where the dynamical system exhibits chaotic motions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Danby, J. M. A.: 1962, Fundamentals of Celestial Mechanics, Macmillan, New York.

    Google Scholar 

  2. Fédoriouk, M.: 1987, Méthodes Asymptotiques pour les Equations Différentielles Ordinaires Linéaires, MIR, Moscow.

    Google Scholar 

  3. Grotta Ragazzo, G., Koiller, J. and Oliva, W. M., Motion of Massive Vortices in Two Dimensions (preprint).

  4. Kyner, W. T.: 1968, ‘Rigorous and Formal Stability of Orbits around an Oblate Planet’, Mem. AMS 81, 1.

    Google Scholar 

  5. Irigoyen, M. and Simó, C.: 1993, ‘Non Integrability of the J 2 Problem’, Cel. Mech. and Dynam. Astron. 55, 281.

    Google Scholar 

  6. Landau, L. D. and Lifschitz, E. M.: 1982, Quantum Mechanics, MIR, Moscow.

    Google Scholar 

  7. Lerman, L. M.: 1991, ‘Hamiltonian Systems with Loops of a Separatrix of a Saddle-Center’, Selecta Math. Sov. 10, 297.

    Google Scholar 

  8. Mielke, A., Holmes, P. and O'Reilly, O.: 1992, ‘Cascades of Homoclinic Orbits to, and Chaos near, a Hamiltonian Saddle Center’, J. Dyn. Diff. Eqs. 4, 95.

    Google Scholar 

  9. Simó, C.: 1991, ‘Measuring the Lack of Integrability of the J 2 Problem for Earth's Satellites’, in A. E. Roy (ed.), Predictability, Stability, and Chaos in N-Body Dynamical Systems, Plenum Press, New York.

    Google Scholar 

  10. Yoshida, H.: 1987, ‘A Criterion for the Non-Existence of an Additional Integral in Hamiltonian Systems with a Homogeneous Potential’, Physica 29D, 128.

    Google Scholar 

  11. Ziglin, S. L.: 1983, ‘Branching of Solutions and Non-Existence of First Integrals in Hamiltonian Mechanics’, Funct. Anal. Appl. 16, 181 and 17, 6.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Dipartimento di Matematica Pura e Applicata, Università di L'Aquila, 1-67100, Coppito, L'Aquila, Italy

    Alessandra Celletti & Piero Negrini

Authors
  1. Alessandra Celletti
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Piero Negrini
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Celletti, A., Negrini, P. Non-integrability of the problem of motion around an oblate planet. Celestial Mech Dyn Astr 61, 253–260 (1995). https://doi.org/10.1007/BF00051896

Download citation

  • Received:

  • Accepted:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF00051896

Key words

Search

Navigation