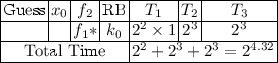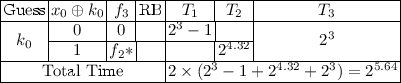Improved Linear Hull Attack on Round-Reduced Simon with Dynamic Key-Guessing Techniques

Abstract

Simon is a lightweight block cipher family proposed by NSA in 2013. It has drawn many cryptanalysts’ attention and varieties of cryptanalysis results have been published, including differential, linear, impossible differential, integral cryptanalysis and so on. In this paper, we give the improved linear attacks on all reduced versions of Simon with dynamic key-guessing technique, which was proposed to improve the differential attack on Simon recently. By establishing the boolean function of parity bit in the linear hull distinguisher and reducing the function according to the property of AND operation, we can guess different subkeys (or equivalent subkeys) for different situations, which decrease the number of key bits involved in the attack and decrease the time complexity in a further step. As a result, 23-round Simon32/64, 24-round Simon48/72, 25-round Simon48/96, 30-round Simon64/96, 31-round Simon64/128, 37-round Simon96/96, 38-round Simon96/144, 49-round Simon128/128, 51-round Simon128/192 and 53-round Simon128/256 can be attacked. As far as we know, our attacks on most reduced versions of Simon are the best compared with the previous cryptanalysis results. However, this does not shake the security of Simon family with full rounds.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

In 2013, NSA proposed a new family of lightweight block cipher with Feistel structure, named as Simon, which is tuned for optimal performance in hardware applications [7]. The Simon family consists of various block and key sizes to match different application requirements. There is no S-box in the round function. The round function consists of AND, rotation and Xor (ARX structure), leading to a low-area hardware requirement.

Related Works. Simon family has attracted a lot of cryptanalysts’ attention since its proposition. Many cryptanalysis results on various versions of Simon were published. For differential attack, Alkhzaimi and Lauridsen [5] gave the first differential attacks on all versions of Simon. The attacks cover 16, 18, 24, 29, 40 rounds for the versions with block size 32, 48, 64, 96 and 128 respectively. At FSE 2014, Abed et al. [3] gave differential attack on variants of Simon reduced to 18, 19, 26, 35, 46 rounds with respective block size 32, 48, 64, 96 and 128. At the same time, Biryukov et al. [9] gave differential attack on several versions of Simon independently. And 19-round Simon32, 20-round Simon48, 26-round Simon64 were attacked. Then Wang et al. [20] proposed better differential attacks with existing differentials, using dynamic key-guessing techniques. As a result, 21-round Simon32/64, 23-round Simon48/72, 24-round Simon48/96, 28-round Simon64/96, 29-round Simon64/128, 37-round Simon96/96, 37-round Simon96/144, 49-round Simon128/128, 49-round Simon128/192, 50-round Simon128/256 were attacked.

For the earlier linear cryptanalysis, 11, 14, 16, 20, 23-round key recovery attacks on Simon with block size 32, 48, 64, 96, 128 were presented in [2]. Then, Alizadeh et al. [4] improved the linear attacks on 13-round Simon32, 15-round Simon48, 19-round Simon64, 28-round Simon96, 35-round Simon128. Recently, Abdelraheem et al. [1] took advantage of the links between linear characteirstics and differential characteristics for Simon and found some linear distinguishers using differential characteristics found earlier. They presented various linear attacks on Simon with linear, multiple linear, linear hull cryptanalysis. The linear hull cryptanalysis has better attack results, which can attack 21-round Simon32/64, 20-round Simon48/72, 21-round Simon48/96, 27-round Simon64/96, 29-round Simon64/128, 36-round Simon96/144, 48-round Simon128/192 and 50-round Simon128/256. Then, with the Mixed-integer Linear Programming based technique, Shi et al. [17] searched new linear trails and linear hulls, and 21, 21, 29 rounds for Simon32/64, Simon48/96, Simon64/128 were attacked respectively. Also, Sun et al. [18] found a 16-round linear hull distinguisher of Simon48, with which he attacked 23-round Simon48/96. Ashur [6] introduced a new way to calculate the correlations of short linear hulls and provided a more accurate estimation for some previously published linear trails. He gave multiple linear cryptanalysis on 24-round Simon32/64, 23-round Simon48/72, 24-round Simon48/96, 24-round Simon64/96 and 25-round Simon64/128. However, it uses the correlation when all the subkeys are zero as the expected correlation under random key situations, which is not exact. Moreover, if the potential of each linear hull of the cipher is smaller than that of random permutations, then the combination of these linear hulls can not distinguish between the cipher and a random permutation.

Table 1. Summary of Linear Hull Attacks on Simon

Also, there are some results with other attack models, such as impossible differential cryptanalysis [4, 10, 12, 21], zero-correlation cryptanalysis [21] and integral cryptanalysis [21].

Our Contributions. In this paper, we give the improved linear hull attacks on all reduced versions of Simon family with dynamic key-guessing technique, which was proposed initially to improve the differential attack on Simon [20], using existing linear hull distinguishers. In linear attack, one important point is to compute the empirical correlations (bias) of the parity bit, which derives from the Xor-sum of the active bits at both sides of the linear hull distinguisher, under some key guess. Our attack on Simon improves this procedure efficiently.

The non-linear part in the round function of Simon is mainly derived from the bitwise AND (&) operation while it has a significant feature. For details, if one of the two elements is equal to zero, the result of their AND will be zero, no matter what value the other element takes. For a function $f=f_1(x_1,k_1) \& f_2(x_2,k_2)$, if we GUESS $k_1$ at first, and SPLIT the all $x=x_1||x_2$ into two cases: case 1, $f_1(x_1,k_1)=0$; case 2, $f_1(x_1,k_1)=1$, there is no need to guess the key bits $k_2$ in case 1, since $f=0$ holds for any value of $f_2$ in case 1. Then, we can compute the correlations in each case with less time and at last, we COMBINE the two correlations together for corresponding key $k=k_1||k_2$.

At first, we give the boolean representations for the parity bit in the linear distinguisher of Simon. And then we apply the GUESS, SPLIT and COMBINE technique in the calculation of the empirical correlations, which mainly exploits the dynamic key-guessing idea to reduce the number of subkey bits guessed significantly. For example, in the attack on 21-round Simon32, 32 subkey bits are involved. With above technique, we can only guess 12.5 bits from the total 32-bit subkey on average to compute the correlations.

As a result, the improved attack results are shown as follows. We can attack 23-round Simon32/64, 24-round Simon48/72, 25-round Simon48/96, 30-round Simon64/96, 31-round Simon64/128, 37-round Simon96/96, 38-round Simon96/144, 49-round Simon128/128, 51-round Simon128/192 and 53-round Simon128/256. This improves the linear attack results for all versions. From the point of number of rounds attacked, the results on most versions are best up to now. The existing and new linear hull attack results on Simon are summarized in Table 1. Also, we implement the 21-round attack on Simon32. In the attack, we can decrease the 32 subkey bits involved in the attack by 8 bits. The experiments show that the attack success probability is about $27.7\,\%$ using $2^{31.19}$ plaintext-ciphertext pairs.

The paper is organised as follows. In Sect. 2, we introduce the linear (hull) cryptanalysis and give the description of Simon family. Section 3 gives the dynamic key-guessing technique used in the linear cryptanalysis. Then the improved attacks on Simon32/64 and all other variants are given in Sect. 4. Finally, we conclude in Sect. 5. Appendix A gives the time complexities to calculate the empirical correlations in some simple situations.

2 Preliminaries

2.1 Linear Cryptanalysis and Linear Hull

$\mathbb {F}_2$ denotes the field with two elements and $\mathbb {F}_2^n$ is the n-dimensional vector space of $\mathbb {F}_2$. Let $g: \mathbb {F}_2^n\rightarrow \mathbb {F}_2$ be a Boolean function. Let $B(g)=\sum _{x\in \mathbb {F}_2^n}(-1)^{g(x)}$. The correlation c(g) of g and 0 (in the following paper, when we say the correlation of a function, it means the correlation of this function and 0) is defined by

$$\begin{aligned} c(g)=2^{-n}\sum _{x\in \mathbb {F}_2^n}(-1)^{g(x)}=2^{-n}B(g). \end{aligned}$$

(1)

(In some situations of the remainder of this paper, we regard B(g) as the correlation for simplicity of description.) The bias of g is defined by half of c(g), which is represented as $\epsilon (g)=\frac{1}{2}c(g)$.

Linear cryptanalysis [13] is a powerful cryptanalytic method proposed in 1993 to cryptanalysis DES. At first, one tries to find a good linear approximation involving some plaintext bits, ciphertext bits and the subkey bits as follows

$$\begin{aligned} \alpha \cdot P \oplus \beta \cdot C = \gamma \cdot K, \end{aligned}$$

(2)

where $\alpha ,\beta ,\gamma$ are masks and P, C, K represent the plaintext, ciphertext and keys. ‘good’ means that the probability of the linear approximations is far away from 1 / 2, which is the probability in random situations. In other words, higher absolute of bias $\epsilon (\alpha \cdot P \oplus \beta \cdot C\oplus \gamma \cdot K)$ leads to better linear crypanalysis result in general. Algorithms 1 and 2 in [13] are two attack models exploiting the linear approximation as distinguisher. $\mathcal {O}(\frac{1}{\epsilon ^2})$ known plaintexts are needed in the key-recovery attacks.

Then in 1994, Nyberg [15] studied the linear approximations with same input mask $\alpha$ and output mask $\beta$, and denoted them as linear hull. The potential of a linear hull is defined as

$$\begin{aligned} ALH(\alpha ,\beta )=\sum _{\gamma } \epsilon ^2(\alpha \cdot P \oplus \beta \cdot C\oplus \gamma \cdot K)=\bar{\epsilon }^2. \end{aligned}$$

(3)

The effect of linear hull is that the final bias $\bar{\epsilon }$ may become significantly higher than that of any individual linear trail. Then the linear attacks with linear hull require less known plaintexts, i.e., $\mathcal {O}(\frac{1}{\bar{\epsilon }^2})$.

Selçuk and Biçak [16] gave the estimation of success probability in linear attack for achieving a desired advantage level. The advantage is the complexity reduction over the exhaustive search. For example, if m-bit key is attacked and the right key is ranked t-th among all $2^m$ candidates, the advantage of this attack is $m-log_2(t)$. Theorem 2 in [16] described the relation between success rate, advantage and number of data samples.

Theorem 1

(Theorem 2 in [16]). Let $P_S$ be the probability that a linear attack, as defined by Algorithm-2 in [13], where all candidates are tried for an m-bit subkey, in an approximation of probability p, with N known plaintext blocks, delivers an a-bit or higher advantage. Assuming that the approximation’s probablity is independent for each key tried and is equal to 1 / 2 for all wrong keys, we have, for sufficiently large m and N,

$$\begin{aligned} P_S=\int ^{\infty }_{-2\sqrt{N}|p-1/2|+\Phi ^{-1}(1-2^{-a-1})}\phi (x)dx, \end{aligned}$$

(4)

independent of m.

2.2 Description of Simon

Simon is a family of lightweight block cipher with Feistel structure designed by NSA, which is tuned for optimal performance in hardware applications [7]. The Simon block cipher with an n-bit word (hence 2n-bit block) is denoted Simon2n, where n is limited to be 16, 24, 32, 48 or 64. The key length is required to be mn where m takes value from 2, 3 and 4. Simon2n with m-word key is referred to Simon2n / mn. There are ten versions in the Simon family and the detailed parameters are listed in Table 2. Before introducing the round functions of Simon, we give some notations of symbols used throughout this paper.

$X^r$	2n-bit output of round r (input of round $r+1$)
$X^r_L$	left half n-bit of $X^r$
$X^r_R$	right half n-bit of $X^r$
$K^r$	subkey used in round $r+1$
$x_i$	the i-th bit of x, begin with bit 0 from right (e.g., $X^r_{L,0}$ is the LSB of $X^r_L$ )
$x_{i_1,\ldots ,i_t}$	the XOR-sum of $x_i$ for $i=i_1,i_2,\ldots ,i_t$ (e.g., $x_{0,1}=x_0\oplus x_1$)
$x\lll i$	left circulant shift by i bits of x
$\oplus$	bitwise XOR
&	bitwise AND
F(x)	$F(x)=((x\lll 1) \& (x\lll 8)) \oplus (x\lll 2)$

The r-th round function of Simon2n is a Feistel map

$$\begin{aligned} F_{K^{r-1}}: \mathbb {F}_2^n\times \mathbb {F}_2^n&\rightarrow \mathbb {F}_2^n\times \mathbb {F}_2^n,\\ (X^{r-1}_L,X^{r-1}_R)&\rightarrow (X^{r}_L,X^{r}_R) \end{aligned}$$

where $X^r_R=X^{r-1}_L$ and $X^r_L=F(X^{r-1}_L) \oplus X^{r-1}_R \oplus K^{r-1}$. The round function of Simon is depicted in Fig. 1. Suppose the number of rounds is T, the whole encryption of Simon is the composition $F_{K^{T-1}}\circ \cdots \circ F_{K^{1}}\circ F_{K^{0}}$. The subkeys are derived from the master key. The key schedules are a little different depending on the key size. However, the master key can be derived from any m consecutive subkeys. Please refer to [7] for more details.

Fig. 1.

Round Function of Simon

Table 2. The Simon Family Block Ciphers

3 Time Reduction in Linear Cryptanalysis for Bit-Oriented Block Cipher

For bit-oriented block cipher, such as Simon, the operations of round function can be seen as the concatenation of some boolean functions. For example, in Simon32, the 0-th bit of $X^r_{L}$ is a boolean function of some bits of $X^{r-1}$ and subkeys as follows,

$$ \begin{aligned} X^r_{L,0}=(X^{r-1}_{L,15} \& X^{r-1}_{L,8}) \oplus X^{r-1}_{L,14}\oplus X^{r-1}_{R,0}\oplus K^{r-1}_0. \end{aligned}$$

(5)

Other bits in $X^r_L$ have similar boolean representations and the bits in $X^r_R$ are same with the bits in $X^{r-1}_L$. The boolean representation of one bit can be extended to multiple rounds.

3.1 Linear Compression

In Matsui’s improved linear cryptanalysis [14], the attacker can pre-construct a table to store the plaintexts and ciphertexts. We call this pre-construction procedure as linear compression, since the purpose is to reduce the size of efficient states by compressing the linear part. The detail of the compression is as follows.

Suppose x is a $l_1$-bit value derived from the n-bit plaintext or ciphertext and k is a $l_2$-bit value derived from the subkey. $y\in \mathbb {F}_2$ is a boolean function of x and k, $y=f(x,k)$. Let V[x] stores the count number of x. We define $B^{k}(y)$ with counter vector V and function $y=f(x,k)$ for k as

$$\begin{aligned} B^{k}(y)=\sum _{x}(-1)^{f(x,k)}V[x]. \end{aligned}$$

(6)

So, $B^k(y)$ is the correlation of y with x under key guess k. One needs to do $2^{l_1+l_2}$ computations of function f to calculate the correlations of y for all k with a straight-forward method at most. If y is linear with some bits of x and k, the time can be decreased.

For simplicity, let $x=x'||x_0$, $k=k'||k_0$ and $y=x_0\oplus k_0\oplus f_1(x',k')$, where both $x_0$ and $k_0$ are single bits. The correlation of y under some k is

$$\begin{aligned} B^k(y)= (-1)^{k_0} \sum _{x'}(-1)^{f_1(x',k')}(V[x'||0]- V[x'||1]). \end{aligned}$$

(7)

It is obvious the correlations of y under same $k'$ and different $k_0$ have same absolute value, and they are different just in the sign. So if we compress the $x_0$ bit at first according to $V'[x']=V[x'||0]-V[x'||1]$, $B^{k'}(y')$ with counter vertor $V'$ and function $y'=g'(x',k')$ for $k'$ can be computed with $2^{l_1+l_2-2}$ calculations of $f_1$. And the correlation $B^k(y)$ can be derived directly from $B^k(y)= (-1)^{k_0}B^{k'}(y')$. We define $k_0$ the related bit. If the absolute correlations are desired, the related bit $k_0$ can be omitted directly, since it has no effect on the absolute values.

If y is linear with multiple bits of x and k, the linear bits can be combined at first, then above linear compression can be applied. For example, $y=(x_0\oplus k_0)\oplus \cdots \oplus (x_t\oplus k_t) \oplus f_t(x'',k'')$ where $x'',k''$ are the other bits of x and k respectively. We can initialize a new counter vector $V'[x''||x_0']$ where $x_0'$ is 1-bit value of the xor sum of $x_0,x_1,\ldots ,x_t$. We set $V'[x''||x_0']=\sum _{x_0\oplus \cdots \oplus x_t=x_0'}V[x]$. Let $k_0'=k_0\oplus \cdots \oplus k_t$. The target value y becomes $y=x_0'\oplus k_0'\oplus f_t(x'',k'')$ with counter vector $V'[x''||x_0']$, which is the case discussed above.

3.2 Dynamic Key-Guessing in Linear Attack: Guess, Split and Combination

Suppose one want to compute $B^k(y)$ with counter vector V and boolean function $y=f(x,k)$, along with the definitions in the above section. With a straight-forward method, the time to compute $B^k(y)$ is $2^{l_1+l_2}$. If for different values of x, different key bits of k are involved in function f(x, k), the time to calculate $B^k(y)$ can be decreased.

Fig. 2.

When $k_G$ is known, the set of x can be splitted to two sets. f is independent of $k_B$ in set $S_A$ and independent of $k_A$ in set $S_B$.

For simplicity, let $k=k_G||k_A||k_B||k_C$, where $k_G,k_A,k_B,k_C$ are $l_2^G,l_2^A,l_2^B$ and $l_2^C$ bits ($l_2^G+l_2^A+l_2^B+l_2^C=l_2$) respectively. Suppose when $k_G$ is known, the all x can be splitted into two sets, i.e. $S_A$ with $N_A$ elements and $S_B$ with $N_B$ elements ($N_A+N_B=2^{l_1}$). And when $x\in S_A$, $f(x,k)=f_A(x,k_A||k_C)$ which is independent of $k_B$; when $x\in S_B$, $f(x,k)=f_B(x,k_B||k_C)$ which is independent of $k_A$ (See Fig. 2). Then, $B^k(y)$ can be obtained from the following combination

$$\begin{aligned} B^k(y)=\sum _{x\in S_A}(-1)^{f_A(x,k_A||k_C)}V[x]+\sum _{x\in S_B}(-1)^{f_B(x,k_B||k_C)}V[x] \end{aligned}$$

(8)

for some guessed $k_G$. The time to compute $\sum (-1)^{f_A(x,k_A||k_C)}V[x]$ for the $x\in S_A$ needs $N_A2^{l_2^G+l_2^A+l_2^C}$ calculations, while $\sum (-1)^{f_B(x,k_B||k_C)}V[x]$ for $x\in S_B$ needs $N_B2^{l_2^G+l_2^B+l_2^C}$. The combination needs $2^{l_2}$ additions. So the time complexity in total is about

$$N_A2^{l_2^G+l_2^A+l_2^C}+N_B2^{l_2^G+l_2^B+l_2^C}+2^{l_2}$$

which improves the time complexity compared with $2^{l_1+l_2}$.

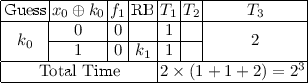
The AND operation in Simon will generate the situations discussed above. Let $x,k\in \mathbb {F}_2^2$ and $y=f(x,k)=(x_0\oplus k_0) \& (x_1\oplus k_1)$. V[x] denotes the count number of x. With a straight-forward method, the calculation of correlations for all k need time $2^{2+2}=2^4$. If one side of the AND in f(x, k) is 0, y would be 0 without knowing the value in the other side. Exploiting this property, we can improve the time complxity for calculating the correlations. At first, we guess one bit of k, e.g. $k_0$. Then we split the x into two sets and compute the correlations in each set. At last, we combine the correlations according to the keys guessed.

• GUESS $k_0$ and SPLIT the x into two sets

  • For the x with $x_0=k_0$, initialize a counter $T_0$ and set $T_0=V[0||x_0]+V[1||x_0]$

  • For the x with $x_0=k_0\oplus 1$, initialize a counter $T_1$ and set $T_1=V[0||x_0]-V[1||x_0]$ (Linear compression)

  • COMBINE $B(y)=T_0+(-1)^{k_1}T_1$ ($k_1$ is a related bit)

So in total, it needs $2(1+1+2)=2^3$ additions to compute the correlations for all the k, which improves the time complexity compared to the straight-forward method. Although there are 2 bits of k involved in the attack, we guess only one bit and make some computations while another bit is just involved in the final combination. This can be viewed as that we reduce the number of key bits guessed from 2 to 1. Morever, this technique adapts to some complicated boolean functions and more key (or equivalent key) bits can be reduced significantly. Some cases have been discussed in Appendix A.

4 Linear Cryptanalysis on Simon

In this section, we will give the improved procedure of linear attack on Simon using existing linear hull distinguishers for all versions of Simon

Table 3. Linear Hulls for Simon

4.1 Linear Hulls of Simon

Some linear hulls have been proposed recently in [1, 17, 18], and they are displayed in Table 3. Abdelraheem et al. [1] took advantage of the connection between linear- and differential- characteristics for Simon and transformed the differential characteristics proposed in [2, 9] to linear characteristics directly. Similarly, differentials can be transformed to the linear hulls. Also, they found a new 14-round linear hull for Simon32 / 64, by constructing squared correlation matrix to compute the average squared correlation. Shi et al. [17] searched the linear characteristics with same input and output masks using the Mixed-integer Linear Programming modelling, which was investigated to search the differential characteristics for bit-oriented block cipher [19] and then extended to search the linear characteristics (hull) later [18].

Similar to the rotational property of integral distinguishers and zero-correlation linear hull shown in [21], more linear hulls can be constructed as follows.

Property 1

Assume that $X^i_{L,j_0^0},\ldots , X^i_{L,j_{t_0}^0}, X^i_{R,j_0^1},\ldots , X^i_{R,j_{t_1}^1}\rightarrow X^{i+r}_{L,j_0^2},\ldots , X^{i+r}_{L,j_{t_2}^2},$ $X^{i+r}_{R,j_0^3},\ldots , X^{i+r}_{R,j_{t_3}^3}$ is a r-round linear hull with potential $\bar{\epsilon }^2$ for Simon2n, where $j_0^0,\ldots ,j_{t_0}^0,j_0^1,\ldots ,j_{t_1}^1,j_0^2,\ldots ,j_{t_2}^2,j_0^3,\ldots ,j_{t_3}^3 \in \{0,\ldots , n-1\}$. Let $j^{p,s}_{q}= (j^{p}_{q}+s) \text { mod } n$, where $p=0,\ldots ,3$, $q=0,\ldots ,t_p$, then for $0\le s \le n-1$, we have that the potential of the r-round linear hull $X^i_{L,j_0^{0,s}},\ldots , X^i_{L,j_{t_0}^{0,s}}, X^i_{R,j_0^{1,s}},\ldots , X^i_{R,j_{t_1}^{1,s}}\rightarrow X^{i+r}_{L,j_0^{2,s}},\ldots , X^{i+r}_{L,j_{t_2}^{2,s}}, X^{i+r}_{R,j_0^{3,s}},\ldots , X^{i+r}_{R,j_{t_3}^{3,s}}$ for Simon2n is also $\bar{\epsilon }^2$.

Observe the two 13-round linear hulls of Simon32 in Table 3 and we can find they are in fact the rotations of same linear hull. The potential of $X^i_{L,6}\rightarrow X^{i+13}_{L,14}$ is estimated as $2^{-31.69}$ in [1] while that of $X^i_{L,5}\rightarrow X^{i+13}_{L,13}$ is estimated as $2^{-30.19}$ in [17]. The difference may come from the different search methods and different linear trails found. Since Simon32 has small block size, we can test the bias (potential) of the 13-round linear hull experimentally. In the experimentation, we choose 600 keys randomly, and compute the corresponding bias from the whole plaintexts space. The results are shown in the following table.

Table 4. Experimental bias for the 13-round linear hull of Simon32

From the table, we know that about $26.4\,\%$ of the keys have $\epsilon ^2 \ge 2^{-30.19}$. So $2^{30.19}$ is a little optimistic for the other $73.6\,\%$ keys. However, this linear hull distinguisher is interesting and in the following, we will give the key recovery procedure using this linear hull. Also, we implement the 21-round attack on Simon32 and the results shows that we can decrease the candidate key space by 8 bits when the potential under the real key is large.

4.2 Improved Key Recovery Attack on Simon32 / 64

We exploit the 13-round linear hull proposed in [17] to make key recovery attack on round-reduced Simon32. The linear hull is

$$X^i_{L,5}\rightarrow X^{i+13}_{R,13}.$$

We mount a key recovery attack on 21-round Simon32 / 64 by adding four rounds before and appending four rounds after the distinguisher. Here let $P=X^{i-4}$ be the plaintext and $C=X^{i+17}$ be the corresponding ciphertext. Suppose the subkeys involved in the first four rounds are $K_P$ and those in the last four rounds are $K_C$. Then $X^{i}_{L,5}$ is a function of P and $K_P$, $X^{i}_{L,5}=E(P,K_P)$. Similarly, $X^{i+13}_{R,13}=D(C,K_C)$ is a function of C and $K_C$. Let $\mathcal {S}$ be the set of N plaintext-ciphertext pairs obtained, the empirical correlation under some key $K_P,K_C$ is

$$\begin{aligned} \bar{c}_{K_P,K_C}=\frac{1}{N}\sum _{P,C\in \mathcal {S}}(-1)^{E(P,K_P)\oplus D(C,K_C)}. \end{aligned}$$

(9)

Table 5. 4 rounds before $X^{i}_{L,5}$ for Simon32

Table 6. 4 rounds after $X^{i+13}_{R,13}$ for Simon32

In a further step, $X^{i}_{L,5}$ can be represented as $X^{i}_{L,5}=f(x,k)$ where

$$ \begin{aligned}&f(x,k)=x_0\oplus k_0\oplus ((x_1\oplus k_1) \& (x_2\oplus k_2))\oplus ((x_3\oplus k_3) \& (x_4\oplus k_4))\oplus \\&[(x_5\oplus k_5\oplus ((x_6\oplus k_6) \& (x_7\oplus k_7))) \& (x_8\oplus k_8\oplus ((x_9\oplus k_9) \& (x_7\oplus k_7)))]\oplus \\&\{(x_{10}\oplus k_{10}\oplus ((x_6\oplus k_6) \& (x_7\oplus k_7))\oplus \\&[(x_{11}\oplus k_{11}\oplus ((x_{12}\oplus k_{12}) \& (x_{13}\oplus k_{13}))) \& (x_{14}\oplus k_{14}\oplus ((x_3\oplus k_3) \& (x_{13}\oplus k_{13})))]) \& \\&(x_{15}\oplus k_{15}\oplus ((x_7\oplus k_7) \& (x_9\oplus k_9))\oplus \\&[(x_{14}\oplus k_{14}\oplus ((x_{13}\oplus k_{13}) \& (x_{3}\oplus k_{3}))) \& (x_{16}\oplus k_{16}\oplus ((x_3\oplus k_3) \& (x_{4}\oplus k_{4})))])\} \end{aligned}$$

where the representation of x and k are 17-bit value shown in Table 5. With the same way, $X^{i+13}_{R,13}$ can also be represented as f(x, k) where the corresponding x and k are described in Table 6. To distinguish them, let $x_P,k_P$ be the x, k described in Table 5 and $x_C,k_C$ be the x, k described in Table 6. The N plaintext-ciphertext pairs in $\mathcal {S}$ can be compressed into a counter vector $V[x_P,x_C]$, which stores the number of $x_P,x_C$. Then there is

$$\begin{aligned} \bar{c}_{k_P,k_C}=\frac{1}{N}\sum _{x_P,x_C}(-1)^{f(x_P,k_P)\oplus f(x_C,k_C)}V[x_P,x_C]. \end{aligned}$$

(10)

Notice that f(x, k) is linear with $x_0\oplus k_0$. According to the linear compression technique, the 0-th bit of $x_P$ and $x_C$ could be compressed initially. Suppose that $x_P'$ is the 16-bit value of $x_P$ without the 0-th bit (same representations for $x_C',k_P',k_C'$). Initialize a new counter vector $V_1$ which has values

$$\begin{aligned} V_1[x_P',x_C'] = \sum _{x_{P,0},x_{C,0}}(-1)^{x_{P,0}\oplus x_{C,0}}V[x_P,x_C]. \end{aligned}$$

(11)

Then the correlation becomes

$$\begin{aligned} \bar{c}_{k_P',k_C'}&=\frac{1}{N}\sum _{x_P',x_C'}(-1)^{f'(x_P',k_P')\oplus f'(x_C',k_C')}V_1[x_P',x_C'] \nonumber \\&=\frac{1}{N}\sum _{x_C'}(-1)^{f'(x_C',k_C')}\sum _{x_P'}(-1)^{f'(x_P',k_P')}V_1[x_P',x_C'], \end{aligned}$$

(12)

where $f'$ is part of f, i.e. $f(x,k)=x_0\oplus k_0\oplus f'(x',k'),x'=(x_{1},\ldots ,x_{16}), k'=(k_{1},\ldots ,k_{16})$.

So we can guess $k_P'$ (16-bit) at first and compress the plaintexts into a counter. Then guess $k_C'$ (16-bit) to decrypt the appending rounds, to achieve the final correlations. In the following, we introduce the attack procedure in the forward rounds in detail. The procedure to compute $\sum _{x_P'}(-1)^{f'(x_P',k_P')}V_1[x_P',x_C']$ for each $x_C'$ is same with the procedure to compute $B^{k'}(y)$ with some counter vector $V_1'[x']$ and boolean function $f'$. Counter vector $V_1'$ is part of counter vector $V_1$. For each specific $x_C'$,

$$V_1'[x'] = V_1[x',x_C'],$$

which means $V_1'[x']$ takes value of $V_1[x_P',x_C']$ where $x_P'=x'$ and $x_C'$ is fixed. Morever, there are relations that $x_{10}=x_3\oplus x_5, x_{15}=x_{4}\oplus x_8$ in Tables 5 and 6, which means there are only 14 independent bits for $x'$ ($x_P'$ or $x_C'$).

Compute $\varvec{B^{k'}(y)}$ with counter vector $\varvec{V_1'[x']}$ and Boolean function $\varvec{f'}$ . (For simplicity, we define this procedure as Procedure A.) Although $x'$ is a 16-bit value, there are only $2^{14}$ possible values for $x'$ as explained above. We use the guess, split and combination technique to decrease the time complexity to compute $B^{k'}(y)$ with counter vector $V_1'[x']$ and boolean function $y=f'$, for $2^{16}$ key vaules $k'$.

• 1. Guess $k_1,k_3,k_7$ and split the plaintexts into 8 sets according to the value $(x_1\oplus k_1, x_3\oplus k_3, x_7\oplus k_7)$. The simplification for $f'(x',k')$ after guessing some keys are shown in Table 7.

  The representation of $f_{ij}$ are as follows,

  $$ \begin{aligned} f_{00}=&((x_5\oplus k_5) \& (x_8\oplus k_8))\oplus \{(x_{10}\oplus k_{10} \oplus [(x_{11}\oplus k_{11}\oplus ((x_{12}\oplus k_{12}) \& (x_{13}\oplus k_{13})))\\& \& (x_{14}\oplus k_{14} )]) \& (x_{15}\oplus k_{15}\oplus [(x_{14}\oplus k_{14}) \& (x_{16}\oplus k_{16})]) \},\\ f_{01}=&((x_{5,6}\oplus k_{5,6}) \& (x_{8,9}\oplus k_{8,9}))\oplus \{ (x_{6,10}\oplus k_{6,10} \oplus [(x_{11}\oplus k_{11}\oplus ((x_{12}\oplus k_{12})\\& \& (x_{13}\oplus k_{13}))) \& (x_{14}\oplus k_{14} )]) \& (x_{9,15}\oplus k_{9,15}\oplus [(x_{14}\oplus k_{14}) \& (x_{16}\oplus k_{16})]) \},\\ f_{10}=&((x_5\oplus k_5) \& (x_8\oplus k_8))\oplus \{(x_{10}\oplus k_{10} \oplus [(x_{11}\oplus k_{11}\oplus ((x_{12}\oplus k_{12}) \& (x_{13}\oplus k_{13})))\\& \& (x_{13,14}\oplus k_{13,14} )]) \& (x_{15}\oplus k_{15}\oplus [(x_{13,14}\oplus k_{13,14}) \& (x_{4,16}\oplus k_{4,16})]) \},\\ f_{11}=&((x_{5,6}\oplus k_{5,6}) \& (x_{8,9}\oplus k_{8,9}))\oplus \{ (x_{6,10}\oplus k_{6,10} \oplus [(x_{11}\oplus k_{11}\oplus ((x_{12}\oplus k_{12}) \& (x_{13}\\&\oplus k_{13}))) \& (x_{13,14}\oplus k_{13,14} )]) \& (x_{9,15}\oplus k_{9,15}\oplus [(x_{13,14}\oplus k_{13,14}) \& (x_{4,16}\oplus k_{4,16})]) \}.\\ \end{aligned}$$

  Table 7. Simplification for $f'(x',k')$ after guessing $k_1,k_3,k_7$

  Table 8. Simplification for $f_{00}$ after guessing $k_5,k_{14}$

  The counter vectors for $x'$ can be compressed in a further step according to the new representations of $f'$. For example, if $(x_1\oplus k_1, x_3\oplus k_3, x_7\oplus k_7)=(0,0,0)$, $f'$ will be equal to the formula $f_{00}$, which is independent of $x_2,x_4,x_6,x_9$. So we compress the corresponding counters into a new counter $V_{000}$, and

  $$V_{000}[x_5,x_8,x_{10}-x_{16}]=\sum _{ x_1=k_1,x_3=k_3,x_7=k_7, x_2\in \mathbb {F}_2,x_4\in \mathbb {F}_2,x_6\in \mathbb {F}_2,x_9 \in \mathbb {F}_2 }V_1'[x'].$$

  Notice $x_{10}=x_3\oplus x_5$, so there are 8 independent x bits for $x_5,x_8,x_{10}-x_{16}$. Notice $x_{15}=x_{4}\oplus x_8$, for some fixed value of $x_5,x_8,x_{10}-x_{16}$, there are 7 times addition in above equation. So generating this new counter vector needs $2^8\times 7$ additions.

     We give another example to illustrate the situations with related key bit. If $(x_1\oplus k_1,x_3\oplus k_3,x_7\oplus k_7)= (1,0,0)$, there is $f'=(x_2\oplus k_2) \oplus f_{00}$. Notice in this subset, $f'$ is linear with $x_2\oplus k_2$ and $x_2$ can be compressed into the new counters with related key $k_2$. So the new counter vector $V_{100}$ is as follows,

  $$V_{100}[x_5,x_8,x_{10}-x_{16}]=\sum _{ x_1=k_1\oplus 1,x_3=k_3,x_7=k_7, x_2\in \mathbb {F}_2,x_4\in \mathbb {F}_2,x_6\in \mathbb {F}_2,x_9 \in \mathbb {F}_2 }(-1)^{x_2}V_1'[x'].$$

  Also, there are 8 independent x bits for $x_5,x_8,x_{10}-x_{16}$. For each fixed $x_5,x_8,x_{10}-x_{16}$, the new counter can be obtained with 7 additions according to above equation.

     The procedures to generate the new counter vectors for other cases are similar as that of case $(x_1\oplus k_1,x_3\oplus k_3, x_7\oplus k_7)=(0,0,0)$ or (1, 0, 0). Morever, the time complexity to split the plaintexts and construct new counter vectors is same for each case. Observing the four functions $f_{00},f_{01},f_{10}$ and $f_{11}$, we know that they are with same form. In the following step, we explain the attack procedure of case $(x_1\oplus k_1,x_3\oplus k_3, x_7\oplus k_7)=(0,0,0)$ in detail and the others can be obtained in the same way.

     Note that, there are 9 subkey bits in each function of $f_{00}, f_{01}, f_{10}$ and $f_{11}$ after guessing $k_1, k_3, k_7$. So this can be viewed as that $3+9=12$ subkey bits are involved in the attack while there are 16 subkey bits are involved initially in $f'$. In the following, the number of key bits can be reduced in a further step.

• 2. For $f_{00}$, guess $k_5,k_{14}$ and split the plaintexts into 4 sets according to the value $(x_5\oplus k_5,x_{14}\oplus k_{14})$. The simplification for $f_{00}$ after guessing some keys are shown in Table 8.

  The time complexity of computing the counters’ value $B^{k_5,k_8,k_{10}-k_{16}}(y)$ with counter vector $V_{000}$ and function $f_{00}$ is as follows:

  • (a) Guess $k_5,k_{14}$ and split the states into four parts

    • i. $(x_5\oplus k_5,x_{14}\oplus k_{14})=(0,0)$

      • A. Since $x_{10}=x_{3}\oplus x_{5}$, $x_5=k_5$ and $x_{3}=k_3$ (the first case in Table 7), so the $x_{10}$ here is fixed. There is one variable bit $x_{15}$ to store. Let $V_{000}^{00}[x_{10},x_{15}]$ store the number of $(x_{10},x_{15})$. There is

        $$V_{000}^{00}[x_{10},x_{15}]=\sum _{x_5=k_5,x_{14}=k_{14}}V_{000}[x_5,x_8,x_{10}-x_{16}].$$

        There are two possible values for $(x_{10},x_{15})$ here and for each value, the above sum needs $2^5-1$ additions (5 variable bits $(x_8, x_{11},x_{12},x_{13},x_{16})$). So generating the new counter vector needs $2 \times (2^{5}-1)=2^6-2$ additions.

      • B. Computing $B_{00}^{k_{10},k_{15}}(y)$ with new function (the first case in Table 8) and vector $V_{000}^{00}$:

        If $k_{10}=x_{10}$, $B_{00}^{k_{10},k_{15}}(y)=V_{000}^{00}[x_{10},0]+V_{000}^{00}[x_{10},1]$; if $k_{10}=x_{10}\oplus 1$, $B_{00}^{k_{10},k_{15}}(y)=(-1)^{k_{15}}(V_{000}^{00}[x_{10},0]-V_{000}^{00}[x_{10},1])$. So in total there are no more than $2^2$ additions.

    • ii. $(x_5\oplus k_5,x_{14}\oplus k_{14})=(0,1)$

      • A. There are 4 variable bits $(x_{10,11}, x_{12}, x_{13}, x_{15,16})$ to store. Let $V_{000}^{01}[x_{10,11},x_{12},x_{13},x_{15,16}]$ store the counter number of $(x_{10,11},x_{12},$ $x_{13},x_{15,16})$. There is

        $$V_{000}^{01}[x_{10,11},x_{12},x_{13},x_{15,16}]=\sum _{x_5=k_5,x_{14}=k_{14}\oplus 1}V_{000}[x_5,x_8,x_{10}-x_{16}].$$

        For each possible value of $(x_{10,11}, x_{12}, x_{13}, x_{15,16})$, the above sum needs $2^2-1$ additions (2 free variables $(x_{8},x_{15})$, $x_{10}$ is fixed, $x_{11}=x_{10}\oplus x_{10,11}$, $x_{16} = x_{15}\oplus x_{15,16}$). So generating the new counter vector needs: $2^4\times (2^2-1)=2^6-2^4$ additions.

      • B. Partial $B_{01}^{k_{10,11},k_{12},k_{13},k_{15,16}}(y)$ with new function and vector $V_{000}^{01}$: $2^{5.64}$ additions. (See $f_3$ in Appendix A)

    • iii. $(x_5\oplus k_5,x_{14}\oplus k_{14})=(1,0)$

      • A. Similar to the first case in Step (2(a)i), let $V_{000}^{10}[x_{10},x_{15}]$ store the number of $(x_{10},x_{15})$. There is

        $$V_{000}^{10}[x_{10},x_{15}]=\sum _{x_5=k_5,x_{14}=k_{14}}V_{000}(-1)^{x_8}[x_5,x_8,x_{10}-x_{16}].$$

        So generating the new counter vector also needs $2 \times (2^{5}-1)=2^6-2$ additions. $k_8$ becomes a related bit.

      • B. Partial $B_{10}^{k_{10},k_{15}}(y)$ with new function and vector $V_{000}^{10}$: $2^2$ additions (same with case (0, 0)).

    • iv. $(x_5\oplus k_5,x_{14}\oplus k_{14})=(1,1)$

      • A. Similar to the second case in Step (2(a)ii), let $V_{000}^{11}[x_{10,11},x_{12},x_{13},$ $x_{15,16}]$ store the counter number of $(x_{10,11},x_{12},$ $x_{13},x_{15,16})$. There is

        $$\begin{aligned}&V_{000}^{11}[x_{10,11},x_{12},x_{13},x_{15,16}]\\ =&\sum _{x_5=k_5,x_{14}=k_{14}\oplus 1}(-1)^{x_8}V_{000}[x_5,x_8,x_{10}-x_{16}]. \end{aligned}$$

        So generating the new counter vector needs: $2^4\times (2^2-1)=2^6-2^4$ additions. $k_8$ becomes a related bit.

      • B. Partial $B_{11}^{k_{10,11},k_{12},k_{13},k_{15,16}}(y)$ with new function and vector $V_{000}^{11}$: $2^{5.64}$ additions. (See $f_3$ in Appendix A)

  • (b) For each of $2^9$ keys involved in $f_{00}$, partial $B^{k_5,k_8,k_{10}-k_{16}}(y)$ with function $y=f_{00}$ and counter vector $V_{000}$ under key guess $k_5,k_{14}$ is

    $$\begin{aligned} B^{k_5,k_8,k_{10}-k_{16}}(y)&=\qquad \qquad \quad (B_{00}^{k_{10},k_{15}}(y)+B_{01}^{k_{10,11},k_{12},k_{13},k_{15,16}}(y))\\&+(-1)^{k_8} \qquad \qquad (B_{10}^{k_{10},k_{15}}(y)+B_{01}^{k_{10,11},k_{12},k_{13},k_{15,16}}(y)). \end{aligned}$$

    We can add $B_{00}^{k_{10},k_{15}}(y)$ and $B_{01}^{k_{10,11},k_{12},k_{13},k_{15,16}}(y)$ at first, then add $B_{10}^{k_{10},k_{15}}(y)$ and $B_{01}^{k_{10,11},k_{12},k_{13},k_{15,16}}(y)$, at last add the two parts according to the index value and $k_8$. The combination phase needs $2^6+2^6+2^7=2^8$ additions in total when $k_5,k_{14}$ are fixed.

  • (c) In total, there are

    $$2^2\times ((2^6-2+2^2+2^6-2^4+2^{5.64})\times 2 + 2^8) \approx 2^{11.19}$$

    additions to compute $B^{k_5,k_8,k_{10}-k_{16}}(y)$ for all $2^9$ possible key values. Note that, about 1 subkey bit is guessed in the first (or third) step of step 2a. In the second (or forth) step of step 2a, 1.5 subkey bits are guessed on average. So, although there are 9 subkey bits in total, only 2+(1+1+1.5+1.5)/4=3.25 bits on average are guessed with dynamic key-guessing technique.

• 3. The time of computing $B^{k'}(y)$ with counter vector $V_1'[x']$ and boolean function $f'$ is shown in Table 9. $T_1$ denotes the time of seperation of the plaintexts according to the guessed bit of k. $T_2$ denotes the time of computation in the inner part. $T_3$ is the time in the combination phase. When $k_1,k_3,k_7$ are fixed, in each case, $T_1=2^8\times 7$ as explainted in Step 1. $T_2$ is $2^{11.19}$ as explained in Step 2. There are 13 bits for $k'$ except $k_1,k_3,k_7$, leading to $T_3=2^{13}\times 7$. For all guesses of $k_1,k_3,k_7$, the total time is about $2^{19.46}$ additions.

In Step 1, 3 key bits are guessed and the plaintexts are splitted into 8 situations. For each situation, 3.25 key bits are guessed as explained above. So on average, about $3+3.25=6.25$ subkey bits are guessed in this procedure, while there are 16 subkey bits involved.

Table 9. Time Complexity of computing $B^{k'}(y)$ with counter vector $V_1'[x']$ and boolean function $f'$

Table 10. Relation between bias and success probability using $2^{31.19}$ data and setting advantage $a=8$

21-Round Attack on Simon $\varvec{32/64}$ .  Adding four rounds and appending four rounds after the 13-round linear hull distinguisher, we give the 21-round linear attack on Simon32 / 64. The estimated potential of the linear hull is $\bar{\epsilon }^2\approx 2^{-30.19}$ in [17], which is a little optimistic for more than half of keys. In the attack, we use $N=2^{31.19}$ plaintext-ciphertext pairs. According to Theorem 1, the relation between the bias and success probability is shown in Table 10 when using $2^{31.19}$ plaintext-ciphertext pairs. So according to Tables 4 and 10, the expected success probability of the attack is larger than

$$0.012*p_0 + 0.035*p_1 + 0.097*p_2 + 0.12*p_3 + 0.173*p_4 \approx 0.22,$$

and it is smaller than

$$(0.012 + 0.035)*p_0 + 0.097*p_1 + 0.12*p_2 + 0.173*p_3 \approx 0.33.$$

There are 32 subkey bits involved in this attack. With our attack method, only about $6.25+6.25=12.5$ bits are guessed on average, which reduces the number of key bits greatly.

Attack:

• 1. Compress the N plaintext-ciphertext pairs into the counter vector $V_1[x_P',x_C']$ of size $2^{14+14}$.

• 2. For each of $2^{14}$ $x_C'$

  • (a) Call Procedure A. Store the counters according to $x_C'$ and $k_P'$

• 3. For each $k_P'$ of $2^{16}$ possible values.

  • (a) Call procedure A. Store the counters according to $k_P'$ and $k_C'$.

• 4. The keys with counter values ranked in the largest $2^{32-8}=2^{24}$ values would be the right subkey candidates. Exploiting the key schedule and guessing some other bits, use two plaintex-ciphertext pairs to check the right key.

Time: (1)$N=2^{31.19}$ times compression (2) $2^{14}\times 2^{19.46}=2^{33.46}$ additions. (3)$2^{16}\times 2^{19.46}=2^{35.46}$ additions. So the time to compute the empirical bias for the subkeys involved is about $2^{35.84}$ while that given in [1] with similar linear hull is $2^{63.69}$. The time is improved significantly. Step (4) is to recovery the master key, which needs $2^{64-8}=2^{56}$ 21-round encryptions. However, [1] does not give this step.

Also we implemented the 21-round attack on Simon32 using $2^{31.19}$ plaintext-ciphertext pairs. (The exhaustive search part of the attack is not included since it would take about $2^{64-8}=2^{56}$ encryptions, which takes too much time.) In the implementation, we set the main key randomly and collect $2^{31.19}$ plaintext-ciphertext pairs (data collection part), then use the dynamic key-guessing techniques to recover 8-bit key information for the 32 subkey bits (recovery part). We store the $2^{32-8} = 2^{24}$ keys with large bias in set S as the right key candidates, then compute the real 32 subkey bits from the main key and check whether it is in S. In the implementation, about 5GB memory is needed. The data collection part ($2^{31.19}$ encryptions) takes about 11 minutes and the recovery part takes about 11 minutes too (using Intel(R) Xeon(R) CPU E5-2620, 2.00GHz). 1000 experiments were done and 277 of them were successful. This derives that the experimental success probability is about $27.7\,\%$, which is consistent with the expected success probability.

22-Round Attack on Simon 32/64. Add one more round before the 21-round attack, we can attack 22-round of Simon32/64. There are 13 active key bits involved in round $i-5$, which is $\kappa _1=(K^{i-5}_0-K^{i-5}_{3},K^{i-5}_5,K^{i-5}_7-K^{i-5}_{12},K^{i-5}_{14},K^{i-5}_{15})$, to obtain the x represented in Table 5.

Attack:

• 1. Guess each of $2^{13}$ $\kappa _1$

  • (a) Encrypt the plaintexts by one round.

  • (b) Do as the first three steps in the 21-round attack

• 2. The keys with counter values ranked in the largest $2^{32+13-8}=2^{37}$ values would be the right subkey candidates. Exploiting the key schedule and guessing some other bits, use two plaintex-ciphertext pairs to check the right key.

Time: (1.a)$2^{13}\times N=2^{44.19}$ one-round encryptions. (1.b) $2^{13}\times 2^{35.84}=2^{48.84}$ additions. (2) Exhaustive phase needs about $2^{64-8}=2^{56}$ 22-round encryptions. So the total time is about $2^{56}$ 22-round encryptions and $2^{48.84}$ additions.

23-round attack on Simon 32/64. Add one more round before and one round after the 21-round attack, we can attack 23-round of SIMON32/64. There are 13 active key bits involved in round $i+17$, which is $\kappa _2=(K^{i+17}_0-K^{i+17}_{3},K^{i+17}_5,$ $K^{i+17}_7-K^{i+17}_{12},K^{i+17}_{14},K^{i+17}_{15})$, to obtain the x represented in Table 6.

Attack:

• 1. Guess each of $2^{13+13}$ $\kappa _1|| \kappa _2$

  • (a) Encrypt the plaintexts by one round and decrypt the ciphertexts by one round.

  • (b) Do as the first three steps in the 21-round attack

• 2. The keys with counter values ranked in the largest $2^{32+26-8}=2^{50}$ values would be the right subkey candidates. Exploiting the key schedule and guessing some other bits, use two plaintex-ciphertext pairs to check the right key.

Time: (1.a)$2^{26}\times N=2^{57.19}$ two-round encryptions. (1.b) $2^{26}\times 2^{35.84}=2^{61.84}$ additions. (2) Exhaustive phase needs about $2^{64-8}=2^{56}$ 23-round encryptions. So the total time complexity is about $2^{56.3}$ 23-round encryptions and $2^{61.84}$ additions.

4.3 Improved Key Recovery Attack on Other Variants of Simon

With the dynamic key-guessing technique shown in above attack, we can also improve the linear hull attacks on all other variants of Simon. The linear hulls used are displayed in Table 3. For Simon48, we exploit the 22-round linear hull proposed in [18], which covers most rounds up to date. For Simon64, the 21-round linear hull with potential $2^{-62.53}$ proposed in [1] is used in the attack. Also, the 31-round (resp. 40-round) linear hull for Simon96 (resp. Simon128) in [1] are used to attack corresponding variant. Due to limited space, we do not give the detail of the attacks (please refer to the full version [11] of this paper for the details). However, the improved results for these variants are listed in Table 1.

4.4 Multiple Linear Hull Attack on Simon

Combining multiple linear cryptanalysis [8] and linear hull together, one can make multiple linear hull attack with improved data complexity. Our attack technique can be used in the multiple linear hull attack of Simon well. According to the rotational property, Property 1, of Simon, lots of linear hulls with high potential can be found. For example, the two 13-round linear hulls for Simon32 in Table 3 are rotations of same linear hull.

Suppose that the time to compute the bias for one linear hull is $\mathcal {T}_1$ and data complexity is $\mathcal {N}$. If m linear hulls with same bias are used in the multiple linear hull attack, the data complexity would be decreased to $\mathcal {N}/m$. But the time complexity would increase to $m\mathcal {T}_1+2^{\mathcal {K}}$, where $\mathcal {K}$ is the size of the independent key bits involved in all m linear hull attacks. For example, there are 32 independent key bits involved in the 21-round attack of Simon32 with linear hull $X^{i}_{L,5}\rightarrow X^{i+13}_{R,13}$. The data complexity is $2^{31.19}$ known plaintext-ciphertext pairs and the time needs about $2^{35.84}$ additions to get the bias. When another linear hull $X^{i}_{L,6}\rightarrow X^{i+13}_{R,14}$ is taken in to make a multiple linear hull attack, the data size will decrease to $2^{30.19}$. There are also 32 independent key bits involved in this linear hull attack. But, the total independent key size of both linear hulls is 48. So the time to compute the bias for the multiple linear hull attack with above two linear hulls needs about $2^{36.84}$ additions and $2^{48}$ combinations.

5 Conclusion

In this paper, we gave the improved linear attacks on all the reduced versions of Simon family with dynamic key-guessing techniques. By establishing the boolean function of parity bit in the linear hull distinguisher and reducing the expressions of function according to the property of AND operation, we decrease the number of key bits involved in the attack and decrease the attack complexity in a further step. As a result, we can attack 23-round Simon32/64, 24-round Simon48/72, 25-round Simon48/96, 30-round Simon64/96, 31-round Simon64/128, 37-round Simon96/96, 38-round Simon96/144, 49-round Simon128/128, 51-round Simon128/192 and 53-round Simon128/256. The differential attack in [20] and our linear hull attack are bit-level cryptanalysis results, which provide the more efficient and precise security estimation results on Simon. It is mentioned that, the bit-level cryptanalysis combining with dynamic key-guessing techniques are applicable to more light-weight block ciphers and hash functions etc.

A Time Complexity in Some Situations

In this section, we give the time complexities of computing the counters $B^k(y)$ for some simple functions of $y=f(x,k)$. This would be the deepest layer’s operation in the linear attack to Simon. Notice in the following, ‘Guess’ denotes the bits guessed at first. The second column $x_i\oplus k_i$ denotes the value of $x_i$ which is used in the splitting phase. The third column denotes the new representation of the target function according to the value of $x_i\oplus k_i$. ‘RB’ is the related bit (defined in Sect. 3). $T_1$ denotes the time of seperation of the plaintexts according to the guessed bit of k. $T_2$ denotes the time of computation in the inner part. $T_3$ is the time in the combination phase. Total Time is the final time complexity, which is twice of the sum of all $T_1,T_2$ and $T_3$. Notice that $T_1,T_2$ and $T_3$ represent the number of addition operations. For simplicity, we denote $f*$ the function with same form of f. For example, if $f_1=(x_0\oplus k_0) \& (x_1\oplus k_1)$ and $f_1'=(x_0\oplus k_0) \& (x_3\oplus k_3)$, we say $f_1'$ is with form $f_1*$. The calculation of B(y) for the functions with same form have same procedures and time complexties.

• 1. $f_1=(x_0\oplus k_0) \& (x_1\oplus k_1)$

  

• 2. $f_2=(x_0\oplus k_0)\oplus (x_1\oplus k_1) \& (x_2\oplus k_2)$

  

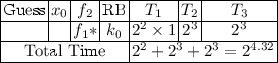
• 3. $f_3=(x_0\oplus k_0) \& ((x_1\oplus k_1)\oplus (x_2\oplus k_2) \& (x_3\oplus k_3 ))$

  

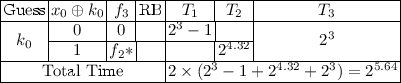
The detail of case 1, where $f_1(x,k)=(x_0\oplus k_0) \& (x_1\oplus k_1)$, has been given in Sect. 3.2. The other cases are derived similarly. For example, in case 2, linear compression is done before any key guessing, leading to the compression of bit $x_0$ and generation of related bit $k_0$.