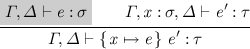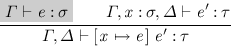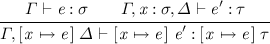Needle & Knot: Binder Boilerplate Tied Up

Abstract

To lighten the burden of programming language mechanization, many approaches have been developed that tackle the substantial boilerplate which arises from variable binders. Unfortunately, the existing approaches are limited in scope. They typically do not support complex binding forms (such as multi-binders) that arise in more advanced languages, or they do not tackle the boilerplate due to mentioning variables and binders in relations. As a consequence, the human mechanizer is still unnecessarily burdened with binder boilerplate and discouraged from taking on richer languages.

This paper presents Knot, a new approach that substantially extends the support for binder boilerplate. Knot is a highly expressive language for natural and concise specification of syntax with binders. Its meta-theory constructively guarantees the coverage of a considerable amount of binder boilerplate for well-formed specifications, including that for well-scoping of terms and context lookups. Knot also comes with a code generator, Needle, that specializes the generic boilerplate for convenient embedding in Coq and provides a tactic library for automatically discharging proof obligations that frequently come up in proofs of weakening and substitution lemmas of type-systems.

Our evaluation shows, that Needle & Knot significantly reduce the size of language mechanizations (by 40 % in our case study). Moreover, as far as we know, Knot enables the most concise mechanization of the POPLmark Challenge (1a + 2a) and is two-thirds the size of the next smallest. Finally, Knot allows us to mechanize for instance dependently-typed languages, which is notoriously challenging because of dependent contexts and mutually-recursive sorts with variables.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The meta-theory of programming language semantics and type-systems is highly complex due to the management of many details. Formal proofs are long and prone to subtle errors that can invalidate large amounts of work. In order to guarantee the correctness of formal meta-theory, techniques for mechanical formalization in proof-assistants have received much attention in recent years.

This paper targets the syntactic approach to programming language metatheory, invented by Wright and Felleisen [42] and popularized by Pierce [25]. An important issue that arises in such formalizations is the treatment of variable binding which typically comprises the better part of the formalization. Most of this variable binding infrastructure is repetitive and tedious boilerplate. By boilerplate we mean mechanical operations and lemmas that appear in many languages, such as: (1) common operations like calculating the sets of free variables or the domain of a typing context, appending contexts and substitutions; (2) lemmas about operations like commutation of substitutions or the interaction between the free-variable calculation and substitution; and (3) lemmas about the well-scoping of terms and preservation of well-scoping under operations.

To alleviate researchers from this burden, multiple approaches have been developed to capture the structure of variable binding and generically take care of the associated boilerplate. These include specification languages of syntax with binding and scoping rules [33], tools or reflection libraries that generate code for proof assistants from specifications [7, 27, 32], generic programming libraries that implement boilerplate using datatype generic functions and proofs [18] and meta-languages that have built-in support for syntax with binding [22, 24, 35].

Yet, despite the multitude of existing approaches, the scope of the available support is still rather limited. Most approaches do not cover rich-binding forms (such as patterns or declaration lists) or the advanced scoping rules (like sequential and recursive scopes) of more complex languages. Those that do still leave most of the boilerplate up to the developer. As a consequence, only drastic simplifications of languages are mechanized, in order to fit the mold of existing tools and make the development cost affordable. For example, multi-variable binders are replaced by single-variable binders and polymorphic languages by monomorphic sublanguages to avoid dealing with multiple distinct namespaces. Obviously, there is a very real danger that these simplifications gloss over actual problems in the original language and give a false sense of security.

This work greatly improves the support for binder boilerplate in the mechanization of programming languages in two dimensions. First, we support a rich class of abstract syntaxes with binders involving advanced binding forms, complex scoping rules and mutually recursive sorts with variables. Secondly, the supported boilerplate for this class goes beyond term-related functions and lemmas: it also generically covers contexts and well-scopedness predicates.

For this purpose, we provide Knot, a language to concisely and naturally specify the abstract syntax and rich binding structure of programming languages. From such a Knot specification, our Needle  tool generates the corresponding Coq code as well as all the derived boilerplate. Our specific contributions are:

• 1. We present Knot, a new approach to automate the treatment of variable binding boilerplate. Knot is a natural and concise specification language for syntax with binders. Knot is highly expressive, supporting multi-binders, advanced scoping rules and mutually recursive sorts with variables.

• 2. We prove that any well-formed Knot specification is guaranteed to produce a considerable amount of binder boilerplate operations and lemmas that include the usual term-level interaction lemmas, but also lemmas for contexts and context lookups and for weakening, strengthening and substitution lemmas of well-scopedness relations. Our mechanized proof consists of a constructive generic implementation which in particular deals with the challenges of mutually recursive definitions.

• 3. Alongside the generic implementation, we provide Needle, a convenient code generator that produces specialized boilerplate for easy embedding in larger Coq formalizations. Needle also provides a library of tactics to simplify and automatically discharge well-scopedness proof obligations.

• 4. We demonstrate the usefulness of Knot with two case studies.

  • (a) We show that the Knot-based approach is on average 40 % smaller than the unassisted approach in a case-study of type-safety mechanizations for 10 languages.

  • (b) We compare the Knot solution of the POPLmark challenge (1A + 2A) to 7 other solutions. Ours is by far the smallest.

The code for Needle and the Coq developments (compatible with Coq 8.4 and 8.5) are available at https://users.ugent.be/~skeuchel/knot.

2 Overview

This section gives an overview of the variable binding boilerplate that arises when proving type preservation of typed programming languages. For this purpose, we use $F_\times$ (i.e., System F with products and destructuring pattern bindings) as the running example. In the following, we elaborate the different steps of the formalization and point out where variable binding boilerplate arises.

2.1 Syntax: Variable Representation

Figure 1 (top) shows the first step in the formalization: the syntax of $F_\times$. Notice that patterns can be nested and can bind an arbitrary number of variables at once. In this grammar the scoping rules are left implicit. The intended rules are that in a type or term abstraction the variable scopes over the body $e$ and in a pattern binding the variables bound by the pattern scope over $e _2$ but not $e _1$.

Fig. 1.

$F_\times$ syntax and de Bruijn representation

The syntax raises the first variable-related issue: how to concretely represent variables, an issue that is side-stepped in Fig. 1 (top). Traditionally, one would use identifiers for variables. However, when formalizing meta-theory this representation requires reasoning modulo $\alpha$-equivalence of terms to an excruciating extent. It is therefore inevitable to choose a different representation.

The goal of this paper is neither to develop a new approach to variable binding nor to compare existing ones, but rather to scale the generic treatment of a single approach to realistic languages. For this purpose, we choose de Bruijn representations [9], motivated by two main reasons. First, reasoning with de Bruijn representations is well-understood and, in particular, the representation of pattern binding and scoping rules is also well-understood [10, 15]. Second, the functions related to variable binding, the statements of properties of these functions and their proofs have highly regular structures with respect to the abstract syntax and the scoping rules of the language. This helps us in treating boilerplate generically and automating proofs.

The term grammar in Fig. 1 (bottom) encodes a de Bruijn representation of $F_\times$. The variable occurrences of binders have been removed in this representation and the referencing occurrences of type and term variables are replaced by de Bruijn indices $n$. These de Bruijn indices point directly to their binders: The index $n$ points to the $n$th enclosing binding position. For instance, the $F_\times$  expression for the polymorphic swap function

$$\varLambda \alpha .\varLambda \beta .\lambda x \mathbin {:}(\alpha ,\beta ).\mathbf {case}\; x \;\mathbf {of}\;( x1 , x2 )\rightarrow ( x2 , x1 )$$

is represented by the de Bruijn term

Again, the order in which de Bruijn indices are bound and the scoping rules are left implicit in the term grammar. Our specification language Knot  for de Bruijn terms from Sect. 3 will make order of binding and scoping rules explicit.

A second example is $tyabs \;( tyabs \;( abs \;( tvar \;\mathrm {1})\;( abs \;( tvar \;\mathrm {0})\;( var \;\mathrm {1})))$ for the polymorphic $const$ function $\varLambda \alpha .\varLambda \beta .\lambda x \mathbin {:}\alpha .\lambda y \mathbin {:}\beta . x$. We use different namespaces for term and type variables and treat indices for variables from distinct namespaces independently: The index for the type variable $\beta$ that is used in the inner $abs$ is $\mathrm {0}$ and not $\mathrm {1}$, because we only count the number of binders for the corresponding namespace and not binders for other namespaces.

2.2 Semantics: Shifting and Substitution

The next step in the formalization is to develop the typical semantic relations for the language of study. In the case of $F_\times$, these comprise a small-step call-by-value operational semantics, as well as a well-scopedness relation for types, a typing relation for terms and a typing relation for patterns. The operational semantics defines the evaluation of term- and type-abstraction by means of $\beta$-reduction.

$$ (\lambda x . e _1)\; e _2 \longrightarrow _\beta [ x \mapsto e _2]\; e _1 \qquad ( \varLambda \alpha .e )\;\tau \longrightarrow _\beta [\alpha \mapsto \tau ]\; e $$

This requires the first boilerplate for the de Bruijn representation: substitution of type variables in types, terms and contexts, and of term variables in terms.

It is necessary to define weakenings first, that adapts the indices of free variables in a term $e$ when its context $\varGamma$ is changed, e.g. when traversing into the right-hand side of a pattern binding that binds $\varDelta$ variables: $\varGamma \vdash e \leadsto \varGamma ,\varDelta \vdash e$.

To only adapt free variables but not bound variables in $e$, we implement weakening by reducing it to a more general operation called shifting that implements insertion of a single variable in the middle of a context [10, 25]

$$ \varGamma ,\varDelta \vdash e \leadsto \varGamma , x ,\varDelta \vdash e \qquad \varGamma ,\varDelta \vdash e \leadsto \varGamma ,\alpha ,\varDelta \vdash e $$

In total, we need to implement four shift functions to adapt type-variable indices in types, terms and contexts and term-variable indices in terms.

Table 1. Lines of Coq code for the $F_\times$  meta-theory mechanization.

2.3 Theorems: Commutation, Weakening and Preservation

Given the definitions from the previous subsection, we are ready to define the semantics and type system of $F_\times$ and move on to formulate and prove type soundness for $F_\times$. We refrain from formulating it here explicitly. The proof of type soundness involves the usual lemmas for canonical forms, typing inversion, pattern-matching definedness as well as progress and preservation [42]. To prove these lemmas, we require a second set of variable binding boilerplate:

• Interaction lemmas for the shift, weaken and substitution operations. These include commutation lemmas for two operations working on distinct indices and the cancellation of a subst and a shift working on the same variables (cf. Sect. 6). In the case of $F_\times$, we only need interaction lemmas for type-variable operations to prove the preservation lemma, but in general these may also involve interactions between two operations in distinct namespaces.

• Weakening and strengthening lemmas about context lookups which in particular need additional interaction lemmas for context concatenation.

• We need to define well-scopedness of types with respect to a context and prove weakening and strengthening properties and the preservation of well-scopedness under well-scoped type-variable substitution.

2.4 Summary

Table 1 summarizes the effort required to formalize type soundness of $F_\times$ in the Coq proof assistant in terms of the de Bruijn representation. It lists the lines of Coq code for the three different parts of the formalization discussed above, divided in binder-related “boilerplate” and the other “useful” code. The table clearly shows that the boilerplate constitutes about two thirds of the formalization. The boilerplate lemmas in particular, while individually fairly short, make up the bulk of the boilerplate and close to half of the whole formalization.

Of course, very similar variable binder boilerplate arises in the formalization of other languages, where it requires a similar unnecessarily large development effort. For instance, Rossberg et al. [30] report that 400 out of 500 lemmas of their mechanization in the locally-nameless style [6] were tedious boilerplate lemmas.

Fortunately, there is much regularity to the boilerplate: it follows the structure of the language’s abstract syntax and its scoping rules. Many earlier works have already exploited this fact in order to automatically generate or generically define part of the boilerplate for simple languages.

2.5 Our Solution: Needle and Knot

The aim of this work is to considerably extend the support for binder boilerplate in language mechanizations on two accounts. First, we go beyond simple single variable binders and tackle complex binding structures, like the nested pattern matches of $F_\times$, recursively and sequentially scoped binders, mutually recursive binders, heterogeneous binders, etc. Secondly, we cover a larger extent of the boilerplate than earlier works, specifically catering to contexts, context lookups and well-scopedness relations.

Our approach consists of a specification language, called Knot, that allows concise and natural specifications of abstract syntax of programming languages and provides rich binding structure. We provide generic definitions and lemmas for the variable binding boilerplate that apply to every well-formed Knot specification. Finally, we complement the generic approach with a code generator, called Needle, that specializes the generic definitions and allows manual customization and extension.

We follow two important principles: Firstly, even though in its most general form, syntax with binders has a monadic structure [3–5], Knot restricts itself to free monadic structures. This allows us to define substitution and all related boilerplate generically and encompasses the vast majority of languages.

Secondly, we hide as much as possible the underlying concrete representation of de Bruijn indices as natural numbers. Instead, we provide an easy-to-use interface that admits only sensible operations and prevents proofs from going astray. In particular, we rule out comparisons using inequalities and decrements, and any reasoning using properties of these operations.

3 The Knot Specification Language

This section introduces Knot, our language for specifying the abstract syntax of programming languages and associated variable binder information. The advantage of specifying programming languages in Knot is straightforward: the variable binder boilerplate comes for free for any well-formed Knot specification.

The syntax of Knot allows programming languages to be expressed in terms of different syntactic sorts, term constructors for these sorts and binding specifications for these term constructors. The latter specify the number of variables that are bound by the term constructors as well as their scoping rules.

Fig. 2.

The syntax of Knot

3.1 Knot  Syntax

Figure 2 shows the grammar of Knot. A Knot  specification $spec$ of a language consists of variable namespace declarations $namedecl$, syntactic sort declarations $sortdecl$, function declarations $fundecl$ and environment declarations $envdecl$.

A namespace declaration introduces a new namespace $\alpha$ and associates it with a particular sort S. This expresses that variables of namespace $\alpha$ can be substituted for terms of sort S. It is possible to associate multiple namespaces with a single sort.

A declaration of S comes with two kinds of constructor declarations $ctordecl$. Variable constructors $K \;( x \mathord {@}\alpha )$ hold a variable reference in the namespace $\alpha$. These are the only constructors where variables can appear free. Regular constructors $K\,\overline{(x : \alpha )}\,\overline{(s : S)}$ contain named variable bindings $\overline{(x : \alpha )}$ and named subterms $\overline{(s : S)}$. Meta-variables $x$ and field names $s$ scope over the constructor declaration. For the sake of presentation, we assume that the variable bindings precede subterms. The distinction between variable and regular constructors follows straightforwardly from our free-monadic view on syntax. This rules out languages for normal forms, but as they require custom behavior (renormalization) during substitution [31, 40] their substitution-related boilerplate cannot be defined generically anyway.

Each subterm $s$ is preceded by a binding specification $bs$ that stipulates which variable bindings are brought in scope of $s$. The binding specification consists of a list of items $bsi$. An item is either a meta-variable $x$ that refers to a singleton variable binding of the constructor or the invocation of a function $f$, that computes which variables in siblings or the same subterm are brought in scope of $s$. Functions serve in particular to specify multi-binders in binding specifications. In regular programming languages the binding specifications will often be empty and can be omitted.

Functions are defined by function declarations $fundecl$. The type signature $f : S \rightarrow [\overline{\alpha }]$ denotes that function f operates on terms of sort S and yields variables in namespaces $\overline{\alpha }$. The function itself is defined by exhaustive case analysis on a term of sort S. A crucial property of Knot is the enforcement of lexical scoping: shifting and substituting variables does not change the scoping of bound variables. To achieve this, functions cannot be defined for sorts that have variable constructors.

Environments E represent a list of variables that are in scope and associate them with additional data such as typing information. To this end, an environment declaration $envdecl$ consists of clauses $\alpha \mapsto \overline{S}$ that stipulate that variables in namespace $\alpha$ are associated to terms of sorts $\overline{S}$.

Fig. 3.

Example specifications of $F_\times$ and ${\lambda _{\text {letrec}}}$

Fig. 4.

Example specifications of ${\uplambda }{\text {LF}}$ and ${\lambda _{\text {tele}}}$

3.2 Examples

Several examples of rich binder forms now illustrate Knot ’s expressive power. Figure 3 (top) shows the Knot  specification of $F_\times$. We start with the declaration of two namespaces: $Tyv$ for type variables and $Tmv$ for term variables, which is followed by the declarations of $F_\times$ ’s three sorts: types, patterns and terms. For readability, we omit empty binding specifications. The Knot  specification contains only four non-empty binding specifications: universal quantification for types and type abstraction for terms bind exactly one type variable, the lambda abstraction for terms binds exactly one term variable and the pattern match binds $bind ~ p$ variables in $t _2$ where $bind$ is a function defined on patterns.

Figure 3 (bottom) shows the specification of a simply-typed lambda calculus with recursive let definitions as they are found in the Haskell programming language. The auxiliary function $bind$ collects the variables bound by a declaration list $ds$. In the term constructor $Let$, we specify that the variables of $ds$ are not only bound in the body $t$ but also recursively in $ds$ itself.

Figure 4 (top) shows the specification of a lambda calculus with first-order dependent types as presented by Aspinall and Hofmann [26]. In this language, terms and types are mutually recursive and have distinct namespaces. Type variables can be declared in the context with a specific kind $K$ but are never bound in the syntax.

The calculus presented in Fig. 4 (top) uses telescopic abstractions. Telescopes were invented to model dependently typed systems [10]. They are lists of variables together with their types $x_1 : T_1, \dots , x_n : T_n$ where each variable scopes over subsequent types. In the abstract syntax, the sequential scoping is captured in the binding specification of the recursive position of the $TCons$ constructor. In the lambda abstraction case $Abs$ and the dependent function type constructor $Pi$ the variables of a telescope are bound simultaneously in the body.

3.3 Well-Formed Knot  Specifications

In this section, we generally define well-formedness of specifications that in particular ensures that meta-variables and field names in binding specifications are always bound and that binding specifications are well-typed. To do so, we make use of several kinds of global information. The global environment $V$ contains the mapping from namespaces to the associated sort. The function environment $\varPhi$ contains the type signatures for all functions $f \mathbin {:} S \rightarrow \overline{\alpha }$.

The global function $depsOf$ maps sort $S$ to the set of namespaces $\overline{\alpha }$ that $S$ depends on. For example, in $F_\times$  terms depend on both type and term variables, but types only depend on type variables. $depsOf$ is the least function that fulfill two conditions:

• 1. For each variable constructor $(K : \alpha \rightarrow S)$: $\alpha \in depsOf \; S$,

• 2. and for each regular constructor $(K : \overline{\alpha }~\overline{T} \rightarrow S)$: $depsOf ~T_i \subseteq depsOf ~S \quad (\forall i)$.

The function $depsOf$ induces a subordination relation on sorts similar to subordination in Twelf [22, 38]. We will use $depsOf$ in the definition of syntactic operations to avoid recursing into subterms in which no variables of interest are to be found and for subordination-based strengthening lemmas.

Figure 5 defines the well-formedness relation $\vdash spec$ for Knot specifications. The single rule WfSpec expresses that a specification is well-formed if each of the constructor declarations inside the sort declarations is and the meta-environment $V$ contains exactly the declared namespaces.

The auxiliary well-sorting relation $\vdash _S ctordecl$ denotes that constructor declaration $ctordecl$ has sort S. There are two rules for this relation, one for each constructor form. Rule WfVar requires that the associated sort of the variable namespace matches the sort of the constructor. Rule WfReg handles regular constructors. It builds a constructor-local meta-environment L for meta-variables with their namespace $x \mathbin {:}\alpha$ and fields with their sorts $s \mathbin {:} S$. The binding specifications of all fields and all functions defined on S are checked against L.

The relation $L \vdash bs : \overline{\alpha }$ in Fig. 5 denotes that binding specification $bs$ is typed heterogeneously with elements from namespaces $\overline{\alpha }$. By rule WfBs a binding specification is well-typed if each of its items is well-typed.

Rule WfSng regulates the well-typing of a singleton variable binding. It is well-typed if the namespace $\beta$ of the binding is among the namespaces $\overline{\alpha }$. Correspondingly, the rule $\textsc {WfCall}$ states that a function call f s is well-typed if the namespace set $\overline{\beta }$ of the function is a subset of $\overline{\alpha }$.

Fig. 5.

Well-formed specifications

In addition to the explicitly formulated well-formedness requirements of Fig. 5, we also require a number of simple consistency properties:

• 1. Constructor names are not repeated for different constructor declarations.

• 2. Field names are not repeated in a constructor declaration.

• 3. For each namespace $\alpha$ there is a unique variable constructor declaration $K \;\alpha$.

• 4. Function declarations are exhaustive and not overlapping.

• 5. There is at most one environment clause per namespace.

The first two requirements avoid ambiguity and follow good practice. The third requirement expresses that every variable belongs to one sort and there is only one way, i.e., one term constructor, to inject it in that sort. The fourth requirement ensures that functions are total. Finally, the last requirement avoids ambiguity by associating variables from a namespace with only one kind of data.

4 Knot Semantics

The previous section has introduced the Knot  specification language for abstract syntax. This section generically defines the semantics of the language in terms of a de Bruijn representation, declare the abstract syntax that is valid with respect to the specification and define the semantics of binding specifications. We assume a given well-formed specification $spec$ in the rest of this section.

Fig. 6.

Grammars of raw de Bruijn terms

4.1 Term Semantics

We assume that information about constructors is available in a global environment. We use $( K \mathbin {:}\alpha \rightarrow S )$ for looking up the type of a variable constructor and $( K \mathbin {:}\overline{\alpha }\rightarrow \overline{ T }\rightarrow S )$ for retrieving the fields types of regular constructors.

Figure 6 contains a term grammar for raw terms of sorts and environments. A sort term consists of either a constructor applied to a de Bruijn index or a term constructor applied to other sort terms. An environment term is either and empty environment or the cons of an environment and a list of associated sort terms. The cons is additionally tagged with a namespace $\alpha$. It is straightforward to define a well-sortedness judgement $\vdash u \mathbin {:} S$ for raw sort terms and $\vdash \varGamma \mathbin {:} E$ for raw environment terms. See also the well-scopedness relation in Fig. 8 that refines well-sortedness.

Fig. 7.

Interpretation of binding specifications and functions

4.2 Binding Specification Semantics

The binding specification $[ bs ]\; t$ for a particular subterm $t$ of a given term constructor $K$ defines the variables that are brought into scope in $t$. For example, the binding specification of the pattern-matching case of $F_\times$ in Fig. 3 states that the pattern variables are bound in the body by means of a function $bind$ that collects these variables. We need to define an interpretation of binding specifications and functions that we can use in the definitions of boilerplate functions.

Figure 7 defines the interpretation $\llbracket \, bs \,\rrbracket _{\vartheta }$ of $bs$ as a meta-level evaluation. Interpretation is always performed in the context of a particular constructor $K$. This is taken into account in the interpretation function: the parameter $\vartheta \mathbin {:}\overline{ t \mapsto u }$ is a mapping from field labels to concrete subterms.

Traditionally, one would use a natural number to count the number of variables that are being bound. Instead, we use heterogeneous variable lists $hvl$ – a refinement of natural numbers – defined in Fig. 7 for dealing with heterogeneous contexts: each successor $S_\alpha$ is tagged with a namespace $\alpha$ to keep track of the number and order of variables of different namespaces. This allows us to model languages with heterogeneous binders, i.e. that bind variables of different namespaces at the same time, for which reordering the bindings is undesirable.

In case the binding specification item is a single-variable binding, the result is a one with the correct tag. In the interesting case of a function call $f \; t _ i$, the evaluation pattern matches on the corresponding subterm $\vartheta \; t _ i$ and interprets the right-hand side of the appropriate function clause with respect to the new subterms. Note that we have ruled out function definitions for variable constructors. Thus, we do not need to handle that case here.

The $hvl$s are term counterparts of environments from which the associated information has been dropped. The function $domain$ in Fig. 7 makes this precise by calculating the underlying $hvl$ of an environment term. In the following, we use the extension of addition from natural numbers to concatenation of $hvl$s – defined in Fig. 7 – and implicitly use its associativity property. In contrast, concatenation is not commutative. We mirror the convention of extending environments to the right at the level of $hvl$ and will always add new variables on the right-hand side of concatenation.

4.3 Well-Scopedness

Part of the semantics is the well-scopedness of terms. It is current practice to define well-scopedness with respect to a typing environment: a term is well-scoped iff all of its free variables are bound in the environment. The environment is extended when going under binders. For example, when going under the binder of a lambda abstraction with a type-signature the conventional rule is:

The rule follows the intention that the term variable should be of the given type. In this regard, well-scopedness is already a lightweight type-system. However, it is problematic for Knot to establish this intention or in general establish what the associated data in the environment should be. Furthermore, we allow the user to define different environments with potentially incompatible associated data. Hence, instead we define well-scopedness by using domains of environments. In fact, this is all we need to establish well-scopedness.

Figure 8 defines the well-scopedness relation on de Bruijn indices as well as sort and environment terms. The relation $h \vdash _\alpha n$ denotes that n is a well-scoped de Bruijn index for namespace $\alpha$ with respect to the variables in h. This is a refinement of $n < h$ in which only the successors for namespace $\alpha$ in h are taken into account. This is accomplished by rule WsHom which strips away one successor in the homogeneous case and rule WsHet that simply skips successors in the heterogeneous case. Rule WsZero forms the base case for $n=0$ which requires that h has a successor tagged with $\alpha$.

Rule WsVar delegates well-scopedness of variable constructors to the well-scopedness of the index in the appropriate namespace. In rule WsCtor, the heterogeneous variable list h is extended for each subterm $u_i$ with the result of evaluating its binding specification $bs _ i$.

The relation $h \vdash \varGamma$ defines the well-scopedness of environment terms with respect to previously existing variables $h$. We will also write $\vdash \varGamma$ as short-hand for $\mathrm {0}\vdash \varGamma$. Note in particular that rule WsCons extends h with the $domain$ of the existing bindings when checking the well-scopedness of associated data.

Fig. 8.

Well-scopedness of terms

5 Infrastructure Operations

In this section, we generically define common infrastructure operations generically over all terms of a specifications. This includes shifting and substitution in sort and environment terms and lookups in environments.

Fig. 9.

Shifting of terms

5.1 Shifting

Shifting adapts indices when a variable $x$ is inserted into the context.

$$ \varGamma ,\varDelta \vdash e \leadsto \varGamma ,( x \mathbin {:}\tau ),\varDelta \vdash e $$

Indices in $e$ for $\alpha$-variables in $\varGamma$ need to be incremented to account for the new variable while indices for variables in $\varDelta$ remain unchanged. The $shift$ function is defined in Fig. 9 implements this. It is parameterized over the namespace $\alpha$ of variable $x$ in which the shift is performed. It takes a cut-off parameter $c$ that is the number of $\alpha$-variable bindings in $\varDelta$. In case of a variable constructor $K \mathbin {:}\alpha \rightarrow S$, the index is shifted using the $shift _\mathbb {N}$ function. For variable constructors of other namespaces, we keep the index unchanged. In the case of a regular constructor, we need to calculate the cut-offs for the recursive calls. This is done by evaluating the binding specification $bs$ and weakening the cut-off. Using the calculated cut-offs, the $shift ?_\alpha$ function can proceed recursively on the subterms that depend on the namespace $\alpha$.

Instead of using the traditional arithmetical implementation

$$\mathbf {if}\; n \mathbin {<} c \;\mathbf {then}\; n \;\mathbf {else}\; n \mathbin {+}\mathrm {1}$$

we use an equivalent recursive definition of $shift _\mathbb {N}$ that inserts the successor constructor at the right place. This follows the inductive structure of $\varDelta$ which facilitates inductive proofs on $\varDelta$.

Weakening. Weakening is the transportation of a term $e$ from a context $\varGamma$ to a bigger context $\varGamma ,\varDelta$ where variables are only added at the end.

$$ \varGamma \vdash e \leadsto \varGamma ,\varDelta \vdash e $$

Figure 9 shows the implementation of $weaken _\alpha$ that iterates the 1-place $shift ?_\alpha$ function. Its second parameter $h$ is the domain of $\varDelta$; the range of $\varDelta$ is not relevant for weakening.

Fig. 10.

Substitution of terms

5.2 Substitution

Next, we define substitution of a single variable $x$ for a term $e$ in some other term $e'$ generically. In the literature, two commonly used variants can be found.

• 1. The first variant keeps the invariant that $e$ and $e'$ are in the same context and immediately weakens $e$ when passing under a binder while traversing $e'$ to keep this invariant. It corresponds to the substition lemma

  

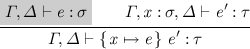
• 2. The second variant keeps the invariant that $e'$ is in a weaker context than $e$. It defers weakening of $e$ until the variable positions are reached to keep the invariant and performs shifting if the variable is substituted. It corresponds to the substitution lemma

  

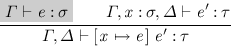
Both variants were already present in de Bruijn’s seminal paper [9], but the first variant has enjoyed more widespread use. However, we will use the second variant because it has the following advantages:

• 1. It supports the more general case of languages with a dependent context:

  

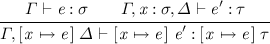
• 2. The parameter $e$ is constant while recursing into $e'$ and hence it can also be moved outside of inductions on the structure of $e$. Proofs become slightly simpler because we do not need to reason about any changes to $s$ when going under binders.

For the definition of substitution, we again need to use a refinement of natural numbers, a different one from before: we need to keep track of variable bindings of the namespaces to transport $e$ into the context of $e'$, i.e. those in $depsOf \; S$ where $S$ is the sort of $e$. Figure 10 contains the refinement, which we call “traces”, a well-formedness condition that expresses the namespace restriction and a $weaken _\alpha$ function for traces.

Figure 10 also contains the definition of substitution. Like for shift, we define substitution by three functions. The function $subst _{\alpha ,\mathbb {N}}\; v \; x \; n$ defines the operation for namespace $\alpha$ on indices by recursing on $x$ and case distinction on $n$. If the index and the trace match, then the result is the term $v$. If the index $n$ is strictly smaller or strictly larger than the trace $x$, then $subst _{\alpha ,\mathbb {N}}$ constructs a term using the variable constructor for $\alpha$. In the recursive cases, $subst _{\alpha ,\mathbb {N}}$ performs the necessary shifts when coming out of the recursion in the same order in which the binders have been crossed. This avoids a multiplace $weaken$ on terms.

The substitution $subst _\alpha$ traverses terms to the variable positions and weakens the trace according to the binding specification. As previously discussed $v$ remains unchanged. The function $subst ?_\alpha$ only recurses into the term if it is interesting to do so.

5.3 Environment Lookups

The paramount infrastructure operation on environments is the lookup of variables and their associated data. Lookup is a partial function. For that reason, we define it as a relation $( n \mathbin {:}\overline{ u })\;\in _\alpha \;\varGamma$ that witnesses that looking up the index $n$ of namespace $\alpha$ in the environment term $\varGamma$ is valid and that $\overline{ u }$ is the associated data. Figure 11 contains the definition.

Rule InHere forms the base case where $n \mathrel {=}\mathrm {0}$. In this case the environment term needs to be a cons for namespace $\alpha$. Note that well-scopedness of the associated data is included as a premise. This reflects common practice of annotating variable cases with with well-scopedness conditions. By moving it into the lookup itself, we free the user from dealing with this obligation explicitly. We need to $weaken$ the result of the lookup to account for the binding.

Rule InThere encodes the case that the lookup is not the last cons of the environment. The rule handles both the homogeneous $\alpha \mathrel {=}\beta$ and the heterogeneous case $\alpha \ne \beta$ by means of weakening the index $n$. The associated data is also shifted to account for the new $\beta$ binding.

Fig. 11.

Environment lookup

6 Infrastructure Lemmas

Programming language mechanizations typically rely on many boilerplate properties of the infrastructure operations that we introduced in the previous section. To further reduce the hand-written boilerplate, we have set up the Knot specification language in such a way that it provides all the necessary information to generically state and prove a wide range of these properties.¹ Below we briefly summarize the three different kinds of ubiquitous lemmas that we cover. In general, it is quite challenging to tackle these boilerplate lemmas generically because their exact statements, and in particular which premises are needed, depend highly on the $depsOf$ function and also on the dependencies of the associated data in environments.

Interaction Lemmas. Formalizations involve a number of interaction boilerplate lemmas between $shift$, $weaken$ and $subst$. These lemmas are for example needed in weakening and substitution lemmas for typing relations. Two operation always commute when they are operating on different variables and a shifting followed by a substitution on the same variable cancel each other out:

$$ subst _\alpha \; v \;\mathrm {0}\;\alpha \;( shift _\alpha \;\mathrm {0}\;\alpha \; u )\mathrel {=} u .$$

Well-Scopedness. The syntactic operations preserve well-scoping. This includes shifting, weakening and substitution lemmas. If a sort does not depend on the namespace of the substitute, we can formulate a strengthening lemma instead:

Environment Lookup. Lemmas for shifting, weakening and strengthening for environment lookups form the variable cases for corresponding lemmas of typing relations. These lemmas also explain how the associated data in the context is changed. For operating somewhere deep in the context we use relations, like for example which denotes that $\varGamma _2$ is the result after inserting a new $\alpha$ variable at cutoff position $c$ in $\varGamma _1$. The shifting lemma for lookups is then:

7 Implementation

This section briefly describes our two implementations of Knot. The first is a generic implementation that acts as a constructive proof of the boilerplate’s existence for all well-formed specifications. The second, called Needle, is a code generator that is better suited to practical mechanization.

7.1 The Generic Knot Implementation

We implemented the boilerplate functions generically for all well-formed Knot specifications in about 4.3k lines of Coq by employing datatype-generic programming techniques [8]. Following our free monad principle, we capture de Bruijn terms in a free monadic structure that is parameterized by namespaces and whose underlying functor covers the regular constructors of sorts. To model the underlying functors, we use the universe of finitary containers [1, 13, 14, 19] Finitary containers closely model our specification language: a set of shapes (constructors) with a finite number of fields. We use an indexed [2] version to model mutually recursive types and use a higher-order presentation to obtain better induction principles for which we assume functional extensionality². We implemented boilerplate operations and lemmas for this universe generically.

7.2 The Needle Code Generator

While the generic Coq definitions presented in the previous sections are satisfactory from a theoretical point of view, they are less so from a pragmatic perspective. The reason is that the generic code only covers the variable binder boilerplate; the rest of a language’s formalization still needs to be developed manually. Developing the latter part directly on the generic form is cumbersome. Working with conversion functions is possible but often reveals too much of the underlying generic representation. As observed by Lee et al. [18], this happens in particular when working with generic predicates.

For this reason, we also implemented a code generation tool, called Needle that generates all the boilerplate in a language-specific non-generic form. Needle  takes a Knot  specification and generates Coq code: the inductive definitions of a de Bruijn representation of the object language and the corresponding specialized boilerplate definitions, lemmas and proofs. Both proof terms and proof scripts are generated. Needle is implemented in about 11k lines of Haskell.

Soundness. We have not formally established that Needle  always generates type-correct code or that the proof scripts always succeed. Nevertheless, a number of important implementation choices bolster the confidence in Needle ’s correctness: First, the generic-programming based implementation is evidence for the existence of type-sound boilerplate definitions and proofs for for every language specified with Knot.

Secondly, the generic implementation contains a small proof-term DSL featuring only the basic properties of equality such as symmetry, reflexivity, transitivity and congruence and additionally stability and associativity lemmas as axioms. The induction steps of proofs on the structure of terms or on the structure of well-scopedness relation on terms in the generic implementation elaborate to this DSL first and then adhere to its soundness lemma. Subsequently, we ported the proof term elaboration to Needle. Hence, we have formally established the correctness of elaboration functions but not their Haskell implementations.

Thirdly, lemmas for which we generate proof scripts follow the structure of the generic proofs. In particular, this includes all induction proofs on natural number- or list-like data because these are less fragile than induction proofs on terms. A companion library contains tactics specialized for each kind of lemma that performs the same proof steps as the generic proof.

Finally and more pragmatically, we have implemented a test suite of Knot  specifications for Needle  that contains a number of languages with advanced binding constructs including languages with mutually recursive and heterogeneous binders, recursive scoping and dependently-typed languages with interdependent namespaces for which correct code is generated.

Nevertheless, the above does not rule out trivial points of failure like name clashes between definitions in the code and the Coq standard library or software bugs in the code generator. Fortunately, when the generated code is loaded in Coq, Coq still performs a type soundness check to catch any issues. In short, soundness never has to be taken at face value.

Table 2. Size statistics of the meta-theory mechanizations.

8 Case Studies

This sections demonstrates the benefits of the Knot approach with two case studies. First, we compare fully manual versus Knot-based mechanizations of type-safety proofs for 10 languages. Second, we compare Knot ’s solution of the POPLmark challenge against various existing ones.

8.1 Manual vs. Knot Mechanizations

We compare manual against Knot-based mechanization of type safety for 10 textbook calculi: (1) the simply-typed lambda calculus, (2) the simply-typed lambda calculus with products, (3) System F, (4) System F with products, (5) System F with sequential lets, (6) $\text {System}~\text {F}_{<:}$ as in the POPLmark challenge 1A + 2A, (7) $\text {System}~\text {F}_{<:}$ with binary products, (8) $\text {System}~\text {F}_{<:}$ with records as in the POPLmark challenge 1B + 2B, (9) the simply-typed lambda calculus with type-operators, and (10) System F with type-operators.

For each language, we have two Coq formalizations: one developed without tool support and one that uses Needle ’s generated code. Table 2 gives a detailed overview of the code sizes (LoC) of the different parts of the formalization for each language and the total and relative amount of boilerplate code.

The Specification column comprises the language specifications. For the manual approach, it is split into an essential part and a boilerplate part. The former comprises the abstract syntax declarations (including binding specifications), the evaluation rules, typing contexts and typing rules and is also captured (slightly more concisely) in the Knot specification. The latter consists of context lookups for the variable typing rule as well as shifting and substitution operators, that are necessary to define $\beta$-reduction and, if supported by the language, type application; all of this boilerplate is generated by Needle and thus not counted towards the Knot-based mechanization.

The essential meta-theoretical Lemmas for type-safety are weakening and substitution lemmas for the typing relations, typing and value inversion as well as progress and preservation and where applicable this includes: pattern-matching definedness, reflexivity and transitivity of subtyping and the Church-Rosser property for type reductions.

We separate the binder boilerplate in these formalizations into two classes:

• 1. Term-related boilerplate consists of interaction lemmas discussed in Sect. 6 and other interaction lemmas between shifting, weakening and the size of terms. This is absent form the mechanizations of $\lambda$ and $\lambda _{\times }$ that do not require them. In all other cases, Needle derives the necessary lemmas. This is about 140 lines of code for each language. The size depends mainly on the number of namespaces, the number of syntactic sorts and the dependency structure between them, which is roughly the same for these languages.

• 2. The boilerplate context lemmas consist of weakening, strengthening and substitution lemmas for term well-scopedness relations and for context lookups. The size depends on the number of namespaces that are handled by the context. In the cases where only single-variable binding is used, we can skip weakening and strengthening lemmas related to multi-binders.

Summary. Table 2 clearly shows that Knot provides substantial savings in each of the language formalizations, ranging up to  74 % for System F. Note that these formalizations of type safety use only a fraction of the lemmas generated by Needle. For instance, none of the above formalization uses any of the interaction lemmas for terms that are generated.

8.2 Comparison of Approaches

Because it is the most widely implemented benchmark for mechanizing metatheory, we use parts 1A + 2A of the POPLmark challenge to compare our work with that of others. These parts prove type-safety for $\text {System}~\text {F}_{<:}$ with algorithmic subtyping. As they involve only single-variable bindings, they are manageable for most existing approaches (though they do not particularly put Knot ’s expressivity to the test). Figure 12 compares 9 different solutions:

• Charguéraud’s [11] developments use the locally-nameless representation and come with proof automation for this representation.

• Vouillon [39] presents a self-contained de Bruijn solution.

• Our manual version from Sect. 8.1.

• GMeta [18] is a datatype-generic library supporting both de Bruijn indices and the locally-nameless representation.

• LNGen [7] is a code-generator that produces Coq code for the locally-nameless representation from an Ott specification.

• Autosubst [32] is a Coq tactic library for de Bruijn indices.

• Our Knot solution from Sect. 8.1.

The figure provides the size (in LoC) for each solution. The LoC counts, generated by coqwc, are separated into proof scripts and other specification lines, except for the Twelf solution were we made the distinction manually. We excluded both library code and generated code. The AutoSubst and Knot  formalizations are significantly smaller than the others due to the uniformity of weakening and substitution lemmas. Knot ’s biggest savings compared to AutoSubst come from the generation of well-scopedness relations and the automation of well-scopedness proof obligations. In summary, the Knot solution is the smallest solutions we are aware of.

Fig. 12.

Sizes (in LoC) of POPLmark solutions

9 Related Work

For lack of space, we cover only work on specification languages for variable binding, and systems and tools for reasoning about syntax with binders.

9.1 Specification Languages

The Ott tool [33] allows the definition of concrete programming language syntax and inductive relations on terms. Its binding specifications have inspired those of Knot. The main difference is that Knot allows heterogeneous binding specification functions instead of being restricted to homogeneous ones. While Ott generates datatype and function definitions for abstract syntax in multiple proof assistants, support for lemmas is absent.

The C$\upalpha$ml tool [28] defines a specification language for abstract syntax with binding specifications from which it generates OCaml definitions and substitutions. A single abstraction construct allows atoms appearing in one subterm to be bound in another. However this rules out nested abstractions and therefore, the telescopic lambdas of Fig. 4 cannot be encoded directly in C$\upalpha$ml. We are not aware of any work that uses C$\upalpha$ml for the purpose of mechanization.

Romeo [34] is a programming language that checks for safe handling of variables in programs. Romeo ’s specification language is based on the concept of attribute grammars [16] with a single implicit inherited and synthesized attribute. In this view, Knot also has a single implicit inherited attribute and binding specification functions represent synthesized attributes. Moreover, we allow multiple functions over the same sort. However, Romeo is a full-fledged programming language while Knot only allows the definition of functions for the purpose of binding specification. Romeo has a deduction system that rules out unsafe usage of binders but is not targeting mechanizations of meta-theory.

Unbound [41] is a Haskell library for programming with abstract syntax. Its specification language consists of a set of reusable type combinators that specify variables, abstractions, recursive and sequential scoping. The library internally uses a locally nameless approach to implement the binding boilerplate which is hidden from the user. The library also has a combinator called $Shift$ which allows to skip enclosing abstractions. This form of non-linear scoping is not supported by Knot. However, the objective of Unbound is to eliminate boilerplate in meta-programs and not meta-theoretic reasoning.

Knot focuses on the kind of abstract syntax representations that are common in mechanizations, which are usually fully resolved and desugared variants of the concrete surface syntax of a language. More work is needed to specify surface languages with complex name resolutions algorithms. In this vein, it would be interesting to extend Knot to synthesize scope graphs [21, 37], which are a recent development to address name resolution in a syntax independent manner.

9.2 Tools for First-Order Representations

Aydemir and Weirich [7] created LNGen, a tool that generates locally-nameless Coq definitions from an Ott specification. It takes care of boilerplate syntax operations, local closure predicates and lemmas. It supports multiple namespaces but restricts itself to single-variable binders.

The DbGen  tool [27] generates de Bruijn representations and boilerplate code. It supports multiple namespaces, mutually recursive definitions and, to a limited extent, multi-variable binders: one can specify that $n$ variables are to be bound in a field, with $n$ either a natural number literal or a natural number field of the constructor. It generates all basic interaction lemmas, but does not deal with well-scopedness or contexts.

GMeta  [18] is a framework for first-order representations of variable binding developed by Lee et al. It is implemented as a library in Coq that makes use of datatype-generic programming concepts to implement syntactic operations and well-scopedness predicates generically. GMeta allows multiple namespaces but is restricted to the single-variable case. The system does not follow our free monad principle to model namespaces explicitly, but rather establishes the connection at variable binding and reference positions by comparing the structure representation of sorts for equality. This raises the question whether the universe models syntax adequately when different sorts have the same structure.

GMeta  contains a reusable library for contexts of one or two sorts. In the case of two sorts, e.g. term and type variables, the binding of type variables can be telescopic which is enough to address the POPLmark challenge. Hence, GMeta  captures the structure of terms generically, but not the structure of contexts and the accompanying library implements only two instances, but admittedly the ones that are used the most.

AutoSubst [32] is a Coq library that derives boilerplate automatically by reflection using Coq ’s built-in tactics language. It supports variable binding annotations in the datatype declarations but is limited to single variable bindings and directly recursive definitions. AutoSubst derives parallel substitution operations which is particularly useful for proofs that rely on more machinery for substitutions than type-safety proofs like logical relation proofs for normalization, parametricity or full-abstraction. We do not support parallel substitutions yet, but plan to do so in the future.

9.3 Languages for Mechanization

Several languages have direct support for variable binding. Logical frameworks such as Abella [12], Hybrid [20], Twelf [22] and Beluga [24] are specifically designed to reason about logics and programming languages. Their specialized meta-logic encourages the use of higher-order abstract syntax (HOAS) to represent object-level variable binding with meta-variable bindings. The advantage is that facts about substitution, $\alpha$-equivalence and well-scoping are inherited from the meta-language. These systems also allow the definition of higher-order judgements to get substitution lemmas for free if the object-language context admits exchange [29]. If it does not admit exchange, the context can still be modeled explicitly [17, 23]. For the POPLmark challenge for instance this becomes necessary to isolate a variable in the middle of the context for narrowing.

Despite the large benefits of these systems, they are generally limited to single variable binding and other constructs like patterns or recursive lets have to be encoded by transforming the object language [29].

Nominal Isabelle [36] is an extension of the Isabelle/HOL framework with support for nominal terms which provides $\alpha$-equivalence for free. At the moment, the system is limited to single variable binding but support for richer binding structure is planned [35].

10 Conclusion

This paper has presented a new approach to mechanizing meta-theory based on Knot, a specification language for syntax with variable binding, and Needle, an infrastructure code generator. Our work distinguishes itself from earlier work on two accounts. First, it covers a wider range of binding constructs featuring rich binding forms and advanced scoping rules. Secondly, it covers a larger extent of the boilerplate functions and lemmas needed for mechanizations. In future work, we want to include support for typing relations.