Abstract
Non-malleable codes are a generalization of classical error-correcting codes where the act of “corrupting” a codeword is replaced by a “tampering” adversary. Non-malleable codes guarantee that the message contained in the tampered codeword is either the original message m, or a completely unrelated one. In the common split-state model, the codeword consists of multiple blocks (or states) and each block is tampered with independently.
The central goal in the split-state model is to construct high rate non-malleable codes against all functions with only two states (which are necessary). Following a series of long and impressive line of work, constant rate, two-state, non-malleable codes against all functions were recently achieved by Aggarwal et al. [2]. Though constant, the rate of all known constructions in the split state model is very far from optimal (even with more than two states).
In this work, we consider the question of improving the rate of split-state non-malleable codes. In the “information theoretic” setting, it is not possible to go beyond rate 1/2. We therefore focus on the standard computational setting. In this setting, each tampering function is required to be efficiently computable, and the message in the tampered codeword is required to be either the original message m or a “computationally” independent one.
In this setting, assuming only the existence of one-way functions, we present a compiler which converts any poor rate, two-state, (sufficiently strong) non-malleable code into a rate-1, two-state, computational non-malleable code. These parameters are asymptotically optimal. Furthermore, for the qualitative optimality of our result, we generalize the result of Cheraghchi and Guruswami [10] to show that the existence of one-way functions is necessary to achieve rate \(>1/2\) for such codes.
Our compiler requires a stronger form of non-malleability, called augmented non-malleability. This notion requires a stronger simulation guarantee for non-malleable codes and simplifies their modular usage in cryptographic settings where composition occurs. Unfortunately, this form of non-malleability is neither straightforward nor generally guaranteed by known results. Nevertheless, we prove this stronger form of non-malleability for the two-state construction of Aggarwal et al. [3]. This result is of independent interest.
S. Agrawal and M. Prabhakaran—Research supported in part by NSF grant 1228856.
D. Gupta and H.K. Maji—Research supported in part from a DARPA/ONR PROCEED award, NSF Frontier Award 1413955, NSF grants 1228984, 1136174, 1118096, and 1065276, a Xerox Faculty Research Award, a Google Faculty Research Award, an equipment grant from Intel, and an Okawa Foundation Research Grant. This material is based upon work supported by the Defense Advanced Research Projects Agency through the U.S. Office of Naval Research under Contract N00014-11- 1-0389. The views expressed are those of the author and do not reflect the official policy or position of the Department of Defense, the National Science Foundation, or the U.S. Government.
D. Gupta, O. Pandey and M. Prabhakaran—This work was done in part while the author was visiting the Simons Institute for the Theory of Computing, supported by the Simons Foundation and by the DIMACS/Simons Collaboration in Cryptography through NSF grant #CNS-1523467.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
- Non-malleable codes
- Split-state
- Explicit construction
- Computational setting
- One-way functions
- Pseudorandom generators
- Authenticated encryption schemes
- Rate 1
1 Introduction
Non-Malleable Codes, introduced by Dziembowski, Pietrzak, and Wichs [18], are a generalization of the classical notion of error detection. Informally, a code is non-malleable if the message contained in a codeword that has been tampered with is either the original message, or a completely unrelated value. Non-Malleable Codes have emerged as a fundamental object at the intersection of coding theory and cryptography.
There are two main directions in this area: design explicit codes that can tolerate a large class of tampering functions, and achieve high rate Footnote 1 for such constructions.
Ideally, we would like to tolerate the class of all tampering functions that can be implemented in \(\mathrm {P} / \mathrm {poly}\). However, this is impossible if the adversary has unrestricted access to the full codewordFootnote 2. Therefore, one must either consider a (much weaker) class of tampering functions, or move to alternative models where the adversary has only restricted access to the codeword.
The most common model for tolerating arbitrary tampering functions is the split state model. In this model, the codeword is “split” into two or more states \(c=(c_1,\ldots ,c_k)\); a tampering function f is viewed as a list of k functions \((f_1,\ldots ,f_k)\) fixed before c is sampled, where each function \(f_i\) tampers with the corresponding component \(c_i\) of the codeword independently, i.e., the tampered codeword is \(c'=(f_1(c_1),\ldots ,f_k(c_k))\). Ideally, we would like to achieve codewords with minimum number of states \(k=2\) while tolerating all possible tampering functions and achieving high-rateFootnote 3.
In a break-through result, Aggarwal et al. [3] presented an explicit non-malleable code for \(k=2\) states for messages of arbitrary length (significantly improving upon [17] which only encodes a single bit). However, their work only achieves rate \(\varOmega (n^{-6/7})\) (or rate 0, asymptotically) where n is the block length of the codeword. Chattopadhyay and Zuckerman [9] present an encoding which has constant rate by increasing the number of states to \(k=10\). Very recently, Aggarwal et al. [2] show that constant rate for such codes can in fact be achieved with only \(k=2\) statesFootnote 4.
Though constant, the rate of codes in [2, 9] is very far from optimal. A natural question is if we can achieve the best parameters, i.e.:
Can we construct explicit, 2-state, non-malleable codes of rate 1 tolerating all tampering functions in \(\mathrm {P}/\mathrm {poly}\)?
In the “information theoretic” setting it is impossible to go beyond rate 1/2. Recall that in the “information theoretic” setting, the tampering function is of the form \((f_1,f_2)\) (restricting ourselves to 2 states), the component functions are not necessarily of polynomial size, and we require that the tampered codeword contains either the original message m or a message statistically independent of m.
We must therefore consider the “computational setting” which is a natural relaxation of the information theoretic setting. More specifically, we make two changes: first, we require that \(f_1,f_2\) are both in \(\mathrm {P}/\mathrm {poly}\); and second the tampered codeword either contains the original message m or a message that is only “computationally independent” of m Footnote 5.
In this work, we show that it is indeed possible to construct rate 1 non-malleable codes in the computational setting with only \(k=2\) states under the standard assumption that one-way functions exist. Our code is explicit and tolerates all tampering functions (in \(\mathrm {P/poly}\)). Furthermore, we complement this result by proving that the existence of non-malleable codes of rate better than 1/2 (in the information theoretic setting) implies one-way functions. Our motivation to rely on the computational setting to go beyond rate 1/2 comes from similar previous works [27, 29] on classical error correcting codes where a computationally bounded channel is considered to correct more than 1 / 4th fraction of the errors.
Our approach actually yields a compiler which converts any 2-state, poor rate (potentially rate 0), non-malleable code into a rate-1 computational non-malleable code. However, this reduction requires the underlying code to have a stronger form of non-malleability: at a high level, it requires a stronger simulation guarantee where the simulator can not only simulate the distribution of the message in the tampered codeword, but also one of the states of the original codeword (say the second state). We formalize this stronger simulation requirement and call the resulting notion augmented non-malleability. Given this stronger form of non-malleability, we can prove the computational non-malleability of our 2-state construction. Augmented non-malleability simplifies the design of non-malleable codes by allowing us to compose them with other cryptographic constructs.
Unfortunately, augmented non-malleability is neither straightforward nor generally guaranteed to hold for known constructions [3, 9]. Nevertheless, we prove this stronger form of non-malleability for the two-state construction of [3]. This gives an explicit code with the desired properties, i.e.:
Informal Theorem 1
Assuming the existence of one-way functions, there exists a rate-1 split-state non-malleable code against computationally efficient tampering functions.
We note that these parameters are asymptotically optimal in the computational setting. In addition, our extension of [3] to augmented non-malleability is of independent interest — it is particularly useful in settings where composition occurs. This is captured in the following theorem:
Informal Theorem 2
For any k and \(\varepsilon \), there exists an efficient (in k and \(\log (\frac{1}{\varepsilon })\)) information-theoretically secure \(\varepsilon \)-augmented-non-malleable code for encoding k-bit messages in the (two-partition) split-state model.
We now present a technical overview of our approach.
1.1 Technical Overview
Improving Rate via Hybrid Encoding. The starting point of our work is to consider the standard “hybrid” approach where we first encode a short cryptographic key K using a low rate 2-state non-malleable code, and then use K along with an appropriate cryptographic object such as a “good rate” encryption scheme.
We note that this hybrid approach has been used in many different works to improve efficiency or the rate. For example, the most well-known example of this approach in cryptography is that of “hybrid encryption,” which improves the efficiency of a (non-malleable) public-key encryption scheme by using it to encrypt a short key for a symmetric-key encryption scheme, and then using the latter to encrypt the actual message (e.g., see [16, 26]). In the context of error-correcting codes and non-malleable codes, this approach has been used to improve the rate in [11, 18, 22], and even by [5] (who obtain information theoretic non-malleability).
In our setting, let us start by considering the following construction: encode a fresh key K using a 2-state information-theoretic non-malleable code of low (potentially 0) rate to obtain the two states say \((c_1,c_2)\), and then generate a third component \(c_3\) which is an encryption of the message m to be encoded, under the key K, using a “high rate” symmetric authenticated encryption scheme. Such encryption schemes can be constructed from pseudorandom functions (implied by one-way functions).
At first, suppose that we can keep more than two states. Then, we can output \(c=(c_1,c_2,c_3)\) as our three-state codeword. We argue that this is already a 3-state computational non-malleable code of rate 1. To see this, fix a tampering function \(f=(f_1,f_2,f_3)\) and recall that each state of the codeword is tampered independently. Let \(c'=(c'_1,c'_2,c'_3)\) be the tampered codeword where \(c'_i=f_i(c_i)\); let \(K'\) denote the “tampered” key in \((c'_1,c'_2)\) and \(m'\) denote the tampered message defined by decryption of \(c'_3\) using \(K'\). Then, intuitively, if \(K'=K\) then \(m'\) must also be equal to m by the security of authenticated encryption. On the other hand, if \(K'\ne K\) yet \(m'\) is not computationally independent of m, then it must be that \(K'\) is also not computationally independent of K. This will violate the non-malleability of the underlying 2-state code for K. This approach is reminiscent of the technique introduced by [18] for rate amplification for the restrictive class of bit-wise tampering functions.
To achieve a 2-state solution, we propose that \(c_2\) and \(c_3\) be kept in a single state and the resulting codeword is \((c_1, c_2\Vert c_3)\). However, this creates a difficult situation: since \(c_2 \Vert c_3\) are now available together, adversary might be able to generate \(c_2' \Vert c_3'\) such that \((c_1',c_2')\) encodes a key \(K'\ne K\), \(K'\) stays independent of K by itself, yet decryption of \(c_3'\) yields a message that depends on m. Unlike the case of 3-states where \(c_3'\) was generated independently of \(c_2'\), in this setting, \((c_2' \Vert c_3')\) now depends on both \(c_2\) and \(c_3\). Therefore, we need a stronger guarantee from non-malleability where not only the distribution of \(K'\), but the distribution of \(K'\) along with state \(c_2\) must be simulatable (and computationally independent of K).
We formalize this stronger simulation requirement and call the resulting notion augmented non-malleability. Given this stronger form of non-malleability, we can prove the computational non-malleability of our 2-state construction. We emphasize that the novelty of this augmented non-malleability is highlighted by the fact that our whole construction only uses one-way functions (in a fully black-box manner) while previous non-malleable code constructions by [19, 28] use CRS and extremely strong cryptographic primitives.
Achieving Augmented Non-malleability. As noted earlier, it is not clear if existing non-malleable codes also satisfy the augmented non-malleability property. In fact, we do not know if this is true in general for all non-malleable codes. We prove in Informal Theorem 2 that augmented non-malleability can be achieved from the 2-state code of [3]. We now describe how we achieve augmented non-malleability.
The main technical ingredient to prove Informal Theorem 2 is the following result.
Informal Theorem 3
Assume \(\mathbb {F}_p\) is a finite field of prime order, \(n\geqslant \mathrm {poly} (\log p))\), L is uniformly random over \(\mathbb {F}_p^n\), and \(f,g:\mathbb {F}_p^n\rightarrow \mathbb {F}_p^n\) are two arbitrary functions. Then, for almost all \(r \in \mathbb {F}_p^n\), the joint distribution \((\langle L,r \rangle ,\langle f(L),g(r) \rangle )\) is “close” to a convex combination (that depends on r) of affine distributions \(\{(U,a U+b)\mid a,b\in \mathbb {F}_p\}\), where U is uniformly random over \(\mathbb {F}_p\).
The formal statement appears in Theorem 3. A similar but weaker statement was shown in [3]. They showed that the above mentioned joint distribution is on average (over \(r \in \mathbb {F}_p^n\)) close to a convex combination of affine-distributions, while we show that this holds individually for almost all \(r \in \mathbb {F}_p^n\).
The proof follows a similar structure as [3] where the ambient space \(\mathbb {F}_p^n \times \mathbb {F}_p^n\) is partitioned into subsets depending on f, g, and then the joint distribution is analyzed over each of these subsets. One crucial difference from [3] is that several steps in their proof relied on the fact that the inner-product is a strong extractor, i.e., \(\langle L,R \rangle \) is close to uniform conditioned on L. While this is sufficient to prove the result for R uniform in \(\mathbb {F}_p^n\), we needed to be more careful since we needed to show the result for almost all \(r\in \mathbb {F}_p^n\), and we cannot claim that \(\langle L, R \rangle \) is close to uniform conditioned on both L, R. Fortunately, however, we could show (refer to Lemmas 3 and 4) that it is sufficient to show that \(\langle L,R \rangle \) is close to uniform conditioned on R and h(L) for some function \(h:\mathbb {F}_p^n \mapsto \mathbb {F}_p\) and this holds since L has sufficient entropy conditioned on h(L).
The proof of Informal Theorem 2 is relatively immediate from Informal Theorem 3 using affine-evasive sets [1, 3].
Necessity of One-Way Functions. We sketch, at a very high level, how we extend the result of Cheraghchi and Guruswami [10] to show the existence of distributional one-way functions if 2-state (information theoretic) non-malleable codes of rate large than 1 / 2 exist. See Sect. 5 for more details.
The following negative result is shown in [10]: Consider the set of tampering functions which depend only on the first \(\alpha n\) bits of the code and tampers it arbitrarily. Then a non-malleable code which protects against this tampering class can have rate at most \(1-\alpha \).
In particular, k-split-state non-malleable code can have at most \(1-1/k\) rate. Otherwise, one can use the same attack in [10] to tamper only the first state appropriately and violate the non-malleability condition.
The result in [10] uses the following idea. If the rate is higher than \(1-\alpha \) then there exists two messages \(s_0\) and \(s_1\), and a set \(X \subseteq {\{0,1\}} ^{\alpha n}\) such that the following condition holds: The first \(\alpha n\) bits of an encoding of \(s_0\) has higher probability to be in X than for an encoding of \(s_1\). So, the tampering function just writes a dummy string w if the first \(\alpha n\) bits belong in X; otherwise it keeps it intact. The decoding of the tampered code is, therefore, identical to the original message or it is an invalid string. Due to the property of X, the tampering function ensures that the decoding is \(\perp \) with higher probability when the message is \(s_0\).
Now consider the following function: \(f(b,r) = Enc(s_b;r)|_{\alpha n}\), i.e. the function which outputs the first \(\alpha n\) bits of the encoding of message \(s_b\) (using randomness r in the encoding procedure). Let y be any string in the domain of \(f(\cdot ,\cdot )\). Suppose B is an oracle which, when queried with y, provides a uniformly reverse sampled pre-image of y. Then we make t calls to B to create a set \(S_y=\{(b_1,r_1), \cdots ,(b_t,r_t)\}\). Counting the number of occurrences of \(b=0\) in \(S_y\) we can test whether \(y\in X\) or not; when t is sufficiently large we have \(y\in X\) implies \(\mathsf {maj} \{b_1,\cdots ,b_t\}=0\) w.h.p. (by Chernoff bounds). Given access to the oracle B, we can emulate the tampering function which performs the tampering of [10] (except with \(\mathsf {negl} (n)\) error).
Now, consider a setting where distributionally one-way functions do not exist. In this case, for \(f(\cdot ,\cdot )\) and suitably large \(p(\cdot )\) (as a function of t), there exists an efficient inverter A which can simulate every call of B, except with error (at most) 1 / p(n). Now, we can replace calls to algorithm B in the previous paragraph, with calls to A while incurring an error of at most t(n) / p(n). By suitably choosing t(n) and p(n), we can construct an efficient tampering on the first \(\alpha n\) bits of the encoding which emulates the tampering of [10] with error t(n) / p(n).
1.2 Prior Work
Cramer et al. [14] introduced the notion of arithmetic manipulation detection (AMD) codes, which is a special case of non-malleable codes against tampering functions with a simple algebraic structure; explicit AMD codes with optimal (second order) parameters have been recently provided by [15]. Dziembowski et al. motivated and formalized the more general notion of non-malleable codes in [18]. They showed existence of a constant rate non-malleable code against the class of all bit-wise independent tampering functions (which are essentially multi-state codes with a large, non-constant, value of k).
The existence of rate-1 non-malleable codes against various classes of tampering functions is now known. For example, existence of such codes with rate \((1-\alpha )\) was shown against any tampering function family of size \(2^{2^{\alpha n}}\); but this scheme has inefficient encoding and decoding [10]. For tampering functions of size \(2^{\mathrm {poly} (n)}\), rate-1 codes (with efficient encoding and decoding) exist, and can be obtained efficiently with overwhelming probability [20].
Very recently, an explicit rate-0 code against a more powerful class of tampering functions, which in addition to tampering with each bit of the codeword independently can also permute the bits of the resulting codeword after tampering, was achieved in [4]. This was further improved to rate 1 by [5].
In the “split state” setting where the codeword is partitioned into k separate blocks and each block can be tampered arbitrarily but independently, an encoding scheme was proposed in [12]. For the case of only two states, an explicit non-malleable code for encoding a single bit was proposed by [17]. Recently, in a break-through result, an explicit scheme (of rate 0) was proposed for arbitrary length messages by [3]. A constant rate construction for 10 states was provided in [9] (and later in [3]). Very recently, Aggarwal et al. [2] show that constant rate for such codes can in fact be achieved with only \(k=2\) states. We note that in this setting it is not possible to go beyond rate 1/2 if one insists upon information theoretic non-malleability. Our present work shows that by relying on computational definition of non-malleability, we can achieve rate 1 with only 2 states (which are necessary). Asymptotically, these are the best possible parameters.
In the computational setting, there has been a sequence of works on improving the rate of error-correcting codes [8, 22, 23, 27, 29, 30] as well as constructing non-malleable codes and its variants [19, 28]. We also note that for the case of bit-wise tampering functions, a hybrid approach was suggested in [18] by relying on authenticated encryption. It is not clear if this approach works for a general class of functions. Chandran et al. [7] also rely on the computational setting in defining their new notion of blockwise non-malleable codes. Blockwise non-malleable codes are a generalization of the split-state model (and the recent lookahead model of [2]) where the adversary tampers with one state at a time.
Non-malleable codes have found interesting cryptographic applications like domain extension of self-destruct CCA-secure public-key encryption [13] and non-malleable commitments [4].
2 Preliminaries
Notation. We denote the security parameter by \({\lambda } \). Probability distributions are represented by capital letters. Given a distribution X, \(x\sim X\) represents that x is sampled according to the distribution X. For a function \(f(\cdot )\), the random variable \(Y=f(X)\) represents the following distribution: sample \(x\sim X\) and output f(x).
For a randomized algorithm A, we write A(z) to denote the distribution of the output of A on an input z. A function \(f: {\mathbb N} \rightarrow {\mathbb R} ^+\) is negligible if for every positive polynomial \(\mathsf {poly} (\cdot )\) and all sufficiently large n, \(f(n) \leqslant 1/\mathsf {poly} (n)\). We use \(\mathsf {negl} (M)\) to denote an (unspecified) negligible function in M. Lastly, all logarithms in this paper are to the base 2.
For two variables \(X,X'\) their statistical distance is \(\varDelta (X;X')=\tfrac{1}{2}\sum _x |\Pr [X=x]-\Pr [X'=x]|\).
The min-entropy of a distribution is \(\mathbf {H}_\infty (D) = \min _x \log (D[x]^{-1})\). For a finite set S, we denote by \(U_S\) the uniform distribution over S. Note that \(\mathbf {H}_\infty (U_S) = \log |S|\). Moreover, if X is a distribution with min-entropy k then X is a convex combination of distributions uniform over sets of size \(2^k\).
Let E be an event. We denote by X|E the conditional random variable, conditioned on E holding. For a set S we shorthand \(X|_S= X|[X \in S]\).
2.1 Non-malleable Codes in the Split-State Model
In this section, we give a stronger definition of non-malleable codes in the split-state model (than what is considered in literature [2, 3, 18]). We call these augmented non-malleable codes, denoted my Aug-NMC. We define Aug-NMC both in the information theoretic setting as well as computational setting.
Let \({\lambda } \) be the security parameter. Let \(N_1({\lambda })\) and \(N_2({\lambda })\) be some fixed polynomials in \({\lambda } \). These will denote the size of the states in the split state setting. We begin by defining the real tampering and ideal simulation experiments against any generic tampering class \({\mathcal F} \) in Fig. 1. We also define the advantage between the real and simulated experiments w.r.t. a class of distinguishers \({\mathcal D} \) in Fig. 1.
Let \({\mathcal D} _\mathsf {all} \) and \({{\mathcal F}}_\mathsf {all} \) denote the class of all distinguishers and all split-state tampering functions, respectively, as in Fig. 1. Similarly, let \({\mathcal D} _\mathsf {eff} \) and \({\mathcal F} _\mathsf {eff} \) denote the class of efficient distinguishers and efficient split-state tampering functions, respectively, as in Fig. 1. That is, there exists polynomials p, q such that for all \({\lambda } \in {\mathbb N} \), the running time of \(f_{\lambda }, g_{\lambda } \) is at most \(p({\lambda })\) and running time of all \(D \in {\mathcal D} _{\mathsf {eff},{\lambda }}\) is at most \(q({\lambda })\). Next, we define \({\textsf {Aug-NMC}} \) w.r.t. experiments defined in Fig. 1.
Definition 1
(Standard \([(N_1,N_2), M, \nu ]\) -Aug-NMC ). Suppose \(\mathsf {Enc}: \{0,1\}^{M} \rightarrow \{0,1\}^{N_1} \times {\{0,1\}} ^{N_2}\) and \(\mathsf {Dec}: \{0,1\}^{N_1} \times {\{0,1\}} ^{N_2} \rightarrow {\{0,1\}} ^M\cup \{\bot \}\) are (possibly randomized) mappings. Then \((\mathsf {Enc},\mathsf {Dec})\) is a (standard) \([(N_1,N_2), M, \nu ]\)-Aug-NMC if the following conditions hold:
-
\(\circ \) Correctness: \(\forall s \in {\{0,1\}} ^M\), \(\mathop {\mathrm {Pr}} [\mathsf {Dec} (\mathsf {Enc} (s))=s ]=1\).
-
\(\circ \) Non-Malleability: \(\mathsf {adv} ^{\mathsf {Enc},\mathsf {Dec}}_{{{\mathcal F}}_\mathsf {all},{\mathcal D} _\mathsf {all}} \leqslant \nu ({\lambda })\). (See Fig. 1 for description.)
We say that the coding scheme is efficient if (\(\mathsf {Enc}\),\(\mathsf {Dec}\)) run in time bounded by a polynomial in \(M\) and \({\lambda } \).
Definition 2
(Computational \([(N_1,N_2), M, \nu ]\) -Aug-NMC ). Suppose \(\mathsf {Enc}: \{0,1\}^{M}\) \(\rightarrow \{0,1\}^{N_1} \times {\{0,1\}} ^{N_2}\) and \(\mathsf {Dec}: \{0,1\}^{N_1} \times {\{0,1\}} ^{N_2} \rightarrow {\{0,1\}} ^M\cup \{\bot \}\) are (possibly randomized) mappings. Then \((\mathsf {Enc},\mathsf {Dec})\) is a computational \([(N_1,N_2), M, \nu ]\)-Aug-NMC if the following conditions hold:
-
\(\circ \) Correctness: \(\forall s \in {\{0,1\}} ^M\), \(\mathop {\mathrm {Pr}} [\mathsf {Dec} (\mathsf {Enc} (s))=s ]=1\).
-
\(\circ \) Non-Malleability: \(\mathsf {adv} ^{\mathsf {Enc},\mathsf {Dec}}_{{\mathcal F} _\mathsf {eff},{\mathcal D} _\mathsf {eff}} \leqslant \nu ({\lambda })\). (See Fig. 1 for description.)
We say that the coding scheme is efficient if (\(\mathsf {Enc}\),\(\mathsf {Dec}\)) run in time bounded by a polynomial in \(M\) and \({\lambda } \).
Remark 1
Note that the only difference between the two definitions is the class of tampering functions and class of distinguishers.
Remark 2
Note that the notion of non-malleable codes considered in literature is implied by our notion of Aug-NMC. In the original notion, the tampering and simulated experiments only output the result of decoding the tampered codeword (without outputting one of the original states).
2.2 Building Blocks
Our construction will build upon two ingredients. We describe these next.
Authenticated Encryption. We describe the notion of a secret key authenticated encryption scheme \((\mathsf {AEnc}, \mathsf {ADec})\). Later we will describe how such a scheme can be constructed using a secret key encryption scheme and a message authentication code, both of which can be based on one-way functions. Let \({\mathcal K} _{\lambda } \), \({\mathcal M} _{\lambda } \) and \({\mathcal C} _{\lambda } \) denote the key, message, and ciphertext space for the authenticated encryption scheme, respectively. The scheme should satisfy the following properties. In each of the following the probability is over the randomness of \(\mathsf {AEnc}, \mathsf {ADec} \) and coins of the adversary.
-
1.
Perfect Correctness: For every \(k \in {\mathcal K} _{\lambda } \), \(m \in {\mathcal M} _{\lambda } \), \(\mathop {\mathrm {Pr}} [\mathsf {ADec} (k,(\mathsf {AEnc} (k,m)) = m] = 1\).
-
2.
Semantic Security: For all PPT adversaries \({\mathcal A} \), for all messages \(m,m' \in {\mathcal M} _{\lambda } \), over a random choice of
 , \(\{\mathsf {AEnc} (k, m)\} \approx _c \{\mathsf {AEnc} (k,m')\}\).
, \(\{\mathsf {AEnc} (k, m)\} \approx _c \{\mathsf {AEnc} (k,m')\}\). -
3.
Unforgeability: For every PPT adversary \({\mathcal A} = ({\mathcal A} _1, {\mathcal A} _2)\),

We call the above authenticated encryption scheme an \([M, K, C]\) scheme if \({\mathcal M} = {\{0,1\}} ^M\), \({\mathcal K} \subseteq {\{0,1\}} ^K\) and \({\mathcal C} \subseteq {\{0,1\}} ^C\).
The scheme described above can be instantiated as follows: Let \((\mathsf {Encrypt}, \mathsf {Decrypt})\) be a semantically-secure secret key encryption scheme with perfect correctness. Let \({\mathcal K} ^{^{{\left( 1\right) }}}_{\lambda }, {\mathcal M} ^{^{{\left( 1\right) }}}_{\lambda }, {\mathcal C} ^{^{{\left( 1\right) }}}_{\lambda } \) be the key, message and ciphertext space, respectively, for the encryption scheme. Let \((\mathsf {Tag}, \mathsf {Verify})\) be a message authentication scheme satisfying perfect correctness and unforgeability. Let \({\mathcal K} ^{^{{\left( 2\right) }}}_{\lambda } \), \({\mathcal M} ^{^{{\left( 2\right) }}}_{\lambda } = {\mathcal C} ^{^{{\left( 1\right) }}}_{\lambda } \) and \({\mathcal T} ^{^{{\left( 2\right) }}}_{\lambda } \) be the key, message and tag space, respectively. Then we can define an authenticated encryption naturally as follows: The key space will be \({\mathcal K} _{\lambda } = {\mathcal K} ^{^{{\left( 1\right) }}}_{\lambda } \times {\mathcal K} ^{^{{\left( 2\right) }}}_{\lambda } \), message space is \({\mathcal M} _{\lambda } = {\mathcal M} ^{^{{\left( 1\right) }}}_{\lambda } \) and the ciphertext space is \({\mathcal C} _{\lambda } = {\mathcal C} ^{^{{\left( 1\right) }}}_{\lambda } \times {\mathcal T} ^{^{{\left( 2\right) }}}_{\lambda } \). For a key  , and \(m \in {\mathcal M} _{\lambda } \), \(\mathsf {AEnc} (k,m) = (c_1, c_2)\) such that \(c_1 \sim \mathsf {Encrypt} (k_1, m)\) and \(c_2 \sim \mathsf {Tag} (k_2, c_1)\).
, and \(m \in {\mathcal M} _{\lambda } \), \(\mathsf {AEnc} (k,m) = (c_1, c_2)\) such that \(c_1 \sim \mathsf {Encrypt} (k_1, m)\) and \(c_2 \sim \mathsf {Tag} (k_2, c_1)\).
It is easy to see that the described authenticated encryption scheme will satisfy the three desired properties. Moreover, such a scheme can be designed assuming only one-way functions. We describe one such construction in our proof of Corollary 1.
\([(N_1,N_2),M,\nu ]\) -Aug-NMC with \(\mathbf{1/}{{\varvec{poly}}}\) rate Based on [3] we prove the following theorem.
Theorem 1
There exists a fixed polynomial p, such that for all \(M\in {\mathbb N} \), there exists an efficient \([(N_1,N_2), M,\nu ]\)-Aug-NMC \((\mathsf {Enc} ^+, \mathsf {Dec} ^+)\) for the message space \({\{0,1\}} ^M\) satisfying Definiion 1 such that \(N_1+N_2\leqslant p(M,{\lambda })\) and \(\nu ({\lambda }) = \mathsf {exp} (-{\lambda })\).
For the proof of the above theorem, refer to Sect. 4.
3 Our Construction
In this section, we give a construction for rate-1 computational non-malleable codes in the split-state model and prove the following theorem.
Theorem 2
Suppose there exists an \([M, K,C]\) authenticated encryption scheme and a standard or computational \([(N_1', N_2'),K,\nu ']\)-Aug-NMC satisfying Theorem 1. Then there exists a computational \([(N_1,N_2), M,\nu ]\)-Aug-NMC such that \(N_1+N_2= N_1'+ (N_2'+ C)\) and \(\nu = \mathsf {negl} ({\lambda })\).
Before we describe our construction, here is a corollary of the above theorem, which is our main result.
Corollary 1
Assuming the existence of one-way functions, there exists a computational \([(N_1,N_2),M,\nu ]\)-Aug-NMC such that \(N_1+N_2= M+ \mathsf {poly} ({\lambda })\).
Proof
The corollary can be obtained from Theorem 2 by using an \([M, K,C]\) authenticated scheme where \(K= 2{\lambda } \) and \(C= M+ \mathsf {poly} ({\lambda })\). Consider \(M= q({\lambda })\) for a fixed polynomial q. Consider a polynomial stretch PRG \(G: {\{0,1\}} ^{\lambda } \rightarrow {\{0,1\}} ^M\) and a pseudorandom function \(\mathsf {PRF}: {\{0,1\}} ^{\lambda } \times {\{0,1\}} ^M\rightarrow {\{0,1\}} ^{\lambda } \). Then the authenticated encryption scheme is as follows: \({\mathcal K} = {\{0,1\}} ^{2{\lambda }}\) and \({\mathcal C} = {\{0,1\}} ^{M+ {\lambda }}\). For a key \((k_1, k_2) \in {\{0,1\}} ^{2{\lambda }}\), \(\mathsf {AEnc} ((k_1, k_2), m) = (c_1, c_2)\) such that \(c_1 = G(k_1)\oplus m\) and \(c_2 = \mathsf {PRF} (k_2, c_1)\). It can be seen that this is a valid authenticated encryption scheme.
Using this scheme in Theorem 2, we get that \(N_1'+ N_2'= p(2{\lambda })\) and \(N_1+N_2= p(2{\lambda }) + (M+ {\lambda }) = M+ r({\lambda })\), where r is some fixed polynomial in \({\lambda } \). The scheme is rate-1 if q is an asymptotically faster growing polynomial than r.
Construction. Let \({\lambda } \) be the security parameter and \({\mathcal M} _{\lambda } = {\{0,1\}} ^M\) be the message space. Let \((\mathsf {AEnc},\mathsf {ADec})\) be an authenticated encryption scheme for message space \({\mathcal M} _{\lambda } \) with key space \({\mathcal K} _{\lambda } \subseteq {\{0,1\}} ^K\) and ciphertext space \({\mathcal C} _{\lambda } \subseteq {\{0,1\}} ^C\). Let \((\mathsf {Enc} ^+,\mathsf {Dec} ^+)\) be a \([(N_1',N_2'),K,\nu ']\) augmented non-malleable encoding scheme for message space \({\{0,1\}} ^K\) guaranteed by Theorem 1. Given these two ingredients, our scheme is as follows.
To encode a message \(s \in {\{0,1\}} ^M\), sample a key k for authenticated encryption scheme and encode it using \(\mathsf {Enc} ^+\) as \((\ell ,r)\). Next, encrypt the message \(s \) using \(\mathsf {AEnc} \) under key k, i.e. \(c\sim \mathsf {AEnc} (k,s)\). Now, the encodings in two states are \(L= \ell \) and \(R= (r,c)\). The decoding function is natural, which first uses \(\mathsf {Dec} ^+(\ell ,r)\) to obtain a key k, which is used to decrypt the ciphertext \(c\) using \(\mathsf {ADec} \).
A formal description of the scheme is provided in Fig. 2.
It is easy to see that the scheme is perfectly correct if the underlying authenticated encryption and augmented non-malleable codes are perfectly correct. In the next section, we prove its non-malleability.
3.1 Proof of Non-malleability
In this section, we prove that the construction in Fig. 2 is a \([(N_1,N_2), M, \nu ]\) computational non-malleable code such that \(\nu = \mathsf {negl} ({\lambda })\) against the tampering functions \({\mathcal F} _\mathsf {eff} ^{(N_1,N_2)}\) according to Definition 2.
We begin by describing our simulator \(\mathsf {Sim} \) required by the definition and then argue via a sequence of hybrids that for any \(s \in {\{0,1\}} ^M\) and any \((F,G) \in {\mathcal F} _\mathsf {eff} \), for any efficient distinguisher \(D \in {\mathcal D} _\mathsf {eff} \),
The simulator \(\mathsf {Sim} \) is defined formally in Fig. 3. At a high level, \(\mathsf {Sim} \) does the following: It samples a key  and generates a ciphertext for message \(0^M\), i.e., \(c= \mathsf {AEnc} (k,0^M)\). It defines a new tampering function \(g_c\) for the underlying augmented non-malleable code by hard-coding the value of \(c\) in tampering function G. Next, it runs the simulator \(\mathsf {Sim} ^{+}(F, g_c)\) to get \((r,\mathsf {ans})\). Then, it computes \(\tilde{R} = G(r, c) = (\tilde{r}, \tilde{c})\). Finally, if \(\mathsf {ans} = \mathsf {same} ^{*} \) and \(\tilde{c} = c\), it outputs \(\mathsf {same} ^{*} \). Else, if \(\mathsf {ans} = k^*\), it outputs \(\mathsf {ADec} (k^*,\tilde{c})\). Otherwise, it outputs \(\bot \).
and generates a ciphertext for message \(0^M\), i.e., \(c= \mathsf {AEnc} (k,0^M)\). It defines a new tampering function \(g_c\) for the underlying augmented non-malleable code by hard-coding the value of \(c\) in tampering function G. Next, it runs the simulator \(\mathsf {Sim} ^{+}(F, g_c)\) to get \((r,\mathsf {ans})\). Then, it computes \(\tilde{R} = G(r, c) = (\tilde{r}, \tilde{c})\). Finally, if \(\mathsf {ans} = \mathsf {same} ^{*} \) and \(\tilde{c} = c\), it outputs \(\mathsf {same} ^{*} \). Else, if \(\mathsf {ans} = k^*\), it outputs \(\mathsf {ADec} (k^*,\tilde{c})\). Otherwise, it outputs \(\bot \).
For ease of description of hybrids, below we first describe \(\mathsf {Hyb} _{0}\) which is same as \(\mathsf {Tamper} _{F,G}^{{\left( s \right) }} \).
\(\mathsf {Hyb} _{0}\): This is same as \(\mathsf {Tamper} _{F,G}^{{\left( s \right) }} \), where we also open up the description of \(\mathsf {Enc} \) and \(\mathsf {Dec} \).
-
1.
Sample
 .
. -
2.
Sample \(c\sim \mathsf {AEnc} (k,s)\).
-
3.
Sample \((\ell ,r) \sim \mathsf {Enc} ^+(k)\).
-
4.
Define \(L= \ell \) and \(R= (r,c)\).
-
5.
Define tampered codeword as:
 and
and  .
. -
6.
Let \(\tilde{k} = \mathsf {Dec} ^+(\tilde{L},\tilde{r})\).
-
7.
If \(\tilde{k} = \bot \), output \(((r,c),\bot )\). Else, output \(((r,c),\mathsf {ADec} (\tilde{k},\tilde{c}))\).
\(\mathsf {Hyb} _{1}\): This hybrid is just a re-write of the previous experiment using \(\mathsf {Tamper} ^{+}(F,g_c,k)\). Hence, the outputs of the two experiments are identical.
-
1.
Sample
 .
. -
2.
Sample \(c\sim \mathsf {AEnc} (k,s)\).
-
3.
Define a function \(g_c: {\{0,1\}} ^{N_2'} \rightarrow {\{0,1\}} ^{N_2'}\) such that \(g_c(x) = \tilde{x}\) if \(G(x,c) = (\tilde{x}, \tilde{c})\).
-
4.
Define \((r,\tilde{k}) \sim \mathsf {Tamper} ^{+}(F,g_c,k)\).
-
5.
Define \((\tilde{r},\tilde{c}) = G(r, c)\).
-
6.
If \(\tilde{k} = \bot \), output \(((r,c),\bot )\). Else, output \(((r,c),\mathsf {ADec} (\tilde{k},\tilde{c}))\).
\(\mathsf {Hyb} _{2}\): In this hybrid, we use \(\mathsf {Copy} _{\mathsf {Sim} ^{+}(F,g_c)}^{{\left( k\right) }} \) instead of \(\mathsf {Tamper} _{F,G}^{{\left( s \right) }} \). The two hybrids are statistically close by Theorem 1.
-
1.
Sample
 .
. -
2.
Sample \(c\sim \mathsf {AEnc} (k,s)\).
-
3.
Define a function \(g_c: {\{0,1\}} ^{N_2'} \rightarrow {\{0,1\}} ^{N_2'}\) such that \(g_c(x) = \tilde{x}\) if \(G(x,c) = (\tilde{x}, \tilde{c})\).
-
4.
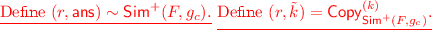
-
5.
Define \((\tilde{r},\tilde{c}) = G(r, c)\).
-
6.
If \(\tilde{k} = \bot \), output \(((r,c),\bot )\). Else, output \(((r,c),\mathsf {ADec} (\tilde{k},\tilde{c}))\).
\(\mathsf {Hyb} _{3}\): In this hybrid, we change last step of how we compute the output for the case when \(\mathsf {ans} = \mathsf {same} ^{*} \).
-
1.
Sample
 .
. -
2.
Sample \(c\sim \mathsf {AEnc} (k,s)\).
-
3.
Define a function \(g_c: {\{0,1\}} ^{N_2'} \rightarrow {\{0,1\}} ^{N_2'}\) such that \(g_c(x) = \tilde{x}\) if \(G(x,c) = (\tilde{x}, \tilde{c})\).
-
4.
Define \((r,\mathsf {ans}) \sim \mathsf {Sim} ^{+}(F,g_c)\).
-
5.
Define \((\tilde{r},\tilde{c}) = G(r, c)\).
-
6.
We have the following cases for \(\mathsf {ans} \):
-
\(\circ \) Case(a) \(\mathsf {ans} = \bot \), output \(((r,c),\bot )\).
-
\(\circ \)

-
\(\circ \) Case(c) \(\mathsf {ans} = k^*\), output \(((r,c),\mathsf {ADec} (k^*, \tilde{c}))\).
-
First note that the cases (a) and (c) are identical in \(\mathsf {Hyb} _{2}\) and \(\mathsf {Hyb} _{3}\). By the unforgeability property of authenticated encryption scheme, case(b) in \(\mathsf {Hyb} _{3}\) is close to \(\mathsf {Hyb} _{2}\) for all efficient tampering functions.
\(\mathsf {Hyb} _{4}\): In this hybrid, we change how we compute the ciphertext \(c\). Instead of computing an encryption of \(s \), we start computing encryption of \(0^M\).
-
1.
Sample
 .
. -
2.

-
3.
Define a function \(g_c: {\{0,1\}} ^{N_2'} \rightarrow {\{0,1\}} ^{N_2'}\) such that \(g_c(x) = \tilde{x}\) if \(G(x,c) = (\tilde{x}, \tilde{c})\).
-
4.
Define \((r,\mathsf {ans}) \sim \mathsf {Sim} ^{+}(F,g_c)\).
-
5.
Define \((\tilde{r},\tilde{c}) = G(r, c)\).
-
6.
We have the following cases for \(\mathsf {ans} \):
-
\(\circ \) Case(a) \(\mathsf {ans} = \bot \), output \(((r,c),\bot )\).
-
\(\circ \) Case(b) \(\mathsf {ans} = \mathsf {same} ^{*} \): If \(\tilde{c} = c\), output \(((r,c),s)\). Else, output \(((r,c),\bot )\).
-
\(\circ \) Case(c) \(\mathsf {ans} = k^*\), output \(((r,c),\mathsf {ADec} (k^*, \tilde{c}))\).
-
By semantic security of the authenticated encryption scheme, hybrid \(\mathsf {Hyb} _{3}\) is computationally close to \(\mathsf {Hyb} _{4}\).
Finally, note that \(\mathsf {Hyb} _{4}\) is identical to \(\mathsf {Copy} _{\mathsf {Sim} ^{+}(F,G)}^{{\left( s \right) }} \), where \(\mathsf {Sim} \) is the simulator described in Fig. 3.
4 Proof of Theorem 1
For proving Theorem 1, we will need the following which is a stronger version of Theorem 3 from [3]. In particular, the proof structure of our result is similar.
Let \(\mathbb {F}_p\) be a finite field of prime order. Let L be uniform in \(\mathbb {F}_p^n\) and let \(r \in \mathbb {F}_p^n\). Let \(f,g:\mathbb {F}_p^n \rightarrow \mathbb {F}_p^n\) be a pair of functions. We consider the following family of distributions
Theorem 3
There exists absolute constants \(c, c' >0\) such that the following holds. For any finite field \(\mathbb {F}_p\) of prime order, and any \(n > c' \log ^6 p\), let \(L \in \mathbb {F}_p^n\) be uniform, and fix \(f,g:\mathbb {F}_p^n \rightarrow \mathbb {F}_p^n\). Then there exists a set \({\mathcal R} \subset \mathbb {F}_p^n\) of cardinality at least \(p^n \cdot (1-2^{-c n^{1/6}})\) such that for all \(r \in {\mathcal R} \), there exist random variables \(A, B\in \mathbb {F}_p\), and U uniform in \(\mathbb {F}_p\) and independent of A, B such that
To prove Theorem 3, we will need the following results from [3].
Claim
Let \(X=(X_1,X_2) \in \mathbb {F}_p\times \mathbb {F}_p\) be a random variable. Assume that for all \(a,b \in \mathbb {F}_p\) not both zero, \(\varDelta (aX_1+bX_2 \ ; \ U_{\mathbb {F}_p}) \leqslant \varepsilon \). Then \(\varDelta ((X_1,X_2) \ ; \ U_{\mathbb {F}_p^2}) \leqslant \varepsilon p^2\).
Claim
Let \(X \in \mathbb {F}_p\) be a random variable. Assume that \(\varDelta (X \ ; \ U_{\mathbb {F}_p}) \geqslant \varepsilon \). Then if \(X'\) is an independent and i.i.d copy of X then
The following is a reformulation of the statement that the inner-product is a strong two-source extractor.
Lemma 1
Let L be a random variable over \(\mathbb {F}_p^n\), and let \(\varepsilon >0\). Then the number of \(r \in \mathbb {F}_p^n\) such that \(\varDelta (\langle L,r \rangle \; ; \; U_{\mathbb {F}_p}) > \varepsilon \) is at most \(\frac{p^{n+1}}{2^{\mathbf {H}_\infty (L)} \cdot \varepsilon ^2}\).
We now prove Theorem 3. Let us fix functions \(f,g:\mathbb {F}_p^n \rightarrow \mathbb {F}_p^n\) and shorthand \(\varphi (L,r)=\varphi _{f,g}(L,r)\). We will use the following notation: for set \({\mathcal P} \subset \mathbb {F}_p^n\) let \(\varphi (L,r)|_{{\mathcal P}}\) denote the conditional distribution of \(\varphi (L,r)\) conditioned on \(L \in {\mathcal P} \). Equivalently, it is the distribution of \(\varphi (L,r)\) for uniformly chosen \(L \in {\mathcal P} \).
The following is a reformulation of Lemma 5 from [3].
Lemma 2
Let U be uniformly random in \(\mathbb {F}_p\). Let \({\mathcal P} \subseteq \mathbb {F}_p^n\), and let \(r \in \mathbb {F}_p^n\). Let \({\mathcal P} _1,\ldots ,{\mathcal P} _k\) be a partition of \({\mathcal P} \). Assume that for all \(1 \leqslant i \leqslant k\) there exist random variables \(A_i, B_i \in \mathbb {F}_p\) independent of U such that,
Then there exist random variables \(A, B \in \mathbb {F}_p\) independent of U such that
Let \(s = \lfloor \frac{n}{10}\rfloor \), and \(t = \lfloor \frac{s^{1/6}}{c_1 \log p} \rfloor \), where \(c_1\) is some constant that will be chosen later. Note that \(s \gg t\). We choose the constant \(c'\) in the statement of Theorem 3 such that \(t\geqslant 3\).
We call \(r \in \mathbb {F}_p^n\) \(({\mathcal P},\alpha )\)-bad if for every pair of random variables \(A, B\in \mathbb {F}_p\), and U uniform in \(\mathbb {F}_p\) and independent of A, B
We consider a partition of \(\mathbb {F}_p^n\) based on g to elements whose output is too popular; and the rest. For \(y \in \mathbb {F}_p^n\) let \(g^{-1}(y)=\{x \in \mathbb {F}_p^n: g(x)=y\}\) be the set of pre-images of y. Define
and set \({\mathcal R} _1 := \mathbb {F}_p^n \setminus {\mathcal R} _0\).
g is close to a constant. We now bound the number of \(r \in {\mathcal R} _0\) such that there \(\varphi (L, r)\) is not close to affine.
Lemma 3
The number of \(r \in {\mathcal R} _0\) that are \((\mathbb {F}_p^n, p^{-t/4})\)-bad is at most \(p^{-t/3} \cdot |{\mathcal R} _0|\).
Proof
Let \(Y = \{y \in \mathbb {F}_p^n: |g^{-1}(y)| \geqslant p^t\}\). We can decompose \({\mathcal R} _0\) as the disjoint union over \(y \in Y\) of \(g^{-1}(y)\). Fix such a \(y \in Y\) and let \({\mathcal R} ^\star =\{r \in \mathbb {F}_p^n : g(r)=y\}\). Since the min-entropy of L conditioned on \(\langle f(L), y \rangle \) is at least \((n-1) \log p\), using Lemma 1, we have that for all but at most \(p^{t/2+2}\) different \(r \in {\mathcal R} ^\star \)
Thus the total number of \(p^{-t/4}\)-bad \(r \in {\mathcal R} _0\) is at most \(p^{t/2 + 2} \cdot |Y|\) which is upper bounded by \(p^{t/2 + 2} \cdot |{\mathcal R} _0| \cdot p^{-t} \leqslant p^{-t/3} \cdot |{\mathcal R} _0|\).
f is close to linear. We now define a partition \({\mathcal L} _1,\ldots ,{\mathcal L} _a\) of \(\mathbb {F}_p^n\) based on f. Intuitively, \({\mathcal L} _i\) for \(1 \leqslant i<a\) will correspond to inputs on which f agrees with a popular linear function; and \({\mathcal L} _a\) will be the remaining elements.
We define \({\mathcal L} _1,\ldots ,{\mathcal L} _a\) iteratively. For \(i \geqslant 1\), given \({\mathcal L} _1,\ldots ,{\mathcal L} _{i-1}\), if there exists a linear map \(A_i:\mathbb {F}_p^n \rightarrow \mathbb {F}_p^n\) for which
then set \({\mathcal L} _i\) to be \(\{x \in \mathbb {F}_p^n: f(x)=A_i x\} \setminus ({\mathcal L} _1 \cup \ldots \cup {\mathcal L} _{i-1})\). If no such linear map exists, set \(a:=i\), \({\mathcal L} _a := \mathbb {F}_p^n \setminus ({\mathcal L} _0 \cup \ldots \cup {\mathcal L} _{a-1})\) and complete the process. Note we obtained a partition \({\mathcal L} _1,\ldots ,{\mathcal L} _a\) of \(\mathbb {F}_p^n\) with \(a \leqslant p^s+1\).
Lemma 4
Fix \(1 \leqslant i < a\). The number of \(r \in {\mathcal R} _1\) that are \(({\mathcal L} _i, p^{-s})\)-bad is at most \(p^{7s}\).
Proof
Let \({\mathcal R} ^\star \) be the set of all \(r \in {\mathcal R} _1\) such that \((\langle L',r \rangle , \langle f(L'),g(r) \rangle )\) is \(p^{-s}\)-close to \(U_{\mathbb {F}_p^2}\). Clearly, no \(r \in {\mathcal R} ^\star \) is \(({\mathcal L} _i, p^{-s})\)-bad.
Let \(L'\) be uniform in \({\mathcal L} _i\). Note that for any \(r \in {\mathcal R} _1 \setminus {\mathcal R} ^\star \),
If \((\langle L',r \rangle , \langle f(L'),g(r) \rangle )\) is not \(p^{-s}\)-close to \(U_{\mathbb {F}_p^2}\) then by Claim 4 there exist \(a,b \in \mathbb {F}_p\), not both zero, such that
Now, by assumption, \(L'\) is uniform over a set of size at least \(p^{n-s}\). By Lemma 1, this implies that \(a r + b A^T g(r)\) can take at most \(p^{3s + 4}\) different values. Let \(Y_{a,b} \in \mathbb {F}_p^n\) be the set of distinct values taken by \(a r + b A^T g(r)\).
Fix a, b and \(y \in Y_{a,b}\) and let \({\mathcal R} ' \subset {\mathcal R} _1 \setminus {\mathcal R} ^\star \) be such that
We will upper bound the number of \(r \in {\mathcal R} '\) that are \(({\mathcal L} _i, p^{-s})\)-bad. If \(b=0\), then clearly \(|{\mathcal R} '| = 1\). If \(b \ne 0\), we can rewrite (and rename the constants for convenience) as
We know that for any \(r \in {\mathcal R} '\), \(\langle f(L'),g(r) \rangle =\langle L',A^T g(r) \rangle = a_1 \langle L',r \rangle + \langle L',y_1 \rangle \).
We know that the min-entropy of \(L'\) given \(\langle L',y_1 \rangle \) is at least \((n-s-1) \log p\). Thus, by Lemma 1, the number of \(r \in {\mathcal R} '\) that are \(({\mathcal L} _i, p^{-s})\)-bad is at most \(p^{3s+2}\).
Enumerating over various possible values of a, b, y, we get that the number of \(r \in {\mathcal R} _1\) that are \(({\mathcal L} _i, p^{-s})\)-bad is at most \(p^{3s+2} \cdot p^{3s + 4} \cdot p^2 \leqslant p^{7s}\).
f is far from linear and g is far from constant. The last partition we need to analyze is \({\mathcal L} _a \times {\mathcal R} _1\), corresponding to the case where f is far from linear and g is far from constant. For this, we need the following result that can be seen as a generalization of the linearity test from [31] that was proved in [3] using results from [6, 21, 32].
Theorem 4
Let p be a prime, and \(n \in \mathbb {N}\). For any \(\varepsilon = \varepsilon (n,p) > 0\), \(\gamma _1 = \gamma _1(n,p) \leqslant 1\), \(\gamma _2 = \gamma _2(n,p) \geqslant 1\), the following is true. For any function \(f: \mathbb {F}_p^n \mapsto \mathbb {F}_p^n\), let \({\mathcal A} \subseteq \{(x, f(x)) \, : \, x \in \mathbb {F}_p^n\} \subseteq \mathbb {F}_p^{2n}\). If \(|{\mathcal A} | \geqslant \gamma _1 \cdot |\mathbb {F}_p^n|\) and there exists some set \({\mathcal B} \) such that \(|{\mathcal B} | \leqslant \gamma _2 \cdot p^n\), and
then there exists a linear map \(M:\mathbb {F}_p^n \rightarrow \mathbb {F}_p^n\) such that
We will now show that, \(\varphi (L,r)|_{{\mathcal L} _a}\) is close to uniform over \(\mathbb {F}_p\times \mathbb {F}_p\) for most \(r \in {\mathcal R} _1\).
Lemma 5
If \(|{\mathcal L} _a| \geqslant p^{n-t}\) then the number of \(r \in {\mathcal R} _1\) that are \(({\mathcal L} _a, p^{-t})\)-bad is at most \(p^{n-t}\).
Proof
Let \(L' \in {\mathcal L} _a\) be uniform. Let \({\mathcal R} '\) be the set of \(r \in {\mathcal R} _1\) such that \(\varphi (L',r)\) is not \(p^{-t}\)-close to \(U_{\mathbb {F}_p\times \mathbb {F}_p}\). Assume that the cardinality of \({\mathcal R} '\) is more than \(p^{n-t}\), and we will show a contradiction.
For any \(r \in {\mathcal R} '\), by Claim 4 there exist \(a,b \in \mathbb {F}_p\), not both zero, so that \(\varDelta (a\langle L',r \rangle +b\langle f(L'), g(r) \rangle \ ; \ U_{\mathbb {F}_p}) \geqslant p^{-t-2}\). Define functions \(F,G:\mathbb {F}_p^n \rightarrow \mathbb {F}_p^{2n}\) as follows
We have that \(\varDelta (\langle F(L'),G(r) \rangle \ ; \ U_{\mathbb {F}_p}) \geqslant p^{-t-2}\). Applying Claim 4, we get that for \(L''\) i.i.d to \(L'\) we have
This implies that for all \(r \in {\mathcal R} '\)
Let \(R'\) be uniform in \({\mathcal R} '\) and define
Let \(B \in {\mathcal B} \) be uniform. Then \(\varDelta (\langle B, G(R') \rangle , U_{\mathbb {F}_p}) \geqslant \frac{1}{p^{2t+6}}\). Also, since g(y) has at most \(p^t\) preimages for any \(y \in \mathbb {F}_p^n\), \(G(R')\) has min-entropy at least \(\log (|{\mathcal R} '| p^{-t}) \geqslant {(n-2t)} \log p\). Hence, by Lemma 1, we have \(\mathbf {H}_\infty (B) \leqslant (n + 6t + 13)\cdot \log p\), which implies \(|{\mathcal B} | \leqslant p^{n+6t+13}\). Furthermore, we have that
So we must have that
Thus, using Theorem 4, we get that there exists a linear map \(M:\mathbb {F}_p^n \rightarrow \mathbb {F}_p^n\) for which
This violates the definition of \({\mathcal L} _a\) whenever \(s \geqslant C(t^6 \log ^6 p)\) for a big enough constant C Footnote 6.
To conclude the proof of Theorem 3, note that from Lemmas 3, 4 and 5, and applying Lemma 2, we have that apart from \(p^{n-t/3} + p^{7s} \cdot p^{s} + p^{n-t} \leqslant p^{n-t/4}\) different elements in \(\mathbb {F}_p^n\), for every other \(r \in \mathbb {F}_p^n\), there exist random variables \(A, B \in \mathbb {F}_p\), and U uniform in \(\mathbb {F}_p\) and independent of A, B, such that the statistical distance of \(\varphi (L, r)\) and \((U, AU + B)\) is at most
To complete the proof of Theorem 1, we will need the notion of an affine-evasive set modulo p and the following result from [1].
Definition 3
A surjective function \(h: \mathbb {F}_p\mapsto {\mathcal M} \cup \{\bot \}\) is called \((\gamma , \delta )\) -affine-evasive if for any \(a, b \in \mathbb {F}_p\) such that \(a \ne 0\), and \((a,b) \ne (1, 0)\), and for any \(m \in {\mathcal M} \),
-
1.
\(\Pr _{U \leftarrow \mathbb {F}_p}(h(aU + b) \ne \bot ) \leqslant \gamma \)
-
2.
\(\Pr _{U \leftarrow \mathbb {F}_p}(h(aU+b) \ne \bot \; | \; h(U) = m) \leqslant \delta \)
-
3.
A uniformly random X such that \(h(X) = m\) is efficiently samplable.
Lemma 6
([1, Lemma 2]). There exists an efficiently computable \((p^{-3/4}, \varTheta (K \log p \cdot p^{-1/4}))\)-affine-evasive function \(h: \mathbb {F}_p\mapsto {\mathcal M} \cup \{\bot \}\).
Additionally, we will need the following from [3].
Claim
Let \(X_1, X_2, Y_1, Y_2 \in {\mathcal A} \) be random variables such that \(\varDelta ((X_1, X_2) ; (Y_1, Y_2)) \leqslant \varepsilon \). Then, for any non-empty set \({\mathcal A} _1 \subseteq {\mathcal A} \), we have
Proof
(Proof of Theorem 1 ). We construct a \(\nu \)-augmented-non-malleable encoding scheme from \({\mathcal M} = \{1, \ldots , K\}\) to \(\mathbb {F}_p^n \times \mathbb {F}_p^n\), where \(\mathbb {F}_p\) is a finite field of prime order p such that \(p \geqslant (\frac{2K}{\nu })^{8}\), and n chosen as \(\left( \lceil \frac{2 \log p}{c} \rceil \right) ^6\) (i.e., such that \(2^{c n^{1/6}} \geqslant p^2\)), where c is the constant from Theorem 3.
The decoding function \(\mathsf {Dec} ^+: \mathbb {F}_p^n \times \mathbb {F}_p^n \mapsto {\mathcal M} \cup \{\bot \}\) is defined using the affine-evasive function h from Lemma 6 as:
The encoding function is defined as \(\mathsf {Enc} ^+(m) := (L, R)\) where L, R are chosen uniformly at random from \(\mathbb {F}_p^n \times \mathbb {F}_p^n\) conditioned on the fact that \(h(\langle L,R \rangle ) = m\).
We will show that our scheme is \(\nu \)-non-malleable with respect to the family of all functions \((f,g):\mathbb {F}_p^n \times \mathbb {F}_p^n \mapsto \mathbb {F}_p^n \times \mathbb {F}_p^n\), where f and g are functions from \(\mathbb {F}_p^n \mapsto \mathbb {F}_p^n\), and \((f, g)(x, y) = (f(x), g(y))\), for all \(x, y \in \mathbb {F}_p^n\).
Simulator. For any functions \(f, g: \mathbb {F}_p^n \mapsto \mathbb {F}_p^n\), we define the distribution \(D_{f,g}\) over \({\mathcal M} \cup \{\bot , \mathsf {same} ^{*} \}\) as the output of the following sampling procedure:
-
1.
Choose \(L, R \leftarrow \mathbb {F}_p^n\).
-
2.
If \(\langle {f(L)},{g(R)} \rangle = \langle L,R \rangle \), then output \((R,\mathsf {same} ^{*})\), else output \(\left( R,h(\langle {f(L)},{g(R)} \rangle )\right) \).
Note that this distribution is efficiently samplable given oracle access to f and g. The distribution \(D_{f, g}\) can also be expressed as:
where \(m' \in {\mathcal M} \cup \{\bot \}\).
Security Proof. The random variable corresponding to the tampering experiment \(\mathsf {Tamper} ^{+}(f,g,m)\) has the following distribution for all \(m' \in {\mathcal M} \cup \{\bot \}\).
The random variable corresponding to the simulator \(\mathsf {Copy} _{\mathsf {Sim} ^{+}(f,g)}^{{\left( m\right) }} \) has the following distribution for all \(m' \in {\mathcal M} \cup \{\bot \}\).
where E is the event \(\langle {f(L)},{g(r)} \rangle = \langle L,r \rangle \)
From Theorem 3, we get that for all but at most \(p^{n-2}\) different \(r \in \mathbb {F}_p^n\) (call these \({\mathcal R} _{\textsf {bad}}\)), there exists random variables \(A, B \in \mathbb {F}_p\) and U uniform in \(\mathbb {F}_p\) and independent of A, B such that
At the cost of an additional error of at most \(\frac{1}{p^2}\), we assume that \(r \notin {\mathcal R} _{\textsf {bad}}\) for the remainder of the proof.
Using Claim 4 and that \(\varDelta \left( \langle L,r \rangle , \langle f(L),g(r) \rangle \ ; \ U, aU+b\right) \leqslant \frac{1}{p^2}\), we get that
where S and T are defined as follows for all \(m' \in {\mathcal M} \cup \{\bot \}\):
Note that if \((A, B) = (1, 0)\), then for all \(m' \in {\mathcal M} \), \(\Pr (T = (r,m')) = \Pr (S = (r,m'))\). Thus, we have that
where the first inequality uses Lemma 6.
Therefore, using the triangle inequality, and including the error \(\frac{1}{p^2}\) that occurs due to \(r \in {\mathcal R} _{\textsf {bad}}\), we have that
thus completing the proof.
5 Necessity of One-Way Functions
We start by recalling the definition of distributional one-way functions.
Definition 4
(Distributionally One-way Functions [24, 25]). A function \(f:{\{0,1\}} ^*\rightarrow {\{0,1\}} ^*\) is a distributionally one-way function if there exists a positive polynomial \(p(\cdot )\) such that for every probabilistic polynomial-time algorithm A and all sufficiently large n’s we have:
Intuitively, it says that if f is a distributionally one-way function, then there exists an associated (fixed) polynomial \(p(\cdot )\) such that no algorithm can uniformly reverse-sample from the pre-image set on average with at most 1 / p(n) error. It was shown that if one-way functions do not exist, then distributionally one-way functions also do not exist [25]. If distributionally one-way functions do not exist, then for every function f and polynomial \(p(\cdot )\), there exists an algorithm A such that (for large enough n) it can ensure: \(\mathrm {SD}\left( {(U_n,f(U_n))},{(A(1^n,f(U_n)),f(U_n))}\right) < \frac{1}{p(n)}\).
We briefly recall the overview of our result (already presented in Sect. 1.1).
Cheraghchi and Guruswami [10] show the following negative result. Consider the set of tampering functions which depend only on the first \(\alpha n\) bits of the code and tampers it arbitrarily. Then a non-malleable code which protects against this tampering class can have rate at most \(1-\alpha \). In particular, k-split-state non-malleable code can have at most \(1-1/k\) rate. Otherwise, one can use the attack of [10] to show that one can tamper only the first state appropriately to violate the non-malleability condition.
The result in [10] uses the following idea. If the rate is higher than \(1-\alpha \) then there exists two messages \(s_0\) and \(s_1\), and a set \(X \subseteq {\{0,1\}} ^{\alpha n}\) such that the following condition holds: The first \(\alpha n\) bits of encoding of \(s_0\) has higher probability to be in X than for an encoding of \(s_1\). So, the tampering function just writes a dummy string w if the first \(\alpha n\) bits belong in X; otherwise it keeps it intact. The decoding of the tampered code is, therefore, identical to the original message or it is an invalid string. Due to the property of X, the tampering function ensures that the decoding is \(\perp \) with higher probability when the message is \(s_0\).
Now consider the following function: \(f(b,r) = Enc(s_b;r)|_{\alpha n}\), i.e. the function which outputs the first \(\alpha n\) bits of the encoding of message \(s_b\) (using randomness r in the encoding procedure). Let y be any string in the domain of \(f(\cdot ,\cdot )\). Suppose B is an oracle which, when queried with y, provides a uniformly reverse sampled pre-image of y. Then we make t calls to B to create a set \(S_y=\{(b_1,r_1), \cdots ,(b_t,r_t)\}\). Counting the number of occurrences of \(b=0\) in \(S_y\) we can test whether \(y\in X\) or not; when t is sufficiently large we have \(y\in X\) implies \(\mathsf {maj} \{b_1,\cdots ,b_t\}=0\) w.h.p. (by Chernoff bounds). Given access to the oracle B, we can emulate the tampering function which performs the tampering of [10] (except with \(\mathsf {negl} (n)\) error).
Now, consider a setting where distributionally one-way functions do not exist. In this case, for \(f(\cdot ,\cdot )\) and suitably large \(p(\cdot )\) (as a function of t), there exists an efficient inverter A which can simulate every call of B, except with error (at most) 1 / p(n). Now, we can replace calls to algorithm B in the previous paragraph with calls to A while incurring an error of at most t(n) / p(n). By suitably choosing t(n) and p(n), we can construct an efficient tampering on the first \(\alpha n\) bits of the encoding which emulates the tampering of [10] with error t(n) / p(n).
Formally, this proves the following theorem:
Theorem 5
Let \(k\in {\mathbb N} \) and suppose there exists a k-split-state non-malleable code with rate \(\geqslant 1 -(1/k) +\delta (n)\) and simulation error \(\varepsilon (n)\). Then there exists \(\delta _0(n)=\varTheta (\log n/n)\) such that if \(\delta (n)\in [\delta _0(n),1/k]\) and \(\varepsilon (n) < k\delta /96 - n^{-c}\) (for some \(c\geqslant 1\)) then one-way functions exist.
Proof
Suppose one-way functions do not exist, \(\delta (n)\in [\delta _0(n),1/k]\) and \(\varepsilon (n) < k\delta /96 - n^{-c}\). Set \(\eta = k\delta /4\) and \(f(b,r) = Enc(s_b;r)|_{\alpha n}\). Cheraghchi and Guruswami [10] proved that there exists a \(w\in {\{0,1\}} ^{\alpha n}\) such that there is no valid codeword which is consistent with w. Let y be the \(\alpha n\) bits in the encoding. Given y in the image of \(f(\cdot ,\cdot )\), the tampering functions does the following: Consider \(t(n)=n^c\) uniformly sampled pre-images such that their image under \(f(\cdot ,\cdot )\) is y. To reverse sample, set \(p(n)=t(n)^2\) to obtain a corresponding efficient reverse sampler A. Let the obtained samples be \(S_y = \{(b_1,r_1),\cdots ,(b_{t(n)},r_{t(n)})\}\). Let \(n_0\) and \(n_1\) be the, respective, number of samples with \(b_i=0\) and \(b_i=1\). If \(n_0/n_1 \geqslant 3/2 - n^{2/3}\), then write w otherwise leave it untampered.
Cheraghchi and Guruswami [10] show that there exists a set \(X_\eta \subseteq {\{0,1\}} ^{\alpha n}\) and inputs \(s_0\) and \(s_1\) such that
-
1.
\(\mathop {\mathrm {Pr}} [f(0,U)\in X_\eta ] \geqslant \eta \),
-
2.
\(\mathop {\mathrm {Pr}} [f(1,U)\in X_\eta ] \leqslant \eta /2\),
and therefore, there exists a set \(Y_\eta \subseteq X_\eta \) (by pigeon hole principle) such that
-
1.
\(\mathop {\mathrm {Pr}} [f(0,U)\in Y_\eta ] \geqslant (3/2) \cdot \mathop {\mathrm {Pr}} [f(1,U)\in Y_\eta ]\), and
-
2.
\(\mathop {\mathrm {Pr}} [f(0,U)\in Y_\eta ] \geqslant \eta /4\).
Note that \(\mathop {\mathrm {Pr}} [f(0,U)\in Y_\eta ] - \mathop {\mathrm {Pr}} [f(1,U)\in Y_\eta ] \geqslant \eta /12\). Instead of \(X_\eta \), using \(Y_\eta \) in the argument of [10] we get a contradiction because \(\varepsilon (n)\geqslant k\delta /(16\cdot (12/2)) - n^{-c}\). Hence, we get the theorem.
Notes
- 1.
Rate refers to the asymptotic ratio of the length of a message to the length of its encoding (in bits), as the message length increases to infinity. The best rate possible is 1; if the length of the encoding is super-linear in the length of the message, the rate is 0.
- 2.
This is because a non-malleable code has efficient encoding and decoding procedures; an adversary can simply decode the message and encode a related value.
- 3.
We note that in this model, one can even tolerate tampering functions beyond \(\mathrm {P}/\mathrm {poly}\). This is the so called “information theoretic” setting.
- 4.
Sometimes, the setting where \(k=2\) is commonly referred to as the split state setting; and when \(k>2\) it is explicitly mentioned and often called multiple split state setting.
- 5.
This is precisely defined by requiring a simulator whose output, in the case where the tampered message is not m, is computationally indistinguishable from a message in the (real) tampered codeword.
- 6.
The constant C here determines the choice of the constant \(c_1\) used while defining the parameter t.
References
Aggarwal, D.: Affine-evasive sets modulo a prime. Inf. Process. Lett. 115(2), 382–385 (2015). http://dx.doi.org/10.1016/j.ipl.2014.10.015
Aggarwal, D., Dodis, Y., Kazana, T., Obremski, M.: Non-malleable reductions and applications. In: Servedio, R.A., Rubinfeld, R. (eds.) Proceedings of the Forty-Seventh Annual ACM on Symposium on Theory of Computing, STOC 2015, Portland, OR, USA, 14–17 June 2015, pp. 459–468. ACM (2015). http://doi.acm.org/10.1145/2746539.2746544
Aggarwal, D., Dodis, Y., Lovett, S.: Non-malleable codes from additive combinatorics. In: STOC, pp. 774–783 (2014)
Agrawal, S., Gupta, D., Maji, H.K., Pandey, O., Prabhakaran, M.: Explicit non-malleable codes against bit-wise tampering and permutations. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015, Part I. LNCS, vol. 9215, pp. 538–557. Springer, Heidelberg (2015)
Agrawal, S., Gupta, D., Maji, H.K., Pandey, O., Prabhakaran, M.: A rate-optimizing compiler for non-malleable codes against bit-wise tampering and permutations. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015, Part I. LNCS, vol. 9014, pp. 375–397. Springer, Heidelberg (2015). http://dx.doi.org/10.1007/978-3-662-46494-6_16
Balog, A., Szemeredi, E.: A statistical theorem for set addition. Combinatorica 14(3), 263–268 (1994)
Chandran, N., Goyal, V., Mukherjee, P., Pandey, O., Upadhyay, J.: Block-wise non-malleable codes. Cryptology ePrint Archive, Report 2015/129 (2015). http://eprint.iacr.org
Chandran, N., Kanukurthi, B., Ostrovsky, R.: Locally updatable and locally decodable codes. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 489–514. Springer, Heidelberg (2014)
Chattopadhyay, E., Zuckerman, D.: Non-malleable codes against constant split-state tampering. In: 55th IEEE Annual Symposium on Foundations of Computer Science, FOCS 2014, Philadelphia, PA, USA, 18–21 October 2014, pp. 306–315. IEEE Computer Society (2014). http://dx.doi.org/10.1109/FOCS.2014.40
Cheraghchi, M., Guruswami, V.: Capacity of non-malleable codes. In: Naor, M. (ed.) ITCS, pp. 155–168. ACM (2014)
Cheraghchi, M., Guruswami, V.: Non-malleable coding against bit-wise and split-state tampering. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 440–464. Springer, Heidelberg (2014)
Choi, S.G., Kiayias, A., Malkin, T.: BiTR: built-in tamper resilience. In: Lee, D.H., Wang, X. (eds.) ASIACRYPT 2011. LNCS, vol. 7073, pp. 740–758. Springer, Heidelberg (2011)
Coretti, S., Maurer, U., Tackmann, B., Venturi, D.: From single-bit to multi-bit public-key encryption via non-malleable codes. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015, Part I. LNCS, vol. 9014, pp. 532–560. Springer, Heidelberg (2015). http://dx.doi.org/10.1007/978-3-662-46494-6_22
Cramer, R., Dodis, Y., Fehr, S., Padró, C., Wichs, D.: Detection of algebraic manipulation with applications to robust secret sharing and fuzzy extractors. In: Smart, N.P. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 471–488. Springer, Heidelberg (2008)
Cramer, R., Padró, C., Xing, C.: Optimal algebraic manipulation detection codes (2014). http://eprint.iacr.org/2014/116
Cramer, R., Shoup, V.: Design and analysis of practical public-key encryption schemes secure against adaptive chosen ciphertext attack. SIAM J. Comput. 33(1), 167–226 (2003). http://dx.doi.org/10.1137/S0097539702403773
Dziembowski, S., Kazana, T., Obremski, M.: Non-malleable codes from two-source extractors. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013, Part II. LNCS, vol. 8043, pp. 239–257. Springer, Heidelberg (2013)
Dziembowski, S., Pietrzak, K., Wichs, D.: Non-malleable codes. In: Yao, A.C.C. (ed.) ICS, pp. 434–452. Tsinghua University Press (2010)
Faust, S., Mukherjee, P., Nielsen, J.B., Venturi, D.: Continuous non-malleable codes. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 465–488. Springer, Heidelberg (2014)
Faust, S., Mukherjee, P., Venturi, D., Wichs, D.: Efficient non-malleable codes and key-derivation for poly-size tampering circuits. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 111–128. Springer, Heidelberg (2014)
Gowers, T.: A new proof of Szemeredi’s theorem for arithmetic progression of length four. Geom. Func. Anal. 8(3), 529–551 (1998)
Guruswami, V., Smith, A.: Codes for computationally simple channels: explicit constructions with optimal rate. In: FOCS, pp. 723–732. IEEE Computer Society (2010)
Hemenway, B., Ostrovsky, R.: Public-key locally-decodable codes. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 126–143. Springer, Heidelberg (2008)
Impagliazzo, R.: Pseudo-random generators for cryptography and for randomized algorithms. Ph.D. thesis, University of California at Berkeley (1989)
Impagliazzo, R., Levin, L.A., Luby, M.: Pseudo-random generation from one-way functions (extended abstracts). In: Johnson, D.S. (ed.) STOC, pp. 12–24. ACM (1989)
Kurosawa, K.: Hybrid encryption. In: Encyclopedia of Cryptography and Security, 2nd edn., pp. 570–572 (2011). http://dx.doi.org/10.1007/978-1-4419-5906-5_321
Lipton, R.J.: A new approach to information theory. In: STACS, pp. 699–708 (1994)
Liu, F.-H., Lysyanskaya, A.: Tamper and leakage resilience in the split-state model. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 517–532. Springer, Heidelberg (2012)
Micali, S., Peikert, C., Sudan, M., Wilson, D.A.: Optimal error correction against computationally bounded noise. In: Kilian, J. (ed.) TCC 2005. LNCS, vol. 3378, pp. 1–16. Springer, Heidelberg (2005)
Ostrovsky, R., Pandey, O., Sahai, A.: Private locally decodable codes. In: Arge, L., Cachin, C., Jurdziński, T., Tarlecki, A. (eds.) ICALP 2007. LNCS, vol. 4596, pp. 387–398. Springer, Heidelberg (2007)
Samorodnitsky, A.: Low-degree tests at large distances. In: ACM Symposium on Theory of Computing, pp. 506–515. ACM (2007)
Sanders, T.: On the Bogolyubov-Ruzsa lemma. Anal. PDE 5, 627–655 (2012)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 International Association for Cryptologic Research
About this paper
Cite this paper
Aggarwal, D., Agrawal, S., Gupta, D., Maji, H.K., Pandey, O., Prabhakaran, M. (2016). Optimal Computational Split-state Non-malleable Codes. In: Kushilevitz, E., Malkin, T. (eds) Theory of Cryptography. TCC 2016. Lecture Notes in Computer Science(), vol 9563. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-49099-0_15
Download citation
DOI: https://doi.org/10.1007/978-3-662-49099-0_15
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-49098-3
Online ISBN: 978-3-662-49099-0
eBook Packages: Computer ScienceComputer Science (R0)






 ,
, 


 .
. and
and  .
. .
. .
.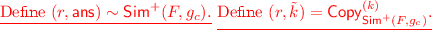
 .
.
 .
.
