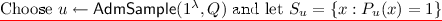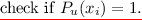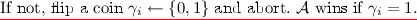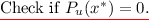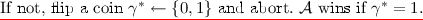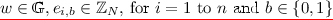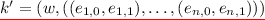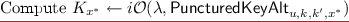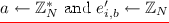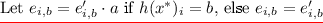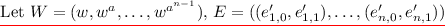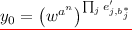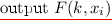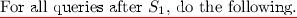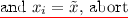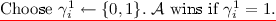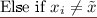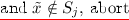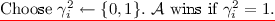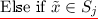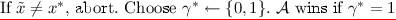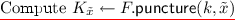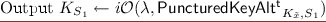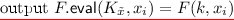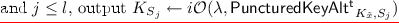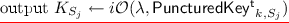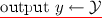Abstract
We study the adaptive security of constrained PRFs in the standard model. We initiate our exploration with puncturable PRFs. A puncturable PRF family is a special class of constrained PRFs, where the constrained key is associated with an element \(x'\) in the input domain. The key allows evaluation at all points \(x\ne x'\).
We show how to build puncturable PRFs with adaptive security proofs in the standard model that involve only polynomial loss to the underlying assumptions. Prior work had either super-polynomial loss or applied the random oracle heuristic. Our construction uses indistinguishability obfuscation and DDH-hard algebraic groups of composite order.
More generally, one can consider a t-puncturable PRF: PRFs that can be punctured at any set of inputs S, provided the size of S is less than a fixed polynomial. We additionally show how to transform any (single) puncturable PRF family to a t-puncturable PRF family, using indistinguishability obfuscation.
S. Hohenberger—Supported by the National Science Foundation CNS-1228443 and CNS-1414023; the Defense Advanced Research Projects Agency (DARPA) and the Air Force Research Laboratory (AFRL) under contract FA8750-11-C-0080, the Office of Naval Research under contract N00014-14-1-0333, and a Microsoft Faculty Fellowship.
B. Waters—Supported by NSF CNS-1228599 and CNS-1414082, DARPA SafeWare, Google Faculty Research award, the Alfred P. Sloan Fellowship, Microsoft Faculty Fellowship, and Packard Foundation Fellowship.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Pseudorandom functions (PRFs) are one of the fundamental building blocks in modern cryptography. A PRF system consists of a keyed function F and a set of keys \(\mathcal {K}\) such that for a randomly chosen key \(k \in \mathcal {K}\), the output of the function F(k, x) for any input x in the input space “looks” random to a computationally bounded adversary, even when given polynomially many evaluations of \(F(k, \cdot )\). Recently, the concept of constrained pseudorandom functions Footnote 1 was proposed in the concurrent works of Boneh and Waters [4], Boyle, Goldwasser and Ivan [6] and Kiayias, Papadopoulos, Triandopoulos and Zacharias [21]. A constrained PRF system is associated with a family of boolean functions \(\mathcal {F}= \{f\}\). As in standard PRFs, there exists a set of master keys \(\mathcal {K}\) that can be used to evaluate the PRF F. However, given a master key k, it is also possible to derive a constrained key \(k_f\) associated with a function \(f \in \mathcal {F}\). This constrained key \(k_f\) can be used to evaluate the function \(F(k, \cdot )\) at all inputs x such that \(f(x)=1\). Intuitively, we would want that even if an adversary has \(k_f\), the PRF evaluation at an input x not accepted by f looks random. Security is captured by an adaptive game between a PRF challenger and an adversary. The adversary is allowed to make multiple constrained key or point evaluation queries before committing to a challenge \(x^*\) not equal to any of the evaluation queries or accepted by any of the functions for which he obtained a constrained key.Footnote 2 The challenger either sends the PRF evaluation at \(x^*\) or an output chosen uniformly at random from the PRF range space, and the adversary wins if he can distinguish between these two cases.
Since their inception, constrained PRFs have found multiple applications. For example, Boneh and Waters [4] gave applications of broadcast encryption with optimal ciphertext length, identity-based key exchange, and policy-based key distribution. Sahai and Waters [24] used constrained PRFs as a central ingredient in their punctured programming methodology for building cryptosystems using indistinguishable obfuscation. Boneh and Zhandry [5] likewise applied constrained PRFs for realizing multi-party key exchange and broadcast systems.
Adaptive Security in Constrained PRFs. In their initial work, Boneh and Waters [4] showed constructions of constrained PRFs for different function families, including one for the class of all polynomial circuits (based on multilinear maps). However, all their constructions offer selective security - a weaker notion where the adversary must commit to the challenge input \(x^*\) before making any evaluation/constrained key queries.Footnote 3 Using complexity leveraging, one can obtain adaptive security by guessing the challenge input \(x^*\) before any queries are made. However, this results in exponential security loss. The works of [6, 21] similarly dealt with selective security.
Recently, Fuchsbauer, Konstantinov, Pietrzak and Rao [11] showed adaptive security for prefix-fixing constrained PRFs, but with quasi-polynomial security loss. Also recently, Hofheinz [16] presented a novel construction that achieves adaptive security for bit-fixing constrained PRFs, but in the random oracle model.
While selective security has been sufficient for some applications of constrained PRFs, including many recent proofs leveraging the punctured programming [24] methodology (e.g., [2, 5, 19, 24]), there are applications that demand adaptive security, where the security game allows the adversary to query the PRF on many inputs before deciding on the point to puncture. For instance, [5] give a construction for multiparty key exchange that is semi-statically secure, and this construction requires adaptively secure constrained PRFs for circuits. We anticipate that the further realization of adaptively secure PRFs will introduce further applications of them.
Our Objective and Results. Our goal is to study adaptive security of constrained PRFs in the standard model. We initiate this exploration with puncturable PRFs, first explicitly introduced in [24] as a specialization of constrained PRFs. A puncturable PRF family is a special class of constrained PRFs, where the constrained key is associated with an element \(x'\) in the input domain. The key allows evaluation at all points \(x\ne x'\). As noted by [4, 6, 21], the GGM tree-based construction of PRFs from one-way functions (OWFs) [14] can be modified to construct a puncturable PRF.Footnote 4 A selective proof of security follows via a hybrid argument, where the reduction algorithm uses the pre-determined challenge query \(x^*\) to “plant” its OWF challenge. However, such a technique does not seem powerful enough to obtain adaptive security with only a polynomial-factor security loss. The difficulty in proving adaptive security arises due to the fact that the reduction algorithm must respond to the evaluation queries, and then output a punctured key that is consistent with the evaluations. This means that the reduction algorithm must be able to evaluate the PRF at a large set S (so that all evaluation queries lie in S with non-negligible probability). However, S cannot be very large, otherwise the challenge \(x^*\) will lie in S, in which case the reduction algorithm cannot use the adversary’s output.
In this work, we show new techniques for constructing adaptively-secure puncturable PRFs in the standard model. A central contribution is to overcome the conflict above, by allowing the reduction algorithm to commit to the evaluation queries, and at the same time, ensuring that the PRF output at the challenge point is unencumbered by the commitment.
Our main idea is to execute a delayed commitment to part of the PRF by partitioning. Initially, in our construction all points are tied to a single (Naor-Reingold [23] style) PRF. To prove security we begin by using the admissible hash function of Boneh and Boyen [3]. We partition the inputs into two distinct sets. The evaluable set which contains about \((1-1/q)\) fraction of inputs, and a challenge set which contains about 1 / q fraction of inputs, where q is the number of point evaluation queries made by the attacker. Via a set of hybrid steps using the computational assumptions of indistinguishability obfuscation and subgroup hiding we modify the construction such that we use one Naor-Reingold PRF function to evaluate points in the evaluable set and a completely independent Naor-Reingold PRF to evaluate points in the challenge set.
After this separation has been achieved, there is a clearer path for our proof of security. At this point the reduction algorithm will create one PRF itself and use it to answer any attacker point query in the evaluable set. If it is asked for a point x in the challenge set, it will simply abort. (The admissible hash function ensures that we get through without abort with some non-negligible probability.) Eventually, the attacker will ask for a punctured key on \(x^*\), which defines \(x^*\) as the challenge input. Up until this point the reduction algorithm has made no commitments on what the second challenge PRF is. It then constructs the punctured key using the a freshly chosen PRF for the challenge inputs. However, when constructing this second PRF it now knows what the challenge \(x^*\) actually is and can fall back on selective techniques for completing the proof.
At a lower level our core PRF will be the Naor-Reingold PRF [23], but based in composite-order groups. Let \({\mathbb G}\) be a group of order \(N = pq\), where p and q are primes. The master key consists of a group element \(v\in {\mathbb G}\) and 2n exponents \(d_{i,b} \in \mathbb {Z}_N\) (for \(i=1\) to n and \(b \in \{0,1\}\)). The PRF F takes as input a key \(k=(v,\{d_{i,b}\})\), an \(\ell \)-bit input x, uses a public admissible hash function \(h : \{0,1\}^{\ell } \rightarrow \{0,1\}^n\) to compute \(h(x) = b_1 \ldots b_n\) and outputs \(v^{\prod _{j=1}^n d_{j, b_j}}\). A punctured key corresponding to \(x'\) derived from master key k is the obfuscation of a program P which has \(k,x'\) hardwired and outputs F(k, x) on input \(x\ne x'\), else it outputs \(\perp \).
We will use a parameterized problem (in composite groups) to perform some of the separation step. Our assumption is that given \(g, g^a, \ldots , g^{a^{n-1}}\) for randomly chosen \(g \in {\mathbb G}\) and \(a \in \mathbb {Z}^*_N\) it is hard to distinguish \(g^{a^{n}}\) from a random group element. While it is somewhat undesirable to base security on a parameterized assumption, we are able to use the recent results of Chase and Meiklejohn [8] to reduce this to the subgroup decision problem in DDH hard composite order groups.
t-puncturable PRFs. We also show how to construct t-puncturable PRFs: PRFs that can be punctured at any set of inputs S, provided \(|S| \le t\) (where \(t(\cdot )\) is a fixed polynomial). We show how to transform any (single) puncturable PRF family to a t-puncturable PRF family, using indistinguishability obfuscation. In the security game for t-puncturable PRFs, the adversary is allowed to query for multiple t-punctured keys, each corresponding to a set S of size at most t. Finally, the adversary sends a challenge input \(x^*\) that lies in all the sets queried, and receives either the PRF evaluation at \(x^*\) or a uniformly random element of the range space.
In the construction, the setup and evaluation algorithm for the t-puncturable PRF are the same as those for the puncturable PRF. In order to puncture a key k at set S, the puncturing algorithm outputs the obfuscation of a program P that takes as input x, checks that \(x\notin S\), and outputs F(k, x).
For the proof of security, we observe that when the first t-punctured key query \(S_1\) is made by the adversary, the challenger can guess the challenge \(\tilde{x} \in S_1\). If this guess is incorrect, then the challenger simply aborts (which results in a 1 / t factor security loss). However, if the guess is correct, then the challenger can now use the punctured key \(K_{\tilde{x}}\) for all future evaluation/t-punctured key queries. From the security of puncturable PRFs, it follows that even after receiving evaluation/t-punctured key queries, the challenger will not be able to distinguish between \(F(k,\tilde{x})\) and a random element in the range space.
We detail this transformation and its proof in Sect. 5.1. We also believe that we can use a similar approach to directly modify our main construction to handle multiple punctured points, however, we choose to focus on the generic transformation.
Related Works. Two recent works have explored the problem of adaptive security of constrained PRFs. Fuchsbauer, Konstantinov, Pietrzak and Rao [11] study the adaptive security of the GGM construction for prefix-free constrained PRFs. They show an interesting reduction to OWFs that suffers only a quasi-polynomial factor \(q^{O(\log n)}\) loss, where q is the number of queries made by the adversary, and n is the length of the input. This beats the straightforward conversion from selective to adaptive security, which results in \(O(2^n)\) security loss.
Hofheinz [16] shows a construction for bit-fixing constrained PRFs that is adaptively secure, assuming indistinguishability obfuscation and multilinear maps in the random oracle model. It also makes novel use of the random oracle for dynamically defining the challenge space based on the output of h. It is currently unclear whether such ideas could be adapted to the standard model.
Fuchsbauer et al. also show a negative result for the Boneh-Waters [4] construction of bit-fixing constrained PRFs. They show that any simple reduction from a static assumption to the adaptive security of the Boneh-Waters [4] bit-fixing constrained PRF construction must have an exponential factor security loss. More abstractly, using their techniques, one can show that any bit-fixing scheme that has the following properties will face this obstacle: (a) fingerprinting queries - By querying for a set of constrained keys, the adversary can obtain a fingerprint of the master key. (b) checkability - It is possible to efficiently check that any future evaluation/constrained key queries are consistent with the fingerprint. While these properties capture certain constructions, small perturbations to them could potentially circumvent checkability.
Partitioning type proofs have been used in several applications including identity-based encryption [1, 3, 17, 25], verifiable random functions [20], and proofs of certain signature schemes [9, 18, 19]. We believe ours is the first to use partitioning for a delayed commitment to parameters. We note that our delayed technique is someway reminiscent to that of Lewko and Waters [22].
Recently, there has been a push to prove security for indistinguishability obfuscation from basic multilinear map assumptions. The recent work of Gentry, Lewko, Sahai and Waters [13] is a step in this direction, but itself requires the use of complexity leveraging. In the future work, we might hope for such reductions with just polynomial loss — perhaps for special cases of functionality. And thus give an end-to-end polynomial loss proof of puncturable PRFs from multilinear maps assumptions.
Two works have explored the notion of constrained verifiable random functions (VRFs). Fuchsbauer [10] and Chandran, Raghuraman and Vinayagamurthy [7] show constructions of selectively secure constrained VRFs for the class of all polynomial sized circuits. The construction in [7] is also delegatable.
Future Directions. A natural question is to construct adaptively-secure constrained PRFs for larger classes of functions in the standard model. Given the existing results of [11, 16], both directions seem possible. While the techniques of [16] are intricately tied to the random oracle model, it is plausible there could be constructions in the standard model that evade the negative result of [11]. On the other hand, maybe the negative result of [11] (which is specific to the [4] construction) can be extended to show a similar lower bound for all constructions of constrained PRFs with respect to function family \(\mathcal {F}\).
2 Preliminaries
First, we recall the notion of admissible hash functions due to Boneh and Boyen [3]. Here we state a simplified definition from [19]. Informally, an admissible hash function family is a function h with a ‘partition sampling algorithm’ \(\mathsf {AdmSample}\). This algorithm takes as input a parameter Q and outputs a ‘random’ partition of the outputs domain, where one of the partitions has 1 / Q fraction of the points. Also, this partitioning has special structure which we will use in our proof.
Definition 1
Let \(l, n\) and \(\theta \) be efficiently computable univariate polynomials, \(h: \{0,1\}^{l(\lambda )} \rightarrow \{0,1\}^{n(\lambda )}\) an efficiently computable function and \(\mathsf {AdmSample}\) a PPT algorithm that takes as input \(1^{\lambda }\) and an integer Q, and outputs a string \(u \in \{0,1, \perp \}^{n(\lambda )}\). For any \(u\in \{0,1,\perp \}^{n(\lambda )}\), define \(P_u:\{0,1\}^{l(\lambda )} \rightarrow \{0,1\}\) as follows: \(P_u(x)=0\) if for all \(1 \le j \le n(\lambda ), h(x)_j \ne u_j\), else \(P_u(x)=1\).
We say that \((h, \mathsf {AdmSample})\) is \(\theta \)-admissible if the following condition holds:
For any efficiently computable polynomial Q, for all \(x_1, \ldots , x_{Q(\lambda )}, x^* \in \{0,1\}^{l(\lambda )}\), where \(x^* \notin \{x_i\}_i\),
where the probability is taken over \(u \leftarrow \mathsf {AdmSample}(1^{\lambda }, Q(\lambda ))\).
Theorem 1
(Admissible Hash Function Family [3], simplified proof in [9]). For any efficiently computable polynomial \(l\), there exist efficiently computable polynomials \(n, \theta \) such that there exist \(\theta \)-admissible function families mapping \(l\) bits to \(n\) bits.
Note that the above theorem is information theoretic, and is not based on any cryptographic assumptions.
Next, we recall the definition of indistinguishability obfuscation from [12, 24]. Let PPT denote probabilistic polynomial time.
Definition 2
(Indistinguishability Obfuscation) A uniform PPT machine \(i\mathcal {O}\) is called an indistinguishability obfuscator for a circuit class \(\{\mathcal {C}_{\lambda }\}\) if it satisfies the following conditions:
-
(Preserving Functionality) For all security parameters \(\lambda \in \mathbb {N}\), for all \({C} \in \mathcal {C}_{\lambda }\), for all inputs x, we have that \({C}'(x) = {C}(x)\) where \({C}' \leftarrow i\mathcal {O}(\lambda , C)\).
-
(Indistinguishability of Obfuscation) For any (not necessarily uniform) PPT distinguisher \(\mathcal {B}= (Samp, \mathcal {D})\), there exists a negligible function \(\text {negl}(\cdot )\) such that the following holds: if for all security parameters \(\lambda \in \mathbb {N}, \Pr [ \forall x,C_0(x) = C_1(x) : ({C}_0; {C}_1; \sigma ) \leftarrow Samp(1^{\lambda })] > 1-\text {negl}(\lambda )\), then
$$\begin{aligned} \vert&\Pr [\mathcal {D}(\sigma , i\mathcal {O}(\lambda , C_0))=1 : ({C}_0; {C}_1; \sigma ) \leftarrow Samp(1^{\lambda })] -\\&\Pr [\mathcal {D}(\sigma , i\mathcal {O}(\lambda , C_1))=1 : ({C}_0; {C}_1; \sigma ) \leftarrow Samp(1^{\lambda })] \vert \le \text {negl}(\lambda ). \end{aligned}$$
In a recent work, [12] showed how indistinguishability obfuscators can be constructed for the circuit class P / poly. We remark that \((Samp, \mathcal {D})\) are two algorithms that pass state, which can be viewed equivalently as a single stateful algorithm \(\mathcal {B}\). In our proofs we employ the latter approach, although here we state the definition as it appears in prior work.
2.1 Assumptions
Let \(\mathcal {G}\) be a PPT group generator algorithm that takes as input the security parameter \(1^{\lambda }\) and outputs \((N, p, q, \mathbb {G}, \mathbb {G}_p\), \(\mathbb {G}_q, g_1, g_2 )\) where \(p,q \in \varTheta (2^{\lambda })\) are primes, \(N=pq\), \(\mathbb {G}\) is a group of order N, \(\mathbb {G}_p\) and \(\mathbb {G}_q\) are subgroups of \(\mathbb {G}\) of order p and q respectively, and \(g_1\) and \(g_2\) are generators of \(\mathbb {G}_p\) and \(\mathbb {G}_q\) respectively.
Assumption 1
(Subgroup Hiding for Composite DDH-Hard Groups). Let \((N, p, q, \mathbb {G}, \mathbb {G}_p, \mathbb {G}_q, g_1, g_2) \leftarrow \mathcal {G}(1^{\lambda })\) and \(b\leftarrow \{0,1\}\). Let \(T \leftarrow \mathbb {G}\) if \(b=0\), else \(T \leftarrow \mathbb {G}_p\). The advantage of algorithm \(\mathcal {A}\) in solving Assumption 1 is defined as
We say that Assumption 1 holds if for all PPT \(\mathcal {A}\), \(\mathsf {Adv}^{\mathrm {SGH}}_{\mathcal {A}}\) is negligible in \(\lambda \).
Note that the adversary \(\mathcal {A}\) gets generators for both subgroups \(\mathbb {G}_p\) and \(\mathbb {G}_q\). This is in contrast to bilinear groups, where, if given generators for both subgroups, the adversary can use the pairing to distinguish a random group element from a random subgroup element.
Analogously, we assume that no PPT adversary can distinguish between a random element of \( {\mathbb G}\) and a random element of \({\mathbb G}_q\) with non-negligible advantage. This is essentially Assumption 1, where prime q is chosen instead of p, and \({\mathbb G}_q\) is chosen instead of \({\mathbb G}_p\).
Assumption 2
This assumption is parameterized with an integer \(n \in \mathbb {Z}\). Let \((N, p, q, \mathbb {G}, \mathbb {G}_p, \mathbb {G}_q, g_1, g_2) \leftarrow \mathcal {G}(1^{\lambda })\), \(g \leftarrow {\mathbb G}\), \(a\leftarrow \mathbb {Z}^*_N\) and \(b \leftarrow \{0,1\}\). Let \(D=(N, \mathbb {G}, \mathbb {G}_p, \mathbb {G}_q, g_1, g_2, g, g^{a}, \ldots , g^{a^{n-1}})\). Let \(T=g^{a^{n}}\) if \(b=0\), else \(T \leftarrow \mathbb {G}\). The advantage of algorithm \(\mathcal {A}\) in solving Assumption 2 is defined as
We say that Assumption 2 holds if for all PPT \(\mathcal {A}\), \(\mathsf {Adv}^{}_{\mathcal {A}}\) is negligible in \(\lambda \).
We will use Assumption 2 for clarity in certain parts of our proof, but we do not give it a name because it is implied by other named assumptions. First, Assumption 2 is implied by the n-Power Decisional Diffie-Hellman Assumption [15]. Second, it is also implied by the non-parameterized Assumption 1. The recent results of Chase and Meiklejohn [8] essentially show this latter implication, but that work focuses on the target groups of bilinear maps, whereas our algebraic focus does not involve bilinear maps.
3 Constrained Pseudorandom Functions
In this section, we define the syntax and security properties of a constrained pseudorandom function family. This definition is similar to the one in Boneh-Waters [4], except that the keys are constrained with respect to a circuit family instead of a set system.
Let \(\mathcal {K}\) denote the key space, \(\mathcal {X}\) the input domain and \(\mathcal {Y}\) the range space. The PRF is a function \(F:\mathcal {K}\times \mathcal {X}\rightarrow \mathcal {Y}\) that can be computed by a deterministic polynomial time algorithm. We will assume there is a Setup algorithm \(F.\textsf {setup}\) that takes the security parameter \(\lambda \) as input and outputs a random secret key \(k\in \mathcal {K}\).
A PRF \(F:\mathcal {K}\times \mathcal {X}\rightarrow \mathcal {Y}\) is said to be constrained with respect to a circuit family \(\mathcal {C}\) if there is an additional key space \(\mathcal {K}_c\), and three algorithms \(F.\textsf {setup}\), \(F.\textsf {constrain}\) and \(F.\textsf {eval}\) as follows:
-
\(F.\textsf {setup}(1^{\lambda })\) is a PPT algorithm that takes the security parameter \(\lambda \) as input and outputs a description of the key space \(\mathcal {K}\), the constrained key space \(\mathcal {K}_c\) and the PRF F.
-
\(F.\textsf {constrain}(k,C)\) is a PPT algorithm that takes as input a PRF key \(k\in \mathcal {K}\) and a circuit \(C\in \mathcal {C}\) and outputs a constrained key \(k_C \in \mathcal {K}_c\).
-
\(F.\textsf {eval}(k_C,x)\) is a deterministic polynomial time algorithm that takes as input a constrained key \(k_C\in \mathcal {K}_c\) and \(x\in \mathcal {X}\) and outputs an element \(y\in \mathcal {Y}\). Let \(k_C\) be the output of \(F.\textsf {constrain}(k,C)\). For correctness, we require the following:
$$\begin{aligned} F.\textsf {eval}(k_C,x) = {\left\{ \begin{array}{ll} F(k,x) &{} \text { if }C(x)=1 \\ \perp &{} \text {otherwise} \end{array}\right. } \end{aligned}$$
Security of Constrained Pseudorandom Functions: Intuitively, we require that even after obtaining several constrained keys, no polynomial time adversary can distinguish a truly random string from the PRF evaluation at a point not accepted by the queried circuits. This intuition can be formalized by the following security game between a challenger and an adversary A.
Let \(F : \mathcal {K}\times \mathcal {X}\rightarrow \mathcal {Y}\) be a constrained PRF with respect to a circuit family \(\mathcal {C}\). The security game consists of three phases.
Setup Phase. The challenger chooses a random key \(k\leftarrow \mathcal {K}\) and \(b\leftarrow \{0,1\}\).
Query Phase. In this phase, A is allowed to ask for the following queries:
-
Evaluation Query A sends \(x\in \mathcal {X}\), and receives F(k, x).
-
Key Query A sends a circuit \(C \in \mathcal {C}\), and receives \(F.\textsf {constrain}(k,C)\).
-
Challenge Query A sends \(x\in \mathcal {X}\) as a challenge query. If \(b=0\), the challenger outputs F(k, x). Else, the challenger outputs a random element \(y\leftarrow \mathcal {Y}\).
Guess. A outputs a guess \(b'\) of b.
Let \(E\subset \mathcal {X}\) be the set of evaluation queries, \(L \subset \mathcal {C}\) be the set of constrained key queries and \(Z \subset \mathcal {X}\) the set of challenge queries. A wins if \(b=b'\) and \(E \cap Z = \phi \) and for all \(C \in L, z\in Z, C(z)=0\). The advantage of A is defined to be \(\mathsf {Adv}^F_A(\lambda ) = Pr[A \text { wins}]\).
Definition 3
The PRF F is a secure constrained PRF with respect to \(\mathcal {C}\) if for all PPT adversaries A \(\mathsf {Adv}^F_{\mathcal {A}}(\lambda )\) is negligible in \(\lambda \).
3.1 Puncturable Pseudorandom Functions
In this section, we define the syntax and security properties of a puncturable pseudorandom function family. Puncturable PRFs are a special class of constrained pseudorandom functions.
A PRF \(F:\mathcal {K}\times \mathcal {X}\rightarrow \mathcal {Y}\) is a puncturable pseudorandom function if there is an additional key space \(\mathcal {K}_{p}\) and three polynomial time algorithms \(F.\textsf {setup}\), \(F.\textsf {eval}\) and \(F.\textsf {puncture}\) as follows:
-
\(F.\textsf {setup}(1^{\lambda })\) is a randomized algorithm that takes the security parameter \(\lambda \) as input and outputs a description of the key space \(\mathcal {K}\), the punctured key space \(\mathcal {K}_p\) and the PRF F.
-
\(F.\textsf {puncture}(k,x)\) is a randomized algorithm that takes as input a PRF key \(k\in \mathcal {K}\) and \(x\in \mathcal {X}\), and outputs a key \(k_x \in \mathcal {K}_{p}\).
-
\(F.\textsf {eval}(k_{x},x')\) is a deterministic algorithm that takes as input a punctured key \(k_{x} \in \mathcal {K}_{p}\) and \(x'\in \mathcal {X}\). Let \(k\in \mathcal {K}\), \(x\in \mathcal {X}\) and \(k_x \leftarrow F.\textsf {puncture}(k,x)\). For correctness, we need the following property:
$$ F.\textsf {eval}(k_x, x') = {\left\{ \begin{array}{ll} F(k,x') &{} \text { if } x\ne x' \\ \perp &{} \text { otherwise} \end{array}\right. } $$
Security of Puncturable PRFs: The security game between the challenger and the adversary A consists of the following four phases.
Setup Phase. The challenger chooses uniformly at random a PRF key \(k\leftarrow \mathcal {K}\) and a bit \(b\leftarrow \{0,1\}\).
Evaluation Query Phase. A queries for polynomially many evaluations. For each evaluation query x, the challenger sends F(k, x) to A.
Challenge Phase. A chooses a challenge \(x^* \in \mathcal {X}\). The challenger computes \(k_{x^*} \leftarrow F.\textsf {puncture}(k, x^*)\). If \(b=0\), the challenger outputs \(k_{x^*}\) and \(F(k,x^*)\). Else, the challenger outputs \(k_{x^*}\) and \(y \leftarrow \mathcal {Y}\) chosen uniformly at random.
Guess. A outputs a guess \(b'\) of b. Let \(E\subset \mathcal {X}\) be the set of evaluation queries. A wins if \(b=b'\) and \(x^* \notin E\). The advantage of A is defined to be \(\mathsf {Adv}^F_A(\lambda ) = Pr[A \text { wins}]\).
Definition 4
The PRF F is a secure puncturable PRF if for all probabilistic polynomial time adversaries A \(\mathsf {Adv}^F_{\mathcal {A}}(\lambda )\) is negligible in \(\lambda \).
t -Puncturable Pseudorandom Functions. The notion of puncturable PRFs can be naturally extended to that of t-puncturable PRFs, where it is possible to derive a key punctured at any set S of size at most t. A formal definition of t-puncturable PRFs can be found in Sect. 5.
4 Construction
We now describe our puncturable PRF family. It consists of the PRF \(F: \mathcal {K}\times \mathcal {X}\rightarrow \mathcal {Y}\) and the three algorithms \(F.\textsf {setup}, F.\textsf {puncture}\) and \(F.\textsf {eval}\). The input domain is \(\mathcal {X}= \{0,1\}^{\ell }\), where \(\ell = \ell (\lambda )\). We define the key space \(\mathcal {K}\) and range space \(\mathcal {Y}\) as part of the setup algorithm described next.
\(\mathbf{F.}{{{\textsf {\textit{setup}}}}}{} \mathbf{(1}^{\lambda }{} \mathbf{)}\) \(F.\textsf {setup}\), on input \(1^{\lambda }\), runs \(\mathcal {G}\) to compute \((N, p, q, {\mathbb G}, {\mathbb G}_p, {\mathbb G}_q, g_1, g_2) \leftarrow \mathcal {G}(1^{\lambda })\). Let \(n, \theta \) be polynomials such that there exists a \(\theta \)-admissible hash function h mapping \(\ell (\lambda )\) bits to \(n(\lambda )\) bits. For simplicity of notation, we will drop the dependence of \(\ell \) and n on \(\lambda \).
The key space is \(\mathcal {K}= {\mathbb G}\times \left( \mathbb {Z}_N^2 \right) ^{n}\) and the range is \(\mathcal {Y}= {\mathbb G}\). The setup algorithm chooses \(v\in {\mathbb G}\), \(d_{i,b} \in \mathbb {Z}_N\), for \(i=1\) to n and \(b \in \{0,1\}\), and sets \(k = \left( v, \left( \left( d_{1,0}, d_{1,1} \right) , \ldots , \left( d_{n,0}, d_{n,1} \right) \right) \right) \).
The PRF F for key k on input x is then computed as follows. Let \(k= \left( v, \left( \left( d_{1,0}, d_{1,1} \right) , \ldots , \left( d_{n,0}, d_{n,1} \right) \right) \right) \in {\mathbb G}\times \left( \mathbb {Z}_N^2 \right) ^n\) and \(h(x) = \left( b_1, \ldots , b_n \right) \), where \(b_i \in \{0,1\}\). Then,
\(\mathbf{F.}{{{\textsf {\textit{puncture}}}}}{} \mathbf{(k,x')}\) \(F.\textsf {puncture}\) computes an obfuscation of \(\mathsf {PuncturedKey}_{k,x'}\) (defined in Fig. 1); that is, \(K_{x'} \leftarrow i\mathcal {O}(\lambda , \mathsf {PuncturedKey}_{k, x'})\) where \(\mathsf {PuncturedKey}_{k,x'}\) is padded to be of appropriate size.Footnote 5
\(\mathbf{F.}{{{\textsf {\textit{eval}}}}} \mathbf{(K_{x'}, x)}\) The punctured key \(K_{x'}\) is a program that takes an \(\ell \)-bit input. We define
4.1 Proof of Security
We will now prove that our construction is a secure puncturable PRF as defined in Definition 4. Specifically, the claim we show is:
Theorem 2
(Main Theorem). Assuming \(i\mathcal {O}\) is a secure indistinguishability obfuscator and the Subgroup Hiding Assumption holds for groups output by \(\mathcal {G}\), the PRF F defined above, together with algorithms \(F.\textsf {setup}\), \(F.\textsf {puncture}\) and \(F.\textsf {eval}\), is a secure punctured pseudorandom function as defined in Definition 4.
Proof
In order to prove this, we define the following sequence of games. Assume the adversary \(\mathcal {A}\) makes \(Q = Q(\lambda )\) evaluation queries (where \(Q(\cdot )\) is a polynomial) before sending the challenge input.
Sequence of Games. We underline the primary changes from one game to the next.
Game 0. This game is the original security game from Definition 4 between the challenger and \(\mathcal {A}\) instantiated by the construction under analysis. Here the challenger first chooses a random PRF key, then \(\mathcal {A}\) makes evaluation queries and finally sends the challenge input. The challenger responds by sending a key punctured at the challenge input, and either a PRF evaluation at the challenged point or a random value.
-
1.
Let \((N, p, q, {\mathbb G}, {\mathbb G}_p, {\mathbb G}_q, g_1, g_2) \leftarrow \mathcal {G}(1^{\lambda })\). Choose \(v \in {\mathbb G}, d_{i,b} \in \mathbb {Z}_N\), for \(i=1\) to n and \(b \in \{0,1\}\), and set \(k=\left( v, \left( \left( d_{1,0}, d_{1,1} \right) , \ldots , \left( d_{n,0}, d_{n,1} \right) \right) \right) \).
-
2.
On any evaluation query \(x_i \in \{0,1\}^{\ell }\), compute \(h(x_i) = b^i_1 \ldots b^i_n\) and output \(v^{\prod _{j=1}^n d_{j,b^i_j}}\).
-
3.
\(\mathcal {A}\) sends challenge input \(x^*\) such that \(x^* \ne x_i\) \(\forall \) \(i\le Q\). Compute \(K_{x^*} \leftarrow i\mathcal {O}(\lambda , \mathsf {PuncturedKey}_{k,x^*})\) and \(h(x^*) = b_1^* \ldots b_n^*\). Let \(y_0 = v^{\prod _{j=1}^n d_{j,b_j^*}}\) and \(y_1 \leftarrow {\mathbb G}\).
-
4.
Flip coin \(\beta \leftarrow \{0,1\}\). Output \((K_{x^*}, y_{\beta })\).
-
5.
\(\mathcal {A}\) outputs \(\beta '\) and wins if \(\beta = \beta '\).
Game 1. This game is the same as the previous one, except that we simulate a partitioning game while the adversary operates and if an undesirable partition arises, we abort the game and decide whether or not the adversary “wins” by a coin flip. This partitioning game works as follows: the challenger samples \(u \in \{0,1,\perp \}^n\) using \(\mathsf {AdmSample}\) and aborts if either there exists an evaluation query x such that \(P_u(x) = 0\) or the challenge query \(x^*\) satisfies \(P_u(x^*)=1\).
-
1.
Let \((N, p, q, {\mathbb G}, {\mathbb G}_p, {\mathbb G}_q, g_1, g_2) \leftarrow \mathcal {G}(1^{\lambda })\). Choose \(v \in {\mathbb G}, d_{i,b} \in \mathbb {Z}_N\), for \(i=1\) to n and \(b \in \{0,1\}\), and set \(k=\left( v, \left( \left( d_{1,0}, d_{1,1} \right) , \ldots , \left( d_{n,0}, d_{n,1} \right) \right) \right) \).
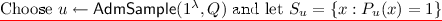
(recall \(P_u(x) = 0\) if \(h(x)_j \ne u_j ~ \forall 1\le j \le n\)).
-
2.
On any evaluation query \(x_i \in \{0,1\}^{\ell }\),
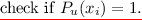
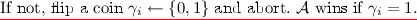
Else compute \(h(x_i) = b^i_1 \ldots b^i_n\) and output \(v^{\prod _{j=1}^n d_{j,b^i_j}}\).
-
3.
\(\mathcal {A}\) sends challenge input \(x^*\) such that \(x^* \ne x_i\) \(\forall \) \(i\le Q\).
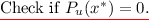
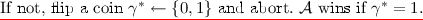
Else compute \(K_{x^*} \leftarrow i\mathcal {O}(\lambda , \mathsf {PuncturedKey}_{k,x^*})\) and \(h(x^*) = b_1^* \ldots b_n^*\). Let \(y_0 = v^{\prod _{j=1}^n d_{j,b_j^*}}\) and \(y_1 \leftarrow {\mathbb G}\).
-
4.
Flip coin \(\beta \leftarrow \{0,1\}\). Output \((K_{x^*}, y_{\beta })\).
-
5.
\(\mathcal {A}\) outputs \(\beta '\) and wins if \(\beta = \beta '\).
Game 2. In this game, the challenger modifies the punctured key and outputs an obfuscation of \(\mathsf {PuncturedKeyAlt}\) defined in Fig. 2. On inputs x such that \(P_u(x)=1\), the altered punctured key uses the same master key k as before. However, if \(P_u(x) = 0\), the altered punctured key uses a different master key \(k'\) that is randomly chosen from the key space.
-
1.
Let \((N, p, q, {\mathbb G}, {\mathbb G}_p, {\mathbb G}_q, g_1, g_2) \leftarrow \mathcal {G}(1^{\lambda })\). Choose \(v \in {\mathbb G}, d_{i,b} \in \mathbb {Z}_N\), for \(i=1\) to n and \(b \in \{0,1\}\).
Set \(k=\left( v, \left( \left( d_{1,0}, d_{1,1} \right) , \ldots , \left( d_{n,0}, d_{n,1} \right) \right) \right) \).
Choose \(u \leftarrow \mathsf {AdmSample}(1^{\lambda }, Q)\).
-
2.
On any evaluation query \(x_i \in \{0,1\}^{\ell }\), check if \(P_u(x_i) = 1\).
If not, flip a coin \(\gamma _i \leftarrow \{0,1\}\) and abort. \(\mathcal {A}\) wins if \(\gamma _i = 1\).
Else compute \(h(x_i) = b^i_1 \ldots b^i_n\) and output \(v^{\prod _{j=1}^n d_{j,b^i_j}}\).
-
3.
\(\mathcal {A}\) sends challenge input \(x^*\) such that \(x^* \ne x_i\) \(\forall \) \(i\le Q\). Check if \(P_u(x^*) = 0\).
If not, flip a coin \(\gamma ^* \leftarrow \{0,1\}\) and abort. \(\mathcal {A}\) wins if \(\gamma ^* = 1\).
Else choose
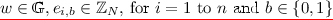
.
Set
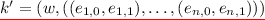
.
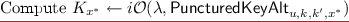
and \(h(x^*) = b_1^* \ldots b_n^*\). Let \(y_0 = w^{\prod _{j=1}^n e_{j,b_j^*}}\) and \(y_1 \leftarrow {\mathbb G}\).
-
4.
Flip coin \(\beta \leftarrow \{0,1\}\). Output \((K_{x^*}, y_{\beta })\).
-
5.
\(\mathcal {A}\) outputs \(\beta '\) and wins if \(\beta = \beta '\).
Game 3. In this game, the challenger changes how the master key \(k'\) is chosen so that some elements contain an a-factor, for use on inputs x where \(P_u(x)=0\).
-
1.
Let \((N, p, q, {\mathbb G}, {\mathbb G}_p, {\mathbb G}_q, g_1, g_2) \leftarrow \mathcal {G}(1^{\lambda })\). Choose \(v \in {\mathbb G}, d_{i,b} \in \mathbb {Z}_N\), for \(i=1\) to n and \(b \in \{0,1\}\), and set \(k=\left( v, \left( \left( d_{1,0}, d_{1,1} \right) , \ldots , \left( d_{n,0}, d_{n,1} \right) \right) \right) \).
Choose \(u \leftarrow \mathsf {AdmSample}(1^{\lambda }, Q)\).
-
2.
On any evaluation query \(x_i \in \{0,1\}^{\ell }\), check if \(P_u(x_i) = 1\).
If not, flip a coin \(\gamma _i \leftarrow \{0,1\}\) and abort. \(\mathcal {A}\) wins if \(\gamma _i = 1\).
Else compute \(h(x_i) = b^i_1 \ldots b^i_n\) and output \(v^{\prod _j d_{j,b^i_j}}\).
-
3.
\(\mathcal {A}\) sends challenge input \(x^*\) such that \(x^* \ne x_i\) \(\forall \) \(i\le Q\). Check if \(P_u(x^*) = 0\).
If not, flip a coin \(\gamma ^* \leftarrow \{0,1\}\) and abort. \(\mathcal {A}\) wins if \(\gamma ^* = 1\).
Else choose \(w \leftarrow {\mathbb G}\),
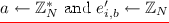
.
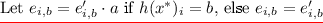
.
Let \(k'\!=\!(w, ((e_{1,0}, e_{1,1}), \ldots , (e_{n,0}, e_{n,1})))\), \(K_{x^*} \!\leftarrow \! i\mathcal {O}(\mathsf {PuncturedKeyAlt}_{u, k,k',x^*})\).
Let \(h(x^*) = b_1^* \ldots b_n^*\) and \(y_0 = w^{\prod _j e_{j,b_j^*}}\) and \(y_1 \leftarrow {\mathbb G}\).
-
4.
Flip coin \(\beta \leftarrow \{0,1\}\). Output \((K_{x^*}, y_{\beta })\).
-
5.
\(\mathcal {A}\) outputs \(\beta '\) and wins if \(\beta = \beta '\).
Game 4. This game is the same as the previous one, except that the altered punctured program contains the constants \(\{w^{^{a^i}}\}_{i=0}^n\) hardwired. These terms are used to compute the output of the punctured program. The punctured key is an obfuscation of \(\mathsf {PuncturedKeyAlt}'\) defined in Fig. 3.
-
1.
Let \((N, p, q, {\mathbb G}, {\mathbb G}_p, {\mathbb G}_q, g_1, g_2) \leftarrow \mathcal {G}(1^{\lambda })\). Choose \(v \in {\mathbb G}, d_{i,b} \in \mathbb {Z}_N\), for \(i=1\) to n and \(b \in \{0,1\}\), and set \(k=\left( v, \left( \left( d_{1,0}, d_{1,1} \right) , \ldots , \left( d_{n,0}, d_{n,1} \right) \right) \right) \).
Choose \(u \leftarrow \mathsf {AdmSample}(1^{\lambda },Q)\).
-
2.
On any evaluation query \(x_i \in \{0,1\}^{\ell }\), check if \(P_u(x_i) = 1\).
If not, flip a coin \(\gamma _i \leftarrow \{0,1\}\) and abort. \(\mathcal {A}\) wins if \(\gamma _i = 1\).
Else compute \(h(x_i) = b^i_1 \ldots b^i_n\) and output \(v^{\prod _j d_{j,b^i_j}}\).
-
3.
\(\mathcal {A}\) sends challenge input \(x^*\) such that \(x^* \ne x_i\) \(\forall \) \(i\le Q\). Check if \(P_u(x^*) = 0\).
If not, flip a coin \(\gamma ^* \leftarrow \{0,1\}\) and abort. \(\mathcal {A}\) wins if \(\gamma ^* = 1\).
Else choose \(w \leftarrow {\mathbb G}\), \(a \leftarrow \mathbb {Z}^*_N\) and \(e'_{i,b} \leftarrow \mathbb {Z}_N \).
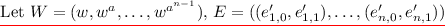
.
Let

, \(h(x^*) \!=\! b_1^* \ldots b_n^*\),
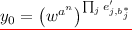
and \(y_1 \leftarrow {\mathbb G}\).
-
4.
Flip coin \(\beta \leftarrow \{0,1\}\). Output \((K''_{x^*}, y_{\beta })\).
-
5.
\(\mathcal {A}\) outputs \(\beta '\) and wins if \(\beta = \beta '\).
Game 5. In this game, we replace the term \(w^{a^n}\) with a random element from \({\mathbb G}\). Hence, both \(y_0\) and \(y_1\) are random elements of \({\mathbb G}\), thereby ensuring that any adversary has zero advantage in this game.
-
1.
Let \((N, p, q, {\mathbb G}, {\mathbb G}_p, {\mathbb G}_q, g_1, g_2) \leftarrow \mathcal {G}(1^{\lambda })\). Choose \(v \in {\mathbb G}, d_{i,b} \in \mathbb {Z}_N\), for \(i=1\) to n and \(b \in \{0,1\}\), and set \(k=\left( v, \left( \left( d_{1,0}, d_{1,1} \right) , \ldots , \left( d_{n,0}, d_{n,1} \right) \right) \right) \).
Choose \(u \leftarrow \mathsf {AdmSample}(1^{\lambda }, Q)\).
-
2.
On any evaluation query \(x_i \in \{0,1\}^{\ell }\), check if \(P_u(x_i) = 1\).
If not, flip a coin \(\gamma _i \leftarrow \{0,1\}\) and abort. \(\mathcal {A}\) wins if \(\gamma _i = 1\).
Else compute \(h(x_i) = b^i_1 \ldots b^i_n\) and output \(v^{\prod _{j=1}^n d_{j,b^i_j}}\).
-
3.
\(\mathcal {A}\) sends challenge input \(x^*\) such that \(x^* \ne x_i\) \(\forall \) \(i\le Q\). Check if \(P_u(x^*) = 0\).
If not, flip a coin \(\gamma ^* \leftarrow \{0,1\}\) and abort. \(\mathcal {A}\) wins if \(\gamma ^* = 1\).
Else choose \(w \leftarrow {\mathbb G}\), \(a \leftarrow \mathbb {Z}_N^*\), and \(e'_{i,b} \leftarrow \mathbb {Z}_N \). Let \(W = (w, w^a, \ldots , w^{a^{n-1}})\),
\(E \!=\! ((e'_{1,0}, e'_{1,1}), \ldots , (e'_{n,0}, e'_{n,1}))\) and \(K_{x^*} \!\leftarrow \! i\mathcal {O}(\lambda , \mathsf {PuncturedKeyAlt}'_{u, W, E, k, x^*})\).
Let \(h(x^*) = b_1^* \ldots b_n^*\).

and \(y_1 \leftarrow {\mathbb G}\).
-
4.
Flip coin \(\beta \leftarrow \{0,1\}\). Output \((K_{x^*}, y_{\beta })\).
-
5.
\(\mathcal {A}\) outputs \(\beta '\) and wins if \(\beta = \beta '\).
Adversary’s Advantage in These Games. Let \(\mathsf {Adv}^i_{\mathcal {A}}\) denote the advantage of adversary \(\mathcal {A}\) in Game i. We will now show that if an adversary \(\mathcal {A}\) has non-negligible advantage in Game i, then \(\mathcal {A}\) has non-negligible advantage in Game \(i+1\). Finally, we show that \(\mathcal {A}\) has advantage 0 in Game 5.
Claim 1
For any adversary \(\mathcal {A}\), \(\mathsf {Adv}^1_{\mathcal {A}} \ge \mathsf {Adv}^0_{\mathcal {A}}/\theta (Q)\).
Proof
This claim follows from the \(\theta \)-admissibility of the hash function h. Recall h is \(\theta \)-admissible if for all \(x_1,\ldots , x_q, x^*\), \(Pr[~\forall i, P_u(x_i) = 1 \wedge P_u(x^*) = 0] \ge 1/\theta (Q)\), where the probability is only over the choice of \(u \leftarrow \mathsf {AdmSample}(1^{\lambda }, Q)\). Therefore, if \(\mathcal {A}\) wins with advantage \(\epsilon \) in Game 0, then \(\mathcal {A}\) wins with advantage at least \(\epsilon /\theta (Q)\) in Game 1.
Claim 2
Assuming \(i\mathcal {O}\) is a secure indistinguishability obfuscator and the Subgroup Hiding Assumption holds, for any PPT adversary \(\mathcal {A}\),
Clearly, the two programs in Game 1 and Game 2 are functionally different (they differ on ‘challenge partition’ inputs x where \(P_u(x) = 0\)), and therefore the proof of this claim involves multiple intermediate experiments. In the first hybrid experiment, we transform the program such that the program computes the output in a different manner, although the output is the same as in the original program. Next, the constants hardwired in the modified program are modified such that the output changes on all ‘challenge partition’ inputs (this step uses Assumption 2). Essentially, both programs use a different base for the challenge partition inputs. Next, using Subgroup Hiding Assumption and Chinese Remainder Theorem, even the exponents can be changed for the challenge partition, thereby ensuring that the original program and final program use different PRF keys for the challenge partition. The formal proof can be found in full version of this paper.
Claim 3
For any PPT adversary \(\mathcal {A}\), \(\mathsf {Adv}^3_{\mathcal {A}} = \mathsf {Adv}^2_{\mathcal {A}}\).
Proof
Game 2 and Game 3 are identical, except for the manner in which the constants \(e_{i,b}\) are chosen. In Game 2, \(e_{i,b} \leftarrow \mathbb {Z}_N\), while in Game 3, the challenger first chooses \(e'_{i,b} \leftarrow \mathbb {Z}_N\), \(a\leftarrow \mathbb {Z}^*_N\), and sets \(e_{i,b} = e'_{i,b} \cdot a\) if \(h(x)_i = b\), else sets \(e_{i,b} = e'_{i,b}\). Since \(a \in \mathbb {Z}^*_N\) (and therefore is invertible), \(e'_{i,b} \cdot a\) is also a uniformly random element in \(\mathbb {Z}_N\) if \(e'_{i,b}\) is. Hence the two experiments are identical.
Claim 4
If there exists a PPT adversary \(\mathcal {A}\) such that \(\mathsf {Adv}^3_{\mathcal {A}} - \mathsf {Adv}^4_{\mathcal {A}} \) is non-negligible in \(\lambda \), then there exists a PPT distinguisher \(\mathcal {B}\) that breaks the security of \(i\mathcal {O}\) with advantage non-negligible in \(\lambda \).
Proof
Suppose there exists a PPT adversary \(\mathcal {A}\) such that \(\mathsf {Adv}^3_{\mathcal {A}} - \mathsf {Adv}^4_{\mathcal {A}} = \epsilon \). We will construct a PPT algorithm \(\mathcal {B}\) that breaks the security of \(i\mathcal {O}\) with advantage \(\epsilon \) by interacting with \(\mathcal {A}\). \(\mathcal {B}\) first sets up the parameters, including u and k, and answers the evaluation queries of \(\mathcal {A}\) exactly as in steps 1 and 2 of Game 3, which are identical to steps 1 and 2 of Game 4. When \(\mathcal {A}\) sends \(\mathcal {B}\) a challenge input \(x^*\), \(\mathcal {B}\) checks that \(P_u(x^*)=0\) and if not aborts (identical in both games).
Next \(\mathcal {B}\) chooses further values to construct the circuits: \(w \leftarrow {\mathbb G}\), \(a \leftarrow \mathbb {Z}^*_N\) and \(e'_{i,b} \leftarrow \mathbb {Z}_N \). Let \(e_{i,b} = e'_{i,b}\cdot a\) if \(h(x^*)_i=b\), else \(e_{i,b} = e'_{i,b}\). Let \(k'=(w, ((e_{1,0}, e_{1,1}), \ldots , (e_{n,0}, e_{n,1})))\), \(W = (w, w^a, \ldots , w^{a^{n-1}})\) and \(E = ((e'_{1,0}, e'_{1,1})\), \(\ldots , (e'_{n,0}, e'_{n,1}))\).
\(\mathcal {B}\) constructs \(C_0 = \mathsf {PuncturedKeyAlt}_{u, k,k',x^*}\), \(C_1 = \mathsf {PuncturedKeyAlt}'_{u, W, E, k, x^*}\), and sends \(C_0, C_1\) to the \(i\mathcal {O}\) challenger. \(\mathcal {B}\) receives \(K_{x^*} \leftarrow i\mathcal {O}(C_b)\) from the challenger. It computes \(h(x^*)=b^*_1 \ldots b^*_n\), \(y_0=w^{\prod _j e_{j,b^*_j}}\), \(y\leftarrow {\mathbb G}\), \(\beta \leftarrow \{0,1\}\), sends \((K_{x^*}, y_{\beta })\) to \(\mathcal {A}\) and receives \(\beta '\) in response. If \(\beta = \beta '\), \(\mathcal {B}\) outputs 0, else it outputs 1.
We will now prove that the circuits \(C_0\) and \(C_1\) have identical functionality. Consider any \(\ell \) bit string x, and let \(h(x) = b_1 \ldots b_n\). Recall \(t_{x*}(x) = | \{ i : b_i = b^*_i\} |\).
For any \(x\in \{0,1\}^{\ell }\) such that \(x = x^*\), both circuits output \(\perp \).
For any \(x\in \{0,1\}^{\ell }\) such that \(x \ne x^*\) and \(P_u(x) = 1\), both circuits output \(v^{\prod _{j=1}^n d_{j,b_j}}\).
For any \(x\in \{0,1\}^{\ell }\) such that \(x \ne x^*\) and \(P_u(x) = 0\), we have
As \(C_0\) and \(C_1\) have identical functionality, \(Pr[\mathcal {B}\text { wins } ]\) = \(Pr[\mathcal {A}\text { wins in Game 3}]~\)-\( Pr[\mathcal {A}\text { wins in Game 4}]\). If \(\mathsf {Adv}^3_{\mathcal {A}} - \mathsf {Adv}^4_{\mathcal {A}} = \epsilon \), then \(\mathcal {B}\) wins the \(i\mathcal {O}\) security game with advantage \(\epsilon \).
Claim 5
If there exists a PPT adversary \(\mathcal {A}\) such that \(\mathsf {Adv}^4_{\mathcal {A}} - \mathsf {Adv}^5_{\mathcal {A}}\) is non-negligible in \(\lambda \), then there exists a PPT adversary \(\mathcal {B}\) that breaks Assumption 2 with advantage non-negligible in \(\lambda \).
Proof
Suppose there exists an adversary \(\mathcal {A}\) such that \(\mathsf {Adv}^4_{\mathcal {A}} - \mathsf {Adv}^5_{\mathcal {A}}=\epsilon \), then we can build an adversary that breaks Assumption 2 with advantage \(\epsilon \). The games are identical except that Game 5 replaces the term \(w^{a^n}\) with a random element of \({\mathbb G}\). On input an Assumption 2 instance \((N, \mathbb {G}, \mathbb {G}_p, \mathbb {G}_q, g_1, g_2, w, w^{a}, \ldots \), \(w^{a^{n-1}})\) together with challenge value T (which is either \(w^{a^n}\) or a random element in \({\mathbb G}\)), use these parameters as in Game 5 with \(\mathcal {A}\). If \(\mathcal {A}\) guesses it was in Game 4, guess that \(T=w^{a^n}\), else guess that T was random.
Observation 1
For any adversary \(\mathcal {A}\), \(\mathsf {Adv}^5_{\mathcal {A}} = 0\).
Proof
If the challenger aborts either during the evaluation or challenge phase, then \(\mathcal {A}\) has 0 advantage, since \(\mathcal {A}\) wins with probability 1 / 2. If the challenger does not abort during both these phases, then \(\mathcal {A}\) receives \((K_{x^*}, y_{\beta })\), and \(\mathcal {A}\) must guess \(\beta \). However, both \(y_0\) and \(y_1\) are uniformly random elements in \({\mathbb G}\), and therefore, \(\mathsf {Adv}^5_{\mathcal {A}} = 0\).
Conclusion of the Main Proof. Given Claims 1–5 and Observation 1, we can conclude that if \(i\mathcal {O}\) is a secure indistinguishability obfuscator and Assumption 1 holds (in the full version of this paper, we show that Assumption 1 implies Assumption 2), then any PPT adversary \(\mathcal {A}\) has negligible advantage in the puncturable PRF security game (i.e., Game 0).
5 t-Puncturable PRFs
Let \(t(\cdot )\) be a polynomial. A PRF \(F_t:\mathcal {K}\times \mathcal {X}\rightarrow \mathcal {Y}\) is a t-puncturable pseudorandom function if there is an additional key space \(\mathcal {K}_{p}\) and three polynomial time algorithms \(F_t.\textsf {setup}\), \(F_t.\textsf {eval}\) and \(F_t.\textsf {puncture}\) defined as follows.
-
\(F_t.\textsf {setup}(1^{\lambda })\) is a randomized algorithm that takes the security parameter \(\lambda \) as input and outputs a description of the key space \(\mathcal {K}\), the punctured key space \(\mathcal {K}_p\) and the PRF \(F_t\).
-
\(F_t.\textsf {puncture}(k,S)\) is a randomized algorithm that takes as input a PRF key \(k\in \mathcal {K}\) and \(S \subset \mathcal {X}\), \(|S| \le t(\lambda )\), and outputs a t-punctured key \(K_S \in \mathcal {K}_{p}\).
-
\(F_t.\textsf {eval}(k_{S},x')\) is a deterministic algorithm that takes as input a t-punctured key \(k_{S} \in \mathcal {K}_{p}\) and \(x'\in \mathcal {X}\). Let \(k\in \mathcal {K}\), \(S\subset \mathcal {X}\) and \(k_S \leftarrow F_t.\textsf {puncture}(k,S)\). For correctness, we need the following property:
$$\begin{aligned} F_t.\textsf {eval}(k_S, x') = {\left\{ \begin{array}{ll} F_t(k,x') &{} \text { if } x'\notin S \\ \perp &{} \text { otherwise} \end{array}\right. } \end{aligned}$$
The security game between the challenger and adversary is similar to the security game for puncturable PRFs. However, in this case, the adversary is allowed to make multiple challenge queries (as in the security game for constrained PRFs). The game consists of the following three phases.
Setup Phase. The challenger chooses a random key \(k\leftarrow \mathcal {K}\) and \(b\leftarrow \{0,1\}\).
Query Phase. In this phase, A is allowed to ask for the following queries:
-
Evaluation Query A sends \(x\in \mathcal {X}\), and receives \(F_t(k,x)\).
-
Key Query A sends a set \(S \subset \mathcal {X}\), and receives \(F_t.\textsf {puncture}(k,S)\).
-
Challenge Query A sends \(x\in \mathcal {X}\) as a challenge query. If \(b=0\), the challenger outputs \(F_t(k,x)\). Else, the challenger outputs a random element \(y\leftarrow \mathcal {Y}\).
Guess A outputs a guess \(b'\) of b.
Let \(x_1,\ldots , x_{q_1} \in \mathcal {X}\) be the evaluation queries, \(S_1, \ldots , S_{q_2} \subset \mathcal {X}\) be the t-punctured key queries and \(x^*_1, \ldots , x^*_s\) be the challenge queries. A wins if \(\forall i\le q_1,j \le s, ~ x_i \ne x^*_j\), \(\forall i\le q_2, j \le s, ~ x^*_j \in S_i\) and \(b'=b\). The advantage of A is defined to be \(\mathsf {Adv}^{F_t}_A(\lambda ) = Pr[A \text { wins}]\).
Definition 5
The PRF \(F_t\) is a secure t-puncturable PRF if for all PPT adversaries \(\mathcal {A}\) \(\mathsf {Adv}^{F_t}_{\mathcal {A}}(\lambda )\) is negligible in \(\lambda \).
5.1 Construction
In this section, we present our construction of t-puncturable PRFs from puncturable PRFs and indistinguishability obfuscation. Let \(F : \mathcal {K}\times \mathcal {X}\rightarrow \mathcal {Y}\) be a puncturable PRF, and \(F.\textsf {setup}\), \(F.\textsf {puncture}\), \(F.\textsf {eval}\) the corresponding setup, puncturing and evaluation algorithms. We now describe our t-puncturable PRF \(F_t\), and the corresponding algorithms \(F_t.\textsf {setup}\), \(F_t.\textsf {puncture}\) and \(F_t.\textsf {eval}\).
\({\mathbf{F_{t}.}{\textsf {setup}}{} \mathbf{(1}^{\lambda }{} \mathbf{)}}\) \(F_t.\textsf {setup}\) is the same as \(F.\textsf {setup}\).
\({\mathbf{F_{t}.}{\textsf {puncture}}{} \mathbf{(k, S)}}\) \(F_t.\textsf {puncture}(k, S)\) computes an obfuscation of the program \(\mathsf {PuncturedKey^t}_{k,S}\) defined in Fig. 4; that is, \(K_{S} \leftarrow i\mathcal {O}(\lambda , \mathsf {PuncturedKey^t}_{k, S})\). As before, the program \(\mathsf {PuncturedKey^t}_{k,S}\) is padded to be of appropriate size.
\({\mathbf{F_{t}.}{\textsf {eval}}{} \mathbf{(K_{S}, x)}}\) The punctured key \(K_{S}\) is a program that takes an input in \(\mathcal {X}\). We define
5.2 Proof of Security
We will now prove that the above construction is a secure t-puncturable PRF as defined in Definition 5.
Theorem 3
Assuming \(i\mathcal {O}\) is a secure indistinguishability obfuscator and F, together with \(F.\textsf {setup}\), \(F.\textsf {puncture}\) and \(F.\textsf {eval}\) is a secure puncturable PRF, the PRF \(F_t\) defined above, together with \(F_t.\textsf {setup}\), \(F_t.\textsf {puncture}\) and \(F_t.\textsf {eval}\), is a secure t-puncturable PRF.
For simplicity, we will assume that the adversary makes \(q_1\) evaluation queries, \(q_2\) punctured key queries and 1 challenge query. As shown by [4], this can easily be extended to the general case of multiple challenge queries via a hybrid argument. We will first define the intermediate hybrid experiments.
Game 0. This game is the original security game between the challenger and adversary \(\mathcal {A}\), where the challenger first chooses a PRF key, then \(\mathcal {A}\) makes evaluation/t-punctured key queries and finally sends the challenge input. The challenger responds with either the PRF evaluation at challenge input, or sends a random element of the range space.
-
1.
Choose a key \(k \leftarrow \mathcal {K}\).
-
2.
\(\mathcal {A}\) makes evaluation/t-punctured key queries.
-
(a)
If \(\mathcal {A}\) sends an evaluation query \(x_i\), then output \(F(k, x_i)\).
-
(b)
If \(\mathcal {A}\) sends a t-punctured key query for set \(S_j\), output the key \(K_{S_j} \leftarrow i\mathcal {O}(\mathsf {PuncturedKey^t}_{k,S_j})\).
-
(a)
-
3.
\(\mathcal {A}\) sends challenge query \(x^*\) such that \(x^* \ne x_i ~ \forall i\le q_1\) and \(x^* \in S_j ~ \forall j\le q_2\). Choose \(\beta \leftarrow \{0,1\}\). If \(\beta =0\), output \(y=F(k,x^*)\), else output \(y\leftarrow \mathcal {Y}\).
-
4.
\(\mathcal {A}\) sends \(\beta '\) and wins if \(\beta = \beta '\).
Game 1. This game is the same as the previous one, except that the challenger introduces an abort condition. When the first t-punctured key query \(S_1\) is made, the challenger guesses the challenge query \(\tilde{x} \leftarrow S_1\). The challenger aborts if any of the evaluation queries are \(\tilde{x}\), if any of the future t-punctured key queries does not contain \(\tilde{x}\) or if the challenge query \(x^* \ne \tilde{x}\).
-
1.
Choose a key \(k \leftarrow \mathcal {K}\).
-
2.
\(\mathcal {A}\) makes evaluation/t-punctured key queries.


.

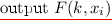
.
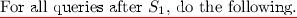
-
(a)
If \(\mathcal {A}\) sends an evaluation query \(x_i\)
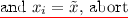
.
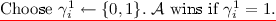
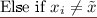
, output \(F(k,x_i)\).
-
(b)
If \(\mathcal {A}\) sends a t-punctured key query for set \(S_j\)
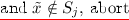
.
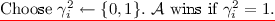
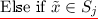
, output \(K_{S_j} \leftarrow i\mathcal {O}(\lambda , \mathsf {PuncturedKey^t}_{k,S_j})\).
-
(a)
-
3.
\(\mathcal {A}\) sends challenge query \(x^*\) such that \(x^* \ne x_i ~ \forall i\le q_1\) and \(x^* \in S_j ~ \forall j\le q_2\).
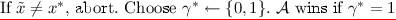
.

, choose \(\beta \leftarrow \{0,1\}\). If \(\beta =0\), output \(y=F(k,x^*)\), else output \(y\leftarrow \mathcal {Y}\).
-
4.
\(\mathcal {A}\) sends \(\beta '\) and wins if \(\beta = \beta '\).
Next, we define \(q_2\) games, Game \(1_l\), \(1\le l \le q_2\). Let Game \(1_0\) = Game 1.
Game \(1_l.\) In this game, the first l punctured key queries use \(K_{\tilde{x}}\), while the remaining use k.
-
1.
Choose a key \(k \leftarrow \mathcal {K}\).
-
2.
\(\mathcal {A}\) makes evaluation/t-punctured key queries.
Let \(S_1\) be the first t-punctured key query. Choose \(\tilde{x} \leftarrow S_1\).
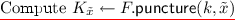
.
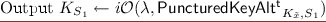
(where \(\mathsf {PuncturedKeyAlt^t}\) is defined in Fig. 5).
For all evaluation queries \(x_i\) before \(S_1\), output \(F(k,x_i)\).
For all queries after \(S_1\), do the following.
-
(a)
If \(\mathcal {A}\) sends an evaluation query \(x_i\) and \(x_i = \tilde{x}\), abort. Choose \(\gamma ^1_i \leftarrow \{0,1\}\). \(\mathcal {A}\) wins if \(\gamma ^1_i = 1\).
Else if \(x_i \ne \tilde{x}\),
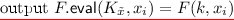
.
-
(b)
If \(\mathcal {A}\) sends a t-punctured key query for set \(S_j\) and \(\tilde{x} \notin S_j\), abort. Choose \(\gamma ^2_i \leftarrow \{0,1\}\). \(\mathcal {A}\) wins if \(\gamma ^2_i = 1\).
Else if \(\tilde{x} \in S_j\)
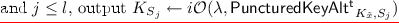
.
Else
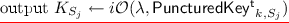
.
-
(a)
-
3.
\(\mathcal {A}\) sends challenge query \(x^*\) such that \(x^* \ne x_i ~ \forall i\le q_1\) and \(x^* \in S_j ~ \forall j\le q_2\).
If \(\tilde{x} \ne x^*\), abort. Choose \(\gamma ^* \leftarrow \{0,1\}\). \(\mathcal {A}\) wins if \(\gamma ^* = 1\).
Else if \(\tilde{x}=x^*\), choose \(\beta \leftarrow \{0,1\}\). If \(\beta =0\), output \(y= F(k,x^*)\), else output \(y\leftarrow \mathcal {Y}\).
-
4.
\(\mathcal {A}\) sends \(\beta '\) and wins if \(\beta = \beta '\).
Game 2. In this game, the challenger outputs a random element as the response to the challenge query.
-
1.
Choose a key \(k \leftarrow \mathcal {K}\).
-
2.
\(\mathcal {A}\) makes evaluation/t-punctured key queries.
Let \(S_1\) be the first t-punctured key query. Choose \(\tilde{x} \leftarrow S_1\) and compute \(K_{\tilde{x}} \leftarrow F.\textsf {puncture}(k, \tilde{x})\).
Output \(K_{S_1} \leftarrow i\mathcal {O}(\lambda , \mathsf {PuncturedKeyAlt^t}_{K_{\tilde{x}},S_1})\).
For all evaluation queries \(x_i\) before \(S_1\), output \(F(k,x_i)\).
For all queries after \(S_1\), do the following.
-
(a)
If \(\mathcal {A}\) sends an evaluation query \(x_i\) and \(x_i = \tilde{x}\), abort. Choose \(\gamma ^1_i \leftarrow \{0,1\}\). \(\mathcal {A}\) wins if \(\gamma ^1_i = 1\).
Else if \(x_i \ne \tilde{x}\), output \(F.\textsf {eval}(K_{\tilde{x}},x_i) = F(k, x_i)\).
-
(b)
If \(\mathcal {A}\) sends a t-punctured key query for set \(S_j\) and \(\tilde{x} \notin S_j\), abort. Choose \(\gamma ^2_i \leftarrow \{0,1\}\). \(\mathcal {A}\) wins if \(\gamma ^2_i = 1\).
Else if \(\tilde{x} \in S_j\), output \(K_{S_j} \leftarrow i\mathcal {O}(\lambda , \mathsf {PuncturedKeyAlt^t}_{K_{\tilde{x}},S_j})\).
-
(a)
-
3.
\(\mathcal {A}\) sends challenge query \(x^*\) such that \(x^* \ne x_i ~ \forall i\le q_1\) and \(x^* \in S_j ~ \forall j\le q_2\).
If \(\tilde{x} \ne x^*\), abort. Choose \(\gamma ^* \leftarrow \{0,1\}\). \(\mathcal {A}\) wins if \(\gamma ^* = 1\).
Else if \(\tilde{x}=x^*\), choose \(\beta \leftarrow \{0,1\}\) and
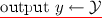
.
-
4.
\(\mathcal {A}\) sends \(\beta '\) and wins if \(\beta = \beta '\).
Adversary’s Advantage in These Games. Let \(\mathsf {Adv}^i_{\mathcal {A}}\) denote the advantage of adversary \(\mathcal {A}\) in Game i.
Observation 2
For any adversary \(\mathcal {A}\), \(\mathsf {Adv}^{1}_{\mathcal {A}} \ge \mathsf {Adv}^{0}_{\mathcal {A}}/t\).
Proof
Since one of the elements of \(S_1\) will be the challenge input, and \(|S_1| \le t\), the challenger’s guess is correct with probability \(1/|S_1| \ge 1/t\). Hence, \(\mathsf {Adv}^1_{\mathcal {A}} \ge \mathsf {Adv}^0_{\mathcal {A}}/t\).
We will now show that Game \(1_{l}\) and Game \(1_{l+1}\) are computationally indistinguishable, assuming \(i\mathcal {O}\) is secure.
Claim 6
If there exists a PPT adversary \(\mathcal {A}\) such that \(\mathsf {Adv}^{1_l}_{\mathcal {A}} - \mathsf {Adv}^{1_{l+1}}_{\mathcal {A}} \) is non-negligible in \(\lambda \), then there exists a PPT distinguisher \(\mathcal {B}\) that breaks the security of \(i\mathcal {O}\) with advantage non-negligible in \(\lambda \).
Proof
Note that the only difference between Game \(1_l\) and Game \(1_{l+1}\) is in the response to the \((l+1)th\) t-punctured key query. In Game \(1_l\), \(\mathsf {PuncturedKey^t}_{k,S_{l+1}}\) is used to compute \(K_{S_{l+1}}\), while in Game \(1_{l+1}\), \(\mathsf {PuncturedKeyAlt^t}_{K_{\tilde{s}}, S_{l+1}}\) is used. Suppose there exists a PPT adversary \(\mathcal {A}\) such that \(\mathsf {Adv}^{1_l}_{\mathcal {A}} - \mathsf {Adv}^{1_{l+1}}_{\mathcal {A}} = \epsilon \). We will construct a PPT algorithm \(\mathcal {B}\) that interacts with \(\mathcal {A}\) and breaks the security of \(i\mathcal {O}\) with advantage \(\epsilon \).
\(\mathcal {B}\) chooses \(k\leftarrow \mathcal {K}\) and for all evaluation queries \(x_i\) before the first t-punctured key query, outputs \(F(k, x_i)\). On receiving the first t-punctured key query \(S_1\), \(\mathcal {B}\) chooses \(\tilde{x} \leftarrow S_1\) and computes \(K_{\tilde{x}} \leftarrow F.\textsf {puncture}(k,\tilde{x})\). The evaluation queries are computed as in Game \(1_l\) and \(1_{l+1}\). The first l t-punctured key queries are constructed using k, while the last \(q_2-l-1\) t-punctured keys are constructed using \(K_{\tilde{x}}\) (as in Game \(1_l\) and Game \(1_{l+1}\)). For the \((l+1)th\) query, \(\mathcal {B}\) does the following. \(\mathcal {B}\) sets \(C_0 = \mathsf {PuncturedKey^t}_{k,S_{l+1}}\) and \(C_1 = \mathsf {PuncturedKeyAlt^t}_{K_{\tilde{x}}, S_{l+1}}\), and sends \(C_0, C_1\) to the \(i\mathcal {O}\) challenger, and receives \(K_{S_{l+1}}\) in response, which it sends to \(\mathcal {A}\).
Finally, after all queries, the challenger sends the challenge query \(x^*\). \(\mathcal {B}\) checks that \(\tilde{x} = x^*\), sets \(y_0 = F(k, x^*)\) and chooses \(y_1\leftarrow \mathcal {Y}, \beta \leftarrow \{0,1\}\). It outputs \(y_{\beta }\) and receives \(\beta '\) in response. If \(\beta = \beta '\), \(\mathcal {B}\) outputs 0, else it outputs 1.
From the correctness property of puncturable PRFs, it follows that \(F.\textsf {eval}(K_{\tilde{x}}, x)\) \(= F(k,x)\) for all \(x\notin S_{l+1}\). Hence, the circuits \(C_0\) and \(C_1\) are functionally identical. This completes our proof.
Next, we show that Game \(1_{q_2}\) and Game 2 are computationally indistinguishable.
Claim 7
If there exists a PPT adversary \(\mathcal {A}\) such that \(\mathsf {Adv}^{1_{q_2}}_{\mathcal {A}} - \mathsf {Adv}^{2}_{\mathcal {A}} \) is non-negligible in \(\lambda \), then there exists a PPT distinguisher \(\mathcal {B}\) that breaks the security of puncturable PRF F with advantage non-negligible in \(\lambda \).
Proof
We will use \(\mathcal {A}\) to construct a PPT algorithm \(\mathcal {B}\) that breaks the security of puncturable PRF F with advantage \(\mathsf {Adv}^{1_{q_2}}_{\mathcal {A}} - \mathsf {Adv}^2_{\mathcal {A}}\). Observe that in Game \(1_{q_2}\), the challenger requires the master key k only for the evaluation queries before the first t-punctured key query. After the first t-punctured key query \(S_1\), the challenger chooses \(\tilde{x} \leftarrow S_1\), computes a punctured key \(K_{\tilde{x}}\), and uses this to compute all future evaluation queries and t-punctured keys.
\(\mathcal {B}\) begins interacting with \(\mathcal {A}\). For each evaluation query \(x_i\) before the first t-punctured key query, \(\mathcal {B}\) sends \(x_i\) to the puncturable PRF challenger, and receives \(y_i\), which it forwards to \(\mathcal {A}\). On receiving the first t-punctured key query \(S_1\), \(\mathcal {B}\) chooses \(\tilde{x} \leftarrow S_1\) and sends \(\tilde{x}\) as challenge input to the puncturable PRF challenger. \(\mathcal {B}\) receives \(K_{\tilde{x}}\) and y. It uses \(K_{\tilde{x}}\) for all remaining queries. On receiving challenge \(x^*\) from \(\mathcal {A}\), \(\mathcal {B}\) checks \(x^* = \tilde{x}\) and sends y. \(\mathcal {B}\) sends \(\mathcal {A}\)’s response to the PRF challenger.
Note that until the challenge query is made, both games are identical and \(\mathcal {B}\) simulates them perfectly. If y is truly random, then \(\mathcal {A}\) receives a response as per Game 2, else it receives a response as per Game \(1_{q_2}\).
Finally, we have the following simple observation.
Observation 3
For any adversary, \(\mathsf {Adv}^3_{\mathcal {A}} = 0\).
From the above claims and observations, we can conclude that if \(i\mathcal {O}\) is a secure indistinguishability obfuscator as per Definition 2, and F, together with \(F.\textsf {setup}, F.\textsf {puncture}, F.\textsf {eval}\) is a secure puncturable PRF as per Definition 4, then any PPT adversary \(\mathcal {A}\) has negligible advantage in Game 0.
6 Conclusion
Puncturable and t-puncturable PRFs have numerous cryptographic applications. This work provides the first constructions and proofs of adaptive security in the standard model. This is an interesting step forward in its own right, and we believe the techniques used to achieve adaptiveness from indistinguishability obfuscation may be useful elsewhere. Moreover, this work resolves for at least the puncturable PRF space, the larger question of characterizing which classes of functions admit an adaptively-secure constrained PRF in the standard model. As noted earlier, the results of [11] and [16] provide intuition both for and against whether this is indeed possible for many other function families.
Notes
- 1.
- 2.
This definition can be extended to handle multiple challenge points. See Sect. 3 for details.
- 3.
- 4.
In fact, the GGM PRF construction can be used to construct prefix-fixing constrained PRFs.
- 5.
Looking ahead, in the proof of security, the program \(\mathsf {PuncturedKey}_{k,x'}\) will be replaced by \(\mathsf {PuncturedKey}'_{V,w,D,u,x'}\), \(\mathsf {PuncturedKeyAlt}_{u,k,k',x'}\) and \(\mathsf {PuncturedKeyAlt}'_{u,W,E,k,x'}\) in subsequent hybrids. Since this transformation relies on \(i\mathcal {O}\) being secure, we need that all programs have same size. Hence, all programs are padded appropriately to ensure that they have the same size.
References
Agrawal, S., Boneh, D., Boyen, X.: Efficient lattice (H)IBE in the standard model. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 553–572. Springer, Heidelberg (2010)
Bitansky, N., Canetti, R., Paneth, O., Rosen, A.: Indistinguishability obfuscation vs. auxiliary-input extractable functions: One must fall. Cryptology ePrint Archive, Report 2013/641 (2013). http://eprint.iacr.org/
Boneh, D., Boyen, X.: Secure identity based encryption without random oracles. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 443–459. Springer, Heidelberg (2004)
Boneh, D., Waters, B.: Constrained pseudorandom functions and their applications. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013, Part II. LNCS, vol. 8270, pp. 280–300. Springer, Heidelberg (2013)
Boneh, D., Zhandry, M.: Multiparty key exchange, efficient traitor tracing, and more from indistinguishability obfuscation. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014, Part I. LNCS, vol. 8616, pp. 480–499. Springer, Heidelberg (2014)
Boyle, E., Goldwasser, S., Ivan, I.: Functional signatures and pseudorandom functions. In: Krawczyk, H. (ed.) PKC 2014. LNCS, vol. 8383, pp. 501–519. Springer, Heidelberg (2014)
Chandran, N., Raghuraman, S., Vinayagamurthy, D.: Constrained pseudorandom functions: Verifiable and delegatable. Cryptology ePrint Archive, Report 2014/522 (2014). http://eprint.iacr.org/
Chase, M., Meiklejohn, S.: Déjà Q: using dual systems to revisit q-type assumptions. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 622–639. Springer, Heidelberg (2014)
Freire, E.S.V., Hofheinz, D., Paterson, K.G., Striecks, C.: Programmable hash functions in the multilinear setting. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013, Part I. LNCS, vol. 8042, pp. 513–530. Springer, Heidelberg (2013)
Fuchsbauer, G.: Constrained verifiable random functions. In: Abdalla, M., De Prisco, R. (eds.) SCN 2014. LNCS, vol. 8642, pp. 95–114. Springer, Heidelberg (2014)
Fuchsbauer, G., Konstantinov, M., Pietrzak, K., Rao, V.: Adaptive security of constrained PRFs. In: Sarkar, P., Iwata, T. (eds.) ASIACRYPT 2014, Part II. LNCS, vol. 8874, pp. 82–101. Springer, Heidelberg (2014)
Garg, S., Gentry, C., Halevi, S., Raykova, M., Sahai, A., Waters, B.: Candidate indistinguishability obfuscation and functional encryption for all circuits. In: FOCS (2013)
Gentry, C., Lewko, A., Sahai, A., Waters, B.: Indistinguishability obfuscation from the multilinear subgroup elimination assumption. Cryptology ePrint Archive, Report 2014/309 (2014). http://eprint.iacr.org/
Goldreich, O., Goldwasser, S., Micali, S.: How to construct random functions (extended abstract). In: FOCS, pp. 464–479 (1984)
Golle, P., Jarecki, S., Mironov, I.: Cryptographic primitives enforcing communication and storage complexity. In: Financial Cryptography, pp. 120–135 (2002)
Hofheinz, D.: Fully secure constrained pseudorandom functions using random oracles. IACR Cryptology ePrint Archive, Report 2014/372 (2014)
Hofheinz, D., Kiltz, E.: Programmable hash functions and their applications. J. Cryptology 25(3), 484–527 (2012)
Hohenberger, S., Sahai, A., Waters, B.: Full domain hash from (Leveled) multilinear maps and identity-based aggregate signatures. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013, Part I. LNCS, vol. 8042, pp. 494–512. Springer, Heidelberg (2013)
Hohenberger, S., Sahai, A., Waters, B.: Replacing a random oracle: full domain hash from indistinguishability obfuscation. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 201–220. Springer, Heidelberg (2014)
Hohenberger, S., Waters, B.: Constructing verifiable random functions with large input spaces. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 656–672. Springer, Heidelberg (2010)
Kiayias, A., Papadopoulos, S., Triandopoulos, N., Zacharias, T.: Delegatable pseudorandom functions and applications. In: ACM Conference on Computer and Communications Security, pp. 669–684 (2013)
Lewko, A., Waters, B.: New proof methods for attribute-based encryption: achieving full security through selective techniques. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 180–198. Springer, Heidelberg (2012)
Naor, M., Reingold, O.: Number-theoretic constructions of efficient pseudo-random functions. J. ACM 51(2), 231–262 (2004)
Sahai, A., Waters, B.: How to use indistinguishability obfuscation: deniable encryption, and more. In: STOC, pp. 475–484 (2014)
Waters, B.: Efficient identity-based encryption without random oracles. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 114–127. Springer, Heidelberg (2005)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2015 International Association for Cryptologc Research
About this paper
Cite this paper
Hohenberger, S., Koppula, V., Waters, B. (2015). Adaptively Secure Puncturable Pseudorandom Functions in the Standard Model. In: Iwata, T., Cheon, J. (eds) Advances in Cryptology -- ASIACRYPT 2015. ASIACRYPT 2015. Lecture Notes in Computer Science(), vol 9452. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-48797-6_4
Download citation
DOI: https://doi.org/10.1007/978-3-662-48797-6_4
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-48796-9
Online ISBN: 978-3-662-48797-6
eBook Packages: Computer ScienceComputer Science (R0)