Leakage Assessment Methodology

Abstract

Evoked by the increasing need to integrate side-channel countermeasures into security-enabled commercial devices, evaluation labs are seeking a standard approach that enables a fast, reliable and robust evaluation of the side-channel vulnerability of the given products. To this end, standardization bodies such as NIST intend to establish a leakage assessment methodology fulfilling these demands. One of such proposals is the Welch’s t-test, which is being put forward by Cryptography Research Inc., and is able to relax the dependency between the evaluations and the device’s underlying architecture. In this work, we deeply study the theoretical background of the test’s different flavors, and present a roadmap which can be followed by the evaluation labs to efficiently and correctly conduct the tests. More precisely, we express a stable, robust and efficient way to perform the tests at higher orders. Further, we extend the test to multivariate settings, and provide details on how to efficiently and rapidly carry out such a multivariate higher-order test. Including a suggested methodology to collect the traces for these tests, we point out practical case studies where different types of t-tests can exhibit the leakage of supposedly secure designs.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The threat of side-channel analysis attacks is well known by the industry sector. Hence, the necessity to integrate corresponding countermeasures into the commercial products has become inevitable. Regardless of the type and soundness of the employed countermeasures, the security evaluation of the prototypes with respect to the effectiveness of the underlying countermeasure in practice is becoming one of the major concerns of the producers and evaluation labs. For example, the power of side-channel analysis as devastating attacks motivated the NIST to hold the “Non-Invasive Attack Testing Workshop” in 2011 to establish a testing methodology capable of robustly assessing the physical vulnerability of cryptographic devices.

With respect to common criteria evaluations – defined and used by governing bodies like ANSSI and BSI – the evaluation labs need to practically examine the feasibility of the state-of-the-art attacks conducted on the device under test (DUT). The examples include but not restricted to the classical differential power analysis (DPA) [12], correlation power analysis (CPA) [4], and mutual information analysis (MIA) [8]. To cover the most possible cases a large range of intermediate values as well as hypothetical (power) models should be examined to assess the possibility of the key recovery. This methodology is becoming more challenging as the number and types of known side-channel attacks are steadily increasing. Trivially, this time-consuming procedure cannot be comprehensive even if a large number of intermediate values and models in addition to several know attacks are examined. In fact, the selection of the hypothetical model is not simple and strongly depends on the expertise of the evaluation labs’ experts. If the models were poorly chosen and as a result none of the key-recovery attacks succeeded, the evaluation lab would issue a favorable evaluation report even though the DUT might be vulnerable to an attack with a more advanced and complex model. This strongly motivates the need for an evaluation procedure which avoids being dependent on attack(s), intermediate value(s), and hypothetical model(s).

On one hand, two information-theoretic tests [5, 6] are known which evaluate the leakage distributions either in a continuous or discrete form. These approaches are based on the mutual information and need to estimate the probability distribution of the leakages. This adds other parameter(s) to the test with respect to the type of the employed density estimation technique, e.g., kernel or histogram and their corresponding parameters. Moreover, they cannot yet focus on a certain statistical order of the leakages. This becomes problematic when e.g., the first-order security of a masking countermeasure is expected to be assessed. On the other hand, two leakage assessment methodologies (specific and non-specific t-tests) based on the Student’s t-distribution have been proposed (at the aforementioned workshop [9]) with the goal to detect any type of leakage at a certain order. A comparative study of these three test vectors is presented in [14], where the performance of specific t-tests (only at the first order) is compared to that of other mutual information-based tests.

In general, the non-specific t-test examines the leakage of the DUT without performing an actual attack, and is in addition independent of its underlying architecture. The test gives a level of confidence to conclude that the DUT has an exploitable leakage. It indeed provides no information about the easiness/hardness of an attack which can exploit the leakage, nor about an appropriate intermediate value and the hypothetical model. However, it can easily and rapidly report that the DUT fails to provide the desired security level, e.g., due to a mistake in the design engineering or a flaw in the countermeasure [2].

Our Contribution. The Welch’s t-test has been used in a couple of research works [2, 3, 13, 16, 20, 21, 23, 26] to investigate the efficiency of the proposed countermeasures, but without extensively expressing the challenges of the test procedure. This document aims at putting light on a path for e.g., evaluation labs, on how to examine the leakage of the DUT at any order with minimal effort and without any dependency to a hypothetical model. Our goal in this work is to cover the following points:

• We try to explain the underlying statistical concept of such a test by a (hopefully) more understandable terminology.

• In the seminal paper by Goodwill et al. [9] it has been shown how to conduct the test at the first order, i.e., how to investigate the first-order leakage of the DUT. The authors also shortly stated that the traces can be preprocessed to run the same test at higher orders. Here we point out the issues one may face to run such a test at higher orders, and provide appropriate solutions accordingly. As a motivating point we should refer to [14], where the t-test is supposed to be able to be performed at only the first order.

• More importantly, we extend the test to cover multivariate leakages and express the necessary formulations in detail allowing us to efficiently conduct t-tests at any order and any variate.

• In order to evaluate the countermeasures (mainly those based on masking at high orders) several million traces might be required (e.g., see [3, 13]). Hence we express the procedures which allow conducting the tests by means of multi-core CPUs in a parallelized way.

• We give details of how to design appropriate frameworks to host the DUT for such tests, including both software and hardware platforms. Particularly we consider a microcontroller as well as an FPGA (SASEBO) for this purpose.

• Depending on the underlying application and platform, the speed of the measurement is a bottleneck which hinders the collection of several million measurements. Due to this reason, the evaluation labs are usually restricted (commonly by common criteria) to measure not more than one million traces from any DUT. We also demonstrate a procedure to accelerate the measurement process allowing the collection of e.g., millions of traces per hour.

2 Statistical Background

A fundamental question in many different scientific fields is whether two sets of data are significantly different from each other. The most common approach to answer such a question is Welch’s t-test in which the test statistic follows a Student’s t distribution. The aim of a t-test is to provide a quantitative value as a probability that the mean $\mu$ of two sets are different. In other words, a t-test gives a probability to examine the validity of the null hypothesis as the samples in both sets were drawn from the same population, i.e., the two sets are not distinguishable.

Hence let $\mathcal {Q}_0$ and $\mathcal {Q}_1$ indicate two sets which are under the test. Let also $\mu _0$ (resp. $\mu _1$) and ${s_0}^2$ (resp. ${s_1}^2$) stand for the sample mean and sample variance of the set $\mathcal {Q}_0$ (resp. $\mathcal {Q}_1$), and $n_0$ and $n_1$ the cardinality of each set. The t-test statistic and the degree of freedom $\mathrm {v}$ are computed as

$$\begin{aligned} \mathrm {t}=\frac{\mu _0-\mu _1}{\sqrt{\frac{{s_0}^2}{n_0}+\frac{{s_1}^2}{n_1}}},~~~~~~~~~~~~~~~~~~~~ \mathrm {v}=\frac{\Big (\frac{{s_0}^2}{n_0}+\frac{{s_1}^2}{n_1}\Big )^2}{ \frac{\Big (\frac{{s_0}^2}{n_0}\Big )^2}{n_0-1}+ \frac{\Big (\frac{{s_1}^2}{n_1}\Big )^2}{n_1-1}}. \end{aligned}$$

(1)

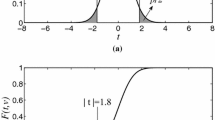
In cases, where ${s_0}\,\approx \,{s_1}$ and $n_0\,\approx \,n_1$, the degree of freedom can be estimated by $\mathrm {v}\,\approx \,n_0+n_1=n$. As the final step, we estimate the probability to accept the null hypothesis by means of Student’s t distribution density function. In other words, based on the degree of freedom v the Student’s t distribution function is drawn

$$\begin{aligned} f(t,v) = \frac{\varGamma (\frac{v+1}{2})}{\sqrt{\pi v}\,\varGamma (\frac{v}{2})} \left( 1+\frac{t^2}{v} \right) ^{-\frac{v+1}{2}}, \end{aligned}$$

where $\varGamma (.)$ denotes the gamma function. Based on the two-tailed Welch’s t-test the desired probability is calculated as

$$ p=2\,\int _{|\mathrm {t}|}^{\infty }f(t,\mathrm {v})\,dt. $$

Figure 1(a) represents a graphical view of such a test.

As an alternative, we can make use of the corresponding cumulative distribution function

$$F(t,v)=\frac{1}{2} + t\, \varGamma \left( \frac{v+1}{2} \right) \frac{\,_2F_1 \left( \frac{1}{2},\frac{v+1}{2};\frac{3}{2};-\frac{x^2}{v} \right) }{\sqrt{\pi v}\,\varGamma \left( \frac{v}{2}\right) },$$

with $_2F_1(.,.;.;.)$ the hypergeometric function. Hence the result of the t-test can be estimated as

$$ p=2\,F(-|\mathrm {t}|,\mathrm {v}). $$

For a graphical view see Fig. 1(b). Note that such a function is available amongst the Matlab embedded functions as

and for R as

Fig. 1.

Student’s t distribution functions and two-tailed Welch’s t-test (examples for $v=10,000$)

Hence, small p values (alternatively big $\mathrm {t}$ values) give evidence to reject the null hypothesis and conclude that the sets were drawn from different populations. For the sake of simplicity, usually a threshold $|\mathrm {t}|$ $> 4.5$ is defined to reject the null hypothesis without considering the degree of freedom and the aforementioned cumulative distribution function. This intuition is based on the fact that $p=2\,F(-4.5,v\,>\,1000)\,<\,0.00001$ which leads to a confidence of $>\,0.99999$ to reject the null hypothesis.

3 Methodology

Suppose that in a side-channel evaluation process, with respect to n queries with associated data (e.g., plaintext or ciphertext) $D_{i\in \{1,\ldots ,n\}}$, n side-channel measurements (so-called traces) are collected while the device under test operates with a secret key that is kept constant. Let us denote each trace by $T_{i\in \{1,\ldots ,n\}}$ containing m sample points $\{t_i^{(1)},\ldots ,t_i^{(m)}\}$.

As a straightforward evaluation process, the traces are categorized into two sets $\mathcal {Q}_0$ and $\mathcal {Q}_1$ and the test is conducted at each sample point $\{1,\ldots ,m\}$ separately. In other words, the test is performed in a univariate fashion. At this step such a categorization is done by means of an intermediate value corresponding to the associated data D. Since the underlying process is an evaluation procedure, the secret key is known and all the intermediate values can be computed. Based on the concept of the classical DPA [12], a bit of an intermediate value (e.g., an Sbox output bit at the first cipher round) is selected to be used in the categorization.

$$\mathcal {Q}_0\,=\,\{T_i\,|\,\mathrm {target\,bit}(D_i)=0\},~~~~~~~ \mathcal {Q}_1\,=\,\{T_i\,|\,\mathrm {target\,bit}(D_i)=1\}.$$

If the corresponding t-test reports that with a high confidence the two trace groups (at certain sample points) are distinguishable from each other, it is concluded that the corresponding DPA attack is – most likely – able to recover the secret key.

Such a test (so-called specific t-test) is not restricted to only single-bit scenarios. For instance, an 8-bit intermediate value (e.g., an Sbox output byte) can be used to categorize the traces as

$$\mathcal {Q}_0\,=\,\{T_i\,|\,\mathrm {target\,byte}(D_i)=\mathrm {x}\},~~~~~~~ \mathcal {Q}_1\,=\,\{T_i\,|\,\mathrm {target\,byte}(D_i)\ne \mathrm {x}\}.$$

In this case, a particular value for $\mathrm {x}$ should be selected prior to the test. Therefore, in case of an 8-bit target intermediate value 256 specific t-tests can be performed. It should be noted that in such tests, $n_0$ and $n_1$ (as the cardinality of $\mathcal {Q}_0$ and $\mathcal {Q}_1$) would be significantly different if the associated data D were drawn randomly. Hence, the accuracy of the estimated (sample) means ($\mu _0$, $\mu _1$) as well as variances (${s_0}^2$, ${s_1}^2$) would not be the same. However, this should not – in general – cause any issue as the two-tailed Welch’s t-test covers such a case.

Therefore, the evaluation can be performed by many different intermediate values. For example, in case of an AES-128 encryption engine by considering the AddRoundKey, SubBytes, ShiftRows, and MixColumns outputs, $4\,\times \,128$ bit-wise tests and $4\,\times \,16\,\times \,256$ byte-wise tests (only at the first cipher round) can be conducted. This already excludes the XOR result between the intermediate values, which depending on the underlying architecture of the DUT (e.g., a serialized architecture) may lead to potential leaking sources. Therefore, such tests suffer from the same weakness as state-of-the-art attacks since both require to examine many intermediate values and models, which prevents a comprehensive evaluation.

To cope with this imperfection a non-specific t-test can be performed, which avoids being dependent on any intermediate value or a model. In such a test the associated data should follow a certain procedure during the trace collection. More precisely a fixed associated data $\mathrm {D}$ is preselected, and the DUT is fed by $\mathrm {D}$ or by a random source in a non-deterministic and randomly-interleaved fashion. As a more clear explanation suppose that before each measurement a coin is flipped, and accordingly $\mathrm {D}$ or a fresh-randomly selected data is given to the DUT. The corresponding t-test is performed by categorizing the traces based on the associated data ($\mathrm {D}$ or random). Hence such a test is also called fixed vs. random t-test.

The randomly-interleaved procedure is unavoidable; otherwise the test may issue a false-positive result on the vulnerability of the DUT. It is mainly due to the fact that the internal state of the DUT at the start of each query should be also non-deterministic. As an example, if the traces with associated data $\mathrm {D}$ are collected consecutively, the DUT internal state is always the same prior to each measurement with $\mathrm {D}$. As another example, if the traces with random associated data and $\mathrm {D}$ are collected one after each other (e.g., $D_i$ being random for even i and $\mathrm {D}$ for odd i), the DUT internal state is always the same prior to each measurement with random associated data.

In order to explain the concept behind the non-specific t-test, assume a specific t-test based on a single-bit intermediate variable w of the underlying process of the DUT and the corresponding sample point $\mathrm {j}$ where the leakage associated to w is measured. Further, let us denote the estimated means of the leakage traces at sample point $\mathrm {j}$ by $\mu _{w=0}$ and $\mu _{w=1}$, i.e., those applied in the specific t-test. If these two means are largely enough different from each other, each of them is also distinguishable from the overall mean $\mu$ ($\approx \,\frac{\displaystyle {\mu _{w=0}\,+\,\mu _{w=1}}}{2}$ supposing $n_0 \approx n_1$).

From another perspective, consider two non-specific t-tests with the fixed associated data $\mathrm {D}_{w=0}$ and $\mathrm {D}_{w=1}$, where $\mathrm {D}_{w=0}$ leads to the intermediate value $w=0$ (respectively for $\mathrm {D}_{w=1}$). Also, suppose that in each of these two tests $\mathcal {Q}_0$ corresponds to the traces with the fixed associated data and $\mathcal {Q}_1$ to those with random. Hence, in the non-specific test with $\mathrm {D}_{w=0}$, the estimated mean $\mu _0$ at sample point $\mathrm {j}$ is close to $\mu _{w=0}$ (respectively to $\mu _{w=1}$ in the test with $\mathrm {D}_{w=1}$). But in both tests the estimated mean $\mu _1$ (of $\mathcal {Q}_1$) is close to $\mu$ (defined above). Therefore, in both tests the statistic ($\mathrm {t}^{non-spec.}$) is smaller than that of the specific test ($\mathrm {t}^{spec.}$) since $\mu _{w=0}\,<\,\mu \,<\,\mu _{w=1}$ (or respectively $\mu _{w=1}\,<\,\mu \,<\,\mu _{w=0}$). However, even supposing $n_0 \approx n_1$ it cannot be concluded that

$$\begin{aligned} |\mathrm {t}^{non-spec.}|\,=\,|\mathrm {t}^{spec.}|/2 \end{aligned}$$

since the estimated overall variance at sample point $\mathrm {j}$ (which is that of $\mathcal {Q}_1$ in both non-specific tests) is

$$\begin{aligned} {s_1}^2\,=\,\frac{(s_{w=0})^2+(s_{w=1})^2}{2}\,+\,\Big (\frac{\mu _{w=0}-\mu _{w=1}}{2}\Big )^2\,\ne \,(s_{w=0/1})^2, \end{aligned}$$

assuming $n_0 \approx n_1$.

As a result if a non-specific t-test reports a detectable leakage, the specific one results in the same conclusion but with a higher confidence. Although any intermediate value (either bit-wise or at larger scales) as well as the combination between different intermediate values are covered by the non-specific t-test, the negative result (i.e., no detectable leakage) cannot be concluded from a single non-specific test due to its dependency to the selected fixed associated data $\mathrm {D}$. In other words, it may happen that a non-specific t-test by a certain $\mathrm {D}$ reports no exploitable leakage, but the same test using another $\mathrm {D}$ leads to the opposite conclusion. Hence, it is recommended to repeat a non-specific test with a couple of different $\mathrm {D}$ to avoid a false-positive conclusion on resistance of the DUT.

The non-specific t-test can also be performed by a set of particular associated data $\mathcal {D}$ instead of a unique $\mathrm {D}$. The associated data in $\mathcal {D}$ are selected in such a way that all of them lead to a certain intermediate value. For example, a set of plaintexts which cause half of the cipher state at a particular cipher round to be constant. In this case $\mathcal {Q}_0$ refers to the traces with associated data – randomly – selected from $\mathcal {D}$ (respectively $\mathcal {Q}_1$ to the traces with random associated data). Such a non-specific t-test is also known as the semi-fixed vs. random test [7], and is particularly useful where the test with a unique $\mathrm {D}$ leads to a false-positive result on the vulnerability of the DUT. We express the use cases of each test in more details in Sect. 6.

Order of the Test. Recalling the definition of first-order resistance, the estimated means of leakages associated to the intermediate values of the DUT should not be distinguishable from each other (i.e., the concept behind the Welch’s t-test). Otherwise, if such an intermediate value is sensitive and predictable knowing the associated data D (e.g., the output of an Sbox at the first cipher round) a corresponding first-order DPA/CPA attack is expected to be feasible. It can also be extended to the higher orders by following the definition of univariate higher-order attacks [17]. To do so (as also stated in [9]) the collected traces need to be preprocessed. For example, for a second-order evaluation each trace – at each sample point independently – should be mean-free squared prior to the t-test. Here we formalize this process slightly differently as follows.

Let us first denote the dth-order raw statistical moment of a random variable X by $M_d=\mathsf {E}(X^d)$, with $\mu =M_1$ the mean and $\mathsf {E}(.)$ the expectation operator. We also denote the dth-order ($d\,>\,1$) central moment by $CM_d=\mathsf {E}\left( \left( X-\mu \right) ^d\right)$, with $s^2=CM_2$ the variance. Finally, the dth-order ($d\,>\,2$) standardized moment is denoted by $SM_d=\mathsf {E}\left( \left( \frac{X-\mu }{s}\right) ^d\right)$, with $SM_3$ the skewness and $SM_4$ the kurtosis.

In a first-order univariate t-test, for each set ($\mathcal {Q}_0$ or $\mathcal {Q}_1$) the mean ($M_1$) is estimated. For a second-order univariate test the mean of the mean-free squared traces $Y=(X-\mu )^2$ is actually the variance ($CM_2$) of the original traces. Respectively, in a third and higher ($d\,>\,2$) order test the standardized moment $SM_d$ is the estimated mean of the preprocessed traces. Therefore, the higher-order tests can be conducted by employing the corresponding estimated (central or standardized) moments instead of the means. The remaining point is how to estimate the variance of the preprocessed traces for higher-order tests. We deal with this issue in Sect. 4.2 and explain the corresponding details.

As stated, all the above given expressions are with respect to univariate evaluations, where the traces at each sample point are independently processed. For a bivariate (respectively multivariate) higher-order test different sample points of each trace should be first combined prior to the t-test, e.g., by centered product at the second order. A more formal definition of these cases is given in Sect. 5.

4 Efficient Computation

As stated in the previous section, the first order t-test requires the estimation of two parameters (sample mean $\mu$ and sample variance $s^2$) for each set $\mathcal {Q}_0$ and $\mathcal {Q}_1$. This can lead to problems concerning the efficiency of the computations and the accuracy of the estimations. In the following we address most of these problems and propose a reasonable solution for each of them. For simplicity we omit to mention the sets $\mathcal {Q}_0$ and $\mathcal {Q}_1$ (and the corresponding indices for the means and variances). All the following expressions are based on focusing on one of these sets, which should be repeated on the other set to complete the required computations of a t-test. Unless otherwise stated, we focus on a univariate scenario. Hence, the given expressions should be repeated at each sample point separately.

Using the basic definitions given in Sect. 3, it is possible to compute the first raw and second central moments ($M_1$ and $CM_2$) for a first order t-test. However, the resulting algorithm is inefficient as it requires to process the whole trace pool (a single point) twice to estimate $CM_2$ since it requires $M_1$ during the computation.

An alternative would be to use the displacement law to derive $CM_2$ from the first two raw moments as

$$\begin{aligned} CM_2\,=\,\mathsf {E}(X^2)-\mathsf {E}(X)^2\,=\,M_2-{M_1}^2. \end{aligned}$$

(2)

whereas it results in a one-pass algorithm, it is still not the optimal choice as it may be numerically unstable [10]. During the computation of the raw moments the intermediate values tend to become very large which can lead to a loss in accuracy. Further, $M_2$ and ${M_1}^2$ can be large values, and the result of $M_2-{M_1}^2$ can also lead to a significant accuracy loss due to the limited fraction significand of floating point formats (e.g., IEEE 754).

In the following we present a way to compute the two required parameters for the t-test at any order in one pass and with proper accuracy. This is achieved by using an incremental algorithm to update the central sums from which the needed parameters are derived.

4.1 Incremental One-Pass Computation of All Moments

The basic idea of an incremental algorithm is to update the intermediate results for each new trace added to the trace pool. This has the advantage that the computation can be run in parallel to the measurements. In other words, it is not necessary to collect all the traces, estimate the mean and then estimate the variance. Since the evaluation can be stopped as soon as the t-value surpasses the threshold, this helps to reduce the evaluation time even further. Finding such an algorithm for the raw moments is trivial. In the following we recall the algorithm of [18] to compute all central moments iteratively, and further show how to derive the standardized moments accordingly.

Suppose that $M_{1,\mathcal {Q}}$ denotes the first raw moment (sample mean) of the given set $\mathcal {Q}$. With y as a new trace to the set, the first raw moment of the enlarged set $\mathcal {Q}'=\mathcal {Q}\cup \{y\}$ can be updated as

$$\begin{aligned} M_{1,\mathcal {Q}'} = M_{1,\mathcal {Q}} + \frac{\varDelta }{n}, \end{aligned}$$

where $\varDelta = y - M_{1,\mathcal {Q}}$, and n the cardinality of $\mathcal {Q}'$. Note that $\mathcal {Q}$ and $M_{1,\mathcal {Q}}$ are initialized with $\emptyset$ and respectively zero.

This method can be extended to compute the central moments at any arbitrary order $d\,>\,1$. We first introduce the term central sum as

$$\begin{aligned} CS_d = \sum \limits _i (x_i-\mu )^d,~~~~~~~\mathrm {where}~CM_d = \frac{CS_d}{n}. \end{aligned}$$

Following the same definitions, the formula to update $CS_d$ can be written as [18]

$$\begin{aligned} CS_{d,\mathcal {Q}'} = CS_{d,\mathcal {Q}} + \sum \limits _{k=1}^{d-2} \left( {\begin{array}{c}d\\ k\end{array}}\right) CS_{d-k,\mathcal {Q}}\left( \frac{-\varDelta }{n}\right) ^k + \left( \frac{n-1}{n}\varDelta \right) ^d\left[ 1-\left( \frac{-1}{n-1}\right) ^{d-1}\right] , \end{aligned}$$

(3)

where $\varDelta$ is still the same as defined above. It is noteworthy that the calculation of $CS_{d,\mathcal {Q}'}$ requires $CS_{i,\mathcal {Q}}$ for $1<i\le d$ as well as the estimated mean $M_{1,\mathcal {Q}}$.

Based on these formulas the first raw and all central moments can be computed efficiently in one pass. Furthermore, since the intermediate results of the central sums are mean free, they do not become significantly large that helps preventing the numerical instabilities. The standardized moments are indeed the central moments which are normalized by the variance. Hence they can be easily derived from the central moments as

$$\begin{aligned} SM_d = \frac{1}{n}\sum _i\left( \frac{x_i-\mu }{s}\right) ^d = \frac{CM_d}{\big (\sqrt{CM_2}\big )^d}. \end{aligned}$$

(4)

Therefore, the first parameter of the t-test (mean of the preprocessed data) at any order can be efficiently and precisely estimated. Below we express how to derive the second parameter for such tests at any order.

4.2 Variance of Preprocessed Traces

A t-test at higher orders operates on preprocessed traces. In particular it requires to estimate the variance of the preprocessed traces. Such a variance does in general not directly correspond to a central or standardized moment of the original traces. Below we present how to derive such a variance at any order from the central and standardized moments.

Equation (2) shows how to obtain the variance given only the first two raw moments. We extend this approach to derive the variance of the preprocessed traces. In case of the second order, the traces are mean-free squared, i.e., $Y=(X-\mu )^2$. The variance of Y is estimated as

$$\begin{aligned} {s_{_Y}}^2&= \frac{1}{n}\sum \Big ((x-\mu )^2-\frac{1}{n}\sum (x-\mu )^2\Big )^2= \frac{1}{n}\sum \Big ((x-\mu )^2-CM_2\Big )^2\nonumber \\&= \frac{1}{n}\sum (x-\mu )^4 - \frac{2}{n}CM_2\sum (x-\mu )^2 + {CM_2}^2\nonumber \\&= CM_4 - {CM_2}^2. \end{aligned}$$

(5)

Therefore, the sample variance of the mean-free squared traces (required for a second-order t-test) can be efficiently derived from the central moments $CM_4$ and $CM_2$. Note that the values processed by the above equations ($CM_4$ and $CM_2$) are already centered hence avoiding the instability issue addressed in Sect. 4. For the cases at the third order, the traces are additionally standardized, i.e., $Z=\big (\frac{X-\mu }{s}\big )^3$. The variance of Z can be written as

$$\begin{aligned} {s_{_Z}}^2&= \frac{1}{n}\sum \Big (\big (\frac{x-\mu }{s}\big )^3-\frac{1}{n}\sum \big (\frac{x-\mu }{s}\big )^3\Big )^2 = \frac{1}{n}\sum \Big (\big (\frac{x-\mu }{s}\big )^3-SM_3\Big )^2\nonumber \\&= \frac{1}{n}\sum \big (\frac{x-\mu }{s}\big )^6 - \frac{2}{n}SM_3\sum \big (\frac{x-\mu }{s}\big )^3 + {SM_3}^2\nonumber \\&= SM_6 - {SM_3}^2 = \frac{CM_6 - {CM_3}^2}{{CM_2}^3}. \end{aligned}$$

(6)

Since the tests at third and higher orders use standardized traces, it is possible to generalize Eq. (6) for the variance of the preprocessed traces at any order $d>2$ as

$$\begin{aligned} SM_{2d} - {SM_d}^2~=~\frac{CM_{2d} - {CM_d}^2}{{CM_2}^d}. \end{aligned}$$

(7)

Therefore, a t-test at order d requires to estimate the central moments up to order 2d. With the above given formulas it is now possible to extend the t-test to any arbitrary order as we can estimate the corresponding required first and second parameters efficiently. In addition, most of the numerical problems are eliminated in this approach. The required formulas for all parameters of the tests up to the fifth order are provided in the extended version of this article [22]. We also included the formulas when the first and second parameters of the tests (up to the fifth order) are derived from raw moments.

In order to give an overview on the accuracy of different ways to compute the parameters for the t-tests, we ran an experiment with 100 million simulated traces with $\thicksim \mathcal {N}(100,25)$, which fits to a practical case where the traces (obtained from an oscilloscope) are signed 8-bit integers. We computed the second parameter for t-tests using (i) three-pass algorithm, (ii) the raw moments, and (iii) our proposed method. Note that in the three-pass algorithm first the mean $\mu$ is estimated. Then, having $\mu$ the traces are processed again to estimate all required central and standardized moments, and finally having all moments the traces are preprocessed (with respect to the desired order) and the variances (of the preprocessed traces) are estimated. The corresponding results are shown in Table 1. In terms of accuracy, our method matches the three-pass algorithm. The raw moments approach suffers from severe numerical instabilities, especially at higher orders where the variance of the preprocessed traces becomes negative.

Table 1. Comparison of the accuracy of different methods to compute the second parameter of the t-tests, 100 million simulated traces $\thicksim \mathcal {N}(100,25)$

4.3 Parallel Computation

Depending on the data complexity of the measurements, it is sometimes favorable to parallelize the computation in order to reduce the time complexity. To this end, a straightforward approach is to utilize a multi-core architecture (a CPU cluster) which computes the necessary central sums for multiple sample points in parallel. This can be achieved easily as the computations on different sample points are completely independent of each other. Consequently, there is no communication overhead between the threads. This approach is beneficial in most measurement scenarios and enables an extremely fast evaluation depending on the number of available CPU cores as well as the number of sample points in each trace. As an example, we are able to calculate all the necessary parameters of five non-specific t-tests (at first to fifth orders) on 100, 000, 000 traces (each with 3, 000 sample points) in 9 hours using two Intel Xeon X5670 CPUs @ 2.93 GHz, i.e., 24 hyper-threading cores.

A different approach can be preferred if the number of points of interest is very low. In this scenario, suppose that the trace collection is already finished and the t-tests are expected to be performed on a small number of sample points of a large number of traces. The aforementioned approach for parallel computing might not be the most efficient way as the degree of parallelization is bounded by the number of sample points. Instead, it is possible to increase the degree by splitting up the computation of the central sums for each sample point. For this, the set of traces of one sample point $\mathcal {Q}$ is partitioned into c subsets $\mathcal {Q}^{*i}$, $i\in \{1,\ldots ,c\}$, and the necessary central sums $CS_{d,\mathcal {Q}^{*i}}$ are computed for each subset in parallel using the equations introduced in Sect. 4.1. Afterward all $CS_{d,\mathcal {Q}^{*i}}$ are combined using the following exemplary equation for $c=2$ [18]:

$$\begin{aligned} CS_{d,\mathcal {Q}} =\;&CS_{d,\mathcal {Q}^{*1}} + CS_{d,\mathcal {Q}^{*2}} +\sum \limits _{k=1}^{d-2} \left( {\begin{array}{c}d\\ k\end{array}}\right) \biggl [\left( -\frac{n^{*2}}{n}\right) ^kCS_{d-k,\mathcal {Q}^{*1}}\nonumber \\&+\left( \frac{n^{*1}}{n}\right) ^kCS_{d-k,\mathcal {Q}^{*2}}\biggl ]{\varDelta _{2,1}}^k + \left( \frac{n^{*1}\,n^{*2}}{n}\varDelta _{2,1}\right) ^d\biggl [\frac{1}{\left( n^{*2}\right) ^{d-1}}-\left( \frac{-1}{n^{*1}}\right) ^{d-1}\biggl ], \end{aligned}$$

with $\mathcal {Q} = \mathcal {Q}^{*1} \cup \mathcal {Q}^{*2}$, $n^{*i} = |\mathcal {Q}^{*i}|$, $n=n^{*1}+n^{*2}$, and $\varDelta _{2,1} = M_{1,\mathcal {Q}^{*2}}-M_{1,\mathcal {Q}^{*1}}$. Further, the mean of $\mathcal {Q}$ can be trivially obtained as

$$\begin{aligned} M_{1,\mathcal {Q}}=\frac{n^{*1}\,M_{1,\mathcal {Q}^{*1}}+n^{*2}\,M_{1,\mathcal {Q}^{*2}}}{n}. \end{aligned}$$

5 Multivariate

The equations presented in Sect. 4 only consider univariate settings. This is typically the case for hardware designs in which the shares are processed in parallel, and the sum of the leakages appear at a sample point. For software implementations this is usually not the case as the computations are sequential and split up over multiple clock cycles.

In this scenario the samples of multiple points in time are first combined using a combination function, and an attack is conducted on the combination’s result. If the combination function (e.g., sum or product) does not require the mean, the extension of the equations to the multivariate case is trivial. It is enough to combine each set of samples separately and compute the mean and variance of the result iteratively as shown in the prior section.

However, this approach does not apply to the optimum combination function, i.e., the centered product [19, 24]. Given d sample point indices $\mathcal {J}~=~\{j_1,...,j_d\}$ as points of interest and a set of sample vectors $\mathcal {Q} = \{{{\varvec{V}}}_{i\in \{1,\ldots ,n\}}\}$ with ${{\varvec{V}}}_i = \left( t_i^{(j)}~|~j\in \mathcal {J}\right)$, the centered product of the i-th trace is defined as

$$\begin{aligned} \prod \limits _{j\in \mathcal {J}}\left( t_i^{(j)} - \mu ^{(j)}_{\mathcal {Q}}\right) , \end{aligned}$$

(8)

where $\mu ^{(j)}_{\mathcal {Q}}$ denotes the mean at sample point j over set $\mathcal {Q}$. The inclusion of the means is the reason why it is not easily possible to extend the equations from Sect. 4 to compute this value iteratively.

There is an iterative algorithm to compute the covariance similar to the aforementioned algorithms. This corresponds to the first parameter in a bivariate second-order scenario, i.e., $d=2$. The covariance $\displaystyle {\frac{C_{2,\mathcal {Q}'}}{n}}$ is computed as shown in [18] with

$$\begin{aligned} C_{2,\mathcal {Q}'} = C_{2,\mathcal {Q}} + \frac{n-1}{n}\left( y^{(1)}-\mu ^{(1)}_{\mathcal {Q}}\right) \left( y^{(2)}-\mu ^{(2)}_{\mathcal {Q}}\right) \end{aligned}$$

(9)

for $\mathcal {Q}' = \mathcal {Q}\cup \{\left( y^{(1)},y^{(2)}\right) \}$, $|\mathcal {Q}'|=n$, and an exemplary index set $\mathcal {J}=\{1,2\}$. Still, even with this formula it is not possible to compute the required second parameter for the t-test. In the following, we present an extension of this approach to d sample points and show how this can be used to compute both parameters for a dth-order d-variate t-test.

First, we define the sum of the centered products which is required to compute the first parameter. For d sample points and a set of sample vectors $\mathcal {Q}$, we denote the sum as

$$\begin{aligned} C_{d,\mathcal {Q},\mathcal {J}} = \sum \limits _{{{\varvec{V}}}\in \mathcal {Q}}\prod \limits _{j\in \mathcal {J}}\left( t^{(j)}-\mu ^{(j)}_{\mathcal {Q}}\right) . \end{aligned}$$

(10)

In addition, we define the k-th order power set of $\mathcal {J}$ as

$$\begin{aligned} \mathcal {P}_k = \{\mathcal {S}~|~\mathcal {S}\in \mathbb {P}(\mathcal {J}),|\mathcal {S}|=k\}, \end{aligned}$$

(11)

where $\mathbb {P}(\mathcal {J})$ refers to the power set of the indices of the points of interest $\mathcal {J}$. Using these definitions we derive the following theorem.

Theorem 1

Let $\mathcal {J}$ be a given set of indices (of d points of interest) and ${{\varvec{V}}}$ the given sample vector with ${{\varvec{V}}} = (y^{(1)},...,y^{(d)})$. The sum of the centered products $C_{d,\mathcal {Q}',\mathcal {J}}$ of the extended set $\mathcal {Q}'=\mathcal {Q}\cup {{\varvec{V}}}$ with $\varDelta ^{(j\in \mathcal {J})} = y^{(j)} - \mu ^{(j)}_{\mathcal {Q}}$ and $|\mathcal {Q}'|=n>0$ can be computed as:

$$\begin{aligned} C_{d,\mathcal {Q}',\mathcal {J}} = C_{d,\mathcal {Q},\mathcal {J}}&+ \left( \sum \limits _{k=2}^{d-1}\sum \limits _{\mathcal {S}\in \mathcal {P}_k}C_{k,\mathcal {Q},\mathcal {S}}\prod \limits _{j\in \mathcal {J}\setminus \mathcal {S}}\left( \frac{\varDelta ^{(j)}}{-n}\right) \right) \nonumber \\&+ \left( \frac{(-1)^d(n-1)+(n-1)^d}{n^d}\prod \limits _{j\in \mathcal {J}}\varDelta ^{(j)}\right) . \end{aligned}$$

(12)

The proof of Theorem 1 is given in the extended version of this article [22]. Equation (12) can be also used to derive the second parameter of the t-tests. To this end, let us first recall the definition of the second parameter in the dth-order d-variate case:

$$\begin{aligned} {s}^2 =&~ \frac{1}{n}\sum \limits _{{{\varvec{V}}} \in \mathcal {Q}}\left( \prod \limits _{j\in \mathcal {J}}\left( t^{(j)}-\mu ^{(j)}_{\mathcal {Q}}\right) - \frac{C_{d,\mathcal {Q},\mathcal {J}}}{n} \right) ^2\nonumber \\ =&~ \frac{1}{n}\left( \sum \limits _{{{\varvec{V}}} \in \mathcal {Q}} \prod \limits _{j\in \mathcal {J}}\left( t^{(j)}-\mu ^{(j)}_{\mathcal {Q}}\right) ^2\right) - \left( \frac{C_{d,\mathcal {Q},\mathcal {J}}}{n}\right) ^2. \end{aligned}$$

(13)

The first term of the above equation can be written as

$$\begin{aligned} \frac{1}{n}\sum \limits _{{{\varvec{V}}}\in \mathcal {Q}} \prod \limits _{j\in \mathcal {J}}\left( t^{(j)}-\mu ^{(j)}_{\mathcal {Q}}\right) ^2&= \frac{1}{n}\sum \limits _{{{\varvec{V}}}\in \mathcal {Q}}\left( \prod \limits _{j\in \mathcal {J}}\left( t^{(j)}-\mu ^{(j)}_{\mathcal {Q}}\right) \prod \limits _{j\in \mathcal {J}}\left( t^{(j)}-\mu ^{(j)}_{\mathcal {Q}}\right) \right) \nonumber \\&= \frac{C_{2d,\mathcal {Q},\mathcal {J}'}}{n}. \end{aligned}$$

(14)

Hence, the iterative algorithm (Eq. (12)) can be performed with multiset $\mathcal {J}' = \{j_1,...,j_d,j_1,...,j_d\}$ to derive the first term of Eq. (13). It is noteworthy that at the first glance Eq. (13) looks like Eq. (2), for which we addressed low accuracy issues. However, data which are processed by Eq. (13) are already centered, that avoids the sums $C_{d,\mathcal {Q},\mathcal {J}}$ being very large values. Therefore, the accuracy issues which have been pointed out in Sect. 4 are evaded.

By combining the results of this section with that of Sect. 4, it is now possible to perform a t-test with any variate and at any order efficiently and with sufficient accuracy. As an example, we give all the formulas required by a second-order bivariate ($d=2$) t-test in the extended version of this article [22].

6 Case Studies

Security evaluations consist of the two phases measurement and analysis. All challenges regarding the second part, which in our scenario refers to the computation of the t-test statistics, have been discussed in detail in the previous sections. However, this alone does not ensure a correct evaluation as malpractice in the measurement phase can lead to faulty results in the analysis. Below, we first describe the pitfalls that can occur during the measurement phase and provide solutions to ensure the correctness of evaluations. After that, two case studies are discussed that exemplary show the applications of our proposed evaluation framework.

6.1 Framework

If the DUT is equipped with countermeasures, the evaluation might require the collection of many (millions of) traces and, thus, the measurement rate (i.e., the number of collected traces per a certain period of time) can become a major hurdle. Following the technique suggested in [7, 11] we explain how the measurement phase can be significantly accelerated. The general scenario (cf. Fig. 2) is based on the assumption that the employed acquisition device (e.g., oscilloscope) includes a feature usually called sequence mode or rapid block mode. In such a mode – depending on the length of each trace as well as the size of the sampling memory of the oscilloscope – the acquisition device can record multiple traces. This is beneficial since the biggest bottleneck in the measurement phase is the low speed of the communication between e.g., the PC and the DUT (usually realized by UART). In the scenario shown in Fig. 2 it is supposed that Target is the DUT, and Control a microcontroller (or an FPGA) which communicates with the DUT as well as with the PC. The terms Target and Control correspond to the two FPGAs of e.g., a SAKURA (SASEBO) platform [1], but in some frameworks these two parties are merged, e.g., a microcontroller-based platform. Further, the PC is already included in modern oscilloscopes.

Fig. 2.

An optimized measurement process

Profiting from the sequence mode the communication between the PC and the DUT can be minimized in such a way that the PC sends only a single request to collect multiple N traces. The measurement rate depends on the size of the oscilloscope’s sampling memory, the length of each trace as well as the frequency of operation of the DUT. As an example, by means of an oscilloscope with $64\,\mathrm {MByte}$ sampling memory (per channel) we are able to measure $N=10,000$ traces per request when each trace consists of 5, 000 sample points. This results in being able to collect 100 million traces (for either a specific or non-specific t-test) in 12 hours. We should point out that the given scenario is not specific to t-test evaluations. It can also be used to speed up the measurement process in case of an evaluation by state-of-the-art attacks when the key is known.

To assure the correctness of the measurements, the PC should be able to follow and verify the processes performed by both Control and the DUT. Our suggestion is to employ a random number generator which can be seeded by the PC¹. This allows the PC to check the consistency of $out_N$ as well as the PRNG state. With respect to Fig. 2, f(., ., .) is defined based on the desired evaluation scheme. For a specific t-test (or any evaluation method where no control over e.g., plaintexts is necessary) our suggestion is:

$$\begin{aligned} in_{i+1}~=~f(\mathtt{INPUT },~out_i,~random)~=~out_i \oplus random. \end{aligned}$$

This allows the PC to verify all N processes of the DUT by examining the correctness of $out_N$. In case of a non-specific t-test, such a function can be realized as

$$ in_{i+1}~=~f(\mathtt{INPUT },~out_i,~random)~=\left\{ \begin{array}{l l} \mathtt{INPUT } &{} \quad \text {if } random_{bit} \text { is } 0\\ random &{} \quad \text {if } random_{bit} \text { is } 1 \end{array} \right. . $$

Note that it should be ensured that $random_{bit}$ is excluded from the random input. Otherwise, the random inputs become biased at a certain bit which may potentially lead to false-positive evaluation results. If a semi-fixed vs. random t-test is conducted, INPUT contains a set of certain fixed inputs (which can be stored in Control to reduce the communications), and the function can be implemented as

$$ in_{i+1}~=~f(\mathtt{INPUT },~out_i,~random)~=\left\{ \begin{array}{l l} \mathtt{INPUT }_{random} &{} \quad \text {if } random_{bit} \text { is } 0 \\ random &{} \quad \text {if } random_{bit} \text { is } 1 \end{array} \right. . $$

If the DUT is equipped with masking countermeasures, all communication between Control and Target (and preferably with the PC as well) should be in a shared form. This prevents the unshared data, e.g., INPUT, from appearing in Control and Target. Otherwise, the leakage associated to the input itself would cause, e.g., a non-specific t-test to report an exploitable leakage regardless of the robustness of the DUT. In hardware platforms such a shared communication is essential due to the static leakage as well [15]. For instance, in a second-order masking scheme (where variables are represented by three shares) INPUT should be a 3-share value $(\mathtt{INPUT }^1,\mathtt{INPUT }^2,\mathtt{INPUT }^3)$, and respectively $in_{i+1}=(in_{i+1}^1,in_{i+1}^2,in_{i+1}^3)$. In such a case, a non-specific t-test (including semi-fixed vs. random) should be handled as

$$\begin{aligned} in_{i+1}~=\;&f(\mathtt{INPUT },~out_i,~random)\\ =\;&\left\{ \begin{array}{l l} (\mathtt{INPUT }^1 \oplus r^1, \mathtt{INPUT }^2 \oplus r^2, \mathtt{INPUT }^3 \oplus r^1 \oplus r^2) &{} \quad \text {if } random_{bit} \text { is } 0\\ (r^1,r^2,r^3) &{} \quad \text {if } random_{bit} \text { is } 1 \end{array} \right. , \end{aligned}$$

with $r^1$ as a short notation of $random^1$. In other words, the fixed input should be freshly remasked before being sent to the DUT. Consequently, the last output $(out^1_N,out^2_N,out^3_N)$ is also sent in a shared form to the PC.

In general we suggest to apply the tests with the following settings:

• non-specific t-test (fixed vs. random): with shared communication between the parties, if the DUT is equipped with masking.

• non-specific t-test (semi-fixed vs. random): without shared communication, if the DUT is equipped with hiding techniques.

• specific t-tests: with the goal of identifying a suitable intermediate value for a key-recovery attack, if the DUT is not equipped with any countermeasures or failed in former non-specific tests. In this case, a shared communication is preferable if the DUT is equipped with masking.

We also provided two practical case studies, one based on an Atmel microcontroller platform (the DPA contest v4.2 [25]) and the other one by means of an FPGA-based platform (SAKURA-G [1]), which are given in details in the extended version of this article [22].

7 Conclusions

Security evaluations using Welch’s t-test have become popular in recent years. In this paper we have extended the theoretical foundations and guidelines regarding the leakage assessment introduced in [9]. In particular we have given more detailed instructions how the test can be applied in a higher-order setting. In this context, problems that can occur during the computation of this test vector have been highlighted. We have proposed solutions to perform the t-test efficiently and accurately at any order and any variate. In addition, we have discussed and given guidelines for an optimized measurement setup which allows high measurement rate and avoids faulty evaluations. As a future work, the presented robust incremental approach can be extended to correlation-based evaluation schemes.