Tweakable Blockciphers with Asymptotically Optimal Security

Abstract

We consider tweakable blockciphers with beyond the birthday bound security. Landecker, Shrimpton, and Terashima (CRYPTO 2012) gave the first construction with security up to $\mathcal {O}(2^{2n/3})$ adversarial queries ($n$ denotes the block size in bits of the underlying blockcipher), and for which changing the tweak does not require changing the keys for blockcipher calls. In this paper, we extend this construction, which consists of two rounds of a previous proposal by Liskov, Rivest, and Wagner (CRYPTO 2002), by considering larger numbers of rounds $r>2$. We show that asymptotically, as $r$ increases, the resulting tweakable blockcipher approaches security up to the information bound, namely $\mathcal {O}(2^n)$ queries. Our analysis makes use of a coupling argument, and carries some similarities with the analysis of the iterated Even-Mansour cipher by Lampe, Patarin, and Seurin (ASIACRYPT 2012).

R. Lampe – This author is partially supported by the French Direction Générale de l’Armement.

Y. Seurin – This author is partially supported by the French National Agency of Research: ANR-11-INS-011.

1 Introduction

Tweakable Blockciphers. Tweakable blockciphers (TBC), introduced by Liskov, Rivest, and Wagner [12], are families of (efficiently invertible) permutations indexed by two functionally distinct parameters: the key (as usual for a blockcipher) and the tweak. Phrased differently, a TBC is a family of blockciphers indexed by a tweak. The tweak is usually seen as a public parameter bringing more versatility to the blockcipher, and in particular is assumed to be under control of the attacker when defining security for a TBC.

There are very few constructions of blockciphers which are tweakable “by-design”. The notable examples are the Hasty Pudding cipher [21], Mercy [3], and Threefish, the blockcipher underlying the Skein hash function [6]. See also Goldenberg et al. [7] who considered how to incorporate a tweak in a Feistel structure. Most of the time however, proposed constructions start from an existing blockcipher (which is assumed to be a secure strong pseudorandom permutation) and build on top of it (in a black-box way) a new family of permutations admitting a tweak. An important property of a TBC is that changing the tweak should be very efficient (this is required for example for applications such as disk or database encryption). Most of the time, changing the key in a blockcipher is a costly operation. Hence, TBC designs where a change in the tweak implies a change in the keys used for calls to the underlying blockcipher tend to be avoided.

Simple constructions of tweakable blockciphers, such as the two proposals made in the original paper by Liskov et al. [12], or the XE and XEX constructions by Rogaway [20], are usually proven secure up to the so-called birthday bound (BB), i.e. up to $\mathcal {O}(2^{n/2})$ adversarial queries for a blockcipher with $n$-bit block length. The first proposal with beyond BB security was made by Minematsu [16], however the construction suffers from a restricted tweak length and requires rekeying the blockcipher when changing the tweak. More recently, Landecker, Shrimpton, and Terashima [11] considered chaining two rounds of the second proposal by [12] (called LRW2 in [11]), which works as follows: given a blockcipher $E$ with keyspace $\mathcal {K}$ and an $\varepsilon \text {-AXU}_2$ family of functions $\mathcal {H}$, the TBC constructed from $E$ through the LRW2 construction has key space $\mathcal {K}\times \mathcal {H}$, and given a key $k\in \mathcal {K}$ and a function $h\in \mathcal {H}$, the encryption of $x$ with tweak $t$ is given by $\widetilde{E}_{k,h}(t,x)=h(t)\oplus E_k(x\oplus h(t))$. Landecker et. al. named CLRW2 the construction resulting from the chaining of two LRW2 constructions, namely:

$$ \widetilde{E}_{(k_1,k_2),(h_1,h_2)}(t,x)=h_2(t)\oplus E_{k_2}\Big (h_1(t)\oplus E_{k_1}\big (x\oplus h_1(t)\big )\oplus h_2(t)\Big )\,. $$

They proved that the resulting TBC is secure (against adaptive chosen-plaintexts and ciphertexts attacks) up to $\mathcal {O}(2^{2n/3})$ queries. Moreover it admits arbitrary tweaks (by choosing a suitable family $\mathcal {H}$) and does not require rekeying the blockcipher $E$ when changing the tweak, hence resulting in a very interesting design.

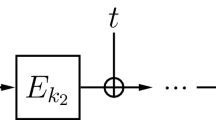
Contributions of This Work. In this paper, we extend the work of Landecker et al. [11] by considering longer chains of the LRW2 construction, with the hope that security increases with the number $r$ of rounds (see Fig. 1 for an idea of the construction). We simply call this the CLRW construction with $r$ rounds ($r$-CLRW for short). And indeed, we show that asymptotically as $r$ goes to $+\infty$, the $r$-CLRW TBC achieves security up to $\mathcal {O}(2^{(1-\varepsilon )n})$ adversarial queries. More precisely, we show the following:

• first, against non-adaptive chosen-plaintexts (NCPA) adversaries, $r$-CLRW achieves security up to $\mathcal {O}(2^{rn/(r+1)})$ queries;

• then, we prove a general “two weak make one strong” composition theorem for TBCs stating that, given two TBCs $\widetilde{E}$ and $\widetilde{E}'$ secure against (information-theoretic) NCPA adversaries, the composition $\widetilde{E}'^{-1}\circ \widetilde{E}$ is secure against adaptive chosen-plaintexts and ciphertexts (CCA) adversaries (care must be taken in how the tweak is handled when composing). We then use this theorem to prove that $r$-CLRW achieves security up to $\mathcal {O}(2^{rn/(r+2)})$ queries against CCA adversaries (in other words, it is a strong tweakable pseudorandom permutation up to this number of queries).

Our proof technique for the first part (NCPA adversaries) of the proof uses a coupling argument. The coupling technique is a very useful tool for upper bounding the statistical distance of the distribution of the outputs of an iterated structure to the uniform distribution, and was previously used in cryptography in [8, 17, 18]. More specifically, our analysis carries some similarities with the analysis of the iterated Even-Mansour cipher by Lampe, Patarin, and Seurin [10], with important differences though. The iterated Even-Mansour cipher [2, 5] (also called key-alternating cipher) is the construction of a blockcipher in the random permutation model defined as follows: given $r$ public permutations $P_1,\ldots ,P_r$ on $\{0,1\}^n$, encryption of $x$ is computed as:

$$ y=k_r\oplus P_r(k_{r-1}\oplus P_{r-1}(\cdots P_1(k_0\oplus x)\cdots ))\,, $$

where $k_0,\ldots ,k_r$ are $r+1$ keys of $n$ bits.¹ This construction was shown to be secure (against CCA adversaries) up to $\mathcal {O}(2^{n/2})$ queries for $r=1$ in [5], and up to $\mathcal {O}(2^{2n/3})$ queries for $r=2$ in [2]. Later, Lampe et al. [10] showed, using a coupling argument, that the construction is secure up to $\mathcal {O}(2^{rn/(r+1)})$ queries against NCPA adversaries, and up to $\mathcal {O}(2^{rn/(r+2)})$ queries against CCA adversaries.

Though these results sound similar to ours, the two settings are quite different. Namely, in the Even-Mansour setting, internal permutations $P_1,\ldots ,P_r$ are publicly accessible by the adversary, whereas in the CLRW setting, $E_{k_1},\ldots ,E_{k_r}$ remain “hidden” in the construction. On the other hand, in the Even-Mansour setting, keys are drawn at random at the beginning of the security experiment and fixed afterwards, whereas in the CLRW setting, values $h_i(t)$ (which may be seen as the analog of keys in the iterated Even-Mansour cipher) can be “refreshed” by the adversary through the tweak $t$. Yet, in both settings, problems that have to be handled in the security proof are collisions at the input of the internal permutations (but the way the adversary provokes such events in both settings is quite different).

Application to MAC and Authenticated Encryption. In [11], the authors defined a nonce-based MAC construction from a TBC called TBC-MAC2 (this is a variant of a previous proposal by [12] called TBC-MAC). This construction preserves the security of the underlying TBC. When instantiated with $r$-CLRW, this directly yields a secure MAC (i.e. a secure PRF) up to $\mathcal {O}(2^{rn/(r+2)})$ queries.² MAC schemes with security beyond the birthday bound are quite rare, and two notable examples have been given by Yasuda [24, 25]. Dodis ans Steinberger [4] also gave an example with security close to $\mathcal {O}(2^n)$ queries. Their construction is more complex, but relies only on the weaker assumption that the underlying blockcipher is unpredictable.

Besides MAC schemes, the $r$-CLRW construction can also be used to obtain an authenticated encryption scheme with security close to the information bound: for example, the OCB1 construction by Rogaway [20] gives an authenticated encryption scheme from a TBC with a tight security bound.

Open Problems. We conjecture that our NCPA bound in fact also holds for CCA adversaries, i.e. that the $r$-CLRW construction is secure up to $\mathcal {O}(2^{rn/(r+1)})$ queries against CCA adversaries. We think that this is probably the main open problem regarding the construction since for $r$ small, this makes a meaningful gap in the bound. For example, we prove security up to $\mathcal {O}(2^{3n/4})$ queries against CCA adversaries only for 6 rounds, but we conjecture that this already holds for 3 rounds. We note that the corresponding problem is equally open for the iterated Even-Mansour cipher. In a recent preprint [23], Steinberger showed that the iterated Even-Mansour cipher with 3 rounds is secure up to $\mathcal {O}(2^{3n/4})$ queries against CCA adversaries. We are currently unable to transfer his proof technique to the $r$-CLRW construction for $r=3$.

We also stress that we view our security proofs more as a feasibility result than a practical one. Indeed, as soon as $r$ is more than 4 or maybe 5, the key size and the number of blockcipher calls of the resulting construction will become too large to be reasonably practical. We think however that it is interesting to see that a relatively simple construction enables to approach the information bound. Moreover, improvements may come which will make the construction more efficient or even practical for larger values of $r$.

Organization. We define the notation and give some useful definitions in Sect. 2. Then, in Sect. 3, we prove our security result for $r$-CLRW against NCPA adversaries. Finally, in Sect. 4, we prove our composition theorem for tweakable blockciphers and apply it to characterize the security of $r$-CLRW against CCA adversaries.

2 Preliminaries

2.1 Notation and Security Definitions

The set of integers $i$ such that $a\le i \le b$ will be denoted $[a;b]$. When $S$ is a non-empty finite set, we write $s\leftarrow _{\$}S$ to mean that a value is sampled uniformly at random from $S$ and assigned to $s$. By $\mathcal {A}^{\mathcal {O}_1,\mathcal {O}_2,\ldots }(x,y,\ldots )\Rightarrow z$ we denote the operation of running the (possibly probabilistic) algorithm $\mathcal {A}$ on inputs $x,y,\ldots$ with access to oracles $\mathcal {O}_1,\mathcal {O}_2,\ldots$ (possibly none), and letting $z$ be the output.

For a set $\mathcal {D}$, we note ${\text {Perm}}({\mathcal {D}})$ the set of permutations of $\mathcal {D}$, and we use ${\text {Perm}}({n})$ to denote the set of permutations of $\mathcal {D}=\{0,1\}^n$. For two sets $\mathcal {D}$ and $\mathcal {K}$, we denote ${\mathsf {BC}}(\mathcal {K},\mathcal {D})$ the set of blockciphers with domain $\mathcal {D}$ and key space $\mathcal {K}$, i.e. the set of functions $E:\mathcal {K}\times \mathcal {D}\rightarrow \mathcal {D}$ such that for all $k\in \mathcal {K}$, $E_k:=E(k,\cdot )\in {\text {Perm}}({\mathcal {D}})$. For three sets $\mathcal {D}$, $\mathcal {K}$, and $\mathcal {T}$, we denote ${\mathsf {TBC}}(\mathcal {K},\mathcal {T},\mathcal {D})$ the set of tweakable blockciphers with domain $\mathcal {D}$, key space $\mathcal {K}$, and tweak space $\mathcal {T}$, i.e. the set of functions $\widetilde{E}:\mathcal {K}\times \mathcal {T}\times \mathcal {D}\rightarrow \mathcal {D}$ such that for each tweak $t\in \mathcal {T}$, $\widetilde{E}(\cdot ,t,\cdot )\in {\mathsf {BC}}(\mathcal {K},\mathcal {D})$. We will use $\widetilde{E}_k(\cdot ,\cdot )$ as a shorthand for $\widetilde{E}(k,\cdot ,\cdot )$. We denote ${\mathsf {BC}}(\mathcal {K},n)$ (resp. ${\mathsf {TBC}}(\mathcal {K},\mathcal {T},n)$) the set of blockciphers (resp. tweakable blockciphers) with domain $\mathcal {D}=\{0,1\}^n$. The perfect cipher over $\mathcal {D}$ is defined as the (inefficient) blockcipher whose key space is ${\text {Perm}}({\mathcal {D}})$. In the following, when the domain is clear ($\mathcal {D}=\{0,1\}^n$ most of the time), we will simply denote $E^*$ the perfect cipher over $\mathcal {D}$. Sampling a random key for $E^*$ simply means sampling a random permutation over $\mathcal {D}$.

Fix an integer $q\le |\mathcal {D}|$. Given a tuple $t=(t_1,\ldots ,t_q)\in \mathcal {T}^q$, we will denote $\varOmega _t\subset \mathcal {D}^q$ the set of possible inputs $x=(x_1,\ldots ,x_q)\in \mathcal {D}^q$ such that all pairs $(t_i,x_i)$ are pairwise distinct:

$$ \varOmega _t=\left\{ x:=(x_1,\ldots ,x_q)\in \mathcal {D}^q: (x_i,t_i)\ne (x_j,t_j), \forall i\ne j\right\} \,. $$

Let $\mathcal {D},\mathcal {K},\mathcal {T}$ be sets, $E\in {\mathsf {BC}}(\mathcal {K},\mathcal {D})$ a blockcipher and $\widetilde{E}\in {\mathsf {TBC}}(\mathcal {K},\mathcal {T},\mathcal {D})$ a tweakable blockcipher. An adversary $\mathcal {A}$ is said to be non-adaptive if it chooses all its queries (possibly randomly) before issuing the first one, and adaptive otherwise. For any $q,\tau$, we define the following advantages (where, depending on the security experiment, one has $k\leftarrow _{\$}\mathcal {K}$, $\pi \leftarrow _{\$}{\text {Perm}}({\mathcal {D}})$, or $\widetilde{\pi }\leftarrow _{\$}{\mathsf {BC}}(\mathcal {T},\mathcal {D})$):

where for ${\mathrm {ncpa}}$ and ${\widetilde{{\mathrm {ncpa}}}}$ (resp. ${\mathrm {cca}}$ and ${\widetilde{{\mathrm {cca}}}}$) the max is taken over non-adaptive (resp. adaptive) adversaries making at most $q$ oracle queries and running in time at most $\tau$. The probabilities are over the random coins of $\mathcal {A}$ and the random draw of $k$, $\pi$ or $\widetilde{\pi }$. In the following, we will refer to $\widetilde{\pi }$ as a tweakable permutation (though this object is syntactically equivalent to a blockcipher) since it takes the tweak as first input rather than the key.

Definition 1

Let $S$ be an arbitrary set. A family of functions $\mathcal {H}$ from $S$ to $\{0,1\}^n$ is said to be $\varepsilon$-almost-2-XOR-universal ($\varepsilon \text {-AXU}_2$) if for all distinct $x,x'\in S$ and all $y\in \{0,1\}^n$, one has $\Pr \left[ {h\leftarrow _{\$}\mathcal {H}\,:\, h(x)\oplus h(x')=y}\right] \le \varepsilon$.

Note that there exists very efficient and well-studied constructions of $\varepsilon \text {-AXU}_2$ function families with $\varepsilon \simeq 2^{-n}$ [22], with short descriptions (i.e. keys). We will stick to the convention of using a notation where the key is implicit in the remaining of the paper.

2.2 Statistical Distance and Coupling

Given a finite event space $\varOmega$ and two probability distributions $\mu$ and $\nu$ defined on $\varOmega$, the statistical distance (or total variation distance) between $\mu$ and $\nu$, denoted $\Vert \mu -\nu \Vert$ is defined as:

$$ \Vert \mu -\nu \Vert =\frac{1}{2}\sum _{x\in \varOmega }|\mu (x)-\nu (x)|\,. $$

The following definitions can easily be seen equivalent:

$$ \Vert \mu -\nu \Vert =\max _{S\subset \varOmega }\left\{ \mu (S)-\nu (S)\right\} =\max _{S\subset \varOmega }\left\{ \nu (S)-\mu (S)\right\} =\max _{S\subset \varOmega }\left\{ |\mu (S)-\nu (S)|\right\} \,. $$

A coupling of $\mu$ and $\nu$ is a distribution $\lambda$ on $\varOmega \times \varOmega$ such that for all $x\in \varOmega$, $\sum \nolimits _{y\in \varOmega } \lambda (x,y)=\mu (x)$ and for all $y\in \varOmega$, $\sum \nolimits _{x\in \varOmega } \lambda (x,y)=\nu (y)$. In other words, $\lambda$ is a joint distribution whose marginal distributions are resp. $\mu$ and $\nu$. The fundamental result of the coupling technique is the following one. For completeness, we provide the proof in Appendix A.

Lemma 1

(Coupling Lemma). Let $\mu$ and $\nu$ be probability distributions on a finite event space $\varOmega$, let $\lambda$ be a coupling of $\mu$ and $\nu$, and let $(X,Y)\sim \lambda$ (i.e. $(X,Y)$ is a random variable sampled according to distribution $\lambda$). Then $\Vert \mu -\nu \Vert \le \Pr [X\ne Y]$.

2.3 Description of the $r$-CLRW Construction

We use and adapt the notation of [11]. Let $\mathcal {K}$ be a set and $E\in {\mathsf {BC}}(\mathcal {K},n)$ a blockcipher. Let $\mathcal {T}$ be a set and $\mathcal {H}$ a set of functions from $\mathcal {T}$ to $\{0,1\}^n$. We define the tweakable blockcipher $\mathtt{LRW}^{E,\mathcal {H}}$ with domain $\{0,1\}^n$, key space $\widetilde{\mathcal {K}}=\mathcal {K}\times \mathcal {H}$, and tweak space $\mathcal {T}$ as follows. For any $(k_1,h_1)\in \mathcal {K}\times \mathcal {H}$, $t\in \mathcal {T}$, and $x\in \{0,1\}^n$, let:

$$ \mathtt{LRW}^{E,\mathcal {H}}((k_1,h_1),t,x)=E_{k_1}\big (x\oplus h_1(t)\big )\oplus h_1(t)\,. $$

We also denote $\mathtt{LRW}^{E,\mathcal {H}}_{k_1,h_1}:=\mathtt{LRW}^{E,\mathcal {H}}((k_1,h_1),\cdot ,\cdot )$ the mapping taking as input $(t,x)\in \mathcal {T}\times \{0,1\}^n$ and returning $y\in \{0,1\}^n$.

This construction was called the LRW2 construction in [11], being the second construction proposed by Liskov et al. in [12] to build a tweakable blockcipher. We simply call it the LRW construction in this paper. In [11], the authors proposed to chain two LRW constructions to increase the security beyond the birthday bound, and called the resulting construction CLRW2. In this paper, we will consider chaining $r$ LRW constructions with $r>2$ to obtain security asymptotically close to the information bound.

Let $r$ be a positive integer. We define the tweakable blockcipher $\mathtt{CLRW}^{r,E,\mathcal {H}}$ with domain $\{0,1\}^n$, key space $\widetilde{\mathcal {K}}=\mathcal {K}^r\times \mathcal {H}^r$, and tweak space $\mathcal {T}$ as follows. For any $k=(k_1, \ldots , k_r)\in \mathcal {K}^r$, $h=(h_1,\ldots ,h_r)\in \mathcal {H}^r$, $t\in \mathcal {T}$, and $x\in \{0,1\}^n$, let $\mathtt{CLRW}^{r,E,\mathcal {H}}((k,h),t,x)$ be defined as the value $y_r$ obtained recursively as:

We also denote $\mathtt{CLRW}^{r,E,\mathcal {H}}_{k,h}:=\mathtt{CLRW}^{r,E,\mathcal {H}}((k,h),\cdot ,\cdot )$ the mapping taking as input $(t,x)\in \mathcal {T}\times \{0,1\}^n$ and returning $y\in \{0,1\}^n$. The construction is depicted on Fig. 1.

Fig. 1.

The $\mathtt{CLRW}^{r,E,\mathcal {H}}$ tweakable blockcipher construction.

Thereafter, we will need the more ideal construction where the blockcipher $E$ is replaced by the perfect cipher $E^*$ over $\{0,1\}^n$ as defined in Sect. 2.1. The resulting (inefficient) TBC will be denoted $\mathtt{CLRW}^{r,E^*,\mathcal {H}}$, and for every $\pi =(\pi _1, \ldots ,\pi _r)\in {\text {Perm}}({n})^r$ and $h=(h_1,\ldots ,h_r)\in \mathcal {H}^r$, we denote $\mathtt{CLRW}^{r,E^*,\mathcal {H}}_{\pi ,h}$ the function defined as $\mathtt{CLRW}^{r,E,\mathcal {H}}_{k,h}$ above, where calls to $E_{k_i}$ are replaced by calls to $\pi _i$.

3 Security Analysis for Non-adaptive Adversaries

In this section, we first deal with non-adaptive chosen-plaintext (NCPA) adversaries. Using a coupling argument, we will prove the following theorem.

Theorem 1

Let $\mathcal {K},\mathcal {T}$ be sets, $E\in {\mathsf {BC}}(\mathcal {K},n)$ be a blockcipher, and $\mathcal {H}$ be an $\varepsilon \text {-AXU}_2$ family of functions from $\mathcal {T}$ to $\{0,1\}^n$. Then one has:

$$ {\mathbf{Adv }}^{{\widetilde{{\mathrm {ncpa}}}}}_{\mathtt{CLRW}^{r,E,\mathcal {H}}}(q,\tau )\le r\cdot {\mathbf{Adv }}^{{\mathrm {ncpa}}}_E(q,\tau +rqT)+\frac{q^{r+1}}{r+1}(2\varepsilon )^r\,, $$

where $T$ is the time to compute $E$ or $E^{-1}$.

Using an $\varepsilon \text {-AXU}_2$ function family with $\varepsilon \simeq 2^{-n}$, one can see that the construction ensures security up to $\mathcal {O}(2^{rn/(r+1)})$ queries (assuming $E$ is sufficiently secure against NCPA adversaries). The remaining of the section is devoted to the proof of Theorem 1.

3.1 An Hybrid Argument

As a first step in the proof, we replace the blockcipher $E$ used in the CLRW construction by the perfect cipher $E^*$, i.e. we replace calls to $E_{k_i}$ for random and independent keys $k_i$ by calls to uniformly random permutations $\pi _i$. If we assume that the blockcipher is a (strong) pseudorandom permutation, the construction using $E$ is only slightly less secure than the construction using $E^*$, as is captured by the following lemma (we also treat the case of CCA adversaries).

Lemma 2

For any $q,\tau$, one has:

$$\begin{aligned}&{\mathbf{Adv }}^{{\widetilde{{\mathrm {ncpa}}}}}_{\mathtt{CLRW}^{r,E,\mathcal {H}}}(q,\tau )\le r\cdot {\mathbf{Adv }}^{{\mathrm {ncpa}}}_{E}(q,\tau +rqT) + {\mathbf{Adv }}^{{\widetilde{{\mathrm {ncpa}}}}}_{\mathtt{CLRW}^{r,E^*,\mathcal {H}}}(q,\tau )\\&{\mathbf{Adv }}^{{\widetilde{{\mathrm {cca}}}}}_{\mathtt{CLRW}^{r,E,\mathcal {H}}}(q,\tau )\le r\cdot {\mathbf{Adv }}^{{\mathrm {cca}}}_{E}(q,\tau +rqT) + {\mathbf{Adv }}^{{\widetilde{{\mathrm {cca}}}}}_{\mathtt{CLRW}^{r,E^*,\mathcal {H}}}(q,\tau )\,, \end{aligned}$$

where $T$ is the time to compute $E$ or $E^{-1}$.

Proof

This is a classical hybrid argument. We only prove the NCPA case, the CCA case is similar. Let $\mathcal {A}$ be a NCPA adversary trying to distinguish $\mathtt{CLRW}^{r,E,\mathcal {H}}$ from a random tweakable permutation. For each $i\in [1;r]$, consider the following adversary $\mathcal {A}_i$ trying to distinguish $E$ from a random permutation. $\mathcal {A}_i$ runs $\mathcal {A}$, answering its queries as follows: it computes the $r$-CLRW construction where the first $i-1$ permutations are uniformly random permutations, the $i$-th permutation is computed by querying $\mathcal {A}_i$’s own oracle, and the last $r-i$ permutations correspond to $E$ with randomly drawn keys. Note that $\mathcal {A}_i$ is non-adaptive, makes at most $q$ queries to its own oracle, and runs in time at most $\tau +rqT$. Denote $\mathcal {O}_i$ the oracle defined as the $r$-CLRW construction where the first $i$ permutations are uniformly random, and the last $r-i$ permutations are $E$ with uniformly random keys. Then, when $\mathcal {A}_i$ is interacting with a random permutation, it answers $\mathcal {A}$’s queries as $\mathcal {O}_{i+1}$, whereas when it is interacting with $E_k$ it implements $\mathcal {O}_i$. Moreover $\mathcal {O}_0=\mathtt{CLRW}^{r,E,\mathcal {H}}$ and $\mathcal {O}_r=\mathtt{CLRW}^{r,E^*,\mathcal {H}}$. By the triangular inequality:

The lemma follows by noting that the $r$ first terms are exactly the advantages of adversaries $\mathcal {A}_i$, which are all upper bounded by ${\mathbf{Adv }}^{{\mathrm {ncpa}}}_{E}(q,\tau +rqT)$. $\quad \square$

Hence to study the security of $\mathtt{CLRW}^{r,E,\mathcal {H}}$, we have to study the security of $\mathtt{CLRW}^{r,E^*,\mathcal {H}}$. This is what we do in the remaining of the proof.

3.2 NCPA Advantage and Statistical Distance

A classical result states that the advantage of a (computationally unbounded) NCPA adversary in distinguishing two systems $S_1$ and $S_2$ with at most $q$ queries is upper bounded by the max over any $q$ inputs of the statistical distance between the outputs of the two systems. The two systems we consider here are $\mathtt{CLRW}^{r,E^*,\mathcal {H}}$ and a random tweakable permutation $\widetilde{\pi }$, and we want to upper bound the statistical distance between the outputs of $\mathtt{CLRW}^{r,E^*,\mathcal {H}}$ and the outputs of a random tweakable permutation for any $q$ queries to these two systems.

Thereafter, we will consider a NCPA-distinguisher $\mathcal {A}$ which chooses all its (plaintexts) queries in advance. We will denote the $i$-th query $(t_i,x_i)$. We denote $\mu _q$ the distribution of the outputs when the distinguisher is accessing the $\mathtt{CLRW}^{r,E^*,\mathcal {H}}$ construction (the distribution is defined by the random draw of $\pi =(\pi _1,\ldots ,\pi _r)\in {\text {Perm}}({n})^r$ and $h=(h_1,\ldots ,h_r)\in \mathcal {H}^r$) and $\mu _0$ the distribution of the outputs when the distinguisher is accessing a uniformly random tweakable permutation $\widetilde{\pi }$. Hence, for any $\tau$ (since this holds even for computationally unbounded adversaries):

$$ {\mathbf{Adv }}^{{\widetilde{{\mathrm {ncpa}}}}}_{\mathtt{CLRW}^{r,E^*,\mathcal {H}}}(q,\tau )\le \Vert \mu _q - \mu _0 \Vert \,. $$

In the following, we will denote $\tau =+\infty$ in the advantage when it applies to computationally unbounded adversaries.

3.3 Dividing the Problem into $q$ Simpler Problems

We now give another way to describe the distribution $\mu _0$. For any $t\in \mathcal {T}$, we do the following experiment: let $I_{t}$ be the set of indexes $i\in [1;q]$ such that $t_i=t$ and let $(u_i)_{i\in I_{t}}$ be uniformly random pairwise distinct elements. We claim that the distribution of the outputs of $(t_1,u_1),\ldots ,(t_q,u_q)$ by any (not necessarily uniform) random tweakable permutation $\widetilde{\pi }'$ whose distribution is independent of the distribution of $(u_i)$ is $\mu _0$, i.e. the distribution of the outputs of $(t_i,x_i)$ by a uniformly random tweakable permutation $\widetilde{\pi }$. Indeed, for every $t$, the values $({\widetilde{\pi }}(t_i,x_i))_{i\in I_{t}}$ and $(\widetilde{\pi }'(t_i,u_i))_{i\in I_t}$ are both uniformly random and pairwise distinct.

Now that we gave this new description of $\mu _0$, we can split the computation of $\Vert \mu _q - \mu _0 \Vert$ in $q$ simpler computations. The idea is to construct a distribution $\mu _\ell$ for every $\ell \le q$ such that $\mu _\ell$ is the distribution of the outputs of a random instance of $\mathtt{CLRW}^{r,E^*,\mathcal {H}}$ queried with $(t_i,x_i)$ for $i=1,\ldots ,\ell$ and the last $q-\ell$ queries keep the same tweak $t_i$ as in adversarial queries, but their last coordinate is uniformly random among unqueried values. More precisely, for each $\ell \in [0;q]$, let $((t_1,z_1),\ldots ,(t_q,z_q))$ be a tuple of queries such that $z_i=x_i$ for $i\le \ell$, and $z_i$ is uniformly random in $\{0,1\}^{n}\setminus \{z_j\,|\,t_j=t_i,j<i\}$ for $i>\ell$. This means that the first $\ell$ queries are the adversary’s queries and the remaining $z_i$ are chosen uniformly at random among the possible values (all queries have to be pairwise distinct). Denoting $\mu _\ell$ the distribution of the tuple of $q$ outputs when a random instance of $\mathtt{CLRW}^{r,E^*,\mathcal {H}}$ receives inputs $((t_1,z_1),\ldots ,(t_q,z_q))$, we have:

$$\begin{aligned} {\mathbf{Adv }}^{{\widetilde{{\mathrm {ncpa}}}}}_{\mathtt{CLRW}^{r,E^*,\mathcal {H}}}(q,\tau =+\infty )\le \Vert \mu _q - \mu _0 \Vert \le \sum _{\ell =0}^{q-1} \Vert \mu _{\ell +1}-\mu _\ell \Vert \,. \end{aligned}$$

(1)

3.4 Coupling of $\mu _{\ell +1}$ and $\mu _\ell$

Restricting to the First $\varvec{\ell }$ + 1 Queries

It remains to upper bound the statistical distance between $\mu _{\ell +1}$ and $\mu _{\ell }$, for each $\ell \in [0;q-1]$. For this, we will construct a suitable coupling of the two distributions. Note that we only have to consider the first $\ell +1$ elements of the two tuples of outputs since for both distributions, the $i$-th inputs for $i>\ell +1$ are sampled uniformly at random. In other words,

$$\begin{aligned} \Vert \mu _{\ell +1}-\mu _{\ell }\Vert =\Vert \mu '_{\ell +1}-\mu '_{\ell }\Vert \,, \end{aligned}$$

(2)

where $\mu '_{\ell +1}$ and $\mu '_{\ell }$ are the respective distributions of the $\ell +1$ first outputs of the $r$-CLRW construction.

Construction of $\varvec{\mu }'_{\varvec{\ell }}$ and $\varvec{\mu }'_{\varvec{\ell } \mathbf{+ 1}}$

To define the coupling of $\mu '_{\ell +1}$ and $\mu '_{\ell }$, we consider a random $\mathtt{CLRW}^{r,E^*,\mathcal {H}}_{\pi ,h}$ (i.e. $\pi =(\pi _1,\ldots ,\pi _r)$ and $h=(h_1,\ldots ,h_r)$ are uniformly random in respectively ${\text {Perm}}({n})^r$ and $\mathcal {H}^r$) that receives inputs $(t_j,x_j)$ for $j=1,\ldots ,\ell +1$ so that the outputs are distributed according to $\mu '_{\ell +1}$, and we consider another random $\mathtt{CLRW}^{r,E^*,\mathcal {H}}_{\pi ',h'}$ (i.e. $\pi '=(\pi '_1,\ldots ,\pi '_r)$ and $h'=(h'_1,\ldots ,h'_r)$ are uniformly random in respectively ${\text {Perm}}({n})^r$ and $\mathcal {H}^r$) with inputs $(t_j,z_j)$ for $j=1,\ldots ,\ell +1$ with $z_j=x_j$ for every $j\le \ell$ and $z_{\ell +1}$ being uniformly random in $\{0,1\}^n\setminus \{x_j\,|\,t_j=t_{\ell +1},j<\ell +1\}$, so that the outputs are distributed according to $\mu '_{\ell }$.

Notation

For every $j\le \ell +1$ and every $i\in [0;r]$, we note $x^i_j$ and $z^i_j$ the values defined by induction:

(3)

In order to apply the Coupling Lemma (Lemma 1), we have to find how to correlate $(\pi ,h)$ and $(\pi ',h')$ so that the outputs of both systems $(x^r_1,\ldots ,x^r_{\ell +1})$ and $(z^r_1,\ldots ,z^r_{\ell +1})$ are equal with high probability. We choose $(\pi ,h)$ uniformly at random and we construct $(\pi ',h')$ as a function of $(\pi ,h)$. We have to pay attention that the distribution of $(\pi ',h')$ remains uniform in order for $(z^r_1,\ldots ,z^r_{\ell +1})$ to be distributed according to $\mu '_{\ell }$.

Coupling of the First $\varvec{\ell }$ Queries

For every $j\le \ell$, the $j$-th queries $x^0_j$ and $z^0_j$ are equal by definition. Considering the system (3), we set $h'=h$ and $\pi '_i(x^i_j\oplus h_i(t_j))=\pi _i(x^i_j\oplus h_i(t_j))$ for every $j\le \ell$ and $i\le r$. This implies that the first $\ell$ outputs $(x^r_1,\ldots ,x^r_{\ell })$ and $(z^r_1,\ldots ,z^r_{\ell })$ are equal.

Coupling of the $\varvec{(\ell }$ + 1)-th Query

For every $i\in [0;r-1]$ we define the coupling for the $\ell +1$-th query as follows:

• (1) if there exists $j\le \ell$ such that $z^i_{\ell +1}\oplus h_i(t_{\ell +1})=z^i_j\oplus h_i(t_j)$ then $\pi '_i(z^i_{\ell +1}\oplus h_i(t_{\ell +1}))$ is already defined. Unless we have coupled $z^i_{\ell +1}$ and $x^i_{\ell +1}$ in a previous round, we cannot couple $z^{i+1}_{\ell +1}$ and $x^{i+1}_{\ell +1}$ at this round.

• (2) else, if $z^i_{\ell +1}\oplus h_i(t_{\ell +1})\ne z^i_j\oplus h_i(t_j)$ for all $j\le \ell$, then:

  • (a) if there exists $j\le \ell$ such that $x^i_{\ell +1}\oplus h_i(t_{\ell +1})=x^i_j\oplus h_i(t_j)$ then we choose $\pi '_i(z^i_{\ell +1}\oplus h_i(t_{\ell +1}))$ uniformly at random in $\{0,1\}^n\setminus \{\pi '_i(z^i_j\oplus h_i(t_j)),j\le \ell \}$. We cannot couple $z^{i+1}_{\ell +1}$ and $x^{i+1}_{\ell +1}$ at this round.

  • (b) else, we define $\pi '_i(z^i_{\ell +1}\oplus h_i(t_{\ell +1}))=\pi _i(x^i_{\ell +1}\oplus h_i(t_{\ell +1}))$. This implies that $z^{i+1}_{\ell +1}=x^{i+1}_{\ell +1}$.

Note that once $z^{i+1}_{\ell +1}=x^{i+1}_{\ell +1}$, $z^{i'}_{\ell +1}=x^{i'}_{\ell +1}$ for any subsequent round $i'\ge i+1$, in particular for $i'=r$, so that the coupling is successful.

Verification that $\varvec{(\pi }\mathbf{'},\varvec{h}\mathbf{')}$ Is Uniformly Random

We set $h'=h$ and $h$ is uniformly random so $h'$ is uniformly random. During the coupling of the first $\ell$ queries, we set $\pi '_i(x^i_j\oplus h_i(t_j))=\pi _i(x^i_j\oplus h_i(t_j))$ for every $j\le \ell$ and $i\le r$ and $\pi _i(x^i_j\oplus h_i(t_j))$ is uniformly random among possible values so $\pi '_i(x^i_j\oplus h_i(t_j))$ is uniformly random among possible values. Rule (1) says that if there is a collision with a previous input of $\pi '_i$, we cannot choose the value of $\pi '_i(z^i_j\oplus h_i(t_j))$ so this does not change anything to the distribution of $\pi '_i$. When conditions of rule (2)(a) are met, we have for some $j\le \ell$:

$$ \left\{ \begin{array}{l} \pi _i(x^i_{\ell +1}\oplus h_i(t_{\ell +1}))=\pi _i(x^i_j\oplus h_i(t_j))=\pi '_i(z^i_j\oplus h_i(t_j))\\ z^i_{\ell +1}\oplus h_i(t_{\ell +1})\ne z^i_{j}\oplus h_i(t_{j})\,, \end{array}\right. $$

which implies that $\pi '_i(z^i_{\ell +1}\oplus h_i(t_{\ell +1}))\ne \pi _i(x^i_j\oplus h_i(t_j))$. This means that the coupling is impossible and we choose $\pi '_i(z^i_{\ell +1}\oplus h_i(t_{\ell +1}))$ uniformly at random among possible values to keep $\pi '_i$ uniformly distributed. Finally, when conditions of rule (2)(b) are met, we have no problem to couple: $\pi _i(x^i_{\ell +1}\oplus h_i(t_{\ell +1}))$ and $\pi '_i(z^i_{\ell +1}\oplus h_i(t_{\ell +1}))$ are both uniformly random among possible values. In conclusion, permutations $\pi _i'$ are uniformly random and independent as wanted, so that $(z_1^r,\ldots ,z_{\ell +1}^r)$ is distributed according to $\mu '_{\ell }$.

Failure Probability of the Coupling

It remains to upper bound the probability that the coupling fails, i.e.

$$ (z_1^r,\ldots ,z_{\ell +1}^r)\ne (x_1^r,\ldots ,x_{\ell +1}^r)\,. $$

For every $i\in [0;r-1]$, we denote $\mathtt{fail}^i$ the event that it exists $j\le \ell$ such that $z^i_{\ell +1}\oplus h_i(t_{\ell +1})=z^i_j\oplus h_i(t_j)$ or $x^i_{\ell +1}\oplus h_i(t_{\ell +1})=x^i_j\oplus h_i(t_j)$. This is the event of failing to couple at round $i$. Then we have:

where the second inequality comes from the $\varepsilon \text {-AXU}_2$ property of $\mathcal {H}$ (note that when $t_{\ell +1}=t_j$, necessarily $z_{\ell +1}^i\ne z_j^i$ and $x_{\ell +1}^i\ne x_j^i$ since all queries must be distinct, so that the probability is zero). Since the functions $h_i$ are independent, we have:

$$\begin{aligned} \displaystyle \Pr \left[ {\bigcap _{i=0}^{r-1} \mathtt{fail}^i}\right] \le (2\ell \varepsilon )^r\,. \end{aligned}$$

(4)

Using the Coupling Lemma and the fact that $z^r_j=x^r_j$ for all $j\le \ell$, we have:

$$\begin{aligned} \Vert \mu '_{\ell +1}-\mu '_\ell \Vert \le \Pr \left[ {(z^r_1,\ldots ,z^r_{\ell +1})\ne (x^r_1,\ldots ,x^r_{\ell +1})}\right] \le \Pr \left[ {z^r_{\ell +1}\ne x^r_{\ell +1}}\right] \,. \end{aligned}$$

(5)

If we succeed to couple the last query at some round $i\le r-1$, we know that $z^{i'}_{\ell +1}$ and $x^{i'}_{\ell +1}$ remain equal in the subsequent rounds so that:

$$\begin{aligned} \Pr \left[ {z^r_{\ell +1}\ne x^r_{\ell +1}}\right] \le \displaystyle \Pr \left[ {\bigcap _{i=0}^{r-1} \mathtt{fail}^i}\right] \,. \end{aligned}$$

(6)

Using (4), (5) and (6), we have:

$$\begin{aligned} \Vert \mu '_{\ell +1}-\mu '_\ell \Vert \le (2\ell \varepsilon )^r\,. \end{aligned}$$

(7)

Finally, using (1), (2) and (7), we obtain:

$$\begin{aligned} {\mathbf{Adv }}^{{\widetilde{{\mathrm {ncpa}}}}}_{\mathtt{CLRW}^{r,E^*,\mathcal {H}}}(q,\tau =+\infty )&\le \sum _{\ell =0}^{q-1} \Vert \mu '_{\ell +1}-\mu '_\ell \Vert \\&\le \sum _{\ell =0}^{q-1} (2\ell \varepsilon )^r\\&\le \int _0^q (2\ell \varepsilon )^r dl\\&=\frac{q^{r+1}}{r+1}(2\varepsilon )^r\,. \end{aligned}$$

Theorem 1 then follows from the above inequality combined with Lemma 2.

4 Security Analysis for Adaptive Adversaries

In this section, we first prove a general composition theorem for tweakable blockciphers similar to the “two weak make one strong” theorem for the composition of usual blockciphers. This theorem roughly states that composing two blockciphers secure against NCPA adversaries yields a blockcipher secure against CCA adversaries [14, 15]. We prove exactly the same result for TBCs, but we stress that the exact way the tweak is used in composition is important: namely, the same tweak must be used in both ciphers. We state this theorem in the information-theoretic setting (i.e. for computationally unbounded adversaries) since we will then apply it to the $\mathtt{CLRW}^{r,E^*\mathcal {H}}$ construction which has information-theoretic security. Corresponding theorems in the computational setting are usually much harder to obtain. Our proof technique is an extension of the “H Coefficients” technique of Patarin [19] to tweakable blockciphers. One could probably use the formalism of random systems [13] to obtain a tight bound in the computational setting as in [15], however subtle problems have been recently found in this proof technique [9] so that we prefer the more simple and straightforward statistical approach. We then apply this result to prove the security of $r$-CLRW against CCA adversaries up to $\mathcal {O}(2^{rn/(r+2)})$ queries.

4.1 Definitions ans Preliminary Results

Fix $\widetilde{E} \in {\mathsf {TBC}}(\mathcal {K},\mathcal {T},\mathcal {D})$. For any $t=(t_1,\ldots ,t_q)\in \mathcal {T}^q$, and any $x=(x_1,\ldots ,x_q)\in \varOmega _t$, we denote $\nu _{(t,x)}$ the distribution on $\varOmega _t$ induced by $\widetilde{E}$ and $\nu ^*_{(t,x)}$ the distribution induced by a random tweakable permutation on inputs $(t_i,x_i)$, namely for $y=(y_1,\ldots ,y_q)\in \varOmega _t$:

Note that $\nu ^*_{(t,x)}$ is uniform over $\varOmega _t$ (the exact cardinality of $\varOmega _t$ depends on $t$). For any $\alpha \in [0,1]$, we note $S_{\alpha ,(t,x)}$ the set of $y\in \varOmega _t$ satisfying $\nu _{(t,x)}(y)\ge (1-\alpha )\nu ^*_{(t,x)}(y)$.

We start by proving two lemmas which will be useful for our main result. The first one says that if, for every $t=(t_1,\ldots ,t_q)$, $x=(x_1,\ldots ,x_q)$, and $y=(y_1,\ldots ,y_q)$, the probability that $\widetilde{E}_k$ maps $(t_i,x_i)$ to $y_i$ for all $i$ is close to the corresponding probability for a random tweakable permutation, then the advantage of any adversary in distinguishing $\widetilde{E}$ from a random tweakable permutation with $q$ queries is small.

Lemma 3

Fix $\widetilde{E} \in {\mathsf {TBC}}(\mathcal {K},\mathcal {T},\mathcal {D})$, and $q\le |\mathcal {D}|$. If there exists $\alpha \in [0,1]$ such that, for all $t\in \mathcal {T}^q$ and for all $x\in \varOmega _t$, $\nu ^*_{(t,x)}(S_{\alpha ,(t,x)})=1$, then

$$ {\mathbf{Adv }}^{{\widetilde{{\mathrm {cca}}}}}_{\widetilde{E}}(q,\tau =+\infty )\le \alpha \,. $$

Proof

Consider a computationally unbounded CCA attacker $\mathcal {A}$ making $q$ queries to an oracle $\mathcal {O}$ acting like $\widetilde{E}$ or like a random tweakable permutation $\widetilde{\pi }$. We assume wlog that $\mathcal {A}$ is deterministic. We note $\delta =(\delta _1,\ldots ,\delta _q)\in \mathcal {D}^q$ the transcript of the attack, defined as follows. If $\mathcal {A}$ makes a direct query $(t_1,x_1)$ and receives an answer $y_1$, one has $\delta _1=y_1$ and then, the attacker continues his attack and receives the next answers $\delta _2, \ldots , \delta _q$. If the attacker makes an inverse query $(t_i,y_i)$ then $\delta _i$ is the answer $x_i$. For each transcript $\delta$, we denote $t(\delta ), x(\delta )$ and $y(\delta )$ the corresponding values of $t_1, \ldots , t_q, x_1, \ldots , x_q, y_1, \ldots , y_q$. We denote $\Sigma$ the set of transcripts $\delta$ such that the attacker outputs $1$. If the oracle is acting like $\widetilde{E}$ then the probability that the attacker outputs $1$ is exactly

$$ \sum _{\delta \in \Sigma }\nu _{t(\delta ),x(\delta )}(y(\delta ))\,. $$

If the oracle is acting like a random tweakable permutation $\widetilde{\pi }$ then the probability that the attacker outputs $1$ is exactly

$$ \sum _{\delta \in \Sigma }\nu ^*_{t(\delta ),x(\delta )}(y(\delta ))\,. $$

We deduce that the advantage of $\mathcal {A}$ equals:

$$\begin{aligned} \left| \sum _{\delta \in \Sigma }\left( \nu _{t(\delta ),x(\delta )}(y(\delta ))-\nu ^*_{t(\delta ),x(\delta )}(y(\delta ))\right) \right| \,. \end{aligned}$$

(8)

Since for every $t\in \mathcal {T}^q$, $x\in \varOmega _t$, and $y\in \varOmega _t$, one has $\nu _{(t,x)}(y)\ge (1-\alpha )\nu ^*_{(t,x)}(y)$, it follows that:

(9)

Finally, it is easy to verify that

(10)

because

$$ \sum _{\delta }\nu _{t(\delta ),x(\delta )}(y(\delta ))=\sum _{\delta }\nu ^*_{t(\delta ),x(\delta )}(y(\delta ))=1\,. $$

Using (8), (9) and (10), we deduce that the advantage of $\mathcal {A}$ is upper bounded by $\alpha$.$\quad \square$

The second lemma says that if the advantage of the best NCPA adversary is small, then, for all $t,x$, almost all $y$ are such that the probability of sending $(t,x)$ to $y$ for a random $\widetilde{E}_k$ is close to the probability of sending $(t,x)$ to $y$ for a random tweakable permutation.

Lemma 4

Fix $\widetilde{E} \in {\mathsf {TBC}}(\mathcal {K},\mathcal {T},\mathcal {D})$ and $q\le |\mathcal {D}|$. If there exists $\beta \in [0,1]$ such that

$$ {\mathbf{Adv }}^{{\widetilde{{\mathrm {ncpa}}}}}_{\widetilde{E}}(q,\tau =+\infty )\le \beta \,, $$

then, for all $t\in \mathcal {T}^q$ and $x\in \varOmega _t$, one has:

$$ \nu ^*_{(t,x)}\left( S_{\sqrt{\beta },(t,x)}\right) \ge 1-\sqrt{\beta }\,. $$

Proof

By contrapositive, suppose there exists $t=(t_1,\ldots ,t_q)\in \mathcal {T}^q$ and $x=(x_1,\ldots ,x_q)\in \varOmega _t$ such that

$$ \nu ^*_{(t,x)}\left( S_{\sqrt{\beta },(t,x)}\right) <1-\sqrt{\beta }\,. $$

Consider the adversary which queries $(t_1,x_1)$, ..., $(t_q,x_q)$ and outputs $0$ if the answers $y=(y_1,\ldots ,y_q)$ are such that $y\in S_{\sqrt{\beta },(t,x)}$ and $1$ otherwise. His advantage is exactly

$$ \left| \sum _{y\notin S_{\sqrt{\beta },(t,x)}}\nu _{(t,x)}(y)-\nu ^*_{(t,x)}(y)\right| \,, $$

and $y\notin S_{\sqrt{\beta },(t,x)}$ means, by definition, that $\nu _{(t,x)}(y)<(1-\sqrt{\beta })\nu ^*_{(t,x)}(y)$, so that the advantage of this adversary is strictly greater than:

$$ \sqrt{\beta }\times \left( 1-\nu ^*_{(t,x)}\left( S_{\sqrt{\beta },(t,x)}\right) \right) > \beta \,, $$

hence the result.$\quad \square$

4.2 A Composition Theorem for Tweakable Blockciphers

Given two TBCs sharing the same set of tweaks and the same domain $\widetilde{E}_1\in {\mathsf {TBC}}(\mathcal {K}_1,\mathcal {T},\mathcal {D})$ and $\widetilde{E}_2\in {\mathsf {TBC}}(\mathcal {K}_2,\mathcal {T},\mathcal {D})$, we define the tweakable blockcipher $\widetilde{E}_2\circ \widetilde{E}_1\in {\mathsf {TBC}}(\mathcal {K}_1\times \mathcal {K}_2,\mathcal {T},\mathcal {D})$ as:

Theorem 2

Let $\widetilde{E}_1\in {\mathsf {TBC}}(\mathcal {K}_1,\mathcal {T},\mathcal {D})$ and $\widetilde{E}_2\in {\mathsf {TBC}}(\mathcal {K}_2,\mathcal {T},\mathcal {D})$ be two TBCs satisfying:

$$ {\mathbf{Adv }}^{{\widetilde{{\mathrm {ncpa}}}}}_{\widetilde{E}_1}(q,\tau =+\infty )\le \beta _1{\text { and }} {\mathbf{Adv }}^{{\widetilde{{\mathrm {ncpa}}}}}_{\widetilde{E}_2}(q,\tau =+\infty )\le \beta _2 \,. $$

Then:

$$ {\mathbf{Adv }}^{{\widetilde{{\mathrm {cca}}}}}_{\widetilde{E}^{-1}_2\circ \widetilde{E}_1}(q,\tau =+\infty )\le 2(\sqrt{\beta _1}+\sqrt{\beta _2}) \,. $$

Proof

We denote $\nu ^1$, $\nu ^2$, and $\nu ^3$ the distributions associated respectively to $\widetilde{E}_1, \widetilde{E}_2$ and $\widetilde{E}^{-1}_2\circ \widetilde{E}_1$. For every $t\in \mathcal {T}^q$, $x\in \varOmega _t$, and $\alpha \in [0,1]$, we denote $S^{\widetilde{E}_i}_{\alpha ,(t,x)}$ the set $S_{\alpha ,(t,x)}$ corresponding to $\widetilde{E}_i$, $i=1,2$.

By Lemma 4, for all $t\in \mathcal {T}^q$, $x\in \varOmega _t$, and $y\in \varOmega _t$, we have:

$$\begin{aligned} \nu ^*_{(t,x)}\left( S^{\widetilde{E}_1}_{\sqrt{\beta _1},(t,x)}\right) \ge 1-\sqrt{\beta _1} \quad {\text {and}} \quad \nu ^*_{(t,y)}\left( S^{\widetilde{E}_2}_{\sqrt{\beta _2},(t,y)}\right) \ge 1-\sqrt{\beta _2}\,. \end{aligned}$$

(11)

Furthermore, for all $(k_1,k_2)\in \mathcal {K}_1\times \mathcal {K}_2$, $\widetilde{E}^{-1}_2\circ \widetilde{E}_1((k_1,k_2),\cdot ,\cdot )$ maps $(t,x)$ to $y$ if and only if for all $i\le q$, $\widetilde{E}_1(k_1,t_i,x_i)=\widetilde{E}_2(k_2,t_i,y_i)$. Denoting $S'=S^{\widetilde{E}_1}_{\sqrt{\beta _1},(t,x)}\cap S^{\widetilde{E}_2}_{\sqrt{\beta _2},(t,y)}$, one has, for any $y\in \varOmega _t$:

$$\begin{aligned} \nu ^3_{(t,x)}(y)&=\sum _{z\in \varOmega _t} \nu ^1_{(t,x)}(z)\cdot \nu ^2_{(t,y)}(z)\\&\ge \sum _{z\in S'} \nu ^1_{(t,x)}(z)\cdot \nu ^2_{(t,y)}(z)\\&\ge \sum _{z\in S'} \left( 1-\sqrt{\beta _1}\right) {\nu ^*}_{(t,x)}(z)\cdot \left( 1-\sqrt{\beta _2}\right) {\nu ^*}_{(t,y)}(z)\\&\ge \left( 1-\sqrt{\beta _1}\right) \left( 1-\sqrt{\beta _2}\right) \frac{|S'|}{|\varOmega _t|^2}\\&=\left( 1-\sqrt{\beta _1}\right) \left( 1-\sqrt{\beta _2}\right) \nu ^*_{(t,x)}(S')\nu ^*_{(t,x)}(y)\,. \end{aligned}$$

By definition of $S'$ and using Eq. 11, one has $\nu ^*_{(t,x)}(S')\ge (1-\sqrt{\beta _1}-\sqrt{\beta _2})$ (note that $\nu ^*$ in fact only depends on $t$), so that:

$$ \nu ^3_{(t,x)}(y)\ge (1-2(\sqrt{\beta _1}+\sqrt{\beta _2}))\nu ^*_{(t,x)}(y)\,. $$

Since this holds for any $t$, $x$, and $y$, the theorem follows by applying Lemma 3 with $\alpha =2(\sqrt{\beta _1}+\sqrt{\beta _2})$.$\quad \square$

4.3 Application to the $r$-CLRW Construction

Finally, we apply the previous result to prove the security of $r$-CLRW against CCA adversaries.

Theorem 3

Let $\mathcal {K},\mathcal {T}$ be sets, $E\in {\mathsf {BC}}(\mathcal {K},n)$ be a blockcipher, and $\mathcal {H}$ be an $\varepsilon \text {-AXU}_2$ family of functions from $\mathcal {T}$ to $\{0,1\}^n$. Then for any even integer $r$, one has:

$$ {\mathbf{Adv }}^{{\widetilde{{\mathrm {cca}}}}}_{\mathtt{CLRW}^{r,E,\mathcal {H}}}(q,\tau )\le r\cdot {\mathbf{Adv }}^{{\mathrm {cca}}}_E(q,\tau +rqT)+\frac{4\sqrt{2}}{\sqrt{r+2}}q^{(r+2)/4}(2\varepsilon )^{r/4}\,, $$

where $T$ is the time to compute $E$ or $E^{-1}$.

Proof

Noting that the inverse of a $r/2$-CLRW construction is again a $r/2$-CLRW construction, we can apply Theorem 2 to get:

$$ {\mathbf{Adv }}^{{\widetilde{{\mathrm {cca}}}}}_{\mathtt{CLRW}^{r,E^*,\mathcal {H}}}(q,\tau =+\infty )\le 4\sqrt{\alpha }\,, $$

where

$$ \alpha := {\mathbf{Adv }}^{{\widetilde{{\mathrm {ncpa}}}}}_{\mathtt{CLRW}^{r/2,E^*,\mathcal {H}}}(q,\tau =+\infty )\le \frac{q^{r/2+1}}{r/2+1}(2\varepsilon )^{r/2} $$

by the results of Sect. 3. The theorem then follows from Lemma 2.$\quad \square$

Again, using an $\varepsilon \text {-AXU}_2$ function family with $\varepsilon \simeq 2^{-n}$, the construction achieves security against CCA adversaries up to $\mathcal {O}(2^{rn/(r+2)})$ queries.

Proof of the Coupling Lemma

The original statement and proof of the Coupling Lemma is due to Aldous [1]. Here we follow closely a proof by Vigoda.³

Let $\lambda$ be a coupling of $\mu$ and $\nu$, and $(X,Y)\sim \lambda$. By definition, we have that for any $z\in \omega$, $\lambda (z,z)\le \min \{\mu (z),\nu (z)\}$. Moreover, $\Pr [X=Y]=\sum _{z\in \varOmega }\lambda (z,z)$. Hence we have:

$$ \Pr [X=Y]\le \sum _{z\in \varOmega } \min \{\mu (z),\nu (z)\}\,. $$

Therefore:

$$\begin{aligned} \Pr [X\ne Y]&\ge 1 -\sum _{z\in \varOmega }\min \{\mu (z),\nu (z)\}\\&= \sum _{z\in \varOmega }\left( \mu (z)-\min \{\mu (z),\nu (z)\}\right) \\&= \sum _{\begin{array}{c} z\in \varOmega \\ \mu (z)\ge \nu (z) \end{array}} (\mu (z)-\nu (z))\\&=\max _{S\subset \varOmega } \{\mu (S)-\nu (S)\}\\&=\Vert \mu -\nu \Vert \,. \end{aligned}$$