Summary
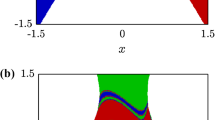
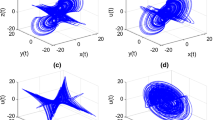
A four-variable ordinary differential equation with hyperchaos is investigated further numerically. A self-similar Sierpinski-type fractal is found in a plane of initial conditions if the prospective fate of each point (whether it escapes through the one or the other escape hole in the exploded hyperchaotic attractor) is used for a coloring criterion. A basin boundary of the same qualitative shape therefore exists in either this equation or a closely related one. All hyper-chaotic systems are eligible for an analogous investigation — both numerically and, if possible, experimentally.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
S. Smale (1967). Bull. Amer. Math. Soc. 73, 747.
B. Mandelbrot, The Fractal Geometry of Nature. Freeman, San Francisco 1983.
O.E. Rössler and C. Mira (1981), Higher-order chaos in a constrained differential equation with an explicit cross section, extended abstract in: Tagungsbericht 40/1981, pp. 9–10. Mathematisches Forschungsinstitut Oberwolfach, 7620 Oberwolfach-Walke, West Germany.
O.E. Rössler (1983). Z. Naturforsch. 38 a, 788.
C. Mira (1978), Complex dynamics generated by a third-order differential equation (in French), in: Proc. “Equadiff 78” ( R. Conti, G. Sestini and G. Villari, Eds.), pp. 25–36. Florence, Italy.
O.E. Rössler (1976). Z. Naturforsch. 31 a, 259.
M. Hénon (1976). Commun. Math. Phys. 50, 69.
C. Mira (1979). C. R. Acad. Sc. Paris 288 A, 591.
I. Gumowski and C. Mira (1975). C. R. Acad. Sc. Paris 280 A, 905.
O.E. Rössler, C. Kahlert, J. Parisi, J. Peinke and B. Röhricht (1986). Z. Naturforsch. 41 a, 819.
O.E. Rössler, J. Hudson, M. Klein and R. Wais (1988), Self-similar basin boundary in an invertible system (folded-towel map), in: Dynamic Patterns in Complex Systems ( J.A.S. Kelso, A.J. Mandell and M.F. Shlesinger, Eds.), pp. 209–218. World Scientific, Singapore.
O.E. Rössler and J.L. Hudson (1989), Self-similarity in hyperchaotic data, in: Chaotic Dynamics in Brain Function ( E. Basar, Ed.), pp. 113–121. Springer-Verlag, Berlin.
O.E. Rössler (1979). Phys. Lett. 71 A, 155.
O.E. Rössler, J.L. Hudson and M. Klein (1989). J. Phys. Chem. 93, 2858.
O.E. Rössler and C. Kahlert (1987). Z. Naturforsch. 42 a, 324.
P.M. Battelino, C. Grebogi, E. Ott, J.A. Yorke and E.D. Yorke (1988). Physica 32 D, 296.
O.E. Rössler (1985), Example of an axiom-A ODE, in: Chaos, Fractals and Dynamics ( P. Fischer and W.R. Smith, Eds.), pp. 105–114. M. Dekker, New York.
F. Moon, Personal communication 1989.
G. Baier, K. Wegmann and J.L. Hudson (1989). Phys. Lett. A (submitted).
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 1990 Springer-Verlags Berlin Heidelberg
About this paper
Cite this paper
Rossler, O.E., Hudson, J.L., Klein, M., Mira, C. (1990). Self-Similar Basin Boundary in a Continuous System. In: Schiehlen, W. (eds) Nonlinear Dynamics in Engineering Systems. International Union of Theoretical and Applied Mechanics. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-83578-0_33
Download citation
DOI: https://doi.org/10.1007/978-3-642-83578-0_33
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-83580-3
Online ISBN: 978-3-642-83578-0
eBook Packages: Springer Book Archive