Abstract
We present “Ouroboros Praos”, a proof-of-stake blockchain protocol that, for the first time, provides security against fully-adaptive corruption in the semi-synchronous setting: Specifically, the adversary can corrupt any participant of a dynamically evolving population of stakeholders at any moment as long the stakeholder distribution maintains an honest majority of stake; furthermore, the protocol tolerates an adversarially-controlled message delivery delay unknown to protocol participants.
To achieve these guarantees we formalize and realize in the universal composition setting a suitable form of forward secure digital signatures and a new type of verifiable random function that maintains unpredictability under malicious key generation. Our security proof develops a general combinatorial framework for the analysis of semi-synchronous blockchains that may be of independent interest. We prove our protocol secure under standard cryptographic assumptions in the random oracle model.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
The design of proof-of-stake blockchain protocols was identified early on as an important objective in blockchain design; a proof-of-stake blockchain substitutes the costly proof-of-work component in Nakamoto’s blockchain protocol [20] while still providing similar guarantees in terms of transaction processing in the presence of a dishonest minority of users, where this “minority” is to be understood here in the context of stake rather than computational power.
The basic stability and security properties of blockchain protocols were first rigorously formulated in [12] and further studied in [15, 21]; these include common prefix, chain quality and chain growth and refer to resilient qualities of the underlying data structure of the blockchain in the presence of an adversary that attempts to subvert them.
Proof-of-stake protocols typically possess the following basic characteristics. Based on her local view, a party is capable of deciding, in a publicly verifiable way, whether she is permitted to produce the next block. Assuming the block is valid, other parties update their local views by adopting the block, and proceed in this way continuously. At any moment, the probability of being permitted to issue a block is proportional to the relative stake a player has in the system, as reported by the blockchain itself.
A particularly challenging design aspect is that the above probabilistic mechanism should be designed so that the adversary cannot bias it to its advantage. As the stake shifts, together with the evolving population of stakeholders, so does the honest majority assumption, and hence the function that appoints stakeholders should continuously take the ledger status into account. Preventing the biasing of the election mechanism in a context of a blockchain protocol is a delicate task that so far has eluded a practical solution that is secure against all attacks.
Our Results. We present “Ouroboros Praos”, a provably secure proof-of-stake protocol that is the first to be secure against adaptive attackers and scalable in a truly practical sense. Our protocol is based on a previous proof-of-stake protocol, Ouroboros [16], as its analysis builds on some of the core combinatorial arguments that were developed to analyze that scheme. Nevertheless, the protocol construction has a number of novel elements that require a significant recasting and generalization of the previous combinatorial analysis. In more detail, our results are as follows.
In Ouroboros Praos, deciding whether a certain participant of the protocol is eligible to issue a block is decided via a private test that is executed locally using a special verifiable random function (VRF) on the current time-stamp and a nonce that is determined for a period of time known as an “epoch”. A special feature of this VRF primitive, novel to our approach, is that the VRF must have strong security characteristics even in the setting of malicious key generation: specifically, if provided with an input that has high entropy, the output of the VRF is unpredictable even when an adversary has subverted the key generation procedure. We call such VRF functions “VRF with unpredictability under malicious key generation” and we present a strong embodiment of this notion with a novel Universal Composable (UC) formulation. We also present a very efficient realization of this primitive under the Computational Diffie Hellman (CDH) assumption in the random oracle model. Beyond this VRF notion, we also formalize in a UC fashion key evolving signatures that provide the forward security that is necessary for handling the adaptive corruption setting.
In more detail, we analyze our protocol in the partial or semi-synchronous model [11, 21]. In this setting, we still divide the protocol execution in time units which, as in [16], are called slots, but there is a maximum delay of \(\varDelta \) slots that is applied to message delivery and it is unknown to the protocol participants.Footnote 1 In order to cope with the \(\varDelta \)-semisynchronous setting we introduce the concept of “empty slots” which occur with sufficient frequency to enable short periods of silence that facilitate synchronization. This feature of the protocol gives also its moniker, “Praos”, meaning “mellow”, or “gentle”. Ensuring that the adversary cannot exploit the stakeholder keys that it possesses to confuse or out-maneuver the honest parties, we develop a combinatorial analysis to show that the simple rule of following the longest chain still enables the honest parties to converge to a unique view with high probability. To accomplish this we revisit and expand the forkable strings and divergence analysis of [16]. We remark that significant alterations are indeed necessary: As we demonstrate in the full version of this paper, the protocol of [16] and its analysis are critically tailored to synchronous operation and is susceptible to a desynchronization attack that can completely violate the common prefix property. Our new combinatorial analysis introduces a new concept of characteristic strings and “forks” that reflects silent periods in protocol execution and network delays. To bound the density of forkable strings in this \(\varDelta \)-semisynchronous setting we establish a syntactic reduction from \(\varDelta \)-semisynchronous characteristic strings to synchronous strings of [16] that preserves the structure of the forks they support. This is followed by a probabilistic analysis that controls the distortion caused by the reduction and concludes that \(\varDelta \)-semisynchronous forkable strings are rare. Finally, we control the effective power of adaptive adversaries in this setting with a stochastic dominance argument that permits us to carry out the analysis of the underlying blockchain guarantees (e.g., common prefix) with a single distribution that provably dominates all distributions on characteristic strings generated by adaptive adversaries. We remark that these arguments yield graceful degradation of the analysis as a function of network delays (\(\varDelta \)), in the sense that the effective stake of the adversary is amplified by a function of \(\varDelta \).
The above combinatorial analysis is nevertheless only sufficient to provide a proof of the static stake case, i.e., the setting where the stake distribution relevant to the honest majority assumption remains fixed at the onset of the computation and prior to the selection of the random genesis data that are incorporated in the genesis block. For a true proof-of-stake system, we must permit the set of stakeholders to evolve over time and appropriately adapt our honest stakeholder majority assumption. Achieving this requires a bootstrapping argument that allows the protocol to continue unboundedly by revising its stakeholder distribution as it evolves. We bootstrap our protocol in two conceptual steps. First we show how bootstrapping is possible if a randomness beacon is available to all participants. The beacon at regular intervals emits a new random value and the participants can reseed the election process so the stakeholder distribution used for sampling could be brought closer to the one that is current. A key observation here is that our protocol is resilient even if the randomness beacon is weakened in the following two ways: (i) it leaks its value to the adversary ahead of time by a bounded number of time units, (ii) it allows the adversary to reset its value if it wishes within a bounded time window. We call the resulting primitive a “leaky resettable beacon” and show that our bootstrapping argument still holds in this stronger adversarial setting.
In the final refinement of our protocol, we show how it is possible to implement the leaky resettable beacon via a simple algorithm that concatenates the VRF outputs that were contributed by the participants from the blockchain and subjects them to a hash function that is modeled as a random oracle. This implementation explains the reasons behind the beacon relaxation we introduced: leakiness stems from the fact that the adversary can complete the blockchain segment that determines the beacon value before revealing it to the honest participants, while resettability stems from the fact that the adversary can try a bounded number of different blockchain extensions that will stabilize the final beacon value to a different preferred value.
Putting all the above together, we show how our protocol provides a “robust transaction ledger” in the sense that an immutable record of transactions is built that also guarantees that new transactions will be always included. Our security definition is in the \(\varDelta \)-semisynchronous setting with full adaptive corruptions. As mentioned above, security degrades gracefully as \(\varDelta \) increases, and this parameter is unknown to the protocol participants.
Note that implementing the beacon via hashing VRF values will make feasible a type of “grinding attack” where the adversary can trade hashing power for a slight bias of the protocol execution to its advantage. We show how this bias can be controlled by suitably increasing the relevant parameters depending on the hashing power that is available to the adversary.
Comparison to related work. The idea of proof-of-stake protocols has been discussed extensively in the bitcoin forum.Footnote 2 The manner that a stakeholder determines eligibility to issue a block is always publicly verifiable and the proof of eligibility is either computed publicly (via a calculation that is verifiable by repeating it) or by using a cryptographic mechanism that involves a secret-key computation and a public-key verification. The first example of the former approach appeared in PPCoin [17], and was followed by others including Ouroboros and Snow White [2, 8, 16]; while the first example of the latter approach (that we also employ in our work) appeared in NXT (cf. Sect. 2.4.1 of [7]) and was then also used elsewhere, most notably in Algorand [19]. The virtue of the latter approach is exactly in its potential to control adaptive corruptions: due to the fact that the adversary cannot predict the eligibility of a stakeholder to issue a block prior to corrupting it, she cannot gain an advantage by directing its corruption quota to specific stakeholders. Nevertheless, none of these previous works isolated explicitly the properties of the primitives that are required to provide a full proof of security in the setting of adaptive corruptions. Injecting high quality randomness in the PoS blockchain was proposed by Bentov et al. [3, 4], though their proposal does not have a full formal analysis. The Ouroboros proof-of-stake protocol [16] is provably secure in a corruption model that excludes fully adaptive attacks by imposing a corruption delay on the corruption requests of the adversary. The Snow White proof-of-stake [8] is the first to prove security in the \(\varDelta \)-semi-synchronous model but—as in the case of Ouroboros—adopts a weak adaptive corruption model.
A recent work close to ours is Algorand [19] that also provides a proof-of-stake ledger that is adaptively secure. It follows an entirely different construction approach that runs a Byzantine agreement protocol for every block and achieves adaptive-corruption security via a novel, appealing concept of player-replaceability. However, Algorand is only secure against a 1 / 3 adversary bound; and while the protocol itself is very efficient, it yields an inherently slower block production rate compared to an “eventual consensus” protocol (like Bitcoin, Snow White, and Ouroboros). In principle, proof-of-stake blockchain protocols can advance at the theoretical maximum speed (of one block per communication round), while protocols relying on Byzantine agreement, like Algorand, would require a larger number of rounds to settle each block.
Sleepy consensus [22] puts forth a technique for handling adaptive corruptions in a model that also encompasses fail-stop and recover corruptions; however, the protocol can be applied directly only in a static stake (i.e., permissioned) setting. We note that in fact our protocol can be also proven secure in such mixed corruption setting, where both fail-stop and recover as well as Byzantine corruptions are allowed (with the former occurring at an arbitrarily high rate); nevertheless this is out of scope for the present exposition and we omit further details.
Note that the possibility of adversarial grinding in Ouroboros Praos is also present in previous work that derives randomness by hashing [8, 19], as opposed to a dedicated coin-tossing protocol as in [16]. Following the examples of [8, 19], we show that security can be guaranteed despite any adversarial bias resulting from grinding. In fact, we show how to use the q-bounded model of [12] to derive a bound that shows how to increase the relevant security parameters given the hashing power that is available to the adversary.
Finally, in the present exposition we also put aside incentives; nevertheless, it is straightforward to adapt the mechanism of input endorsers from the protocol of [16] to our setting and its approximate Nash equilibrium analysis can be ported directly.
2 Preliminaries
We say a function \(negl(x)\) is negligible if for every \(c>0\), there exists an \(n > 0\) such that \(negl(x)< {1}/{x^c}\) for all \(x \ge n\). The length of a string w is denoted by |w|; \(\varepsilon \) denotes the empty string. We let \(v\,\Vert \,w\) denote concatenation of strings.
2.1 Transaction Ledger Properties
We adopt the same definitions for transaction ledger properties as [16]. A protocol \(\varPi \) implements a robust transaction ledger provided that the ledger that \(\varPi \) maintains is divided into “blocks” (assigned to time slots) that determine the order with which transactions are incorporated in the ledger. It should also satisfy the following two properties.
-
Persistence. Once a node of the system proclaims a certain transaction tx in the stable part of its ledger, the remaining nodes, if queried, will either report tx in the same position of that ledger or report a stable ledger which is a prefix of that ledger. Here the notion of stability is a predicate that is parameterized by a security parameter k; specifically, a transaction is declared stable if and only if it is in a block that is more than k blocks deep in the ledger.
-
Liveness. If all honest nodes in the system attempt to include a certain transaction then, after the passing of time corresponding to u slots (called the transaction confirmation time), all nodes, if queried and responding honestly, will report the transaction as stable.
In [15, 21] it was shown that persistence and liveness can be derived from the following three elementary properties provided that protocol \(\varPi \) derives the ledger from a data structure in the form of a blockchain.
-
Common Prefix (CP); with parameters \(k\in \mathbb {N}\). The chains \(\mathcal {C}_1,\mathcal {C}_2\) possessed by two honest parties at the onset of the slots \(sl_1 < sl_2\) are such that \( \mathcal {C}_1^{\lceil k} \preceq \mathcal {C}_2\), where \(\mathcal {C}_1^{\lceil k}\) denotes the chain obtained by removing the last k blocks from \(\mathcal {C}_1\), and \(\preceq \) denotes the prefix relation.
-
Chain Quality (CQ); with parameters \(\mu \in (0,1]\) and \(k\in \mathbb {N}\). Consider any portion of length at least k of the chain possessed by an honest party at the onset of a round; the ratio of blocks originating from the adversary is at most \(1-\mu \). We call \(\mu \) the chain quality coefficient.
-
Chain Growth (CG); with parameters \(\tau \in (0,1],s\in \mathbb {N}\). Consider the chains \(\mathcal {C}_1, \mathcal {C}_2\) possessed by two honest parties at the onset of two slots \(sl_1,sl_2\) with \(sl_2\) at least s slots ahead of \(sl_1\). Then it holds that \(\mathrm {len}(\mathcal {C}_2) - \mathrm {len}(\mathcal {C}_1) \ge \tau {\cdot }s\). We call \(\tau \) the speed coefficient.
2.2 The Semi-synchronous Model
On a high level, we consider the security model of [16] with simple modifications to account for adversarially-controlled message delays and immediate adaptive corruption. Namely, we allow the adversary \(\mathcal {A}\) to selectively delay any messages sent by honest parties for up to \(\varDelta \in \mathbb {N}\) slots; and corrupt parties without delay.
Time and slots. We consider a setting where time is divided into discrete units called slots. A ledger, described in more detail above, associates with each time slot (at most) one ledger block. Players are equipped with (roughly) synchronized clocks that indicate the current slot: we assume that any clock drift is subsumed in the slot length. This will permit them to carry out a distributed protocol intending to collectively assign a block to this current slot. In general, each slot \(sl_r\) is indexed by an integer \(r \in \{1,2,\ldots \}\), and we assume that the real time window that corresponds to each slot has the following two properties: (1) The current slot is determined by a publicly-known and monotonically increasing function of current time. (2) Each player has access to the current time. Any discrepancies between parties’ local time are insignificant in comparison with the length of time represented by a slot.
Security Model. We adopt the model introduced by [12] for analysing security of blockchain protocols enhanced with an ideal functionality \(\mathcal {F}\). We note that multiple different “functionalities” can be encompassed by \(\mathcal {F}\). In our model we employ the “Delayed Diffuse” functionality, which allows for adversarially-controlled delayed delivery of messages diffused among stakeholders.
The Diffuse Functionality. This functionality is parameterized by \(\varDelta \in \mathbb {N}\) and denoted as \(\mathsf {DDiffuse}_\varDelta \). It keeps rounds, executing one round per slot. \(\mathsf {DDiffuse}_\varDelta \) interacts with the environment \(\mathcal {Z}\), stakeholders \(U_1,\ldots ,U_n\) and an adversary \(\mathcal {A}\), working as follows for each round:
-
1.
\(\mathsf {DDiffuse}_\varDelta \) maintains an incoming string for each party \(U_i\) that participates. A party, if activated, is allowed at any moment to fetch the contents of its incoming string, hence one may think of this as a mailbox. Furthermore, parties can give an instruction to the functionality to diffuse a message. Activated parties are allowed to diffuse once in a round.
-
2.
When the adversary \(\mathcal {A}\) is activated, it is allowed to: (a) Read all inboxes and all diffuse requests and deliver messages to the inboxes in any order it prefers; (b) For any message m obtained via a diffuse request and any party \(U_i\), \(\mathcal {A}\) may move m into a special string \(\mathsf {delayed}_i\) instead of the inbox of \(U_i\). \(\mathcal {A}\) can decide this individually for each message and each party; (c) For any party \(U_i\), \(\mathcal {A}\) can move any message from the string \(\mathsf {delayed}_i\) to the inbox of \(U_i\).
-
3.
At the end of each round, the functionality also ensures that every message that was either (a) diffused in this round and not put to the string \(\mathsf {delayed}_i\) or (b) removed from the string \(\mathsf {delayed}_i\) in this round is delivered to the inbox of party \(U_i\). If any message currently present in \(\mathsf {delayed}_i\) was originally diffused at least \(\varDelta \) slots ago, then the functionality removes it from \(\mathsf {delayed}_i\) and appends it to the inbox of party \(U_i\).
-
4.
Upon receiving \((\mathsf {Create},U,\mathcal {C})\) from the environment, the functionality spawns a new stakeholder with chain \(\mathcal {C}\) as its initial local chain (as it was the case in [16]).
Modelling Protocol Execution and Adaptive Corruptions. Given the above we will assume that the execution of the protocol is with respect to a functionality \(\mathcal {F}\) that incorporates \(\mathsf {DDiffuse}\) as well as possibly additional functionalities to be explained in the following sections. The environment issues transactions on behalf of any stakeholder \(U_i\) by requesting a signature on the transaction as described in Protocol \(\pi _{{\text {SPoS}}}\) of Fig. 4 and handing the transaction to stakeholders to put them into blocks. Beyond any restrictions imposed by \(\mathcal {F}\), the adversary can only corrupt a stakeholder \(U_i\) if it is given permission by the environment \(\mathcal {Z}\) running the protocol execution. The permission is in the form of a message \((\mathsf {Corrupt}, U_i)\) which is provided to the adversary by the environment. Upon receiving permission from the environment, the adversary immediately corrupts \(U_i\) without any delay, differently from [8, 16], where corruptions only take place after a given delay. Note that a corrupted stakeholder \(U_i\) will relinquish its entire state to \(\mathcal {A}\); from this point on, the adversary will be activated in place of the stakeholder \(U_i\). The adversary is able to control transactions and blocks generated by corrupted parties by interacting with \(\mathcal {F}_{\mathsf {DSIG}}\), \(\mathcal {F}_{\mathsf {KES}}\) and \(\mathcal {F}_{\mathsf {VRF}}\), as described in Protocol \(\pi _{{\text {SPoS}}}\) of Sect. 3. In summary, regarding activations we have the following: (a) At each slot \(sl_j\), the environment \(\mathcal {Z}\) activates all honest stakeholders.Footnote 3 (b) The adversary is activated at least as the last entity in each \(sl_j\) (as well as during all adversarial party activations and invocations from the ideal functionalities as prescribed); (c) If a stakeholder does not fetch in a certain slot the messages written to its incoming string from the diffuse functionality they are flushed.
Restrictions imposed on the environment. It is easy to see that the model above confers such sweeping power on the adversary that one cannot establish any significant guarantees on protocols of interest. It is thus important to restrict the environment suitably (taking into account the details of the protocol) so that we may be able to argue security. We require that in every slot, the adversary does not control more than \(50\%\) of the stake in the view of any honest stakeholder. This transaction data, including the required signatures by each stakeholder, is obtained by the environment as specified in the protocol. If this is violated, an event \({\textsf {Bad}}^{\frac{1}{2}}\) becomes true for the given execution. When the environment spawns a new stakeholder by sending message \((\mathsf {Create},U,\mathcal {C})\) to the Key and Transaction functionality, the initial local chain \(\mathcal {C}\) can be the chain of any honest stakeholder even in the case of “lazy honest” stakeholders without requiring this stakeholder to have been online in the past slot as in [16]. Finally, we note that in all our proofs, whenever we say that a property Q holds with high probability over all executions, we will in fact argue that \(Q \vee {\textsf {Bad}}^{\frac{1}{2}}\) holds with high probability over all executions. This captures the fact that we exclude environments and adversaries that trigger \({\textsf {Bad}}^{\frac{1}{2}}\) with non-negligible probability.
Random Oracle. We also assume the availability of a random oracle. As usually, this is a function \(\mathsf {H}:\{0,1\}^*\rightarrow \{0,1\}^w\) available to all parties that answers every fresh query with an independent, uniformly random string from \(\{0,1\}^w\), while any repeated queries are answered consistently.
Erasures. We assume that honest users can do secure erasures, which is argued to be a reasonable assumption in protocols with security against adaptive adversaries, see e.g., [18].
3 The Static Stake Protocol
We first consider the static stake case, where the stake distribution is fixed throughout protocol execution. The general structure of the protocol in the semi-synchronous model is similar to that of (synchronous) Ouroboros [16] but introduces several fundamental modifications to the leader selection process: not all slots will be attributed a slot leader, some slots might have multiple slot leaders, and slot leaders’ identities remain unknown until they act. The first modification is used to deal with delays in the semi-synchronous network as the empty slots—where no block is generated—assist the honest parties to synchronize. The last modification is used to deal with adaptive corruptions, as it prevents the adversary from learning the slot leaders’ identity ahead of time and using this knowledge to strategically corrupt coalitions of parties with large (future) influence. Moreover, instead of using concrete instantiations of the necessary building blocks, we describe the protocol with respect to ideal functionalities, which we later realize with concrete constructions. This difference allows us to reason about security in the ideal model through a combinatorial argument without having to deal with the probability that the cryptographic building blocks fail. Before describing the specifics of the new leader selection process and the new protocol, we first formally define the static stake scenario and introduce basic definitions as stated in [16] following the notation of [12].
In the static stake case, we assume that a fixed collection of n stakeholders \(U_{1},\ldots ,U_{n}\) interact throughout the protocol. Stakeholder \(U_{i}\) is attributed stake \(s_i\) at the beginning of the protocol.
Definition 1 (Genesis Block)
The genesis block \(B_0\) contains the list of stakeholders identified by a label \(U_i\), their respective public keys and respective stakes
and a nonce \(\eta \).
We note that the nonce \(\eta \) will be used to seed the slot leader election process and that \(v^{\mathrm {vrf}}_i,v^{\mathrm {kes}}_i,v^{\mathrm {dsig}}_i\) will be determined by \(\mathcal {F}_{\mathsf {VRF}}\), \(\mathcal {F}_{\mathsf {KES}}\) and \(\mathcal {F}_{\mathsf {DSIG}}\), respectively.
Definition 2 (Epoch, State, Block Proof, Block, Blockchain)
An epoch is a set of \(R\) adjacent slots \(S=\{sl_1,\ldots ,sl_{R}\}\). (The value \(R\) is a parameter of the protocol we analyze in this section.) A state is a string \(st\in \{0,1\}^\lambda \). A block proof is a value (or set of values) \({B_\pi }\) containing information that allows stakeholders to verify if a block is valid. A block \(B=(sl_j,st,d,{B_\pi }_j,\sigma _j)\) generated at a slot \(sl_j \in \{sl_1,\ldots ,sl_{R}\}\) contains the current state \(st\in \{0,1\}^\lambda \), data \(d \in \{0,1\}^{*}\), the slot number \(sl_j\), a block proof \({B_\pi }_j\) and \(\sigma _j\), a signature on \((st,d,sl_j,{B_\pi }_j)\) under the signing key for the time period of slot \(sl_j\) of the stakeholder \(U_{i}\) generating the block.
A blockchain (or simply chain) relative to the genesis block \(B_0\) is a sequence of blocks \(B_1,\ldots , B_n\) associated with a strictly increasing sequence of slots for which the state \(st_i\) of \(B_i\) is equal to \(H(B_{i-1})\), where H is a prescribed collision-resistant hash function. The length of a chain \(\mathrm {len}(\mathcal {C}) = n\) is its number of blocks. The block \(B_n\) is the head of the chain, denoted \(\mathrm {head}(\mathcal {C})\). We treat the empty string \(\varepsilon \) as a legal chain and by convention set \(\mathrm {head}(\varepsilon ) = \varepsilon \). Let \(\mathcal {C}\) be a chain of length n and k be any non-negative integer. We denote by \(\mathcal {C}^{\lceil k}\) the chain resulting from removal of the k rightmost blocks of \(\mathcal {C}\). If \(k \ge \mathrm {len}(\mathcal {C})\) we define \(\mathcal {C}^{\lceil k} = \varepsilon \). We let \(\mathcal {C}_1 \preceq \mathcal {C}_2\) indicate that the chain \(\mathcal {C}_1\) is a prefix of the chain \(\mathcal {C}_2\).
We consider as valid blocks that are generated by a stakeholder in the slot leader set of the slot to which the block is attributed. Later in Sect. 3.3 we discuss slot leader sets and how they are selected.
Definition 3 (Absolute and Relative Stake)
Let \(U_\mathcal {P}\), \(U_\mathcal {A}\) and \(U_\mathcal {H}\) denote the sets of all stakeholders, the set of stakeholders controlled by an adversary \(\mathcal {A}\), and the remaining (honest) stakeholders, respectively. For any party (resp. set of parties) X we denote by \(s_X^{+}\) (resp. \(s_X^{-}\)) the maximum (resp. minimum) absolute stake controlled by X in the view of all honest stakeholders at a given slot, and by \(\alpha ^{+}_X\triangleq s^{+}_X/s_\mathcal {P}\) and \(\alpha ^{-}_X\triangleq s^{-}_X/s_\mathcal {P}\) its relative stake taken as maximum and minimum respectively across the views of all honest stakeholders. For simplicity, we use \(s_X^\mathrm {s}, \alpha _X^\mathrm {s}\) instead of \(s_{U_X}, \alpha _{U_X}\) for all \(X\in \{\mathcal {P},\mathcal {A},\mathcal {H}\}, \mathrm {s}\in \{+,-\}\). We also call \(\alpha _\mathcal {A}\triangleq \alpha _\mathcal {A}^{+}\) and \(\alpha _\mathcal {H}\triangleq \alpha _\mathcal {H}^{-} \) the adversarial stake ratio and honest stake ratio, respectively.
3.1 Forward Secure Signatures and \(\mathcal {F}_{\mathsf {KES}}\)
In regular digital signature schemes, an adversary who compromises the signing key of a user can generate signatures for any messages it wishes, including messages that were (or should have been) generated in the past. Forward secure signature schemes [1] prevent such an adversary from generating signatures for messages that were issued in the past, or rather allows honest users to verify that a given signature was generated at a certain point in time. Basically, such security guarantees are achieved by “evolving” the signing key after each signature is generated and erasing the previous key in such a way that the actual signing key used for signing a message in the past cannot be recovered but a fresh signing key can still be linked to the previous one. This notion is formalized through key evolving signature schemes, which allow signing keys to be evolved into fresh keys for a number of time periods. We remark that efficient constructions of key evolving signature schemes with forward security exist [13] but no previous work has fully specified them in the UC setting.
We present a UC definition of the type of key-evolving signatures that we will take advantage of in our constructions. \(\mathcal {F}_{\mathsf {KES}}\) allows us to achieve forward security with erasures (i.e., assuming that parties securely delete old signing keys as the protocol proceeds). This functionality embodies ideal key evolving signature schemes allowing an adversary that corrupts the signer to forge signatures only under the current and future signing keys, but not under a previous signing key that has been updated. Our starting point for \(\mathcal {F}_{\mathsf {KES}}\) is the standard digital signature functionality defined in [5] with the difference that packs together with the signing operation a key-evolving operation. During verification, \(\mathcal {F}_{\mathsf {KES}}\) lets the adversary set the response to a verification query (taking as input a given time period) only if no key update has been performed since that time period and no entry exists in its internal table for the specific message, signature and time period specified in the query. We present \(\mathcal {F}_{\mathsf {KES}}\) in Fig. 1. In the full version, we show that \(\mathcal {F}_{\mathsf {KES}}\) can be realized by a construction based on key evolving signature schemes.
3.2 UC-VRFs with Unpredictability Under Malicious Key Generation
The usual pseudorandomness definition for VRFs captures the fact that an attacker, seeing a number of VRF outputs and proofs for adversarially chosen inputs under a key pair that is correctly generated by a challenger, cannot distinguish the output of the VRF on a new (also adversarially chosen) input from a truly random string. This definition is too weak for our purposes for two reasons: first, we need a simulation-based definition so that the VRF can be composed directly within our protocol; second, we need the primitive to provide some level of unpredictability even under malicious key generation, i.e., against adversaries who are allowed to generate the secret and pubic key pair.
Our UC formulation of VRFs cannot be implied by the standard VRF security definition or even the simulatable VRF notion of [6]. For instance, the VRF proofs in our setting have to be simulatable without knowledge of the VRF output (which is critical as we would like to ensure that the VRF output is not leaked to the adversary prematurely); it is easy to construct a VRF that is secure in the standard definition, but it is impossible to simulate its proofs without knowledge of the VRF output. Furthermore, if the adversary is allowed to generate its own key pair it is easy to see that the distribution of the VRF outputs cannot be guaranteed. Indeed, even for known constructions (e.g. [10]), an adversary that maliciously generates keys can easily and significantly skew the output distribution.
We call the latter property unpredictability under malicious key generation and we present, in Fig. 2, a UC definition for VRF’s that captures this stronger security requirement.Footnote 4 The functionality operates as follows. Given a key generation request from one of the stakeholders, it returns a new verification key v that is used to label a table. Two methods are provided for computing VRF values. The first provides just the VRF output and does not interact with the adversary. In the second, whenever invoked on an input m that is not asked before by a stakeholder that is associated to a certain table labeled by v, the functionality will query the adversary for the value of the proof \(\pi \), and subsequently sample a random element \(\rho \) to associate with m. Verification is always consistent and will validate outputs that have already being inserted in a table. Unpredictability against malicious key generation is captured by imposing the same random selection of outputs even for the function tables that correspond to keys of corrupted stakeholders. Finally, the adversary is allowed to query all function tables maintained by the functionality for which either a proof has been computed, or they correspond to adversarial keys. In the full version, we show how to realize \(\mathcal {F}_{\mathsf {VRF}}\) in the random oracle model under the CDH assumption based on the 2-Hash-DH verifiable oblivious PRF construction of [14].
3.3 Oblivious Leader Selection
As in (synchronous) Ouroboros, for each \(0 < j \le R\), a slot leader \(E_j\) is a stakeholder who is elected to generate a block at \(sl_j\). However, our leader selection process differs from Ouroboros [16] in three points: (1) potentially, multiple slot leaders may be elected for a particular slot (forming a slot leader set); (2) frequently, slots will have no leaders assigned to them; and (3) a priori, only a slot leader is aware that it is indeed a leader for a given slot; this assignment is unknown to all the other stakeholders—including other slot leaders of the same slot—until the other stakeholders receive a valid block from this slot leader. The combinatorial analysis presented in Sect. 4 shows (with an honest stake majority) that (i.) blockchains generated according to these dynamics are well-behaved even if multiple slot leaders are selected for a slot and that (ii.) sequences of slots with no leader provide sufficient stability for honest stakeholders to effectively synchronize. As a matter of terminology, we call slots with an associated nonempty slot leader set active slots and slots that are not assigned a slot leader empty slots.
The idealized slot leader assignment and the active slots coefficient. The fundamental leader assignment process calls for a stakeholder \(U_i\) to be independently selected as a leader for a particular slot \(sl_j\) with probability \(p_i\) depending only on its relative stake. (In this static-stake analysis, relative stake is simply determined by the genesis block \(B_0\).) The exact relationship between \(p_i\) and the relative stake \(\alpha _i\) is determined by a parameter f of the protocol which we refer to as the active slots coefficient. Specifically,
where \(\alpha _i\) is the relative stake held by stakeholder \(U_i\). We occasionally drop the subscript f and write \(\phi (\alpha _i)\) when f can be inferred from context. As the events “\(U_i\) is a leader for \(sl_j\)” are independent, this process may indeed generate multiple (or zero) leaders for a given slot.
Remarks about \(\phi _f(\cdot )\). Observe that \(\phi _f(1) = f\); in particular, the parameter f is the probability that a party holding all the stake will be selected to be a leader for given slot. On the other hand, \(\phi _f()\) is not linear, but slightly concave. To motivate the choice of the function \(\phi _f\), we note that it satisfies the “independent aggregation” property:
In particular, when leadership is determined according to \(\phi _f\), the probability of a stakeholder becoming a slot leader in a particular slot is independent of whether this stakeholder acts as a single party in the protocol, or splits its stake among several “virtual” parties. In particular, consider a party U with relative stake \(\alpha \) who contrives to split its stake among two virtual subordinate parties with stakes \(\alpha _1\) and \(\alpha _2\) (so that \(\alpha _1 + \alpha _2 = \alpha \)). Then the probability that one of these virtual parties is elected for a particular slot is \(1 - (1 - \phi (\alpha _1))(1 - \phi (\alpha _2))\), as these events are independent. Property (2) guarantees that this is identical to \(\phi (\alpha )\). Thus this selection rule is invariant under arbitrary reapportionment of a party’s stake among virtual parties.
3.4 The Protocol in the \(\mathcal {F}_{\mathsf {INIT}}\)-Hybrid Model
We will construct our protocol for the static stake case in the \(\mathcal {F}_{\mathsf {INIT}}\)-hybrid model, where the genesis stake distribution \(\mathbb {S}_0\) and the nonce \(\eta \) (to be written in the genesis block \(B_0\)) are determined by the ideal functionality \(\mathcal {F}_{\mathsf {INIT}}\) defined in Fig. 3. Moreover, \(\mathcal {F}_{\mathsf {INIT}}\) also incorporates the diffuse functionality from Sect. 2.2, which is implicitly used by all parties to send messages and keep synchronized with a global clock. \(\mathcal {F}_{\mathsf {INIT}}\) also takes stakeholders’ public keys from them and packages them into the genesis block at the outset of the protocol. Note that \(\mathcal {F}_{\mathsf {INIT}}\) halts if it is not possible to create a genesis block; all security guarantees we provide later in the paper are conditioned on a successful creation of the genesis block.
Blocks are signed with a forward secure signature scheme modelled by \(\mathcal {F}_{\mathsf {KES}}\), while transactions are signed with a regular EUF-CMA secure digital signature modelled by a standard signature functionality \(\mathcal {F}_{\mathsf {DSIG}}\), deferred to the full version due to space constraints.
Notice that the implicit leader assignment process described in \(\pi _{{\text {SPoS}}}\) calls for a party \(U_i\) to act as a leader for a slot \(sl_j\) when \(y < T_i\); this is an event that occurs with probability (exponentially close to) \(\phi _f(\alpha _i)\) as y is uniform according to the functionality \(\mathcal {F}_{\mathsf {VRF}}\).
We are interested in applications where transactions are inserted in the ledger. For simplicity, transactions are assumed to be simple assertions of the form “Stakeholder \(U_i\) transfers stake s to Stakeholder \((U_j, v^{\mathrm {vrf}}_j,v^{\mathrm {kes}}_j,v^{\mathrm {dsig}}_j)\)” (In an implementation the different public-keys can be hashed into a single value). Protocol \(\pi _{{\text {SPoS}}}\) ensures that the environment learns every stakeholder’s public keys and provides an interface for the environment to request signatures on arbitrary transactions. A transaction will consist of a transaction template tx of this format accompanied by a signature of tx by stakeholder \(U_i\). We define a valid transaction as follows:
Definition 4 (Valid Transaction)
A pair \((tx,\sigma )\) is considered a valid transaction by a verifier \(\mathsf {V}\) if the following holds:
-
The transaction template tx is of the format “Stakeholder \(U_i\) transfers stake s to Stakeholder \((U_j, v^{\mathrm {vrf}}_j,v^{\mathrm {kes}}_j,v^{\mathrm {dsig}}_j)\)” where \(U_i\) and \(U_j\) are stakeholders identified by tuples \((U_i,v^{\mathrm {vrf}}_i,v^{\mathrm {kes}}_i,v^{\mathrm {dsig}}_i)\) and \((U_j,v^{\mathrm {vrf}}_j,v^{\mathrm {kes}}_j,v^{\mathrm {dsig}}_j)\) contained in the current stake distribution \(\mathbb {S}\) and \(x \in \mathbb {Z}\).
-
The verifier V obtains
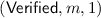 as answer upon sending
as answer upon sending  to \(\mathcal {F}_{\mathsf {DSIG}}\).
to \(\mathcal {F}_{\mathsf {DSIG}}\). -
Stakeholder \(U_i\) possesses x coins at the moment the transaction is issued (or registered in the blockchain) according to the view of the verifier \(\mathsf {V}\).
Given Definitions 2 and 4, we define a valid chain as a blockchain (according to Definition 2) where all transactions contained in every block are valid (according to Definition 4). The stakeholders \(U_{1},\ldots ,U_{n}\) interact among themselves and with \(\mathcal {F}_{\mathsf {INIT}}\) through Protocol \(\pi _{{\text {SPoS}}}\) described in Fig. 4. The protocol relies on a \(\mathsf {maxvalid}_S(\mathcal {C},\mathbb {C})\) function that chooses a chain given the current chain \(\mathcal {C}\) and a set of valid chains \(\mathbb {C}\) that are available in the network. In the static stake case we analyze the simple “longest chain” rule.
Function \(\mathsf {maxvalid}(\mathcal {C},\mathbb {C})\): Returns the longest chain from \(\mathbb {C}\cup \{\mathcal {C}\}\). Ties are broken in favor of \(\mathcal {C}\), if it has maximum length, or arbitrarily otherwise.
4 Combinatorial Analysis of the Static Stake Protocol
Throughout this section, we focus solely on analysis of the protocol \(\pi _{{\text {SPoS}}}\) using the idealized functionalities \(\mathcal {F}_{\mathsf {VRF}}\) and \(\mathcal {F}_{\mathsf {KES}}\) for VRFs and digital signatures, respectively—we refer to it as the hybrid experiment. Any property of the protocol that we prove true in the hybrid experiment (such as achieving common prefix, chain growth and chain quality) will remain true (with overwhelming probability) in the setting where \(\mathcal {F}_{\mathsf {VRF}}\) and \(\mathcal {F}_{\mathsf {KES}}\) are replaced by their real-world implementations—in the so-called real experiment.
The hybrid experiment yields a stochastic process for assigning slots to parties which we now abstract and study in detail. Our analysis of the resulting blockchain dynamics proceeds roughly as follows: We begin by generalizing the framework of “forks” [16] to our semi-synchronous setting—forks are a natural bookkeeping tool that reflect the chains possessed by honest players during an execution of the protocol. We then establish a simulation rule that associates with each execution of the semi-synchronous protocol an execution of a related “virtual” synchronous protocol. Motivated by the special case of a static adversary—which simply corrupts a family of parties at the outset of the protocol—we identify a natural “generic” probability distribution for this simulation theorem which we prove controls the behavior of adaptive adversaries by stochastic domination. Finally, we prove that this simulation amplifies the effective power of the adversary in a controlled fashion and, furthermore, permits forks of the semi-synchronous protocol to be projected to forks of the virtual protocol in a way that preserves their relevant combinatorial properties. This allows us to apply the density theorems and divergence result of [16, 23] to provide strong common prefix, chain growth, and chain quality (Sect. 4.4) guarantees for the semi-synchronous protocol with respect to an adaptive adversary.
We begin in Sect. 4.1 with a discussion of characteristic strings, semi-synchronous forks, and their relationship to executions of \(\pi _{{\text {SPoS}}}\) in the hybrid experiment. Section 4.2 then develops the combinatorial reduction from the semi-synchronous to the synchronous setting. The “generic, dominant” distribution on characteristic strings is then motivated and defined in Sect. 4.3, where the effect of the reduction on this distribution is also described. Section 4.4, as described above, establishes various guarantees on the resulting blockchain under the dominant distribution. The full power of adaptive adversaries is considered in Sect. 4.5. Finally, in preparation for applying the protocol in the dynamic stake setting, we formulate a “resettable setting” which further enlarges the power of the adversary by providing some control over the random nonce that seeds the protocol.
4.1 Chains, Forks and Divergence
We begin by suitably generalizing the framework of characteristic strings, forks, and divergence developed in [16] to our semi-synchronous setting.
The leader assignment process given by protocol \(\pi _{{\text {SPoS}}}\) in the hybrid experiment assigns leaders to slots with the following guarantees: (i.) a party with relative stake \(\alpha \) becomes a slot leader for a given slot with probability \(\phi _f(\alpha ) \triangleq 1 - (1 - f)^\alpha \); (ii.) the event of becoming a slot leader is independent for each party and for each slot (both points follow from the construction of \(\pi _{{\text {SPoS}}}\) and the independent random sampling of every new output in \(\mathcal {F}_{\mathsf {VRF}}\)). Clearly, these dynamics may lead to slots with multiple slot leaders and, likewise, slots with no slot leader. For a given (adaptive) adversary \(\mathcal {A}\) and environment \(\mathcal {Z}\), we reflect the outcome of this process with a characteristic string, as described below.
Definition 5 (Execution)
For an (adaptive) adversary \(\mathcal {A}\) and an environment \(\mathcal {Z}\), an execution \(\mathcal {E}\) of \(\pi _{{\text {SPoS}}}\) is a transcript including the inputs provided by \(\mathcal {Z}\), the random coins of the parties, the random coins of the adversary, the responses of the ideal functionalities and the random oracle. This data determines the entire dynamics of the protocol: messages sent and delivered, the internal states of the parties at each step, the set of corrupt parties at each step, etc.
Definition 6 (Characteristic string)
Let \(S=\{sl_{1},\ldots ,sl_{R}\}\) be a sequence of slots of length R and \(\mathcal {E}\) be an execution (with adversary \(\mathcal {A}\) and environment \(\mathcal {Z}\)). For a slot \(sl_j\), let \(\mathcal {P}(j)\) denote the set of parties assigned to be slot leaders for slot j by the protocol \(\pi _{{\text {SPoS}}}\) (specifically, those parties \(U_i\) for which \(y< 2^{\ell _{\mathsf {VRF}}} \phi _f(\alpha _i)\), where \((y,\pi ) \leftarrow \mathsf {Prove}_{\mathsf {VRF}.sk_i}(\eta \,\Vert \,sl_j)\)). We define the characteristic string \(w \in \{0,1,\bot \}^{R}\) of S to be the random variable so that
For such a characteristic string \(w \in \{0,1,\bot \}^*\) we say that the index j is uniquely honest if \(w_j = 0\), tainted if \(w_j = 1\), and empty if \(w_j = \bot \). We say that an index is active if \(w_j \in \{0,1\}\). Note that an index is “tainted” according to this terminology in cases where multiple honest parties (and no adversarial party) have been assigned to it.
We denote by \(\mathcal {D}^f_{\mathcal {Z},\mathcal {A}}\) the distribution of the random variable \(w=w_1\ldots w_R\) in the hybrid experiment with the active slots coefficient f, adversary \(\mathcal {A}\), and environment \(\mathcal {Z}\). For a fixed execution \(\mathcal {E}\), we denote by \(w_\mathcal {E}\) the (fixed) characteristic string resulting from that execution.
We emphasize that in an execution of \(\pi _{{\text {SPoS}}}\), the resulting characteristic string is determined by both the nonce (and the effective leader selection process), the adaptive adversary \(\mathcal {A}\), and the environment \(\mathcal {Z}\) (which, in particular, determines the stake distribution).
From Executions to Forks. The notion of a “fork”, defined in [16], is a bookkeeping tool that indicates the chains broadcast by honest players during an idealized execution of a blockchain protocol. We now adapt the synchronous notion of [16] to reflect the effect of message delays.
An execution of Protocol \(\pi _{{\text {SPoS}}}\) induces a collection of blocks broadcast by the participants. As we now focus merely on the structural properties of the resulting blockchain, for each broadcast block we now retain only two features: the slot associated with the block and the previous block to which it is “attached” by the idealized digital signature \(\sigma _j\). (Of course, we only consider blocks with legal structure that meet the verification criteria of \(\pi _{{\text {SPoS}}}\).) Note that multiple blocks may be associated with a particular slot, either because multiple parties are assigned to the slot or an adversarial party is assigned to a slot (who may choose to deviate from the protocol by issuing multiple blocks). In any case, these blocks induce a natural directed tree by treating the blocks as vertices and introducing a directed edge between each pair of blocks \((b, b')\) for which \(b'\) identifies b as the previous block. In the \(\varDelta \)-semisynchronous setting, the \(\mathsf {maxvalid}\) rule enforces a further critical property on this tree: the depth of any block broadcast by an honest player during the protocol must exceed the depths of any honestly-generated blocks from slots at least \(\varDelta \) in the past. (This follows because such previously broadcast blocks would have been available to the honest player, who always builds on a chain of maximal length.) We call a directed tree with these structural properties a \(\varDelta \)-fork, and define them precisely below.
We may thus associate with any execution of \(\pi _{{\text {SPoS}}}\) a fork. While this fork disregards many of the details of the execution, any violations of common prefix are immediately manifested by certain diverging paths in the fork. A fundamental element of our analysis relies on controlling the structure of the forks that can be induced in this way for a given characteristic string (which determines which slots have been assigned to uniquely honest parties). In particular, we prove that common prefix violations are impossible for “typical” characteristic strings generated by \(\pi _{{\text {SPoS}}}\) with an adversary \(\mathcal {A}\) by establishing that such diverging paths cannot exist in their associated forks.
Definition 7
(\(\varvec{\varDelta }\)-fork). Let \(w \in \{0,1,\bot \}^k\) and \(\varDelta \) be a non-negative integer. Let \(A = \{ i \mid w_i \ne \bot \}\) denote the set of active indices, and let \(H = \{ i \mid w_i = 0\}\) denote the set of uniquely honest indices. A \(\varDelta \)-fork for the string w is a directed, rooted tree \(F = (V, E)\) with a labeling \(\ell : V \rightarrow \{0\} \cup A\) so that (i) the root \(r \in V\) is given the label \(\ell (r) = 0\); (ii) each edge of F is directed away from the root; (iii) the labels along any directed path are strictly increasing; (iv) each uniquely honest index \(i \in H\) is the label of exactly one vertex of F; (v) the function \(\mathbf {d}: H \rightarrow \{1,\ldots ,k\}\), defined so that \(\mathbf {d}(i)\) is the depth in F of the unique vertex v for which \(\ell (v) = i\), satisfies the following \(\varDelta \)-monotonicity property: if \(i, j \in H\) and \(i + \varDelta < j\), then \(\mathbf {d}(i) < \mathbf {d}(j)\).
As a matter of notation, we write \(F \vdash _\varDelta w\) to indicate that F is a \(\varDelta \)-fork for the string w. We typically refer to a \(\varDelta \)-fork as simply a “fork”.
Also note that our notion of a fork deliberately models honest parties that do not necessarily exploit all the information available to them thanks to the delivery guarantees provided by the \(\mathsf {DDiffuse}\) functionality. Nonetheless, it remains true that any execution of the hybrid experiment leads to a fork as we defined it, a relationship that we make fully formal in the full version. Given this relationship, we can later focus on investigating the properties of the distribution \(\mathcal {D}^f_{\mathcal {Z},\mathcal {A}}\). Roughly speaking, if we prove that a characteristic string sampled from \(\mathcal {D}^f_{\mathcal {Z},\mathcal {A}}\), with overwhelming probability, does not allow for any “harmful” forks, then this also implies that a random execution with overwhelming probability results in a “harmless” outcome.
Now we continue with the adaptation of the framework from [16] to the semi-synchronous setting.
Definition 8
(Tines, length, and viability). A path in a fork F originating at the root is called a tine. For a tine t we let \({{\mathrm{length}}}(t)\) denote its length, equal to the number of edges on the path. For a vertex v, we call the length of the tine terminating at v the depth of v. For convenience, we overload the notation \(\ell (\cdot )\) so that it applies to tines by defining \(\ell (t) \triangleq \ell (v)\), where v is the terminal vertex on the tine t. We say that a tine t is \(\varDelta \)-viable if \({{\mathrm{length}}}(t) \ge \max _{\begin{array}{c} h + \varDelta \le \ell (t) \end{array}} \mathbf {d}(h)\), this maximum extended over all uniquely honest indices h (appearing \(\varDelta \) or more slots before \(\ell (t)\)). Note that any tine terminating in a uniquely honest vertex is necessarily viable by the \(\varDelta \)-monotonicity property.
Remarks on viability and divergence. The notion of viability, defined above, demands that the length of a tine t be no less than that of all tines broadcast by uniquely honest slot leaders prior to slot \(\ell (t) - \varDelta \). Observe that such a tine could, in principle, be selected according to the \(\mathsf {maxvalid}()\) rule by an honest player online at time \(\ell (t)\): in particular, if all blocks broadcast by honest parties in slots \(\ell (t) - \varDelta , \ldots , \ell (t)\) are maximally delayed, the tine can favorably compete with all other tines that the adversary is obligated to deliver by slot \(\ell (t)\). The major analytic challenge, both in the synchronous case and in our semisynchronous setting, is to control the possibility of a common prefix violation, which occurs when the adversary can manipulate the protocol to produce a fork with two viable tines with a relatively short common prefix. We define this precisely by introducing the notion of divergence.
Definition 9
(Divergence). Let F be a \(\varDelta \)-fork for a string \(w \in \{0,1,\bot \}^*\). For two \(\varDelta \)-viable tines \(t_1\) and \(t_2\) of F, define their divergence to be the quantity
where \(t_1 \cap t_2\) denotes the common prefix of \(t_1\) and \(t_2\). We extend this notation to the fork F by maximizing over viable tines: \({{\mathrm{div}}}_\varDelta (F) \triangleq \max _{\begin{array}{c} t_1,t_2 \end{array}} {{\mathrm{div}}}(t_1,t_2)\), taken over all pairs of \(\varDelta \)-viable tines of F. Finally, we define the \(\varDelta \)-divergence of a characteristic string w to be the maximum over all \(\varDelta \)-forks: \({{\mathrm{div}}}_\varDelta (w) \triangleq \max _{F \,\vdash _\varDelta w} {{\mathrm{div}}}_\varDelta (F)\).
Our primary goal in this section is to prove that, with high probability, the characteristic strings induced by protocol \(\pi _{{\text {SPoS}}}\) have small divergence and hence provide strong guarantees on common prefix.
The Synchronous Case. The original development of [16] assumed a strictly synchronous environment. Their definitions of characteristic string, fork, and divergence correspond to the case \(\varDelta = 0\), where characteristic strings are elements of \(\{0,1\}^*\). As this setting will play an important role in our analysis—fulfilling the role of the “virtual protocol” described at the beginning of this section—we set down some further terminology for this synchronous case and establish a relevant combinatorial statement based on a result in [16] that we will need for our analysis.
Definition 10
(Synchronous characteristic strings and forks). A synchronous characteristic string is an element of \(\{0,1\}^*\). A synchronous fork F for a (synchronous) characteristic string w is a 0-fork \(F \vdash _0 w\).
An immediate conclusion of the results obtained in [16, 23] is the following bound on the probability that a synchronous characteristic string drawn from the binomial distribution has large divergence.
Theorem 1
Let \(\ell ,k \in \mathbb {N}\) and \(\epsilon \in (0,1)\). Let \(w \in \{0,1\}^\ell \) be drawn according to the binomial distribution, so that \(\Pr [w_i = 1] = (1 - \epsilon )/2\). Then \(\Pr [{{\mathrm{div}}}_0(w) \ge k] \le \exp (\ln \ell - \varOmega (k))\).
4.2 The Semisynchronous to Synchronous Reduction
We will make use of the following mapping, that maps characteristic strings to synchronous characteristic strings.
Definition 11 (Reduction mapping)
For \(\varDelta \in \mathbb {N}\), we define the function \(\rho _\varDelta :\{0,1,\bot \}^*\rightarrow \{0,1\}^{*}\) inductively as follows: \(\rho _\varDelta (\varepsilon ) = \varepsilon \), \(\rho _\varDelta (\bot \,\Vert \,w') = \rho _\varDelta (w')\),

We call \(\rho _\varDelta \) the reduction mapping for delay \(\varDelta \).
A critical feature of the map \(\rho _\varDelta \) is that it monotonically transforms \(\varDelta \)-divergence to synchronous divergence. We state this in the following lemma, proven in the full version.
Lemma 1
Let \(w \in \{0,1,\bot \}^*\). Then \({{\mathrm{div}}}_\varDelta (w) \le {{\mathrm{div}}}_0(\rho _\varDelta (w))\).
4.3 The Dominant Characteristic Distribution
The high-probability results for our desired chain properties depend on detailed information about the distribution on characteristic strings \(\mathcal {D}^f_{\mathcal {Z},\mathcal {A}}\) determined by the adversary \(\mathcal {A}\), the environment \(\mathcal {Z}\), and the parameters f and R. In this section we define a distinguished distribution on characteristic strings which we will see “dominates” the distributions produced by any static adversary. Later in Sect. 4.5 we show that the same is true also for adaptive adversaries. We then study the effect of \(\rho _\varDelta \) on this distribution in preparation for studying common prefix, chain growth, and chain quality.
Motivating the Dominant Distribution: Static Adversaries. To motivate the dominant distribution, consider the distribution induced by a static adversary who corrupts—at the outset of the protocol—a set \(U_\mathcal {A}\) of parties with total relative stake \(\alpha _\mathcal {A}\). (Formally, one can model this by restricting to environments that only allow static corruption.) Recalling Definition 1, a party with relative stake \(\alpha _i\) is independently assigned to be a leader for a slot with probability
The function \(\phi _f\) is concave since
Considering that \(\phi _f(0) = 0\) and \(\phi _f(1) = f\), concavity implies that \(\phi _f(\alpha ) \ge f \alpha \) for \(\alpha \in [0,1]\). As \(\phi _f(0) \ge 0\) and \(\phi _f\) is concave, the function \(\phi _f\) is subadditive. This immediately implies the following proposition that will be useful during the analysis.
Proposition 1
The function \(\phi _f(\alpha )\) satisfies the following properties.
Recalling Definition 6, this (static) adversary \(\mathcal {A}\) determines a distribution \(\mathcal {D}_{\mathcal {Z},\mathcal {A}}^f\) on strings \(w \in \{0, 1, \bot \}^R\) by independently assigning each \(w_i\) so that
Here \(\mathcal {H}\) denotes the set of all honest parties in the stake distribution \(\mathcal {S}\) determined by \(\mathcal {Z}\). As before, \(\mathcal {P}\) denotes the set of all parties.
It is convenient to work with some bounds on the above quantities that depend only on “macroscopic” features of \(\mathcal {S}\) and \(\mathcal {A}\): namely, the relative stake of the honest and adversarial parties, and the parameter f. For this purpose we note that
where \(\alpha _{\mathcal {H}}\) denotes the total relative stake of the honest parties. Note that this bound applies to all static adversaries \(\mathcal {A}\) that corrupt no more than a \(1 - \alpha _\mathcal {H}\) fraction of all stake. With this in mind, we define the dominant distribution as follows.
Definition 12
(The dominant distribution \({\varvec{\mathcal {D}}}_{\varvec{\alpha }}^{{\varvec{f}}}\)). For two parameters f and \(\alpha \), define \(\mathcal {D}_{\alpha }^f\) to be the distribution on strings \(w \in \{0, 1, \bot \}^R\) that independently assigns each \(w_i\) so that \(p_\bot \triangleq \Pr [w_i = \bot ] = 1 - f\), \(p_0 \triangleq \Pr [w_i = 0] = \phi (\alpha ) \cdot (1-f)\), and \(p_1 \triangleq \Pr [w_i = 1] = 1 - p_\bot - p_0\).
The distribution \(\mathcal {D}^{f}_\alpha \) “dominates” \(\mathcal {D}^f_{\mathcal {Z},\mathcal {A}}\) for any static adversary \(\mathcal {A}\) that corrupts no more than a relative \(1 - \alpha \) share of the total stake, in the sense that nonempty slots are more likely to be tainted under \(\mathcal {D}^{f}_{\alpha }\) than they are under \(\mathcal {D}^f_{\mathcal {Z},\mathcal {A}}\).
To make this relationship precise, we introduce the partial order \(\preceq \) on the set \(\{\bot , 0, 1\}\) so that \(x \preceq y\) if and only if \(x = y\) or \(y = 1\). We extend this partial order to \(\{\bot , 0, 1\}^R\) by declaring \(x_1 \ldots x_R \preceq y_1 \ldots y_R\) if and only if \(x_i \preceq y_i\) for each i. Intuitively, the relationship \(x \prec y\) asserts that y is “more adversarial than” x; concretely, any legal fork for x is also a legal fork for y. We record this in the lemma below, which follows directly from the definition of \(\varDelta \)-fork and \({{\mathrm{div}}}_\varDelta \).
Lemma 2
Let x and y be characteristic strings in \(\{0, 1, \bot \}^R\) for which \(x \preceq y\). Then (1.) for every fork F, \(F \vdash _\varDelta x \Longrightarrow F \vdash _\varDelta y\); (2.) for every \(\varDelta \), \({{\mathrm{div}}}_\varDelta (x) \le {{\mathrm{div}}}_\varDelta (y)\).
Finally, we define a notion of stochastic dominance for distributions on characteristic strings, and \(\alpha \)-dominated adversaries.
Definition 13
(Stochastic dominance). We say that a subset \(E \subseteq \{\bot , 0, 1\}^R\) is monotone if \(x \in E\) and \(x \preceq y\) implies that \(y \in E\). Let \(\mathcal {D}\) and \(\mathcal {D}'\) be two distributions on the set of characteristic strings \(\{\bot , 0, 1\}^R\). Then we say that \(\mathcal {D}'\) dominates \(\mathcal {D}\), written \(\mathcal {D}\preceq \mathcal {D}'\), if \(\Pr _{\mathcal {D}}[E] \le \Pr _{\mathcal {D}'}[E]\) for every monotone set E. An adversary \(\mathcal {A}\) is called \(\alpha \)-dominated if the distribution \(\mathcal {D}^f_{\mathcal {Z},\mathcal {A}}\) that it induces on the set of characteristic strings satisfies \(\mathcal {D}^f_{\mathcal {Z},\mathcal {A}} \preceq \mathcal {D}_\alpha ^f\).
In our application, the events of interest are \(D_\varDelta = \{ x \mid {{\mathrm{div}}}_\varDelta (x) \ge k\}\) which are monotone by Lemma 2. We note that any static adversary that corrupts no more than a \(1 - \alpha \) fraction of stake is \(\alpha \)-dominated, and it follows that \(\Pr _{\mathcal {D}^f_{\mathcal {Z},\mathcal {A}}}[{{\mathrm{div}}}_\varDelta (w) \ge k] \le \Pr _{\mathcal {D}_\alpha ^f}[{{\mathrm{div}}}_\varDelta (w) \ge k]\). This motivates a particular study of the “dominant” distribution \(\mathcal {D}^f_\alpha \).
The Induced Distribution \({\varvec{\rho }}_{\varvec{\varDelta }}({\varvec{\mathcal {D}}}_{\varvec{\alpha }}^{{\varvec{f}}}\)). The dominant distribution \(\mathcal {D}_{\alpha }^f\) on \(\{0, 1, \bot \}^R\) in conjunction with the definition of \(\rho _\varDelta \) of (4) above implicitly defines a family of random variables \(\rho _\varDelta (w) = x_1 \ldots x_\ell \in \{0,1\}^*\), where \(w \in \{0,1,\bot \}^R\) is distributed according to \(\mathcal {D}_{\alpha }^f\). Observe that \(\ell = R - \#_\bot (w)\) is precisely the number of active indices of w. We now note a few properties of this resulting distribution that will be useful to us later (their proofs are presented in the full version). In particular, we will see that the \(x_i\) random variables are roughly binomially distributed, but subject to an exotic stochastic “stopping time” condition in tandem with some distortion of the last \(\varDelta \) variables.
Lemma 3
(Structure of the induced distribution). Let \(x_1\ldots x_\ell = \rho _\varDelta (w)\) where \(w \in \{0, 1, \bot \}^R\) is distributed according to \(\mathcal {D}_{\alpha }^f\). There is a sequence of independent random variables \(z_1, z_2, \ldots \) with each \(z_i \in \{0,1\}\) so that
(Note that while the \(z_i\) are independent with each other, they are not independent with w.)
Divergence for the Dominant Distribution. Our goal is to apply the reduction \(\rho _\varDelta \), Lemma 1, and Theorem 1 to establish an upper bound on the probability that a string drawn from the dominant distribution \(\mathcal {D}^f_\alpha \) has large \(\varDelta \)-divergence. The difficulty is that the distribution resulting from applying \(\rho _\varDelta \) to a string drawn from \(\mathcal {D}^f_\alpha \) is no longer a simple binomial distribution, so we cannot apply Theorem 1 directly. We resolve this obstacle in the proof of the following theorem, also given in the full version.
Theorem 2
Let \(f\in (0,1]\), \(\varDelta \ge 1\), and \(\alpha \) be such that \(\alpha (1 - f)^\varDelta = (1+\epsilon )/2\) for some \(\epsilon >0\). Let w be a string drawn from \(\{0,1,\bot \}^R\) according to \(\mathcal {D}^f_\alpha \). Then we have \(\Pr [{{\mathrm{div}}}_\varDelta (w) \ge k + \varDelta ] = 2^{-\varOmega (k) + \log R}\).
Remark. Intuitively, the theorem asserts that sampling the characteristic string in the \(\varDelta \)-semisynchronous setting with protocol parameter f according to \(\mathcal {D}^f_\alpha \) is, for the purpose of analyzing divergence, comparable to the synchronous setting in which the honest stake has been reduced from \(\alpha \) to \(\alpha (1 - f)^\varDelta \). Note that this can be made arbitrarily close to \(\alpha \) by adjusting f to be small; however, this happens at the expense of longer periods of silence in the protocol.
4.4 Common Prefix, Chain Growth, and Chain Quality
Our results on \(\varDelta \)-divergence from the previous section allow us to easily establish the following three statements, their proofs are again postponed to the full version.
Theorem 3 (Common prefix)
Let \(k,R, \varDelta \in \mathbb {N}\) and \(\varepsilon \in (0,1)\). Let \(\mathcal {A}\) be an \(\alpha \)-dominated adversary against the protocol \(\pi _{{\text {SPoS}}}\) for some \(\alpha \) satisfying \(\alpha (1 - f)^\varDelta \ge (1+\epsilon )/2\). Then the probability that \(\mathcal {A}\), when executed in a \(\varDelta \)-semisynchronous environment, makes \(\pi _{{\text {SPoS}}}\) violate the common prefix property with parameter k throughout a period of R slots is no more than \(\exp (\ln R + \varDelta - \varOmega (k))\). The constant hidden by the \(\varOmega (\cdot )\)-notation depends on \(\epsilon \).
To obtain a bound on the probability of a violation of the chain growth property, we again consider the \(\varDelta \)-right-isolated uniquely honest slots introduced in Sect. 4.2. Intuitively, we argue that the leader of such a slot has already received all blocks that were created in all previous such slots and therefore the block it creates will be having depth larger than all these blocks. It then follows that the length of the chain grows by at least the number of such slots.
Theorem 4 (Chain growth)
Let \(k,R, \varDelta \in \mathbb {N}\) and \(\varepsilon \in (0,1)\). Let \(\mathcal {A}\) be an \(\alpha \)-dominated adversary against the protocol \(\pi _{{\text {SPoS}}}\) for some \(\alpha >0\). Then the probability that \(\mathcal {A}\), when executed in a \(\varDelta \)-semisynchronous environment, makes \(\pi _{{\text {SPoS}}}\) violate the chain growth property with parameters \(s\ge 4 \varDelta \) and \(\tau =c \alpha / 4\) throughout a period of R slots, is no more than \(\exp \left( -{c\alpha s}/{(20 \varDelta )} + \ln R\varDelta + O(1)\right) \), where c denotes the constant \( c:=c(f,\varDelta )=f (1-f)^\varDelta \).
Our chain quality statement of Theorem 5 is a direct consequence of Lemma 4, which observes that a sufficiently long sequence of consecutive blocks in an honest party’s chain will most likely contain a block created in a \(\varDelta \)-right-isolated uniquely honest slot.
Lemma 4
Let \(k, \varDelta \in \mathbb {N}\) and \(\epsilon \in (0,1)\). Let \(\mathcal {A}\) be an \(\alpha \)-dominated adversary against the protocol \(\pi _{{\text {SPoS}}}\) for some \(\alpha >0\) satisfying \(\alpha (1-f)^\varDelta =(1+\epsilon )/2\). Let \(B_1,\ldots ,B_k\) be a sequence of consecutive blocks in a chain C possessed by an honest party. Then at least one block \(B_i\) was created in a \(\varDelta \)-right-isolated uniquely honest slot, except with probability \(\exp (-\varOmega (k))\).
Theorem 5 (Chain quality)
Let \(k,R, \varDelta \in \mathbb {N}\) and \(\epsilon \in (0,1)\). Let \(\mathcal {A}\) be an \(\alpha \)-dominated adversary against the protocol \(\pi _{{\text {SPoS}}}\) for some \(\alpha >0\) satisfying \(\alpha (1 - f)^\varDelta \ge (1+\epsilon )/2\). Then the probability that \(\mathcal {A}\), when executed in a \(\varDelta \)-semisynchronous environment, makes \(\pi _{{\text {SPoS}}}\) violate the chain quality property with parameters k and \(\mu =1/k\) throughout a period of R slots, is no more than \(\exp (\ln R - \varOmega (k))\).
4.5 Adaptive Adversaries
The statements in the previous sections give us guarantees on the common prefix, chain growth, and chain quality properties as long as the adversary is \(\alpha \)-dominated for some suitable value of \(\alpha \). In Sect. 4.3 we argued that any static adversary that corrupts at most \((1-\alpha )\)-fraction of stake is \(\alpha \)-dominated. In this section we extend this claim also to adaptive adversaries, showing that as long as they corrupt no more than \((1-\alpha )\)-fraction of stake adaptively throughout the whole execution, they are still \(\alpha \)-dominated. The proof is deferred to the full version.
Theorem 6
Every adaptive adversary \(\mathcal {A}\) that corrupts at most \((1-\alpha )\)-fraction of stake throughout the whole execution is \(\alpha \)-dominated.
Theorems 3, 4, 5 and 6 together give us the following corollary.
Corollary 1
Let \(\mathcal {A}\) be an adaptive adversary against the protocol \(\varPi _{{\text {SPoS}}}\) that corrupts at most \((1-\alpha )\)-fraction of stake. Then the bounds on common prefix, chain growth and chain quality given in Theorems 3, 4, 5 are satisfied for \(\mathcal {A}\).
4.6 The Resettable Protocol
With the analysis of these basic structural events behind us, we remark that the same arguments apply to a modest generalization of the protocol which permits the adversary some control over the nonce. Specifically, we introduce a “resettable” initialization functionality \(\mathcal {F}_{\mathsf {INIT}}^r\), which permits the adversary to select the random nonce from a family of r independent and uniformly random nonces. Specifically, \(\mathcal {F}_{\mathsf {INIT}}^r\) is identical to \(\mathcal {F}_{\mathsf {INIT}}\), with the following exception:
-
Upon receiving the first request of the form
 from some stakeholder \(U_{i}\), \(\mathcal {F}_{\mathsf {INIT}}^r\) samples a nonce
from some stakeholder \(U_{i}\), \(\mathcal {F}_{\mathsf {INIT}}^r\) samples a nonce 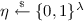 , defines a “nonce candidate” set \(H = \{ \eta \}\), and permits the adversary to carry out up to \(r-1\) reset events: each reset event draws an independent element from \(\{0,1\}^{\lambda }\), adds the element to the set H, and permits the adversary to replace the current nonce \(\eta \) with any element of H. Finally,
, defines a “nonce candidate” set \(H = \{ \eta \}\), and permits the adversary to carry out up to \(r-1\) reset events: each reset event draws an independent element from \(\{0,1\}^{\lambda }\), adds the element to the set H, and permits the adversary to replace the current nonce \(\eta \) with any element of H. Finally,  is sent to \(U_i\). Later requests from any stakeholder are answered using the same value \(\eta \).
is sent to \(U_i\). Later requests from any stakeholder are answered using the same value \(\eta \).
Looking ahead, our reason to introduce the resettable functionality \(\mathcal {F}_{\mathsf {INIT}}^r\) is to capture the limited grinding capabilities of the adversary. A simple application of the union bound shows that this selection of \(\eta \) from among a set of size r uniformly random candidate nonces can inflate the probability of events during the run of \(\pi _{{\text {SPoS}}}\) by a factor no more than r. We record this as a corollary below.
Corollary 2
(Corollary to Theorems 3, 4, 5). The protocol \(\varPi _{{\text {SPoS}}}\), with initialization functionality \(\mathcal {F}_{\mathsf {INIT}}^r\), satisfies the bounds of Theorems 3, 4, 5 with all probabilities scaled by r.
5 The Full Protocol
In this section, we construct a protocol that handles the dynamic case, where the stake distribution changes as the protocol is executed. As in Ouroboros [16], we divide protocol execution in a number of independent epochs during which the stake distribution used for sampling slot leaders remains unchanged. The strategy we use to bootstrap the static protocol is, at a high level, similar: we first show how the protocol can accommodate dynamic stake utilizing an ideal “leaky beacon” functionality and then we show this beacon functionality can be simulated via an algorithm that collects randomness from the blockchain.
In order to facilitate the implementation of our beacon, we need to allow the leaky beacon functionality to be adversarially manipulated by allowing a number of “resets” to be performed by the adversary. Specifically, the functionality is parameterized by values \(\tau \) and r. First, it leaks to the adversary, up to \(\tau \) slots prior to the end of an epoch, the beacon value for the next epoch. (Looking ahead, we remark that it is essential that the stake distribution used for sampling slot leaders in the next epoch is determined prior to this leakage.) Second, the adversary can reset the value returned by the functionality as many as r times. As expected for a beacon, it reports to honest parties the beacon value only once the next epoch starts. After the epoch is started no more resets are allowed for the beacon value. This mimics the functionality \(\mathcal {F}_{\mathsf {INIT}}\) and its resettable version \(\mathcal {F}_{\mathsf {INIT}}^r\). Note that the ability of the adversary to reset the beacon can be quite influential in the protocol execution: for instance, any event that depends deterministically on the nonce of an epoch and happens with probability 1/2 can be easily forced to happen almost always by the adversary using a small number of resets.
Naturally, we do not want to assume the availability of a randomness beacon in the final protocol, even if it is leaky and resettable. In our final iteration of the protocol we show how it is possible to simulate such beacon using a hash function that is modeled as a random oracle. This hash function is applied to the concatenation of VRF values that are inserted into each block, using values from all blocks up to and including the middle \(\approx 8k\) slots of an epoch that lasts approximately 24k slots in entirety. (The “quiet” periods before and after this central block of slots that sets the nonce will ensure that the stake distribution, determined at the beginning of the epoch, is stable, and likewise that the nonce is stable before the next epoch begins.) The verifiability of those values is a key property that we exploit in the proof.
Our proof strategy is to reduce any adversary against the basic properties of the blockchain to a resettable-beacon adversary that will simulate the random oracle. The key point of this reduction is that whenever the random oracle adversary makes a query with a sequence of values that is a candidate sequence for determining the nonce for the next epoch, the resettable attacker detects this as a possible reset opportunity and resets the beacon; it obtains the response from the beacon and sets this as the answer to the random oracle query.
The final issue is to bound the number of resets: towards this, note that the adversary potentially controls a constant fraction of the \({\approx }8k\) slots associated with nonce selection, and this allows him to explore an a priori large space of independent random potential nonces (and, ultimately, select one as the next epoch nonce). The size of this space is however upper-bounded by the number of random oracle queries that the adversary can afford during the sequence of \({\approx }8k\) slots. To formalize this bound we utilize the q-bounded model of [12] that bounds the number of queries the adversary can pose per round: in that model, the adversary is allowed q queries per adversarial party per round (“slot” in our setting).Footnote 5 Assuming that the adversary controls t parties, we obtain a bound equal to \({\approx }8qtk\).
5.1 The Dynamic Stake Case with a Resettable Leaky Beacon
First we construct a protocol for the dynamic stake case assuming access to a resettable leaky beacon that provides a fresh nonce for each epoch. This beacon is leaky in the sense that it allows the adversary to obtain the nonce for the next epoch before the epoch starts, and resettable in the sense that it allows the adversary to reset the nonce a number of times. We model the resettable leaky randomness beacon in functionality \(\mathcal {F}_{RLB}^{\tau ,r}\) presented in Fig. 5.
We now describe protocol \(\pi _{{\text {DPoS}}}\), which is a modified version of \(\pi _{{\text {SPoS}}}\) that updates its genesis block \(B_0\) (and thus the assignment of slot leader sets) for every new epoch. The protocol also adopts an adaptation of the static \(\mathsf {maxvalid}_S\) function, defined so that it narrows selection to those chains which share common prefix. Specifically, it adopts the following rule, parametrized by a prefix length k:
Function \(\mathsf {maxvalid}(\mathcal {C},\mathbb {C})\). Returns the longest chain from \(\mathbb {C}\cup \{\mathcal {C}\}\) that does not fork from \(\mathcal {C}\) more than k blocks (i.e., not more than k blocks of \(\mathcal {C}\) are discarded). If multiple exist it returns \(\mathcal {C}\), if this is one of them, or it returns the one that is listed first in \(\mathbb {C}\).
The protocol \(\pi _{{\text {DPoS}}}\) is described in Fig. 6 and functions in the \(\mathcal {F}_{RLB}^{\tau ,r}\)-hybrid model.
Lazy players. Note that while the protocol \(\pi _{{\text {DPoS}}}\) in Fig. 6 is stated for a stakeholder that is permanently online, this requirement can be easily relaxed. Namely, it is sufficient for an honest stakeholder to join at the beginning of each epoch, determine whether she belongs to the slot leader set for any slots within this epoch (using the \(\mathsf {Eval}\) interface of \(\mathcal {F}_{\mathsf {VRF}}\)), and then come online and act on those slots while maintaining online presence at least every k slots. We sketch this variant of the protocol in the full version.
We proceed to the security analysis of the full protocol in the hybrid world where the functionality \(\mathcal {F}_{RLB}^{\tau ,r}\) is available to the protocol participants. A key challenge is that in the dynamic stake setting, the honest majority assumption that we have in place refers to the stakeholder view of the honest stakeholders in each slot. Already in the first few slots this assumption may diverge rapidly from the stakeholder distribution that is built-in the genesis block.
To accommodate the issues that will arise from the movement of stake throughout protocol execution, we recall the notion of stake shift defined in [16].
Definition 14
Consider two slots \(sl_1, sl_2\) and an execution \(\mathcal {E}\). The stake shift between \(sl_1, sl_2\) is the maximum possible statistical distance of the two weighted-by-stake distributions that are defined using the stake reflected in the chain \(\mathcal {C}_1\) of some honest stakeholder active at \(sl_1\) and the chain \(\mathcal {C}_2\) of some honest stakeholder active at \(sl_2\).
Finally, the security of \(\pi _{{\text {DPoS}}}\) is stated below and proven in the full version. We slightly abuse the notation from previous sections and denote by \(\alpha _\mathcal {H}\) a lower bound on the honest stake ratio throughout the whole execution.
Theorem 7
(Security of \(\pi _{{\text {DPoS}}}\) with access to \(\mathcal {F}_{RLB}^{\tau ,r}\)). Fix parameters \(k, R, \varDelta , L\in \mathbb {N}, \epsilon ,\sigma \in (0,1)\) and r. Let \(R\ge 16k/f\) be the epoch length, L the total lifetime of the system, and
The protocol \(\pi _{{\text {DPoS}}}\), with access to \(\mathcal {F}_{RLB}^{\tau ,r}\), with \(\tau \le 8k/f \) satisfies persistence with parameters k and liveness with parameters \(u=8k/f \) throughout a period of L slots of \(\varDelta \)-semisynchronous execution with probability \(1 - \exp (\ln L + \varDelta + \log (r) - \varOmega (k))\) assuming that \(\sigma \) is the maximum stake shift over \(2R\) slots.
Note that while Theorem 7 (and also Corollary 3 below) formulates the bound (11) in terms of the overall upper bound on honest stake ratio \(\alpha _\mathcal {H}\) and maximum stake shift \(\sigma \) over any 2R-slots interval, one could easily prove more fine-grained statements that would only require inequality (11) to hold for each epoch (with respect to the honest stake ratio in that epoch, and the stake shift occurring for that epoch’s stake distribution).
5.2 Instantiating \(\mathcal {F}_{RLB}^{\tau ,r}\)
In this section, we show how to substitute the oracle \(\mathcal {F}_{RLB}^{\tau ,r}\) of protocol \(\pi _{{\text {DPoS}}}\) with a subprotocol \(\pi _{RLB}\) that simulates \(\mathcal {F}_{RLB}^{\tau ,r}\). The resulting protocol can then operate directly in the \(\mathcal {F}_{\mathsf {INIT}}\)-hybrid model as in Sect. 3 (without resets) while utilizing a random oracle \(\mathsf {H}(\cdot )\). The sub-protocol \(\pi _{RLB}\) is described in Figure 7.
We will show next that the sub-protocol \(\pi _{RLB}\) can safely substitute \(\mathcal {F}_{RLB}^{\tau ,r}\) when called from protocol \(\pi _{{\text {DPoS}}}\). We will perform our analysis in the q-bounded model of [12] assuming that the adversary is capable of issuing q queries per each round of protocol execution per corrupted party and there are t corrupted parties. The proof is deferred to the full version.
Lemma 5
Consider the event of violating one of common prefix, chain quality, chain growth in an execution of \(\pi _{{\text {DPoS}}}\) using sub-protocol \(\pi _{RLB}\) in the \(\mathcal {F}_{\mathsf {INIT}}\)-hybrid model with adversary \(\mathcal {A}\) and environment \(\mathcal {Z}\) with the same parameter choices as Theorem 7. We construct an adversary \(\mathcal {A}^\prime \) so that the corresponding event happens with the same probability in an execution of \(\pi _{{\text {DPoS}}}\) in the \(\mathcal {F}_{RLB}^{\tau ,r}\)-hybrid world with adversary \(\mathcal {A}^\prime \) and environment \(\mathcal {Z}\) assuming that \(r = 8tqk/f\).
Based on the above lemma, it is now easy to revisit Theorem 7, and show that the same result holds for r in the q-bounded model assuming \(r= 8tkq/f\) and \(\tau \le 8k/f\) which permits to set our epoch length R to 24k / f.
Corollary 3
(Security of \(\pi _{{\text {DPoS}}}\) with subprotocol \(\pi _{RLB}\)). Fix parameters \(k, R, \varDelta , L\in \mathbb {N}, \epsilon ,\sigma \in (0,1)\). Let \(R= 24k/f\) be the epoch length, L the total lifetime of the system, and \((\alpha _\mathcal {H}-\sigma )(1 - f)^\varDelta \ge (1+\epsilon )/2\). The protocol \(\pi _{{\text {DPoS}}}\) using subprotocol \(\pi _{RLB}\) in the \(\mathcal {F}_{\mathsf {INIT}}\)-hybrid model satisfies persistence with parameters k and liveness with parameters \(u=8k/f\) throughout a period of L slots of \(\varDelta \)-semisynchronous execution with probability \(1 - \exp (\ln L + \varDelta - \varOmega (k - \log tkq))\) assuming that \(\sigma \) is the maximum stake shift over \(2R\) slots.
Notes
- 1.
It is worth pointing out that the notion of slots we use in this work can be substantially shorter in terms of real time elapsed compared to the slots of [16], where each slot represented a full round of interaction between all participants.
- 2.
Refer e.g., to the posts by QuantumMechanic and others from 2011 https://bitcointalk.org/index.php?topic=27787.0 (Last Accessed 19/09/2017).
- 3.
We assume this to simplify our formal treatment, a variant of our protocol can actually accommodate “lazy honesty” as introduced in [19]. In this variant, honest stakeholders only come online at the beginning of each epoch and at a few infrequent, predictable moments, see the full version.
- 4.
In fact our UC formulation captures a stronger notion: even for adversarial keys the VRF function will act as a random oracle. We note that while we can achieve this notion in the random oracle model, a weaker condition of mere unpredictability can be sufficient for the security of our protocol. A UC version of the notion of verifiable pseudorandom permutations, cf. [9], could potentially be used towards a standard model instantiation of the primitive.
- 5.
Note that we utilize the q-bounded model only to provide a more refined analysis; given that the total length of the execution is polynomial in \(\lambda \) one may also use the total execution length as a bound.
References
Bellare, M., Miner, S.K.: A forward-secure digital signature scheme. In: Wiener, M. (ed.) CRYPTO 1999. LNCS, vol. 1666, pp. 431–448. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48405-1_28
Bentov, I., Gabizon, A., Mizrahi, A.: Cryptocurrencies without proof of work. CoRR, abs/1406.5694 (2014)
Bentov, I., Gabizon, A., Mizrahi, A.: Cryptocurrencies without proof of work. In: Clark, J., Meiklejohn, S., Ryan, P.Y.A., Wallach, D., Brenner, M., Rohloff, K. (eds.) FC 2016. LNCS, vol. 9604, pp. 142–157. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53357-4_10
Bentov, I., Lee, C., Mizrahi, A., Rosenfeld, M.: Proof of activity: extending bitcoin’s proof of work via proof of stake. SIGMETRICS Perform. Eval. Rev. 42(3), 34–37 (2014)
Canetti, R.: Universally composable signature, certification, and authentication. In: 17th IEEE Computer Security Foundations Workshop, (CSFW-17 2004), p. 219. IEEE Computer Society (2004)
Chase, M., Lysyanskaya, A.: Simulatable VRFs with applications to multi-theorem NIZK. In: Menezes, A. (ed.) CRYPTO 2007. LNCS, vol. 4622, pp. 303–322. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-74143-5_17
The NXT Community. Nxt whitepaper, July 2014. https://bravenewcoin.com/assets/Whitepapers/NxtWhitepaper-v122-rev4.pdf
Daian, P., Pass, R., Shi, E.: Snow white: provably secure proofs of stake. Cryptology ePrint Archive, Report 2016/919 (2016). http://eprint.iacr.org/2016/919
Dodis, Y., Puniya, P.: Feistel networks made public, and applications. In: Naor, M. (ed.) EUROCRYPT 2007. LNCS, vol. 4515, pp. 534–554. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-72540-4_31
Dodis, Y., Yampolskiy, A.: A verifiable random function with short proofs and keys. In: Vaudenay, S. (ed.) PKC 2005. LNCS, vol. 3386, pp. 416–431. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-30580-4_28
Dwork, C., Lynch, N.A., Stockmeyer, L.J.: Consensus in the presence of partial synchrony. J. ACM 35(2), 288–323 (1988)
Garay, J., Kiayias, A., Leonardos, N.: The bitcoin backbone protocol: analysis and applications. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9057, pp. 281–310. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46803-6_10
Itkis, G., Reyzin, L.: Forward-secure signatures with optimal signing and verifying. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 332–354. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44647-8_20
Jarecki, S., Kiayias, A., Krawczyk, H.: Round-optimal password-protected secret sharing and T-PAKE in the password-only model. In: Sarkar, P., Iwata, T. (eds.) ASIACRYPT 2014. LNCS, vol. 8874, pp. 233–253. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-45608-8_13
Kiayias, A., Panagiotakos, G.: Speed-security tradeoffs in blockchain protocols. Cryptology ePrint Archive, Report 2015/1019 (2015). http://eprint.iacr.org/2015/1019
Kiayias, A., Russell, A., David, B., Oliynykov, R.: Ouroboros: a provably secure proof-of-stake blockchain protocol. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10401, pp. 357–388. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_12
King, S., Nadal, S.: PPCoin: peer-to-peer crypto-currency with proof-of-stake, August 2012. https://peercoin.net/assets/paper/peercoin-paper.pdf
Lindell, A.Y.: Adaptively secure two-party computation with erasures. In: Fischlin, M. (ed.) CT-RSA 2009. LNCS, vol. 5473, pp. 117–132. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-00862-7_8
Micali, S.: ALGORAND: the efficient and democratic ledger. CoRR, abs/1607.01341 (2016)
Nakamoto, S.: The proof-of-work chain is a solution to the byzantine generals’ problem. The Cryptography Mailing List, November 2008. https://www.mail-archive.com/cryptography@metzdowd.com/msg09997.html
Pass, R., Seeman, L., Shelat, A.: Analysis of the blockchain protocol in asynchronous networks. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10211, pp. 643–673. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56614-6_22
Pass, R., Shi, E.: The sleepy model of consensus. Cryptology ePrint Archive, Report 2016/918 (2016). http://eprint.iacr.org/2016/918
Russell, A., Moore, C., Kiayias, A., Quader, S.: Forkable strings are rare. Cryptology ePrint Archive, Report 2017/241 (2017). http://eprint.iacr.org/2017/241
Acknowledgements
We thank Christian Badertscher and the anonymous reviewers for several useful suggestions improving the presentation of the paper.
Peter Gaži partly worked on this project while being a postdoc at IST Austria, supported by the ERC consolidator grant 682815-TOCNeT. Aggelos Kiayias was partly supported by H2020 Project #653497, PANORAMIX.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 International Association for Cryptologic Research
About this paper
Cite this paper
David, B., Gaži, P., Kiayias, A., Russell, A. (2018). Ouroboros Praos: An Adaptively-Secure, Semi-synchronous Proof-of-Stake Blockchain. In: Nielsen, J., Rijmen, V. (eds) Advances in Cryptology – EUROCRYPT 2018 . EUROCRYPT 2018. Lecture Notes in Computer Science(), vol 10821. Springer, Cham. https://doi.org/10.1007/978-3-319-78375-8_3
Download citation
DOI: https://doi.org/10.1007/978-3-319-78375-8_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-78374-1
Online ISBN: 978-3-319-78375-8
eBook Packages: Computer ScienceComputer Science (R0)








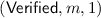 as answer upon sending
as answer upon sending  to
to 
 from some stakeholder
from some stakeholder 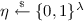 , defines a “nonce candidate” set
, defines a “nonce candidate” set  is sent to
is sent to 


