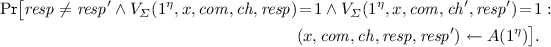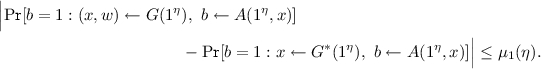Post-quantum Security of Fiat-Shamir

Abstract

The Fiat-Shamir construction (Crypto 1986) is an efficient transformation in the random oracle model for creating non-interactive proof systems and signatures from sigma-protocols. In classical cryptography, Fiat-Shamir is a zero-knowledge proof of knowledge assuming that the underlying sigma-protocol has the zero-knowledge and special soundness properties. Unfortunately, Ambainis, Rosmanis, and Unruh (FOCS 2014) ruled out non-relativizing proofs under those conditions in the quantum setting.

In this paper, we show under which strengthened conditions the Fiat-Shamir proof system is still post-quantum secure. Namely, we show that if we require the sigma-protocol to have computational zero-knowledge and statistical soundness, then Fiat-Shamir is a zero-knowledge simulation-sound proof system (but not a proof of knowledge!). Furthermore, we show that Fiat-Shamir leads to a post-quantum secure unforgeable signature scheme when additionally assuming a “dual-mode hard instance generator” for generating key pairs.

1 Introduction

1.1 Background

Fiat-Shamir signatures. Signatures are (next to encryption) probably one of the most important constructs in modern cryptography. In search for efficient signature schemes, Fiat-Shamir [12] gave a construction for transforming many three-round identification schemes into signatures, using the random oracle. (The transformation was stated only for a specific case, but the general construction is an easy generalization. [12] also does not contain a complete security proof, but a proof was later provided by Pointcheval and Stern [20].) The Fiat-Shamir transform and variations thereof have since been used in a large number of constructions (signatures [21, 23], group signatures [7], anonymous credentials [10], e-voting [1], anonymous attestation [9], etc.) The benefit of the Fiat-Shamir transform is that it combines efficiency with universality: The underlying identification scheme can be any so-called sigma-protocol (see below), this allows for great flexibility in how public and secret key are related and enables the construction of more advanced signature schemes and related schemes such as group signatures, etc.

Non-interactive zero-knowledge proofs. At the first glance unrelated, but upon closer inspection intimately connected to signatures are non-interactive zero-knowledge proof of knowledge (NIZKPoK). In fact, Fiat-Shamir can also be seen as a highly efficient construction for NIZKPoKs in the random oracle model [11]. Basically, a NIZKPoK allows a prover to show his knowledge of a witness $sk$ that stands in a given relation to a publicly known statement $pk$. From a NIZKPoK, we can derive a signature scheme: To sign a message m, the signer constructs a proof that he knows the secret key corresponding to the public key $pk$. (Of course, the message m needs to be included in the proof as well, we omit the details for now.) For this construction to work, the NIZKPoK needs to satisfy certain advanced security notions (“simulation-sound extractability”);¹ Fiat-Shamir satisfies this notion in the classical setting [11]. Thus Fiat-Shamir doubles both as a signature scheme and as a NIZKPoK, leading to simple and highly efficient constructions of both.

The construction. In order to understand the rest of this introduction more easily, we sketch the construction of Fiat-Shamir (the precise definition is given in Definition 11). We will express it as a NIZKPoK since this makes the analysis more modular. (We study Fiat-Shamir as a signature scheme in Sect. 6.)

A sigma-protocol $\varSigma$ is a three-message protocol: The prover (given a statement x and a corresponding valid witness w) sends a message $com$, called “commitment”, to the verifier. The verifier (who knowns only the statement x) responds with a uniformly random “challenge” $ch$. Then the prover answers with his “response” $resp$, and the verifier checks whether $( com , ch , resp )$ is a valid interaction. If so, he accepts the proof of the statement x. In the following, we will assume that $ch$ has superlogarithmic length, i.e., there are superpolynomially many different challenges. This can always be achieved by parallel-composing the sigma-protocol.

Given the sigma-protocol $\varSigma$, the Fiat-Shamir transform yields a non-interactive proof system: The prover $P_{FS}$ internally executes the prover of the sigma-protocol to get the commitment $com$. Then he computes the challenge as $ch :=H(x\Vert com )$ where H is a hash function, modeled as a random oracle. That is, instead of letting the verifier generate a random challenge, the prover produces it by hashing. This guarantees, at least on an intuitively level, that the prover does not have any control over the challenge, it is as if it was chosen randomly. Then the prover internally produces the response $resp$ corresponding to $com$ and $ch$ and sends the non-interactive proof $com \Vert resp$ to the verifier.

The Fiat-Shamir verifier $V_{FS}$ computes $ch :=H(x\Vert com )$ and checks whether $( com , ch , resp )$ is a valid interaction of the sigma-protocol.

Note that numerous variants of the Fiat-Shamir are possible. For example, one could compute $ch :=H( com )$ (omitting x). However, this variant of Fiat-Shamir is malleable, see [11].

Difficulties with Fiat-Shamir. The Fiat-Shamir transform is a deceptively simple construction, but proving its security turns out to be more involved that one would anticipate. To prove security (specifically, the unforgeability property in the signature setting, or the extractability in the NIZKPoK setting), we need simulate the interaction of the adversary with the random oracle, and then rerun the same interaction with slightly changed random oracle responses (“rewinding”). The first security proof by Fiat and Shamir [12] overlooked that issue.² Bellare and Rogaway [5, Sect. 5.2] also prove the security of the Fiat-Shamir transform (as a proof system) but simply claim the soundness without giving a proof (we assume that they also overlooked the difficulties involved).³ The first complete security proof of the Fiat-Shamir as a signature scheme is by Pointcheval and Stern [20] who introduced the so-called “forking lemma”, a central tool for analyzing the security of Fiat-Shamir (it allows us to analyze the rewinding used in the security proof). When considering Fiat-Shamir as a NIZKPoK, the first proof was given by Faust et al. [11]; they showed that Fiat-Shamir is zero-knowledge and simulation-sound extractable.⁴ This short history of the security proofs indicates that Fiat-Shamir is more complicated than it may look at the first glance.

Further difficulties were noticed by Shoup and Gennaro [24] who point out that the fact that the Fiat-Shamir security proof uses rewinding can lead to considerable difficulties in the analysis of more complex security proofs (namely, it may lead to an exponential blowup in the running time of a simulator; Pointcheval and Stern [19] experienced similar problems). Fischlin [13] notes that the rewinding also leads to less tight reductions, which in turn may lead to longer key sizes etc. for protocols using Fiat-Shamir.

Another example of unexpected behavior: Assume Alice gets a n pairs of public keys $( pk _{i0}, pk _{i1})$, and then can ask for one of the secret keys for each pair (i.e., $sk _{i0}$ or $sk _{i1}$ is revealed, never both), and then Alice is supposed to prove using Fiat-Shamir that he knows both secret keys for one of the pairs. Intuitively, we expect Alice not to be able to do that (if Fiat-Shamir is indeed a proof of knowledge), but as we show in the full version [27], Fiat-Shamir does not guarantee that Alice cannot successfully produce a proof in this situation!

To circumvent all those problems, Fischlin [13] gave an alternative construction of NIZKPoKs and signature schemes in the random oracle model whose security proof does not use rewinding. However, their construction seems less efficient in terms of the computation performed by the prover (although this is not fully obvious if the tightness of the reduction is taken into account), and their construction requires an additional property (unique responses⁵) from the underlying sigma-protocol.

We do not claim that those difficulties in proving and using Fiat-Shamir necessarily speak against Fiat-Shamir. But they show one needs to carefully analyze which precise properties Fiat-Shamir provably has, and not rely on what Fiat-Shamir intuitively achieves.

Post-quantum security. In this paper we are interested in the post-quantum security of Fiat-Shamir. That is, under what conditions is Fiat-Shamir secure if the adversary has a quantum computer? In the post-quantum setting, the random oracle has to be modeled as a random function that can be queried in superposition⁶ since a normal hash function can be evaluated in superposition as well (cf. [8]). Ambainis et al. [2] showed that in this model, Fiat-Shamir is insecure in general. More precisely, they showed that relative to certain oracles, there are sigma-protocols such that: The sigma-protocol satisfies the usual security properties. (Such as zero-knowledge and special soundness. These are sufficient for security in the classical case.) But when applying the Fiat-Shamir transform to it, the resulting NIZKPoK is not sound (and thus, as a signature, not unforgeable). Since this negative result is relative to specific oracles, it does not categorically rule out a security proof. However, it shows that no relativizing security proof exists, and indicates that it is unlikely that Fiat-Shamir can be shown post-quantum secure in general. Analogous negative results [2] hold for Fischlin’s scheme [13].

Unruh [26] gave a construction of a NIZKPoK/signature scheme in the random oracle model that is avoids these problems and is post-quantum secure (simulation-sound extractable zero-knowledge/strongly unforgeable). However, Unruh’s scheme requires multiple executions of the underlying sigma-protocol, leading to increased computational and communication complexity in comparison with Fiat-Shamir which needs only a single execution.⁷ Furthermore, Fiat-Shamir is simpler (in terms of the construction, if not the proof), and more established in the crypto community. In fact, a number of papers have used Fiat-Shamir to construct post-quantum secure signature schemes (e.g., [3, 4, 15,16,17,18]). The negative results by Ambainis et al. show that the post-quantum security of these schemes is hard to justify.⁸ Thus the post-quantum security of Fiat-Shamir would be of great interest, both from a practical and theoretical point of view.

Is there a possibility to show the security of Fiat-Shamir notwithstanding the negative results from [2]? There are two options (besides non-relativizing proofs): (a) Unruh [25] introduced an additional condition for sigma-protocols, so-called “perfectly unique responses”.⁹ Unique responses means that for any commitment and challenge in a sigma-protocol, there exists at most one valid response. They showed that a sigma-protocol that additionally has perfect unique responses is a proof of knowledge while [2] showed that without unique responses, a sigma protocol will not in general be a proof of knowledge (relative to some oracle). Similarly, [2] does not exclude that Fiat-Shamir is post-quantum secure when the underlying sigma-protocol has perfectly unique responses.¹⁰ (b) If we do not require extractability, but only require soundness (i.e., if we only want to prove that there exists a witness, not that we know it), then [2] does not exclude a proof that Fiat-Shamir is sound based on a sigma-protocol with perfect special soundness (but (computational) special soundness is not sufficient). In this paper, we mainly follow approach (b), but we also have some results related to research direction (a).

1.2 Our Contribution

Security of Fiat-Shamir as a proof system. We prove that Fiat-Shamir is post-quantum secure as a proof system. More precisely, we prove that it is zero-knowledge (using random-oracle programming techniques from [26]), and that it is sound (i.e., a proof of knowledge, using a reduction to quantum search). More precisely:

Theorem 1

(Post-quantum security of Fiat-Shamir – informal). Assume that $\varSigma$ has honest-verifier zero-knowledge and statistical soundness.

Then the Fiat-Shamir proof system $(P_{FS},V_{FS})$ is zero-knowledge and sound.¹¹

The assumptions are the same as in the classical setting, except that instead of computational special soundness (as in the classical case), we need statistical soundness.¹² This is interesting, because it means that we need one of the properties of the sigma-protocol to hold unconditionally, even though we only want computational security in the end. However, [2] shows that this is necessary: when assuming only computational (special) soundness, they construct a counter-example to the soundness of Fiat-Shamir (relative to some oracle).

Simulation-soundness. In addition to the above, we also show that Fiat-Shamir has simulation-soundness. Simulation-soundness is a property that guarantees non-malleability, i.e., that an adversary cannot take a proof gotten from, say, an honest participant and transform it into a different proof (potentially for a different but related statement).¹³ This is particularly important when using Fiat-Shamir to construct signatures (see below) because we would not want the adversary to transform one signature into a different signature. Our result is:

Theorem 2

(Simulation-soundness of Fiat-Shamir – informal). Assume that $\varSigma$ has honest-verifier zero-knowledge, statistical soundness, and unique responses.

Then the Fiat-Shamir proof system $(P_{FS},V_{FS})$ has simulation-soundness.

Note that unique responses are needed for this result even in the classical case. If we only require a slightly weaker form of simulation-soundness (“weak” simulation-soundness), then we can omit that requirement.

Signatures. Normally, the security of Fiat-Shamir signatures is shown by reducing it to the simulation-sound extractability of Fiat-Shamir (implicitly or explicitly). Unfortunately, we do not know whether Fiat-Shamir is extractable in the quantum setting. Thus, we need a new proof of the security of Fiat-Shamir signatures that only relies on simulation-soundness. We can do so by making additional assumptions about the way the key generator works: We call an algorithm G a “dual-mode hard instance generator” if G outputs a key pair $( pk , sk )$ in such a way that $pk$ is computationally indistinguishable from an invalid $pk$ (i.e., a $pk$ that has no corresponding $sk$). An example of such an instance generator would be: $sk$ is chosen uniformly at random, and $pk :=F( sk )$ for a pseudo-random generator F. Then we have:

Theorem 3

(Fiat-Shamir signatures – informal). Assume that G is a dual-mode hard instance generator. Fix a sigma-protocol $\varSigma$ (for showing that a given public key has a corresponding secret key). Assume that $\varSigma$ has honest-verifier zero-knowledge, statistical soundness.

Then the Fiat-Shamir signature scheme is unforgeable.

Note that classically, we only require that G is a hard instance generator. That is, given $pk$, it is hard to find $sk$. We leave it as an open problem whether this is sufficient in the post-quantum setting, too.

Organization. In Sect. 2, we fix some simple notation. In Sect. 3, we discuss the (relatively standard) security notions for sigma-protocols used in this paper. In Sect. 4, we define security notions for non-interactive proof systems in the random oracle model. In Sect. 5 we give out main results, the security properties of Fiat-Shamir (zero-knowledge, soundness, simulation-soundness, ...). In Sect. 6, we show how to construct signature schemes from non-interactive zero-knowledge proof systems, in particular from Fiat-Shamir.

Readers who are interested solely in conditions under which Fiat-Shamir signatures are post-quantum secure but not in the security proofs may restrict their attention to Sects. 3 and 6 (in particular Corallary 23).

A full version with additional material on extractability appears online [27].

2 Preliminaries

$\mathrm {Fun}(n,m)$ is the set of all functions from $\{0,1\}^{n}$ to $\{0,1\}^{m}$. $a\oplus b$ denotes the bitwise XOR between bitstrings (of the same length).

If H is a function, we write $H(x:=y)$ for the function $H'$ with $H'(x)=y$ and $H'(x')=H(x')$ for $x'\ne x$. We call a list $ass =(x_1:=y_1,\dots ,x_n:=y_n)$ an assignment-list. We then write $H( ass )$ for $H(x_1:=y_1)(x_2:=y_2)\dots (x_n:=y_n)$. (That is, H is updated to return $y_i$ on input $x_i$, with assignments occurring later in $ass$ taking precedence.)

We write $x\leftarrow A(\dots )$ to denote that the result of the algorithm/measurement A is assigned to x. We write $Q\leftarrow |\varPsi \rangle$ or $Q\leftarrow \rho$ to denote that the quantum register Q is initialized with the quantum state $|\varPsi \rangle$ or $\rho$, respectively. We write $x{\mathop {\leftarrow }\limits ^{\scriptscriptstyle \$}}M$ to denote that x is assigned a uniformly randomly chosen element of the set M.

If H is a classical function, then $A^H$ means that A has oracle access to H in superposition (i.e., to the unitary $|x,y\rangle \rightarrow |x,y\oplus H(x)\rangle$).

Theorem 4

(Random oracle programming [26]). Let $\ell ^{in},\ell ^{out}\ge 1$ be a integers, and $H{\mathop {\leftarrow }\limits ^{\scriptscriptstyle \$}}\mathrm {Fun}(\ell ^{in}_\eta ,\ell ^{out}_\eta )$. Let $A_C$ be an algorithm, and $A_0,A_2$ be oracles algorithms, where $A_0^{ H}$ makes at most $q_A$ queries to H, $A_C$ is classical, and the output of $A_C$ has collision-entropy at least k given $A_C$’s initial state (which is classical). $A_0,A_C,A_2$ may share state. Then

Lemma 5

(Hardness of search [27]). Let $H:\{0,1\}^{n}\rightarrow \{0,1\}^{m}$ be a uniformly random function. For any q-query algorithm A, it holds that $\Pr [H(x)=0:x\leftarrow A^H()]\le 32 \cdot 2^{-m}\cdot (q+1)^2$.

3 Sigma Protocols

In this paper, we will consider only proof systems for fixed-length relations . A fixed-length relation $R_\eta$ is a family of relations on bitstrings such that:

For every $\eta$, there are values $\ell ^x_\eta$ and $\ell ^w_\eta$ such that $(x,w)\in R_\eta$ implies $|x|=\ell ^x_\eta$ and $|w|=\ell ^w_\eta$, and such that $\ell ^x_\eta ,\ell ^w_\eta$ can be computed in time polynomial in $\eta$. Given x, w, it can be decided in polynomial-time in $\eta$ whether $(x,w)\in R_\eta$.

We now define sigma protocols and related concepts. The notions in this section are standard in the classical setting, and easy to adapt to the quantum setting. Note that the definitions are formulated without the random oracle, we only use the random oracle later for constructing non-interactive proofs out of sigma protocols.

A sigma protocol for a fixed-length relation $R_\eta$ is a three-message proof system. It is described by the lengths $\ell ^{com}_\eta ,\ell ^{ch}_\eta ,\ell ^{resp}_\eta$ of the “commitments”, “challenges”, and “responses” (those lengths may depend on $\eta$), by a quantum-polynomial-time¹⁴ prover $(P_\varSigma ^1,P_\varSigma ^2)$ and a deterministic polynomial-time verifier $V_\varSigma$. We will commonly denote statement and witness with x and w (with $(x,w)\in R$ in the honest case). The first message from the prover is $com \leftarrow P_\varSigma ^1(1^{\eta },x,w)$ and is called the commitment and satisfies $com \in \{0,1\}^{\ell ^{com}}$, the uniformly random reply from the verifier is $ch {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \$}}\{0,1\}^{\ell ^{ch}}$ (called challenge ), and the prover answers with a message $resp \leftarrow P_\varSigma ^2(1^{\eta },x,w, ch )$ (the response ) that satisfies $resp \in \{0,1\}^{\ell ^{resp}}$. We assume $P_\varSigma ^1,P_\varSigma ^2$ to share classical or quantum state. Finally $V_\varSigma (1^{\eta },x, com , ch , resp )$ outputs 1 if the verifier accepts, 0 otherwise.

Definition 6

(Properties of sigma protocols). Let be a sigma protocol. We define:

• Completeness: For any quantum-polynomial-time algorithm A, there is a negligible $\mu$ such that for all $\eta$,

  

• Statistical soundness: There is a negligible $\mu$ such that for any stateful classical (but not necessarily polynomial-time) algorithm A and all $\eta$, we have that

  $$\begin{aligned} \Pr [ ok =1\wedge x\notin L_R:{}&(x, com )\leftarrow A(1^{\eta }),\ ch {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \$}}\{0,1\}^{\ell ^{ch}},\\&resp \leftarrow A(1^{\eta }, ch ), ok \leftarrow V_\varSigma (1^{\eta },x, com , ch , resp )] \le \mu (\eta ). \end{aligned}$$

• Honest-verifier zero-knowledge (HVZK): There is a quantum-polynomial-time algorithm $S_\varSigma$ (the simulator) such that for any stateful quantum-polynomial-time algorithm A there is a negligible $\mu$ such that for all $\eta$ and $(x,w)\in R_\eta$,

  

• Perfectly unique responses: There exist no values $\eta ,x, com , ch , resp , resp '$ with $resp \ne resp '$ and $V_\varSigma (1^{\eta },x, com , ch , resp )=1$ and $V_\varSigma (1^{\eta },x, com , ch ', resp ')=1$.

• Unique responses: For any quantum-polynomial-time A, the following is negligible:

  

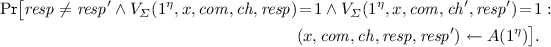
• Unpredictable commitments: The commitment has superlogarithmic collision-entropy. In other words, there is a negligible $\mu$ such that for all $\eta$ and $(x,w)\in R_\eta$,

  $$ \Pr [ com _1= com _2: com _1\leftarrow P_\varSigma ^1(1^{\eta },x,w),\ com _2\leftarrow P_\varSigma ^1(1^{\eta },x,w)] \le \mu (\eta ). $$

Note: the “unpredictable commitments” property is non-standard, but satisfied by all sigma-protocols we are aware of. However, any sigma-protocol without unpredictable commitments can be transformed into one with unpredictable commitments by appending superlogarithmically many random bits to the commitment (that are then ignored by the verifier).

4 Non-interactive Proof Systems (Definitions)

In the following, let H always denote a function $\{0,1\}^{\ell ^{in}_\eta }\rightarrow \{0,1\}^{\ell ^{out}_\eta }$ where $\ell ^{in}_\eta ,\ell ^{out}_\eta$ may depend on the security parameter $\eta$. Let $\mathrm {Fun}(\ell ^{in}_\eta ,\ell ^{out}_\eta )$ denote the set of all such functions.

A non-interactive proof system (P, V) for a relation $R_\eta$ consists of a quantum-polynomial-time algorithm P and a deterministic polynomial-time algorithm V, both taking an oracle $H\in \mathrm {Fun}(\ell ^{in}_\eta ,\ell ^{out}_\eta )$. $\pi \leftarrow P^H(1^{\eta },x,w)$ is expected to output a proof $\pi$ for the statement x using witness w. We require that $|\pi |=\ell ^\pi _\eta$ for some length $\ell ^\pi _\eta$. (i.e., the length of a proof $\pi$ depends only on the security parameter.) And $ok \leftarrow V^H(1^{\eta },x,\pi )$ is supposed to return $ok =1$ if the proof $\pi$ is valid for the statement x. Formally, we define:

Definition 7

(Completeness). (P, V) has completeness for a fixed-length relation $R_\eta$ iff for any polynomial-time oracle algorithm A there is a negligible $\mu$ such that for all $\eta$,

For the following definition, a simulator is a classical stateful algorithm S. Upon invocation, $S(1^{\eta },x)$ returns a proof $\pi$. Additionally, S may reprogram the random oracle. That is, S may choose an assignment-list $ass$, and H will then be replaced by $H( ass )$.

Definition 8

(Zero-knowledge). Given a simulator S, the oracle $S'(x,w)$ runs $S(1^{\eta },x)$ and returns the latter’s output. Given a prover P, the oracle $P'(x,w)$ runs $P(1^{\eta },x,w)$ and returns the latter’s output.

A non-interactive proof system (P, V) is zero-knowledge iff there is a quantum-polynomial-time simulator S such that for every quantum-polynomial-time oracle algorithm A there is a negligible $\mu$ such that for all $\eta$ and all normalized density operators $\rho$,

(1)

Here we quantify only over A that never query $(x,w)\notin R$ from the $P'$ or $S'$-oracle.

Definition 9

(Soundness). A non-interactive proof system (P, V) is sound iff for any quantum-polynomial-time oracle algorithm A, there is a negligible function $\mu$, such that for all $\eta$ and all normalized density operators $\rho$,

$$ \Pr [ ok _V=1\wedge x\notin L_R: (x,\pi )\leftarrow A^H(1^{\eta },\rho ),\ ok _V\leftarrow V^H(1^{\eta },x,\pi ) ] \le \mu (\eta ). $$

Here $L_R:= \{x:\exists w. (x,w)\in R\}$.

In some applications, soundness as defined above is not sufficient. Namely, consider a security proof that goes along the following lines: We start with a game in which the adversary interacts with an honest prover. We replace the honest prover by a simulator. From the zero-knowledge property it follows that this leads to an indistinguishable game. And then we try to use soundness to show that the adversary in the new game cannot prove certain statements.

The last proof step will fail: soundness guarantees nothing when the adversary interacts with a simulator that constructs fake proofs. Namely, it could be that the adversary can take a fake proof for some statement and changes it into a fake proof for another statement of its choosing. (Technically, soundness cannot be used because the simulator programs the random oracle, and Definition 9 provides no guarantees if the random oracle is modified.)

An example where this problem occurs is the proof of Theorem 21 below (unforgeability of Fiat-Shamir signatures).

To avoid these problems, we adapt the definition of simulation-soundness [22] to the quantum setting. Roughly speaking, simulation-soundness requires that the adversary cannot produce wrong proofs $\pi$, even if it has access to a simulator that it can use to produce arbitrary fake proofs. (Of course, it does not count if the adversary simply outputs one of the fake proofs it got from the simulator. But we require that the adversary cannot produce any other wrong proofs.)

Definition 10

(Simulation-soundness). A non-interactive proof system (P, V) is simulation-sound with respect to the simulator S iff for any quantum-polynomial-time oracle algorithm A, there is a negligible function $\mu$, such that for all $\eta$ and all normalized density operators $\rho$,

(2)

Here the oracle $S''(x)$ invokes $S(1^{\eta },x)$. And $H_{final}$ refers to the value of the random oracle H at the end of the execution (recall that invocations of S may change H). $\mathsf{S}\text {-}\mathsf{queries}$ is a list containing all queries made to $S''$ by A, as pairs of input/output. (Note that the input and output of $S''$ are classical, so such a list is well-defined.)

We call (P, V) weakly simulation-sound if the above holds with the following instead of (2), where $\mathsf{S}\text {-}\mathsf{queries}$ contains only the query inputs to $S''$:

(3)

When considering simulation-sound zero-knowledge proof systems, we will always implicitly assume that the same simulator is used for the simulation-soundness and for the zero-knowledge property.

5 Fiat-Shamir

For the rest of this paper, fix a sigma-protocol $\varSigma =(\ell ^{com}_\eta ,\ell ^{ch}_\eta ,\ell ^{resp}_\eta ,P_\varSigma ^1,P_\varSigma ^2,V_\varSigma )$ for a fixed-length relation $R_\eta$. Let $H:\{0,1\}^{\ell ^x_\eta +\ell ^{com}_\eta }\rightarrow \{0,1\}^{\ell ^{ch}_\eta }$ be a random oracle.

Definition 11

The Fiat-Shamir proof system $(P_{FS},V_{FS})$ consists of the algorithms $P_{FS}$ and $V_{FS}$ defined in Fig. 1.

Fig. 1.

Prover $P_{FS}$ and verifier $V_{FS}$ of the Fiat-Shamir proof system. $S_{FS}$ is the simulator constructed in the proof of Theorem 14.

In the remainder of this section, we show the following result, which is an immediate combination of Theorems 14, 16, 17, and Lemma 13 below.

Theorem 12

If $\varSigma$ has completeness, unpredictable commitments, honest-verifier zero-knowledge, statistical soundness, then Fiat-Shamir $(P_{FS},V_{FS})$ has completeness, zero-knowledge, and weak simulation-soundness.

If $\varSigma$ additionally has unique responses, then Fiat-Shamir has simulation-soundness.

5.1 Completeness

Lemma 13

If $\varSigma$ has completeness and unpredictable commitments, then Fiat-Shamir $(P_{FS},V_{FS})$ has completeness.

Interestingly, without unpredictable commitments, the lemma does not hold. Consider the following example sigma-protocol: Let $R_\eta :=\{(x,w):|x|=|w|=\eta \}$, $\ell ^{com}:=\ell ^{ch}:=\ell ^{resp}:=\eta$. Let $P_\varSigma ^1(1^{\eta },x,w)$ output $com :=0^\eta$. Let $P_\varSigma ^2(1^{\eta },x,w, ch )$ output $resp := ch$ if $ch \ne w$, and $resp :=\overline{ ch }$ else ($\overline{ ch }$ is the bitwise negation of $ch$). Let $V_\varSigma (1^{\eta },x, com , ch , resp )=1$ iff $|x|=\eta$ and $ch = resp$. This sigma-protocol has all the properties from Definition 6 except unpredictable commitments. Yet $(P_{FS},V_{FS})$ does not have completeness: A can chose $x:=0^\eta$ and $w:=H(0^\eta \Vert 0^\eta )$. For those choices of (x, w), $P_{FS}(x,w)$ will chose $com =0^\eta$ and $ch =H(x\Vert com )=w$ and thus $resp =\overline{ ch }$ and return $\pi =( com ,\overline{ ch })$. This proof will be rejected by $V_{FS}$ with probability 1.

Proof

of Lemma 13. Fix a polynomial-time oracle algorithm A. We need to show that $\Pr [ win =1:$ Game 1] is negligible for the following game:

Game 1

(Completeness). $H{\mathop {\leftarrow }\limits ^{\scriptscriptstyle \$}}\mathrm {Fun}(\ell ^{in}_\eta ,\ell ^{out}_\eta )$, $(x,w)\leftarrow A^{ H}(1^{\eta })$, $\pi \leftarrow P_{FS}^{ H}(1^{\eta },x,w)$, $ok _V\leftarrow V_{FS}^{ H}(1^{\eta },x,\pi )$, $win :=((x,w)\in R_\eta \wedge ok _V=0)$.

Let $P_\varSigma ^{1, class },P_\varSigma ^{2, class }$ be classical implementations of $P_\varSigma ^1,P_\varSigma ^2$. (I.e., $P_\varSigma ^{1, class },P_\varSigma ^{2, class }$ have the same output distribution but do not perform quantum computations or keep a quantum state. $P_\varSigma ^{1, class },P_\varSigma ^{2, class }$ might not be polynomial-time, and the state they keep might not be polynomial space.)

We use Theorem 4 to transform Game 1. For a fixed $\eta$, let $A_0^{ H}$ run $(x,w)\leftarrow A^{ H}(1^{\eta })$ (and return nothing). Let $A_C()$ run $com \leftarrow P_\varSigma ^{1, class }(1^{\eta },x,w)$ and return $x\Vert com$. Let $A_2^{H}( ch )$ run $resp \leftarrow P_\varSigma ^{2, class }(1^{\eta },x,w, ch )$ and $ok _V\leftarrow V_\varSigma (1^{\eta },x, com , ch , resp )$ and return $b:= win :=((x,w)\in R_\eta \wedge ok _V=0)$. (Note: $A_C$ and $A_2^H$ are not necessarily polynomial-time, we will only use that $A_0^H$ is polynomial-time.)

Let $p_1,p_2$ denote the first and second probability in Theorem 4, respectively. By construction, $p_1=\Pr [ win =1:$ Game 1].

Furthermore, $p_2=\Pr [ win =1:$ Game 2] for the following game:

Game 2

$H{\mathop {\leftarrow }\limits ^{\scriptscriptstyle \$}}\mathrm {Fun}(\ell ^{in}_\eta ,\ell ^{out}_\eta )$, $(x,w)\leftarrow A^{ H}(1^{\eta })$, $com \leftarrow P_\varSigma ^1(1^{\eta },x,w)$, $ch {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \$}}\{0,1\}^{\ell ^{ch}}$, $resp \leftarrow P_\varSigma ^2(1^{\eta },x,w, ch )$, $ok _V\leftarrow V_\varSigma (1^{\eta },x, com , ch , resp )$, $win :=((x,w)\in R_\eta \wedge ok _V=0)$.

Then Theorem 4 implies that

$$\begin{aligned} \bigl | \Pr [ win \!=\!1: \text {Game 1}] - \Pr [ win \!=\!1: \text {Game 2}] \bigr | \!=\! |p_1-p_2|\le (4+\sqrt{2})\sqrt{q_A}2^{-k/4}=:\mu \end{aligned}$$

(4)

where $q_A$ is the number of queries performed by $A_0^{ H}$, and k the collision-entropy of $x\Vert com$. Since A is polynomial-time, $q_A$ is polynomially bounded. And since $\varSigma$ has unpredictable commitments, k is superlogarithmic. Thus $\mu$ is negligible.

Since $\varSigma$ has completeness, $\Pr [ win =1:$ Game 2] is negligible. From (4) it then follows that $\Pr [ win =1:$ Game 1] is negligible. This shows that $(P_{FS},V_{FS})$ has completeness.    $\square$

5.2 Zero-Knowledge

Theorem 14

(Fiat-Shamir is zero-knowledge). Assume that $\varSigma$ is honest-verifier zero-knowledge and has completeness and unpredictable commitments.

Then the Fiat-Shamir proof system $(P_{FS},V_{FS})$ is zero-knowledge.

Proof

In this proof, we will in many places omit the security parameter $\eta$ for readability. (E.g., we write $\{0,1\}^{\ell ^{ch}}$ instead of $\{0,1\}^{\ell ^{ch}_\eta }$ and $S_\varSigma (x)$ instead of $S_\varSigma (1^{\eta },x)$.) It is to be understood that this is merely a syntactic omission, the variables and algorithms still depend on $\eta$.

To show that Fiat-Shamir is zero-knowledge, we first define a simulator $S_{FS}$, see Fig. 1. In the definition of $S_{FS}$ we use the honest-verifier simulator $S_\varSigma$ for $\varSigma$ (see Definition 6) which exists since $\varSigma$ is HVZK by assumption. Fix a quantum-polynomial-time adversary A, and a quantum state $\rho$ (that may depend on $\eta$). Let $q_H$ and $q_P$ denote polynomial upper bounds on the number of queries performed by A to the random oracle H and the prover/simulator, respectively. We need to show that (1) is negligible (with $P:=P_{FS}$ and $S:=S_{FS}$). For this, we transform the lhs of (1) into the rhs of (1) using a sequences of games.

Game 1

(Real world). $b\leftarrow A^{ H,P_{FS}}(\rho )$.

Game 2

(Programming H ). $b\leftarrow A^{ H,P^*}(\rho )$ with the following oracle $P^*$:

$P^*(x,w)$ runs $com \leftarrow P_\varSigma ^1(x,w)$, $ch {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \$}}\{0,1\}^{\ell ^{ch}}$, $H(x\Vert com ):= ch$, $resp \leftarrow P_\varSigma ^2(x,w, ch )$. Then it returns $\pi := com \Vert resp$.

Notice that $P^*$ reprograms the random oracle in a similar way as the simulator does. Thus, $P^*$ is not a valid prover any more, but the game is well-defined nonetheless.

In order to relate Games 1 and 2, we define a hybrid game:

Game 3

${\!\!\!}_i$ (Hybrid). $b\leftarrow A^{ H,P'}(\rho )$ where $P'$ behaves as $P_{FS}$ in the first i invocations, and as $P^*$ (see Game 2) in all further invocations.

Fix some $i\ge 0$ and some $\eta$. We will now bound $\bigl |\Pr [b=1: \text {Game 3}_i]-\Pr [b=1: \text {Game 3}_{i+1}]\bigr |$ by applying Theorem 4. Let $A_0^{ H}()$ be an algorithm that executes $A^{ H,P'}(\rho )$ until just before the i-th query to $P'$.¹⁵ Note that at that point, the query input x, w for the $(i+1)$-st $P'$-query are fixed. Let $P_\varSigma ^{1, class },P_\varSigma ^{2, class }$ be classical implementations of $P_\varSigma ^1,P_\varSigma ^2$. (I.e., $P_\varSigma ^{1, class },P_\varSigma ^{2, class }$ have the same output distribution but do not perform quantum computations or keep a quantum state. $P_\varSigma ^{1, class },P_\varSigma ^{2, class }$ might not be polynomial-time.) Let $A_C()$ compute $com \leftarrow P_\varSigma ^{1, class }(x,w)$ and return $x\Vert com$ if $(x,w)\in R$. (If $(x,w)\notin R$, $A_C()$ instead outputs a $\eta$ uniformly random bits.) Let $A_2^{ H}( ch )$ compute $resp \leftarrow P_\varSigma ^{2, class }(x,w, ch )$, set $\pi := com \Vert resp$, and then finish the execution of $A^{ H}$ using $\pi$ as the response of the $(i+1)$-st $P'$-query. $A_2^{ H}$ outputs the output of $A^{ H}$. Note that in the execution of $A_2^{ H}$, $P'$ will actually behave like $P^*$ and thus reprogram the random oracle H. $A_2^{ H}$ does not actually reprogram H (it only has readonly access to it), but instead maintains a list of all changes performed by $P^*$ to simulate queries to H performed by A accordingly.

Since $\varSigma$ has unpredictable commitments, the output of $P_\varSigma ^1$ has collision-entropy $\ge k(\eta )$ for some superlogarithmic k, assuming $(x,w)\in R$. Hence the output of $A_C$ has collision-entropy $\ge k':=\min \{\eta ,k\}$.

Since A makes at most $q_H$ queries to H, and at most $q_P$ queries to the prover, and since $P_{FS}$ and $P^*$ make one and zero queries to H, respectively, $A_0^{ H}$ makes at most $q_A:=q_H+q_P$ queries to H.

Let

$$\begin{aligned} P_{lhs}:=\Pr [b=1:{}&H{\mathop {\leftarrow }\limits ^{\scriptscriptstyle \$}}\mathrm {Fun}(\ell ^x+\ell ^{com},\ell ^{ch}), A_0^{ H}(), x\Vert com \leftarrow A_C(), \\ {}&ch :=H(x\Vert com ), b\leftarrow A_2^{ H}( ch )],\\ P_{rhs} := \Pr [b=1:{}&H{\mathop {\leftarrow }\limits ^{\scriptscriptstyle \$}}\mathrm {Fun}(\ell ^x+\ell ^{com},\ell ^{ch}), A_0^{ H}(), x\Vert com \leftarrow A_C(), \\ {}&ch {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \$}}\{0,1\}^{\ell ^{ch}}, H(x\Vert com ):= ch , b\leftarrow A_2^{ H}( ch )] \end{aligned}$$

Then, by Theorem 4,

$$\begin{aligned} \bigl |P_{lhs}-P_{rhs}\bigr | \le (4+\sqrt{2})\sqrt{q_A}2^{-k/4} =: \mu _1. \end{aligned}$$

(5)

Since k is superlogarithmic, and $q_A=q_H+q_P$ is polynomially bounded, we have that $\mu _1$ is negligible.

With those definitions, we have that

$$\begin{aligned} P_{lhs} =\Pr [b=1: \text {Game 3}_{i+1}] \end{aligned}$$

(6)

because $x\Vert com \leftarrow A_C(), ch :=H(x\Vert com )$ together with the steps $resp \leftarrow P_\varSigma ^{2, class }(x,w, ch )$ and $\pi := com \Vert resp$ executed by $A_2^{ H}$ compute what $P_{FS}$ would compute,¹⁶ hence the $(i+1)$-st query is exactly what it would be in Game 3$_{i+1}$.

And we have that

$$\begin{aligned} P_{rhs} = \Pr [b=1: \text {Game 3}_{i}] \end{aligned}$$

(7)

because $x\Vert com \leftarrow A_C()$, $ch {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \$}}\{0,1\}^{\ell ^{ch}}$, $H(x\Vert com ):= ch$, together with the steps $resp \leftarrow P_\varSigma ^{2, class }(x,w, ch )$ and $\pi := com \Vert resp$ executed by $A_2^{ H}$ compute what $P^*$ would compute, hence the i-st query is exactly what it would be in Game 3$_{i}$.

From (5)–(7), we have (for all i and $\eta$):

$$\begin{aligned} \bigl | \Pr [b=1: \text {Game 3}_{i+1}] - \Pr [b=1: \text {Game 3}_{i}] \bigr | \le \mu _1 \end{aligned}$$

(8)

Furthermore, we have that

$$\begin{aligned} \begin{aligned}&\Pr [b=1: \text {Game 3}_0] = \Pr [b=1:\text {Game 2}] \\ \text {and}\qquad&\Pr [b=1: \text {Game 3}_{q_P}] = \Pr [b=1: \text {Game 1}] \end{aligned} \end{aligned}$$

(9)

by definition of the involved games. (For the second equality, we use that $A^{ H,P'}$ makes at most $q_P$ queries to $P'$.)

Thus we have

(10)

Since $\mu _1$ is negligible and $q_P$ is polynomially bounded, $\mu _2$ is negligible.

Game 4

$b\leftarrow A^{ H,P^{**}}(\rho )$ with the following oracle $P^{**}$:

$P^{**}(x,w)$ runs: $com \leftarrow P_\varSigma ^1(x,w)$, $ch {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \$}}\{0,1\}^{\ell ^{ch}}$, $resp \leftarrow P_\varSigma ^2(x,w, ch )$, if $V_\varSigma (x, com , ch , resp )=1$ then $H(x\Vert com ):= ch$. Then it returns $\pi := com \Vert resp$.

By assumption, $\varSigma$ has completeness. Furthermore, A never queries $(x,w)\notin R$ from $P^{**}$ (see Definition 8). Thus with overwhelming probability, $V_\varSigma (x, com , ch , resp )=1$ holds in each query to $P^{**}$. Thus with overwhelming probability, the condition $V_\varSigma (x, com , ch , resp )=1$ in the if-statement is satisfied in each invocation of $P^{**}$, and $P^{**}$ performs the same steps as $P^*$. Thus for some negligible $\mu _3$ we have

$$\begin{aligned} \bigl |\Pr [b=1: \text {Game 2}]-\Pr [b=1:\text {Game 4}]\bigr | \le \mu _3. \end{aligned}$$

(11)

Let $S_{FS}$ be as in Fig. 1.

Game 5

$b\leftarrow A^{ H,S_{FS}'}$. (Here $S_{FS}'(x,w)$ runs $S_{FS}(x)$, analogous to $S'$ in Definition 8.)

By definition, $P^{**}(x,w)$ performs the following steps:

• $com \leftarrow P_\varSigma ^1(x,w)$, $ch \leftarrow \{0,1\}^{\ell ^{ch}}$, $resp \leftarrow P_\varSigma ^2(x,w, ch )$, if $V_\varSigma (x, com , ch , resp )=1$ then $H(x\Vert com ):= ch$.

In constract, $S_{FS}'$ performs:

• $( com , ch , resp )\leftarrow S_\varSigma (x)$, if $V_\varSigma (x, com , ch , resp )=1$ then $H(x\Vert com ):= ch$.

By definition of honest-verifier zero-knowledge, $( com , ch , resp )$ as chosen in the first item is indistinguishable by a quantum-polynomial-time algorithm from $( com , ch , resp )$ as chosen second item, assuming $(x,w)\in R$. (And $(x,w)\in R$ is guaranteed since by Definition 8, A only queries $(x,w)\in R$ from the prover/simulator.) A standard hybrid argument then shows that no quantum-polynomial-time adversary can distinguish oracle access to $P^{**}$ from oracle access to $S_{FS}'$. Hence

$$\begin{aligned} \bigl |\Pr [b=1:\text {Game 4}]-\Pr [b=1:\text {Game 5}]\bigr | \le \mu _4 \end{aligned}$$

(12)

for some negligible $\mu _4$.

Altogether, we have

Since $\mu _2$, $\mu _3$, and $\mu _4$ are negligible, so is $\mu _2+\mu _3+\mu _4$. Thus (1) from Definition 8 is negligible. This shows that $S_{FS}$ is a simulator as required by Definition 8, thus Fiat-Shamir is zero-knowledge.    $\square$

5.3 Soundness

Theorem 15

Assume that $\varSigma$ has statistical soundness. Then the Fiat-Shamir proof system $(P_{FS},V_{FS})$ is sound.

It may seem surprising that we need an information-theoretical property (statistical soundness of $\varSigma$) to get a computational property (soundness of $(P_{FS},V_{FS})$). Might it not be sufficient to assume that $\varSigma$ has computational soundness (or the somewhat stronger, computational special soundness)? Unfortunately, [2] shows that (relative to certain oracles), there is a sigma-protocol $\varSigma$ with computational special soundness such that $(P_{FS},V_{FS})$ is not sound. So, we cannot expect Theorem 15 to hold assuming only computational special soundness, at least not with a relativizing proof.¹⁷

The proof is based on the following observation: To produce a fake Fiat-Shamir proof, the adversary needs to find an input $(x, com )$ to the random oracle H such that $ch :=H(x\Vert com )$ is a challenge for which there exists a valid response. We call such a challenge promising. (Additionally, the adversary needs to also find that response, but we do not make use of that fact.) So, to show that forging a proof is hard, we need to show that outputs of H that are promising are hard to find. Since the sigma-protocol has statistical soundness, there cannot be too many promising challenges (otherwise, an unlimited adversary would receive a promising challenge with non-negligible probability, compute the corresponding response, and break the statistical soundness of the sigma-protocol). By reduction to existing bounds on the quantum hardness of search in a random function, we then show that finding a promising challenge in H is hard.

Proof

of Theorem 15. In this proof, we will in most places omit the security parameter $\eta$ for readability. (E.g., we write $\ell ^{ch}$ instead of $\ell ^{ch}_\eta$ and $S_\varSigma (x)$ instead of $S_\varSigma (\eta ,x)$.) It is to be understood that this is merely a syntactic omission, the variables and algorithms still depend on $\eta$.

Let $x\in \{0,1\}^{\ell ^x}, com \in \{0,1\}^{ com }$. We call a $ch \in \{0,1\}^{\ell ^{ch}}$ promising for $(x, com )$ iff there exists a $resp \in \{0,1\}^{\ell ^{resp}}$ such that $V_\varSigma (x, com , ch , resp )=1$.

Claim 1

There is a negligible $\mu$ such that for any $x\in \{0,1\}^{\ell ^x}\setminus L_R$ and any $com \in \{0,1\}^{\ell ^{com}}$, there exist at most $\mu 2^{\ell ^{ch}}$ promising $ch$.

Since $\varSigma$ has statistical soundness, by definition (Definition 6) there exists a negligible function $\mu$ such that for all $x\notin L_R$, all $com \in \{0,1\}^{\ell ^{com}}$, and all A, we have:

$$\begin{aligned} \Pr [ V_\varSigma (x, com , ch , resp )=1 :{} ch {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \$}}\{0,1\}^{\ell ^{ch}}, resp \leftarrow A(x, com , ch )] \le \mu . \end{aligned}$$

(13)

Let A be the adversary that, given $(x, com , ch )$ outputs some $resp$ with $V_\varSigma (x, com , ch , resp )=1$ if it exists, and an arbitrary output otherwise. That is, whenever $ch$ is promising for $(x, com )$, A outputs $resp$ such that $V_\varSigma (x, com , ch , resp )=1$. For any $x, com$, let $prom _{x, com }$ denote the number of promising $ch$. Then for all $x\notin L_R$ and all $com \in \{0,1\}^{\ell ^{com}}$, we have

This shows the claim.

We now define an auxiliary distribution $\mathcal D$ on functions $f:\{0,1\}^{\ell ^x+\ell ^{com}}\rightarrow \{0,1\}^{\ell ^{ch}}$ as follows: For each x, $com$, let $f(x\Vert com )$ be an independently chosen uniformly random promising $ch$. If no promising $ch$ exists for $(x, com )$, $f(x\Vert com ):=0^{\ell ^{ch}}$.

Let A be a quantum-polynomial-time adversary that breaks the soundness of Fiat-Shamir given some initial state $\rho$. That is, $\delta$ is non-negligible where

$$\begin{aligned} \delta := \Pr [ ok _V=1\wedge x\notin L_R: (x, com \Vert resp )\leftarrow A^H(\rho ),\ ok _V\leftarrow V_{FS}^H(x, com \Vert resp ) ]. \end{aligned}$$

By definition of $V_{FS}$, we have that $ok _V=1$ implies that $V_\varSigma (x, com , ch , resp )=1$ where $ch :=H(x\Vert com )$. In particular, $ch =H(x\Vert com )$ is promising for $(x, com )$. Thus, if $ok _V=1\wedge x\notin L_R$ then $f(x\Vert com )=H(x\Vert com )$ with probability at least $1/(\mu 2^{\ell ^{ch}})$ for $f\leftarrow \mathcal D$. Hence for uniformly random H,

$$\begin{aligned} \Pr [f(x\Vert com )=H(x\Vert com ) : (x, com \Vert resp )\leftarrow A^H(\rho )] \ge \frac{\delta }{\mu 2^{\ell ^{ch}}}. \end{aligned}$$

(14)

Let $B^H(\rho )$ perform the following steps: It defines $H'(x\Vert com ):=H(x\Vert com )\oplus f(x\Vert com )$. It invokes $(x, com \Vert resp )\leftarrow A^{H'}(\rho )$. It returns $x\Vert com$.

Let q be a polynomial upper bound for the number of queries performed by A. Although B may not be quantum-polynomial-time (f may not be efficiently computable), B performs only q queries since each query to $H'$ can be implemented using one query to H.¹⁸

If H is uniformly random, then $H'$ is uniformly random. Thus by (14), $H'(x\Vert com )=f(x\Vert com )$ with probability $\ge 2^{-\ell ^{ch}}\delta /\mu$. Thus $H(x\Vert com )=0^{\ell ^{ch}}$ with probability $\ge 2^{-\ell ^{ch}}\delta /\mu$. In other words, B finds a zero-preimage of H with probability $\ge 2^{-\ell ^{ch}}\delta /\mu$. By Lemma 5, this implies that $2^{-\ell ^{ch}}\delta /\mu \le 32\cdot 2^{-\ell ^{ch}}\cdot (q+1)^2$. Hence $\delta \le 32\mu \cdot (q+1)^2$. Since q is polynomially bounded (as A is quantum-polynomial-time) and $\mu$ is negligible, we have that $\delta$ is negligible.

Since this holds for all quantum-polynomial-time A, it follows that $(P_{FS},V_{FS})$ is sound.    $\square$

5.4 Simulation-Soundness

We give two theorems on simulation-soundness, depending on whether the sigma-protocol has unique responses or not.

Theorem 16

(Fiat-Shamir is weakly simulation-sound). Assume that $\varSigma$ has statistical soundness.

Then the Fiat-Shamir proof system $(P_{FS},V_{FS})$ is weakly simulation-sound with respect to the simulator $S_{FS}$ from Fig. 1.

Proof

In this proof, we will in most places omit the security parameter $\eta$ for readability. (E.g., we write $\ell ^{ch}$ instead of $\ell ^{ch}_\eta$ and $S_\varSigma (x)$ instead of $S_\varSigma (\eta ,x)$.) It is to be understood that this is merely a syntactic omission, the variables and algorithms still depend on $\eta$. For brevity, we will also omit the choosing of the random oracle H from all games. That is, every game implicitly starts with $H{\mathop {\leftarrow }\limits ^{\scriptscriptstyle \$}}\mathrm {Fun}(\ell ^{in},\ell ^{out})$.

Fix a quantum-polynomial-time adversary A, and a density operator $\rho$. Let $q_H$ and $q_P$ denote polynomial upper bounds on the number of queries performed by A to the random oracle H and the prover/simulator, respectively. We need to show that (3) holds with $V:=V_{FS}$ and $S:=S_{FS}$ for some negligible $\mu$. For this, we transform the game from (3) using a sequence of games until we reach a game where the adversary has a negligible success probability. The following game encodes the game from (3): (We write $com \Vert resp$ instead of $\pi$ to be able to explicitly refer to the two components of $\pi$.)

Game 1

(Real world). $S_A\leftarrow \rho$. $x\Vert com \Vert resp \leftarrow A^{H,S_{FS}}(S_A)$. $ok _V\leftarrow V_{FS}^{H_{final}}(x, com \Vert resp )$. $win :=\bigl ( ok _V=1\wedge x\notin L_R\wedge x\notin \mathsf{S}\text {-}\mathsf{queries}\bigr )$.

Here we use H to refer to the initial value of the random oracle H, and $H_{final}$ to the value of H after it has been reprogrammed by $S_{FS}$. (See Definition 10.)

We now show that in Game 1, we have

(15)

Assume for contradiction that (15) does not hold, i.e., that $V_{FS}^{H_{final}}(x, com \Vert resp )=1$ and ${x}\notin \mathsf{S}\text {-}\mathsf{queries}$, but $V_{FS}^{H}(x, com \Vert resp )=0$ in some execution of Game 1. Since $V_{FS}^{H}$ queries H only for input $x\Vert com$, this implies that $H_{final}(x\Vert com )\ne H(x\Vert com )$. Since H is only reprogrammed by invocations of $S_{FS}$, $H(x\Vert com )$ must have been reprogrammed by $S_{FS}$. Consider the last query to $S_{FS}$ that programmed $H(x\Vert com )$ (in case there are several). By construction of $S_{FS}$, that query had input x, in contradiction to $x\notin \mathsf{S}\text {-}\mathsf{queries}$. Thus our assumption that (15) does not hold was false. Thus (15) follows.

We now consider a variant of Game 1 where the verifier in the end gets access to H instead of $H_{final}$. (That is, we can think of H being reset to its original state without the simulator’s changes.)

(In this and the following games, we will not need to refer to $com$ and $resp$ individually any more, so we just write $\pi$ instead of $com \Vert resp$.)

Game 2

(Unchanged H ). $S_A\leftarrow \rho$. $x\Vert \pi \leftarrow A^{H,S_{FS}}(S_A)$. $ok _V\leftarrow V_{FS}^{H}(x,\pi )$. $win :=\bigl ( ok _V=1\wedge x\notin L_R\wedge x\notin \mathsf{S}\text {-}\mathsf{queries}\bigr )$.

By (15), we get

$$\begin{aligned} \Pr [ win :\text {Game 2}] \ge \Pr [ win :\text {Game 1}]. \end{aligned}$$

(16)

Furthermore, we have

$$\begin{aligned} \Pr [ ok _V=1\wedge x\notin L_R:\text {Game 2}] \ge \Pr [ win :\text {Game 2}]. \end{aligned}$$

We define an oracle algorithm B. When invoked as $B^H(S_A)$, it simulates an execution of $A^{H,S_{FS}}(S_A)$. Note that $S_{FS}$ can program the random oracle H. In order to simulate this, $B^H$ keeps track of the assignments $ass _S$ made by $S_{FS}$, and then provides A with the oracle $H( ass _S)$ (i.e., H reprogrammed according to the assignment-list $ass _S$) instead of H. Then $B^H(S_A)$ will have the same distribution of outputs as $A^{H,S_{FS}}(S_A)$. (But of course, any reprogramming of H performed by the $S_{FS}$ simulated by B will not have any effect beyond the execution of B. That is, the function H before and after the invocation of $B^H$ will be the same.)

By construction of B (and because $V_{FS}$ gets access to H and not $H_{final}$ in (16)), we then have

$$\begin{aligned} \Pr [ win :\text {Game 3}] = \Pr [ ok _V=1\wedge x\notin L_R:\text {Game 2}]. \end{aligned}$$

Game 3

(Adversary B ). $S_A\leftarrow \rho$. $x\Vert \pi \leftarrow B^{H}(S_A)$. $ok _V\leftarrow V_{FS}^{H}(x,\pi )$. $win :=\bigl ( ok _V=1\wedge x\notin L_R\bigr )$.

By Theorem 15, $(P_{FS},V_{FS})$ is sound. Furthermore, since A and $S_{FS}$ are quantum-polynomial-time, B is quantum-polynomial-time. Thus by definition of soundness (Definition 9), there is a negligible $\mu$ such that

$$\begin{aligned} \Pr [ win :\text {Game 3}] \le \mu . \end{aligned}$$

Combining the inequalities from this proof, we get $\Pr [ win :\text {Game 1}] \le \mu +\mu '.$ And $\mu +\mu '$ is negligible. Since Game 1 is the game from the definition of weak simulation soundness (Definition 10) for $(P_{FS},V_{FS})$, and since A was an arbitrarily quantum-polynomial-time oracle algorithm, it follows that $(P_{FS},V_{FS})$ is weakly simulation-sound.    $\square$

If we add another assumption about the sigma-protocol, we even can get (non-weak) simulation-soundness:

Theorem 17

(Fiat-Shamir is simulation-sound). Assume that $\varSigma$ has statistical soundness and unique responses.

Then the Fiat-Shamir proof system $(P_{FS},V_{FS})$ is simulation-sound with respect to the simulator $S_{FS}$ from Fig. 1.

Unique responses are necessary in this theorem. As pointed out in [11], if $\varSigma$ does not have unique responses, it cannot be simulation-sound, even in the classical case. Namely, if we do not require unique responses, it could be that whenever $( com , ch , resp \Vert 0)$ is a valid proof in $\varSigma$, so is $( com , ch , resp \Vert 1)$, and vice versa. Thus any valid Fiat-Shamir proof $com \Vert ( resp \Vert 0)$ could be efficiently transformed into another valid Fiat-Shamir proof $com \Vert ( resp \Vert 1)$ for the same statement. This would contradict the simulation-soundness of $(P_{FS},V_{FS})$.

Proof

In this proof, we will in most places omit the security parameter $\eta$ for readability. (E.g., we write $\ell ^{ch}$ instead of $\ell ^{ch}_\eta$ and $S_\varSigma (x)$ instead of $S_\varSigma (\eta ,x)$.) It is to be understood that this is merely a syntactic omission, the variables and algorithms still depend on $\eta$. For brevity, we will also omit the choosing of the random oracle H from all games. That is, every game implicitly starts with $H{\mathop {\leftarrow }\limits ^{\scriptscriptstyle \$}}\mathrm {Fun}(\ell ^{in},\ell ^{out})$.

Fix a quantum-polynomial-time adversary A, and a density operator $\rho$. Let $q_H$ and $q_P$ denote polynomial upper bounds on the number of queries performed by A to the random oracle H and the prover/simulator, respectively. We need to show that (2) holds with $V:=V_{FS}$ and $S:=S_{FS}$ for some negligible $\mu$. For this, we transform the game from (2) using a sequence of games until we reach a game where the adversary has a negligible success probability. The following game encodes the game from (2): (We write $com \Vert resp$ instead of $\pi$ to be able to explicitly refer to the two components of $\pi$.)

Game 4

(Real world). $S_A\leftarrow \rho$. $x\Vert com \Vert resp \leftarrow A^{H,S_{FS}}(S_A)$. $ok _V\leftarrow V_{FS}^{H_{final}}(x, com \Vert resp )$. $win :=\bigl ( ok _V=1\wedge x\notin L_R\wedge (x, com \Vert resp )\notin \mathsf{S}\text {-}\mathsf{queries}\bigr )$.

Here we use H to refer to the initial value of the random oracle H, and $H_{final}$ to the value of H after it has been reprogrammed by $S_{FS}$. (See Definition 10.)

We define a variant of the random variable $\mathsf{S}\text {-}\mathsf{queries}$. Let $\mathsf{S}\text {-}\mathsf{queries}^*$ be the list of all $S_{FS}$-queries $(x', com '\Vert resp ', ch ')$ where $x'$ was the input to $S_{FS}$, $com '\Vert resp '$ was the response of $S_{FS}$, and $ch '$ was the value of $H(x'\Vert com ')$ right after the query to $S_{FS}$. (Note that $H(x'\Vert com ')$ may change later due to reprogramming.) Notice that the only difference between $\mathsf{S}\text {-}\mathsf{queries}$ and $\mathsf{S}\text {-}\mathsf{queries}^*$ is that in the latter, we additionally track the values $ch '=H(x'\Vert com ')$.

Let $\mathsf {RespConflict}$ denote the event that $V_\varSigma (x, com ,H_{final}(x\Vert com ), resp )=1$ and that there is a query $(x', com '\Vert resp ', ch ')\in \mathsf{S}\text {-}\mathsf{queries}$ with $x'=x$, $com '= com$, $ch '=H_{final}(x\Vert com )$, and $resp '\ne resp$ and $V_\varSigma (x, com , ch ', resp ')=1$.

Since $\varSigma$ has unique responses, it follows that

$$ \Pr [\mathsf {RespConflict}:\text {Game 4}] \le \mu ' $$

for some negligible $\mu '$. (Otherwise, we could construct an adversary that simulates Game 4, and then searches for $(x, com \Vert resp ', ch )\in \mathsf{S}\text {-}\mathsf{queries}$ with $V_\varSigma (x, com , ch , resp ')=1$ and $resp '\ne resp$.)

Thus

$$ \Bigl | \Pr [ win :\text {Game 4}] - \Pr [ win \wedge \lnot \mathsf {RespConflict}:\text {Game 4}] \Bigr | \le \mu '. $$

We now show that in Game 4, we have

$$\begin{aligned} V_{FS}^{H_{final}}(x, com \Vert resp )=1 \ \wedge \ (x, com \Vert resp )\notin \mathsf{S}\text {-}\mathsf{queries}\ \wedge \ \lnot \mathsf {RespConflict}\\ \implies V_{FS}^{H}(x, com \Vert resp )=1. \end{aligned}$$

(17)

Assume for contradiction that (17) does not hold, i.e., that $V_{FS}^{H_{final}}(x, com \Vert resp )=1$ and $(x, com \Vert resp )\notin \mathsf{S}\text {-}\mathsf{queries}$ and $\lnot \mathsf {RespConflict}$, but $V_{FS}^{H}(x, com \Vert resp )=0$ in some execution of Game 4. Since $V_{FS}^{H}$ queries H only for input $x\Vert com$, this implies that $H_{final}(x\Vert com )\ne H(x\Vert com )$. Since H is only reprogrammed by invocations of $S_{FS}$, $H(x\Vert com )$ must have been reprogrammed by $S_{FS}$. Consider the last query to $S_{FS}$ that programmed $H(x\Vert com )$ (in case there are several). By construction of $S_{FS}$, that query had input x, and returns $( com , resp ')$ for some $resp '$. In particular, $(x, com \Vert resp ')\in \mathsf{S}\text {-}\mathsf{queries}$. Let $ch$ be the challenge chosen by $S_{FS}$ in that query. Then $(x, com \Vert resp ', ch )\in \mathsf{S}\text {-}\mathsf{queries}^*$. By construction of $S_{FS}$, we have $V_\varSigma (x, com , ch , resp ')=1$ (else H would not have been reprogrammed in that query) and $H_{final}(x\Vert com )= ch$ (because we are considering the last $S_{FS}$-query that programmed $H(x\Vert com )$). Since $(x, com \Vert resp )\notin \mathsf{S}\text {-}\mathsf{queries}$ and $(x,com\Vert resp ')\in \mathsf{S}\text {-}\mathsf{queries}$, we have $resp \ne resp '$. Since $V_{FS}^{H_{final}}(x, com \Vert resp )=1$ and $ch =H_{final}(x\Vert com )$, we have that $V_\varSigma (x, com , ch , resp )=1$ by definition of $V_{FS}$. Summarizing, we have $V_\varSigma (x, com , ch , resp )=1$ and $ch =H_{final}(x\Vert com )$ and $V_\varSigma (x, com , ch , resp ')=1$ and $(x, com \Vert resp ', ch )\in \mathsf{S}\text {-}\mathsf{queries}^*$ and $resp \ne resp '$. By definition of $\mathsf {RespConflict}$, this contradicts $\lnot \mathsf {RespConflict}$. Thus our assumption that (17) does not hold was false. Thus (17) follows.

We now consider a variant of Game 4 where the verifier in the end gets access to H instead of $H_{final}$. (That is, we can think of H being reset to its original state without the simulator’s changes.)

(In this and the following games, we will not need to refer to $com$ and $resp$ individually any more, so we just write $\pi$ instead of $com \Vert resp$.)

Game 5

(Unchanged H ). $S_A\leftarrow \rho$. $x\Vert \pi \leftarrow A^{H,S_{FS}}(S_A)$. $ok _V\leftarrow V_{FS}^{H}(x,\pi )$. $win :=\bigl ( ok _V=1\wedge x\notin L_R\wedge (x,\pi )\notin \mathsf{S}\text {-}\mathsf{queries}\bigr )$.

By (17), we get

$$\begin{aligned} \Pr [ win :\text {Game 5}] \ge \Pr [ win \wedge \lnot \mathsf {RespConflict}:\text {Game 4}] . \end{aligned}$$

(18)

Furthermore, we have

$$\begin{aligned} \Pr [ ok _V=1\wedge x\notin L_R:\text {Game 5}] \ge \Pr [ win :\text {Game 5}]. \end{aligned}$$

We define an oracle algorithm B. When invoked as $B^H(S_A)$, it simulates an execution of $A^{H,S_{FS}}(S_A)$. Note that $S_{FS}$ can program the random oracle H. In order to simulate this, $B^H$ keeps track of the assignments $ass _S$ made by $S_{FS}$, and then provides A with the oracle $H( ass _S)$ (i.e., H reprogrammed according to the assignment-list $ass _S$) instead of H. Then $B^H(S_A)$ will have the same distribution of outputs as $A^{H,S_{FS}}(S_A)$. (But of course, any reprogramming of H performed by the $S_{FS}$ simulated by B will not have any effect beyond the execution of B. That is, the function H before and after the invocation of $B^H$ will be the same.)

By construction of B (and because $V_{FS}$ gets access to H and not $H_{final}$ in (18)), we then have

$$\begin{aligned} \Pr [ win :\text {Game 6}] = \Pr [ ok _V=1\wedge x\notin L_R:\text {Game 5}]. \end{aligned}$$

Game 6

(Adversary B ). $S_A\leftarrow \rho$. $x\Vert \pi \leftarrow B^{H}(S_A)$. $ok _V\leftarrow V_{FS}^{H}(x,\pi )$. $win :=\bigl ( ok _V=1\wedge x\notin L_R\bigr )$.

By Theorem 15, $(P_{FS},V_{FS})$ is sound. Furthermore, since A and $S_{FS}$ are quantum-polynomial-time, B is quantum-polynomial-time. Thus by definition of soundness (Definition 9), there is a negligible $\mu$ such that

$$\begin{aligned} \Pr [ win :\text {Game 6}] \le \mu . \end{aligned}$$

Combining the inequalities from this proof, we get $\Pr [ win :\text {Game 4}] \le \mu +\mu '.$ And $\mu +\mu '$ is negligible. Since Game 4 is the game from Definition 10 for $(P_{FS},V_{FS})$, and since A was an arbitrarily quantum-polynomial-time oracle algorithm, it follows that $(P_{FS},V_{FS})$ is simulation-sound.    $\square$

6 Signatures

Originally, Fiat-Shamir was constructed as a signature scheme [12]. Only later, [5] used the same idea to construct a non-interactive zero-knowledge proof. The fact that Fiat-Shamir gives rise to a secure signature scheme can be seen as a special case of its properties as a proof system. Namely, any non-interactive zero-knowledge proof system with simulation-sound extractability can be used as a signature scheme. In the quantum setting, [26] showed that their construction of simulation-sound extractable non-interactive proofs gives rise to a signature scheme in the same way. However, this approach does not show that Fiat-Shamir gives rise to a secure signature scheme because we are not able to prove that Fiat-Shamir is extractable. For analyzing Fiat-Shamir, we show under which conditions a simulation-sound zero-knowledge non-interactive proof system gives rise to a signature scheme. Combined with our results from Sect. 5, this implies security for Fiat-Shamir based signatures.

The basic idea of the construction of signatures from non-interactive proof systems (e.g., Fiat-Shamir) is the following: To sign a message m, one needs to show the knowledge of one’s secret key. Thus, we need a relation $R_\eta$ between public and secret keys, and we need an algorithm G to generate public/secret key pairs such that it is hard to guess the secret key (a “hard instance generator”). We formalize the definition below (Definition 20).

An example of a hard instance generator would be: $R_\eta :=\{(x,w):|w|=\eta \wedge x=f(w)\}$ for some quantum-one-way function f, and G picks w uniformly from $\{0,1\}^{\eta }$, sets $x:=f(w)$, and returns (x, w).

Now a signature is just a proof of knowledge of the secret key. That is, the statement is the public key, and the witness is the secret key. However, a signature should be bound to a particular message. For this, we include the message m in the statement that is proven. That is, the statement that is proven consists of a public key and a message, but the message is ignored when determining whether a given statement has a witness or not. (In the definition below, this is formalized by considering an extended relation $R'$.) The simulation-soundness of the proof system will then guarantee that a proof/signature with respect to one message cannot be transformed into a proof/signature with respect to another message because this would mean changing the statement.

A signature scheme consists of three oracle algorithms: Keys are generated with $( pk , sk )\leftarrow KeyGen ^{H}(1^{\eta })$. The secret key $sk$ is used to sign a message m using the signing algorithm $\sigma \leftarrow Sign ^{H}(1^{\eta }, sk ,m)$ to get a signature $\sigma$. And the signature is considered valid iff $Verify ^{H}(1^{\eta }, pk ,\sigma ,m)=1$.

An instance generator for a relation $R_\eta$ is an algorithm G such that $G(1^\eta )$ outputs $(x,w)\in R_\eta$ with overwhelming probability.

We now describe how to use a simulation-sound zero-knowledge protocol (e.g., Fiat-Shamir) to construct a signature scheme:

Definition 18

(Signatures from non-interactive proofs). Let G be an instance generator for a relation $R_\eta$. Fix a length $\ell ^m_\eta$. Let $R'_\eta :=\{(x\Vert m,w):|m|=\ell ^m_\eta \wedge (x,w)\in R_\eta \}$. Let (P, V) be a non-interactive proof system for $R'_\eta$ (in the random oracle model). Then we construct the signature scheme $( KeyGen , Sign , Verify )$ with message space $\{0,1\}^{\ell ^m_\eta }$ as follows:

• $KeyGen ^{H}(1^{\eta })$: Pick $(x,w)\leftarrow G(1^{\eta })$. Let $pk :=x$, $sk :=(x,w)$. Return $( pk , sk )$.

• $Sign ^{H}(1^{\eta }, sk ,m)$ with $sk =(x,w)$: Run $\sigma \leftarrow P^{H}(1^{\eta },x\Vert m,w)$. Return $\sigma$.

• $Verify ^{H}(1^{\eta }, pk ,\sigma ,m)$ with $pk =x$: Run $ok \leftarrow V^{H}(1^{\eta },x\Vert m,\sigma )$. Return $ok$.

Note that we use a proof system for the relation $R'_\eta$ instead of $R_\eta$. However, in most cases (including Fiat-Shamir) it is trivial to construct a proof system for $R'_\eta$ given one for $R_\eta$. This is because any sigma-protocol for $R_\eta$ is also a sigma-protocol for $R'_\eta$.¹⁹ The only reason why we need to use $R'_\eta$ is that we want to include the message m inside the statement (without logical significance), and $R'_\eta$ allows us to do precisely that. (In the case of Fiat-Shamir, the overall effect will simply be to include m in the hash, see Definition 22.)

The security property we will prove is unforgeability. Unforgeability comes in two variants: weak unforgeability that ensures that the adversary cannot forge a signature for a message that has not been signed before, and strong unforgeability that additionally ensures that the adversary cannot even produce a different signature for a message that has been signed before. (Weak unforgeability is often just called unforgeability.) The definitions are standard, we include them here for completeness:

Definition 19

(Strong/weak unforgeability). A signature scheme $( KeyGen , Sign , Verify )$ is strongly unforgeable iff for all polynomial-time oracle algorithms A there exists a negligible $\mu$ such that for all $\eta$, we have

(19)

Here $\mathbf {Sig}$ is a classical ²⁰ oracle that upon classical input m returns $Sign ^H(1^{\eta }, sk ,m)$. (But queries to H are quantum.) And $\mathbf {Sig}\text {-}{{\textsf {\textit{queries}}}}$ is the list of all queries made to $\mathbf {Sig}$. (I.e., when $\mathbf {Sig}$ is queried with m and $\sigma$, $(m,\sigma )$ is added to the list $\mathbf {Sig}\text {-}{{\textsf {\textit{queries}}}}$.) And $\ell ^{in}_\eta ,\ell ^{out}_\eta$ denote the input/output length of the random oracle used by the signature scheme.

We call $( KeyGen , Sign , Verify )$ weakly unforgeable if the above holds with the following instead of (19), where $\mathbf {Sig}\text {-}{{\textsf {\textit{queries}}}}$ contains only the query inputs made to $\mathbf {Sig}$ (i.e., m instead of $(m,\sigma )$):

In [26], a hard instance generator was defined as an algorithm that outputs a statement/witness pair such that it is hard on average to find a valid witness given only the statement. However, since we will do not assume a proof system with extractability, we need a stronger variant of this definition: A dual-mode hard instance generator requires more. While a hard instance generator requires that is it hard to find a witness for x, a dual-mode hard instance generator requires that it is hard to distinguish whether x even has a witness. In other words, we should not be able to distinguish x as returned by G from $x^*$ as returned by an algorithm $G^*$ that returns statements that do not have a witness (except with negligible probability). Formally:

Definition 20

(Dual-mode hard instance generator). We call an algorithm G a dual-mode hard instance generator for a fixed-length relation $R_\eta$ iff

• G is quantum-polynomial-time, and

• there is a negligible $\mu$ such that for every $\eta$, $\Pr [(x,w)\in R_\eta :(x,w)\leftarrow G(1^{\eta })]\ge 1-\mu (\eta )$, and

• for all quantum-polynomial-time algorithm A, there is a quantum-polynomial-time algorithm $G^*$ and negligible $\mu _1,\mu _2$ such that for all $\eta$,

  

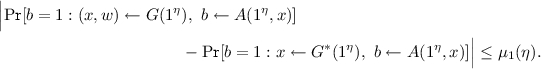
  and

  $$\begin{aligned} \Pr [x\in L_R:x\leftarrow G^*(1^{\eta })] \le \mu _2(\eta ). \end{aligned}$$

Note that we allow $G^*$ to depend on A. This is a slightly weaker requirement than requiring a universal $G^*$. We chose the weaker variant because it is sufficient for our proof below.

An example of a dual-mode hard instance generator is: Let $R_\eta :=\{(x,w):|w|=\eta \wedge x=F(w)\}$ for some quantum pseudorandom generator $F:\{0,1\}^{\eta }\rightarrow \{0,1\}^{2\eta }$, and G picks w uniformly from $\{0,1\}^{\eta }$, sets $x:=F(w)$, and returns (x, w). The conditions from Definition 20 are satisfied for $G^*$ which returns $x{\mathop {\leftarrow }\limits ^{\scriptscriptstyle \$}}\{0,1\}^{2\eta }$.

With this definition, we can state the main results of this section, namely the strong (weak) unforgeability of signatures constructed from non-interactive zero-knowledge proof systems that are (weakly) simulation-sound:

Theorem 21

(Unforgeability from simulation-soundness). Fix a relation $R_\eta$. Let $R'_\eta$ be defined as in Definition 18. If (P, V) is zero-knowledge and simulation-sound (weakly simulation-sound) for $R'_\eta$, and G is a dual-mode hard instance generator for $R_\eta$, then the signature scheme $( KeyGen , Sign , Verify )$ from Definition 18 is strongly unforgeable (weakly unforgeable).

The proof is given in Sect. 6.1 below.

Fiat-Shamir. The two preceding theorems are formulated for generic simulation-sound zero-knowledge proof systems. By specializing Theorem 21 to the case that (P, V) is the Fiat-Shamir proof system, we get a signature scheme based on a dual-mode hard instance generator and a zero-knowledge sigma-protocol with statistical soundness. The resulting signature scheme is the following:

Definition 22

(Fiat-Shamir signatures). Let G be an instance generator for a relation $R_\eta$. Fix a length $\ell ^m_\eta$. Then we construct the signature scheme $( KeyGen , Sign , Verify )$ with message space $\{0,1\}^{\ell ^m_\eta }$ as follows:

• $KeyGen ^{H}(1^{\eta })$: Pick $(x,w)\leftarrow G(1^{\eta })$. Let $pk :=x$, $sk :=(x,w)$. Return $( pk , sk )$.

• $Sign ^{H}(1^{\eta }, sk ,m)$ with $sk =(x,w)$: $com \leftarrow P_\varSigma ^1(1^{\eta },x,w)$. $resp \leftarrow P_\varSigma ^2(1^{\eta },x,w,H(x\Vert m\Vert com ))$. Return $\sigma := com \Vert resp$.

• $Verify ^{H}(1^{\eta }, pk ,\sigma ,m)$ with $pk =x$ and $\sigma = com \Vert resp$: Run $ok \leftarrow V_\varSigma (1^{\eta },x, com ,H(x\Vert m\Vert com ), resp )$. Return $ok$.

Corollary 23

(Fiat-Shamir signatures). Assume that $\varSigma$ is honest-verifier zero-knowledge, has completeness, has unpredictable commitments, and has statistical soundness for $R_\eta$, and that $\ell ^{ch}_\eta$ is superlogarithmic. Assume that G is a dual-mode hard instance generator for $R_\eta$.

Then the signature scheme $( KeyGen _{FS}, Sign _{FS}, Verify _{FS})$ from Definition 22 is weakly unforgeable.

If $\varSigma$ additionally has unique responses, the signature scheme is strongly unforgeable.

Proof

Let $\varSigma '$ be the following sigma-protocol for $R'$: The message lengths $\ell ^{com}_\eta ,\ell ^{ch}_\eta ,\ell ^{resp}_\eta$ are the same as for $\varSigma$. For $x\in \{0,1\}^{\ell ^x_\eta }$, $m\in \{0,1\}^{\ell ^m_\eta }$, the prover $P_{\varSigma '}^{1}(1^{\eta },(x\Vert m),w)$ runs $P_\varSigma ^1(1^{\eta },x,w)$, and $P_{\varSigma '}^{2}(1^{\eta },(x\Vert m),w, ch )$ runs $P_\varSigma ^2(1^{\eta },x,w, ch )$. And $V_{\varSigma '}(1^{\eta },x\Vert m, com , ch , resp )$ runs $V_\varSigma (1^{\eta },x, com , ch , resp )$.

It is easy to check that $\varSigma '$ is honest-verifier zero-knowledge, has completeness, has unpredictable commitments, and has statistical soundness for $R'_\eta$. (Using the fact that $\varSigma$ has these properties for $R_\eta$.) And $\ell ^{ch}$ is superlogarithmic.

We apply the Fiat-Shamir construction (Definition 11) to $\varSigma '$. The resulting proof system $(P_{FS},V_{FS})$ is zero-knowledge and weakly simulation-sound for $R'_\eta$ by Theorems 14 and 16. Then we apply the construction of signatures (Definition 18) to $(P_{FS},V_{FS})$ and G. By Theorem 21, the resulting signature scheme S is weakly unforgeable.

Finally, notice that this signature scheme S is the signature scheme from Definition 22. (By explicitly instantiating the constructions from Definition 11 and Definition  18 and the definition of $\varSigma '$.)

If $\varSigma$ additionally has unique responses, then $\varSigma '$ also has unique responses. Thus by Theroem 17, $(P_{FS},V_{FS})$ is simulation-sound. Hence by Theorem 21, S is strongly unforgeable.    $\square$

6.1 Security Proof

Proof

of Theorem 21. We prove the case of strong unforgeability (assuming simulation-soundness). The case of weak unforgeability is proven almost identically, we just have to replace all occurrences of $(m^*,\sigma ^*)\notin \mathbf {Sig}\text {-}\mathsf{queries}$ by $m^*\notin \mathbf {Sig}\text {-}\mathsf{queries}$ and $(x^*,\pi ^*)\notin \mathsf{S}\text {-}\mathsf{queries}$ by $x^*\notin \mathsf{S}\text {-}\mathsf{queries}$.

In this proof, we will in many places omit the security parameter $\eta$ for readability. (E.g., we write $\ell ^m$ instead of $\ell ^m_\eta$ and $Sign ( sk ,m)$ instead of $Sign (1^{\eta }, sk ,m)$.) It is to be understood that this is merely a syntactic omission, the variables and algorithms still depend on $\eta$.

In the following, H will always denote a uniformly random function from $\mathrm {Fun}(\ell ^{in},\ell ^{out})$. That is, every game written below implicitly starts with $H{\mathop {\leftarrow }\limits ^{\scriptscriptstyle \$}}\mathrm {Fun}(\ell ^{in},\ell ^{out})$.

Fix a polynomial-time oracle algorithm A. By definition of strong unforgeability (Definition 19), we need to show

$$\begin{aligned} \Pr [ win =1 : \text {Game 1} ] \le \mu (\eta ) \end{aligned}$$

for some negligible $\mu$ and the following game:

Game 1

(Unforgeability). $( pk , sk )\leftarrow KeyGen ^{H}()$, $(\sigma ^*,m^*)\leftarrow A^{H,\mathbf {Sig}}( pk )$, $ok \leftarrow Verify ^{H}( pk ,\sigma ^*,m^*)$. $win := ( ok =1\ \wedge \ (m^*,\sigma ^*)\notin \mathbf {Sig}\text {-}{{\textsf {\textit{queries}}}})$.

We will transform this game in several steps. First, we inline the definitions of $\mathbf {Sig}$ (Definition 19) and $KeyGen$, $Sign$, and $Verify$ (Definition 18). This leads to the following game:

Game 2

$(x,w)\leftarrow G(1^{\eta })$. $(x^*,\pi ^*)\leftarrow B^{H,P^{H}}(x,w)$. $ok \leftarrow V^{H}(x^*,\pi ^*)$. $win := ( ok =1\ \wedge \ (x^*,\pi ^*)\notin \mathsf{S}\text {-}\mathsf{queries})$.

Here B is a polynomial-time oracle algorithm that runs A with input $pk :=x$, and that, whenever A queries $\mathbf {Sig}$ with input m, invokes $P^{H}$ with input $(x\Vert m,w)$ instead. And when A returns some $(m^*,\sigma ^*)$, then B returns $(x^*,\pi ^*)$ with $x^*:=x\Vert m^*$ and $\pi ^*:=\sigma ^*$. And $\mathsf{S}\text {-}\mathsf{queries}$ is the list of queries made to $P^{H}$. More precisely, when $P^H$ is invoked with $(x',w')$ and responds with $\pi '$, then $(x',\pi ')$ is appended to $\mathsf{S}\text {-}\mathsf{queries}$.

We then have:

$$\begin{aligned} \Pr [ win =1 : \text {Game 1} ] = \Pr [ win =1 : \text {Game 2} ] \end{aligned}$$

We now use the zero-knowledge property of (P, V). Let S be the simulator whose existence is guaranteed by Definition 8. Let $S'$ be the oracle that on input $(x,w)\in R'$ runs S(x) and returns the latter’s output (as in Definition 8).

Then

$$\begin{aligned} \Bigl | \Pr [ win =1 : \text {Game 2} ] - \Pr [ win =1 : \text {Game 3} ] \Bigr | \le \mu _1 \end{aligned}$$

for some negligible $\mu _1$, and with the following game:

Game 3

$(x,w)\leftarrow G(1^{\eta })$. $(x^*,\pi ^*)\leftarrow B^{H,S'^{H}}(x,w)$. $ok \leftarrow V^{H_{final}}(x^*,\pi ^*)$. $win := ( ok =1\ \wedge \ (x^*,\pi ^*)\notin \mathsf{S}\text {-}\mathsf{queries})$.

Here $H_{final}$ is as in Definition 10, i.e., the value of the random oracle H after it has been reprogrammed by S.

By $x\le x^*$, we mean that x consists of the first $\ell ^x$ bits of $x^*$. (I.e., $x^*=x\Vert m$ for some m.)

Game 4

$(x,w)\leftarrow G(1^{\eta })$. $(x^*,\pi ^*)\leftarrow B^{H,S'^{H}}(x,w)$. $ok \leftarrow V^{H_{final}}(x^*,\pi ^*)$. $win := ( ok =1\ \wedge \ x\le x^* \ \wedge \ (x^*,\pi ^*)\notin \mathsf{S}\text {-}\mathsf{queries})$.

Since B by construction always outputs $x^*=x\Vert m^*$, we have

$$ \Pr [ win =1:\text {Game 3}] = \Pr [ win =1:\text {Game 4}]. $$

Let $C^{H,S^{H}}(x)$ be a polynomial-time oracle algorithm that runs A with input $pk :=x$, and that, whenever A queries $\mathbf {Sig}$ with input m, instead invokes $S^{H}$ with input $x\Vert m$. And when A returns some $(m^*,\sigma ^*)$, then C returns $(x^*,\pi ^*)$ with $x^*:=x\Vert m^*$ and $\pi ^*:=\sigma ^*$.

Note that there are two differences between $B^{H,{S'}^{H}}$ and $C^{H,{S}^{H}}$: First, C does not take w as input. Second, C invokes $S^{H}$ instead of ${S'}^{H}$. Since $S'(x\Vert m,w)$ invokes $S(x\Vert m)$ whenever $(x\Vert m,w)\in R'$, B and C will differ only when $(x\Vert m,w)\notin R'$. By definition of $R'$, this happens only when $(x,w)\notin R$. And this, in turn, happens with negligible probability since (x, w) are chosen by G, and G is a dual-mode hard instance generator. Thus there exists a negligible $\mu _2$ such that

Game 5

$(x,w)\leftarrow G(1^{\eta })$. $(x^*,\pi ^*)\leftarrow C^{H,S^{H}}(x)$. $ok \leftarrow V^{H_{final}}(x^*,\pi ^*)$. $win := ( ok =1\ \wedge \ x\le x^*\ \wedge \ (x^*,\pi ^*)\notin \mathsf{S}\text {-}\mathsf{queries})$.

Since G is a dual-mode hard instance generator, and since the computation in Game 5 after $(x,w)\leftarrow G(1^{\eta })$ is quantum-polynomial-time²¹ and does not use w, we have (by Definition 20) that there exists a quantum-polynomial-time $G^*$ and a negligible $\mu _3$ such that:

Game 6

$x\leftarrow G^*(1^{\eta })$. $(x^*,\pi ^*)\leftarrow C^{H,S^{H}}(x)$. $ok \leftarrow V^{H_{final}}(x^*,\pi ^*)$. $win := ( ok =1\ \wedge \ x\le x^*\ \wedge \ (x^*,\pi ^*)\notin \mathsf{S}\text {-}\mathsf{queries})$.

Since $G^*$ was chosen as in Definition 20, we have that $x\in L_R$ with some negligible probability $\mu _4$ in Game . Thus

Game 7

$x\leftarrow G^*(1^{\eta })$. $(x^*,\pi ^*)\leftarrow C^{H,S^{H}}(x)$. $ok \leftarrow V^{H_{final}}(x^*,\pi ^*)$. $win := ( ok =1\ \wedge x\notin L_R\ \wedge \ x\le x^*\ \wedge \ (x^*,\pi ^*)\notin \mathsf{S}\text {-}\mathsf{queries})$.

By definition of $R'$, we have that $x\notin L_R\wedge x\le x^* \implies x^*\notin L_R.$ Thus

$$ \Pr [ win :\text {Game 7}] \le \Pr [ ok =1\wedge x^*\notin L_R\wedge (x^*,\pi ^*)\notin \mathsf{S}\text {-}\mathsf{queries}:\text {Game 7}]. $$

Since (P, V) is simulation-sound (Definition 10), and “$x\leftarrow G^*(1^{\eta })$. $(x^*,\pi ^*)\leftarrow C^{H,S^{H}}(x)$” can be executed by a quantum-polynomial-time oracle algorithm with oracle access to H and $S^H$, we have that there is a negligible $\mu _5$ such that

$$\begin{aligned} \Pr [ ok =1\wedge x^*\notin L_R\wedge (x^*,\pi ^*)\notin \mathsf{S}\text {-}\mathsf{queries}:\text {Game 7}] \le \mu _5. \end{aligned}$$

Combining all inequalities from this proof, we get that

$$\begin{aligned} \Pr [ win :\text {Game 1}] \le \mu _1+\dots +\mu _5 =: \mu . \end{aligned}$$

The function $\mu$ is negligible since $\mu _1,\dots ,\mu _5$ are. Since A was arbitrary and quantum-polynomial-time, and Game 1 is the game from Definition 19, it follows that $( KeyGen , Sign , Verify )$ is strongly unforgeable.    $\square$