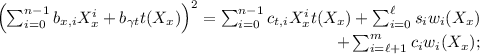Snarky Signatures: Minimal Signatures of Knowledge from Simulation-Extractable SNARKs

Abstract

We construct a pairing based simulation-extractable SNARK (SE-SNARK) that consists of only 3 group elements and has highly efficient verification. By formally linking SE-SNARKs to signatures of knowledge, we then obtain a succinct signature of knowledge consisting of only 3 group elements.

SE-SNARKs enable a prover to give a proof that they know a witness to an instance in a manner which is: (1) succinct - proofs are short and verifier computation is small; (2) zero-knowledge - proofs do not reveal the witness; (3) simulation-extractable - it is only possible to prove instances to which you know a witness, even when you have already seen a number of simulated proofs.

We also prove that any pairing based signature of knowledge or SE-NIZK argument must have at least 3 group elements and 2 verification equations. Since our constructions match these lower bounds, we have the smallest size signature of knowledge and the smallest size SE-SNARK possible.

J. Groth—The research leading to these results has received funding from the European Research Council under the European Union’s Seventh Framework Programme (FP/2007-2013)/ERC Grant Agreement n. 307937

M. Maller—Supported by a scholarship from Microsoft Research.

1 Introduction

Non-Interactive Zero-Knowledge (NIZK) arguments enable a prover to convince a verifier that they know a witness to an instance being member of a language in NP, whilst revealing no information about this witness. Recent works have looked into building NIZK arguments that are efficient enough to use in scenarios where a large number of proofs need to be stored and where verifiers have limited computational resources. Such arguments are called succinct NIZK arguments, or zk-SNARKs (zero-knowledge Succinct Non-interactive Arguments of Knowledge). A weakness of zk-SNARKs is that they are, currently without exception, susceptible to man-in-the-middle attacks. As a result, any application intending to use zk-SNARKs has to take additional measures to ensure security e.g. signing the instance and proof. Conversely, schemes that do not require succinctness can take advantage of a primitive called Signatures of Knowledge (SoKs).

Signatures of knowledge [16, 17] generalise signatures by replacing the public key with an instance in an NP-language. A signer who holds a witness for the instance can create signatures, and somebody who does not know a witness for the instance cannot sign. SoKs should not reveal the witness, since this would enable others to sign with respect to the same witness. Chase and Lysyanskaya [17] therefore define signatures of knowledge to be simulatable: if you have a trapdoor associated with some public parameters, you can simulate the signature without the witness, and hence the signature cannot be disclosing information about the witness. Moreover, in the spirit of strong existential unforgeability for digital signatures, we want it to be the case that even after seeing many signatures under different instances, it should still not be possible to create a new signature unless you know a witness. Chase and Lysyanskaya capture this property through the notion of simulation-extractability where you may obtain arbitrary simulated signatures, but still not create a new signature not seen before unless you know the witness for the instance.

Both zk-SNARKs and SoKs are key building blocks in cryptographic applications, including but not limited to: ring signatures, group signatures, policy based signatures, cryptocurrencies, anonymous delegatable credentials and direct anonymous attestation [3, 5, 6, 22, 44].

Our Contribution. We construct a succinct simulation-extractable NIZK argument, or an SE-SNARK. Our construction is pairing based. Given three groups with a bilinear map $e: \mathbb {G}_1\times \mathbb {G}_2\mapsto \mathbb {G}_T$, our proofs consist of only 3 group elements from the source groups: 2 from $\mathbb {G}_1$ and 1 from $\mathbb {G}_2$. The proofs also have fast verification with verifiers needing to check just 2 pairing product equations.

By exploring the link between SoKs and SE-NIZK arguments, we show that our construction also yields a succinct SoK. We formally define the notions of succinct SoKs and SE-SNARKs. Then we construct SoKs from SE-NIZK arguments and collision resistant hash functions, and also prove the reverse implication that SoKs give rise to SE-NIZK arguments. Our SoK inherits the high efficiency of the SE-SNARK, in particular that it consists of only 3 group elements.

We also prove a lower bound: a pairing based SE-NIZK argument for a non-trivial language in NP must have at least 2 verification equations and 3 group elements. Due to our proof that any pairing based SoK yields a pairing based SE-NIZK (where the signature size equals the proof size and the number of verification equations are equal), this lower bound also applies to the signature size and the number of verification equations in SoKs. Our constructions are therefore optimal with respect to size and number of verification equations. We note that the lower bound improves on previous lower bounds on standard NIZK arguments by explicitly taking advantage of the simulation-extractability properties in the proof.

Our construction of an SE-NIZK argument compares well with the state of the art pairing based zk-SNARKs. Groth [36] gave a 3 element zk-SNARK, however, it is not simulation-extractable and it only has a proof of security in the generic group model. While we pay a price in computational efficiency, our simulation-extractable SNARK matches the size of Groth’s zk-SNARK. We also get comparable verification complexity and unlike Groth’s zk-SNARK we give a security proof based on concrete intractability assumptions instead of relying on the full generic group model. Ben-Sasson, Chiesa, Tromer, and Virza gave an 8 element zk-SNARK which is also not simulation extractable, however they do have smaller prover computation [4]. Compared to other pairing based zk-SNARKs in the literature we have both the simulation-extractability property and also better efficiency. In Table 1 we give a comparison of our simulation-extractable SNARK with these prior zk-SNARKs.

Table 1. Comparison for arithmetic circuit satisfiability with $\ell$ element instance, m wires, n multiplication gates. Since our work uses squarings gates, we have conservatively assumed n multiplication gates translate to 2n squaring gates; if a circuit natively has many squaring gates our efficiency would therefore improve compared to Groth and BCTV. Units: $\mathbb {G}$ means group elements, E means exponentiations and P means pairings.

Our construction of a succinct signature of knowledge is the first in any computational model. This reduces the size of the signatures, albeit at the expense of having more public parameters. For applications where the public parameters need only be generated once, such as DAA and anonymous cryptocurrencies, this can be advantageous. A comparison with the most efficient prior signature of knowledge by Bernhard, Fuchsbauer and Ghadafi [6] is given in Table 2. The BFG scheme uses standard assumptions, as opposed to ours which uses knowledge extractor assumptions. It is difficult to directly compare computational efficiency since the languages are different; our work uses arithmetic circuits whereas the BFG scheme uses satisfiability of a set of pairing product equations. Therefore, we get better efficiency for arithmetic circuits and they get better efficiency for pairing product equations. However, what is clear is that we make big efficiency gains in terms of the signature size and the number of verification equations.

Table 2. Comparison of signatures of knowledge schemes. We use m and n for the number of wires and multiplication gates in our arithmetic curcuit, $\lambda$ refers to the security parameter; $|\varvec{w}|$ is the witness size and $n_p$ is the number of pairing product equations in BFG (one can translate an arithmetic circuit to pairing product equations, in which case $n_p=n$). Size is measured in number of group elements and computation in the number of exponentiations.

Techniques and Challenges. Standard definitions of signatures of knowledge [17] and simulation-extractable NIZK proofs [34] assume the ability to encrypt the witness, which can then be decrypted using a secret extraction key. However, since we are interested in having succinct signatures and proofs, we do not have space to send a ciphertext. Instead we give new definitions that use non-black-box extraction. Roughly, the definitions say that given the signer’s or prover’s state it is possible to extract a witness if it succeds in creating a valid signature or proof.

To formalise the close link between SoKs and SE-NIZK arguments, we illustrate how to build a relation which includes the signature’s message as part of the instance to be proved. Given an SE-NIZK for this relation, we build an SoK for the same relation only without the message encoded. This SoK is built solely from a collision resistant hash function and the SE-NIZK argument. The SoK is proven to be simulation-extractable directly from the definition of simulation-extractability of the NIZK argument. Once this link has been formalized, the rest of the paper focuses on how to build SE-SNARKs with optimum efficiency.

Our SE-SNARK is pairing based. The common reference string describes a bilinear group and some group elements, the proofs consist of group elements, and the verifier checks that the exponents of the proofs satisfy quadratic equations by calculating products of pairings. The underlying relation is a square arithmetic program, which is a SNARK-friendly characterisation of arithmetic circuits. Square arithmetic programs are closely related to quadratic arithmetic programs [30], but use only squarings instead of arbitrary multiplications. As suggested by Groth [36] the use of squarings give nice symmetry properties, which in our case makes it possible to check different parts of the proof against each other and hence make it intractable for an adversary to modify them without knowing a witness.

The security of our construction is based on concrete intractability assumptions. For standard knowledge soundness our strongest intractability assumption is similar to the power knowledge of exponent assumption used in [19]. To go beyond knowledge soundness to the stronger simulation-extractability property requires a stronger assumption, probably unavoidably so. We formulate the eXtended Power Knowledge of Exponent (XPKE) assumption, which assumes that an adversary cannot find elements in two source groups that have a linear relationship between each other unless it already knows what this relationship is - not even if it can query an oracle for functions of these exponents.

Finally, we rely on Groth’s [36] definition of pairing based non-interactive arguments and rule out the existence of SE-NIZK arguments with 1 verification equation or 2 group elements. Groth [36] already ruled out 1 element NIZK arguments by exploiting that if there is only one group element then the verification equations are linear in the exponents and easy to fool. It is an open problem from [36] whether regular NIZK arguments can have 2 group element proofs, a more difficult problem since a pairing of two group elements gives rise to quadratic verification equations in the exponents. We show that in the case of SE-NIZK arguments 2 group elements is not possible by leveraging the simulation-extractability property to deal also with quadratic verification equations.

Related Work. Signatures of knowledge are a core ingredient in many cryptographic protocols. For example, [6, 7, 15, 26, 29, 52] are DAA schemes that use SoKs. Anonymous cryptocurrencies can also be constructed using signatures of knowledge, for example Zero-Coin [44]. In order to make sufficient efficiency gains so that it could be deployed, the Zcash cryptocurrency [48] instead uses zk-SNARKs. To use zk-SNARKs, Zcash has to take extra steps to avoid malleability (MiTM) attacks. Specifically, Zcash samples a key pair for a one-time signature scheme; computes MACs to “tie” the signing key to the identities secret keys; modifies the instance to include signature verifying key and the MACs; and finally uses the signing key to sign the transaction. However, the use of succinct SoKs for cryptocurrencies would yield the same, if not better, efficiency as the use of zk-SNARKs and the resulting models would be simpler.

NIZK proofs originated with Blum, Feldman and Micali [2, 12] and there has been many works making both theoretical advances and efficiency improvements [18, 20, 21, 25, 31, 35, 37, 41]. Groth, Ostrovsky and Sahai [38] proposed the first pairing based NIZK proofs and subsequent works [34, 39] have yielded efficient NIZK proofs that can be used in pairing based protocols. NIZK proofs with unconditional soundness need to be linear in the witness size. However, for NIZK arguments with computational soundness it is possible to get succinct proofs that are smaller than the size of the witness [40, 43].

The practical improvements have been accompanied by theoretical works on how SNARKs compose [4, 8, 51] and on the necessity of using strong cryptographic assumptions when building SNARKs [1, 9, 11, 14, 32]. The latter works give methods to take SNARKs with long common reference strings and build SNARKs with common reference string size that is independent of the instance size, i.e., fully succinct SNARKs. Using these techniques on our simulation-extractable SNARK, which has a long common reference string, gives a fully succinct SE-SNARK.

Simulation-soundness of NIZK proofs was a notion introduced by Sahai [47] to capture the notion that even after seeing simulated proofs it is not possible to create a fake proof for a false instance unless copying a previous simulated proof. Combining this with proofs of knowledge, Groth [34] defined the even stronger security notion that we should be able to extract a witness from an adversary that creates a valid new proof, even if this adversary has seen many simulated proofs for arbitrary instances. Faust, Kohlweiss, Marson, and Venturi discuss how to achieve simulation soundness in the random oracle model [24]. Kosba et al. [46] discuss how to lift any zk-SNARK into a simulation-extractable one, however they do so by appending an encryption of the witness to the proof, so the result is not succinct.

Camenisch [16] coined the term signatures of knowledge to capture zero-knowledge protocols relying on techniques used in Schnorr signatures [49]. Signatures of knowledge have been used in many constructions albeit without a precise security definition. Chase and Lysyanskaya [17] gave the first formal definition of signatures of knowledge. They also broke the tight connection with Schnorr signatures and NIZK arguments based on cyclic groups and the Fiat-shamir heuristic and instead provided a general construction from simulation-sound NIZK proofs and dense public key encryption. An alternative definition of signatures of knowledge was given by Fischlin and Onete [27] which requires witness indistinguishability as opposed to full zero-knowledge.

2 Definitions

2.1 Notation

We write $y=A(x;r)$ when algorithm A on input x and randomness r, outputs y. We write $y\leftarrow A(x)$ for the process of picking randomness r at random and setting $y=A(x;r)$. We use the abbreviation PPT for probabilistic polynomial time. We also write $y\leftarrow S$ for sampling y uniformly at random from the set S. We will assume it is possible to sample uniformly at random from sets such as $\mathbb {Z}_p$. For an algorithm $\mathcal {A}$ we define $\mathsf {trans}_\mathcal {A}$ to be a list containing all of $\mathcal {A}$’s inputs and outputs, including random coins.

When considering security of our cryptographic schemes, we will assume there is an adversary $\mathcal {A}$. The security of our schemes will be parameterised by a security parameter $\lambda \in \mathbb {N}$. The intuition is that the larger the security parameter, the better security we get. For functions $f,g: \mathbb {N}\rightarrow [0;1]$ we write $f(\lambda )\approx g(\lambda )$ if $|f(\lambda )-g(\lambda )|=\lambda ^{-\omega (1)}$. We say a function f is negligible if $f(\lambda )\approx 0$ and overwhelming if $f(\lambda )\approx 1$. We will always implicitly assume all participants and the adversary know the security parameter, i.e., from their input they can efficiently compute the security parameter in unary representation $1^\lambda$.

We use games in security definitions and proofs. A game $\mathcal {G}$ has a number of procedures including a main procedure. The main procedure outputs either 0 or 1 depending on whether the adversary succeeds or not. $\Pr [\mathcal {G}]$ denotes the probability that this output is 1.

2.2 Relations

Let $\mathcal {R}$ be a relation generator that given a security parameter $\lambda$ in unary returns a polynomial time decidable relation $R\leftarrow \mathcal {R}(1^\lambda )$ in NP. For $(\varvec{\phi }, \varvec{w}) \in R$ we call $\varvec{\phi }$ the instance and $\varvec{w}$ the witness. We define $\mathcal {R}_\lambda$ to be the set of possible relations $\mathcal {R}(1^\lambda )$ might output.

2.3 Hard Decisional Problems

A relation R is sampleable if there are two algorithms, $\mathsf {Yes}$ and $\mathsf {No}$ such that:

• $\mathsf {Yes}$ samples instances and witnesses in the relation.

• $\mathsf {No}$ samples instances outside the language $L_R$ defined by the relation.

When proving our lower bounds for the efficiency of SE-NIZK arguments, we will assume the existence of sampleable relations where it is hard to tell whether an instance $\phi$ has been sampled by $\mathsf {Yes}$ or $\mathsf {No}$.

Definition 2.1

Let $\mathcal {R}$ a relation generator, and let $\mathsf {Yes}$, $\mathsf {No}$ be two PPT algorithms such that for $(R,\mathsf {aux})\leftarrow \mathcal {R}(1^\lambda )$ we have $\mathsf {Yes}(R)\rightarrow (\varvec{\phi },\varvec{w})\in R$ and $\mathsf {No}(R) \rightarrow \varvec{\phi }\not \in L_R$, and let $\mathcal {A}$ be an adversary. Define $\mathbf {Adv}^{DP}_{\mathcal {R}, \mathsf {Yes}, \mathsf {No}, \mathcal {A}}(1^{\lambda })$ $=$ $2\Pr [\mathcal {G}_{\mathcal {R},\mathsf {Yes},\mathsf {No},\mathcal {A}}^{DP}(1^\lambda )]-1$ where $\mathcal {G}_{\mathcal {R},\mathsf {Yes},\mathsf {No},\mathcal {A}}^{DP}(1^\lambda )$ is given by

We say $\mathsf {Yes},\mathsf {No}$ is a hard decisional problem for $\mathcal {R}$ if for all PPT adversaries $\mathcal {A}$, $\mathbf {Adv}_{\mathcal {R},\mathsf {Yes},\mathsf {No},\mathcal {A}}^{DP}(1^\lambda ) \approx \frac{1}{2}$.

2.4 Signatures of Knowledge

Signatures of knowledge [17] (SoKs) generalise digital signatures by replacing the public key with an instance in a language in NP. If you have a witness for the instance, you can sign a message. If you do not know a witness, then you cannot sign. The notion of SoKs mimic digital signatures with strong existential unforgeability; even if you have seen many signatures on arbitrary messages under arbitrary instances, you cannot create a new signature not seen before without knowing the witness for the instance.

Signatures of knowledge are closely related to simulation-extractable NIZK arguments and previous constructions have also explored the link between SoKs and NIZK proofs. In the following, we define signatures of knowledge, simulation-extractable NIZK arguments, and give a formal proof that signatures of knowledge can be constructed from simulation-extractable NIZK arguments. When we later in the article construct compact and easy to verify SE-NIZK arguments, i.e., simulation-extractable SNARKs, we will therefore automatically obtain compact and easy to verify SoKs.

For our definition of a simulation-extractable signature of knowledge, we follow the game based definitions of Chase and Lysyanskaya [17]. However, Chase and Lysyanskaya define their relations with respect to Turing Machines, whereas in our definitions the use of Turing Machines is implicit in the relation generator. Another more important difference is that since we want compact signatures, we give a non-black-box of simulation-extractability.

Definition 2.2

Let $\mathcal {R}$ be a relation generator and let $\{\mathcal {M}_\lambda \}_{\lambda \in \mathbb {N}}$ be a sequence of message spaces. Then the quintet of efficient algorithms $(\mathsf {SSetup}, \mathsf {SSign},\mathsf {SVfy}, \mathsf {SSimSetup}, \mathsf {SSimSign})$ is a simulation-extractably secure signature of knowledge scheme for $\mathcal {R}$ and $\{\mathcal {M}_\lambda \}_{\lambda \in \mathbb {N}}$ if it is correct, simulatable and simulation-extractable (defined below) and works as follows:

• $\varvec{pp}\leftarrow \mathsf {SSetup}(R)$: the setup algorithm is a PPT algorithm which takes as input a relation $R \in \mathcal {R}_\lambda$ and returns public parameters $\varvec{pp}$.

• $\varvec{\sigma }\leftarrow \mathsf {SSign}(\varvec{pp}, \varvec{\phi }, \varvec{w}, m)$: the signing algorithm is a PPT algorithm which takes as input the public parameters, a pair $(\varvec{\phi }, \varvec{w}) \in R$ and a message $m\in \mathcal {M}_\lambda$ and returns a signature $\varvec{\sigma }$.

• $0/1 \leftarrow \mathsf {SVfy}(\varvec{pp}, \varvec{\phi }, m, \varvec{\sigma })$: the verification algorithm is a deterministic polynomial time algorithm, which takes as input some public parameters $\varvec{pp}$, an instance $\varvec{\phi }$, a message $m \in \mathcal {M}_{\lambda }$, and a signature $\varvec{\sigma }$ and outputs a 0 or a 1 depending on whether it considers the signature to be valid or not.

• $(\varvec{pp},\varvec{\tau }) \leftarrow \mathsf {SSimSetup}(R):$ the simulated setup algorithm is a PPT algorithm which takes as input a relation $R\in \mathcal {R}_\lambda$ and returns public parameters $\varvec{pp}$ and a trapdoor $\varvec{\tau }$.

• $\varvec{\sigma }\leftarrow \mathsf {SSimSign}(\varvec{pp}, \varvec{\tau }, \varvec{\phi }, m):$ the simulated signing algorithm is a PPT algorithm which takes as input some public parameters $\varvec{pp}$, a simulation trapdoor $\varvec{\tau }$, and an instance $\varvec{\phi }$ and returns a signature $\varvec{\sigma }$.

Perfect Correctness: A signer with a valid witness can always produce a signature that will convince the verifier.

Definition 2.3

A signature of knowledge scheme is perfectly correct if for all $\lambda \in \mathbb {N}$, for all $R \in \mathcal {R}_\lambda$, for all $(\varvec{\phi },\varvec{w})\in R$, and for all $m\in \mathcal {M}_\lambda$

$$\Pr [\varvec{pp}\leftarrow \mathsf {SSetup}(R); \varvec{\sigma }\leftarrow \mathsf {SSign}(\varvec{pp}; \varvec{\phi }, \varvec{w}, m): \mathsf {SVfy}(\varvec{pp}, \varvec{\phi }, m, \varvec{\sigma })=1]=1.$$

Perfect Simulatability: The verifier should learn nothing from a signature about the witness that it did not already know. The secrecy of the witness is modelled by the ability to simulate signatures without the witness. More precisely, we say the signatures of knowledge are simulatable if there is a simulator that can create good looking public parameters and signatures without the witness.

Definition 2.4

For a signature of knowledge SoK, define $\mathbf {Adv}_{\textit{SoK},\mathcal {A}}^{\textit{simul}}(\lambda )=2\Pr [\mathcal {G}_{\textit{SoK},\mathcal {A}}^{\textit{simul}}(\lambda )]-1$ where the game $\mathcal {G}_{\textit{SoK},\mathcal {A}}^{\textit{simul}}$ is defined as follows

A signature of knowledge SoK is perfectly simulatable if for any PPT adversary $\mathcal {A}$, $\mathbf {Adv}_{\textit{SoK},\mathcal {A}}^{\textit{simul}}(\lambda )=\frac{1}{2}$.

Simulation-Extractability: An adversary should not be able to issue a new signature unless it knows a witness. This should hold even if the adversary gets to see signatures on arbitrary messages under arbitrary instances. We model this notion in a strong sense, by letting the adversary see simulated signatures for arbitrary messages and instances, which potentially includes false instances. Even under this strong attack model, we require that whenever the adversary outputs a valid signature not seen before, it is possible to extract a witness for the instance if you have access to the internal data of the adversary.

Definition 2.5

For a signature of knowledge SoK, define $\mathbf {Adv}_{\textit{SoK},\mathcal {A},\chi _\mathcal {A}}^{\textit{sig-ext}}(\lambda )=\Pr [\mathcal {G}_{\textit{SoK},\mathcal {A},\chi _\mathcal {A}}^{\textit{sig-ext}}(\lambda )]$ where the game $\mathcal {G}_{\textit{SoK},\mathcal {A},\chi _\mathcal {A}}^{\textit{sig-ext}}$ is defined as follows

A signature of knowledge SoK is simulation-extractable if for any PPT adversary $\mathcal {A}$, there exists a PPT extractor $\chi _\mathcal {A}$ such that $\mathbf {Adv}_{\textit{SoK},\mathcal {A},\chi _\mathcal {A}}^{\textit{sig-ext}}(\lambda )\approx 0$.

2.5 Non-interactive Zero-Knowledge Arguments of Knowledge

Definition 2.6

Let $\mathcal {R}$ be a relation generator. A NIZK argument for $\mathcal {R}$ is a quadruple of algorithms $(\mathsf {ZSetup}, \mathsf {ZProve},\mathsf {ZVfy},\mathsf {ZSimProve})$, which is complete, zero-knowledge and knowledge sound (defined below) and works as follows:

• $(\mathbf {crs}, \varvec{\tau })\leftarrow \mathsf {ZSetup}(R)$: the setup algorithm is a PPT algorithm which takes as input a relation $R \in \mathcal {R}_{\lambda }$ and returns a common reference string $\mathbf {crs}$ and a simulation trapdoor $\varvec{\tau }$.

• $\varvec{\pi }\leftarrow \mathsf {ZProve}(\mathbf {crs}, \varvec{\phi },\varvec{w})$: the prover algorithm is a PPT algorithm which takes as input a common reference string $\mathbf {crs}$ for a relation R and $(\varvec{\phi },\varvec{w})\in R$ and returns a proof $\varvec{\pi }$.

• $0/1 \leftarrow \mathsf {ZVfy}(\mathbf {crs},\varvec{\phi },\varvec{\pi })$: the verifier algorithm is a deterministic polynomial time algorithm which takes as input a common reference string $\mathbf {crs}$, an instance $\varvec{\phi }$ and a proof $\varvec{\pi }$ and returns 0 (reject) or 1 (accept).

• $\varvec{\pi }\leftarrow \mathsf {ZSimProve}(\mathbf {crs},\varvec{\tau }, \varvec{\phi })$: the simulator is a PPT algorithm which takes as input a common reference string $\mathbf {crs}$, a simulation trapdoor $\varvec{\tau }$ and an instance $\varvec{\phi }$ and returns a proof $\varvec{\pi }$.

Perfect Completeness: Perfect completeness says that given a true statement, a prover with a witness can convince the verifier.

Definition 2.7

$(\mathsf {ZSetup}, \mathsf {ZProve}, \mathsf {ZVfy},\mathsf {ZSimProve})$ is a perfectly complete argument system for $\mathcal {R}$ if for all $\lambda \in \mathbb {N}$, for all $R \in \mathcal {R}_\lambda$ and for all $(\varvec{\phi },\varvec{w}) \in R:$

$$\Pr {\big [}(\mathbf {crs}, \varvec{\tau })\leftarrow \mathsf {ZSetup}(R); \varvec{\pi }\leftarrow \mathsf {ZProve}(\mathbf {crs},\varvec{\phi },\varvec{w}): \mathsf {ZVfy}(\mathbf {crs}, \varvec{\phi },\varvec{\pi })=1{\big ]}=1.$$

Note that the simulation trapdoor $\varvec{\tau }$ is kept secret and is not known to either prover or verifier in normal use of the NIZK argument, but it enables the simulation of proofs when we define zero-knowledge below.

Perfect Zero-Knowledge: An argument system has perfect zero-knowledge if it does not leak any information besides the truth of the instance. This is modelled a simulator that does not know the witness but has some trapdoor information that enables it to simulate proofs.

Definition 2.8

For $\mathfrak {A}=(\mathsf {ZSetup}, \mathsf {ZProve}, \mathsf {ZVfy},\mathsf {ZSimProve})$ an argument system, define $\mathbf {Adv}_{\mathfrak {A},\mathcal {A}}^{\textit{zk}}(\lambda )=2\Pr [\mathcal {G}_{\mathfrak {A},\mathcal {A}}^{\textit{zk}}(\lambda )]-1$ where the game $\mathcal {G}_{\mathfrak {A},\mathcal {A}}^{\textit{zk}}$ is defined as follows

The argument system $\mathfrak {A}$ is perfectly zero knowledge if for any PPT adversary $\mathcal {A}$, $\mathbf {Adv}_{\mathfrak {A},\mathcal {A}}^{\textit{zk}}(\lambda )=\frac{1}{2}$.

Computational Knowledge Soundness: An argument system is computationally knowledge sound if whenever somebody produces a valid argument it is possible to extract a valid witness from their internal data.

Definition 2.9

For $\mathfrak {A}=(\mathsf {ZSetup}, \mathsf {ZProve}, \mathsf {ZVfy},\mathsf {ZSimProve})$ an argument system, define $\mathbf {Adv}_{\mathfrak {A},\mathcal {A},\chi _\mathcal {A}}^{\textit{sound}}(\lambda )=\Pr [\mathcal {G}_{\mathfrak {A},\mathcal {A},\chi _\mathcal {A}}^{\textit{sound}}(\lambda )]$ where the game $\mathcal {G}_{\mathfrak {A},\mathcal {A},\chi _\mathcal {A}}^{\textit{sound}}$ is defined as follows

An argument system $\mathfrak {A}$ is computationally knowledge sound if for any PPT adversary $\mathcal {A}$, there exists a PPT extractor $\chi _\mathcal {A}$ such that $\mathbf {Adv}_{\mathfrak {A},\mathcal {A},\chi _\mathcal {A}}^{\textit{sound}}(\lambda )\approx 0$.

Simulation-Extractability: Zero-knowledge and soundness are core security properties of NIZK arguments. However, it is conceivable that an adversary that sees a simulated proof for a false instance might modify the proof into another proof for a false instance. This scenario is actually very common in security proofs for cryptographic schemes, so it is often desirable to have some form of non-malleability that prevents cheating in the presence of simulated proofs.

Traditionally, simulation-extractability is defined with respect to a decryption key associated with the common reference string that allows the extraction of a witness from a valid proof. However, in succinct NIZK arguments the proofs are too small to encode the full witness. We will therefore instead define simulation-extractable NIZK arguments using a non-black-box extractor that can deduce the witness from the internal data of the adversary.

Definition 2.10

Let $\mathfrak {A}=(\mathsf {ZSetup}, \mathsf {ZProve}, \mathsf {ZVfy},\mathsf {ZSimProve})$ be a NIZK argument for $\mathcal {R}$. Define $\mathbf {Adv}_{\mathfrak {A},\mathcal {A},\chi _\mathcal {A}}^{\textit{proof-ext}}(\lambda )=\Pr [\mathcal {G}_{\mathfrak {A},\mathcal {A},\chi _\mathcal {A}}^{\textit{proof-ext}}(\lambda )]$ where the game $\mathcal {G}_{\mathfrak {A},\mathcal {A},\chi _\mathcal {A}}^{\textit{proof-ext}}$ is defined as follows

A NIZK argument $\mathfrak {A}$ is simulation-extractable if for any PPT adversary $\mathcal {A}$, there exists a PPT extractor $\chi _\mathcal {A}$ such that $\mathbf {Adv}_{\mathfrak {A},\mathcal {A},\chi _\mathcal {A}}^{\textit{proof-ext}}(\lambda )\approx 0$.

We observe that simulation-extractability implies knowledge soundness, since the latter corresponds to a simulation-extractability adversary that is not allowed to use the simulation oracle.

Definition 2.11

A succinct argument system is one in which the proof size is polynomial in the security parameter and the verifier’s computation time is polynomial in the security parameter and the instance size.

Terminology:

• A Succinct Non-interactive ARgument of Knowledge is a SNARK.

• A zk-SNARK is a zero-knowledge SNARK, or a succinct NIZK argument.

• A simulation-extractable NIZK argument is an SE-NIZK.

• A succinct SE-NIZK argument is an SE-SNARK.

Benign Relation Generators. Bitansky et al. [10] showed that indistinguishability obfuscation implies that there are potential auxiliary inputs to the adversary that allow it to create a valid proof in an obfuscated way such that it is impossible to extract the witness. Boyle and Pass [14] show that assuming the stronger notion of public coin differing input obfuscation there is even auxiliary inputs that defeat witness extraction for all candidate SNARKs. These counter examples, however, rely on specific input distributions for the adversary. We will therefore in the following assume the relationship generator is benign such that the relation (and the potential auxiliary inputs included in it) are distributed in such a way that the SNARKs we construct can be simulation extractable.

3 Signatures of Knowledge from SE-NIZKs

Signatures of knowledge and SE-NIZK arguments are closely related. We will now show how to construct a signature of knowledge scheme for messages in $\{0,1\}^*$ from an SE-NIZK argument and a public coin collision-resistant hash-function. This means that in the rest of the article we can focus our efforts on constructing succinct SE-NIZK arguments, which is a slightly simpler notion than signatures of knowledge since it does not involve a message.

We will be using collision-resistant hash-functions, where the key for the hash-function can be sampled from a source of public coins.

Definition 3.1

(Public coin collision-resistant hash-function). We say the polynomial time algorithm $H:\{0,1\}^{\phi (\lambda )}\times \{0,1\}^*\rightarrow \{0,1\}^\lambda$, with $\phi$ being a polynomial in $\lambda$, is collision resistant if for all PPT adversaries $\mathcal {A}$, $\mathbf {Adv}_\mathcal {A}^{\textit{hash}} \approx 0$ where $\mathbf {Adv}_\mathcal {A}^{\textit{hash}}$ is given by

$$\Pr [K\leftarrow \{0,1\}^{\phi (\lambda )};(m_0,m_1)\leftarrow \mathcal {A}(K): m_0\ne m_1 \ \wedge \ H_K(m_0)=H_K(m_1)]$$

Suppose $\mathcal {R}'$ is a relation generator which, on input of a security parameter $\lambda$, outputs a relation $R'$. We define a corresponding relation

$$R = \{((h, \varvec{\phi }), \varvec{w}): h \in \{0,1\}^\lambda \ \wedge \ (\varvec{\phi }, \varvec{w}) \in R'\}.$$

In the following, we let $\mathcal {R}$ be the relation generator that runs $R'\leftarrow \mathcal {R}'(1^\lambda )$ and returns R as defined above. Let H be a public coin collision-resistant hash function and $(\mathsf {ZSetup}, \mathsf {ZProve}, \mathsf {ZVfy}, \mathsf {ZSimProve})$ be a SE-NIZK argument for $\mathcal {R}$. Then Fig. 1 describes a signature of knowledge for $\mathcal {R}'$.

Fig. 1.

SoK scheme based on collision-resistant hash-function and SE-NIZK argument.

Proposition 3.1

If H is a public coin collision-resistant hash-function and $\mathfrak {A}=(\mathsf {ZSetup}, \mathsf {ZProve}, \mathsf {ZVfy}, \mathsf {ZSimProve})$ is an SE-NIZK argument for $\mathcal {R}$, then the scheme $(\mathsf {SSetup}, \mathsf {SSign}, \mathsf {SVfy})$ given in Fig. 1 is a signature of knowledge for $\mathcal {R}'$ with respect to the message space $\mathcal {M}= \{0,1\}^\lambda$.

Proof

We shall show that the signature of knowledge is perfectly correct, perfectly simulatable and that it is simulation extractable.

Perfect Correctness: Suppose that $\lambda \in \mathbb {N}$, $R' \in \mathcal {R}_{\lambda }'$, $(\varvec{\phi }, \varvec{w}) \in R'$ and $m\in \{0,1\}^*$. Running $\varvec{pp}\leftarrow \mathsf {SSetup}(R')$, $\varvec{\sigma }\leftarrow \mathsf {SSign}(\varvec{pp}, \varvec{\phi }, \varvec{w},m)$ and checking that $\mathsf {SVfy}(\varvec{pp}, \varvec{\phi },m, \varvec{\sigma })$ outputs 1 corresponds to running $K\leftarrow \{0,1\}^{\phi (\lambda )}$, $(\mathbf {crs},\varvec{\tau })\leftarrow \mathsf {ZSetup}(R)$, $\varvec{\pi }\leftarrow \mathsf {ZProve}(\mathbf {crs},(H_K(m),\varvec{\phi }),\varvec{w})$ and checking that $\mathsf {ZVfy}(\mathbf {crs}, (H_K(m), \varvec{\phi }), \varvec{\pi })$ outputs 1. As the NIZK argument is perfectly complete this check will always pass.

Perfect Simulatability: We show that for any PPT adversary $\mathcal {A}$ there exists a PPT adversary $\mathcal {B}$ such that $\mathbf {Adv}^{\text {simul}}_{SoK, \mathcal {A}}(\lambda )$ $\le$ $\mathbf {Adv}_{\mathfrak {A}, \mathcal {B}}^{\text {zk}}(1^\lambda )$ for all $\lambda \in \mathbb {N}$. Since an SE-NIZK is perfectly zero-knowledge, this implies that $\mathbf {Adv}^{\text {simul}}_{SoK, \mathcal {A}}$ is negligible in $\lambda$ i.e. if $\mathcal {A}$ breaks simulatability for $\text {SoK}$ then $\mathcal {B}$ breaks the zero-knowledge for $\mathfrak {A}$.

Let $\mathcal {A}$ be a PPT adversary against $\mathcal {G}_{SoK,\mathcal {A}}^{\text {simul}}$. Define the PPT adversary $\mathcal {B}$ that uses the output of $\mathcal {A}$ to attack the zero-knowledge of $\mathfrak {A}$ and behaves as follows:

We argue that if $P^b_{\mathbf {crs},\varvec{\tau }}$ is defined to be the oracles in $\mathcal {G}^{\text {zk}}_{\mathfrak {A},\mathcal {B}}$ then $P'^{b}_{(K,\mathbf {crs}),\varvec{\tau }}$ behaves exactly as the oracles in $\mathcal {G}^{\text {simul}}_{\text {SoK}, \mathcal {A}}$. To see this first note that if $(\varvec{\phi }_i, \varvec{w}_i)\not \in R$ then $P'^{b}$ returns $\bot$. If $(\varvec{\phi }_i,\varvec{w}_i)\in R$ then the following holds.

• when $b=0$, $P^{b}_{\mathbf {crs},\varvec{\tau }}$ returns $\varvec{\pi }_i \leftarrow \mathsf {ZProve}(\mathbf {crs}, (H_K(m_i),\varvec{\phi }),\varvec{w}_i)$. This corresponds exactly to sampling $\varvec{\sigma }_i \leftarrow \mathsf {SSign}((K,\mathbf {crs}), \varvec{\phi }, m_i, \varvec{w}_i)$.

• when $b=1$, $P^{b}_{\mathbf {crs},\varvec{\tau }}$ returns $\varvec{\pi }_i \leftarrow \mathsf {ZSimProve}(\mathbf {crs},\varvec{\tau }, ( H_K(m_i),\varvec{\phi }))$. This corresponds exactly to sampling $\varvec{\sigma }_i \leftarrow \mathsf {SSimSign}((K,\mathbf {crs}), \varvec{\tau }, \varvec{\phi }_i, m_i)$.

Hence whenever $\mathcal {A}$ succeeds at $\mathcal {G}^{\text {simul}}_{\text {SoK},\mathcal {A}}$, $\mathcal {B}$ succeeds at $\mathcal {G}^{\text {zk}}_{\mathfrak {A},\mathcal {B}}$ and the result holds.

Simulation-Extractability: We show that for all PPT adversaries $\mathcal {A}$, there exists a PPT adversary $\mathcal {B}$ such that for all PPT extractors $\chi _\mathcal {B}$, there exists a PPT extractor $\chi _\mathcal {A}$ such that $\mathbf {Adv}_{\text {SoK},\mathcal {A},\chi _\mathcal {A}}^{sig-ext}(\lambda ) \le \mathbf {Adv}_{\mathfrak {A},\mathcal {B},\chi _\mathcal {B}}^{\text {proof-ext}} + \mathbf {Adv}_\mathcal {B}^{\text {hash}}$ for all $\lambda \in \mathbb {N}$. By simulation-extractability of the SE-NIZK, we have that for any choice of $\mathcal {B}$, there exists a PPT $\chi _\mathcal {B}$ such that the above is negligible in $\lambda$, meaning that there exists a $\chi _\mathcal {A}$ such that $\mathbf {Adv}_{\text {SoK},\mathcal {A},\chi _\mathcal {A}}^{sig-ext}(\lambda )$ is negligible in $\lambda$. In other words, we construct an adversary $\mathcal {B}$ such that if $\mathcal {A}$ breaks simulation-extractability for $\text {SoK}$ then $\mathcal {B}$ breaks simulation extractability for $\mathfrak {A}$.

Let $\mathcal {A}$ be a PPT adversary that on input of some public parameters outputs an instance, a message and a signature. Define the PPT adversary $\mathcal {B}$ that uses $\mathcal {A}$ to attack simulation-extractability of $\mathfrak {A}$ and behaves as follows.

Where $\mathcal {A}$ is given K as well as all of $\mathcal {B}$’s oracle responses, $\mathsf {trans}_\mathcal {B}$ contains no information that cannot be calculated in polynomial time from $\mathsf {trans}_\mathcal {A}$. We need to design an extractor $\chi _\mathcal {A}$ that uses $\chi _B$’s output to break simulation-extractability for $\mathfrak {A}$. Let T be such that $\mathsf {trans}_\mathcal {B}= T(\mathsf {trans}_\mathcal {A})$. Let $\chi _\mathcal {B}$ be a PPT extractor that on input of $\mathsf {trans}_\mathcal {B}$ outputs some $\varvec{w}$. Define $\chi _\mathcal {A}$ as follows.

For all PPT $\mathcal {A}$, if $\mathcal {B}$ is defined as above, then for all PPT $\chi _\mathcal {B}$, if $\chi _\mathcal {A}$ is defined as above, then $\mathcal {B}$ succeeds at $\mathcal {G}^{\text {prove-ext}}_{\mathfrak {A},\mathcal {B},\chi _\mathcal {B}}$ whenever $\mathcal {A}$ succeeds at $\mathcal {G}^{\text {sig-ext}}_{\text {SoK},\mathcal {A},\chi _\mathcal {A}}$. To see this observe that

• 1. If $((\varvec{\phi }, h), \varvec{\sigma })\in Q$ then either $(\phi ,m,\varvec{\sigma })\in Q'$ or $\mathcal {A}$ outputs some m such that $H_{K}(m)=H_{K}(m_i)$ (for $m_i$ one of the queried messages) but $m \ne m_i$. The latter happens with negligible probability when $H_K$ is collision resistant.

• 2. $(\varvec{\phi },\varvec{w})\in R' \iff ((h,\varvec{\phi }),\varvec{w})\in R$.

• 3. $\mathsf {SVfy}((K,\mathbf {crs}),\varvec{\phi },m,\varvec{\sigma })=\mathsf {ZVfy}(\mathbf {crs}, (H_K(m),\varvec{\phi }),\varvec{\pi })$.

This completes the proof.   $\square$

In the other direction, it is easy to see that an SoK scheme can be used to construct an SE-NIZK argument by using the default message $m=0$.

Proposition 3.2

If an SoK scheme is simulation-extractably secure for a relation generator $\mathcal {R}$ then the NIZK for the relation generator $\mathcal {R}$ described in Fig. 2 has perfect completeness, perfect zero-knowledge and is simulation-extractable.

Proof

This holds directly from the perfect correctness, perfect simulatability and simulation-extractability of the SoK scheme.

Fig. 2.

SE-NIZK construction from an SoK.

4 Bilinear Groups and Assumptions

Definition 4.1

A bilinear group generator $\mathcal {BG}$ takes as input a security parameter in unary and returns a bilinear group $gk = (p,\mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_T,e)$ consisting of cyclic groups $\mathbb {G}_1$, $\mathbb {G}_2$, $\mathbb {G}_T$ of prime order p and a bilinear map $e:\mathbb {G}_1\times \mathbb {G}_2\rightarrow \mathbb {G}_T$ such that

• there are efficient algorithms for computing group operations, evaluating the bilinear map, deciding membership of the groups, and sampling generators of the groups;

• the map is bilinear, i.e., for all $G\in \mathbb {G}_1$ and $H\in \mathbb {G}_2$ and for all $a,b\in \mathbb {Z}$ we have $e(G^a,H^b)=e(G,H)^{ab}$;

• and the map is non-degenerate, i.e., if $e(G,H)=1$ then $G=1$ or $H=1$.

Usually bilinear groups are constructed from elliptic curves equipped with a pairing, which can be tweaked to yield a non-degenerate bilinear map. There are many ways to set up bilinear groups both as symmetric bilinear groups where $\mathbb {G}_1=\mathbb {G}_2$ and as asymmetric bilinear groups where $\mathbb {G}_1\ne \mathbb {G}_2$. We will be working in the asymmetric setting, in what Galbraith, Paterson and Smart [28] call the Type III setting where there is no efficiently computable non-trivial homomorphism in either direction between $\mathbb {G}_1$ and $\mathbb {G}_2$. Type III bilinear groups are the most efficient type of bilinear groups and hence the most relevant for practical applications.

4.1 Intractability Assumptions

We will now specify the intractability assumptions used to prove our pairing based SE-SNARK secure.

The eXtended Power Knowledge of Exponent Assumption

Our strongest assumption is the extended power knowledge of exponent (XPKE) assumption, which is a knowledge extractor assumption. We consider an adversary that gets access to source group elements that have discrete logarithms that are polynomials evaluated on secret random variables. The assumption then says that the only way the adversary can produce group elements in the two source groups with matching discrete logarithms, i.e., $G^a \in \mathbb {G}_1$ and $H^b\in \mathbb {G}_2$ with $a=b$, is if it knows that b is the evaluation of a known linear combination of the polynomials.

Assumption 4.1

Let $\mathcal {A}$ be an adversary and let $\chi _\mathcal {A}$ be an extractor. Define $\mathbf {Adv}_{\mathcal {BG}, d(\lambda ),q(\lambda ),\mathcal {A},\chi _A}^{\textit{XPKE}}(\lambda )=\Pr [\mathcal {G}^{\textit{XPKE}}_{\mathcal {BG},d(\lambda ),q(\lambda ),\mathcal {A},\chi _\mathcal {A}}(\lambda )]$ where $\mathcal {G}^{\textit{XPKE}}_{\mathcal {BG}, d(\lambda ),q(\lambda ),\mathcal {A},\chi _\mathcal {A}}$ is defined by

The $(d(\lambda ),q(\lambda ))\text {-}\mathsf {XPKE}$ assumption holds relative to $\mathcal {BG}$ if for all PPT adversaries $\mathcal {A}$, there exists a PPT algorithm $\chi _\mathcal {A}$ such that $\mathbf {Adv}_{\mathcal {BG},d(\lambda ),q(\lambda ),\mathcal {A},\chi _A}^{\textit{XPKE}}(\lambda )$ is negligible in $\lambda$.

The Computational Polynomial Assumption

The computational polynomial (Poly) assumption is related to the d-linear assumption of Escala, Herold, Kiltz, Ràfols and Villar [23]. In the univariate case, the Poly assumption says that for any $G \in \mathbb {G}_1^*$, given $G^{g_1(z)}, \ldots , G^{g_I(z)}$, an adversary cannot compute $G^{g(z)}$ for a polynomial g that is linearly independent from $g_1, \ldots , g_I$ - even if it knows $H^{g(z)}$ for $H \in \mathbb {G}_2^*$.

Assumption 4.2

Let $\mathcal {A}$ be a PPT algorithm and define $\mathbf {Adv}_{\mathcal {BG}, d(\lambda ),q(\lambda ),\mathcal {A}}^{\textit{Poly}}(\lambda )=\Pr [\mathcal {G}^{\textit{Poly}}_{\mathcal {BG},d(\lambda ),q(\lambda ),\mathcal {A}}(\lambda )]$ where $\mathcal {G}^{\textit{Poly}}_{\mathcal {BG}, d(\lambda ),q(\lambda ),\mathcal {A}}$ is defined by

The $(d(\lambda ),q(\lambda ))\text {-}\mathsf {Poly}$ assumption holds relative to $\mathcal {BG}$ if for all PPT adversaries $\mathcal {A}$ we have $\mathbf {Adv}_{Poly,d(\lambda ),q(\lambda ),\mathcal {A}}^{\textit{XPKE}}(\lambda )$ is negligible in $\lambda$.

Plausibility of the assumptions

To be plausible an assumption should not be trivial to break using generic group operations. There are various ways to formalize generic group models that restrict the adversary to such operations [42, 45, 50]. Using the framework from [13] it is easy to show the following proposition.

Proposition 4.1

The $(d(\lambda ),q(\lambda ))\text {-}\mathsf {XPKE}$ and $(d(\lambda ),q(\lambda ))\text {-}\mathsf {Poly}$ assumptions both hold in the generic group model.

We will in the following construct a pairing based SE-SNARK. The simulation extractability of the SE-SNARK will rely on the XPKE and Poly assumptions. It is instructive to consider also the assumption requirements for the weaker notion of knowledge soundness of the SNARK. To prove our SNARK has standard knowledge soundness, it suffices to consider the XPKE and Poly assumptions where the adversary has non-adaptive oracle access. We can reformulate this as the adversary specifies all the polynomials it wants to query, and then submits all queries at once and gets the matching oracle responses. The non-adaptive Poly assumption is a computational target assumption [33] and is implied by the $q-\text {BGDHE}_2$ assumption for sufficiently large q, which says given $G,G^x,\ldots ,G^{x^2q} \in \mathbb {G}_1$ and $H,H^x,\ldots ,H^{x^{q-1}},H^{x^{q+1}},\ldots ,H^{x^2q\in \mathbb {G}_2}$ it is hard to compute $H^{x^q}$. The non-adaptive XPKE assumption bears resemblance to the power knowledge of exponent (PKE) assumption from [19]. It is also worth noting that we only want to ensure the if the response $G^a$ and $H^b$ has $a=b$ then it is beceause b is some known linear combination of the queried polynomials, whereas in the only previous 3 element zk-SNARK [36] it is necessary in the proof of knowledge soundness to also consider elements where the exponent has a quadratic relationship to the queried polynomials.

To get simulation-extractability, we strengthened both the XPKE and Poly assumptions to make them interactive. We conjecture this is unavoidable, simulation extractability is interactive in nature and we do not see how to base it on non-interactive assumptions.

5 SE-SNARK

We will now construct an SE-SNARK for square arithmetic program (SAP) generators, which we define below. Any arithmetic circuit over a finite field can be efficiently converted into an SAP over the same field, see Appendix B, so this gives us SE-SNARKs for arithmetic circuit satisfiability.

Before giving our SE-SNARK, let us first provide some intuition as to why pairing based zk-SNARKs are, typically speaking, not simulation extractable. The problem is that an adversary that sees a proof is often able to modify it into a different proof for the same instance. Suppose that (A, B, C) are three of the group elements in the proof (there might be more) that satisfy the verification equations of some SNARK scheme. At least two of the proof elements must satisfy some quadratic constraint of the form

$$e(A,B)=T.$$

In the first generic attack, the adversary takes $A' = A^r$ and $B'= B^{\frac{1}{r}}$ for any value r. These new components will also satisfy the quadratic constraint. Hence, an SE-SNARK must have an additional constraint on the pairs of components that satisfy a quadratic constraint, since otherwise it is possible to forge a new proof for a previously proved statement. This is at the heart of why an SE-SNARK must have at least two verification equations. The second generic attack involves any constraint of the form

$$e(A,B) = e(C, H^\delta ),$$

where H is a generator of $\mathbb {G}_2$ given in the common reference string. This constraint can also be satisfied by $A' = A$, $B' = B H^{r\delta }$, $C' = A^rC$.

To build an SE-SNARK we need to neutralize both of these generic attacks. In our scheme, we include a constraint of the form

$$e(A,B)= e(C,H)$$

as well as a linear constraint to ensure $\log _G A = \log _H B$. The CRS will be designed to contain H, $G^\gamma$ and $H^\gamma$ but not G. That way, if the adversary sets $B' = B H^{r}$, then the only possible value for $A'$ is $A G^{r}$ - which means that r must depend on $\gamma$. This in turn forces the adversary to include a factor of $\gamma ^2$ in $C'$. By limiting the information we give the adversary about $\gamma ^2$, we ensure that the adversary cannot calculate the required value of $C'$. The full SE-SNARK verifications then also include parts to ensure the instance is correctly incorporated.

5.1 Square Arithmetic Programs

Formally, we will be working with square arithmetic programs R that have the following description

$$R=\left( \mathbb {Z}_p,gk,\ell ,\{u_i(X),w_i(X)\}_{i=0}^{m},t(X)\right) ,$$

where the bilinear group $gk=(p,\mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_T,e)$ is included as auxiliary information, $1\le \ell \le m$, $u_i(X),w_i(X),t(X)\in \mathbb {Z}_p[X]$ and $u_i(X),w_i(X)$ have strictly lower degree than n, the degree of t(X). Furthermore, suppose that the set $S=\{u_i(X): 0\le i\le \ell \}$ is linearly independent and that any $u_i \in S$ is also linearly independent from the set $\{u_j(X): \ell < j \le m\}$. A square arithmetic program with such a description defines the following binary relation, where we define $s_0=1$,

We say $\mathcal {R}$ is a square arithmetic program generator if it generates relations of the form given above with $p> 2^{\lambda -1}$.

5.2 The Construction

• $(\mathbf {crs}, \varvec{\tau }) \leftarrow \mathsf {ZSetup}(R)$:

• $\text{ Pick } \alpha , \beta , \gamma , x \leftarrow \mathbb {Z}_p^*; \ G \leftarrow \mathbb {G}_1^*; \ H \leftarrow \mathbb {G}_2^* \text { such that } t(x)\ne 0 \text { and set}$

  

• $\varvec{\pi } \leftarrow \mathsf {ZProve}(\mathbf {crs}, \varvec{\phi }, \varvec{w}):$

• Pick $r \leftarrow \mathbb {Z}_p$ and compute $\varvec{\pi } = (A,B,C)$ such that

  $$A= G^{\gamma \left( \sum _{i=0}^m s_iu_i(x)+ r\cdot t(x) \right) }, \qquad B= H^{\gamma \left( \sum _{i=0}^m s_iu_i(x)+ r\cdot t(x) \right) }$$
  $$C= G^{f(\varvec{w}) + r^2 \gamma ^2 (t(x))^2 + r(\alpha +\beta )\gamma t(x) + \gamma ^2 t(x)\left[ h(x)+2r\sum _{i=0}^{m}s_iu_i(x)\right] }$$

• where $f(\varvec{w})= \sum _{i=l+1}^{m} s_i(\gamma ^2 w_i(x)+(\alpha +\beta )\gamma u_i(x))$.

• $0/1 \leftarrow \mathsf {ZVfy}(\mathbf {crs}, \varvec{\phi }, \varvec{\pi }):$

• Check that

  $$\begin{aligned} e(AG^{\alpha }, BH^{\beta }) = e(G^{\alpha }, H^{\beta })e(G^{\varphi (\varvec{\phi })}, H^\gamma )e(C, H) \end{aligned}$$

  (1)
  $$\begin{aligned} e(A, H^{\gamma }) = e(G^{\gamma }, B) \end{aligned}$$

  (2)

• where $\varphi (\varvec{\phi })=\sum _{i=0}^\ell s_i(\gamma w_i(x) + (\alpha +\beta ) u_i(x))$. Accept the proof if and only if both the tests pass.

• $\varvec{\pi } \leftarrow \mathsf {ZSimProve}(\varvec{\tau }, \varvec{\phi }):$

• Pick $\mu \leftarrow \mathbb {Z}_p$ and compute $\varvec{\pi } = (A,B,C)$ such that

  $$A=G^{\mu }, \quad B=H^{\mu }, \quad C=G^{\mu ^2+(\alpha +\beta )\mu -\gamma \varphi (\varvec{\phi })}.$$

5.3 Efficiency

The proof size is 2 elements in $\mathbb {G}_1$ and 1 element in $\mathbb {G}_2$. The common reference string contains a description of R (which includes the bilinear group), $m+2n+5$ elements in $\mathbb {G}_1$ and $n+3$ elements in $\mathbb {G}_2$.

Although the verifier is modelled as knowing the whole common reference string, actually it only needs to know

$$\begin{aligned}&\mathbf {crs}_V= \\&\left( p, \mathbb {G}_1, \mathbb {G}_2, \mathbb {G}_T, e, H, G^\alpha , H^\beta , G^{\gamma }, H^\gamma , \{G^{\gamma w_i(x) + (\alpha +\beta )u_i(x)}\}_{i=0}^\ell , e(G^\alpha , H^\beta ) \right) . \end{aligned}$$

Thus the verifier’s common reference string only contains a description of the bilinear group $\mathcal {G}$, $\ell + 3$ elements from $\mathbb {G}_1$, 3 elements from $\mathbb {G}_2$, and 1 element from $\mathbb {G}_T$.

The verification consists of checking that the proof contains 3 appropriate group elements and checking 2 pairing product equations. The verifier computes $\ell$ exponentiations in $\mathbb {G}_1$ (noting that $s_0=1$), 4 group multiplications and 5 pairings (assuming $e(G^\alpha , H^\beta )$ is precomputed in the verifier’s common reference string).

The prover has to compute the polynomial h(X). It depends on the relation how long time this computation takes; if it arises from an arithmetic circuit where each multiplication gate connects to a constant number of wires, the relation will be sparse and the computation will be linear in n. The prover also computes the coefficients of $\sum _{i=0}^ms_iu_i(X)$. Having all the coefficients, the prover does $m+2n-\ell$ exponentiations in $\mathbb {G}_1$ and n exponentiations in $\mathbb {G}_2$.

5.4 Security Proof

Theorem 5.1

The protocol given above is a non-interactive zero knowledge argument of knowledge with perfect completeness, perfect zero knowledge and it has simulation-extractability (implying it also has knowledge soundness) provided that the $(d(\lambda ),q(\lambda ))\text {-}\mathsf {XPKE}$ and $(d(\lambda ),q(\lambda ))\text {-}\mathsf {Poly}$ assumptions hold.

Proof

Perfect Completeness

Perfect completeness holds by direct verification. Given the number of variables and the length of the equations in the exponent, we have included this verification in Appendix A for completeness.

Zero-Knowledge

To see that this scheme has perfect zero knowledge, suppose that $\pi =(A,B,C)$ is a valid proof for the instance $(s_1, \dots s_{\ell })$. If A was constructed by the prover then it is uniformly random as it depends on the random element r. The element B is then completely determined by A due to the second verification equation and C is completely determined by A and B due to the first verification equation. Similarly, when A is constructed by the simulator, A is random because it depends on the random exponent $\mu$. The element B is then completely determined by A since it can be seen to satisfy the second verification equation and C is completely determined by A and B since it can be seen to satisfy the first verification equation. Thus, real proofs and simulated proofs have identical probability distributions.

Simulation Extractability

To show simulation extractability, we shall show that any adversary that breaks simulation extractability for our scheme can also either break the $(d(\lambda ),q(\lambda ))$-XPKE assumption or break the $(d(\lambda ),q(\lambda ))$-Poly assumption. To put this formally in terms of the games $\mathcal {G}^{\text {prove-ext}}$, $\mathcal {G}^{\text {XPKE}}$ and $\mathcal {G}^{\text {Poly}}$, we observe that the relation generator $\mathcal {R}$ corresponds to a bilinear group generator where the values $\ell$, $\{u_i(X), w_i(X)\}_{i=0}^m$, t(X) are auxiliary information. Formally, we will show that for all PPT adversaries $\mathcal {A}$, there exists PPT algorithms $\mathcal {B}$, $\mathcal {C}$ such that for all PPT extractors $\chi _\mathcal {B}$, there exists a PPT extractor $\chi _\mathcal {A}$ such that for all $\lambda \in \mathbb {N}$

$$\begin{aligned} \mathbf {Adv}_{\text {Arg},\mathcal {A},\chi _\mathcal {A}}^{\text {prove-ext}}(\lambda ) \le \mathbf {Adv}_{\mathcal {R},d(\lambda ),q(\lambda ),\mathcal {B},\chi _B}^{\text {XPKE}}(\lambda )+\mathbf {Adv}_{\mathcal {R},d(\lambda ),q(\lambda ),\mathcal {C}}^{\text {Poly}}(\lambda )+\epsilon \end{aligned}$$

(3)

where $\epsilon$ is some negligible function in $\lambda$. By the $(d(\lambda ),q(\lambda ))-$XPKE and the $(d(\lambda ),q(\lambda ))-$Poly assumption we then have that for any choice of $\mathcal {B}$, $\mathcal {C}$ there exists $\chi _\mathcal {B}$ such that the RHS of 3 is negligible in $\lambda$. Thus there exists $\chi _\mathcal {A}$ such that $\mathbf {Adv}_{\text {Arg},\mathcal {A},\chi _\mathcal {A}}^{\text {prove-ext}}$ is negligible in $\lambda$.

Choosing the algorithms $\mathcal {B}$ and $\mathcal {C}$ :

To begin, we choose two PPT algorithms $\mathcal {B}$ and $\mathcal {C}$ such that whenever $\mathcal {A}$ outputs a verifying $(\varvec{\phi }, G^a,H^b,G^c)$, $\mathcal {B}$ outputs elements $(G^a,H^b)$ such that $a=b$ and $\mathcal {C}$ outputs $G^c$. Both of these algorithms will run the algorithm $\mathcal {D}$ below as a sub-protocol. The PPT adversary $\mathcal {D}$ takes a bilinear group gk as input, is given access to the oracles described in $\mathcal {G}^{\text {XPKE}}$ (or $\mathcal {G}^{\text {Poly}}$), and is defined as follows.

Then the adversaries $\mathcal {B}$ and $\mathcal {C}$ are given by

where the algorithm $\chi _\mathcal {C}$ outputs $g(\varvec{X})$ specified in (4).

Choosing the algorithm $\chi _\mathcal {C}$ :

Define $\chi _\mathcal {C}$ such that if it receives $\mathsf {trans}_\mathcal {C}$ as input and then it outputs

(4)

Possible $\chi _\mathcal {B}$ such that $\mathcal {A}$ ’s output verifies and $\mathcal {B}$ fails at $\mathcal {G}^\mathbf{XPKE }$ :

Let $\chi _\mathcal {B}$ be a PPT extractor for $\mathcal {B}$. If $\mathcal {A}$ were to output $(\varvec{\phi },G^a, H^b, G^c)$ such that $\mathsf {ZVfy}(\mathbf {crs}, G^a, H^b, G^c)=1$, then a must equal b due to the second verification equation. Thus either $\mathcal {B}$ succeeds at $\mathcal {G}^{\text {XPKE}}_{\mathcal {R},d(\lambda ),q(\lambda ),\mathcal {B},\chi _\mathcal {B}}$ or $\chi _\mathcal {B}(\mathsf {trans}_\mathcal {B})$ outputs

$$\varvec{\eta }=\left( b_0, b_\beta , b_{\gamma ,t}, \{b_{x,i}\}_{i=0}^{n-1},\{b_j\}_{j=1}^{|Q'|} \right) \in \mathbb {Z}^{3+n+|Q'|}$$

such that

$$b=b_0 \cdot 1 + b_\beta \cdot \beta + b_{\gamma , t}\cdot \gamma t(x) + \sum _{i=0}^{n-1} b_{x,i} \cdot x^i\gamma +\sum _{j=1}^{|Q'|}b_j\cdot \mu _j.$$

Choosing the extractor $\chi _\mathcal {A}$ :

Since $\mathcal {A}$ receives all of $\mathcal {C}$’s oracle responses and $\mathcal {C}$ does not use any random coins to calculate anything else, there is no information in $\mathsf {trans}_\mathcal {C}$ that cannot be calculated from $\mathsf {trans}_\mathcal {A}$. Let T be such that $T(\mathsf {trans}_\mathcal {A})=\mathsf {trans}_\mathcal {C}$. Define the PPT extractor $\chi _\mathcal {A}$ as follows¹

Contrapositive - if $\mathcal {B}$ and $\mathcal {C}$ fail then $\mathcal {A}$ fails:

Suppose that $\mathcal {A}$ outputs $(\varvec{\phi },G^a, H^b, G^c)$ with $\mathsf {ZVfy}(\mathbf {crs},\varvec{\phi }, G^a, H^b, G^c)=1$, and both $\mathcal {B}$ and $\mathcal {C}$ output 0 for $\mathcal {G}^{\text {XPKE}}_{\mathcal {R},d(\lambda ),q(\lambda ),\mathcal {B},\chi _\mathcal {B}}$ and $\mathcal {G}^{\text {Poly}}_{\mathcal {R},d(\lambda ),q(\lambda ),\mathcal {C}}$ respectively. We shall show that either

• 1. $(\varvec{\phi }, G^a, H^b, G^c) \in Q'$;

• 2. the extractor $\chi _\mathcal {A}$ outputs a valid witness for $\varvec{\phi }$.

Consequently, $\mathcal {A}$ fails at the $\mathcal {G}_{\text {Arg},\mathcal {A},\chi _\mathcal {A}}^{prove-etr}$ game. This suffices to show that (3) holds. We consider two cases: the case where the vector extracted by $\chi _\mathcal {B}$, $\varvec{\eta }$, is such that $b_k \ne 0$ for some $1 \le k \le |Q'|$; and the case where $\varvec{\eta }$ is such that $b_j=0$ for all $1 \le j \le |Q'|$. In the first case we shall show that $(\varvec{\phi }, G^a, H^b, G^c) \in Q'$ and in the second case we shall show that $\chi _\mathcal {A}$ outputs a valid witness for $\varvec{\phi }$.

Relating $\chi _\mathcal {B}$ ’s and $\chi _\mathcal {C}$ ’s outputs when $\mathcal {B}$ and $\mathcal {C}$ fail:

If $\mathcal {A}$ outputs $(\varvec{\phi },G^a, H^b, G^c)$ such that $\mathsf {ZVfy}(\mathbf {crs},\varvec{\phi }, G^a, H^b, G^c)=1$, and if both $\mathcal {B}$ and $\mathcal {C}$ fail at $\mathcal {G}^{\text {XPKE}}_{\mathcal {R},d(\lambda ),q(\lambda ),\mathcal {B},\chi _\mathcal {B}}$ and $\mathcal {G}^{\text {Poly}}_{\mathcal {R},d(\lambda ),q(\lambda ),\mathcal {C}}$ respectively, then $\chi _\mathcal {B}$ and $\chi _\mathcal {C}$ output $\varvec{\eta }$ and $g(\varvec{X})$ as above such that, with $b=\varvec{\eta }\cdot (\mathbf {crs}_{\mathbb {G}_1}, \varvec{\mu })$,

$$\begin{aligned} g(\varvec{z})=b^2 + (\alpha + \beta )b - \gamma \varphi (\varvec{\phi }). \end{aligned}$$

(5)

If $\chi _\mathcal {B}$ outputs $\varvec{\eta }$ with $b_k \ne 0$ then $\mathcal {A}$ outputs $(\varvec{\phi },G^a,G^b,G^c)\in Q'$ :

Suppose that $\chi _\mathcal {B}$ outputs $\varvec{\eta }$ is such that $b_k \ne 0$ for some integer $1 \le k \le |Q'|$.

Table 3 gives lists the coefficients of the terms that must cancel out if (5) holds. The coefficients in b relating to the all but the $k^{th}$ simulated proofs must cancel because else $b^2$ would contain a term $\mu _j\mu _k$ and $\mathcal {C}$ does not query $X_{\mu _j}X_{\mu _k}$ for $j \ne k$. Thus $g(\varvec{z})$ cannot contain any $C_{A_j}$, $C_{C_j}$ terms for $j \ne k$. Similarly, b cannot contain any $b_\beta , b_{\gamma t}, \{b_{x, i}\}_{i=0}^{n-1}$ terms because $\mathcal {C}$ does not query $X_{\beta }^2$ or $X_{\mu _k}X_\gamma$. We also have that $b_0$ is cancelled because $\mathcal {C}$ does not query $\mathcal {O}^1_{G, \varvec{z}}$ on 1.

Table 3. Table of coefficients of terms that cancel.

We can now use that the remaining terms in the RHS of (5) contain either a factor of $\gamma ^2$, $\alpha \gamma$, $\beta \gamma$, $\gamma \mu _k$, or $\mu _k^2$; and that none of them contain a factor of $x^n$. The terms involving $c_\alpha$, $c_\beta$ and $\{c_i\}_{i=0}^\ell$, $\{c_{x,i}\}_{i=0}^{n-1}$, $c_{A_k}$ do not involve $X_\gamma ^2$, $X_{\alpha \gamma }$, $X_{\beta \gamma }$, $X_{\gamma \mu _k}$, or $X_{\mu _k}^2$ terms, and so must cancel. The terms involving $c_{\gamma t}$, $\{c_{t,i}\}_{i=0}^{n-1}$ include the polynomial $t(X_x)$, which is a degree n polynomial, so they must cancel too. Denote the instance $\varvec{\phi }$ output by $\mathcal {A}$ as $(s_1, \ldots , s_\ell )$ and the instances that $\mathcal {A}$ queries the $\mathsf {ZSimProve}_{\mathbf {crs},\tau }$ oracle on as $\varvec{\phi }_j=(s_{j1}, \ldots , s_{j\ell })$. The remaining terms in (5) are,

(6)

Looking separately at the terms involving $X_{\mu _k}^2$, $X_\alpha X_{\mu _k}$, and $X_\alpha X_\gamma$ yields the three simultaneous equations

• 1. $b_k^2 = c_{C_k}$;

• 2. $b_k=c_{C_k}$;

• 3. $\sum _{i=0}^\ell (s_i-c_{C_k}s_{ki})u_i(X_x) - \sum _{i=\ell +1}^m c_iu_i(X_x) =0$.

Since $b_k \ne 0$, the first two equations mean that $b_k = c_{C_k}=1$. Also, where the polynomials $\{u_i(X)\}_{i=0}^{\ell }$ are independent from each other as well as independent from the polynomials $\{u_i(X)\}_{i=\ell +1}^{m}$, the third equation gives us that $s_i = s_{ki}$ for $0 \le i \le \ell$ and $\sum _{i=\ell +1}^m C_iu_i(x) =0$.

This is precisely the situation where $\varvec{\phi }= \varvec{\phi }_k$ and $a=\mu _k$, $b=\mu _k$, $c=\mu _k^2+(\alpha +\beta )\mu _k-\gamma \varphi (\varvec{\phi }_k)$. Hence $(\varvec{\phi }, G^a, G^b, G^c)\in Q'$.

If $\chi _\mathcal {B}$ outputs $\varvec{\eta }$ with all $b_k = 0$ then $\chi _\mathcal {A}$ outputs valid $\varvec{w}$ :

Suppose that $\chi _\mathcal {B}$ outputs $\varvec{\eta }$ is such that $b_k = 0$ for all $1 \le j \le |Q'|$.

Table 4 gives lists the coefficients of the terms that must cancel out if (5) holds. We have that $g(\varvec{X})$ cannot contain any $\{C_{A_j}, C_{C_j}\}_{i=1}^{|Q'|}$ as b contains no terms involving $\{\mu _j\}_{j=1}^{|Q'|}$. Also, b cannot contain any $b_\beta , b_0$ terms because $\mathcal {C}$ does not query $X_{\beta }^2$ or 1.

Table 4. Table of coefficients of terms that cancel.

We can now use that the remaining terms in the RHS of (5) contain either a factor of $\gamma$. The terms involving $c_\alpha$, $c_\beta$ and $\{c_i\}_{i=0}^\ell$ do not involve $X_\gamma$ so must cancel. This means that we from the remaining coefficients in (5), dividing both sides by $X_\gamma$ yields

Looking separately at the terms involving $X_\gamma$ and $X_\alpha$ provides the two simultaneous equations

• 1.

  

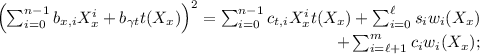
• 2. $\sum _{i=0}^{n-1}b_{x,i}X_x^i+ b_{\gamma t}t(X_x) = \sum _{i=0}^{\ell }s_i u_i(X_x) + \sum _{i=\ell +1}^m c_i u_i(X_x)$.

The first equation means that $b_{\gamma t} = 0$ because the term $b_{\gamma t}^2t^2(X_x)$ is a degree 2n polynomial in $X_x$, whereas all other polynomials in $X_x$ in that equation have maximum degree $2n-1$. Set $h(X_x)=\sum _{i=0}^{n-1}c_{t,i}X_x^i$. Then these two equations ensure that the witness $\varvec{w}= (c_{\ell +1}, \ldots , c_m)$ is a valid witness for $\varvec{\phi }$.    $\square$

6 Lower Bounds

Our pairing based simulation-extractable SNARK construction in Sect. 5 is optimal in the number of group elements and verification equations. In the full paper, we prove that in the generic group model it is impossible to have a pairing based SE-NIZK with just one verification equation or have proofs with just 2 group elements. Consequently, it is impossible to have a pairing based SoK with one verification equation or with 2 group elements. This stands in contrast to standard knowledge sound NIZK arguments, for which there are constructions consisting of just one verification equation [36].

Theorem 6.1

If $\mathcal {R}$ is a relation generator with hard decision problems and $(\mathsf {ZSetup},\mathsf {ZProve},\mathsf {ZVfy},\mathsf {ZSimProve})$ is a pairing based (as defined by Groth [36]) SE-NIZK for $\mathcal {R}$ then $\mathsf {ZVfy}$ must consist of at least 2 verification equations and the proofs must consist of at least 3 group elements.

We refer to the full paper for the proof.

Appendices

A  Completeness of the SE-SNARK in Sect. 5

Here we show perfect completeness of the SE-SNARK presented in Sect. 5. Suppose that

$$A= G^{\gamma \left( \sum _{i=0}^m s_iu_i(x)+ r\cdot t(x) \right) }, \qquad B= H^{\gamma \left( \sum _{i=0}^m s_iu_i(x)+ r\cdot t(x) \right) }$$

$$C= G^{f(\varvec{w}) + r^2 \gamma ^2 (t(x))^2 + r(\alpha +\beta )\gamma t(x) + \gamma ^2 t(x)\left[ h(x)+2r\sum _{i=0}^{m}s_iu_i(x)\right] }$$

where $f(\varvec{w})= \sum _{i=l+1}^{m} s_i(\gamma ^2 w_i(x)+(\alpha +\beta )\gamma u_i(x))$.

It is easy to see the second verification equation $e(A, H^{\gamma }) = e(G^{\gamma }, B)$ holds. Here we show that so does the first verification equation

$$e(AG^{\alpha }, BH^{\beta }) = e(G^{\alpha }, H^{\beta })e(G^{\varphi (\varvec{\phi })}, H^\gamma )e(C, H),$$

where $\varphi (\varvec{\phi })=\sum _{i=0}^\ell s_i(\gamma w_i(x) + (\alpha +\beta ) u_i(x))$. Taking discrete logarithms, this is equivalent to showing that

(7)

Combining the sums, the right hand side of (7) can be rewritten as

$$\begin{aligned} \alpha \beta + \gamma (\alpha +\beta \!&) \left( \sum _{i=0}^m s_i\left( u_i(x)\right) + r \cdot t(x)\right) \nonumber \\ +&\gamma ^2\left( \sum _{i=0}^{m} s_i\left( w_i(x) + 2 r \cdot t(x) u_i(x)\right) + r^2 (t(x))^2 + t(x)h(x)\right) . \end{aligned}$$

(8)

Expanding the left hand side of (7) yields

$$\alpha \beta + \gamma \left( \alpha + \beta \right) \left( \sum _{i=0}^m s_iu_i(x)+ r\cdot t(x) \right) + \gamma ^2 \left( \sum _{i=0}^m s_iu_i(x)+ r\cdot t(x) \right) ^2.$$

Since $(s_0, \ldots , s_m)$ is a valid witness for R, we have that $\left( \sum _{i=0}^m s_i u_i(X)\right) ^2 = \sum _{i=0}^m s_i w_i(X)+ h(X)t(X)$ for all $X \in \mathbb {Z}_p$. In particular this means that the left hand side of (7) is equal to

$$\begin{aligned} \alpha \beta + \gamma \,\big (\alpha + \beta&\!\!\big )\left( \sum _{i=0}^m s_iu_i(x)+ r\cdot t(x)\right) \\&+\, \gamma ^2 \left( \sum _{i=0}^m s_i\left( w_i(x)+ 2r\cdot t(x)u_i(x)\right) +r^2 (t(x))^2 +h(x)t(x) \right) . \end{aligned}$$

This is identical to the expression in (8), which gives us that the left hand side and the right hand side of (7) are equal.

B  Square Arithmetic Programs

We defined Square Arithmetic Program (SAP) relations in Sect. 5. We will now show how any arithmetic circuit with fan-in 2 gates over a finite field $\mathbb {Z}_p$ can be expressed as a SAP over the same finite field. The conversion is largely the same as the conversions described in [19, 30], however we also discuss how to instantiate the trick of replacing multiplications with squarings that was mentioned in [36].

Gennaro, Gentry, Parno and Raykova [30] introduced quadratic span programs (QSPs) and quadratic arithmetic programs (QAPs). These define NP-complete languages specified by a quadratic equation over polynomials. QSPs characterise boolean circuits and QAPs characterise arithmetic circuits in a natural way. Danezis, Fournet, Groth and Kohlweiss [19] noticed that by replacing each of the constraints in QSPs with 2 other constaints, it is possible to design a square span program (SSP), which is a QSP in which the two sets of polynomials involved in the quadratic term are identical. Using this technique they were able to reduce the number of proof elements and verification equations (at the cost of a circuit with twice as many gates) by having the quadratic proof components on each side of the pairing be replicas. We use SAPs in a similar way to make the group elements A and B in our proof symmetric.

An arithmetic circuit can be described as a set of equations over the wires $s_1,\ldots ,s_m$. We fix the constant $s_0=1$, use $s_1,\ldots ,s_\ell \in \mathbb {Z}_p$ to describe the instance, and the rest of the wires $s_{\ell +1},\ldots ,s_m$ can be viewed as the (extended) witness. Generalising from the simple equations that arise in arithmetic circuit, we can consider a set of equations of the form

$$\sum _{i=0}^{m} s_iu_{i,q} \cdot \sum _{i=0}^m s_iv_{i,q}=\sum _{i=0}^m s_iw_{i,q},$$

where $u_{i,q},v_{i,q},w_{i,q}$ are constants in $\mathbb {Z}_p$ specifying the qth equation.

Our SAP is based on a simplification of systems of arithmetic constraints, where all multiplications are replaced with squarings. As suggested by [36], we can write a product $ab=\frac{(a+b)^2-(a-b)^2}{4}$. A system with n multiplication constraints can therefore be rewritten as a system with at most 2n squaring constraints. To be precise, for each multiplication constraint $\sum _{i=0}^m s_iu_{i,q} \cdot \sum _{i=0}^m s_iv_{i,q}=\sum _{i=0}^m s_iw_{i,q}$ we introduce a new variable $s_{m+q}$ and replace it with two squaring constraints

• 1. $\left( \sum _{i=0}^m s_i(u_{i,q}+v_{i,q})\right) ^2=4\sum _{i=0}^m s_iw_{i,q}+s_{m+q}$;

• 2. $\left( \sum _{i=0}^m s_i(u_{i,q}-v_{i,q})\right) ^2=s_{m+q}$.

Given n squaring constraints $\left\{ \left( \sum _{i=0}^ms_iu_{i,q}\right) ^2=\sum _{i=0}^ms_iw_{i,q}\right\} _{q=1}^n$ we can now pick arbitrary distinct $r_1,\ldots ,r_n\in \mathbb {Z}_p$ and define $t(x)=\prod _{q=1}^n(x-r_q)$. Furthermore, let $u_i(x),w_i(x)$ be degree $n-1$ polynomials such that

$$u_i(r_q)=u_{i,q} \quad \text { and } \quad w_i(r_q)=w_{i,q} \qquad \text {for} \quad i=0,\ldots ,m, q=1,\ldots ,n.$$

We now have that $s_0=1$ and the variables $s_1,\ldots ,s_m\in \mathbb {F}$ satisfy the n equations if and only if in each point $r_1,\ldots ,r_q$

$$\left( \sum _{i=0}^ms_iu_i(r_q)\right) ^2=\sum _{i=0}^ms_iw_i(r_q).$$

Since t(X) is the lowest degree monomial with $t(r_q)=0$ in each point, we can reformulate this condition as

$$\left( \sum _{i=0}^ms_iu_i(X)\right) ^2 \equiv \sum _{i=0}^ms_iw_i(X)\ \bmod t(X).$$

This gives rise to a SAP as defined in Sect. 5.

Formally, we work with square arithmetic programs R that have the following description

$$R=\left( \mathbb {Z}_p,\mathrm {aux},\ell ,\{u_i(X),w_i(X)\}_{i=0}^{m},t(X)\right) ,$$

where p is a prime, $\mathrm {aux}$ is some auxiliary information, $1\le \ell \le m$,

$u_i(X),w_i(X),t(X)\in \mathbb {Z}_p[X]$ and $u_i(X),w_i(X)$ have strictly lower degree than n, the degree of t(X). A square arithmetic program with such a description defines the following binary relation, where we define $s_0=1$,

We say $\mathcal {R}$ is a square arithmetic program generator if it generates relations of the form given above with $p>2^{\lambda -1}$.

Relations can arise in many different ways in practice. It may be that the relationship generator is deterministic or it may be that it is randomized. It may be that first the prime p is generated and then the rest of the relation is built on top of the $\mathbb {Z}_p$. Or it may be that the polynomials are specified first and then a random field $\mathbb {Z}_p$ is chosen. To get maximal flexibility we have chosen our definitions to be agnostic with respect to the exact way the field and the relation is generated, the different options can all be modelled by appropriate choices of relation generators.

In our pairing-based NIZK arguments the auxiliary information $\mathrm {aux}$ specifies a bilinear group. It may seem a bit surprising to make the choice of bilinear group part of the relation generator but this provides a better model of settings where the relation is built on top of an already existing bilinear group. Again, there is no loss of generality in this choice, one can think of a traditional setting where the relation is chosen first and then the bilinear group is chosen at random as the special case where the relation generator works in two steps, first choosing the relation and then picking a random bilinear group. Of course letting the relation generator pick the bilinear group is another good reason that we need to assume it is benign; an appropriate choice of bilinear group is essential for security.

We use in the security proofs that the polynomials $u_0(X), \ldots , u_\ell (X)$ are linearly independent from each other and linearly independent from $u_{\ell +1}(X),\ldots ,u_m(X)$. When constructing the square arithmetic program from squaring constraints, we can achieve this by introducing the constraint $s_i\cdot 1 = s_{i}$ for any $u_i(X)$ that is not already linearly independent. This makes $u_i(X)$ linearly independent from all the other $u_j(X)$ since $u_i(r_{m+i})=1$, while $u_j(r_{m+i})=0$ for all $j\ne i$.

Finally, we note that given the square arithmetic program defining $R'$, we can formulate the square arithmetic program defining

$$R=\{((h, \varvec{\phi }), \varvec{w}): \quad h \in \{0,1\}^\lambda \ \wedge \ (\varvec{\phi }, \varvec{w}) \in R' \}$$

by introducing another new variable h and adding the constraint that $h \cdot 1 =h$. This means that from a simulation-extractable NIZK for relation R, we can build a simulation extractable signature of knowledge as in Sect. 3.