Abstract
A distributed computation in which nodes are connected by a partial communication graph is called topology-hiding if it does not reveal information about the graph (beyond what is revealed by the output of the function). Previous results [Moran, Orlov, Richelson; TCC’15] have shown that topology-hiding computation protocols exist for graphs of logarithmic diameter (in the number of nodes), but the feasibility question for graphs of larger diameter was open even for very simple graphs such as chains, cycles and trees.
In this work, we take a step towards topology-hiding computation protocols for arbitrary graphs by constructing protocols that can be used in a large class of large-diameter networks, including cycles, trees and graphs with logarithmic circumference. Our results use very different methods from [MOR15] and can be based on a standard assumption (such as DDH).
A. Akavia—Work partly supported by the ERC under the EU’s Seventh Framework Programme (FP/2007-2013) ERC Grant Agreement no. 307952.
T. Moran—Supported by ISF grant no. 1790/13.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
When theoretical cryptographers think about privacy and computation, the first thing that comes to mind is usually secure multiparty computation (MPC), in which multiple parties can compute an arbitrary function of their inputs without revealing anything but the function’s output. In the original definitions (and constructions) of MPC, the participants were connected by a full communication graph (a broadcast channel and/or point-to-point channels between every pair of parties). In real-world settings, however, the actual communication graph between parties is usually not complete, and parties may be able to communicate directly with only a subset of the other parties. Moreover, in some cases the graph itself is sensitive information (e.g., if you communicate directly only with your friends in a social network).
A natural question is whether we can successfully perform a joint computation over a partial communication graph while revealing no (or very little) information about the graph itself. In the information-theoretic setting, in which a variant of this question was studied by Hinkelman and Jakoby [10], the answer is mostly negative.
The situation is better in the computational setting. Moran, Orlov and Richelson showed that topology-hiding computation is possible against static, semi-honest adversaries [12]. However, their protocol is restricted to communication graphs with small diameter. Specifically, their protocol addresses networks with diameter \(d=O(\log n)\) logarithmic in the number of nodes n (where the diameter is the maximal distance between two nodes in the graph). For many natural network topologies the question remains open, including for wireless and ad-hoc sensor networks [4, 14], where topology is modeled by random geometric graphs [13] whose diameter is large with high probability [5], as well as for very simple topologies such as chains, cycles and trees (note that topology-hiding computation isn’t trivial even if the overall topology of the network is known; in a cycle, for example, the order of the nodes may still be sensitive).
1.1 Our Results
In this work we take a step towards topology-hiding computation protocols for arbitrary graphs by constructing protocols that can be used in a large class of large-diameter networks. As in [12], our protocols actually implement topology-hiding broadcast—given this primitive, standard MPC protocols can then be used for generic topology-hiding computation.
-
We construct a protocol for topology-hiding broadcast on directed cycles, given an upper bound on the number of nodes in the cycle. This protocol uses completely different techniques than those of [12], and in particular does not require generic MPC (it borrows ideas from mix networks). The security of this protocol can be based on standard assumptions, e.g., the Decisional Diffie-Hellman assumption.
-
We show that given (black-box) access to a protocol for topology-hiding broadcast on a cycle, we can construct a protocol for topology-hiding broadcast on arbitrary graphs if nodes are given an auxiliary information specifying their neighbors in a spanning tree of the graph (this information will be used to compute a cycle traversing all nodes of the graph). Our security guarantee in this case is that our protocol reveals nothing beyond what can be learned from the auxiliary information. For arbitrary graphs, we do not know how to compute the auxiliary information in a topology-hiding manner, so this protocol would require a trusted setup phase for those graphs. Any class of graphs for which we can construct a protocol to compute this auxiliary information locally will give us a topology-hiding broadcast for that class of graphs. In particular, for trees, the “auxiliary information” for computing a spanning tree is trivial and does not require trusted setup; thus, together with our cycle protocol this result gives us a protocol for topology-hiding broadcast on trees.
This construction makes only black-box use of the cycle protocol, and does not require additional assumptions.
-
We define information-local computation; loosely speaking this is a distributed computation in which the outputs of each party can depend only on information available in their “local neighborhood”. We prove that information-local computations can be performed in a topology-hiding way on arbitrary graphs given a topology-hiding computation protocol for small-diameter graphs.
-
We construct an information-local computation for computing consistent local views of a spanning tree in arbitrary small-circumference graphs (in which the length of the longest cycle is bounded by k). This gives a protocol for topology-hiding broadcast on small-circumference graphs. This protocol makes black-box use of both the small-diameter topology-hiding computation protocol and almost-black-box use of the topology-hiding broadcast on the cycle (we require the existence of an efficient circuit to compute the next-message function of the cycle protocol).
Assumptions. Our basic protocol for topology-hiding broadcast on a cycle can be based on the Decisional Diffie-Hellman (DDH) assumption. Our further reductions are black box, and do not require additional assumptions. Elaborating on the former, all we require for our basic protocol is the existence of an CPA-secure encryption scheme with some special properties (aka, hPKCR-enc); we show that such a scheme exists based on DDH. The properties we require from a hPKCR-enc are essentially that ciphertexts are rerandomizable (given the public-key), that it is key-commutative when given the secret-key (we name the latter property privately key-commutative), and that it is homomorphic w.r. to a single operation; see details in Sect. 3.
Voting vs. Broadcast. We also present protocols for topology-hiding voting (rather than broadcast) for all aforementioned graph topologies; for full security, these require the exact number of nodes for the cycle topology to be known (rather than an upper-bound). We note that for our voting protocols we do not require the homomorphism property of the underlying hPKCR-enc scheme. Recall that voting means that each player \(P_i\) has at the beginning of the protocol an input vote \(v_i\), and receives at the termination of the protocol a list of all votes in a randomly permuted order \((v_{\pi _i(1)},\ldots ,v_{\pi _i(n)})\) for \(\pi _i:[n]\rightarrow [n]\) a uniformly random permutation.
We summarize our results in the following theorems. For brevity we use the shorthand notation “TH-\({{\mathcal {F}}}\)” standing for “an efficient topology-hiding protocol realizing functionality \({{\mathcal {F}}}\) against a statically-corrupting semi-honest adversary”. Denote by \(\left| G \right| \) the number of nodes in a graph G.
Theorem 1
(Topology-hiding on cycle). Under DDH assumption, for every network of cycle topology C, there exist the following protocols:
-
Broadcast. A TH-\(\mathcal {F}_{\text {Broadcast}}\), provided parties are given an upper-bound on \(\left| C \right| \).
-
Voting. A TH-\(\mathcal {F}_{\text {Vote}}\), provided parties are given the exact size \(\left| C \right| \).
Theorem 2
(Reductions to other topologies). Suppose there exists TH-\({{\mathcal {F}}}\) for networks of cycle-topology C when given upper-bound on (resp. exact size of) \(\left| C \right| \). Then there exists TH-\({{\mathcal {F}}}\) for the following (connected, undirected) network graphs G, when given an upper-bound on (resp. exact size of) \(\left| G \right| \):
-
Every graph G, provided parties are given their neighbors in a (globally consistent) spanning tree of G.
-
Every tree G.
-
Every graph G with circumference at most k, provided there exists TH-\(\mathcal {F}_{\text {Broadcast}} \) for graphs of diameter at most k.
Combining the above theorems and employing a TH-\(\mathcal {F}_{\text {Broadcast}}\) protocol for low-diameter graphs [12] we conclude:
Corollary 1
Under the DDH assumption, there exists TH-\(\mathcal {F}_{\text {Broadcast}}\) (resp. TH-\(\mathcal {F}_{\text {Vote}}\)) for the following (connected, undirected) network graphs G, when given an upper-bound on (resp. exact size of) \(\left| G \right| \):
-
Every cycle G.
-
Every graph G, provided parties are given their neighbors in a (globally consistent) spanning tree of G.
-
Every tree G.
-
Every graph G with circumference at most \(O(\log \left| G \right| )\).
1.2 High-Level Overview of Our Techniques
In the following we first give an overview of the our approach and challenges, then an overview for our protocols for topology-hiding voting, and conclude by describing their modification yielding our protocols for topology-hiding broadcast.
Our Approach and Challenges. Recall that in a broadcast protocol a bit \(b\in \left\{ {0,1} \right\} \) is given as input to a single player called the broadcasting player, and the protocol terminates with all players receiving this bit b as output. Our starting point is the “OR-and-Forward” protocol, in which at the first round the broadcasting player forwards its bit b to all its neighbors, and at each following round the players OR their received bits and forward the resulting bit to their neighbors. Note that the bit b reaches all players once the number of rounds exceeds the network diameter.
This “OR-and-Forward” protocol is of course not topology-hiding. For one, distance to the broadcaster leaks from the round number t when a node i first receives a message. To prevent this leakage-by-timing attack, we change the protocol to have all players send messages at all rounds, where the change is simply by asking the non-broadcasting players to send the neutral bit 0 in the first round.
The latter protocol is still not topology-hiding, e.g., because distance to the broadcaster leaks from the round number t when a node i first receives a non-zero message. To prevent this leakage-by-content attack, we’d like to encrypt all transmitted messages, so that the players (nodes) cannot identify when their received messages are transformed from 0 to 1.
Encrypting the transmitted messages raises new challenges. First, when using such an encryption, who has the secret-key for decryption?! If every player has the secret key, then encryption hides nothing; and if not, then how do players decrypt to get the output? Second, how can we compute the OR of encrypted messages? To address these challenges we first restrict our attention to the cycle topology, and use key-homomorphic and message-homomorphic encryption (e.g., ElGamal). Our first protocol realizes a voting functionality rather than broadcast—its output is a shuffled list of all parties’ inputs. On the cycle topology, encryption/decryption can be computed jointly by all players via going around the cycle where every player adds/peels-of their own encryption layer (using the key-homomorphism property). This protocol requires us to know the exact length of the cycle in order to prevent leaking topology information. We then show how to use the homomorphic operation to OR ciphertexts together in a way that hides topology even if the exact cycle length is not known.
Topology-Hiding Voting on Directed Cycles. At the beginning of the voting protocol each player i has a secret input \(v_i\) (her vote). The protocol then proceeds in two phases, aggregation and mix-and-decrypt. Loosely speaking, in the aggregation phase votes are aggregated by passing around the cycle an array of encrypted votes, to which each party adds their own vote and then adds an extra layer of encryption before sending it on to the next party. At the end of this phase, each party has an array of all n votes, encrypted under the a public key whose secret key is shared between all parties. In the mix-and-decrypt phase, the parties successively remove the layer of encryption they are responsible for, mix the votes and rerandomize the remaining layers of encryption before passing the array back to the previous party. Upon the termination of this phase, each player i has a list of all votes in a randomly permuted order \((v_{\pi _i(1)},\ldots ,v_{\pi _i(n)})\) (for \(\pi _i:[n]\rightarrow [n]\) a uniformly random permutation). For details, see Sect. 4.
From Voting to Broadcast. Relaxing the input to consist of an upper bound \(n'\) on the number of nodes n in the cycle (rather than the exact number) is the main challenge in devising our topology-hiding broadcast protocol. Subsequently, our reductions from the cycle topology to other topologies go through as is.
Our first attempt was to execute our voting protocol as is, while using \(n'\) instead of n; but this fails to be topology-hiding. In particular, topology information leaks from the output now consisting of multiple votes from some parties.Footnote 1 We remark that correctness is also undermined by receiving multiple votes from some players; this could be fixed (say, by augmenting the vote with an anonymous identifier and post-processing to remove multiple votes), yet, this fix is of course not topology-hiding.
Our topology-hiding broadcast is a modification of the above approach where we combine the list of votes into a single bit—the OR of all input bits, thus avoiding the aforementioned votes counting attack. Specifically, the aggregation phase in our topology-hiding broadcast combines each additional vote to a single ciphertext being passed around, where this ciphertext either holds the neutral message or a random group element (interpreted as a broadcast of 0 or 1 respectively). To combine the votes we require the underlying hPKCR-enc to be homomorphic with respect to a single operation. The “mix-and-decrypt” phase is a degenerate version of the mix-and-decrypt phase in our topology-hiding voting protocol, where the players peel off decryption layers and re-randomize, but with no need for mixing ciphertexts (as now only a single ciphertext is being passed around).
The additional wrinkle here is that, when we know only an upper bound \(n'\) on the number of nodes, using a simple homomorphic multiplication (or addition) to OR bits together is not topology hiding. To see this, suppose the broadcaster chooses the value m as the non-neutral element representing a 1 bit. Every time the encrypted bit passes around the cycle it is multiplied by m, so the output will be \(m^c\), where c is the number of passes through the broadcasting party. Thus, the output leaks a tighter estimate for n, as well as information on the distance from the broadcasting party (for example, parties i, j receiving outputs \(m^2\), m, respectively, can conclude that i appears first on the path from the broadcasting party).
To prevent this leakage-by-output attack, we require that all parties randomize their message m before passing it forward (and then re-randomize also the ciphertext). Our message randomization is by raising m to a random power r (using homomorphic multiplication, and exponentiation-by-squaring algorithm for efficiency), this in turn maps the identity to itself while mapping other elements m to uniformly random group elements \(m^r\) (choosing the message space to be a prime order group).
For space considerations, a detailed description and analysis of our broadcast protocol is deferred to the full version of the paper.
From Cycles to Graphs Given Spanning-Tree Neighbors and Tree. The main idea for this reduction is that given a tree, we can compute a cycle-traversal of the graph by having each node independently decide on a local ordering of edges. Each node will appear exactly d times in the cycle (where d is the degree of the node). The predecessor of the \(i^{th}\) instance of the node in the cycle is the neighbor adjacent to its \(i^{th}\) edge; the successor is the neighbor adjacent to the next edge. In Sect. 5.2, we prove that for any numbering of edges, this always generates a cycle-traversal of the graph, and that this traversal can be used to execute any protocol for topology-hiding computation on directed cycles.
Topology-Hiding Computation for Information-Local Functions. The intuition behind this reduction is simple: if a node’s output depends only on information from a node’s k-neighborhood, then we can use a topology-hiding computation protocol for small-diameter graphs to compute it by limiting the protocol to the node’s k-neighborhood. The reason this isn’t quite that straightforward is that we want to hide the topology of the k-neighborhoods. This means the node participating in the protocol shouldn’t be able to tell who else is participating with it in the protocol. In particular, this means we can’t assign a global session id to distinguish between multiple concurrent instances of the protocol (we need to run multiple instances since each node will need to compute the function given its own local neighborhood).
Our main innovation here is the use of relative session ids, where the session id depends on the node’s relative location in its neighborhood, and each node applies a transformation on the session ids sent and received so that they remain in the correct relative framework. In Sect. 7 we describe our protocol in detail and prove that we can use it to compute an arbitrary information-local function in parallel in all k-neighborhoods.
From Graphs Given Spanning-Tree Neighbors to Small-Circumference Graphs. For this reduction, we combine several of our previous results. There are two main ideas here. First, we prove that for graphs whose circumference is bounded by k, we can compute local views of a spanning tree using a k-information-local function (this is not trivial, since local views must be globally consistent with a single spanning tree). Together with our result on topology-hiding computation given a spanning tree, and our result on computation of information-local functions, this already gives a protocol for topology-hiding computation on small-circumference graphs. This naïve way of running the protocol reveals the local view of the spanning tree to each node, which can give information about the graph topology. However, we show it is possible to compose the protocols into a single computation that does not reveal the spanning-tree information (at the cost of higher complexity). Due to space considerations, the details of this reduction are deferred to the full version of the paper.
1.3 Related Work
Topology-Hiding MPC in Computational Settings. The most relevant related work is that of Moran, Orlov and Richelson [12], who gave the first feasibility results for topology-hiding computation in the computational setting, giving a protocol for topology-hiding broadcast secure against static, semi-honest adversaries, as well as a protocol secure against fail-stop adversaries that do not disconnect the graph. However, their protocol is restricted to communication graphs with diameter logarithmic in the total number of parties.
The main idea behind their protocol is a series of nested multiparty computations, in which each node is replaced with a secure computation in its local neighborhood that simulates that node. In contrast, our cycle protocol uses ideas from the cryptographic voting literature—it hides the order of the nodes in the cycle by “mixing” encrypted inputs before decrypting them.
Other related works include a concurrent work by Hirt et al. [11] that achieves better efficiency than [12] for topology-hiding computation, albeit still restricted to low diameter networks as in [12]. The work by Chandran et al. [3] addresses the question of hiding the communication network in the context of secure multi-party computation, but with a different goal than topology-hiding: their goal is to reduce communication complexity by allowing each party to communicate with a small (sublinear in the total number of parties) number of its neighbors.
Topology-Hiding MPC in Information Theoretic Settings. Hinkelmann and Jakoby [10] considered the question of topology-hiding secure computation while focusing on the information theoretic setting. Their main result is negative: any MPC protocol in the information-theoretic setting must inherently leak information about G to an adversary. They do, however, prove a nice positive result: if we are allowed to leak a routing table of the network, one can construct an MPC protocol which leaks no further information.
Secure Multiparty Computation with General Interaction Patterns. Halevi et al. [8] presented a unified framework for studying secure MPC with arbitrarily restricted interaction patterns (generalizing models for MPC with specific restricted interaction patterns [1, 7, 9]). The questions they study, however, are independent of our topology-hiding focus. Their starting point is the observation that an adversary controlling the final players \(P_i,\ldots ,P_n\) in the interaction pattern can learn the output of the computed function on several inputs (as the adversary can rewind and execute the protocol over any possible values for the inputs \(x_i,\ldots ,x_n\) for the corrupted players while fixing the inputs \(x_1,\ldots ,x_{i-1}\) for the preceding parties). The question they ask is therefore when is it possible to prevent the adversary from learning the output of the function on multiple inputs. In contrast to ours, their model allows complete knowledge on the underlying interaction patterns, and does not hide the topology.
2 Preliminaries
2.1 Computation and Adversarial Models
We model a network by a directed graph \(G=(V,E)\) that is not fully connected. We consider a system with \(n=\text {poly}(\kappa )\) parties (where \(\kappa \) is the security parameter), denoted \(P_1,\dots ,P_n\). We often implicitly identify V with the set of parties \(\{P_1,\dots ,P_n\}\). We consider a static and computationally bounded (PPT) adversary that controls some subset of parties (any number of parties). That is, at the beginning of the protocol, the adversary corrupts a subset of the parties and may instruct them to deviate from the protocol according to the corruption model. Throughout this work, we consider only semi-honest adversaries. In addition, we assume that the adversary is rushing; that is, in each round the adversary sees the messages sent by the honest parties before sending the messages of the corrupted parties for this round. For general MPC definitions including in-depth descriptions of the adversarial models we consider see [6].
2.2 Definitions of Graph Terms
Let \(G=(V,E)\) be an undirected graph. For \(v\in V\) we let \(N(v)=\{w\in V:(v,w)\in E\}\) denote the neighborhood of v; and similarly, the closed neighborhood of v, \(N^{}[{v}] =N(v)\cup \{v\}\). We sometimes refer to \(N^{}[{v}] \) as the closed 1-neighborhood of v, and for \(k\ge 1\) we define the k-neighborhood of v as the set of all nodes within distance k of v. Formally, we can define this recursively:
The k-neighborhood graph of v in G is the subgraph \(G^{({k})}[{v}] \) of G on the k-neighborhood of v, defined by
2.3 UC Security
As in [12], we prove security in the UC model [2]. Proving security in the UC model allows our protocols to be composed with other protocols, and makes it easier to use as a subprotocol in more complex constructions. For details about the UC framework, we refer the reader to [2]. We note that although the UC model requires setup for security against general adversaries, this is not necessary for security against semi-honest adversaries, so we also get a protocol that is secure in the plain model.
2.4 Topology Hiding—The Simulation-Based Definition
To help make the paper more self-contained, in this section we reproduce the simulation-based definition for topology hiding computation from [12].
The UC model usually assumes all parties can communicate directly with all other parties. To model the restricted communication setting, [12] define the \({{\mathcal {F}}}_{\text {graph}}\)-hybrid model, which employs a special “graph party,” \(P_{\text {graph}}\). Figure 1 shows \({{\mathcal {F}}}_{\text {graph}}\)’s functionality: at the start of the functionality, \({{\mathcal {F}}}_{\text {graph}}\) receives the network graph from \(P_{\text {graph}}\), and then outputs, to each party, that party’s neighbors. Then, \({{\mathcal {F}}}_{\text {graph}}\) acts as an “ideal channel” for parties to communicate with their neighbors, restricting communications to those allowed by the graph.
Since the graph structure is an input to one of the parties in the computation, the standard security guarantees of the UC model ensure that the graph structure remains hidden (since the only information revealed about parties’ inputs is what can be computed from the output). Note that the \(P_{\text {graph}}\) party serves only to specify the communication graph, and does not otherwise participate in the protocol.
Since \({{\mathcal {F}}}_{\text {graph}}\) provides local information about the graph to all corrupted parties, any ideal-world adversary must have access to this information as well (regardless of the functionality we are attempting to implement). To capture this, we define the functionality \({{\mathcal {F}}}_{\text {graphInfo}}\), that is identical to \({{\mathcal {F}}}_{\text {graph}}\) but contains only the initialization phase. For any functionality \({{\mathcal {F}}}\), we define a “composed” functionality \(({{\mathcal {F}}}_{\text {graphInfo}}|| {{\mathcal {F}}})\) that adds the initialization phase of \({{\mathcal {F}}}_{\text {graph}}\) to \({{\mathcal {F}}}\). We can now define topology-hiding MPC in the UC framework:
Definition 1
We say that a protocol \(\varPi \) securely realizes a functionality \({{\mathcal {F}}}\) hiding topology if it UC-realizes \(({{\mathcal {F}}}_{\text {graphInfo}}|| {{\mathcal {F}}})\) in the \({{\mathcal {F}}}_{\text {graph}}\)-hybrid model.
Note that this definition can also capture protocols that realize functionalities depending on the graph (e.g., find a shortest path between two nodes with the same input, or count the number of triangles in the graph).
3 Privately Key-Commutative and Rerandomizable Encryption
We require a public key encryption scheme with the properties of being homomorphic (w.r. to a single operation), privately key-commutative, and re-randomizable. In this section we first formally define the properties we require, and then show how they can be achieved based on the Decisional Diffie-Hellman assumption.
We call an encryption scheme satisfying the latter two properties, i.e., privately key-commutative and re-randomizable, a hPKCR-enc; and call an encryption scheme satisfying all three properties, i.e., homomorphic, privately key-commutative and re-randomizable, a hPKCR-enc.
3.1 Required Properties
Let \(\textsf {KeyGen}:\left\{ {0,1} \right\} ^*\mapsto \mathcal {PK}\times \mathcal {SK}, \textsf {Enc}:\mathcal {PK}\times {{\mathcal {M}}}\times \left\{ {0,1} \right\} ^*\mapsto \mathcal {C}, \textsf {Dec}:\mathcal {SK}\times \mathcal {C}\mapsto {{\mathcal {M}}}\) be the encryption scheme’s key generation, encryption and decryption functions, respectively, where \(\mathcal {PK}\) is the space of public keys, \(\mathcal {SK}\) the space of secret keys, \({{\mathcal {M}}}\) the space of plaintext messages and \(\mathcal {C}\) the space of ciphertexts.
We will use the shorthand \(\left[ {m} \right] _{k}\) to denote an encryption of the message m under public-key k. We assume that for every secret key \(sk\in \mathcal {SK}\) there is associated a single public key \(pk\in \mathcal {PK}\) such that (pk, sk) are in the range of \(\textsf {KeyGen} \). We slightly abuse notation and denote the public key corresponding to sk by pk(sk).
Rerandomizable. We require that there exists a ciphertexts “re-randomizing” algorithm \(\textsf {Rand}:\mathcal {C}\times \mathcal {PK}\times \left\{ {0,1} \right\} ^*\mapsto \mathcal {C}\) satisfying the following:
-
1.
Randomization: For every message \(m\in {{\mathcal {M}}}\), every public key \(pk\in \mathcal {PK}\) and ciphertext \(c=\left[ {m} \right] _{pk}\), the distributions \((m,pk,c,\textsf {Rand}\left( {c,pk,U^*}\right) )\) and \((m,pk,c,\textsf {Enc} _{pk}(m;U^*))\) are computationally indistinguishable.
-
2.
Neutrality: For every ciphertext \(c\in \mathcal {C}\), every secret key \(sk\in \mathcal {SK}\) and every \(r\in \left\{ {0,1} \right\} ^*\),
$$\begin{aligned} \textsf {Dec} _{sk}(c)=\textsf {Dec} _{sk}(\textsf {Rand}\left( {c,pk(sk),r}\right) ). \end{aligned}$$
Furthermore, we require that public-keys are “re-randomizable” in the sense that the product \(k\circledast k'\) of an arbitrary public key k with a public-key \(k'\) generated using KeyGen is computationally indistinguishable from a fresh public-key generated by KeyGen.
Privately Key-Commutative. The set of public keys \(\mathcal {PK}\) form an abelian (commutative) group. We denote the group operation \(\circledast \). Given any \(k_1,k_2\in \mathcal {PK}\), there exists an efficient algorithm to compute \(k_1\circledast k_2\). We denote the inverse of k by \(k^{-1}\) (i.e., \(k^{-1}\circledast k\) is the identity element of the group). Given a secret key sk, there must be an efficient algorithm to compute the inverse of its public key \((pk(sk))^{-1}\).
There exist a pair of algorithms \(\textsf {AddLayer}:\mathcal {C}\times \mathcal {SK}\mapsto \mathcal {C}\) and \(\textsf {DelLayer}:\mathcal {C}\times \mathcal {SK}\mapsto \mathcal {C}\) that satisfy:
-
1.
For every public key \(k\in \mathcal {PK}\), every message \(m\in {{\mathcal {M}}}\) and every ciphertext \(c=\left[ {m} \right] _{k}\),
$$\begin{aligned} \textsf {AddLayer}\left( {c,sk}\right) = \left[ {m} \right] _{k\circledast pk(sk)}. \end{aligned}$$ -
2.
For every public key \(k\in \mathcal {PK}\), every message \(m\in {{\mathcal {M}}}\) and every ciphertext \(c=\left[ {m} \right] _{k}\),
$$\begin{aligned} \textsf {DelLayer}\left( {c,sk}\right) = \left[ {m} \right] _{k\circledast (pk(sk))^{-1}}. \end{aligned}$$
We call this privately key-commutative since adding and deleting layers both require knowledge of the secret key.
Note that since the group \(\mathcal {PK}\) is commutative, adding and deleting layers can be done in any order.
Homomorphism. We require the message space \({{\mathcal {M}}}\) forms a group with operation denoted \(\cdot \), and require that the encryption scheme is homomorphic with respect this operation \(\cdot \) in the sense that there exist an efficient algorithm \(\textsf {hMult}:\mathcal {C}\times \mathcal {C}\mapsto \mathcal {C}\) that, given two ciphertexts \(c = \left[ {m} \right] _{pk}\) and \(c' = \left[ {m'} \right] _{pk}\), returns a ciphertext \(c'' \leftarrow \textsf {hMult}{c_1, c_2}\) s.t. \(\textsf {Dec} _{sk}(c'') = m \cdot m'\) (for sk the secret-key associated with public-key pk).
3.2 Instantiation of PKCR-enc and hPKCR-enc Under DDH
We use standard ElGamal, augmented by the additional required functions. The \(\textsf {KeyGen} \), \(\textsf {Dec} \) and \(\textsf {Enc} \) functions are the standard ElGamal functions, except that to obtain a one-to-one mapping between public keys and secret keys, we fix the group G and the generator g, and different public keys vary only in the element \(h=g^x\). Below, g is always the group generator. The \(\textsf {Rand}\) function is also the standard rerandomization function for ElGamal:

We use the shorthand notation of writing \(\textsf {Rand}\left( {c,pk}\right) \) when the random coins r are chosen independently at random during the execution of Rand. We note that the distribution of public-keys outputted by KeyGen is uniform, and thus the requirement for “public-key rerandomization” indeed holds. ElGamal public keys are already defined over an abelian group, and the operation is efficient. For adding and removing layers, we define:

Every ciphertext \(\left[ {m} \right] _{pk}\) has the form \((g^r, pk^r\cdot m)\) for some element \(r\in \mathbb {Z} _{ord(g)}\). So
It is easy to verify that the corresponding requirement is satisfied for DelLayer as well.
ElGamal message space already defined over an abelian group with homomorphic multiplication, specifically:

Recalling that the input ciphertext have the form \(c =(g^r,pk^r \cdot m)\) and \(c' = (g^{r'},pk^{r'} \cdot m')\) for messages \(m,m'\in \mathbb {Z} _{ord(g)}\), it is easy to verify that decrypting the ciphertext \(c'' = (g^{r+r'}, pk^{r+r'} \cdot m \cdot m')\) returned from hMult yields the product message \(\textsf {Dec} _{sk}(c'') = m\cdot m'\).
Finally, to obtain a negligible error probability in our broadcast protocols, we take G a prime order group of size satisfying that \(1/\left| G \right| \) is negligible in the security parameter \(\kappa \).
4 Topology-Hiding Voting for Cycle Topology
In this section we present our topology-hiding voting protocol for the cycle topology. That is, we consider networks where the n players are numbered by indices \(1,\ldots ,n\), and communication is only between players with consecutive indices, i.e., player i can communicate with players \(i+1\) and \(i-1\) (where addition is modulo n). We remind the reader that cycles have a large diameter (diameter n/2), and are therefore not handled by prior works on topology hiding protocols.
4.1 Topology Hiding Voting for Cycle Topology from PKCR-Enc
The Protocol. Recall that each player i has a secret input \(v_i\) (her vote). To simplify notation, we omit the modulus when specifying the party (i.e., we let \(P_{n+1}=P_1\) and \(P_0=P_n\)). The protocol is composed of two main phases:
-
In the first phase the votes are aggregated in encrypted form. This phase consists of n rounds. At the first round each player i encrypts its vote \(v_i\) and sends it to player \(i+1\) together with the public-key \(pk_i^{(1)}\). At every following round t, upon receiving from player \(i-1\) a list L of encrypted votes together their encryption key k, player i does the following. (a) Encrypt its vote \(v_i\) under key k, and add the resulting ciphertext to the list L, (b) Add an encryption layer to every vote in the list using its keys \((pk_i^{(t)},sk_i^{(t)})\), (c) Compute the new key \(k'=k\circledast pk_i^{(t)}\), and (d) Sends the updated list \(L'\) and key \(k'\) to \(i+1\). We note that player i uses fresh keys \((pk_i^{(t)},sk_i^{(t)})\) at each round t, this is necessary for security.
-
In the second phase the players each remove an encryption layer to reveal the votes in plaintext, while also shuffling the votes and re-randomizing their ciphertexts so that the votes in the resulting lists are not traceable to the voters.
See Protocol 1 for details.
A Note Regarding Notation. We use the superscript (i : t) to denote variables set by party i in iteration t; e.g., the notation \(k^{(i:t)}\) denotes the key party i receives from party \(i-1\) in iteration t of the Aggregate phase. When the identity of the party is clear, we will sometimes use the shorter versions \(k^{(t)}\). For clarity we also omit the modular arithmetic for party indices, identifying party 0 with party n and party \(n+1\) with party 1.

4.2 Correctness and Topology-Hiding
We formally prove the following theorems about Protocol 1.
Theorem 3
(Completeness). Protocol 1 is complete.
Theorem 4
(Topology-Hiding). If the underlying encryption PKCR scheme is CPA-secure then Protocol 1 realizes the functionality \(\mathcal {F}_{\text {Vote}}\) in a topology-hiding way against a statically-corrupting, semi-honest adversary.
The proofs of these theorems appear in Sect. 6.
5 Dealing with General (Connected, Undirected) Graphs
In this section we show that topology-hiding computation on a cycle is a useful stepping stone to other large-diameter graphs. Given a protocol for computing a (symmetric) functionality \(\mathcal {F}_{f} \) on a cycle, we show how to construct a topology-hiding protocol for computing the functionality on arbitrary graphs, as long as every node is also given some auxiliary data: a local view of a cycle-traversal of the graph (the computed function is a “multiple-input” version of the original, see below for details).
A corollary is that we can construct a topology-hiding voting and broadcast protocols for every network topology for which the aforementioned auxiliary information can be efficiently found in a topology-hiding way. Chains, trees and small-circumference graphs are a special case of the latter.
We remark that in our results using auxiliary information, this information may be given to the players once-and-for-all during setup (as it depends only of the network topology and not on the input to the voting protocol). Clearly, the auxiliary information reveals properties of the graphs; in this case, the topology-hiding property of our protocols ensures that no additional information is revealed.
Multiple-Input Extension. Our reductions to \(\mathcal {F}_{f} \) on a cycle realize a slightly different functionality—we realize a “multiple-input” version of \(\mathcal {F}_{f} \) which we denote \(\mathcal {F}_{f^*} \). Loosely speaking, the “multiple-input” extension of a function allows each party to give several inputs to the function, with the number of inputs depending on the number of times the party appears in the cycle traversal. Formally, let \(\left\{ {f_n} \right\} \) be a class of symmetric functions on n inputs (i.e., in which the order of inputs does not matter). For every n and \(g:[n]\mapsto \mathbb {N} \), we define \(f^*_{g,n}\) to be \(f_{\sum _{i=1}^n g(n)}\) where the \(i^{th}\) input to \(f^*_{g,n}\) is a vector of g(i) inputs to \(f_{\sum _{i=1}^n g(n)}\). In our case, g will always map each party to the number of times the party appears in the cycle traversal; we will omit g and n for brevity and write \(\mathcal {F}_{f^*} \) as the functionality we are computing.
5.1 Dealing with General Graphs, Given Local Views of a Cycle-Traversal
In this section we first observe that for every (connected, undirected) graph G there exists a cycle traversing all its nodes;Footnote 2 we call such a cycle a cycle-traversal of G, denoted \(C_G\). We then show that if all nodes of G are given their local view of the cycle as auxiliary information, then they can execute a topology-hiding protocol to compute \(\mathcal {F}_{f^*} \) on G simply by executing a topology-hiding protocol for \(\mathcal {F}_{f} \) on its cycle-traversal, \(C_G\).
A cycle-traversal is sure to exist as it can be explicitly found, e.g., by running Depth-First-Search (DFS) to find a DFS-tree spanning all nodes of the graph, and then converting this tree to a cycle-traversal using Protocol 4.
The local view of the cycle traversal \(C_G\) is specified for each node i by its successor function \(\textsf {Succ}_i:N(i)\mapsto N(i)\cup \left\{ {\bot } \right\} \). Note that each node may appear more than once on the cycle, so the successor function is defined \(\textsf {Succ}_i(v) = u\) if-and-only-if \((v\rightarrow i \rightarrow u)\) is part of the cycle \(C_G\) (if the edge (v, i) is not on \(C_G\), then \(\textsf {Succ}_i(v) = \bot \)).
Theorem 5
(Cycle-traversal known, realizing \(\mathcal {F}_{f^*} \) ). Suppose there exists a topology-hiding protocol \(\varPi \) that realizes the functionality \(\mathcal {F}_{f} \) on directed cycles. Then there exists a topology-hiding protocol \(\varPi '\) realizing the functionality \(\mathcal {F}_{f^*} \) on any (connected, undirected) graph G, when given as auxiliary input local views of a cycle-traversal \(C_G\) of G.
We remark that for protocols \(\varPi \) requiring auxiliary information aux (e.g., the cycle length m) Theorem 5 still holds, provided that aux is included in \(\varPi '\)’s auxiliary information. The only change in the proof is that the protocol \(\varPi '\) provides aux to \(\varPi \) when calling it.
Proof
(sketch for Theorem 5 ). Our protocol \(\varPi '\) for G (c.f. Prototcol 2) simply runs \(\varPi \) on the cycle \(C_G\), where each node \(i\in V\) plays the role of all its \(w_i\) occurrences on the cycle (in parallel). Recall that in the functionality \(\mathcal {F}_{f^*} \), the input to player \(P_i\) is a vector \((v_{i,1},\cdots ,v_{i,w_i})\). Player \(P_i\) executes as \(w_i\) independent players in \(\varPi \), with each occurrence \(\ell \) using input \(v_{i,\ell }\), and where sending forward (backward) messages received from \(j \in N(i)\) is executed by sending them to the corresponding successor (predecessor) on the cycle \(C_{G}\).

We note that the when \(\mathcal {F}_{f} =\mathcal {F}_{\text {Vote}} \) is the voting functionality, the above protocol realizes the weighted-vote functionality \(\mathcal {F}_{f^*} =\mathcal {F}_{\text {WVote}} \) that accepts as input a list of \(w_i\) votes from each party i (where \(w_i\) the number of times party i appears on \(C_G\)), and outputs a list of all \(m=\sum _{i=1}^n w_i\) votes in a randomly permuted order. Nevertheless, in the semi-honest setting, the standard voting functionality \(\mathcal {F}_{\text {Vote}}\) can be easily reduced to \(\mathcal {F}_{\text {WVote}}\) by letting each party submit only one “real” vote and use a \(\bot \) value for the additional votes. For the broadcast functionality, the multiple-input version gives the same output as the original (without modification).
Due to space considerations, the details and formal analysis are deferred to the full version of the paper. \(\square \)
5.2 Dealing with General Graphs, Given Local Views of a Spanning-Tree
In this section we show that if there exists a topology-hiding protocol for \(\mathcal {F}_{f} \) on a cycle, and for some spanning-tree \(T=(V,F\subseteq E)\) of a graph \(G=(V,E)\), all nodes are given as auxiliary information their neighbors in T, then there exists a topology-hiding protocol realizing the functionality \(\mathcal {F}_{f^*}\) on G. The main idea is that given a spanning tree, nodes can locally compute (their local views of) a cycle-traversal of G. Thus, we can reduce this problem to the previously solved one of topology-hiding computation given a cycle-traversal of G.
Let \(G=(V,E)\) be a connected undirected graph describing the network topology.
Theorem 6
(Spanning-tree known, realizing \(\mathcal {F}_{f^*} \) ). If there exists a protocol \(\varPi \) that realizes \(\mathcal {F}_{f} \) in a topology-hiding way, given as input a local view of a cycle-traversal of G and \(m=|C_G|\) (the cycle length), then, using \(\varPi \) as a black box, Protocol 3 realizes \(\mathcal {F}_{f^*} \) when given as inputs a local view of a spanning tree T of G and n (the number of nodes in G).
Proof
Our proof follows from the existence of a local translation from local views of a spanning-tree T to local views of a cycle-traversal \(C_G\). Protocol 3 simply executes this translation and then runs \(\varPi \) using the auxiliary information about the cycle-traversal.
The auxiliary input conversion is local in the sense that each node executes the computation while using only its own auxiliary information. Specifically, the conversion executed by node i takes as input its neighbors \(N_T(i)\) in the spanning T, and returns as output its successor function \(\textsf {Succ}_i\) on the cycle \(C_G\) of G. In our execution of Protocol 2 we use the cycle length m and the successor functions \(\textsf {Succ}_i\) as the auxiliary information of node i.

Completeness. In Lemma 1 we show that our conversion procedure is correct; i.e., there exists a length m cycle-traversal of G such that the output for each node i is indeed its successor function on this cycle. Thus, by completeness of Protocol 2 the output of each node is indeed the output of the \(\mathcal {F}_{f^*} \) functionality.
Security follows immediately from the security of Protocol 1. \(\square \)
Lemma 1
(Tree to cycle). There exists a length m cycle-traversal \(C_G\) of G such that for every node \(i\in V\), its output \(\textsf {Succ}_i\) in the conversion procedure (c.f. line 5 in Protocol 3) equals its successor function on this cycle \(C_G\).
Proof
We show that the functions \(\textsf {Succ}_i\) returned by the conversion procedure are the successor functions for a length m cycle-traversal of G. For this purpose, we exhibit an algorithm that, given a spanning-tree T, outputs a length cycle-traversal \(C_T\) of T (c.f. Protocol 4 and Claims 1 and 2). Next we prove that \(\textsf {Succ}_i\) are successor functions for the graph \(C_T\) returned by Protocol 4 (c.f. Claim 3).
Specifically, Protocol 4 first initializes \(C_T\) to consist of a single node \(C_T = \langle x \rangle \) (for an arbitrary \(x\in V\)). Next, while there exists a node u in \(C_T\) with a neighbor \(v\in N(u)\) not included in \(C_T\), the algorithm pastes to \(C_T\) in place of u a cycle \(C_v\) defined as follows. The cycle \(C_v = \langle w_1,v,w_2,v,\ldots ,v,w_d,v,w_1 \rangle \) is a cycle traversing all neighbors \(N_T(v)=\left\{ {w_1,\ldots ,w_d} \right\} \) of v (where neighbors order on the cycle is ascending, and the starting point is chosen to be \(w_1=u\)). That is, for \((v_1,v_2,\ldots ,v_d)\) the neighbors of v in ascending order where \(u=v_j\) we define \((w_1,w_2,\ldots ,w_d) = (v_j,v_{j+1},\ldots ,v_d,v_1,\ldots ,v_{j-1})\). We remark that the requirement of traversing neighbors of v is ascending order is not essential; we use it merely to facilitate notations in demonstrating the correspondence between the cycle \(C_T\) returned from Protocol 4 and the successor function \(\textsf {Succ}_i\) returned from line 5 Protocol 3 (c.f. Claim 3).

\(\square \)
Claim 1
The output \(C_T\) of Protocol 4 is a cycle-traversal of G.
Proof
Observe that \(C_T\) visits all nodes of T, and thus all nodes of G. Else, if there is an unvisited node y, then there is a path from x to y (since T is connected), and on this path there must be a node u with neighbor \(v\notin C_T\). A contradiction to the termination of the while loop.
Next, observe that \(C_T\) is a cycle. This is proved by induction. The base case \(\langle x \rangle \) is a cycle of length zero. The induction hypothesis say that the content of \(C_T\) throughout the first t iterations of the while loop is a cycle. The induction step shows that \(C_T\) remains a cycle after pasting \(C_v = \langle u,v,w_2,v,\ldots ,v,w_d,v,u \rangle \). For this purpose note that \(C_v\) is a cycle starting at node u, and thus when it is pasted in place of u in \(C_T = \langle \ldots a,u,b \ldots \rangle \) (which is a cycle, by induction hypothesis) the resulting \(C_T' = \langle \ldots a,u,v,w_2,v,\ldots ,v,w_d,v,u,b \ldots \rangle \) remains a cycle.
We conclude that \(C_T\) of is a cycle-traversal of G. \(\square \)
Claim 2
The output \(C_T\) of Protocol 4 has length \(m=2(n-1)\).
Proof
To show that \(C_T\) has length \(m=2(n-1)\) we recall that there are \(n-1\) edges in a spanning-tree for a graph with \(n=\left| V \right| \) nodes, and argue that the cycle \(C_T\) goes through each edge of the spanning-tree exactly twice. Thus resulting in a total of \(2(n-1)\) edges on the cycle.
To complete the above argument we first prove by induction that throughout the first t iterations of the while loop, the number of times \(C_T\) goes through every edge of T is either 0 or 2. Base case (\(t=0)\): At the initialization, \(C_T = \langle x \rangle \) passes through every edges exactly 0 times. Induction step: Note that the cycle to be pasted \(C_v\) goes over each edge connecting v to its neighbor exactly twice. Moreover, these edges (v, w) were not included in \(C_T\) prior to pasting \(C_v\) by the choice of v as a node not appearing in \(C_T\). Next, we note that to traverse all notes of the tree, \(C_T\) must go through each edge at least once. We conclude therefore that \(C_T\) goes through each edge exactly twice. \(\square \)
Claim 3
The output \(\textsf {Succ}_i\) in the conversion procedure (c.f. line 5 in Protocol 3) is the successor function for the cycle \(C_T\) output by Protocol 4.
Proof
Recall first that the output \(\textsf {Succ}_i\) returned from the conversion procedure (c.f. Line 5 in Protocol 3) is defined to be
for \((v_1,\ldots ,v_d)\) an ascending ordering of the neighbors N(i) of i (and where we identify \(v_{d+1}\mathop {=}\limits ^{\cdot }v_1\)). Namely, this successor function corresponds to the cycle \(C_i = (v_1,i,v_2,i,\ldots ,i,v_d)\) where the nodes \(v_1,\ldots ,v_d\) are in ascending order.
Recall also that in the cycle \(C_T\) returned from Protocol 4 the edges passing through node i were added by pasting a cycle \(C_i' = (u,i,w_2,i,\ldots ,i,w_d)\) passing through the neighbors \(u,w_1,\ldots ,w_d\) of i in ascending order shifted to start with neighbor u. Since this is a cycle, we may view each point as the starting point. Choosing to view the smallest neighbor as the starting point we see that \(C_i'\) is the same as the cycle \(C_i\).
We conclude that the function \(\textsf {Succ}_i\) is identical to the successor function for the cycle \(C_T\) outputted by Protocol 4. \(\square \)
5.3 Dealing with Trees
A simple corollary of Theorem 6 is that if G is a tree T (i.e., connected and acyclic), then there exists a topology-hiding protocol realizing the voting functionality \(\mathcal {F}_{f^*} \) on G. The proof is derived from the fact that when G is a tree, the players can trivially find their neighbors in its spanning tree, without needing to get it as an auxiliary input:
Corollary 2
(Trees). Suppose there exists a topology-hiding protocol realizing the functionality \(\mathcal {F}_{f} \) on directed cycles, when given (a bound on) the cycle length. Then there exists a topology-hiding protocol realizing the functionality \(\mathcal {F}_{f^*} \) on every tree T, when given (a bound on) the number of nodes in T.
6 Topology-Hiding Voting for Cycle Topology—Formal Proofs
In this section we give the formal proofs of correctness and security for Protocol 1.
6.1 Correctness Analysis
Denote \(k^{(0)}\mathop {=}\limits ^{\cdot }1\), the identity element of the group. Then:
Claim 4
For every party i and all \(t\in \left\{ {0,\cdots ,n-1} \right\} \):
Proof
Let i be an arbitrary party index. The proof is by induction on t. For \(t=0\) it is trivially true. Assume it is true for all i up to some \(t\in \left\{ {0,\cdots ,n-2} \right\} \), then in iteration t of the Aggregate loop, party \(i-1\) will have \(k^{(i-1:t)}=\prod _{j=1}^t pk^{({i-1-j}:{j})} \), and will send \(k^{(i-1:t)}\circledast pk^{({i-1}:{t+1})} =\prod _{j=1}^{t+1} pk^{({i-j}:{j})} \) to party i in line 7. Thus, for party i, \(k^{(i:t+1)}\) will also have the required form. \(\square \)
Claim 5
For every party i and all \(t\in \left\{ {1,\cdots ,n-1} \right\} \):
Proof
Let i be an arbitrary party index. The proof is also by induction on t. For \(t=1\), \(c^{(i:1)}=\left[ {v_{i-1}} \right] _{pk^{({i-1}:{1})}}\) (as sent by party \(i-1\) in line 4). Assume the hypothesis is true for all i up to iteration t. The values party i receives at lines 6 and 9 in iteration \(t+1\) of the Aggregate phase are those sent by party \(i-1\) in line 7 of iteration t:
confirming the hypothesis for iteration \(t+1\).
\(\square \)
Claim 6
For every party i and all \(t\in \left\{ {1,\cdots ,n-1} \right\} \):
where \(\sigma ^{({i}:{t})} =\pi ^{({i}:{t})} \circ \cdots \circ \pi ^{({i+n-t-1}:{n-1})} \).
Proof
We note that it’s enough to show the claim holds for the h values, since the corresponding d values are computed from them by peeling off the outer key layer (by calling DelLayer with the key \(sk^{({i}:{t})} \)).
The proof is by induction on t (we run the induction backwards, starting at \(t=n-1\)). Let i be an arbitrary party. First, note that by the initial assignment to the d values in lines 11 and 12 of the MixAndDecrypt phase, and using Claim 5, we have
Thus, \(t=n-1\) and all \(i,j\in \left\{ {1,\cdots ,n} \right\} \):
which is the required value of \(h^{(i:n-1)}\) according to the induction hypothesis. Since this is true for all i, it also holds for the values of \(h^{(i+1:n-1)}\) received in line 19. Hence, it follows that for the \(d^{i:n-2}\) values computed in line 21 we have:
as required by the induction hypothesis.
Assume the hypothesis holds for all i down to some t. Then for iteration \(t-1\), the \(h^{i:t-1}\) values computed in line 16 are a rerandomized permutation of \(d^{(i:t-1)}\), hence by the induction hypothesis they are:
Since this is true for all i, the \(h^{(i+1:t-1)}\) values received in line 19 also satisfy the equation, hence the \(d^{(i:t-2)}\) values satisfy
(the details are exactly as in the proof of the base case). \(\square \)
Proof
(of Theorem 3 ). The theorem follows directly from Claim 6, setting \(t=1\) the outputs of party i are the values \(d^{(i:0)}_1,\cdots ,d^{(i:0)}_n\). \(\square \)
6.2 Security Analysis
Proof
(of Theorem 4 ). To prove Theorem 4, we first describe the ideal-world simulator \(\mathcal {S}\) (that “lives” in the ideal world in which all honest parties are dummy parties and there exists only the composed \(\mathcal {F}_{\text {Vote}} ||\mathcal {F}_{\text {Graph}} \) functionality). We will then prove, via a hybrid argument, that the environment’s interactions with \(\mathcal {S}\) are computationally indistinguishable from an interaction with the real-world adversary \(\mathcal {A}\) that “lives” in the real world in which the parties execute Protocol 1 and only the \(\mathcal {F}_{\text {Graph}} \) functionality exists.
Simulator Description. \(\mathcal {S}\) works as follows:
-
1.
Let \({{\mathcal {Q}}}\) be the set of corrupt parties. Note that we are in the semi-honest model with static corruptions, so \({{\mathcal {Q}}}\) and the input to each party in \({{\mathcal {Q}}}\) is available at the start of the protocol, and the adversary must play “according to protocol” with these inputs.
-
2.
\(\mathcal {S}\) sends the inputs for the parties in \({{\mathcal {Q}}}\) to \(\mathcal {F}_{\text {Vote}} \) and receives the output of \(\mathcal {F}_{\text {Vote}} \) (i.e., a random permutation of all the parties’ inputs). Let \(out_1,\cdots ,out_n\) be the output \(\mathcal {F}_{\text {Vote}} \) sends to \(\mathcal {S}\).
-
3.
\(\mathcal {S}\) receives the local neighborhood information from \(\mathcal {F}_{\text {Graph}}\) for all parties in \({{\mathcal {Q}}}\). For \(P\in {{\mathcal {Q}}}\), let \(\textsf {pred}\left( {P}\right) \) denote the party preceding P on the cycle and \(\textsf {succ}\left( {P}\right) \) the party succeeding P on the cycle.
-
4.
The adversary partitions \({{\mathcal {Q}}}\) into “segments”, where each segment consists of a sequence of corrupt parties that appear consecutively on the cycle. The segments are separated on the cycle by one or more honest parties (if it’s more than one, \(\mathcal {S}\) can’t tell how many, or in which order the segments appear on the cycle). Let
 be the set of corrupt parties that are first in their segment, i.e.,
be the set of corrupt parties that are first in their segment, i.e., 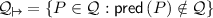 ) and
) and  the set of parties that are last in their segment.
the set of parties that are last in their segment. -
5.
Within each segment, \(\mathcal {S}\) simulates the corrupt parties exactly according to protocol. However, \(\mathcal {S}\) must still simulate the inputs to the parties in
 and
and  that are generated by honest parties.
that are generated by honest parties. -
6.
Simulating messages from honest parties in the AGGREGATE phase, for party
 :
:
-
(a)
\(\mathcal {S}\) generates \(n-1\) key pairs:
$$\begin{aligned} (pk^{({\textsf {pred}\left( {P}\right) }:{1})},sk^{({\textsf {pred}\left( {P}\right) }:{1})}),\cdots ,(pk^{({\textsf {pred}\left( {P}\right) }:{n-1})},sk^{({\textsf {pred}\left( {P}\right) }:{n-1})}) \end{aligned}$$for the honest party preceding P (by honestly running KeyGen).
-
(b)
To simulate the \(n-1\) messages sent by \(\textsf {pred}\left( {P}\right) \) in lines and 7, for each \(t\in \left\{ {0,\cdots ,n-2} \right\} \), \(\mathcal {S}\) simulates \(\textsf {pred}\left( {P}\right) \) sending:
$$\begin{aligned} \underbrace{\left[ {0} \right] _{pk^{({{\mathbf {pred}}[P]}:{t+1})}},\cdots ,\left[ {0} \right] _{pk^{({{\mathbf {pred}}[P]}:{t+1})}}}_{t\, +\, 1 \text {independent ciphertexts}} {\text {and}}\, pk^{({\textsf {pred}\left( {P}\right) }:{t+1})}, \end{aligned}$$where each encryption of 0 is generated honestly using Enc with independent random coins (note that line 4 is covered by \(t=0\).)
-
(a)
-
7.
Simulating messages from honest parties in the MIXANDDECRYPT phase, for party
 : To simulate the \(n-1\) messages sent by \(\textsf {succ}\left( {P}\right) \) in line 18, for each \(t\in \left\{ {n-1,\cdots ,1} \right\} \), \(\mathcal {S}\)
: To simulate the \(n-1\) messages sent by \(\textsf {succ}\left( {P}\right) \) in line 18, for each \(t\in \left\{ {n-1,\cdots ,1} \right\} \), \(\mathcal {S}\)
-
(a)
Chooses a random permutation

-
(b)
Simulates \(\textsf {succ}\left( {P}\right) \) sending:
$$\begin{aligned} \left[ {out_{\pi '^{({t})} (1)}} \right] _{k^{(t-1)}\circledast pk^{({P}:{t})}},\cdots ,\left[ {out_{\pi '^{({t})} (n)}} \right] _{k^{(t-1)}\circledast pk^{({P}:{t})}}\!. \end{aligned}$$(Recall that \(k^{(0)}\mathop {=}\limits ^{\cdot }1\) is defined to be the identity for the key group; and \(out_1,\cdots ,out_n\) are the outputs \(\mathcal {F}_{\text {Vote}} \) sent to \(\mathcal {S}\)).
-
(a)
Proof of Transcript Indistinguishability. A real-world protocol transcript is fully defined by the following information:
-
1.
The messages received by corrupt parties during the protocol (including the messages from \(\mathcal {F}_{\text {Graph}}\))
-
2.
The outputs of the honest parties.
Since \(\mathcal {S}\) faithfully simulates corrupt parties exactly according to the real-world protocol, if the input messages to the corrupt parties are indistinguishable in the ideal and real world, so are their output messages.
We will construct a sequence of hybrid worlds. Assume \(\mathcal {S}\) has access to the honest parties inputs and neighborhoods in these hybrids (in the final hybrid it will not make use of this information, and will be identical to the ideal-world simulator described above):
-
1.
Hybrid 1: \(\mathcal {S}\) simulates the real-world protocol exactly. (The transcript is identically distributed to a real-world transcript).
-
2.
Hybrid 2: For each honest party \(H=\textsf {pred}\left( {P}\right) \) that precedes a corrupt party P, \(\mathcal {S}\) generates \(n-1\) “simulated” key pairs
$$\begin{aligned} ({pk'^{({H}:{1})}},{sk'^{({H}:{1})}}),\cdots ,({pk'^{({H}:{n-1})}},{sk'^{({H}:{n-1})}}) \end{aligned}$$using KeyGen (exactly as in step 6a of the simulation). In line 4 of the Aggregate phase, instead of simulating H exactly according to the protocol \(\mathcal {S}\) simulates H sending \(\left[ {v_H} \right] _{pk'^{({H}:{1})}}\) and \(pk'^{({H}:{1})} \) to P, while in the \(t^{th}\) iteration of line 7, it sends
$$\begin{aligned} \left[ {v_{\textsf {pred}^{(1)}(P)}} \right] _{pk'^{({H}:{t+1})}},\cdots , \left[ {v_{\textsf {pred}^{(t+1)}(P)}} \right] _{pk'^{({H}:{t+1})}} \text { and } pk'^{({H}:{t+1})} \end{aligned}$$to P.
-
3.
Hybrid 3: In this hybrid (compared to the previous one), every simulated ciphertext sent by \(\mathcal {S}\) in step 6b of the simulation is replaced by a fresh, independent, encryption of 0, under the same key.
-
4.
Hybrid 4: In this hybrid (compared to the previous one), in line 16 of the Aggregate phase, instead of mixing as required by the protocol, \(\mathcal {S}\) sets the \(h^{(i:t)}\) values as follows:
$$\begin{aligned} h^{(i:t)}_j\leftarrow \left[ {out_{\pi '^{({t})} (j)}} \right] _{k^{(i:t)}}. \end{aligned}$$That is, it replaces the mix and re-randomize step with a new, fresh set of ciphertexts (under the same public key), permuted according to a fresh, random permutation \(\pi '\). (This hybrid is identically distributed to the transcript of the simulated execution in the ideal world.)
Indistinguishability of Hybrids.
-
1.
In Hybrid 1 (the real-world protocol), the adversary’s view contains, for each
 , the following sequence of messages sent by \(\textsf {pred}\left( {P}\right) \) (each row is a message): $$\begin{aligned} \begin{array}{lcl} k^{(1)}=pk^{({\textsf {pred}^{(1)}(P)}:{1})} &{} \text {and} &{} \left[ {v_{\textsf {pred}^{(1)}(P)}} \right] _{k^{(1)}} \\ k^{(2)}=pk^{({\textsf {pred}^{(2)}(P)}:{1})} \circledast pk^{({\textsf {pred}^{(1)}(P)}:{2})} &{} \text {and} &{} \left[ {v_{\textsf {pred}^{(1)}(P)}} \right] _{k^{(2)}}, \left[ {v_{\textsf {pred}^{(2)}(P)}} \right] _{k^{(2)}} \\ \vdots &{} &{} \vdots \\ k^{(n-1)}=pk^{({\textsf {pred}^{(n-1)}(P)}:{1})} &{} &{}\\ \qquad \qquad \circledast \cdots \circledast pk^{({\textsf {pred}^{(1)}(P)}:{n-1})} &{} \text {and} &{} \left[ {v_{\textsf {pred}^{(1)}(P)}} \right] _{k^{(n-1)}},\cdots , \left[ {v_{\textsf {pred}^{(n-1)}(P)}} \right] _{k^{(n-1)}} \end{array} \end{aligned}$$
, the following sequence of messages sent by \(\textsf {pred}\left( {P}\right) \) (each row is a message): $$\begin{aligned} \begin{array}{lcl} k^{(1)}=pk^{({\textsf {pred}^{(1)}(P)}:{1})} &{} \text {and} &{} \left[ {v_{\textsf {pred}^{(1)}(P)}} \right] _{k^{(1)}} \\ k^{(2)}=pk^{({\textsf {pred}^{(2)}(P)}:{1})} \circledast pk^{({\textsf {pred}^{(1)}(P)}:{2})} &{} \text {and} &{} \left[ {v_{\textsf {pred}^{(1)}(P)}} \right] _{k^{(2)}}, \left[ {v_{\textsf {pred}^{(2)}(P)}} \right] _{k^{(2)}} \\ \vdots &{} &{} \vdots \\ k^{(n-1)}=pk^{({\textsf {pred}^{(n-1)}(P)}:{1})} &{} &{}\\ \qquad \qquad \circledast \cdots \circledast pk^{({\textsf {pred}^{(1)}(P)}:{n-1})} &{} \text {and} &{} \left[ {v_{\textsf {pred}^{(1)}(P)}} \right] _{k^{(n-1)}},\cdots , \left[ {v_{\textsf {pred}^{(n-1)}(P)}} \right] _{k^{(n-1)}} \end{array} \end{aligned}$$In Hybrid 2, the difference is that instead of the sequence of keys
$$\begin{aligned} pk^{({\textsf {pred}^{(1)}(P)}:{1})},\cdots , pk^{({\textsf {pred}^{(n-1)}(P)}:{1})} \circledast \cdots \circledast pk^{({\textsf {pred}^{(1)}(P)}:{n-1})}, \end{aligned}$$the public keys seen are \(pk'^{({\textsf {pred}\left( {P}\right) }:{1})},\cdots ,pk'^{({\textsf {pred}\left( {P}\right) }:{n-1})} \), and the ciphertexts are fresh encryptions of the same values. Note that in the Hybrid 1 key sequence, each product contains one entirely new independent key, that hasn’t been included in any transcript prefix (the \(t^{th}\) product contains \(pk^{({\textsf {pred}^{(1)}(P)}:{t})} \)). Thus, we can think of this key as being chosen randomly and independently at that point. Since the keys are randomly chosen, each product is itself a random, independent key, hence identically distributed to \(pk'^{({\textsf {pred}\left( {P}\right) }:{t})} \). As for the ciphertexts, the indistinguishability property of \(\textsf {AddLayer}\) ensures that fresh encryptions under the composed key are indistinguishable from the ciphertexts produced by adding layers sequentially.
-
2.
The difference between Hybrid 2 and 3 is that ciphertexts containing actual votes are replaced with encryptions of 0 under the same key. However, these ciphertexts are all encrypted under an honest public key (generated by \(\mathcal {S}\)), whose corresponding secret key is never revealed to the adversary. Moreover, every ciphertext received from an honest party is re-randomized, so is indistinguishable from a fresh encryption of that value. Thus, by the semantic security of the encryption scheme, the hybrids are indistinguishable.
-
3.
Finally, the differences between Hybrid 3 and 4 are that \(\mathcal {S}\) chooses a new random permutation in place of \(\sigma ^{({i}:{t})} \) (by Claim 7 this is distributed identically) and instead of calling \(\textsf {Rand}\) it generates new ciphertexts (these are indistinguishable by the security properties of \(\textsf {Rand}\)).
To complete the proof we use Claim 7. \(\square \)
Claim 7
For every party  and all \(t\in \left\{ {1,\cdots ,n-1} \right\} \), the permutation \(\sigma ^{({i+1}:{t})} \) (as defined in Claim 6) is random even conditioned on everything else in the adversary’s view up to iteration t.
and all \(t\in \left\{ {1,\cdots ,n-1} \right\} \), the permutation \(\sigma ^{({i+1}:{t})} \) (as defined in Claim 6) is random even conditioned on everything else in the adversary’s view up to iteration t.
Proof
By Claim 6, \(\sigma ^{({i+1}:{t})} =\pi ^{({i+1}:{t})} \circ \cdots \circ \pi ^{({i+n-t}:{n-1})} \). Since \(\pi ^{({i+1}:{t})} \) is chosen uniformly at random by the honest party \(i+1\) at iteration t, its composition with an arbitrary permutation is still uniformly random. \(\square \)
7 Topology-Hiding Computation of Information-Local Functions
In Sect. 5, we showed how to reduce the topology-hiding computation problem in general graphs to (1) computing local views of a spanning tree and (2) solving the problem for cycles. This leads us to ask: “when can we compute local views of a spanning tree in a topology-hiding way?”. More generally, what can be computed in a topology hiding way for arbitrary graphs, without relying in a circular manner on a generic protocol for topology-hiding computation?
With this motivation in mind, we define:
Definition 2
(Information-local Function). We say a function computed over a communication graph \(G=(V,E)\) is k-information-local if the output of every node \(v\in V\) can be (efficiently) computed from the inputs and random coins of \(N^{({k})}[{v}] \) (v’s k-neighborhood).
Note that information-locality is a property of the function computed, not the protocol used to compute it—although if a function is information-local, an immediate consequence of the definition is that there exists an information-local protocol to compute it (i.e., a protocol involving only nodes in v’s k-neighborhood).
In this section, we show that any k-information-local protocol can be computed in a topology-hiding way on a general graph, given a protocol for topology-hiding computation on depth-k trees (as long \(d_{\text {max}} ^k=poly(\kappa )\), where \(d_{\text {max}} \) is a bound on the degree of the graph). This will allow us to leverage previous results for topology-hiding computation for small-diameter graphs.
We then show that we can construct a k-information-local protocol for computing a spanning tree for graphs of circumference k, and can combine this step with the cycle protocol itself in a secure computation so that nodes don’t ever learn the results of the spanning tree computation. Due to space considerations, the details are deferred to the full version of the paper.
7.1 High-Level Overview of Our Protocol
Let f be a k-information-local function. By Definition 2, the output of every node can be computed from the inputs and random coins of its k-neighborhood. Thus, we can construct a generic protocol for computing f, by having every node v “collect” the required information from its k-neighborhood and locally compute its output. Every node can run multiple instances of the protocol in parallel—once as the center of the k-neighborhood (this will give it its output) and an additional instance for each member of its k-neighborhood as a “helper instance” that only serves as an information source.
Executing the generic protocol described above is not topology-hiding, and in fact requires knowledge of the graph topology (for example, in order to determine how many instances a node must execute as a helper instance). To hide the topology information, we will run each instance of the protocol under a topology-hiding MPC whose participants are the k-neighborhoods.
Even this does not completely solve the problem, however, since the naïve way of determining the participants in the MPC requires knowledge of the graph topology. To achieve a full topology-hiding execution, we have to be able to run a protocol between all parties in a k-neighborhood in such a way that individual nodes do not learn anything about which other nodes (beyond their immediate neighbors) are participating in the protocol.
Our solution to the problem is to have every node “pretend” its k-neighborhood is a complete \(d_{\text {max}} \)-ary tree of depth k. If this were actually the case, it would know exactly how many nodes are in its k-neighborhood and could refer to all other nodes in its neighborhood using relative notation (by the unique path to reach that node). Of course, in the actual k-neighborhood of v not all nodes have maximal degree, and there may be cycles. To reduce to the ideal tree setting, every node with less than maximal degree will simulate any missing neighbors as subtrees of depth \(k-1\) consisting of “dummy” nodes with default inputs (the simulation is not recursive; the simulated dummy nodes participate only in helper instances whose output instance is not a dummy node, so in particular they will not need inputs from nodes outside the original simulated subtree).
In order to allow nodes to match messages received from their neighbors with the specific instance of the protocol, we introduce relative session identifiers (sids). That is, instead of using a global sid to denote the protocol instance, each node will have a different sid for the same instance. When receiving (or sending) a message, the node will translate the received sid into its “local frame of reference”. In more detail, we identify each execution instance with the central node of the depth-k tree, and the sid of the node for that execution will be the (relative) path in the tree from that node to the center. For example, suppose a node u is running an instance with \(sid=(dist=3,e_1=1,e_2=2,e_3=1)\); that is, to reach the center of this execution’s tree from u, take edge 1 from u, then take edge 2 from the next node, and finally edge 1 from the third node (each node fixes some random numbering of its edges). When node u sends a message to v, then:
- Case 1::
-
v is “upstream”; i.e., (u,v) is edge 1 from u: In this case u will send the sid \((\text {up}:dist=2,e^*_1=2,e_2=1)\) (that is, remove the edge (u, v) from the path to get an sid relative to v for the same execution). v will still have to renumber \(e^*_1\), since u’s numbering omits the edge (u, v) on which the message was received by v.
- Case 2::
-
v is “downstream”: In this case, u will send the sid \((\text {down}:dist=4,e_1=?,e_2=1,e_2=3,e_4=1)\). Note that u doesn’t know the numbering of v’s edge to u, so v will have to fill that in when receiving the message).
By matching sids in this way, each execution will be a complete \(d_{\text {max}} \)-ary tree of depth k. If the neighborhood contains cycles, however, some nodes will have several different sids participating in the same execution instance. This because when cycles exist, the relative directions to its neighbors are not unique. We deal with this issue by requiring the underlying function to be invariant with respect to the number of actual inputs (otherwise the function itself reveals the size of the k-neighborhood) and transforming the function to make it invariant with respect to duplicate inputs. That is, suppose \(f_v\) is a k-information-local function that receives the input \(x_u\) from every \(u\in N^{({k})}[{v}] \). We will modify the input from each party to be the pair \(x'_u=(u,x_u)\), where u is the id of node u in the original graph G, and compute the function \(f'(X')\) that computes f on the “deduplicated” inputs
where \(X'\) is the set of “raw” inputs that may contain duplicates.
Due to space considerations, the formal description of the protocol and its analysis are deferred to the full version of the paper.
8 Discussion and Open Questions
This work leaves several natural open questions.
Topology-Hiding Computation for Arbitrary Graphs. This work extends the feasibility results for topology-hiding computation to graphs with large diameter, but the class of graphs we can handle is still restricted. The question of whether a topology-hiding computation protocol exists for any graph (without additional auxiliary information) is still open.
Topology-Hiding Computation for Large-Diameter Graphs in the Fail-Stop Model. All of our protocols are proven secure in the semi-honest model. This is an inherent restriction for cycles and trees, since topology-hiding computation is known to be impossible in the fail-stop model unless the adversary cannot disconnect the graph [12]. Thus, our approach does not give a feasibility result for topology-hiding computation for large-diameter graphs in the fail-stop model. This remains an interesting open question.
Notes
- 1.
For example, for \(n'=n+3\), the output of player i consists of double votes from players \(i, i+1,i+2\), implying that non-neighboring corrupted players i, j can identify whether \(j=i+2\) by letting j place a unique vote \(v^*\) and then count whether this vote \(v^*\) appears once in the output of i (implying \(j\ne i+2\)) or twice (implying \(j=i+2\)).
- 2.
Note that, unlike Eulerian or Hamiltonian cycles, we do not require a single pass through each edge or vertex. This relaxation in turn guarantees that the cycle-traversal always exists and can be found efficiently (when given the graph as input).
References
Beimel, A., Gabizon, A., Ishai, Y., Kushilevitz, E., Meldgaard, S., Paskin-Cherniavsky, A.: Non-interactive secure multiparty computation. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8617, pp. 387–404. Springer, Heidelberg (2014). doi:10.1007/978-3-662-44381-1_22
Canetti, R.: Universally composable security: a new paradigm for cryptographic protocols. In: FOCS, pp. 136–145. IEEE Computer Society (2001)
Chandran, N., Chongchitmate, W., Garay, J. A., Goldwasser, S., Ostrovsky, R. Zikas, V.: The hidden graph model: communication locality and optimal resiliency with adaptive faults. In: Proceedings of the 2015 Conference on Innovations in Theoretical Computer Science, ITCS 2015, pp. 153–162. ACM, New York (2015)
Estrin, D., Govindan, R., Heidemann, J., Kumar, S.: Next century challenges: scalable coordination in sensor networks. In: Proceedings of the 5th annual ACM/IEEE International Conference on Mobile Computing and Networking, pp. 263–270. ACM (1999)
Friedrich, T., Sauerwald, T., Stauffer, A.: Diameter and broadcast time of random geometric graphs in arbitrary dimensions. Algorithmica 67(1), 65–88 (2013)
Goldreich, O.: Foundations of Cryptography: Basic Applications, vol. 2. Cambridge University Press, New York (2004)
Goldwasser, S., Gordon, S.D., Goyal, V., Jain, A., Katz, J., Liu, F.-H., Sahai, A., Shi, E., Zhou, H.-S.: Multi-input functional encryption. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 578–602. Springer, Heidelberg (2014). doi:10.1007/978-3-642-55220-5_32
Halevi, S., Ishai, Y., Jain, A., Kushilevitz, E., Rabin, T.: Secure multiparty computation with general interaction patterns. In: Proceedings of the ACM Conference on Innovations in Theoretical Computer Science, ITCS 2016, pp. 157–168. ACM, New York (2016)
Halevi, S., Lindell, Y., Pinkas, B.: Secure computation on the web: computing without simultaneous interaction. In: Rogaway, P. (ed.) CRYPTO 2011. LNCS, vol. 6841, pp. 132–150. Springer, Heidelberg (2011). doi:10.1007/978-3-642-22792-9_8
Hinkelmann, M., Jakoby, A.: Communications in unknown networks: preserving the secret of topology. Theoret. Comput. Sci. 384(2–3), 184–200 (2007). Structural Information and Communication Complexity (SIROCCO 2005)
Hirt, M., Maurer, U., Tschudi, D., Zikas, V.: Network-hiding communication and applications to multi-party protocols. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9815, pp. 335–365. Springer, Heidelberg (2016). doi:10.1007/978-3-662-53008-5_12
Moran, T., Orlov, I., Richelson, S.: Topology-hiding computation. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9014, pp. 169–198. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46494-6_8
Penrose, M.: Random Geometric Graphs, 5th edn. Oxford University Press, Oxford (2003)
Pottie, G.J., Kaiser, W.J.: Wireless integrated network sensors. Commun. ACM 43(5), 51–58 (2000)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 International Association for Cryptologic Research
About this paper
Cite this paper
Akavia, A., Moran, T. (2017). Topology-Hiding Computation Beyond Logarithmic Diameter. In: Coron, JS., Nielsen, J. (eds) Advances in Cryptology – EUROCRYPT 2017. EUROCRYPT 2017. Lecture Notes in Computer Science(), vol 10212. Springer, Cham. https://doi.org/10.1007/978-3-319-56617-7_21
Download citation
DOI: https://doi.org/10.1007/978-3-319-56617-7_21
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-56616-0
Online ISBN: 978-3-319-56617-7
eBook Packages: Computer ScienceComputer Science (R0)






 be the set of corrupt parties that are first in their segment, i.e.,
be the set of corrupt parties that are first in their segment, i.e.,  ) and
) and  the set of parties that are last in their segment.
the set of parties that are last in their segment. and
and  that are generated by honest parties.
that are generated by honest parties. :
:
 : To simulate the
: To simulate the 
 , the following sequence of messages sent by
, the following sequence of messages sent by 