Quantum Authentication with Key Recycling

Abstract

We show that a family of quantum authentication protocols introduced in [Barnum et al., FOCS 2002] can be used to construct a secure quantum channel and additionally recycle all of the secret key if the message is successfully authenticated, and recycle part of the key if tampering is detected. We give a full security proof that constructs the secure channel given only insecure noisy channels and a shared secret key. We also prove that the number of recycled key bits is optimal for this family of protocols, i.e., there exists an adversarial strategy to obtain all non-recycled bits. Previous works recycled less key and only gave partial security proofs, since they did not consider all possible distinguishers (environments) that may be used to distinguish the real setting from the ideal secure quantum channel and secret key resource.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

1.1 Reusing a One-Time Pad

A one-time pad can famously be used only once [31], i.e., a secret key as long as the message is needed to encrypt it with information-theoretic security. But this does not hold anymore if the honest players can use quantum technologies to communicate. A quantum key distribution (QKD) protocol [5, 30] allows players to expand an initial short secret key, and thus encrypt messages that are longer than the length of the original key. Instead of first expanding a key, and then using it for encryption, one can also swap the order if the initial key is long enough: one first encrypts a message, then recycles the key. This is possible due to the same physical principles as QKD: quantum states cannot be cloned, so if the receiver holds the exact cipher that was sent, the adversary cannot have a copy, and thus does not have any information about the key either, so it may be reused. This requires the receiver to verify the authenticity of the message received, and if this process fails, a net key loss occurs—the same happens in QKD: if an adversary tampers with the communication, the players have to abort and also lose some of the initial secret key.

1.2 Quantum Authentication and Key Recycling

Some ideas for recycling encryption keys using quantum ciphers were already proposed in 1982 [6]. Many years later, Damgård et al. [13] (see also [14, 18]) showed how to encrypt a classical message in a quantum state and recycle the key. At roughly the same time, the first protocol for authenticating quantum messages was proposed by Barnum et al. [3], who also proved that quantum authentication necessarily encrypts the message as well. Gottesman [20] then showed that after the message is successfully authenticated by the receiver, the key can be leaked to the adversary without compromising the confidentiality of the message. And Oppenheim and Horodecki [25] adapted the protocol of [3] to recycle key. But the security definitions in these initial works on quantum authentication have a major flaw: they do not consider the possibility that an adversary may hold a purification of the quantum message that is encrypted. This was corrected by Hayden, Leung and Mayers [21], who give a composable security definition for quantum authentication with key recycling. They then show that the family of protocols from [3] are secure, and prove that one can recycle part of the key if the message is accepted.

The security proof from [21] does however not consider all possible environments. Starting in works by Simmons in the 80’s and then Stinson in the 90’s (see, for example, [33,34,35,36]) the classical literature on authentication studies two types of attacks: substitution attacks—where the adversary obtains a valid pair of message and cipher¹ and attempts to substitute the cipher with one that will decode to a different message—and impersonation attacks—where the adversary directly sends a forged cipher to the receiver, without knowledge of a valid message-cipher pair. To the best of our knowledge, there is no proof showing that security against impersonation attacks follows from security against substitution attacks, hence the literature analyzes both attacks separately.² This is particularly important in the case of composable security, which aims to prove the security of the protocol when used in any arbitrary environment, therefore also in an environment that first sends a forged cipher to the receiver, learns wether it is accepted or rejected, then provides a message to the sender to be authenticated, and finally obtains the cipher for this message. This is all the more crucial when key recycling is involved, since the receiver will already recycle (part of) the key upon receiving the forged cipher, which is immediately given to the environment. The work of Hayden et al. [21] only considers environments that perform substitution attacks—i.e., first provide the sender with a message, then change the cipher, and finally learn the outcome of the authentication as well as receive the recycled key. Hence they do not provide a complete composable security proof of quantum authentication, which prevents the protocol from being composed in an arbitrary environment.³

More recently, alternative security definitions for quantum authentication have been proposed, both without [9, 17] and with [19] key recycling (see also [2]). These still only consider substitution attacks, and furthermore, they are, strictly speaking, not composable. While it is possible to prove that these definitions imply security in a composable framework (if one restricts the environment to substitution attacks), the precise way in which the error $\varepsilon$ carries over to the framework has not been worked out in any of these papers. If two protocols with composable errors $\varepsilon$ and $\delta$ are run jointly (e.g., one is a subroutine of the other), the error of the composed protocol is bounded by the sum of the individual errors, $\varepsilon +\delta$. If a security definition does not provide a bound on the composable error, then one cannot evaluate the new error after composition.⁴ For example, quantum authentication with key recycling requires a backwards classical authentic channel, so that the receiver may tell the sender that the message was accepted, and allow her to recycle the key. The error of the complete protocol is thus the sum of errors of the quantum authentication and classical authentication protocols. Definitions such as those of [9, 17, 19] are not sufficient to directly obtain a bound on the error of such a composed protocol.

In the other direction, it is immediate that if a protocol is $\varepsilon$-secure according to the composable definition used in this work, then it is secure according to [9, 17, 19] with the same error $\varepsilon$. More precisely, proving that the quantum authentication scheme constructs a secure channel is sufficient to satisfy [9, 17]—i.e., the ideal functionality is a secure channel which only allows the adversary to decide if the message is delivered, but does not leak any information about the message to the adversary except its length (confidentiality), nor does it allow the adversary to modify the message (authenticity). And proving that the scheme constructs a secure channel that additionally generates fresh secret key is sufficient to satisfy the definition of total authentication from [19]. Garg et al. [19] also propose a definition of total authentication with key leakage, which can be captured in a composable framework by a secure channel that generates fresh key and leaks some of it to the adversary. This is however a somewhat unnatural ideal functionality, since it requires a deterministic leakage function, which may be unknown or not exist, e.g., the bits leaked can depend on the adversary’s behavior—this is the case for the trap code [8, 9], which we discuss further in Sect. 4. The next natural step for players in such a situation is to extract a secret key from the partially leaked key, and thus the more natural ideal functionality is what one obtains after this privacy amplification step [7, 29]: a secure channel that generates fresh secret key, but where the key generated may be shorter than the key consumed. The ideal functionality used in the current work provides this flexibility: the amount of fresh key generated is a parameter which may be chosen so as to produce less key than consumed, the same amount, or even more.⁵ Hence, with one security definition, we encompass all these different cases—no key recycling, partial key recycling, total key recycling, and even a net gain of secret key. Furthermore, having all these notions captured by ideal functionalities makes for a particularly simple comparison between the quite technical definitions appearing in [9, 17, 19].

1.3 Contributions

In this work we use the Abstract Cryptography (AC) framework [23] to model the composable security of quantum authentication with key recycling. AC views cryptography as a resource theory: a protocol constructs a (strong) resource given some (weak) resources. For example, the quantum authentication protocols that we analyze construct two resources: a secure quantum channel—a channel that provides both confidentiality and authenticity—and a secret key resource that shares a fresh key between both players. In order to construct these resources, we require shared secret key, an insecure (noiseless) quantum channel and a backwards authentic classical channel. These are all resources, that may in turn be constructed from weaker resources, e.g., the classical authentic channel can be constructed from a shared secret key and an insecure channel, and noiseless channels are constructed from noisy channels. Due to this constructive aspect of the framework, it is also called constructive cryptography in the literature [22, 24].

Although this approach is quite different from the Universal Composability (UC) framework [10, 11], in the setting considered in this work—with one dishonest player and where recipients are denoted by classical strings⁶—the two frameworks are essentially equivalent and the same results could have been derived with a quantum version of UC [37]. In UC, the constructed resource would be called ideal functionality, and the resources used in the construction are setup assumptions.

We thus first formally define the ideal resources constructed by the quantum authentication protocol with key recycling—the secure channel and key resource mentioned in this introduction—as well as the resources required by this construction. We then prove that a family of quantum authentication protocols proposed by Barnum et al. [3] satisfy this construction, i.e., no distinguisher (called environment in UC) can distinguish the real system from the ideal resources and simulator except with an advantage $\varepsilon$ that is exponentially small in the security parameter. This proof considers all distinguishers allowed by quantum mechanics, including those that perform impersonation attacks.

We show that in the case where the message is accepted, every bit of key may be recycled. And if the message is rejected, one may recycle all the key except the bits used to one-time pad the cipher.⁷ We prove that this is optimal for the family of protocols considered, i.e., an adversary may obtain all non-recycled bits of key. This improves on previous results, which recycled less key and only considered a subset of possible environments. More specifically, Hayden et al. [21], while also analyzing protocols from [3], only recycle part of the key in case of an accept, and lose all the key in case of a reject. Garg et al. [19] propose a new protocol, which they prove can recycle all of the key in the case of an accept, but do not consider key recycling in the case of a reject either. The protocols we analyze are also more key efficient than that of [19]. We give two instances which need $\varTheta (m +\log 1/\varepsilon )$ bits of initial secret key, instead of the $\varTheta ((m +\log 1/\varepsilon )^2)$ required by [19], where m is the length of the message and $\varepsilon$ is the error. Independently from this work, Alagic and Majenz [2] proved that one of the instances analyzed here satisfies the weaker security definition of [19].

Note that the family of protocols for which we provide a security proof is a subset of the (larger) family introduced in [3]. More precisely, Barnum et al. [3] define quantum authentication protocols by composing a quantum one-time pad and what they call a purity testing code—which, with high probability, will detect any noise that may modify the encoded message—whereas we require a stricter notion, a strong purity testing code—which, with high probability, will detect any noise. This restriction on the family of protocols is necessary to recycle all the key. In fact, there exists a quantum authentication scheme, the trap code [8, 9], which is a member of the larger class from [3] but not the stricter class analyzed here, and which leaks part of the key to the adversary, even upon a successful authentication of the message—this example is discussed in Sect. 4.

We then give two explicit instantiations of this family of quantum authentication protocols. The first is the construction used in [3], which requires an initial key of length $2m+2n$, where m is the length of the message and n is the security parameter, and has error $\varepsilon \le 2^{-n/2+1} \sqrt{2m/n+2}$. The second is an explicit unitary 2-design [15, 16] discovered by Chau [12], which requires $5m+4n$ bits of initial key⁸ and has error $\varepsilon \le 2^{-n/2+1}$. Both constructions have a net loss of $2m+n$ bits of key if the message fails authentication. Since several other explicit quantum authentication protocols proposed in the literature are instances of this family of schemes, our security proof is a proof for these protocols as well—this is discussed further in Sect. 4.

In the full version of this paper [27], we additionally show how to construct the resources used by the protocol from nothing but insecure noisy channels and shared secret key, and calculate the joint error of the composed protocols. We also show how to compensate for the bits of key lost in the construction of the backwards authentic channel, so that the composed protocol still has a zero net key consumption if no adversary jumbles the communication. Finally, the full version [27] also contains a security proof of quantum without key recycling, which is valid for weak purity testing codes and achieves an optimal error.

1.4 Structure of This Paper

In Sect. 2 we give a brief introduction to the main concepts of AC, which are necessary to understand the notion of cryptographic construction and corresponding security defintion. In Sect. 3 we then define the resources constructed and used by a quantum authentication scheme with key recycling. We introduce the family of protocols from [3] that we analyze in this work, and then prove that they construct the corresponding ideal resources. We also prove that the number of recycled bits is optimal. Finally, in Sect. 4 we discuss the relation between some quantum authentication schemes that have appeared in the literature and those analyzed here, as well as some open problems.

2 Constructive Cryptography

As already mentioned in Sect. 1.3, the AC framework [23] models cryptography as a resource theory. In this section we give a brief overview of how these constructive statements are formalized. We illustrate this with an example taken from [26], namely authentication of classical messages with message authentication codes (MAC). An expanded version of this introduction to AC is provided in the full version of this paper [27].

In an n player setting, a resource is an object with n interfaces, that allows every player to input messages and receive other messages at her interface. The objects depicted in Fig. 1 are examples of resources. The insecure channel in Fig. 1a allows Alice to input a message at her interface on the left and allows Bob to receive a message at his interface on the right. Eve can intercept Alice’s message and insert a message of her choosing at her interface. The authentic channel resource depicted in Fig. 1b also allows Alice to send a message and Bob to receive a message, but Eve’s interface is more limited than for the insecure channel: she can only decide if Bob receives the message or not, but not tamper with the message being sent. The key resource drawn in Fig. 1c provides each player with a secret key when requested. If two resources $\mathcal {K}$ and $\mathcal {C}$ are both available to the players, we write $\mathcal {K}\Vert \mathcal {C}$ for the resource resulting from their parallel composition—this is to be understood as the resources being merged into one: the interfaces belonging to player i are simultaneously accessible to her as one new interface, which we depict in Fig. 1d. In the full version of this work [27] we provide a more detailed description of the resources from Fig. 1 along a discussion of how to model them mathematically.

Fig. 1.

Some examples of resources. The insecure channel on the top left could transmit either classical or quantum messages. The authentic channel on the top right is necessarily classical, since it clones the message.

Converters capture operations that a player might perform locally at her interface. For example, if the players share a key resource and an insecure channel, Alice might decide to append a MAC to her message. This is modeled as a converter $\pi ^\text {auth}_A$ that obtains the message x at the outside interface, obtains a key at the inside interface from a key resource $\mathcal {K}$ and sends $(x,h_k(x))$ on the insecure channel $\mathcal {C}$, where $h_k$ is taken from a family of strongly 2-universal hash functions [36, 39]. We illustrate this in Fig. 2. Converters are always drawn with rounded corners. If a converter $\alpha _i$ is connected to the i interface of a resource $\mathcal {R}$, we write $\alpha _i\mathcal {R}$ or $\mathcal {R}\alpha _i$ for the new resource obtained by connecting the two.⁹

Fig. 2.

The real system for a MAC protocol. Alice authenticates her message by appending a MAC to it. Bob checks if the MAC is correct and either accepts or rejects the message.

A protocol is then defined by a set of converters, one for every honest player. Another type of converter that we need is a filter. The resources illustrated in Fig. 1 depict a setting with an adversary that has some control over these resources. For a cryptographic protocol to be useful it is not sufficient to provide guarantees on what happens when an adversary is present, one also has to provide a guarantee on what happens when no adversary is present, e.g., if no adversary tampers with the message on the insecure channel, then Bob will receive the message that Alice sent. We model this setting by covering the adversarial interface with a filter that emulates an honest behavior. In Fig. 3 we draw an insecure and an authentic channel with filters $\sharp _E$ and $\lozenge _E$ that transmit the message to Bob. In the case of the insecure channel, one may want to model an honest noisy channel when no adversary is present. This is done by having the filter $\sharp _E$ add some noise to the message. A dishonest player removes this and has access to a noiseless channel as in Fig. 1a.

We use the term filtered resource to refer to a pair of a resource $\mathcal {R}$ and a filter $\sharp _E$, and often write $\mathcal {R}_\sharp = (\mathcal {R},\sharp _E)$. Such an object can be thought of as having two modes: it is characterized by the resource $\mathcal {R}\sharp _E$ when no adversary is present and by the resource $\mathcal {R}$ when the adversary is present.

The final object that is required by the AC framework to define the notion of construction and prove that it is composable, is a (pseudo-)metric defined on the space of resources that measures how close two resources are. In the following, we use a distinguisher based metric, i.e., the maximum advantage a distinguisher has in guessing whether it is interacting with resource $\mathcal {R}$ or $\mathcal {S}$, which we write $d(\mathcal {R},\mathcal {S})$. More specifically, let $\mathcal {D}$ be a distinguisher, and le $\mathcal {D}[\mathcal {R}]$ and $\mathcal {D}[\mathcal {S}]$ be the binary random variables corresponding to $\mathcal {D}$’s output when connected to $\mathcal {R}$ and $\mathcal {S}$, respectively. Then the distinguishing advantage between $\mathcal {R}$ and $\mathcal {S}$ is defined as

$$\begin{aligned} d(\mathcal {R},\mathcal {S}) := \sup _{\mathcal {D}} \left| \Pr \left[ \mathcal {D}[\mathcal {R}] = 0 \right] - \Pr \left[ \mathcal {D}[\mathcal {S}] = 0 \right] \right| . \end{aligned}$$

Since we study information-theoretic security in this work, the supremum is taken over the set of all possible distinguishers allowed by quantum mechanics. This is discussed further in the full version of this work [27].

Fig. 3.

Channels with filters. The two channels from Fig. 1a and b are represented with filters on Eve’s interface emulating an honest behavior, i.e., when no adversary is present.

We are now ready to define the security of a cryptographic protocol. We do so in the three player setting, for honest Alice and Bob, and dishonest Eve. Thus, in the following, all resources have three interfaces, denoted A, B and E, and a protocol is then given by a pair of converters $(\pi _A,\pi _B)$ for the honest players. We refer to [23] for the general case, when arbitrary players can be dishonest.

Definition 1

(Cryptographic security [23]). Let $\pi _{AB} = (\pi _A,\pi _B)$ be a protocol and $\mathcal {R}_\sharp = (\mathcal {R},\sharp )$ and $\mathcal {S}_\lozenge = (\mathcal {S},\lozenge )$ denote two filtered resources. We say that $\pi _{AB}$ constructs $\mathcal {S}_{\lozenge }$ from $\mathcal {R}_\sharp$ within $\varepsilon$, which we write $\mathcal {R}_\sharp \xrightarrow {\pi ,\varepsilon } \mathcal {S}_\lozenge$, if the two following conditions hold:

• (i) We have

  $$\begin{aligned} d(\pi _{AB}\mathcal {R}\sharp _E,\mathcal {S}\lozenge _E) \le \varepsilon . \end{aligned}$$

• (ii) There exists a converter¹⁰ $\sigma _E$—which we call simulator—such that

  $$\begin{aligned} d(\pi _{AB}\mathcal {R},\mathcal {S}\sigma _E) \le \varepsilon . \end{aligned}$$

If it is clear from the context what filtered resources $\mathcal {R}_\sharp$ and $\mathcal {S}_\lozenge$ are meant, we simply say that $\pi _{AB}$ is $\varepsilon$-secure.

The first of these two conditions measures how close the constructed resource is to the ideal resource in the case where no malicious player is intervening, which is often called correctness in the literature. The second condition captures security in the presence of an adversary. For example, to prove that the MAC protocol $\pi ^\text {auth}_{AB}$ constructs an authentic channel $\mathcal {A}_{\lozenge }$ from a (noiseless) insecure channel $\mathcal {C}_\square$ and a secret key $\mathcal {K}$ within $\varepsilon$, we need to prove that the real system (with filters) $\pi ^\text {auth}_{AB}(\mathcal {K}\Vert \mathcal {C}\square _E)$ cannot be distinguished from the ideal system $\mathcal {A}\lozenge _E$ with advantage greater than $\varepsilon$, and we need to find a converter $\sigma ^\text {auth}_E$ such that the real system (without filters) $\pi ^\text {auth}_{AB}(\mathcal {K}\Vert \mathcal {C})$ cannot be distinguished from the ideal system $\mathcal {A}\sigma ^\text {auth}_E$ with advantage greater than $\varepsilon$. For the MAC protocol, correctness is satisfied with error 0 and the simulator $\sigma ^\text {auth}_E$ drawn in Fig. 4 satisfies the second requirement if the family of hash functions $\{h_k\}_k$ is $\varepsilon$-almost strongly 2-universal [26].

Fig. 4.

The ideal system with simulator for a MAC protocol. The simulator $\sigma ^\text {auth}_E$ picks its own key and generates the MAC. If the value input by Eve is different from the output at her interface (or is input before an output is generated), the simulator prevents Bob from getting Alice’s message.

Remark 2

The protocols and simulators discussed in this work are all efficient. The protocols we consider are either trivially efficient or taken from other work, in which case we refer to these other works for proofs of efficiency. The efficiency of the simulator used to prove the security of quantum authentication has been analyzed in [9]. All other simulators used in the security proofs run the corresponding honest protocols, and are thus efficient because the protocols are. We therefore do not discuss efficiency any further in this work.

3 Quantum Authentication

We start with some technical preliminaries in Sect. 3.1, where we introduce (strong) purity testing codes, which are a key component of the family of quantum authentication protocols of [3]. In Sect. 3.2 we give a constructive view of quantum authentication with key recycling: we define the resources that such a protocol is expected to construct, as well as the resources that are required to achieve this. In Sect. 3.3 we describe the family of protocols that we analyze in this work, along with a variant in which the order of the encryption and encoding operations has been swapped, which we prove to be equivalent. In Sect. 3.4 we give a security proof for the family of quantum authentication protocols defined earlier. And in Sect. 3.5 we show that the number of recycled key bits is optimal. Finally, in Sect. 3.6 we give two explicit constructions of purity testing codes and get the exact parameters of the quantum authentication protocols with these codes.

3.1 Technical Preliminaries

Pauli Operators. To denote a Pauli operator on n qubits we write either $P_{x,z}$ or $P_\ell$, where x and z are n-bit strings indicating in which positions bit and phase flips occur, and $\ell = (x,z)$ is the concatenation of x and z, which is used when we do not need to distinguish between x and z. Two Pauli operators $P_{j}$ and $P_{\ell }$ with $j = (x,z)$ and $\ell = (x',z')$ commute (anti-commute) if the symplectic inner product

$$\begin{aligned} (j,\ell )_{\text {Sp}} := x \cdot z' - z \cdot x' \end{aligned}$$

(1)

is 0 (is 1),where $x \cdot z$ is the scalar product of the vectors and the arithmetic is done modulo 2. Hence, for any $P_j$ and $P_\ell$

$$\begin{aligned} P_j P_\ell = (-1)^{(j,\ell )_{\text {Sp}}} P_\ell P_j. \end{aligned}$$

We use several times the following equality

$$\begin{aligned} \sum _{j \in \{0,1\}^n} (-1)^{(j,\ell )_{\text {Sp}}} = {\left\{ \begin{array}{ll} 2^n &{} \text {if}\,\, \ell = 0,\\ 0 &{} \text {otherwise}, \end{array}\right. } \end{aligned}$$

(2)

where $\ell = 0$ means that all bits of the string $\ell$ are 0.

Purity Testing Code. An error correcting code (ECC) that encodes an m qubit message in a $m+n$ qubit code word is generally defined by an isomorphism from $\mathbb {C}^{2^m}$ to $\mathbb {C}^{2^{m+n}}$. In this work we define an ECC by a unitary $U : \mathbb {C}^{2^{m+n}} \rightarrow \mathbb {C}^{2^{m+n}}$. The code word for a state ${|\psi \rangle }$ is obtained by appending a n qubit state ${|0\rangle }$ to the message, and applying U, i.e., the encoding of ${|\psi \rangle }$ is $U ({|\psi \rangle } \otimes {|0\rangle })$. We do not need to use the decoding properties of ECCs in this work, we only use the them to detect errors, i.e., given a state ${|\varphi \rangle } \in \mathbb {C}^{2^{m+n}}$, we apply the inverse unitary $U^\dag$ and measure the last n qubits to see if they are ${|0\rangle }$ or not.

The first property we require of our codes, is that they map any Pauli error $P_\ell$ into another Pauli error $P_{\ell '}$, i.e.,

$$\begin{aligned} U^\dag P_\ell U = e^{i\theta _\ell } P_{\ell '}, \end{aligned}$$

(3)

for some global phase $e^{i\theta _\ell }$. This is always the case for any U that can be implemented with Clifford operators. In particular, all stabilizer codes have this property, which are used in [3] to define purity testing codes. Note that the mapping from $\ell$ to $\ell '$ defined by (3) is a permutation on the set of indices $\ell \in \{0,1\}^{2m+2n}$ that depends only on the choice of code.

A code will detect an error $P_\ell$ if $P_{\ell '} = P_{x,z} \otimes P_{s,z'}$ for $s \ne 0$, where $P_{x,z}$ acts on the first m qubits and $P_{s,z'}$ on the last n. Measuring these last qubits would yield the syndrome s, since $P_{s,z'}$ flips the bits in the positions corresponding to the bits of s. And an error $P_\ell$ will act trivially on the message if $P_{\ell '} = P_{0,0} \otimes P_{s,z}$. In particular, if $P_{\ell '} = P_{0,0} \otimes P_{0,z}$, then this error will not be detected, but not change the message either.

For a code indexed by a key k, we denote by $\mathcal {P}_k$ the set of Pauli errors that are not detected by this code, and by $\mathcal {Q}_k \subset \mathcal {P}_k$ we denote the undetected errors which act trivially on the message. A purity testing code is a set of codes $\{U_k\}_{k \in \mathcal {K}}$ such that when a code $U_k$ is selected uniformly at random, it will detect with high probability all Pauli errors which act non-trivially on the message.

Definition 3

(Purity testing code [3]). A purity testing code with error $\varepsilon$ is a set of codes $\{U_k\}_{k \in \mathcal {K}}$, such that for all Pauli operators $P_\ell$,

$$\begin{aligned} \frac{\left| \left\{ k \in \mathcal {K}: P_\ell \in \mathcal {P}_k \setminus \mathcal {Q}_k \right\} \right| }{|\mathcal {K}|} \le \varepsilon . \end{aligned}$$

As mentioned in Sect. 1.3, we use a stricter definition of purity testing code in this work. We require that all non-identity Paulis get detected with high probability, even those that act trivially on the message. Intuitively, the reason for this is that, with the original definition of purity testing, if the adversary introduces some noise $P_\ell$, by learning whether the message was accepted or not, she will learn whether that error acts trivially on the message or not, and thus learn something about the ECC used. This means that the adversary learns something about the key used to choose the ECC, and hence it cannot be recycled in its entirety.¹¹

Definition 4

(Strong purity testing code). A strong purity testing code with error $\varepsilon$ is a set of codes $\{U_k\}_{k \in \mathcal {K}}$, such that for all non-identity Pauli operators $P_\ell$,

$$\begin{aligned} \frac{\left| \left\{ k \in \mathcal {K}: P_\ell \in \mathcal {P}_k \right\} \right| }{|\mathcal {K}|} \le \varepsilon . \end{aligned}$$

In Sect. 3.6 we provide explicit constructions of strong purity testing codes.

3.2 Secure Channel and Secret Key Resource

The main result in this paper is a proof that the family of quantum authentication protocols of Barnum et al. [3] restricted to strong purity testing codes can be used to construct a resource that corresponds to the parallel composition of a secure quantum channel $\mathcal {S}^m$ and a secret key resource $\bar{\mathcal {K}}^{\nu _{\textsf {rej}},\nu _{\textsf {acc}}}$, which are illustrated in Fig. 5 and explained in more detail in the following paragraphs.

Fig. 5.

We depict here the filtered resource $(\mathcal {S}^m \Vert \bar{\mathcal {K}}^{\nu _{\textsf {acc}},\nu _{\textsf {rej}}},\flat _E)$ constructed by the quantum authentication protocols analyzed in this work. It can be seen as the composition of a secure channel $\mathcal {S}^m$ (Fig. 5a) and a secret key resource $\bar{\mathcal {K}}^{\nu _{\textsf {acc}},\nu _{\textsf {rej}}}$ (Fig. 5b). The filter $\flat _E$ that emulates an honest behavior is drawn in Fig. 5c.

The secure quantum channel, $\mathcal {S}^m$, drawn in Fig. 5a, allows an m-qubit message $\rho$ to be transmitted from Alice to Bob, which Alice may input at her interface. Since in general the players cannot prevent Eve from learning that a message has been sent, Eve’s interface has one output denoted by a dashed arrow, which notifies her that Alice has sent a message. But the players cannot prevent Eve from jumbling the communication lines either, which is captured in the resource $\mathcal {S}^m$ by allowing Eve to input a bit that decides if Bob gets the message or an error symbol $\bot$ —Eve may also decide not to provide this input (Eve cuts the communication lines), in which case the system is left waiting and Bob obtains neither the message nor an error. Note that the order in which messages are input to the resource $\mathcal {S}^m$ is not fixed, Eve may well provide her bit before Alice inputs a message. In this case, Bob immediately receives an error $\bot$ regardless of the value of Eve’s bit.

The secret key resource, $\bar{\mathcal {K}}^{\nu _{\textsf {rej}},\nu _{\textsf {acc}}}$, depicted in Fig. 5b distributes a uniformly random key to Alice and Bob. Unlike the simplified key resource from Fig. 1c, here the adversary has some control over the length of the key produced. This is because in the real setting Eve can prevent the full key from being recycled by jumbling the message. This is reflected at Eve’s interface of $\bar{\mathcal {K}}^{\nu _{\textsf {rej}},\nu _{\textsf {acc}}}$ allowing her to decide if the key generated is of length $\nu _{\textsf {rej}}$ or $\nu _{\textsf {acc}}$. Furthermore, if in the real setting Alice were to recycle her key before Bob receives the cipher, Eve could use the information from the recycled key to modify the cipher without being detected. So Alice must wait for a confirmation of reception from Bob, which Eve can jumble, preventing Alice from ever recycling the key. This translates in the ideal setting to Eve having another control bit, deciding whether Alice receives the key or an error $\bot$. Note that if Eve provides her two bits in the wrong order, Alice always gets an error $\bot$. This key resource is modeled so that the honest players must request the key to obtain its value. If Bob does this before Eve has provided the bit deciding the key length, he gets an error instead of a key. If Alice makes the request before Eve has provided both her bits, she also gets an error. Otherwise they get the key k.

If no adversary is present, a filter $\flat _E$ covers Eve’s interface of the resources $\mathcal {S}^m$ and $\bar{\mathcal {K}}^{\nu _{\textsf {rej}},\nu _{\textsf {acc}}}$, which is drawn in Fig. 5c. This filter provides the inputs to the resources that allow Bob to get Alice’s message and generate a key of length $\nu _{\textsf {acc}}$ that is made available to both players.

To construct the filtered resource $(\mathcal {S}^m \Vert \bar{\mathcal {K}}^{\nu _{\textsf {rej}},\nu _{\textsf {acc}}})_\flat$, the quantum authentication protocol will use a shared secret key to encrypt and authenticate the message. This means that the players must share a secret key resource. For simplicity we assume the players have access to a resource $\mathcal {K}^\mu$ as depicted in Fig. 1c, that always provides them with a key of length $\mu$.¹² Note that the security of the protocol is not affected if the players only have a weaker resource which might shorten the key or not deliver it to both players—such as the one constructed by the protocol, $\bar{\mathcal {K}}^{\nu _{\textsf {rej}},\nu _{\textsf {acc}}}$—because if either of the players does not have enough key, they simply abort, which is an outcome Eve could already achieve by cutting or jumbling the communication.

They also need to share an insecure quantum channel, which is used to send the message, and is illustrated in Fig. 1a without a filter and in Fig. 3a with a filter. The authentication protocol we consider is designed to catch any error, so if it is used over a noisy channel, it will always abort, even though no adversary is tampering with the message. We thus assume that the players share a noiseless channel, which we denote $\mathcal {C}_{\square }$, i.e., $\mathcal {C}$ is controlled by the adversary as in Fig. 1a. But if no adversary is present, the filter $\square _E$ is noiseless. In the full version of this work [27] we explain how to compose the protocol with an error correcting code so as to run it over a noisy channel.

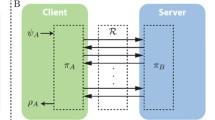
Finally, the players need a backwards authentic channel, that can send one bit of information from Bob to Alice. This is required so that Alice may learn whether the message was accepted and recycle the corresponding amount of key. The authentic channel and its filter $\mathcal {A}_\lozenge$ are drawn in Figs. 1b and 3b. Putting all this together in the case of an active adversary, we get Fig. 6, where the converters for Alice’s and Bob’s parts of the quantum authentication protocol are labeled $\pi ^{\text {q-auth}}_A$ and $\pi ^{\text {q-auth}}_B$, respectively.

According to Definition 1, a protocol $\pi ^\text {q-auth}_{AB} = (\pi ^\text {q-auth}_A,\pi ^\text {q-auth}_B)$ is then a quantum authentication protocol (with key recycling) with error $\varepsilon ^{\text {q-auth}}$ if it constructs $(\mathcal {S}^m \Vert \bar{\mathcal {K}}^{\nu _{\textsf {rej}},\nu _{\textsf {acc}}})_\flat$ from $\mathcal {C}_\square \Vert \mathcal {A}_\lozenge \Vert \mathcal {K}^\mu$ within $\varepsilon ^{\text {q-auth}}$, i.e.,

$$\begin{aligned} \mathcal {C}_\square \Vert \mathcal {A}_\lozenge \Vert \mathcal {K}^{\mu } \xrightarrow {\pi ^\text {q-auth}_{AB},\varepsilon ^{\text {q-auth}}} (\mathcal {S}^m \Vert \bar{\mathcal {K}}^{\nu _{\textsf {rej}},\nu _{\textsf {acc}}})_\flat . \end{aligned}$$

(4)

In Sect. 3.3 we describe the protocol, and in Sect. 3.4 we prove that (4) is satisfied and provide the parameters $\mu ,\nu _\textsf {rej},\nu _\textsf {acc},\varepsilon ^\text {q-auth}$.

3.3 Generic Protocol

The family of quantum authentication protocols from [3] consists in first encrypting the message to be sent with a quantum one-time pad, then encoding it with a purity testing code and a random syndrome. We do the same, but with a strong purity testing code. We also extend the protocol so that the players recycle all the key if the message is accepted, and the key used to select the strong purity testing code if the message is rejected. So that Alice may also recycle the key, Bob uses the backwards authentic classical channel to notify her of the outcome. We refer to this as the “encrypt-then-encode” protocol, the details of which are provided in Fig. 7.

Alternatively, one may perform the encoding and encryption in the opposite order: Alice first encodes her message with the strong purity testing code with syndrome 0, then does a quantum one-time pad on the resulting $m+n$ qubit state. This “encode-then-encrypt” protocol is described in Fig. 8.

Fig. 6.

The real system for quantum authentication with key recycling. Upon receiving a message $\rho$, $\pi ^\text {q-auth}_A$ encrypts it with a key that it obtains from $K^\mu$ and sends it on the insecure channel. Upon receiving a quantum state on the insecure channel, $\pi ^\text {q-auth}_B$ checks whether it is valid, and outputs the corresponding message $\rho '$ or an error message $\bot$. It may then recycle (part of) the key, $k'$, and uses the authentic channel to notify $\pi ^{\text {q-auth}}_A$ whether the message was accepted or not. $\pi ^{\text {q-auth}}_A$ then recycles the key as well. Concrete protocols for this are given in Sect. 3.3.

The pseudo-code described in Figs. 7 and 8 can easily be translated into converters as used in the AC formalism, i.e., the objects $\pi ^{\text {q-auth}}_A$ and $\pi ^{\text {q-auth}}_B$ from Fig. 6. More precisely, if $\pi ^{\text {q-auth}}_A$ receives a message at its outer interface, it requests a key from the key resource, encrypts the message as described and sends the cipher on the insecure channel. It may receive three symbols from the backwards authentic channel: an error $\bot$, in which case it does not recycle any key, a message 0 saying that $\pi ^{\text {q-auth}}_B$ did not receive the correct state, in which case it recycles the part of the key used to choose the code, or a message 1 saying that $\pi ^{\text {q-auth}}_B$ did receive the correct state, in which case it recycles all the key. If $\pi ^{\text {q-auth}}_A$ first receives a message on the backwards authentic channel before receiving a message to send, it will not recycle any key. Similarly, when $\pi ^{\text {q-auth}}_B$ receives a cipher on the insecure channel, it requests a key from the key resource, performs the decryption, outputs either the message or an error depending on the result of the decryption, and sends this result back to $\pi ^{\text {q-auth}}_A$ on the authentic channel.

Fig. 7.

This protocol is identical to the scheme from [3], except that the players use a strong purity testing code, recycle key, and have a backwards authentic channel so that Alice may learn the outcome.

Fig. 8.

This protocol is similar to the protocol from Fig. 7, except that the order of the encryption and encoding have been reversed. To do this, the players need an extra n bits of key.

The encode-then-encrypt protocol uses n bits more key, and since these bits are not recycled in case of a reject, it is preferable to use the encrypt-then-encode protocol. These protocols are however identical: no external observer can detect which of the two is being run. This holds, because the encode-then-encrypt protocol performs phase flips on a syndrome that is known to be in a computational basis state ${|s\rangle }$. Thus, they have no effect and can be skipped. Likewise, Bob performs phase flips on S before measuring in the computational basis—he might as well skip these phase flips, since they have no effect either. We formalize this statement by proving (in Lemma 5) that the converters corresponding to the two different protocols are indistinguishable. This result is similar in spirit to proofs that some prepare-and-measure quantum key distribution (QKD) protocols are indistinguishable from entanglement-based QKD protocols, and thus security proofs for one are security proofs for the other [32].

Since these two protocols are indistinguishable, we provide a security proof in Sect. 3.4 for the encode-then-encrypt protocol. However, in Sect. 3.6, when we count the number of bits of key consumed, we count those of the encrypt-then-encode protocol.

Lemma 5

Let $(\bar{\pi }^\text {q-auth}_A,\bar{\pi }^\text {q-auth}_B)$ and $(\pi ^\text {q-auth}_A,\pi ^\text {q-auth}_B)$ denote the pairs of converters modeling Alice’s and Bob’s behavior in the encrypt-then-encode and encode-then-encrypt protocols, respectively. Then

$$\begin{aligned} d(\bar{\pi }^\text {q-auth}_A,\pi ^\text {q-auth}_A) = d(\bar{\pi }^\text {q-auth}_B,\pi ^\text {q-auth}_B) = 0. \end{aligned}$$

Proof

We start with Alice’s part of the protocol. Let $\bar{\pi }^\text {q-auth}_A$ and $\pi ^\text {q-auth}_A$ receive keys k, $\ell$ and s as in the protocol from Fig. 7, as well as an extra key z of length n that is needed by $\pi ^\text {q-auth}_A$, since it requires more key. The distinguisher prepares a state $\rho ^{RA}$, and sends the A part to the system. $\bar{\pi }^\text {q-auth}_A$ outputs

$$\begin{aligned}&U^{AS}_k P^A_\ell \left( \rho ^{RA} \otimes {|s\rangle \!\langle s|}^S \right) P^A_\ell \left( U^{AS}_k\right) ^\dag \\&\qquad = U^{AS}_k \left( P^A_\ell \otimes P^S_{s,0} \right) \left( \rho ^{RA} \otimes {|0\rangle \!\langle 0|}^S \right) \left( P^A_\ell \otimes P^S_{s,0} \right) \left( U^{AS}_k\right) ^\dag \\&\qquad = U^{AS}_k \left( P^A_\ell \otimes P^S_{s,z} \right) \left( \rho ^{RA} \otimes {|0\rangle \!\langle 0|}^S \right) \left( P^A_\ell \otimes P^S_{s,z} \right) \left( U^{AS}_k\right) ^\dag \\&\qquad = P^{AS}_{\ell '}U^{AS}_k \left( \rho ^{RA} \otimes {|0\rangle \!\langle 0|}^S \right) \left( U^{AS}_k\right) ^\dag P^{AS}_{\ell '}, \end{aligned}$$

where in the last line we used (3). This is exactly the state output by $\pi ^\text {q-auth}_A$ if when receiving the key $k,\ell ,s,z$, the protocol uses the Pauli $P_{\ell '}$ for the quantum one-time pad.

For Bob’s part of the protocol, let the distinguisher prepare a state $\sigma ^{RAS}$ and send the AS part to the system. The subnormalized state held jointly by $\bar{\pi }^\text {q-auth}_B$ and the distinguisher after decoding and performing the measurement is given by

$$\begin{aligned}&{\langle s|} P^A_\ell \left( U^{AS}_k\right) ^\dag \sigma ^{RAS} U^{AS}_k P^A_\ell {|s\rangle }\\&\qquad = {\langle 0|} \left( P^A_\ell \otimes P^S_{s,0}\right) \left( U^{AS}_k\right) ^\dag \sigma ^{RAS} U^{AS}_k \left( P^A_\ell \otimes P^S_{s,0}\right) {|0\rangle } \\&\qquad = {\langle 0|} \left( P^A_\ell \otimes P^S_{s,z}\right) \left( U^{AS}_k\right) ^\dag \sigma ^{RAS} U^{AS}_k \left( P^A_\ell \otimes P^S_{s,z}\right) {|0\rangle } \\&\qquad = {\langle 0|} \left( U^{AS}_k\right) ^\dag P^{AS}_{\ell '} \sigma ^{RAS} P^{AS}_{\ell '} U^{AS}_k {|0\rangle }. \end{aligned}$$

We again obtain the state that is jointly held by $\pi ^\text {q-auth}_B$ and the distinguisher if when receiving the key $k,\ell ,s,z$, the protocol uses the Pauli $P_{\ell '}$ for the quantum one-time pad.    $\square$

Remark 6

If part of the message is classical—i.e., it is diagonal in the computational basis and known not to have a purification held be the distinguisher—then running the same proof as Lemma 5, one can show that it is sufficient to perform bit flips on that part of the message, the phase flips are unnecessary. This is used in the full version of this work [27] to save some key in a construction that involves a message that is part classical.

3.4 Security Proof

Suppose that there exists a strong purity testing code $\{U_k\}_{k \in \mathcal {K}}$ of size $\log |\mathcal {K}| = \nu$ and with error $\varepsilon$ that encodes an m qubit message in an $m+n$ qubit cipher. And let $\pi ^{\text {q-auth}}_{AB} = (\pi ^{\text {q-auth}}_A,\pi ^{\text {q-auth}}_A)$ denote Alice and Bob’s converters when running the encode-then-encrypt protocol from Fig. 8. We are now ready to state the main theorem, namely that $\pi ^{\text {q-auth}}_{AB}$ is a secure authentication scheme with key recycling.

Theorem 7

Let $\pi ^{\text {q-auth}}_{AB}$ denote converteres corresponding to the protocol from Fig. 8. Then $\pi ^{\text {q-auth}}_{AB}$ constructs the secure channel and secret key filtered resource $(\mathcal {S}^m \Vert \bar{\mathcal {K}}^{\nu ,\nu +2m+2n})_\flat$, given an insecure quantum channel $\mathcal {C}_{\square }$, a backwards authentic channel $\mathcal {A}_{\lozenge }$ and a secret key $\mathcal {K}^{\nu +2m+2n}$, i.e.,

$$\mathcal {C}_\square \Vert \mathcal {A}_\lozenge \Vert \mathcal {K}^{\nu +2m+2n} \xrightarrow {\pi ^\text {q-auth}_{AB},\varepsilon ^{\text {q-auth}}} (\mathcal {S}^m \Vert \bar{\mathcal {K}}^{\nu ,\nu +2m+2n})_\flat ,$$

with $\varepsilon ^{\text {q-auth}} = \sqrt{\varepsilon }+\varepsilon /2$, where $\varepsilon$ is the error of the strong purity testing code.

In order to prove this theorem, we need to find a simulator such that the real and ideal systems are indistinguishable except with advantage $\sqrt{\varepsilon }+\varepsilon /2$. The simulator that we use is illustrated in Fig. 9, and works as follows. When it receives a notification from the ideal resource that a message is sent, it generates EPR pairs ${|\varPhi \rangle }^{CR}$ and outputs half of each pair (the C register) at its outer interface. Once it receives a modified cipher (denoted $C'$ in the picture), it measures this state and the half of the EPR pairs it kept in the Bell basis to decide if they were modified. It accordingly activates the switches on the two resources controlling whether Bob gets the message and the length of the key generated, and outputs the bit of backward communication from Bob to Alice—which is always leaked to Eve. If it first receives the register $C'$ before generating the EPR pairs, it always notifies the ideal resource to output an error and outputs 0 as the leak on the backwards authentic channel.

Fig. 9.

The ideal quantum authentication system consisting of the constructed resources $\mathcal {S}^m$ and $\bar{\mathcal {K}}^{\nu ,\nu +2m+2n}$, and the simulator $\sigma ^\text {q-auth}_E$.

Proof

It is trivial to show that correctness holds with error 0, namely that

$$\begin{aligned} d\left( \pi ^{\text {q-auth}}_{AB} \left( \mathcal {C}\square _E \Vert \mathcal {A}\lozenge _E \Vert \mathcal {K}^{\nu +2m+2n} \right) , (\mathcal {S}^m \Vert \bar{\mathcal {K}}^{\nu ,\nu +2m+2n}) \flat _E \right) = 0. \end{aligned}$$

(5)

We now prove the case of security, i.e.,

$$\begin{aligned} d\left( \pi ^{\text {q-auth}}_{AB} \left( \mathcal {C}\Vert \mathcal {A}\Vert \mathcal {K}^{\nu +2m+2n} \right) , (\mathcal {S}^m \Vert \bar{\mathcal {K}}^{\nu ,\nu +2m+2n}) \sigma ^\text {q-auth}_E \right) \le \sqrt{\varepsilon }+\varepsilon /2. \end{aligned}$$

(6)

The real and ideal systems, drawn in Figs. 6 and 9 have 5 inputs. The distinguisher thus has the choice between 5! possible orders for providing inputs. However, most of these orders are redundant and do not need to be analyzed. Providing the requests for the secret keys before they are ready is pointless. So it is sufficient to look at the case where these requests are made as soon as the keys are available for recycling, i.e., after Bob has received the message from Alice and after Alice has received the confirmation from Bob. What is more, neither sending Alice an error on the backwards authentic channel nor allowing her to get Bob’s confirmation will help either way, since the distinguisher already knows what output Alice will produce, so we can completely ignore this input. That leaves only 2 in-ports, and thus 2 orders to analyze:

• 1. The distinguisher first inputs a message at Alice’s interface, gets the cipher at Eve’s interface, inputs a possibly modified cipher at Eve’s interface, gets the output at Bob’s interface, and requests the recycled key.

• 2. The distinguisher first inputs a fake cipher at Eve’s interface, gets the output at Bob’s interface, makes a request for his recycled key, then inputs a message at Alice’s interface and receives the cipher for that message.

We start with the first case, the initial message is sent to Alice. The distinguisher prepares a message ${|\psi \rangle }^{ME}$ and inputs the M part at Alice’s interface. The ideal channel then notifies the simulator that a message has been input. The simulator prepares a maximally entangled state ${|\varPhi \rangle }^{CR}$ of dimension $2^{2m+2n}$ and outputs the C register at Eve’s interface. The distinguisher now holds a bipartite state in CE, to which it applies a unitary $U^{CE}$. Without loss of generality, one may write the unitary as $U^{CE} = \sum _j P^C_j \otimes E^E_j$, where $P^C_j$ are Paulis acting on the cipher register C and $E^E_j$ act on the distinguisher’s internal memory E. The resulting state in the C register is input back in the E interface. The simulator now measures CR in the Bell basis defined by the projectors $\{P_j \otimes I {|\varPhi \rangle \!\langle \varPhi |}^{CR} P_j \otimes I\}_j$. If the outcome is $j = 0$—where $P_0 = I$—it tells the two resources that the cipher was not modified. In which case the contents of the register M is output at Bob’s interface with an $\textsf {acc}$ flag. Furthermore, it generates a fresh uniform key $(k,\ell )$, where $|k| = \nu$ and $|\ell | = 2m+2n$. If the outcome is $j \ne 0$, then the simulator notifies the channel to delete the message and output a $\textsf {rej}$ flag, and tells the key resource to prepare only the shorter key k. The distinguisher then sends a request to obtain the fresh key. So the final state held by the distinguisher interacting with the ideal system is

$$\begin{aligned} \zeta = {|\textsf {acc}\rangle \!\langle \textsf {acc}|} \otimes \tau ^{K} \otimes \tau ^L \otimes \left[ \left( I^M \otimes E^E_0 \right) {|\psi \rangle \!\langle \psi |}^{ME} \left( I^M \otimes \left( E^E_0\right) ^\dag \right) \right] \nonumber \\ {}+ \sum _{j \ne 0} {|\textsf {rej}\rangle \!\langle \textsf {rej}|} \otimes \tau ^{K} \otimes E^E_j \rho ^E \left( E^E_j\right) ^\dag , \end{aligned}$$

(7)

where $\tau ^K$ and $\tau ^L$ are fully mixed states and $\rho ^E = {{\mathrm{tr}}}_{M}({|\psi \rangle \!\langle \psi |}^{ME})$. One could append states $\bot ^L$ and $\bot ^M$ in the $\textsf {rej}$ branch of (7) so that both terms have the same number of registers; we omit them for simplicity.

In the real system, for the secret key $(k,\ell )$, the state before Bob’s measurement of the syndrome is given by

$$\begin{aligned}{|\varphi _{k,\ell }\rangle }^{SME}&= \sum _j \left( \left( U_k^{SM}\right) ^\dag P^{SM}_\ell P^{SM}_j P^{SM}_\ell U^{SM}_k \otimes E^E_j \right) {|0\rangle }^S {|\psi \rangle }^{ME} \\&= \sum _j (-1)^{(j,\ell )_{\text {Sp}}}\left( \left( U_k^{SM}\right) ^\dag P^{SM}_j U^{SM}_k \otimes E^E_j \right) {|0\rangle }^S {|\psi \rangle }^{ME}, \end{aligned}$$

where $(\cdot ,\cdot )_{\text {Sp}}$ denotes the symplectic product defined in (1). Let $\mathcal {J}^k_s$ be the set of indices j such that the error $P^{SM}_j$ produces a syndrome s when code k is used, i.e., $\left( U^{SM}_k \right) ^\dag P^{SM}_jU^{SM}_k = e^{i \theta _{k,j}}P^{S}_{s,z} \otimes P^M_{j'}$ for some $\theta _{k,j}$ (see (3) and discussion thereafter). For $j \in \mathcal {J}^k_s$, let

$$\begin{aligned} {|s\rangle }^S{|\psi _{j,k}\rangle }^{ME}&:= \left( \left( U^{SM}_k\right) ^\dag P^{SM}_j U^{SM}_k \otimes E^E_j \right) {|0\rangle }^S {|\psi \rangle }^{ME} \\&\; = e^{i \theta _{k,j}} \left( P^{S}_{s,z} \otimes P^M_{j'} \otimes E^E_j \right) {|0\rangle }^S {|\psi \rangle }^{ME}. \end{aligned}$$

Then

$$\begin{aligned} {|\varphi _{k,\ell }\rangle }&= \sum _s \sum _{j \in \mathcal {J}^k_s} (-1)^{(j,\ell )_{\text {Sp}}}\left( \left( U_k^{SM}\right) ^\dag P^{SM}_j U^{SM}_k \otimes E^E_j \right) {|0\rangle }^S {|\psi \rangle }^{ME} \\&= \sum _s \sum _{j \in \mathcal {J}^k_s} (-1)^{(j,\ell )_{\text {Sp}}} {|s\rangle }^S {|\psi _{j,k}\rangle }^{ME}. \end{aligned}$$

The next step in Bob’s protocol consists in measuring the syndrome. If $s=0$ is obtained, he outputs the message as well as the key $(k,\ell )$ and a flag $\textsf {acc}$. Otherwise he deletes the message, outputs k with the flag $\textsf {rej}$. The final state held be the distinguisher in this case is

$$\begin{aligned} \xi =&{|\textsf {acc}\rangle \!\langle \textsf {acc}|} \otimes \frac{1}{2^{\nu +2m+2n}} \sum _{k,\ell }{|k,\ell \rangle \!\langle k,\ell |} \\&\qquad \qquad \qquad \qquad \qquad \qquad \quad \otimes \sum _{j_1,j_2 \in \mathcal {J}^k_0} (-1)^{(j_1 \oplus j_2,\ell )_{\text {Sp}}}{|\psi _{j_1,k}\rangle \!\langle \psi _{j_2,k}|}^{ME} \\&{}+ {|\textsf {rej}\rangle \!\langle \textsf {rej}|} \otimes \frac{1}{2^{\nu +2m+2n}} \sum _{k,\ell }{|k\rangle \!\langle k|} \\&\qquad \qquad \qquad \qquad \qquad \qquad \otimes \sum _{s \ne 0} \sum _{j_1,j_2 \in \mathcal {J}^k_s} (-1)^{(j_1 \oplus j_2,\ell )_{\text {Sp}}} E^E_{j_1} \rho ^E \left( E^E_{j_2}\right) ^\dag , \end{aligned}$$

where we have used ${|\psi _{j,k}\rangle }^{ME} = \left( V^M_{k,j}\otimes E^E_j\right) {|\psi \rangle }^{ME}$ for some unitary $V^M_{k,j}$.

Setting

$$\begin{aligned} \zeta ^\textsf {acc}&:= \left( I^M \otimes E^E_0\right) {|\psi \rangle \!\langle \psi |}^{ME} \left( I^M \otimes \left( E_0^E\right) ^\dag \right) , \\ \zeta ^\textsf {rej}&:= \sum _{j \ne 0} E^E_j \rho ^E \left( E_j^E\right) ^\dag , \\ \xi ^\textsf {acc}_{k,\ell }&:= \sum _{j_1,j_2 \in \mathcal {J}^k_0} (-1)^{(j_1 \oplus j_2,\ell )_{\text {Sp}}}{|\psi _{j_1,k}\rangle \!\langle \psi _{j_2,k}|}^{ME}, \\ \xi ^\textsf {rej}_{k}&:= \frac{1}{2^{2m+2n}} \sum _{\ell ,s \ne 0} \sum _{j_1,j_2 \in \mathcal {J}^k_s} (-1)^{(j_1 \oplus j_2,\ell )_{\text {Sp}}} E^E_{j_1} \rho ^E \left( E_{j_2}^E\right) ^\dag , \end{aligned}$$

the distance between real and ideal systems may be written as

$$\frac{1}{2} \left\| \zeta -\xi \right\| _{{{\mathrm{tr}}}} = \frac{1}{2\cdot 2^{\nu +2m+2n}} \sum _{k,\ell }\left\| \zeta ^\textsf {acc}-\xi ^\textsf {acc}_{k,\ell }\right\| _{{{\mathrm{tr}}}} + \frac{1}{2 \cdot 2^{\nu }} \sum _{k}\left\| \zeta ^\textsf {rej}-\xi ^\textsf {rej}_{k}\right\| _{{{\mathrm{tr}}}}. $$

$\zeta ^\textsf {acc}$ and $\xi ^\textsf {acc}_{k,\ell }$ are both pure states, so using the fact that¹³

$$\begin{aligned} \frac{1}{2} \left\| {|\psi \rangle \!\langle \psi |} - {|\varphi \rangle \!\langle \varphi |}\right\| _{{{\mathrm{tr}}}} \le \left\| {|\psi \rangle }-{|\varphi \rangle }\right\| , \end{aligned}$$

(8)

we bound their distance as

$$\begin{aligned} \frac{1}{2} \left\| \zeta ^\textsf {acc}-\xi ^\textsf {acc}_{k,\ell }\right\| _{{{\mathrm{tr}}}}&\le \left\| \left( I^M \otimes E^E_0\right) {|\psi \rangle }^{ME} - \sum _{j \in \mathcal {J}^k_0} (-1)^{(j,\ell )_{\text {Sp}}} {|\psi _{j,k}\rangle }^{ME}\right\| \\&= \left\| \sum _{j \in \mathcal {J}^k_0 \setminus \{0\}} (-1)^{(j,\ell )_{\text {Sp}}} {|\psi _{j,k}\rangle }^{ME}\right\| \\&= \sqrt{\sum _{j_1,j_2 \in \mathcal {J}^k_0 \setminus \{0\}} (-1)^{(j_1 \oplus j_2,\ell )_{\text {Sp}}} {\langle \psi _{j_1,k}|\psi _{j_2,k}\rangle }}, \end{aligned}$$

where $\left\| {|a\rangle }\right\| = \sqrt{{\langle a|a\rangle }}$ is the vector 2-norm and we used the fact that ${|\psi _{0,k}\rangle }^{ME} = \left( I^M \otimes E^E_0\right) {|\psi \rangle }^{ME}$. From Jensen’s inequality and using (2) we obtain

$$\begin{aligned} \frac{1}{2 \cdot 2^{\nu +2m+2n}} \sum _{k,\ell } \left\| \zeta ^\textsf {acc}-\xi ^\textsf {acc}_{k,\ell }\right\| _{{{\mathrm{tr}}}}\qquad \qquad \qquad \quad \qquad \qquad \qquad \qquad \\ \begin{aligned}&\le \sqrt{ \frac{1}{2^{\nu +2m+2n}} \sum _{k,\ell } \sum _{j_1,j_2 \in \mathcal {J}^k_0 \setminus \{0\}} (-1)^{(j_1 \oplus j_2,\ell )_{\text {Sp}}} {\langle \psi _{j_1,k}|\psi _{j_2,k}\rangle }} \\&= \sqrt{ \frac{1}{2^{\nu }} \sum _{k} \sum _{j \in \mathcal {J}^k_0 \setminus \{0\}} {\langle \psi _{j,k}|\psi _{j,k}\rangle }}. \end{aligned} \end{aligned}$$

Finally, because the code is a strong purity testing code with error $\varepsilon$ and that ${\langle \psi _{j,k}|\psi _{j,k}\rangle } = {{\mathrm{tr}}}(E^E_j \rho ^E \left( E^E_j\right) ^\dag ) =: p_j$ with $\sum _j p_j = 1$, we get

$$\begin{aligned} \frac{1}{2|\mathcal {K}\Vert |\mathcal {L}|} \sum _{k,\ell } \left\| \zeta ^\textsf {acc}-\xi ^\textsf {acc}_{k,\ell }\right\| _{{{\mathrm{tr}}}}&\le \sqrt{ \frac{1}{|\mathcal {K}|} \sum _{j \ne 0} \sum _{k : j \in \mathcal {J}^k_0} {\langle \psi _{j,k}|\psi _{j,k}\rangle }} \\&= \sqrt{ \frac{1}{|\mathcal {K}|} \sum _{j \ne 0} \sum _{k : j \in \mathcal {J}^k_0} p_j} \\&\le \sqrt{\sum _{j \ne 0} \varepsilon p_j } \le \sqrt{\varepsilon }. \end{aligned}$$

In the reject branch of the real system we have

$$\begin{aligned} \xi ^\textsf {rej}_{k}&= \frac{1}{2^{2m+2n}} \sum _{\ell ,s \ne 0} \sum _{j_1,j_2 \in \mathcal {J}^k_s} (-1)^{(j_1 \oplus j_2,\ell )_{\text {Sp}}} E^E_{j_1} \rho ^E \left( E^E _{j_2}\right) ^\dag \\&= \sum _{s \ne 0} \sum _{j \in \mathcal {J}^k_s} E^E_{j} \rho ^E \left( E^E _{j}\right) ^\dag \\&= \sum _{j \notin \mathcal {J}^k_0} E^E_{j} \rho ^E \left( E^E _{j}\right) ^\dag , \end{aligned}$$

where we used again (2). Thus

$$\begin{aligned} \frac{1}{2 \cdot 2^{\nu }} \sum _{k}\left\| \zeta ^\textsf {rej}-\xi ^\textsf {rej}_{k}\right\| _{{{\mathrm{tr}}}}&= \frac{1}{2 \cdot 2^{\nu }} \sum _k \left\| \sum _{j \in \mathcal {J}^k_0 \setminus \{0\}} E^E_{j} \rho ^E \left( E^E _{j}\right) ^\dag \right\| _{{{\mathrm{tr}}}} \\&\le \frac{1}{2 \cdot 2^{\nu }} \sum _k \sum _{j \in \mathcal {J}^k_0 \setminus \{0\}} p_j \le \varepsilon /2. \end{aligned}$$

Putting all this together we get

$$\begin{aligned} \frac{1}{2} \left\| \zeta -\xi \right\| _{{{\mathrm{tr}}}} \le \sqrt{\varepsilon } + \varepsilon /2. \end{aligned}$$

We now consider the second case: the distinguisher first prepares a state ${|\psi \rangle }^{CE}$ and inputs the C part at Eve’s interface, then obtains the output at Bob’s interface. Note that in the ideal case the channel always outputs a $\textsf {rej}$ message at Bob’s interface. Thus, if the cipher is accepted by Bob—who outputs a state $\zeta ^\textsf {acc}$—the distinguisher must be interacting with the real system and can already output this guess. In the case of a rejection, it now holds a bipartite system KE—the recycled key K and its purifying system E. It then applies an isometry $U : \mathcal {H}_{KE} \rightarrow \mathcal {H}_{KME}$ to this system and inputs the M part of the resulting state at Alice’s interface. After which it obtains a cipher at Eve’s interface and holds the tripartite system KCE—the recycled key K, the cipher C and its internal memory E. We denote this state $\zeta$ in the ideal case and $\xi ^\textsf {rej}$ in the real case, and we need to bound

$$ \frac{1}{2} \left\| \zeta - \xi ^\textsf {rej}\right\| _{{{\mathrm{tr}}}} + \frac{1}{2} \left\| \xi ^\textsf {acc}\right\| _{{{\mathrm{tr}}}}.$$

In a first step, we assume that the state ${|\psi \rangle }^{CE}$ prepared by the distinguisher is an antisymmetric fully entangled state, which we denote ${|\varPsi ^-\rangle }^{CE} = \sum _x (-1)^{w(x)}{|x,\bar{x}\rangle }^{CE}$, where w(x) is the Hamming weight of $x \in \{0,1\}^{m+n}$ and $\bar{x}$ is the string x with all bits flipped. In the ideal case the simulator notifies the channel to reject the cipher, and the state ${|\textsf {rej}\rangle \!\langle \textsf {rej}|} \otimes \tau ^K$ is output at Bob’s interface. The distinguisher then holds $\zeta = \tau ^K \otimes \tau ^E$. In the real case, Bob applies the decoding algorithm, i.e., first a Pauli $P^C_\ell$, then a unitary $\left( U^C_k\right) ^\dag$ and finally measures n bits of the syndrome in the computational basis. Since the antisymmetric state is invariant under $U \otimes U$, one could equivalently apply the inverse operation, $P_\ell U_k$, to the E system, i.e., the state after Bob’s measurement is given by

$$\begin{aligned} \frac{1}{2^{\nu +3m+3n}} \sum _{k,\ell ,s,x_1,x_2} (-1)^{w(x_1) \oplus w(x_2)} {|k,\ell \rangle \!\langle k,\ell |}\qquad \qquad \qquad \qquad \quad \qquad \\ {}\otimes \left( I^C \otimes P^E_\ell U^E_k \right) {|s,x_1,\bar{s},\bar{x}_1\rangle \!\langle s,x_2,\bar{s},\bar{x}_1|}^{CE} \left( I^C \otimes \left( U _k^E\right) ^\dag P^E_\ell \right) . \end{aligned}$$

If $s=0$ Bob accepts the cipher as being valid, which happens with probability $2^{-n}$, i.e., $\left\| \xi ^\textsf {acc}\right\| _{{{\mathrm{tr}}}} = 2^{-n}$. In the case where $s \ne 0$, he deletes the cipher, so the remaining state is given by

$$\begin{aligned} \frac{1}{2^{\nu +3m+3n}} \sum _{k,\ell ,s \ne 0,x} {|k,\ell \rangle \!\langle k,\ell |} \otimes \left( I^C \otimes P^E_\ell U^E_k \right) {|\bar{s},\bar{x}\rangle \!\langle \bar{s},\bar{x}|}^{CE} \left( I^C \otimes \left( U_k^E\right) ^\dag P^E_\ell \right) \\ = \tau ^K \otimes \tau ^L \otimes \tau ^E - \rho ^{KLE}, \end{aligned}$$

where

$$ \rho ^{KLE} = \frac{1}{2^{\nu +3m+3n}} \sum _{k,\ell ,x} {|k,\ell \rangle \!\langle k,\ell |} \otimes P^E_\ell U^E_k {|\bar{0},\bar{x}\rangle \!\langle \bar{0},\bar{x}|}^{E} \left( U^E_k\right) ^\dag P^E_\ell ,$$

K is made public and the L system is the part of the key kept secret by the players.

Let $\mathcal {E}$ denote the completely positive, trace-preserving (CPTP) map consisting of the distinguisher’s next step—the isometry $U : \mathcal {H}_{KE} \rightarrow \mathcal {H}_{KME}$—and the final operation of the ideal system—deleting the message system M that is input at Alice’s interface and outputting a fully mixed state $\tau ^C$. Let $\mathcal {F}$ denote the CPTP map consisting of the distinguisher’s next step and the final operation of the real system—encoding the message system M according to the protocol and outputting the resulting cipher. We have $\zeta = \mathcal {E}\left( \tau ^K \otimes \tau ^E \right)$ and $\xi ^\textsf {rej}= \mathcal {F}\left( \tau ^K \otimes \tau ^L \otimes \tau ^E \right) -\mathcal {F}\left( \rho ^{KLE}\right)$. Thus,

$$\begin{aligned} \frac{1}{2} \left\| \zeta - \xi ^\textsf {rej}\right\| _{{{\mathrm{tr}}}} \le \frac{1}{2} \left\| \mathcal {E}\left( \tau ^K \otimes \tau ^E \right) - \mathcal {F}\left( \tau ^K \otimes \tau ^L \otimes \tau ^E \right) \right\| _{{{\mathrm{tr}}}} + \frac{1}{2}2^{-n}, \end{aligned}$$

since $\left\| \rho ^{KLE}\right\| _{{{\mathrm{tr}}}} = 2^{-n}$. Finally, note that we have

$$\begin{aligned} \mathcal {E}\left( \tau ^K \otimes \tau ^E \right) = \mathcal {F}\left( \tau ^K \otimes \tau ^L \otimes \tau ^E \right) = \tau ^C \otimes \sigma ^{KE} \end{aligned}$$

for $\sigma ^{KE} = {{\mathrm{tr}}}_{M}\left[ U \left( \tau ^K \otimes \tau ^E\right) U^\dag \right]$, since the random Pauli $P_\ell$ applied by the encryption algorithm completely decouples the cipher from KE. Putting this together, we get

$$\begin{aligned} \frac{1}{2} \left\| \zeta - \xi \right\| _{{{\mathrm{tr}}}} \le 2^{-n} \le \sqrt{\varepsilon } , \end{aligned}$$

since a strong purity testing code will always have an error $\varepsilon \ge \frac{2^{2m+n}-1}{2^{2m+2n}-1} \ge 2^{-2n}$.

The final case that remains to consider is when the distinguisher prepares a state ${|\psi \rangle }^{CE}$ that is not the antisymmetric state. We will reduce this case to that of the entangled antisymmetric by using the entangled state ${|\Psi ^-\rangle }^{CE}$ to teleport the $C'$ part of any state ${|\psi \rangle }^{C'E'}$. Due to space restrictions, the proof of this case is provided in the full version of this work [27].    $\square$

3.5 Optimality of the Recycled Key Length

It follows from Lemma 5 that Theorem 7 is also a proof of security for the encrypt-then-encode protocol from Fig. 7, i.e.,

$$\mathcal {C}_\square \Vert \mathcal {A}_\lozenge \Vert \mathcal {K}^{\nu +2m+n} \xrightarrow {\bar{\pi }^\text {q-auth}_{AB},\varepsilon ^{\text {q-auth}}} (\mathcal {S}^m \Vert \bar{\mathcal {K}}^{\nu ,\nu +2m+n})_\flat ,$$

with $\varepsilon ^{\text {q-auth}} = \sqrt{\varepsilon }+\varepsilon /2$. Thus, in the case where the message is not accepted by Bob, $2m+n$ bits of key are lost. We prove here that this is optimal: one cannot recycle any extra bit of key.

Lemma 8

There exists an adversarial strategy to obtain all the secret bits that are not recycled in the encrypt-then-encode protocol.

Proof

The distinguisher prepares EPR pairs ${|\varPhi \rangle }^{ME}$ and provides the M part to Alice. It then receives the cipher and thus holds the state

$$ U^{SM}_k P^M_{\ell } \left( {|s\rangle }^S \otimes {|\varPhi \rangle }^{ME} \right) , $$

which it keeps. It then sends a bogus cipher to Bob, and obtains the key k after Bob recycles it. It applies the decoding unitary $\left( U^{SM}_k\right) ^\dag$, measures the S register to get the secret key s and measures the joint ME register in the Bell basis to get the secret key $\ell$.    $\square$

3.6 Explicit Constructions

The protocols we have given in Sect. 3.3 use strong purity testing codes, and the parameters of the key used, key recycled and error depend on the parameters of these codes. In this section we give two constructions of purity testing codes. The first requires less initial secret key, the second has a better error parameter. Both have the same net consumption of secret key bits.

The first construction is from Barnum et al. [3]. They give an explicit strong purity testing code with $\nu = n$ and $\varepsilon = \frac{2m/n+2}{2^n}$.¹⁴ Plugging this in the parameters from Theorem 7 with the encrypt-then-encode protocol, we get the following.

Corollary 9

The encrypt-then-encode protocol with the purity testing code of [3] requires an initial key of length $2m+2n$. It recycles all bits if the message is accepted, and n bits if the message is rejected. The error is

$$\varepsilon ^{\text {q-auth}} =\sqrt{\frac{2m/n+2}{2^{n}}} + \frac{m/n+1}{2^n}.$$

The second construction we give is based on an explicit purity testing code by Chau [12]—though he does not name it this way. Chau [12] finds a set of unitaries $\mathcal {U}= \{U_k\}$ in dimension d such that, if k is chosen uniformly at random, any non-identity Pauli is mapped to every non-identity Pauli with equal frequency, i.e., $\forall P_j,P_\ell$ with $P_j \ne I$ and $P_\ell \ne I$,

$$\left| \left\{ U_k \in \mathcal {U}: U_k P_j U^\dag _k = e^{i \theta _{j,k,\ell }} P_\ell \right\} \right| = \frac{|\mathcal {U}|}{d^2-1},$$

where $e^{i \theta _{j,k,\ell }}$ is some global phase.

We prove in the full version of this work [27] that this is a strong purity testing code with $\varepsilon = 2^{-n}$ for $d = 2^{m + n}$. It also has $|\mathcal {U}| = 2^{m+n} \left( 2^{2m+2n} - 1\right)$, hence $\nu = m+n+\log \left( 2^{2m+2n} -1 \right) \le 3m+3n$. Note that when composed with Paulis as in the encode-then-encrypt protocol, $\{P_\ell U_k\}_{k,\ell }$ is a unitary 2-design [15, 16]. It follows that any (approximate) unitary t-design is a good quantum authentication scheme (see the full version of this work [27] for a formal proof).

Corollary 10

The encrypt-then-encode protocol with the purity testing code of [12] requires an initial key of length $5m+4n$. It recycles all bits if the message is accepted, and $3m+3n$ bits if the message is rejected. The error is $\varepsilon ^{\text {q-auth}} = 2^{-n/2} + 2^{-n-1}$.

4 Discussion and Open Questions

The family of quantum authentication protocols of Barnum et al. [3] as well as the subset analyzed in this work are large classes, which include many protocols appearing independently in the literature. The signed polynomial code [1, 4], the Clifford code [1, 9, 17] (which is a unitary 3-design [38, 40]) and the unitary 8-design scheme from [19] and all instances which use a strong purity testing code. Our results apply directly to the Clifford and unitary 8-design schemes—which have in the same error as the unitary 2-design scheme from Corollary 10. But the signed polynomial code uses an ECC on qudits, not qubits, so our proof does not cover this case, and would have to be adapted to do so.

The trap code [8, 9] is an example of a quantum authentication scheme that uses a purity testing code that is not a strong purity testing code, i.e., errors which do not modify the message do not necessarily provoke an abort. For example, if the adversary performs a simple bit flip in one position, this will provoke an abort with probability 2 / 3 in the variant from [8] and with probability 1 / 3 in the variant from [9], but leaves the message unmodified if no abort occurs. If the adversary learns whether Bob accepted the message or not, she will learn whether the ECC used detects that specific bit flip or not, and thus learn something about the key used to select the ECC. Hence, the players cannot recycle the entire key, even in the case where the message is accepted. The restriction to strong purity testing codes is thus necessary to recycle every bit. It remains open how many bits of key can be recycled with the trap code, but we conjecture that this bit leaked due the decision to abort or not is the only part of the key leaked, and the rest can be recycled.

Another quantum authentication scheme, Auth-QFT-Auth, has been proposed in [19], where the authors prove that some of the key can be recycled as well. We do not know if this scheme fits in the family from [3] or not.

In the classical case, almost strongly 2-universal hash functions [36, 39] are used for authentication, and any new family of such functions immediately yields a new MAC. Likewise, any new purity testing code provides a new quantum authentication scheme. However, it is unknown whether all quantum authentication schemes can be modeled as a combination of a one-time pad and a purity testing code, or whether there exist interesting schemes following a different pattern.

We have proven that a loss of $2m+n$ bits of key is inevitable with these schemes if the adversary tampers with the channel. In the case of the unitary 2-design scheme, which has the smallest error, this is $2m + 2 \log 1/\varepsilon + 2$ bits of key which are consumed. A loss of 2m bits will always occur, since these are required to one-time pad the message. It remains open whether there exist other schemes—which do not fit the one-time pad + purity testing code model—which recycle more key.

The initial preprint of this work suggested that one should also investigate whether it is possible to find a prepare-and-measure scheme to encrypt and authenticate a classical message in a quantum state, so that all of the key may be recycled if it is successfully authenticated. At the time of writing, a possible solution had already been found by Fehr and Salvail [18]. Their protocol is however not known to be composable, and it remains open to prove that it achieves the desired result in such a setting.