Abstract
Operational support as an area of process mining aims to predict the performance of individual cases and the overall business process. Although seasonal effects, delays and performance trends are well-known to exist for business processes, there is up until now no prediction model available that explicitly captures seasonality. In this paper, we introduce time series Petri net models. These models integrate the control flow perspective of Petri nets with time series prediction. Our evaluation on the basis of our prototypical implementation demonstrates the merits of this model in terms of better accuracy in the presence of time series effects.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Companies need to analyze their business processes to manage their operations and to tailor effective process-aware information systems. The amount and detail of available data on business processes has substantially increased with a more intensive usage of information systems in various domains of business and private life. Process mining techniques make use of such process data in facilitating automatic discovery, conformance analysis and operational support based on log data of actual process executions [2].
While discovery and conformance have been intensively studied recently, there exists a gap of work that approaches operational support from a time prediction perspective. The few examples in this area include a performance prediction model that captures levels of load as a context factor [9], queueing networks to model business processes with waiting lines [25], or time prediction based on transition systems and log data [4]. On the other hand, it is well established that business process performance is often influenced by periodic effects, trends and delays that can range from intra-day variance of task performance of a process participant to storm season in Australia multiplying lodged insurance claims [3]. Up until now, there is no model that allows us to integrate such effects with the control flow of a process.
Against this background, we introduce a formal model that combines Petri nets with the analytical power of time series analysis. In this way, we are able to directly represent periodic effects, trends and delays together with the control flow specification. Our model can be described as a specific kind of a stochastic Petri net, in which the distribution and weight of each transition is replaced with time series models. The formalism is flexible, in that it can use very simple statistical models, for example the average of durations, or also more complex time series models with seasonality and trend components. We extensively evaluate this model in synthetic settings and with a case study from real-life. This current paper supersedes our earlier work [23].
The remainder of this paper is structured as follows. Section 2 presents an introductory example and summarizes prior research on predictive models for operational support in business processes. The formal model with its semantics and the methods to enrich it is presented in Sect. 3. Then, in Sect. 4, we present the evaluation setting and results. Finally, we conclude in Sect. 5 and outline challenges for future research.
2 Background
This section discusses the background of our research. Section 2.1 presents an example to illustrate the problem. Section 2.2 summarizes prior research that combines Petri nets with time. Finally, Sect. 2.3 classifies approaches to time series analysis.
2.1 Illustrative Example
Business processes are subject to seasonality [4] and effects of delaying [25]. Such effects can be modeled as time series. Figure 1 shows a respective time series for the number of airline passengers per month in thousands. This dataset is from the textbook by Box et al. [6]. Note that there is an upwards trend denoting an overall increase. Also seasonal effects are visible in this data, which hints at more or less busy periods in the calendar year.
Monthly airline passenger counts in thousands [6]. The data shows a clear trend and also a yearly seasonal component can be observed.
Let us consider a travel agency that operates a call center to handle airline passenger bookings in this seasonal setting. A corresponding Petri net model is depicted in Fig. 2. It shows a call center process from the view of the customer calling. Places are depicted as circles and transitions as boxes. We have two kinds of transitions in this model. The transitions depicted as white boxes correspond to process events (e.g., a customer call is received, the voice receiving unit is left, the service ended). These transitions signal a change in the process state and correspond to progress of the case. The gray transitions are invisible to the system. When a customer calls, the voice receiving unit takes the call and provides routing to the corresponding service station. Customers can hang up, or be routed forward. Depending on whether the service station is busy, the customer needs to enter a queue first. If the customer is tired of waiting, they can hang up. They can also finish waiting in the queue to be served. Finally, the customer is connected to a service employee and when the service is finished, the process terminates.
Throughout this paper, we will use the Petri net formalism for modeling and prediction of business processes, more precisely the specific class of workflow nets [1]. We always assume the workflow net properties in this paper, and use the term Petri net instead. Petri nets are a versatile tool that allow us to capture behavioral relations, like concurrency, conflict and sequential behavior. They also allow us to capture repeated cycles in a process in a compact form. All common process modeling languages, no matter if imperative like BPMN, EPC, or UML Activity Diagram [15], or declarative such as Declare models [20] can be mapped to Petri nets. Therefore, by building on Petri nets, we effectively offer a means to predict durations for any model that has a Petri net representation.
2.2 Petri Nets and Time
Although there has been extensive research on combining Petri nets with time, there is until now no model available that directly integrates it with time series characteristics. However, various extensions to Petri nets have been proposed to capture the non-functional properties—like temporal performance—of systems.
After various approaches to incorporate fixed temporal aspect (e.g., fixed temporal durations for transitions, or interval bounded durations) researchers tried to better accommodate the fact that durations often have a stochastic nature. One of the first extensions in this direction was to enrich each transition in a Petri net with exponential firing rates and the resulting models are called stochastic Petri nets (SPN) [16]. These models are memory-less in their firing behavior. That is, their behavior is independent of the time spent in a certain state. This property makes SPN isomorphic to Markov chains [19]. To overcome this simplification and allow to natively model non-exponential durations, non-Markovian stochastic Petri nets were proposed. Latter allow for general modeling of the duration distributions of transitions [10]. All these models assume independence of durations within a process instance, and also between cases. An extension to capture dependence on the history of the current case was introduced in the notion of History dependent stochastic Petri nets [24]. Latter models allow us to capture an often encountered phenomenon in business processes with cycles: the probability to leave a cycle increases with each iteration. Note that Petri nets allow us to capture the dependence between cases and processes, by modeling all the cases and processes in one system. In this scenario, resources (e.g., human process participants, machines) can be represented as tokens that synchronize shared activities or create realistic queueing for scarce resources. Example works in this direction are from van der Alast [26] or the textbook by Zhou and Venkatesh [27]. Even queueing theory found its way into Petri nets by [5], where places in the net are representing queueing stations.
Besides Petri net based models, more abstract models building on transition systems were also proposed to predict remaining process durations [4]. These type of approaches extract a state s from the given observed process trace, and predict the average remaining durations of former cases that also passed through state s. Extensions to make these methods more accurate have been devised, for example to cluster cases based on the system load (i.e., the number of currently active process instances of a process) [9]. Another approach to predict the remaining time is based on feature-based regression of different characteristics of the case and works well, if the features are correlated to the remaining duration [7]. These methods work well, if process data is available to the process engine, and an extension of our approach with regression is certainly worthwhile to investigate, but out of scope for this paper.
These models, however, are unable to capture seasonality and trends in data. To our knowledge, we present in the following the first work integrating time series and Petri nets.
2.3 Time Series
Time series data arise naturally when monitoring processes over a given period of time. Time series analysis methods have the advantage of accounting for the fact that data observed over time might have an underlying internal structure. Hence, the goal of time series analysis is the understanding of this underlying structure and of the forces driving the observed data as well as forecasting of future events. More formally, a time series is defined as a sequence of observations at given times. We use the following notation to describe the past \(N\) observations: \(y _1, \ldots , y _{N}\). Further, we are interested in the value of a time series \(h\) steps ahead in the future, that is, we predict \(y _{N +h}\). The parameter \(h\) is called horizon, as it marks how far we would like to look ahead into the future to predict the parameter in question.
Observed time series data can be decomposed into several potential components: a random or shock component, a trend component (a systematic linear or non-linear tendency in the time series), and a seasonal component (patterns that repeat themselves in systematic time intervals). Other patterns in time series data might include autocorrelation (correlation with different lags of the data), also known as autoregressive AR processes, correlation with different lags of the shocks, called moving average (MA) processes, or both. Latter are called ARMA processes. One property necessary for predicting and modeling time series is stationarity, which requires a constant mean of the series. In general, non-stationary data is transformed to stationary data by differentiation.
There are different techniques for modeling and forecasting time series data [11]. The most popular ones include Exponential Smoothing and the Box-Jenkins ARIMA (AutoRegressive Integrated Moving Average) models, which except for incorporating AR and MA patterns can also account for seasonality components. Further, there are several naive approaches to forecasting, e.g., simply using the last observed value of the current time series as forecast. The large body of research dealing with forecasting for time series is concisely summarized in the review by de Gooijer and Hyndman [11].
In the following, we will denote as \(\mathbf {Y}\) the universe of time series models, i.e., models that when provided with a given time series \(\{y _1,\ldots ,y _{N} \}\) can be used to generate a prediction for the given forecast horizon. Note that we will not restrict the kind of models that can be used to certain kinds of time series models. In fact, in the evaluation, we will compare different approaches, from naive predictors to the automatic selection of a fitting ARIMA model.
3 Time Series Petri Nets
In this section, we describe the underlying model that we propose for encoding seasonality and trends in Petri nets. Consequently, we can use these enhanced model for example to predict remaining time of business processes. Section 3.1 introduces the time series Petri net (TSPN) model. Section 3.2 discusses the challenges of enriching Petri nets towards TSPN models. Section 3.3 clarifies our design decisions.
3.1 Definition and Semantics
In contrast to previous approaches that use Petri nets for performance modeling, we allow the model to encode correlations to previous observed values at given stations in the process, i.e., at the transitions. In this sense, the model we propose builds on the one of Schonenberg et al. [24], into which we integrate time series concepts such as correlations to previous instances which passed through the same part of the model. This allows us to capture seasonality in durations and decisions. For example, at Christmas more customers choose the gift wrapping option in the order process than normally. The choice between conflicting transitions is captured by dynamic weights which depend on time and on the previous trends or seasonal patterns that can be observed.
Given a plain model of a Petri net model as \( PN = (P,T,F,M _0)\), the TSPN is a model is defined as follows:
Definition 1 (Time Series Petri Net)
A TSPN is a six-tuple: TSPN \(= (P, T, F, M _0, \mathcal {C}, \mathcal {D})\), where \((P,T,F,M _0)\) is the basic underlying Petri net.
-
\(P \) is a set of places.
-
The set of transitions \(T= T_{I} \cup T_{T} \) is partitioned into immediate transitions \( T_{I} \) and timed transitions \( T_{T} \)
-
\(F\subseteq (P \times T) \cup (T\times P)\) is a set of connecting arcs representing flow relations.
-
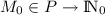 is an initial marking.
is an initial marking. -
\(\mathcal {C}: T_{I} \rightarrow \mathbf {Y} \) assigns to the immediate transitions their corresponding time series model that represents their firing rate (which can vary over time).
-
\(\mathcal {D}: T_{T} \rightarrow \mathbf {Y} \) is an assignment of time series models to timed transitions reflecting the durations of the corresponding process states.
This definition of TSPN models is aligned with the well-established generalized stochastic Petri net (GSPN) [18] model, where immediate transitions are responsible for routing decisions, and timed transitions represent durations between states in the process. The execution semantics of the TSPN model can be chosen from the combinations of conflict resolution and firing memory policies, as it is also available for non-Markovian stochastic Petri nets [17]. Without loss of generality, we assume that conflicts between immediate transitions are resolved probabilistically with respect to their estimated firing rates as forecast by their time series, and conflicts between concurrently enabled timed transitions are resolved by a race policy, that is, the fastest transition fires first. Those transitions that lose a race can keep their progress (i.e., we use the enabling memory policy) until they get disabled. Note that this choice is not binding, and other execution semantics (e.g., the preselection method), as discussed by Marsan could be substituted [17]. The approach does not specifically depend on a specific policy.
3.2 Challenges of Enriching Time Series Petri Nets
The enrichment process is closely following the algorithm as described for generally distributed transition stochastic Petri nets [21]. In a nutshell, the event log that contains the collected execution information of a process is replayed on the corresponding Petri net model. This Petri net can be either manually provided, or discovered from the event log by process mining techniques [2]. During the replay, we obey the semantics of the TSPN model, which are flexibly selected by the user. This way, we gather for every transition the time at which it fired, and also the time at which another conflicting transition fired instead. This information can be used to estimate the firing rates of transitions which possible change over time. The result is an enriched Petri net, where for each transition we collected the durations from enabling to firing with the associated timestamp of firing. This information then can be used to train (possibly time-dependent) models.
Various challenges and modeling options have to be considered for the construction of an appropriate model. We encountered the following challenges for enriching Petri net models to TSPN models.
Immediate Transitions. Without prior knowledge, transitions in Petri net models can be either immediate or timed transitions. Only by careful analysis of the durations can we decide whether a transition is immediate.
Irregularly Spaced Observations. Note that in contrast to common time series data, we consider durations of activities (or more generally durations of certain process states), where the gathered observations are irregularly spaced. See Fig. 3, which shows the durations for transport containers remaining at a harbor. In this case, the density of the collected observations clearly demonstrates that we collected more data points in August than in March.
Outliers. It can happen that the duration of an activity is a rather extreme value compared to the other values. There can be many possible reasons for outliers—e.g., coordination problems of process participants, rare cases that require more work than normally. Because outliers can negatively impact the accuracy of learned models, it can be beneficial to first remove outliers before learning the model parameters of a time series from data.
Decision Probabilities. In business processes that capture choices with regard to the following path in the process, decisions can be modeled as probabilistic choices. We need to find a way that allows us to capture temporal patterns and dependencies in the decision probabilities. Typically, immediate transitions are equipped with static weights that do not capture this aspect.
Hidden Patterns and Model Selection. It is no trivial task to identify the appropriate model that fits the observed data well and also generalizes to future data. Sometimes, it is surprising how complex models with many parameters are fitted to data, but do not generalize well to new observations. The difficulty lies in the balance between overfitting and generalization [12].
Negative Values. Time series models are usually agnostic of the sign of the data (be it positive or negative). That is, they usually have no mechanism to stay in the positive region. In our setting, we have durations and firing rates of transitions, which need always be positive.
Besides these challenges, we highlight an important technical detail, as it might be easily missed when constructing time series from such collected data: The collected data is recorded when the transitions fire. However, as the model should represent the duration of a transition in dependence of the time, we need to shift the observation to the point in time when the state was entered.
3.3 Design Decisions for the Enrichment of Time Series Petri Nets
In this section, we discuss possible solutions to these challenges, and the solutions we chose to implement for a prototypical evaluation.
Detecting Immediate Transitions. Our proposed solution to identify immediate transitions is to check whether the a specific percentile (e.g. the 95th percentile) of the collected values is below a user defined (small) threshold. This way, the method is robust to minor differences in system times in distributed settings, and also robust to a limited number of outliers in the data (e.g., 5%).
Avoiding Irregularly Spaced Observations. We apply a straight-forward technique to convert irregularly spaced time series into equidistant observations, which is aggregation to a coarser grained time unit. For example, one can aggregate the durations of a given activity to an hourly basis using the average of the observations in each hour as the aggregate value. By this transformation, seasonal patterns are easier to identify, as the averages of each morning at 10 am are 24 observations apart, with a weekly period of \(24 \cdot 7 = 168\). Note that the best granularity of abstraction (e.g., hourly, daily, weekly) depends on the frequency of observations and will vary between processes, and perhaps also between different transitions in one model.
Removing Outliers and Missing Values. One way to deal with outliers is to remove them from the training data to which we want to fit the time series models. There exist ways to detect temporal outliers in business processes [22], which we could use to identify a certain number of the most extreme values. Further, there also exists an implementation in R, which we use to remove outliers and missing values from time series data.Footnote 1
Using Time Series to Model Decision Probabilities. Our goal is to keep the model consistent. That is, we also want to be able to capture decision probabilities that vary over time, not only to allow for durations of activities to be dependent on time. Thus, in contrast to [21], we do not only count the number of times a certain decision was taken in comparison to the conflicting decisions, but capture the count of transition firings as the time series of the immediate transition. Let us consider a case of two conflicting transitions. By aggregating the counts on an hourly basis, we can determine the firing rate of these transitions in the next hour as the ratio between the two forecasts of the corresponding time series models. Thereby, we can effectively capture temporal patterns (e.g., seasonal components, trends) in the decision probabilities of TSPN models.
Identifying Hidden Patterns and Selecting Models. To create a plausible prediction model, we need to integrate domain knowledge of experts, who understand the business processes. There is no silver bullet solution for modeling the data, although the recent advancements in computational power and techniques enable us to automate parts of the analyses that statisticians do—see for example the automatic statistician research projectFootnote 2. Here, we keep the implementation of the model open such that any model that can be applied to time series data can be plugged into the transitions.
As a use case, we selected the auto.arima() function provided in the forecast package in R [14]. The auto.arima() function fits a number of different ARIMA time series models with varying parameters and selects the one that yields the best tradeoff in accuracy and model complexity. Additionally, we implemented further naive time series predictors to compare prediction accuracies.
Avoiding Negative Values. Imagine a negative trend in the durations of an activity—perhaps caused by a process participant getting more efficient in handling cases over time. If we simply extrapolate a negative trend when forecasting, we will eventually forecast negative duration values, which we need to avoid. To prevent this effect, whenever a model forecasts negative durations, we replace these negative forecast values with 0. Alternative solutions would be to use log-transforms data and predict in the log-space, and then to transform the predictions back by exponentiation. We did not use the latter approach, as it has problems with dealing with zero values. Zero values occur naturally in our setting, e.g., when a transition is not fired in a time unit of aggregation, the count value is 0. This would then entail more complex treatment.
Now that we discussed possible solutions to the challenges, let us focus on the most critical challenge for integrating time series approaches with business process models: the challenge of irregularly spaced data points. Note that ignoring this issue and simply treating the inter-arrival times between cases at a processing step would destroy the option to capture seasonality. Thus, we seek another solution that maintains the temporal patterns and allows us to capture patterns as introduced in Fig. 1.
There is an important trade-off, which we need to keep in mind using the approach of aggregation. On the one hand, we gain efficiency, that is, we can reuse a forecast value for one hour for all the cases that need a forecast in that hour. On the other hand, we lose the patterns inside the unit of aggregation. Additionally, if we choose a too narrow time unit, we will end up with a lot of time units with missing values (time units, in which no single case was observed). Therefore, the aggregation level should be based on the expected granularity of the seasonal patterns. In the following, we shall evaluate the TSPN formalism with respect to its predictive performance in synthetic and real settings.
4 Evaluation
In the previous section, we presented a novel approach to capture temporal dependencies within business processes. To evaluate its usefulness in the business process domain, we first evaluate the model’s predictive performance with synthetic process models. This way, we are able to identify possible conceptual advantages of the model given clean data that follows seasonal patterns. That is, we are interested in answering the question of how much better a time series model would be in comparison to models that do not incorporate temporal dependency structures, in a setting with clear temporal dependency structures. Section 4.1 defines the setting of our experiments. Section 4.2 describes the compared models. Section 4.3 shows the results. Section 4.4 discusses the merits of our model.
4.1 Experimental Setting
To conduct the experiment, we created TSPN models with 10 activities in sequence (we do not use complex control flow structures, because we want to isolate the prediction performance and not distort the results with synchronization effects). The activities have either a sinusoidal pattern (representing a seasonal pattern) of follow a random ARMA process. More specifically, the process parameters are randomly drawn according for the following processes.
The sinusoidal process uses the following equation given a time point \(t \):
Here, \(\alpha \) is the intercept or mean value, \(\gamma \) is the amplitude and \(\beta \) is the frequency. Additionally, the process has an attached normally distributed error term \(\epsilon \).
The ARMA process is generated by the following process:
This process consists of an autoregressive part with order n and parameters \(\alpha _1,\ldots ,\alpha _n\), and a moving average part with order m and parameters \(\beta _1,\ldots ,\beta _m\). It also includes a normally distributed error term \(\epsilon \).
We implemented the TSPN formalism in the open-source process mining software ProMFootnote 3. The package is freely available as open-source software and the synthetic data sets are provided for testing as well. Figure 4 shows a screenshot of the plug-in visualizing an enriched sinusoidal TSPN process. The main window shows the process structure, and the lower windows project some statistical information about the durations. From right to left this is the duration plotted as a scatter plot against the system load (i.e., the number of concurrently active cases), an aggregate plot of the collected duration values as a probability density function (middle), and the activity durations of the observed cases in relation to time (left). In this lower left screen, analysts can quickly identify temporal patterns in their process data, insofar as these are present.
After the creation of the synthetic models with their corresponding processes, we sample 10, 000 process instances from each model and thereby obtain the simulated event logs. We will use these logs to test how different time series models and time agnostic models for prediction based on Petri nets [21] are able to capture the patterns in the processes.
For the evaluation, we need to ensure that our predictions are only based on available data. Notably, we cannot rely on a usual cross-validation approach when using time series data. Instead, we need a rolling forecasting origin approach. With a rolling forecasting origin, the first k observations \(y _{1},\ldots ,y _{k}\) are used as training set to train the models that are then used to predict the next value with a forecast horizon \(h \). This procedure is repeated with the next forecast using the next observations \(y _{1+h},\ldots ,y _{k+h}\). In our case, we use 10% as training data and repeat this procedure for every further event in the event log.
Let us illustrate the approach with the example of predicting the duration of a single activity, which translates to predicting the firing time of the corresponding transition of the Petri net. In this case, the previous observations of that transition’s duration are aggregated into a time series of the desired granularity—in our case into hourly averages. These aggregates are used as training data to fit the models that we want to compare.
Having fit the models, we then want to predict the duration of an activity. Therefore, we check the timestamp at the prediction time and compare it to the last observation’s timestamp. The difference of the timestamps in hours is the forecast horizon h. For example, if we want to predict the duration of the service station for a customer that just called on Monday morning at 8 am, and the last observation was on Friday evening at 6 pm, then the forecast horizon h is \(6+24+24+8 = 62\) h.
4.2 Compared Models
As mentioned in the previous section, we selected the auto.arima() based model, which ideally selects the best fitting representative of a family of ARIMA models. But we also implemented four naive predictors common to time series analysis [13, Chap. 2.3]. Let us denote the number of observations in the time series as \(N \), the predicted value of a model as \(\hat{y}\), and the forecast horizon as \(h \).
The average method completely ignores any temporal patterns. It predicts the next observation as the average of the values observed so far and is defined as:
The naive method uses the last observation as next predictor and ignores the horizon:
The seasonal naive method (with a season-parameter \(m \)) is similar to the naive one, but it uses the observation from the last season to predict the duration:
The drift method, allows the forecasts to linearly increase or decrease over time, where the amount of change over time (called the drift) is set as the average change of the historical data. So the forecast for time \(t +h \) is given by:
This is equivalent to drawing a line between the first and last observation, and extrapolating it into the future.
Further, we added two Petri net based time prediction models which do not consider seasonal or trend effects in the data. Namely, a GSPN model using exponential distributions, and a generally distributed transition stochastic Petri net (GDT_SPN) model based on a non-parametric Gaussian kernel regression for the distribution of the duration observations. These models serve as a reference for models without time series features.
Prediction results for the sequential process with (a) sinusoidal duration patterns and (b) random ARMA processes generating transition durations. All competing models were run with the rolling forecasting origin method. The prediction is made at each new observed event based on an event log of 10,000 cases and a rolling forecasting window of 1,000 cases.
4.3 Evaluation Results
We are interested in how well the models can predict the observed behavior out of sample. For each prediction iteration (i.e., when a new event is observed) we compare the predicted remaining process duration to the actual remaining duration recorded in the log. The difference between the forecast an the actual value is called prediction error. By aggregating the errors in certain measures, we can weight the prediction quality of the different models against each other.
Therefore, we measure the precision of the model as the bias, which is represented by the mean error, and look at two accuracy measures: The mean absolute error (MAE) and the root mean square error (RMSE). Latter is more sensitive to our model predicting values far off the observed values, while the MAE is an easily interpretable measure: It tells us that on average, our model makes an error of the size of the MAE.
Figure 5 shows the prediction results of the competing models for the sinusoidal duration pattern Fig. 5a and the ARMA-driven duration process Fig. 5b. It can be read from the plots showing the RMSEs and MAEs that the auto.arima() based model fits the sinusoidal pattern well in comparison to the naive methods. In the ARMA case, the auto.arima() method does not fully capture the pattern of the underlying process. We also see that the two naive methods (the naive method using the last observation and the drift method that adjusts the last observation with a drift) are converging. This is expected, as the prediction horizon is mostly only one step, because there are no gaps in the data.
Note that the TSPN based approaches taking into account temporal relationships outperform those comparison methods in terms of accuracy of prediction that cannot make use of the temporal patterns in the data (i.e., the GSPN, GDT_SPN, and the simple average TSPN models).
With these promising results on the synthetic data sets, we next return to our example that we introduced in Sect. 2.1. We use the Petri net depicted in Fig. 2 and a corresponding event log capturing 28 439 process instances of a call center process recorded in January 1999Footnote 4.
Prediction results for the call center case study. All competing models were run with the rolling forecasting origin method. The prediction is made at each new observed event for the model in Fig. 2 and an event log containing 28,439 cases from January 1999.
Figure 6 shows the prediction results for the call center case study. We conducted the same experiment as with the synthetic processes (i.e., first 10% cases as training data, then rolling forecasting for the next cases). Here, we observe that the differences of the various competing models are not substantial with the RMSE values of the predictors being in a similar range. This indicates, that this process does not have a temporal autocorrelation on hourly aggregate values that the compared forecast methods could exploit. However, it has to be noted that all time series predictors except for the auto.arima() perform equally well even without time series effects in the data. Latter creates a positive bias in the predictions and overestimates the durations, as can be seen on the graph for the right hand side in Fig. 6.
4.4 Discussion of the Results
The results presented here can be summarized as follows. In the presence of time series effects as in the synthetic logs, our TSPN models can effectively exploit these for making better predictions than standard stochastic Petri nets. In the absence of time series effects as in the real-life log case study, time series models perform equally well as the baseline. We observe that the auto.arima() function appears to be less robust in this case with partially creating biased estimates. Furthermore, it has to be noted that the temporal granularity might have an influence on the visibility of time series effects. For the case of the real-life data, we worked with hourly aggregates. At this stage, we cannot rule out that time series effects might be visible on a finer level. General guidelines for the choice of a specific aggregation level depend on the frequency of observations, but have to be inspected in future research.
5 Conclusion
With this paper we introduced the first model that integrates seasonal aspects and trends with the control flow structure of business process modeling. We provided the formal model with its semantics, enrichment and an open-source implementation accompanied by the synthetic test data.
There remain some open research challenges to analyze in future work. For example, the results in the selected case study imply that there is potential for improvement on how to best capture the exhibited patterns. One branch of future research is to investigate more sophisticated methods in time series that are able to capture irregularly spaced time series data [8]. Another branch is to automatically find the appropriate abstraction levels per transition. To tackle the overfitting issue, coarser grained time series models can be used and combined with the finer grained models in a weighted average fashion.
We feel that the potentials of time series methods are not yet fully unleashed with our approach. Different parameter settings influence the predictions. Optimal selection of parameters and time series models is an open challenge. To further increase the accuracy of predictions, the timetables and availabilities of resources could be captured. For that purpose, we envision an automatic integration of holidays and of working schedules into the models. Alternatively, an integration with resource-aware models (e.g., discovered queueing networks [25] would combine resource-based and seasonal effects.
Notes
- 1.
The tsclean() method in the forecast package in R provides automatic interpolation of missing values and removal of outliers.
- 2.
The Automatic Statistician project: http://www.automaticstatistician.com.
- 3.
See StochasticPetriNet package in ProM: http://www.promtools.org/.
- 4.
The data of the call center process is available at http://ie.technion.ac.il/ Labs/Serveng.
References
van der Alast, W.M.P.: The application of petri nets to workflow management. J. Circ. Syst. Comput. 8(1), 21–66 (1998)
van der Alast, W.M.P.: Process Mining - Discovery, Conformance and Enhancement of Business Processes. Springer, Heidelberg (2011)
van der Alast, W.M.P., Rosemann, M., Dumas, M.: Deadline-based escalation in process-aware information systems. Decis. Support Syst. 43(2), 492–511 (2007)
van der Alast, W.M.P., Schonenberg, H., Song, M.: Time prediction based on process mining. Inf. Syst. 36(2), 450–475 (2011)
Bause, F.: Queueing petri nets-a formalism for the combined qualitative and quantitative analysis of systems. In: 5th International Workshop on Petri Nets and Performance Models, Proceedings, pp. 14–23. IEEE (1993)
Box, G.E., Jenkins, G.M., Reinsel, G.C., Ljung, G.M.: Time Series Analysis: Forecasting and Control, 4th edn. Wiley, New York (2013)
Dongen, B.F., Crooy, R.A., van der Aalst, W.M.P.: Cycle time prediction: when will this case finally be finished? In: Meersman, R., Tari, Z. (eds.) OTM 2008. LNCS, vol. 5331, pp. 319–336. Springer, Heidelberg (2008). doi:10.1007/978-3-540-88871-0_22
Engle, R.F., Russell, J.R.: Autoregressive conditional duration: a new model for irregularly spaced transaction data. Econometrica 66(5), 1127–1162 (1998)
Folino, F., Guarascio, M., Pontieri, L.: Discovering context-aware models for predicting business process performances. In: Meersman, R., et al. (eds.) OTM 2012. LNCS, vol. 7565, pp. 287–304. Springer, Heidelberg (2012). doi:10.1007/978-3-642-33606-5_18
German, R.: Non-Markovian analysis. In: Brinksma, E., Hermanns, H., Katoen, J.-P. (eds.) EEF School 2000. LNCS, vol. 2090, pp. 156–182. Springer, Heidelberg (2001). doi:10.1007/3-540-44667-2_4
de Gooijer, J.G., Hyndman, R.J.: 25 years of time series forecasting. Int. J. Forecast. 22(3), 443–473 (2006)
Hand, D., Mannila, H., Smyth, P.: Principles of Data Mining. MIT press, Cambridge (2001)
Hyndman, R.J., Athanasopoulos, G.: Forecasting: principles and practice. OTexts (2014). https://www.otexts.org/book/fpp
Hyndman, R.J., Khandakar,Y.: Automatic time series for forecasting: the forecast package for R. Technical report, Monash University, Department of Econometrics and Business Statistics (2007)
Lohmann, N., Verbeek, E., Dijkman, R.: Petri net transformations for business processes – a survey. In: Jensen, K., Aalst, W.M.P. (eds.) Transactions on Petri Nets and Other Models of Concurrency II. LNCS, vol. 5460, pp. 46–63. Springer, Heidelberg (2009). doi:10.1007/978-3-642-00899-3_3
Marsan, M.A.: Stochastic petri nets: an elementary introduction. In: Rozenberg, G. (ed.) APN 1988. LNCS, vol. 424, pp. 1–29. Springer, Heidelberg (1990). doi:10.1007/3-540-52494-0_23
Balbo, G., Bobbio, A., Chiola, G., Conte, G., Cumani, A.: The effect of execution policies on the semantics and analysis of stochastic petri nets. IEEE Trans. Softw. Eng. 15, 832–846 (1989)
Marsan, M.A., Conte, G., Balbo, G.: A class of generalized stochastic petri nets for the performance evaluation of multiprocessor systems. ACM TOCS 2(2), 93–122 (1984)
Molloy, M.K.: On the integration of delay and throughput measures in distributed processing models. Ph.D. thesis, University of California, Los Angeles (1981)
Prescher, J., Ciccio, C.D., Mendling, J.: From declarative processes to imperative models. In: Proceedings of the 4th International Symposium on Data-driven Process Discovery and Analysis (SIMPDA), pp. 162–173 (2014)
Rogge-Solti, A., van der Aalst, W.M.P., Weske, M.: Discovering stochastic petri nets with arbitrary delay distributions from event logs. In: Lohmann, N., Song, M., Wohed, P. (eds.) BPM 2013. LNBIP, vol. 171, pp. 15–27. Springer, Heidelberg (2014). doi:10.1007/978-3-319-06257-0_2
Rogge-Solti, A., Kasneci, G.: Temporal anomaly detection in business processes. In: Sadiq, S., Soffer, P., Völzer, H. (eds.) BPM 2014. LNCS, vol. 8659, pp. 234–249. Springer, Heidelberg (2014). doi:10.1007/978-3-319-10172-9_15
Rogge-Solti, A., Vana, L., Mendling, J.: Time series petri net models - enrichment and prediction. In: Proceedings of the 5th International Symposium on Data-driven Process Discovery and Analysis (SIMPDA), Vienna, Austria, December 9–11, pp. 109–123 (2015)
Schonenberg, H., Sidorova, N., van der Aalst, W.M.P., Hee, K.: History-dependent stochastic petri nets. In: Pnueli, A., Virbitskaite, I., Voronkov, A. (eds.) PSI 2009. LNCS, vol. 5947, pp. 366–379. Springer, Heidelberg (2010). doi:10.1007/978-3-642-11486-1_31
Senderovich, A., Weidlich, M., Gal, A., Mandelbaum, A.: Queue mining for delay prediction in multi-class service processes. Inf. Syst. 53, 278–295 (2015)
van der Aalst, W.M.P.: Petri net based scheduling. Oper. Res. Spektrum 18(4), 219–229 (1996)
Zhou, M., Venkatesh, K.: Modeling, Simulation, and Control of Flexible Manufacturing Systems - A Petri Net Approach. vol. 6 of Series in Intelligent Control and Intelligent Automation. World Scientific, Singapore (1999)
Acknowledgement
This work was partially supported by the European Union’s Seventh Framework Programme (FP7/2007-2013) grant 612052 (SERAMIS).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 IFIP International Federation for Information Processing
About this paper
Cite this paper
Solti, A., Vana, L., Mendling, J. (2017). Time Series Petri Net Models . In: Ceravolo, P., Rinderle-Ma, S. (eds) Data-Driven Process Discovery and Analysis. SIMPDA 2015. Lecture Notes in Business Information Processing, vol 244. Springer, Cham. https://doi.org/10.1007/978-3-319-53435-0_6
Download citation
DOI: https://doi.org/10.1007/978-3-319-53435-0_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-53434-3
Online ISBN: 978-3-319-53435-0
eBook Packages: Computer ScienceComputer Science (R0)







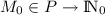 is an initial marking.
is an initial marking.


