Abstract
In this chapter the properties of descriptor revision, as defined in Chapter 4, are further explored. Several alternative selection mechanisms are presented, and the properties of the resulting operations are investigated. In one of these variants, the choice function is based on a relation on belief sets that can be interpreted as representing distances from the current belief set. In another, descriptor revision is constructed from a blockage relation on the outcome set (set of potential outcomes). A belief set blocks another belief set if the latter is ineligible as a revision outcome whenever the first is available. The different variants of descriptor revision are axiomatically characterized with plausible postulates. The controversial axioms discussed in Chapter 3 do not hold in the new framework. Finally, a binary relation on descriptors, the relation of epistemic proximity, is introduced. A descriptor is more epistemically proximate than another descriptor if some belief set satisfying it is closer at hand for the agent, or it can be satisfied with a less far-reaching change. For instance, \(\mathfrak {B}_p \succeq \lnot \mathfrak {B}_q\) denotes that it is closer at hand for the epistemic agent to believe in p than not to believe in q. Relations of epistemic proximity (between descriptors) generalize the relations of epistemic entrenchment (between sentences) that have been developed in the AGM framework. The translation is straight-forward: p is less entrenched than q if and only if \(\lnot \mathfrak {B}_p\) is more proximate than \(\lnot \mathfrak {B}_q\). The chapter also contains a section about indeterministic descriptor revision, in which the operation does not specify a single outcome for each input, but only a set of possible outcomes.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
In [124] the abbreviation \(\widehat{C}(\Psi )\) was used for \(\widehat{C}(\{X\in \mathbb {X}\mid X\Vdash \Psi \})\). The notation used here has the advantage of making it more clear among what objects the choice is made.
- 2.
On outcome sets, see also [121].
- 3.
Properties similar to uniformity have been employed in studies of operations on belief bases, see for instance [83, 88, 89].
- 4.
If we wish to avoid uniformity, then we can replace \(\widehat{C}\) by a function S on descriptors such that
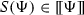 whenever
whenever  .
. - 5.
Similar density properties of the outcome sets of AGM operations are discussed in [121].
- 6.
Sentential belief revision and contraction have been criticized for credulity in this sense, see Section 3.2.
- 7.
Cf. Section 7.6.
- 8.
Relative success for sentential revision, “either \(K*p\vdash p\) or \(K*p=K\)”, was introduced in [213, p. 54] and used for instance in [137]. The corresponding postulate for contraction, “\(K\div p\nvdash p\) or \(K\div p=K\)” was introduced in [51]. Regularity for sentential revision, “If \(K*q\vdash p\) then \(K*p\vdash p\)” was introduced in [137]. It is used in Chapter 8. The corresponding principle for contraction, “If \(K\div q\nvdash p\) then \(K\div p\nvdash p\)” was introduced in [51] under the name “persistence”. It is used in Chapters 9 and 10. Related properties are discussed in [179].
- 9.
A descriptor \(\Psi \) is truthful if and only if \(T\Vdash \Psi \), where T is the set of all true sentences.
- 10.
Similar constructions have been used in studies of non-prioritized sentential change, e.g. the set of retractable sentences in [51] and the set of credible sentences in [137]. David Makinson employed the converse notion of a core protected from change in [179].
- 11.
The global access set is the set of descriptors that can be satisfied after a finite number of applications of \(\circ \), \(\{\Psi \mid (\exists \Xi _1)...(\exists \Xi _n)(K \circ \Xi _1 \circ {\dots } \circ \Xi _n \Vdash \Psi )\}\). For a modal account of this notion of access, see Section 7.6.
- 12.
This is analogous to single sentence logical closure in sentential revision, see [137, p. 1583] and [99, p. 31].
- 13.
The sentential cumulativity postulate seems to have appeared in the belief revision literature for the first time in [184, p. 198]. It has often been divided into two parts,
If \(K*p\vdash q\) then \( K*p\subseteq K*(p \& q)\) (cautious monotony) and
If \(K*p\vdash q\) then \( K*(p \& q)\subseteq K*p\) (cut),
whose names derive from their close relationships with patterns of nonmonotonic reasoning with the same names. [213, p. 49] On these postulates, see also [217].
- 14.
Reciprocity seems to have been introduced independently in [3, p. 32] and [67, p. 97]. It has been further discussed for instance in [174, p. 354] where it was called the Stalnaker property, and in [184, p. 198], [217, p. 110], and [222].
- 15.
The deterministic variant of this construction will be investigated in detail in Chapter 8.
- 16.
To prove this note that \(\text {Cn}(\{p\})\cap \text {Cn}(\{q\})=\text {Cn}(\{p\vee q\})\), thus \(\text {Cn}(\{p\})\cap \text {Cn}(\{q\})\subseteq \text {Cn}(\{r, p\vee q\})\). –Too be more precise: For all sentences \(x \in \text {Cn}(\{p\})\cap \text {Cn}(\{q\})\): (1) If \(x\in \text {Cn}(\varnothing )\), then \(K*x=K\). (2) If \(x\notin \text {Cn}(\varnothing )\), then \(K*x=\text {Cn}(\{r, p\vee q\})\).
- 17.
Suppose there is some sentence x such that \(K*x\) will not be the same in the two constructions. (1) x must be an element of at least one of the four elements of \(\mathbb {X}\) since otherwise \(K*x=K\) in both constructions. (2) x cannot be an element of either K or \(\text {Cn}(\{r, p\vee q\})\), since then the outcome would be the same in both constructions. (3) x cannot be an element of both \(\text {Cn}(\{p\})\) and \(\text {Cn}(\{q\})\) since then either \(K*x=K\) in both constructions (if x is a tautology) or (else) \(K*x=\text {Cn}(\{r, p\vee q\})\) in both constructions, for the reasons given in footnote 16. (4) If \(\text {Cn}(\{p\})\) is the only element of \(\mathbb {X}\) that contains x, then \(K*x=\text {Cn}(\{p\})\) in both constructions. (5) If \(\text {Cn}(\{q\})\) is the only element of \(\mathbb {X}\) that contains x, then \(K*x=\text {Cn}(\{q\})\) in both constructions.
- 18.
This follows from Theorem 8.8.
- 19.
Blockage relations were first introduced in [116] where they were used to construct an operation of contraction.
- 20.
Cf. [116, pp. 418-419], [130, 222].
- 21.
To see this, let \(\mathbb {X}=\{K,X,Y,Z, W\}\), and let \(\circ \) be based on a monoselective choice function \(\widehat{C}\) such that \(\widehat{C}(\mathbb {Y})=K\) whenever \(K\in \mathbb {Y}\subseteq \mathbb {X}\) and that \(\widehat{C}(\{X, Y\})=X\), \(\widehat{C}(\{X, Z\})=Z\), \(\widehat{C}(\{X, W\})=X\), \(\widehat{C}(\{Y, Z\})=Y\), \(\widehat{C}(\{Y, W\})=W\), \(\widehat{C}(\{Z, W\})=Z\), \(\widehat{C}(\{X,Y, Z\})=X\), \(\widehat{C}(\{X,Z, W\})=W\), \(\widehat{C}(\{Y,Z, W\})=Z\), \(\widehat{C}(\{X,Y, W\})=W\), and \(\widehat{C}(\{X,Y,Z, W\})=Y\). Furthermore, let \(\widehat{C}'\) coincide with \(\widehat{C}\) with the sole exception that \(\widehat{C}'(\{X, Y\})=Y\), and let \(\circ '\) be based on \(\widehat{C}'\). Then \(\circ \) and \(\circ '\) give rise to the same blockage relation namely \(\rightharpoondown =\{\langle K,X,\rangle ,\langle K,Y\rangle ,\langle K,Z\rangle , \langle K, W\rangle \}\). However, \(K\circ (\Pi _X\veebar \Pi _Y)=X\) and \(K\circ '(\Pi _X\veebar \Pi _Y)=Y\).
- 22.
This applies to deterministic revision. In indeterministic blockage revision all unblocked elements of
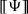 will be elements of \(K\check{\circ }\Psi \), and case (3) does not apply.
will be elements of \(K\check{\circ }\Psi \), and case (3) does not apply. - 23.
If this assumption is not made, then the outcome set is equal to \(\{K \} \cup \{X \in \mathbb {X} \mid X \rightharpoondown \!\!\!\!\!\! \hbox {\small {/}} \,\,\,\,\, X \}\), where \(\mathbb {X}\) is the repertoire.
- 24.
Its sentential analogue, “If \(K*p=K*q\) then \(K*p=K*(p\vee q)\)”, holds for transitively relational AGM revision. It does not seem to have been referred to in the belief revision literature, but it is a trivial consequence of the postulate of disjunctive factoring (Either \(K*(p\vee q)=K*p\) or \(K*(p\vee q)=K*q\) or \(K*(p\vee q)=K*p\cap K*q\)) that holds for transitively relational AGM revision. (Disjunctive factoring was proved by Hans Rott and first reported in [69, pp. 57, 212, and 244].)
- 25.
A relation
 satisfies weak connectedness if and only if it holds for all X and Y that if \(X\ne Y\), then either
satisfies weak connectedness if and only if it holds for all X and Y that if \(X\ne Y\), then either  or
or  . See [56, p. 11].
. See [56, p. 11]. - 26.
- 27.
To see that \(\bigcup \{\Psi \mid \Psi \simeq \mathfrak {B}{\scriptstyle \top }\}\) is maxispecified, note that for all \(p\in \mathcal {L}\), due to amplification either \(\{\mathfrak {B}{\scriptstyle \top },\mathfrak {B}p\} \simeq \{\mathfrak {B}{\scriptstyle \top }\}\) or \(\{\mathfrak {B}{\scriptstyle \top },\lnot \mathfrak {B}p\} \simeq \{\mathfrak {B}{\scriptstyle \top }\}\). It follows that for all \(p\in \mathcal {L}\), either \(\mathfrak {B}p \in \bigcup \{\Psi \mid \Psi \simeq \mathfrak {B}{\scriptstyle \top }\}\) or \(\lnot \mathfrak {B}p \in \bigcup \{\Psi \mid \Psi \simeq \mathfrak {B}{\scriptstyle \top }\}\). It remains to show that \(\bigcup \{\Psi \mid \Psi \simeq \mathfrak {B}{\scriptstyle \top }\}\) specifies a belief set. If not, then there is some p with \(\mathfrak {B}{\scriptstyle \top }\simeq \mathfrak {B}p\) and \(\mathfrak {B}{\scriptstyle \top }\simeq \lnot \mathfrak {B}p\). Due to coupling and transitivity,
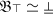 . Due to counter-dominance, \(\mathfrak {B}{\scriptstyle \top }\succeq \Psi \) for all \(\Psi \), and transitivity yields
. Due to counter-dominance, \(\mathfrak {B}{\scriptstyle \top }\succeq \Psi \) for all \(\Psi \), and transitivity yields  for all \(\Psi \), contrary to absurdity avoidance.
for all \(\Psi \), contrary to absurdity avoidance. - 28.
This is explained in Section 9.3.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this chapter
Cite this chapter
Hansson, S.O. (2017). Local Descriptor Revision. In: Descriptor Revision. Trends in Logic, vol 46. Springer, Cham. https://doi.org/10.1007/978-3-319-53061-1_5
Download citation
DOI: https://doi.org/10.1007/978-3-319-53061-1_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-53060-4
Online ISBN: 978-3-319-53061-1
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


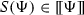 whenever
whenever  .
.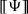 will be elements of
will be elements of  satisfies weak connectedness if and only if it holds for all X and Y that if
satisfies weak connectedness if and only if it holds for all X and Y that if  or
or  . See [56, p. 11].
. See [56, p. 11].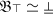 . Due to counter-dominance,
. Due to counter-dominance,  for all
for all