Efficient Continuous Relaxations for Dense CRF

Abstract

Dense conditional random fields (CRF) with Gaussian pairwise potentials have emerged as a popular framework for several computer vision applications such as stereo correspondence and semantic segmentation. By modeling long-range interactions, dense CRFs provide a more detailed labelling compared to their sparse counterparts. Variational inference in these dense models is performed using a filtering-based mean-field algorithm in order to obtain a fully-factorized distribution minimising the Kullback-Leibler divergence to the true distribution. In contrast to the continuous relaxation-based energy minimisation algorithms used for sparse CRFs, the mean-field algorithm fails to provide strong theoretical guarantees on the quality of its solutions. To address this deficiency, we show that it is possible to use the same filtering approach to speed-up the optimisation of several continuous relaxations. Specifically, we solve a convex quadratic programming (QP) relaxation using the efficient Frank-Wolfe algorithm. This also allows us to solve difference-of-convex relaxations via the iterative concave-convex procedure where each iteration requires solving a convex QP. Finally, we develop a novel divide-and-conquer method to compute the subgradients of a linear programming relaxation that provides the best theoretical bounds for energy minimisation. We demonstrate the advantage of continuous relaxations over the widely used mean-field algorithm on publicly available datasets.

Joint first authors.

1 Introduction

Discrete pairwise conditional random fields (CRFs) are a popular framework for modelling several problems in computer vision. In order to use them in practice, one requires an energy minimisation algorithm that obtains the most likely output for a given input. The energy function consists of a sum of two types of terms: unary potentials that depend on the label for one random variable at a time and pairwise potentials that depend on the labels of two random variables.

Traditionally, computer vision methods have employed sparse connectivity structures, such as 4 or 8 connected grid CRFs. Their popularity lead to a considerable research effort in efficient energy minimisation algorithms. One of the biggest successes of this effort was the development of several accurate continuous relaxations of the underlying discrete optimisation problem [1, 2]. An important advantage of such relaxations is that they lend themselves easily to analysis, which allows us to compare them theoretically [3], as well as establish bounds on the quality of their solutions [4].

Recently, the influential work of Krähenbühl and Koltun [5] has popularised the use of dense CRFs, where each pair of random variables is connected by an edge. Dense CRFs capture useful long-range interactions thereby providing finer details on the labelling. However, modeling long-range interactions comes at the cost of a significant increase in the complexity of energy minimisation. In order to operationalise dense CRFs, Krähenbühl and Koltun [5] made two key observations. First, the pairwise potentials used in computer vision typically encourage smooth labelling. This enabled them to restrict themselves to the special case of Gaussian pairwise potentials introduced by Tappen et al. [6]. Second, for this special case, it is possible to obtain a labelling efficiently by using the mean-field algorithm [7]. Specifically, the message computation required at each iteration of mean-field can be carried out in O(N) operations where N is the number of random variables (of the order of hundreds of thousands). This is in contrast to a naïve implementation that requires $O(N^2)$ operations. The significant speed-up is made possible by the fact that the messages can be computed using the filtering approach of Adams et al. [8].

While the mean-field algorithm does not provide any theoretical guarantees on the energy of the solutions, the use of a richer model, namely dense CRFs, still allows us to obtain a significant improvement in the accuracy of several computer vision applications compared to sparse CRFs [5]. However, this still leaves open the intriguing possibility that the same filtering approach that enabled the efficient mean-field algorithm can also be used to speed-up energy minimisation algorithms based on continuous relaxations. In this work, we show that this is indeed possible.

In more detail, we make three contributions to the problem of energy minimisation in dense CRFs. First, we show that the conditional gradient of a convex quadratic programming (QP) relaxation [1] can be computed in O(N) complexity. Together with our observation that the optimal step-size of a descent direction can be computed analytically, this allows us to minimise the QP relaxation efficiently using the Frank-Wolfe algorithm [9]. Second, we show that difference-of-convex (DC) relaxations of the energy minimisation problem can be optimised efficiently using an iterative concave-convex procedure (CCCP). Each iteration of CCCP requires solving a convex QP, for which we can once again employ the Frank-Wolfe algorithm. Third, we show that a linear programming (LP) relaxation [2] of the energy minimisation problem can be optimised efficiently via subgradient descent. Specifically, we design a novel divide-and-conquer method to compute the subgradient of the LP. Each subproblem of our method requires one call to the filtering approach. This results in an overall run-time of $O(N\log (N))$ per iteration as opposed to an $O(N^2)$ complexity of a naïve implementation. It is worth noting that the LP relaxation is known to provide the best theoretical bounds for energy minimisation with metric pairwise potentials [2].

Using standard publicly available datasets, we demonstrate the efficacy of our continuous relaxations by comparing them to the widely used mean-field baseline for dense CRFs.

2 Related Works

Krähenbühl and Koltun popularised the use of densely connected CRFs at the pixel level [5], resulting in significant improvements both in terms of the quantitative performance and in terms of the visual quality of their results. By restricting themselves to Gaussian edge potentials, they made the computation of the message in parallel mean-field feasible. This was achieved by formulating message computation as a convolution in a higher-dimensional space, which enabled the use of an efficient filter-based method [8].

While the original work [5] used a version of mean-field that is not guaranteed to converge, their follow-up paper [10] proposed a convergent mean-field algorithm for negative semi-definite label compatibility functions. Recently, Baqué et al. [11] presented a new algorithm that has convergence guarantees in the general case. Vineet et al. [12] extended the mean-field model to allow the addition of higher-order terms on top of the dense pairwise potentials, enabling the use of co-occurence potentials [13] and $P^n$-Potts models [14].

The success of the inference algorithms naturally lead to research in learning the parameters of dense CRFs. Combining them with Fully Convolutional Neural Networks [15] has resulted in high performance on semantic segmentation applications [16]. Several works [17, 18] showed independently how to jointly learn the parameters of the unary and pairwise potentials of the CRF. These methods led to significant improvements on various computer vision applications, by increasing the quality of the energy function to be minimised by mean-field.

Independently from the mean-field work, Zhang and Chen [19] designed a different set of constraints that lends itself to a QP relaxation of the original problem. Their approach is similar to ours in that they use continuous relaxation to approximate the solution of the original problem but differ in the form of the pairwise potentials. The algorithm they propose to solve the QP relaxation has linearithmic complexity while ours is linear. Furthermore, it is not clear whether their approach can be easily generalised to tighter relaxations such as the LP.

Wang et al. [20] derived a semi-definite programming relaxation of the energy minimisation problem, allowing them to reach better energy than mean-field. Their approach has the advantage of not being restricted to Gaussian pairwise potentials. The inference is made feasible by performing low-rank approximation of the Gram matrix of the kernel, instead of using the filter-based method. However, while the complexity of their algorithm is the same as our QP or DC relaxation, the runtime is significantly higher. Furthermore, while the SDP relaxation has been shown to be accurate for repulsive pairwise potentials (encouraging neighbouring variables to take different labels) [21], our LP relaxation provides the best guarantees for attractive pairwise potentials [2].

In this paper, we use the same filter-based method [8] as the one employed in mean-field. We build on it to solve continuous relaxations of the original problem that have both convergence and quality guarantees. Our work can be viewed as a complementary direction to previous research trends in dense CRFs. While [10–12] improved mean-field and [17, 18] learn’t the parameters, we focus on the energy minimisation problem.

3 Preliminaries

Before describing our methods for energy minimisation on dense CRF, we establish the necessary notation and background information.

Dense CRF Energy Function. We define a dense CRF on a set of N random variables $\mathcal {X} = \left\{ X_{1}, \dots , X_{N}\right\}$ each of which can take one label from a set of M labels $\mathcal {L} = \left\{ l_{1}, \dots \, l_{M}\right\}$. To describe a labelling, we use a vector $\mathbf {x}$ of size N such that its element $x_{a}$ is the label taken by the random variable $X_{a}$. The energy associated with a given labelling is defined as:

$$\begin{aligned} E(\mathbf {x}) = \sum _{a=1}^{N}\phi _{a}(x_{a}) + \sum _{a=1}^{N}\sum _{\begin{array}{c} b=1\\ b \ne a \end{array}}^{N} \psi _{a,b}(x_{a}, x_{b}). \end{aligned}$$

(1)

Here, $\phi _{a}(x_{a})$ is called the unary potential for the random variable $X_{a}$ taking the label $x_{a}$. The term $\psi _{a,b}(x_{a}, x_{b})$ is called the pairwise potential for the random variables $X_{a}$ and $X_{b}$ taking the labels $x_{a}$ and $x_{b}$ respectively. The energy minimisation problem on this CRF can be written as:

$$\begin{aligned} \mathbf {x}^{\star } = \mathop {{{\mathrm{\arg \!\min }}}}\limits _{\mathbf {x}} E(\mathbf {x}). \end{aligned}$$

(2)

Gaussian Pairwise Potentials. Similar to previous work [5], we consider arbitrary unary potentials and Gaussian pairwise potentials. Specifically, the form of the pairwise potentials is given by:

$$\begin{aligned} \psi _{a,b}(i,j)= & {} \mu (i, j) \sum _{m} w^{(m)} k(\mathbf {f}^{(m)}_{a}, \mathbf {f}^{(m)}_{b}), \end{aligned}$$

(3)

$$\begin{aligned} k(\mathbf {f}_{a}, \mathbf {f}_{b})= & {} \exp \left( \frac{-\Vert \mathbf {f}_{a} - \mathbf {f}_{b}\Vert ^{2}}{2}\right) \end{aligned}$$

(4)

We refer to the term $\mu (i,j)$ as a label compatibility function between the labels i and j. An example of a label compatibility function is the Potts model, where $\mu _{\text {potts}}(i, j) = [i \ne j]$, that is $\mu _{potts}(i,j) = 1$ if $i \ne j$ and 0 otherwise. Note that the label compatibility does not depend on the image. The other term, called the pixel compatibility function, is a mixture of gaussian kernels $k(\cdot ,\cdot )$. The coefficients of the mixture are the weights $w^{(m)}$. The $\mathbf {f}^{(m)}_{a}$ are the features describing the random variable $X_{a}$. Note that the pixel compatibility does not depend on the labelling. In practice, similar to [5], we use the position and RGB values of a pixel as features.

IP Formulation. We now introduce a formulation of the energy minimisation problem that is more amenable to continuous relaxations. Specifically, we formulate it as an Integer Program (IP) and then relax it to obtain a continuous optimisation problem. To this end, we define the vector $\mathbf {y}$ whose components $y_{a}(i)$ are indicator variables specifying whether or not the random variable $X_{a}$ takes the label i. Using this notation, we can rewrite the energy minimisation problem as an IP:

$$\begin{aligned} \min \quad&\sum _{a=1}^{N} \sum _{i \in \mathcal {L}} \phi _{a}(i) y_{a}(i) + \sum _{a=1}^{N} \sum _{\begin{array}{c} b=1\\ b \ne a \end{array}}^{N} \sum _{i,j \in \mathcal {L}} \psi _{a,b}(i,j) y_{a}(i)y_{b}(j),\nonumber \\ \text {s.t. }&\sum _{i \in \mathcal {L}} y_{a}(i) = 1 \quad \forall a \in [1, N],\nonumber \\&y_{a}(i) \in \{0,1\} \quad \forall a \in [1, N] \quad \forall i \in \mathcal {L}. \end{aligned}$$

(5)

The first set of constraints model the fact that each random variable has to be assigned exactly one label. The second set of constraints enforce the optimisation variables $y_{a}(i)$ to be binary. Note that the objective function is equal to the energy of the labelling encoded by $\mathbf {y}$.

Filter-Based Method. Similar to [5], a key component of our algorithms is the filter-based method of Adams et al. [8]. It computes the following operation:

$$\begin{aligned} \forall a \in [1, N], \quad v^{\prime }_{a} = \sum _{b=1}^{N} k(\mathbf {f}_{a}, \mathbf {f}_{b}) v_{b}, \end{aligned}$$

(6)

where $v_{a}^{\prime }, v_{b} \in \mathbb {R}$ and $k(\cdot ,\cdot )$ is a Gaussian kernel. Performing this operation the naïve way would result in computing a sum on N elements for each of the N terms that we want to compute. The resulting complexity would be $\mathcal {O}(N^2)$. The filter-based method allows us to perform it approximately with $\mathcal {O}(N)$ complexity. We refer the interested reader to [8] for details. The accuracy of the approximation made by the filter-based method is explored in the supplementary material.

4 Quadratic Programming Relaxation

We are now ready to demonstrate how the filter-based method [8] can be used to optimise our first continuous relaxation, namely the convex quadratic programming (QP) relaxation.

Notation. In order to concisely specify the QP relaxation, we require some additional notation. Similar to [10], we rewrite the objective function with linear algebra operations. The vector $\varvec{\phi }$ contains the unary terms. The matrix $\varvec{\mu }$ corresponds to the label compatibility function. The Gaussian kernels associated with the m-th features are represented by their Gram matrix $\mathbf {K}^{(m)}_{a,b} = k(\mathbf {f}_{a}^{(m)}, \mathbf {f}_{b}^{(m)})$. The Kronecker product is denoted by $\otimes$. The matrix $\varvec{\varPsi }$ represents the pairwise terms and is defined as follows:

$$\begin{aligned} \varvec{\varPsi } = \varvec{\mu } \otimes \left( \sum _{m} \mathbf {K}^{(m)} - \mathbf {I}_{N} \right) , \end{aligned}$$

(7)

where $\mathbf {I}_{N}$ is the identity matrix. Under this notation, the IP (5) can be concisely written as

$$\begin{aligned} \min \quad&\varvec{\phi }^{T} \mathbf {y} + \mathbf {y}^{T} \varvec{\varPsi } \mathbf {y},\nonumber \\ \text { s.t. } \quad&\mathbf {y} \in \mathcal {I}, \end{aligned}$$

(8)

with $\mathcal {I}$ being the feasible set of integer solution, as defined in Eq. (5).

Relaxation. In general, IP such as (8) are NP-hard problems. Relaxing the integer constraint on the indicator variables to allow fractional values between 0 and 1 results in the QP formulation. Formally, the feasible set of our minimisation problem becomes:

$$\begin{aligned} \mathcal {M} = \left\{ \mathbf {y} \quad \text {such that} \quad \begin{aligned} \sum _{i \in \mathcal {L}} y_{a}(i)&= 1 \quad&\forall a \in [1, N],\\ y_{a}(i)&\ge 0&\forall a \in [1, N], \forall i \in \mathcal {L} \end{aligned}\right\} . \end{aligned}$$

(9)

Ravikumar and Lafferty [1] showed that this relaxation is tight and that solving the QP will result in solving the IP. However, this QP is still NP-hard, as the objective function is non-convex. To alleviate this difficulty, Ravikumar and Lafferty [1] relaxed the QP minimisation to the following convex problem:

$$\begin{aligned} \min&S_{cvx}(\mathbf {y}) = (\varvec{\phi } - \mathbf {d})^{T} \mathbf {y} + \mathbf {y}^{T}(\varvec{\varPsi } + \mathbf {D}) \mathbf {y},\nonumber \\ \text {s.t.}&\mathbf {y} \in \mathcal {M}, \end{aligned}$$

(10)

where the vector $\mathbf {d}$ is defined as follows

$$\begin{aligned} d_{a}(i) = \sum _{\begin{array}{c} b=1 \\ b \ne a \end{array}}^{N} \sum _{j \in \mathcal {L}} |\psi _{a,b}(i,j)|, \end{aligned}$$

(11)

and $\mathbf {D}$ is the square diagonal matrix with $\mathbf {d}$ as its diagonal.

Minimisation. We now introduce a new method based on the Frank-Wolfe Algorithm [9] to minimise problem (10). The Frank-Wolfe algorithm allows to minimise a convex function f over a convex feasible set $\mathcal {M}$. The key steps of the algorithm are shown in Algorithm 1. To be able to use the Frank-Wolfe algorithm, we need a way to compute the gradient of the objective function (Step 3), a method to compute the conditional gradient (Step 4) and a strategy to choose the step size (Step 5).

Gradient Computation

Since the objective function is quadratic, its gradient can be computed as

$$\begin{aligned} \nabla S_{\text {cvx}}(\mathbf {y}) = (\varvec{\phi } - \mathbf {d}) + 2 (\varvec{\varPsi } + \mathbf {D}) \mathbf {y}. \end{aligned}$$

(12)

What makes this equation expensive to compute in a naïve way is the matrix product with $\varvec{\varPsi }$. We observe that this operation can be performed using the filter-based method in linear time. Note that the other matrix-vector product, $\mathbf {D} \mathbf {y}$, is not expensive (linear in N) since $\mathbf {D}$ is a diagonal matrix.

Conditional Gradient

The conditional gradient is obtained by solving

$$\begin{aligned} \mathop {{{\mathrm{\arg \!\min }}}}\limits _{\mathbf {s} \in \mathcal {M}} \langle \mathbf {s}, \nabla S_{\text {cvx}}(\mathbf {y}) \rangle . \end{aligned}$$

(13)

Minimising such an LP would usually be an expensive operation for problems of this dimension. However, we remark that, once the gradient has been computed, exploiting the properties of our problem allows us to solve problem (13) in a time linear in the number of random variables (N) and labels (M). Specifically, the following is an optimal solution to problem (13).

$$\begin{aligned} \mathbf {s}_{a}(i) = {\left\{ \begin{array}{ll} 1 \quad \text {if } i = {{\mathrm{\arg \!\min }}}_{i \in \mathcal {L}} \frac{\partial S_{\text {cvx}}}{\partial y_{a}(i)}\\ 0 \quad \text {else.} \end{array}\right. }. \end{aligned}$$

(14)

Step Size Determination

In the original Frank-Wolfe algorithm, the step size $\alpha$ is simply chosen using line search. However we observe that, in our case, the optimal $\alpha$ can be computed by solving a second-order polynomial function of a single variable, which has a closed form solution that can be obtained efficiently. This observation has been previously exploited in the context of Structural SVM [22]. The derivations for this closed form solution can be found in supplementary material. With careful reutilisation of computations, this step can be performed without additional filter-based method calls. By choosing the optimal step size at each iteration, we reduce the number of iterations needed to reach convergence.

The above procedure converges to the global minimum of the convex relaxation and resorts to the filter-based method only once per iteration during the computation of the gradient and is therefore efficient. However, this solution has no guarantees to be even a local minimum of the original QP relaxation. To alleviate this, we will now introduce a difference-of-convex (DC) relaxation.

5 Difference of Convex Relaxation

5.1 DC Relaxation: General Case

The objective function of a general DC program can be specified as

$$\begin{aligned} S_{\text {CCCP}}(\mathbf {y}) = p(\mathbf {y}) - q(\mathbf {y}). \end{aligned}$$

(15)

One can obtain one of its local minima using the Concave-Convex Procedure (CCCP) [23]. The key steps of this algorithm are described in Algorithm 2. Briefly, Step 3 computes the gradient of the concave part. Step 4 minimises a convex upper bound on the DC objective, which is tight at $\mathbf {y}^{t}$.

In order to exploit the CCCP algorithm for DC programs, we observe that the QP (8) can be rewritten as

$$\begin{aligned} \begin{aligned} \min _{\mathbf {y}} \quad&\varvec{\phi }^{T} \mathbf {y} + \mathbf {y}^{T} (\varvec{\varPsi + \mathbf {D}}) \mathbf {y} - \mathbf {y}^{T}\mathbf {D}\mathbf {y},\\ \text { s.t. } \quad&\mathbf {y} \in \mathcal {M}. \end{aligned} \end{aligned}$$

(16)

Formally, we can define $p(\mathbf {y}) = \varvec{\phi }^{T} \mathbf {y} + \mathbf {y}^{T}(\varvec{\varPsi } + \mathbf {D}) \mathbf {y}$ and $q(\mathbf {y}) = \mathbf {y}^{T} \mathbf {D} \mathbf {y}$, which are both convex in $\mathbf {y}$.

We observe that, since $\mathbf {D}$ is diagonal and the matrix product with $\varvec{\varPsi }$ can be computed using the filter based method, the gradient $\nabla q(\mathbf {y}^{t}) = 2 \mathbf {D} \mathbf {y}$ (Step 3) is efficient to compute. The minimisation of the convex problem (Step 4) is analogous to the convex QP formulation (10) presented above with different unary potentials. Since we do not place any restrictions on the form of the unary potentials, (Step 4) can be implemented using the method described in Sect. 4.

The CCCP algorithm provides a monotonous decrease in the objective function and will converge to a local minimum [24]. However, the above method will take several iterations to converge, each necessitating the solution of a convex QP, and thus requiring multiple calls to the filter-based method. While the filter-based method [8] allows us to compute operations on the pixel compatibility function in linear time, it still remains an expensive operation to perform. As we show next, if we introduce some additional restriction on our potentials, we can obtain a more efficient difference of convex decomposition.

5.2 DC Relaxation: Negative Semi-definite Compatibility

We now introduce a new DC relaxation of our objective function that takes advantage of the structure of the problem. Specifically, the convex problem to solve at each iteration does not depend on the filter-based method computations, which are the expensive steps in the previous method. Following the example of Krähenbühl and Koltun [10], we look at the specific case of negative semi-definite label compatibility function, such as the commonly used Potts model. Taking advantage of the specific form of our pairwise terms (7), we can rewrite the problem as

$$\begin{aligned} S(\mathbf {y}) = \varvec{\phi }^{T} \mathbf {y} - \mathbf {y}^{T}(\varvec{\mu } \otimes \mathbf {I}_{N}) \mathbf {y}^{T} + \mathbf {y}^{T} (\varvec{\mu } \otimes \sum _{m} \mathbf {K}^{(m)}) \mathbf {y}. \end{aligned}$$

(17)

The first two terms can be verified as being convex. The Gaussian kernel is positive semi-definite, so the Gram matrices $\mathbf {K}^{(m)}$ are positive semi-definite. By assumption, the label compatibility function is also negative semi-definite. The results from the Kronecker product between the Gram matrix and $\mathbf {\mu }$ is therefore negative semi-definite.

Minimisation. Once again we use the CCCP Algorithm. The main difference between the generic DC relaxation and this specific one is that Step 3 now requires a call to the filter-based method, while the iterations required to solve Step 4 do not. In other words, each iteration of CCCP only requires one call to the filter based method. This results in a significant improvement in speed. More details about this operation are available in the supplementary material.

6 LP Relaxation

This section presents an accurate LP relaxation of the energy minimisation problem and our method to optimise it efficiently using subgradient descent.

Relaxation. To simplify the description, we focus on the Potts model. However, our approach can easily be extended to more general pairwise potentials by approximating them using a hierarchical Potts model. Such an extension, inspired by [25], is presented in the supplementary material. We define the following notation: $K_{a,b} = \sum _{m} w^{(m)}k^{(m)}(\mathbf {f}^{(m)}_{a}$, $\mathbf {f}^{(m)}_{b})$, $\sum _{a} = \sum _{a=1}^{N}$ and $\sum _{b<a} = \sum _{b=1}^{a-1}$. With these notations, a LP relaxation of (5) is:

$$\begin{aligned} \min&S_{LP}(\mathbf {y}) = \underbrace{\sum _{a} \sum _{i} \phi _{a}(i) y_{a}(i)}_{unary} + \underbrace{\sum _{a} \sum _{b \ne a} \sum _{i} K_{a,b} \frac{|y_{a}(i) - y_{b}(i)|}{2}}_{pairwise}, \nonumber \\ \text {s.t.}&\mathbf {y} \in \mathcal {M}. \end{aligned}$$

(18)

The feasible set remains the same as the one we had for the QP and DC relaxations. In the case of integer solutions, $S_{LP}(\mathbf {y})$ has the same value as the objective function of the IP described in (5). The unary term is the same for both formulations. The pairwise term ensures that for every pair of random variables $X_{a}, X_{b}$, we add the cost $K_{a,b}$ associated with this edge only if they are not associated with the same labels.

Minimisation. Kleinberg and Tardos [2] solve this problem by introducing extra variables for each pair of pixels to get a standard LP, with a linear objective function and linear constraints. In the case of a dense CRF, this is infeasible because it would introduce a number of variables quadratic in the number of pixels. We will instead use projected subgradient descent to solve this LP. To do so, we will reformulate the objective function, derive the subgradient, and present an algorithm to compute it efficiently.

Reformulation

The absolute value in the pairwise term of (5) prevents us from using the filtering approach. To address this issue, we consider that for any given label i, the variables $y_{a}(i)$ can be sorted in a descending order: $a \ge b \implies y_{a}(i) \le y_{b}(i)$. This allows us to rewrite the pairwise term of the objective function (18) as:

$$\begin{aligned} \sum _{i} \sum _{a} \sum _{a \ne b} K_{a,b} \frac{|y_{a}(i) - y_{b}(i)|}{2} = \sum _{i} \sum _{a} \sum _{b > a} K_{a,b} y_{a}(i) - \sum _{i} \sum _{a} \sum _{b < a} K_{a,b} y_{a}(i). \end{aligned}$$

(19)

A formal derivation of this equality can be found in supplementary material.

Subgradient.

From (19), we rewrite the subgradient:

$$\begin{aligned} \frac{\partial S_{LP}}{\partial y_{c}(k)}(\mathbf {y}) = \phi _{c}(k) + \sum _{a > c} K_{a,c} - \sum _{a < c} K_{a,c}. \end{aligned}$$

(20)

Note that in this expression, the dependency on the variable $\mathbf {y}$ is hidden in the bounds of the sum because we assumed that $y_{a}(k) \le y_{c}(k)$ for all $a>c$. For a different value of $\mathbf {y}$, the elements of $\mathbf {y}$ would induce a different ordering and the terms involved in each summation would not be the same.

Subgradient Computation

What prevents us from evaluating (20) efficiently are the two sums, one over an upper triangular matrix ($\sum _{a > c} K_{a,c}$) and one over a lower triangular matrix ($\sum _{a<c} K_{a,c}$). As opposed to (6), which computes terms $\sum _{a,b}K_{a,b}v_b$ for all a using the filter-based method, the summation bounds here depend on the random variable we are computing the partial derivative for. While it would seems that the added sparsity provided by the upper and lower triangular matrices would simplify the operation, it is this sparsity itself that prevents us from interpreting the summations as convolution operations. Thus, we cannot use the filter-based method as described by Adams et al. [8].

We alleviate this difficulty by designing a novel divide-and-conquer algorithm. We describe our algorithm for the case of the upper triangular matrix. However, it can easily be adapted to compute the summation corresponding to the lower triangular matrix. We present the intuition behind the algorithm using an example. A rigorous development can be found in the supplementary material. If we consider $N=6$ then $a,c \in \{1,2,3,4,5,6\}$ and the terms we need to compute for a given label are:

$$\begin{aligned} \left( \begin{array}{c} \sum _{a> 1} K_{a,1}\\ \sum _{a> 2} K_{a,2}\\ \sum _{a> 3} K_{a,3}\\ \sum _{a> 4} K_{a,4}\\ \sum _{a> 5} K_{a,5}\\ \sum _{a > 6} K_{a,6}\\ \end{array} \right) = \underbrace{ \left( \begin{array}{ccc|ccc} \text { }0\text { }&{} K_{2,1} &{} K_{3,1} &{} K_{4,1} &{} K_{5,1} &{} K_{6,1}\\ 0 &{} 0 &{} K_{3,2} &{} K_{4,2} &{} K_{5,2} &{} K_{6,2}\\ 0 &{} 0 &{} 0 &{} K_{4,3} &{} K_{5,3} &{} K_{6,3}\\ \hline 0 &{} 0 &{} 0 &{} 0 &{} K_{5,4} &{} K_{6,4}\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} K_{6,5}\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ \end{array} \right) }_{\mathbf {U}} \cdot \left( \begin{array}{c} 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ \end{array} \right) \end{aligned}$$

(21)

We propose a divide and conquer approach that solves this problem by splitting the upper triangular matrix $\mathbf {U}$. The top-left and bottom-right parts are upper triangular matrices with half the size. We solve these subproblems recursively. The top-right part can be computed with the original filter based method. Using this approach, the total complexity to compute this sum is $\mathcal {O}(N \log \,(N))$.

With this algorithm, we have made feasible the computation of the subgradient. We can therefore perform projected subgradient descent on the LP objective efficiently. Since we need to compute the subgradient for each label separately due to the necessity of having sorted elements, the complexity associated with taking a gradient step is $\mathcal {O}(M N \log ( N ))$. To ensure the convergence, we choose as learning rate $(\beta ^{t})_{t=1}^{\infty }$ that is a square summable but not a summable sequence such as $(\frac{1}{1+t})_{t=1}^{\infty }$. We also make use of the work by Condat [26] to perform fast projection on the feasible set. The complete procedure can be found in Algorithm 3. Step 3 to 7 present the subgradient computation for each label. Using this subgradient, Step 8 shows the update rule for $y^{t}$. Finally, Step 9 project this new estimate onto the feasible space.

The algorithm that we introduced converges to a global minimum of the LP relaxation. By using the rounding procedure introduced by Kleinberg and Tardos [2], it has a multiplicative bound of 2 for the dense CRF labelling problem on Potts models and $\mathcal {O}(\log \,(M))$ for metric pairwise potentials.

7 Experiments

We now demonstrate the benefits of using continuous relaxations of the energy minimisation problem on two applications: stereo matching and semantic segmentation. We provide results for the following methods: the Convex QP relaxation ($\mathbf {QP_{cvx}}$), the generic and negative semi-definite specific DC relaxations ($\mathbf {DC_{gen}}$ and $\mathbf {DC_{neg}}$) and the LP relaxation (LP). We compare solutions obtained by our methods with the mean-field baseline (MF).

7.1 Stereo Matching

Data. We compare these methods on images extracted from the Middlebury stereo matching dataset [27]. The unary terms are obtained using the absolute difference matching function of [27]. The pixel compatibility function is similar to the one used by Krähenbühl and Koltun [5] and is described in the supplementary material. The label compatibility function is a Potts model.

Fig. 1.

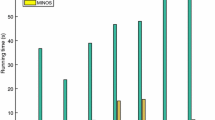
Evolution of achieved energies as a function of time on a stereo matching problem (Teddy Image). While the QP method leads to the worst result, using it as an initialisation greatly improves results. In the case of negative semi-definite potentials, the specific DC $_{neg}$ method is as fast as mean-field, while additionally providing guarantees of monotonous decrease. (Best viewed in colour) (Color figure online)

Results. We present a comparison of runtime in Fig. (1a), as well as the associated final energies for each method in Table (1b). Similar results for other problem instances can be found in the supplementary materials.

We observe that continuous relaxations obtain better energies than their mean-field counterparts. For a very limited time-budget, MF is the fastest method, although DC $_{neg}$ is competitive and reach lower energies. When using LP, optimising a better objective function allows us to escape the local minima to which $\mathbf {DC_{neg}}$ converges. However, due to the higher complexity and the fact that we need to perform divide-and-conquer separately for all labels, the method is slower. This is particularly visible for problems with a high number of labels. This indicates that the LP relaxation might be better suited to fine-tune accurate solutions obtained by faster alternatives. For example, this can be achieved by restricting the LP to optimise over a subset of relevant labels, that is, labels that are present in the solutions provided by other methods. Qualitative results for the Teddy image can be found in Fig. 2 and additional outputs are present in supplementary material. We can see that lower energy translates to better visual results: note the removal of the artifacts in otherwise smooth regions (for example, in the middle of the sloped surface on the left of the image).

Fig. 2.

Stereo matching results on the Teddy image. Continuous relaxation achieve smoother labeling, as expected by their lower energies

7.2 Image Segmentation

Data. We now consider an image segmentation task evaluated on the PASCAL VOC 2010 [28] dataset. For the sake of comparison, we use the same data splits and unary potentials as the one used by Krähenbühl and Koltun [5]. We perform cross-validation to select the best parameters of the pixel compatibility function for each method using Spearmint [29].

Results. The energy results obtained using the parameters cross validated for $\mathbf {DC_{neg}}$ are given in Table 1. MF5 corresponds to mean-field ran for 5 iterations as it is often the case in practice [5, 12].

Table 1. Percentage of images the row method outperforms the column method on final energy, average energy over the test set and Segmentation performance. Continuous relaxations dominate mean-field approaches on almost all images and improve significantly more compared to the Unary baseline. Parameters tuned for $\mathbf {DC_{neg}}$

Once again, we observe that continuous relaxations provide lower energies than mean-field based approaches. To add significance to this result, we also compare energies image-wise. In all but a few cases, the energies obtained by the continuous relaxations are better or equal to the mean-field ones. This provides conclusive evidence for our central hypothesis that continuous relaxations are better suited to the problem of energy minimisation in dense CRFs.

For completeness, we also provide energy and segmentation results for the parameters tuned for MF in the supplementary material. Even in that unfavourable setting, continuous relaxations still provide better energies. Note that, due to time constraints, we run the LP subgradient descent for only 5 iterations of subgradient descent. Moreover, to be able to run more experiments, we also restricted the number of labels by discarding labels that have a very small probability to appear given the initialisation.

Fig. 3.

Segmentation results on sample images. We see that $\mathbf {DC_{neg}}$ leads to better energy in all cases compared to MF. Segmentation results are better for MF for the MF-tuned parameters and better for $\mathbf {DC_{neg}}$ for the $\mathbf {DC_{neg}}$-tuned parameters

Some qualitative results can be found in Fig. 3. When comparing the segmentations for MF and $\mathbf {DC_{neg}}$, we can see that the best one is always the one we tune parameters for. A further interesting caveat is that although we always find a solution with better energy, it does not appear to be reflected in the quality of the segmentation. While in the previous case with stereo vision, better energy implied qualitatively better reconstruction it is not so here. Similar observation was made by Wang et al [20].

8 Discussion

Our main contribution are four efficient algorithms for the dense CRF energy minimisation problem based on QP, DC and LP relaxations. We showed that continuous relaxations give better energies than the mean-field based approaches. Our best performing method, the LP relaxation, suffers from its high runtime. To go beyond this limit, move making algorithms such as $\alpha$-expansion [30] could be used and take advantage of the fact that this relaxation solves exactly the original IP for the two label problem. In future work, we also want to investigate the effect of learning specific parameters for these new inference methods using the framework of [18].