Non-rigid 3D Shape Retrieval via Large Margin Nearest Neighbor Embedding

Abstract

In this paper, we propose a highly efficient metric learning approach to non-rigid 3D shape analysis. From a training set of 3D shapes from different classes, we learn a transformation of the shapes which optimally enforces a clustering of shapes from the same class. In contrast to existing approaches, we do not perform a transformation of individual local point descriptors, but a linear embedding of the entire distribution of shape descriptors. It turns out that this embedding of the input shapes is sufficiently powerful to enable state of the art retrieval performance using a simple nearest neighbor classifier. We demonstrate experimentally that our approach substantially outperforms the state of the art non-rigid 3D shape retrieval methods on the recent benchmark data set SHREC’14 Non-Rigid 3D Human Models, both in classification accuracy and runtime.

1 Introduction

The analysis of 3D shapes is becoming more and more important with increasing amounts of 3D shape data becoming available through novel 3D scanning technology and 3D modeling software. Among the numerous challenges in 3D shape analysis, we will focus on the problems of non-rigid shape similarity and non-rigid 3D shape retrieval: Given a set of 3D shapes and a previously unobserved query shape, we would like to efficiently determine the similarity of the query to all shapes in the database and identify the most similar shapes in the database – see Fig. 1. The computation of shape similarity is a difficult problem, in particular if we wish to allow for non-rigid deformations of the shapes. Under such deformations the appearance of the object may change significantly. For many real-world retrieval applications on large 3D shape databases, it is of importance that the retrieval of similar shapes can be computed efficiently.

Fig. 1.

Example of shape retrieval from SHREC’14 Humans - real (scanned) dataset. The query model (top left) belongs to class 16. The top row shows the best five matches retrieved by the Supervised Dictionary Learning method [1]. The best five matches retrieved by the proposed method (CSD+LMNN) are shown in the bottom row. The blue color indicates that the retrieved model corresponds to the correct class (i.e. 16) and the red color indicates an incorrect class. The quantitative experiments in Sect. 3 show that the proposed method outperforms the state of the art methods significantly on the SHREC’14 Humans dataset. (Color figure online)

1.1 Related Work

Much like in image analysis, the analysis of 3D shapes often starts with the extraction of local feature descriptors which are invariant to rigid and robust to non-rigid transformations of the shape. Popular descriptors include the Heat Kernel Signature [2], the Wave Kernel Signature [3] and the scale-invariant Heat Kernel Signature [4]. For computing a correspondence between 3D shapes, the shape analysis community has devised a variety of machine learning approaches to learn optimal point descriptors [5–8].

Learning approaches have also been used for shape retrieval as in [9] and [1]. In [1] the authors define a dictionary of point descriptors and use it to compute sparse representations of the point descriptors of each shape. Then they obtain global shape descriptors by sum pooling. The distances between them are considered to be the dis-similarity between the shapes. The authors go on to use unsupervised and supervised learning methods to optimize the classification results. In the supervised case, the authors try to minimize a loss function as in [10] using a subset of the pooled descriptors as a training set. They actually propagate the error back to the dictionary of point descriptors. This means their objective is to learn an optimal dictionary of point descriptors for the specific task of shape retrieval and similarity ranking. Although this approach yielded state of the art results, as shown in [11], the computation time needed to learn the optimal dictionary (3–4 h) prohibits it from being used for larger datasets. In [9] the main purpose of the method is to learn the invariant representation of each shape of a given dataset. The authors use a statistical framework to address classification tasks. While achieving state of the art performance, a major drawback of this method, from a learning point of view, is that it uses a large subset of the shapes (even 90 %) for training.

1.2 Contribution

In this work, we propose a 3D shape retrieval method which provides state of the art performance while being substantially faster than previous techniques. We achieve this using a novel combination of stacked shape descriptors and a linear embedding of their distribution by means of a metric learning approach. In contrast to the approach by Litman et al. [1], we do not employ dictionary learning to obtain shape descriptors from sparse point descriptors, but instead use weighted averaging directly on the point descriptors of a shape. We then learn a metric for the resulting shape descriptors so that samples from the same class are closer to each other than samples from different classes. Letting the learning process operate only on shape descriptors reduces our overall runtime tremendously. One of the main insights of our work is that the stacked shape descriptor alone does not lead to better performance, but in combination with the Large Margin Nearest Neighbor (LMNN) approach for metric learning, classification performance is significantly higher, reaching almost 98 % mean average precision on the challenging “SHREC’ 14 Humans - scanned” data set. Furthermore, our method is much faster than previous methods, as the individual steps require comparably only a few computations: Rather than several hours, our approach only needs approximately 4 min to learn the optimal embedding of shapes using only 40 % of the shapes.

2 Approach

Our problem dictates to compare non-rigid shapes therefore we aim to obtain representations that capture their intrinsic properties. Our goal is to find representations such that similar shapes have proportionally similar descriptors. This becomes a particularly challenging problem when considering all possible deformations a single shape can have. In the next paragraphs we explain in detail every tool that we use. First we present an overview of our pipeline as illustrated in Fig. 2.

Fig. 2.

Overview: Schematic illustration of the proposed method.

2.1 Overview

A commonly used scheme in shape analysis is to model a shape $\mathcal {S}$ as a two-dimensional manifold $\mathcal {M}$ and representing it as a triangular mesh with a set of n vertices $\mathcal {V} = \{v_1, v_2, \ldots , v_n \}$, a set of triangular faces $\mathcal {F} \subset \mathcal {V}^3$ and a set of edges $\mathcal {E} \subset \mathcal {V}^2$ between adjacent vertices.

At first, we compute the Laplace-Beltrami operator (LBO) for each mesh in our dataset. We then compute a point descriptor d(x) - based on the LBO - for each vertex of our mesh. There are different descriptors that can be utilized. We use the Wave Kernel Signature [3] and the scale-invariant Heat Kernel Signature [4]. The reason to choose LBO-based descriptors is their inherent invariance to isometric deformations.

As a mesh can have several thousands vertices and datasets contain a large number of meshes, it becomes intractable to compare all point descriptors. Therefore we compute a weighted average of the point descriptors of each mesh and obtain a q-dimensional descriptor $y_f$ for each shape. The shape descriptors $y_f$ can either be the averaged siHKS, the averaged WKS or a combination of them. Our rational for the particular choice of descriptors is that siHKS captures global, while WKS focuses on local shape features. We argue that a stacked combination of them contains diverse information that can be fully exploited by a metric learning algorithm.

In the end we feed a subset of our shape descriptors $y_f$ along with their labels to a supervised metric learning algorithm (LMNN). The algorithm learns a linear mapping L of the shape descriptors such that shapes with different labels are easier to distinguish from one another in the new space.

Now when we want to classify a new shape, all we need to do is to compute the same type of shape descriptor $y_f$ as the one we trained our classifier with and transform it into the new space by applying the learned mapping L. The labels of the k closest shapes in the transformed space determine the predicted label for our query shape.

2.2 The Laplace-Beltrami Operator

The Laplace-Beltrami operator (LBO) is a natural generalization of the Laplace operator for Riemannian manifolds. Like the Laplacian, it is defined as the (negative) divergence of the gradient, and it is a linear operator mapping functions to functions. Therefore the LBO is often also simply referred to as the Laplacian. Formally, given a smooth scalar field $f: \mathcal {M} \rightarrow \mathbb {R}$ on the manifold $\mathcal {M}$ associated to shape $\mathcal {S}$, the Laplace-Beltrami operator $\varDelta$ is defined as

$$\begin{aligned} \varDelta f := - \text {div} ( \nabla f ). \end{aligned}$$

(1)

One of the most important properties of the Laplacian is that it is invariant under isometric deformations. Particularly useful are the eigenvalues $\lambda _i \in \mathbb {R}$ and the eigenfunctions $\phi _i: \mathcal {M} \rightarrow \mathbb {R}$ of the Laplacian, i.e.

$$\begin{aligned} \varDelta \phi _i := \lambda _i \phi _i . \end{aligned}$$

(2)

The eigenvalues $\lambda _i$ of Eq. (2) – known as the Helmholtz equation – are non-negative and represent a discrete set $(0 = \lambda _0 \le \lambda _1 \le \lambda _2 \le \ldots \le + \infty )$. The corresponding eigenfunctions can be chosen to form an orthonormal basis:

$$\begin{aligned} \langle \phi _i, \phi _j \rangle = \int _{\mathcal {M}} \phi _i(x) \phi _j(x) dx = {\left\{ \begin{array}{ll} 0 ,&{} \text {if } i\ne j\\ 1 ,&{} \text {if } i = j . \end{array}\right. } \end{aligned}$$

(3)

Discretization. A popular discretization of the LBO is the cotangent scheme [12, 13]. It allows to compute the eigenvalues $\lambda _i$ and eigenvectors $\phi _i$ as the solutions to the generalized eigenvalue problem

$$\begin{aligned} A\phi _i = \lambda _i B \phi _i, \end{aligned}$$

(4)

where $A\in \mathbb {R}^{n\times n}$ is the stiffness matrix and $B\in \mathbb {R}^{n\times n}$ is the mass matrix. Concretely, A is defined as

$$\begin{aligned} A_{ij} = {\left\{ \begin{array}{ll} \frac{\cot \alpha _{ij} + \cot \alpha _{ji} }{2} ,&{} \text {if } (v_i,v_j) \in \mathcal {E}\\ - \mathop {\sum }\nolimits _{k \in N(i)} A_{ik} ,&{} \text {if } i = j, \end{array}\right. } \end{aligned}$$

(5)

where $\alpha _{ij}$ and $\alpha _{ji}$ are the two angles opposite of the edge $(v_i,v_j)$ and N(i) is the one-ring neighborhood of vertex $v_i$. The mass matrix B is defined as

$$\begin{aligned} B_{ij} = {\left\{ \begin{array}{ll} \frac{a(T_1) + a(T_2)}{12} ,&{} \text {if } (v_i,v_j) \in \mathcal {E}\\ \frac{\sum _{k \in N(i)} a(T_k)}{6} ,&{} \text {if } i = j, \end{array}\right. } \end{aligned}$$

(6)

where $T_1, T_2$ are the triangles that share the edge $(v_i, v_j)$, and a(T) is the area of triangle T. Often a simplified “lumped" diagonal version of the mass matrix is used:

$$\begin{aligned} B_{ii} = \frac{\sum _{k \in N(i)} a(T_k)}{3}, \end{aligned}$$

(7)

i.e. $B_{ii}$ is considered as the corresponding area element of vertex $v_i$. The geometric concepts of these formulas are depicted in Fig. 3.

Fig. 3.

Stiffness Matrix (left): The entries $A_{ij}$ of the stiffness matrix A contain the average of the cotangents of the angles $\alpha _{ij}, \alpha _{ji}$ opposite to the edge $(v_i, v_j)$. Thus the name cotangent scheme. Mass Matrix (right): The diagonal entries $B_{ii}$ of the mass matrix B correspond to the Voronoi area around vertex $v_i$.

2.3 Point Descriptors

Local feature descriptors have been proven particularly useful in shape analysis tasks such as shape matching (point-to-point correspondence) and shape retrieval. In the following we describe three of the most used ones.

Heat Kernel Signature. The HKS [2] is - as the name indicates - based on the heat diffusion process on a surface S which is governed by the Heat equation:

$$\begin{aligned} \varDelta u(x,t) = - \frac{\partial }{\partial t} u(x,t) \text {.} \end{aligned}$$

(8)

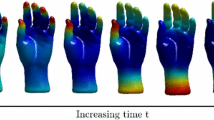
The solution $k_t(x,x)$ can be interpreted as the amount of heat that remains at point x of surface S after time t when starting with a unit heat source $u_0$ concentrated at x at $t_0=0$. The eigen-decomposition of the Heat Kernel is

$$\begin{aligned} k_t(x,y) = \sum _{k=0}^{\infty } e^{-\lambda _k t} \phi _k(x) \phi _k(y) , \end{aligned}$$

(9)

so the HKS is just

$$\begin{aligned} k_t(x,x) = \sum _{k=0}^{K-1} e^{-\lambda _k t} \phi _k(x)^2 , \end{aligned}$$

(10)

as we truncate the basis to the first K eigenfunctions of the LBO. Concatenating the solutions for different times $\{t_1, t_2, \ldots , t_T \}$ we obtain a descriptor of the form

$$\begin{aligned} HKS(x) = (k_{t_1}(x,x), k_{t_2}(x,x), \ldots , k_{t_T}(x,x)) \text {.} \end{aligned}$$

(11)

Scale Invariant Heat Kernel Signature. Bronstein and Kokkinos [4] developed a scale-invariant version of the Heat Kernel Signature (siHKS) using the logarithm, the derivative and the Fourier transform moving from the time domain to the frequencies domain. Assuming a shape is scaled by a factor $\beta$, and rewriting time t as $\alpha ^\tau$, the heat kernel of the scaled shape would only be shifted in $\tau$ by $2\log _\alpha \beta$. The authors first constructed a scale-covariant heat kernel:

$$\begin{aligned} scHKS(x,x) = - \frac{\sum \limits _{k = 1}^{K} \lambda _k \alpha ^\tau \log \alpha e^{-\lambda _k \alpha ^\tau } \phi _k(x)^2}{\sum \limits _{k = 1}^{K} e^{-\lambda _k \alpha ^\tau } \phi _k(x)^2} \text {.} \end{aligned}$$

(12)

In the Fourier domain this shift results in a complex phase ${H}(\omega ) e^{-i \omega 2 \log _\alpha \beta }$ where ${H}(\omega )$ denotes the Fourier transform of scHKS w.r.t. $\tau$. Finally the scale-invariant HKS is constructed by taking the absolute value of ${H}(\omega )$ (thus undoing the phase) and then sampling $|{H}(\omega )|$ at q frequencies $\{ \omega _1, \ldots , \omega _q \}$ [1]:

$$\begin{aligned} siHKS(x) = (|{H}(\omega _1)|, \ldots , |{H}(\omega _q)| )^T \text {.} \end{aligned}$$

(13)

Wave Kernel Signature. The Wave Kernel Signature (WKS) [3] - inspired by quantum mechanics - describes the average probability over time to locate a particle with a certain energy distribution $f_E$ at point x. The movement of a quantum particle on a surface is governed by the wave function $\psi ( x, t )$ which is a solution of the Schrödinger equation

$$\begin{aligned} \frac{\partial \psi (x,t)}{\partial t} = i \varDelta \psi (x,t) . \end{aligned}$$

(14)

The energy distribution of a quantum particle depends on the LBO eigenvalues. Therefore the wave equation for a particle can be written as

$$\begin{aligned} \psi _E(x,t) = \sum \limits _{k=0}^{\infty } e^{i \lambda _k t} \phi _k(x) f_E(\lambda _k) \text {.} \end{aligned}$$

(15)

The probability to locate the particle at point x is then $| \psi _E(x,t) |^2$. Therefore the average probability over time is

$$\begin{aligned} p(x) = \lim \limits _{T \rightarrow \infty } \frac{1}{T} \int _{0}^{T} | \psi _E(x,t) |^2 = \sum \limits _{k=1}^{\infty } \phi _k(x)^2 f_E(\lambda _k)^2 \text {.} \end{aligned}$$

(16)

As we described, the LBO and its spectrum capture intrinsic properties of a shape. Therefore different choices of $f_E$ give us shape properties at different scales. Evaluating with energy distributions $\{e_1, \ldots , e_q \}$ we get the vector for the Wave Kernel Signature:

$$\begin{aligned} WKS(E,x) = (p_{e_1}(x), \ldots , p_{e_q}(x) )^T \text {.} \end{aligned}$$

(17)

Note that as with the HKS we must truncate the sum at the first K eigenvalues. Typical values for K are 50 or 100.

2.4 Weighted Average

Our aim is to use the shape descriptors mentioned above and the learned distance metric to classify shapes. However, for a given shape so far we only have a number of point descriptors, but for classification we would prefer to have one descriptor for the whole shape. To achieve this, we compute a weighted average over all point descriptors d(x) computed from the points x of a given shape $\mathcal {S}$. Thus, our shape descriptor is defined as

$$\begin{aligned} y_f(\mathcal {S}) = \sum _{x\in \mathcal {S}} w_x d({x}) \quad \text {with} \quad w_x = \frac{a_x}{ \sum _{y\in \mathcal {S}} a_y }, \end{aligned}$$

(18)

where $a_x$ is the area element associated with vertex ${x}\in \mathcal {S}$. This weighted averaging is inspired by the pooling step proposed by Litman et al. [1], however with the difference that we do not use sparse coding.

In the case of WKS we normalize the point descriptors by the $L_2$-norm. Both averaged shape descriptors are also normalized by the $L_2$-norm. We compared 3 different shape descriptors, the averaged WKS, the averaged siHKS and a combination of them we refer to as Combined Spectral Descriptor (CSD):

$$\begin{aligned} y_{CSD}(\mathcal {S}) = \begin{pmatrix} y_{WKS}(\mathcal {S}) \\ y_{siHKS}(\mathcal {S}) \\ \end{pmatrix} \text {.} \end{aligned}$$

(19)

2.5 Large Margin Nearest Neighbor

Large Margin Nearest Neighbor (LMNN) is a machine learning algorithm that was first introduced in 2005 [14]. The authors keep updating the algorithm and their implementation is very efficient even for applications with very large datasets [15]. As of the latest version that we used, the L-BFGS algorithm is used for optimization by default.

LMNN utilizes both the concept of SVMs of margin maximization and the well known k-NN algorithm. It is specifically conceived to learn a Mahalanobis (semi-)metric $\mathcal {D}_M$ that improves the accuracy of k-NN classification. This metric is represented by the positive semi-definite matrix $M\in \mathbb {R}^{n\times n}$, such that

$$\begin{aligned} \mathcal {D}_M(\varvec{x},\varvec{y}) = \langle {M(\varvec{x}-\varvec{y}),(\varvec{x}-\varvec{y})} \rangle ^{\frac{1}{2}}\text {.} \end{aligned}$$

(20)

Equivalently $\mathcal {D}_M(\varvec{x},\varvec{y})$ can be seen as the Euclidean distance between the points $\varvec{x}, \varvec{y}$ transformed by the linear transformation $L \in \mathbb {R}^{m \times n}$, i.e.

$$\begin{aligned} \mathcal {D}_L(\varvec{x},\varvec{y}) = \Vert {L\varvec{x}-L\varvec{y}} \Vert \text {,} \end{aligned}$$

(21)

as the positive semi-definiteness of M allows a decomposition $M=L^\top L$.

The main idea of the algorithm is to find a mapping L so that for each input $\varvec{x}_i$ there are at least k neighbors that share its label $y_i$ (see Fig. 4). This is facilitated by choosing target neighbors of $\varvec{x}_i$, i.e. samples that are desired to be closest to $\varvec{x}_i$. The target neighbors for every input are fixed during the whole learning process. Note that target neighbors are not symmetric. For instance if $\varvec{x}_j$ is a target neighbor of $\varvec{x}_i$ it is not necessary that $\varvec{x}_i$ is also a target neighbor of $\varvec{x}_j$.

Fig. 4.

Large Margin Nearest Neighbor (LMNN) finds the best positive semi-definite matrix M, such that the induced Mahalanobis (semi-)norm $\mathcal {D}_M(\varvec{x}_i, \varvec{x}_j)=\langle {M\varvec{x}_i-\varvec{x}_j, \varvec{x}_i-\varvec{x}_j} \rangle ^{{\frac{1}{2}}}$ separates the different classes as good as possible.

Furthermore, LMNN tries to ensure that differently labeled inputs are farther away from the target neighbors so that they do not get selected by k-NN. Samples that violate this rule are called impostors. Ideally we would like to create a large margin between the perimeter around each input and its target neighbors, and all differently labeled inputs as illustrated in Fig. 4 on the right. This goal also explains the name of the algorithm.

Loss Function. The loss function consists of two competing terms. The first one pulls target neighbors together:

$$\begin{aligned} \epsilon _{\text {pull}} (L) = \sum _{i, j \rightsquigarrow i} ||L(\varvec{x}_i - \varvec{x}_j)||^2 . \end{aligned}$$

(22)

The notation in Eq. (22) implies that $\varvec{x}_j$ are target neighbors of $\varvec{x}_i$. The pull loss penalizes large distances between inputs and their target neighbors. This is an important difference of LMNN compared to other algorithms where large distances to all other similarly labeled samples are penalized. The second term pushes impostors away:

$$\begin{aligned} \begin{aligned} \epsilon _{\text {push}} (L) = \sum _{i, j \rightsquigarrow i} \sum _{l} (1 - y_{il}) [1 + ||L(\varvec{x}_i - \varvec{x}_j)||^2 - ||L(\varvec{x}_i - \varvec{x}_l)||^2]_+ \end{aligned} \text {,} \end{aligned}$$

(23)

where $[x]_+ = \max (x,0)$ denotes the standard hinge loss and $y_{il}$ is 1 only when $y_i = y_l$ and 0 otherwise. Note that the choice of the unit margin is an arbitrary convention that sets the scale for the linear transformation L. If a different margin $c > 0$ was enforced, the loss function would be minimized by the same linear transformation up to an overall scale factor $\sqrt{c}$. Combining both terms we get the LMNN loss function:

$$\begin{aligned} \epsilon (L) = \mu \epsilon _{\text {pull}} (L) + (1 - \mu ) \epsilon _{\text {push}} (L) \text {,} \end{aligned}$$

(24)

where $\mu \in [0,1]$ is a trade-off parameter between small intra-class and large inter-class distances. Although $\mu$ can be estimated with cross validation, in practice setting $\mu =0.5$ works well. There are several similarities with the SVM’s loss function:

• One term penalizes the norm of the parameter vector (i.e., w in SVMs, L in LMNN)

• The hinge loss is only triggered by samples near the decision boundary

• Both loss functions can be rewritten to utilize the kernel trick

• Both problems can be reformulated as convex optimization problems.

Convex Optimization. While $\epsilon (L)$ is quadratic in L, Eqs. (20) and (21) allow us to restate the loss of $\epsilon$ of Eq. (24) in terms of M. Minimizing this loss becomes a semi-definite program (SDP) which is a convex problem that can be solved globally in polynomial time. For the SDP formulation the authors of [10] introduced slack variables $\{ \xi _{ijl} \}$ for all triplets of target neighbors $\varvec{x}_i, \varvec{x}_j$ and impostors $\varvec{x_l}$. The slack variables measure the level of margin violation. Therefore the SDP can be defined as:

where the last constraint implies that the matrix M must be positive semi-definite. The authors created their own solver for the SDP in order to take advantage of the sparsity of the slack variables. This leads to much faster solutions.

Optimal Training Parameters. The LMNN optimization process requires three parameters to be specified beforehand: the dimension m of the lower-dimensional space into which the samples are mapped by L, the number of neighbors k to consider, and the number of iterations r of the L-BFGS optimizer. To find good values for these parameters, a validation set is used, which is a part of the original training data. Then, the LMNN optimization is run on the remaining data with different parameter settings, that are chosen using Bayesian optimization, and evaluated on the validation set. After a given number of iterations, the parameter set that achieved the highest performance on the validation set is used to run LMNN training on the entire training set.

Classification. For classification, we use the k nearest-neighbor classifier in the m-dimensional target space. Thus, for a given test shape we compute its descriptor, map it into $\mathbb {R}^m$ using the mapping L found in the training step, and assign to it the most frequent label of the k closest, by the Euclidean distance, mapped training samples.

3 Experiments

Datasets. We evaluated our approaches on 2 datasets from SHREC’14 - Shape Retrieval of Non-Rigid 3D Human Models [11]. Of the two main datasets, one consists of synthetic and one of real (scanned) 3D human models. Each class represents a human model and each instance of a class is a different pose of that model. This is a different setting than most classification problems where distinct classes correspond to naturally separate categories (like humans, dogs, cats, etc.). This property along with the fact that some models contain self-intersections makes these datasets particularly challenging.

We used the provided evaluation code from [11] that computes several accuracy metrics: nearest neighbor, first tier, second tier, discounted cumulative gain, e-measure, f-measure, precision and recall.

All meshes were down-sampled to 20.000 faces with Meshlab [16].

Evaluation Setting. We scaled the shapes as indicated in the available code that accompanies [1]. We truncated the bases of the LBO to the first 100 eigenfunctions. Based on them we computed 50-dimensional siHKS descriptors with the same settings as in [1] and 100-dimensional WKS descriptors, setting the variance to 6. We used 40 % of the shape descriptors to train the LMNN classifier and tested on the rest. We used 25 % of the training set as a validation set to find the optimal parameters for LMNN.¹

Table 1. CSD and CSD+LMNN evaluation on the SHREC’14 real dataset.

Table 2. CSD and CSD+LMNN evaluation on the SHREC’14 synthetic dataset.

Table 3. Comparison of retrieval methods in terms of mean average precision (mAP, in %) on the SHREC’14 3D Human Models datasets. In the upper part of the table, results of methods that participated in the SHREC’14 contest are documented as in [11] and the most recent learning approach proposed in [9]. In the lower part, we report the results of our approaches, averaged over 5 runs (different training/testing sets splits).

Our CSD approach gives remarkable results, when combined with LMNN (Tables 1 and 2). Even though the SHREC’14 datasets are considered extremely challenging, our algorithm performed better than the methods that participated in the SHREC’14 contest (see Table 3) and the most recent learning approach proposed in [9]. This is a significant result since our approach is comparatively simpler and the computation time very low.

Figure 5 shows the result of the LMNN learning step. As one can see, LMNN is able to capture the discriminative features of the classes despite the information loss from the projection onto three dimensions, which is done to facilitate the visualization.

We noticed that using both the siHKS and the WKS performed worse than using each descriptor separately. Nevertheless, when used as input to a metric learning algorithm, the performance of the combined descriptor improved considerably. The CSD with LMNN performs better than either individual descriptor with LMNN (see Table 3). In particular, we observe that even if we add a seemingly harmful descriptor, as in the case of the WKS for the real dataset, LMNN is able to select the most useful - in terms of k-NN classification - dimensions of both descriptors, thereby achieving a better accuracy than the siHKS+LMNN approach. This confirms our hypothesis that metric learning can utilize the additional information contained in the combined descriptor. Adding other descriptors to the CSD such as the GPS [17] led to no improvement.

Fig. 5.

Visualization of the shape descriptors before and after learning: Each circle corresponds to the descriptor of one shape. The colors correspond to the 40 classes of the SHREC’14 Real dataset (top row) or the 15 classes of the SHREC’14 Synthetic dataset (bottom row). It can be seen by even visualizing only two dimensions that the transformation L, learned by LMNN, results in a much better clustering of the shapes. This is in line with the quantitative evaluation on the datasets. (Color figure online)

Fig. 6.

Precision-Recall comparison on the SHREC’14 real dataset.

Fig. 7.

Precision-Recall comparison on SHREC’14 synthetic dataset.

Note that in our CSD+LMNN-approach the most time-consuming part is finding the optimal parameters for LMNN. Still the total time needed for the algorithm - excluding the computation of point descriptors - is approximately 2 min. In the worst case it never exceeded 4 min on a machine with a 2.0 GHz CPU. This is an extremely small amount of time compared to the supervised dictionary learning approach proposed in [1] which needs nearly 4 hours to converge on a machine with a 3.2 GHz CPU.

4 Conclusion

In this paper we showed that metric learning can significantly improve the classification accuracy of well known descriptors. Given a large number of features, a learning algorithm such as LMNN can select the most informative ones and weight them appropriately for the problem that we aim to solve, in this case shape retrieval. Our approach is both considerably faster and more accurate than the state of the art. The comparison in Fig. 1 demonstrates that our approach is more robust, as it is able to find the true inherent similarities between objects and does not get confused by different classes, even if they are very similar by human standards.