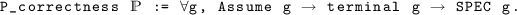Abstract
We propose a framework to build certified proofs of self-stabilizing algorithms using the proof assistant Coq. We first define in Coq the locally shared memory model with composite atomicity, the most commonly used model in the self-stabilizing area. We then validate our framework by certifying a non-trivial part of an existing self-stabilizing algorithm which builds a k-hop dominating set of the network. We also certify a quantitative property related to its output: we show that the size of the computed k-hop dominating set is at most \(\lfloor \frac{n-1}{k+1} \rfloor + 1\), where n is the number of nodes. To obtain these results, we developed a library which contains general tools related to potential functions and cardinality of sets.
This work has been partially supported by project PADEC (AGIR 2015 Pôle MSTIC).
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
In 1974, Dijkstra introduced the notion of self-stabilizing algorithm [12] as any distributed algorithm which resumes correct behavior within finite time, regardless of the initial configuration of the system. A self-stabilizing algorithm can withstand any finite number of transient faults. Indeed, after transient faults hit the system and place it in some arbitrary configuration — where, for example, the values of some variables have been arbitrarily modified — a self-stabilizing algorithm is guaranteed to resume correct behavior within finite time.
For more than 40 year, a vast literature on self-stabilizing algorithms has been developed. Self-stabilizing solutions have been proposed for many kinds of distributed problems, e.g., token circulation [15], spanning tree construction [5], etc. Moreover, self-stabilizing algorithms have been designed to handle various environments, e.g., wired networks [15], wireless sensor networks [1], peer-to-peer systems [3], etc. Progresses in self-stabilization led to researchers consider more and more adversarial environments. As an illustrative example, the three first algorithms proposed by Dijkstra in 1974 [12] were designed for oriented ring topologies and assuming sequential executions only, while nowadays most self-stabilizing algorithms are designed for fully asynchronous arbitrary connected networks, e.g., [15]. Consequently, the design of self-stabilizing algorithms becomes more and more intricate, and accordingly, the proofs of their respective correctness and complexity are now often tricky to establish. However, proofs in distributed algorithmics, in particular in self-stabilization, are commonly written by hand, based on informal reasoning. This potentially leads to errors when arguments are not perfectly clear, as explained by Lamport in its position paper [18]. So, in the current context, such methods are clearly pushed to their limits, justifying then the use of a proof assistant, a tool which allows to develop certified proofs interactively and check them mechanically.
Contribution. In this paper, we propose a general framework to build certified proofs of self-stabilizing algorithms for wired networks using the proof assistant Coq [19].
We first define in Coq the locally shared memory model with composite atomicity introduced by Dijkstra [12], the most common model in self-stabilization. Our modeling is versatile, e.g., it supports any class of network topologies (including arbitrary ones), the diversity of anonymity levels (from fully anonymous to fully identified), and various levels of asynchrony (e.g., sequential, synchronous, fully asynchronous).
We validate our framework by certifying a non-trivial part of an existing silent self-stabilizing algorithm which builds a k-hop dominating set of the network [8]. Starting from an arbitrary configuration, a silent algorithm [13] converges in finite time to a configuration from which all communication variables are fixed. This class of self-stabilizing algorithms is important, as self-stabilizing algorithms that build distributed data structures (e.g., spanning tree or clustering) often achieve the silent property, and these silent self-stabilizing data structures are widely used as basic building blocks in more complex self-stabilizing solutions.
Using a classical scheme, the certified proof consists of two main parts, one relying on termination and the other on partial correctness. For the termination part, we developed tools on potential functions and termination at a fine-grained level. Precisely, we define a potential function as a multiset containing a local potential per node. We then exploit two criteria that are sufficient to meet the conditions for using the Dershowitz-Manna well-founded ordering on multisets. Note that the termination proof we propose assumes a distributed unfair daemon, the most general scheduling assumption of the model. By contrast, the proof given in [8] assumes a stronger daemon: a distributed weakly fair daemon. Finally, we certify a quantitative property, since we show that the size of the computed k-hop dominating set is at most \(\lfloor \frac{n-1}{k+1} \rfloor + 1\), where n is the number of nodes in the network. To obtain this result, we had to write a library dealing with cardinality of sets in general and properties on cardinals of finite sets w.r.t. basic set operations, e.g., Cartesian product, disjoint union, subset inclusion, etc. This work represents about 12,250 lines of code (as computed by coqwc: 4k lines of specifications, 7k lines of proofs) written in Coq 8.4pl4, compiled with OCaml 3.11.2.
Related Work. Several works have shown that proof assistants (in particular Coq) are well-suited to certification of distributed algorithms in various contexts [4, 7, 16]. Now, to the best of our knowledge, only three works deal with certification of self-stabilizing algorithms [6, 10, 17]. A formal correctness proof of Dijkstra’s seminal self-stabilizing algorithm [12] is conducted with the proof assistant PVS [17], however only sequential executions are considered. In [6], Courtieu proposes a general setting for reasoning on self-stabilization in Coq. However, he restricts his study to very simple self-stabilizing algorithms, such as the 4-states algorithm of Ghosh [14], working on networks of very restrictive topologies i.e., lines and rings. So, these two works address too simple cases to draw a general framework. Finally, Deng and Monin [10] propose to certify in Coq self-stabilizing population protocols. Population protocols are used as a theoretical model for a collection of tiny mobile agents that interact with one another to carry out a computation. In such a model, communication is implicit, as there is no notion of communication network: all pairs of agents interact infinitely often. Hence, this latter work is not relevant for wired networks, as considered here.
Roadmap. The rest of the paper is organized as follows. In Sect. 2, we describe how we define the locally shared memory model with composite atomicity in Coq. In Sect. 3, we express the definitions of self-stabilization and silence in Coq. In Sect. 4, we provide general results in Coq to certify termination of distributed algorithms. In Sect. 5, we present our case study. Section 6 is dedicated to the proof in Coq of our case study. We certify a bound on the size of the k-hop dominating set computed by our case-study algorithm in Sect. 7. We make concluding remarks in Sect. 8.
In this paper, we present our work together with a few pieces of Coq code that we simplify in order to make them readable. In particular, we intend to use notations, as defined in the model and algorithm, in those pieces of code. The Coq definitions, lemmas, theorems, and documentation related to the paper are available as an online browsing and a technical report available at http://www-verimag.imag.fr/~altisen/PADEC/. All source codes are also available at this address. We encourage the reader to visit this webpage for a deeper understanding of our work.
2 Locally Shared Memory Model with Composite Atomicity
Distributed Systems. A distributed system is a finite set of interconnected nodes. Each node has its own private memory, runs its own code, and can interact with other nodes via interconnections. Our model in Coq reflects this defining two independent classes: Network and Algorithm. A Network is equipped with a type Node, representing nodes, and defines functions and properties that depict its topology, i.e., interconnections between nodes. Those interconnections are specified using the type Channel. The Algorithm of a node p is equipped with a type State, which describes memory state of p. Its main function, run, specifies how p executes and interacts with each other nodes through channels (type Channel).
Network and Topology. We view the communication network as a simple directed graph \(G = (V, E)\), where V is a set of vertices representing nodes and \(E\subseteq V\times V\) is a set of edges representing interconnections between distinct nodes. We note \(n = |V|\) the numbers of nodes. Two distinct nodes p and q are said to be neighbors if \((p, q)\in E\). From a computational point of view, p uses a distinct channel \(c_{p, q}\) to communicate with each of its neighbors q: it does not have direct access to q. In the type Network, the topology is defined using this narrow point of view, i.e., interconnections are represented using channels only. In particular, the neighborhood of p is encoded with the set \(\mathcal {N}_{p}\) which contains all channels \(c_{p, q}\) outgoing from p. The sets \(\mathcal {N}_{p}\), for all p, are modeled in Coq as lists. The function (peer: Node \(\rightarrow \) Channel \(\rightarrow \) option Node) returns the destination neighbor for a given channel name: (peer p \(c_{p, q}\) ) returns (Some q ), or \(\bot \) Footnote 1 if the name is unused.
Communications can be made bidirectional, assuming a property called sym_net, which states that for all nodes \(p_1\) and \(p_2\), the network defines a channel from \(p_1\) to \(p_2\) if and only if it also defines a channel from \(p_2\) to \(p_1\). In case of bidirectional links (p, q) and (q, p) in E, p can access its channel name at q using the function ( \(\rho _p\): Channel \(\rightarrow \) Channel). Thus, we have: \(\rho _p(c_{p, q})\) equals \(c_{q, p} \in \mathcal {N}_{q}\) and \(\rho _q(c_{q, p})\) equals \(c_{p, q} \in \mathcal {N}_{p}\). Finally, we suppose that, since the number of nodes in the network is finite, we have a list all_nodes containing all the nodes.
Computational Model. In the locally shared memory model with composite atomicity, nodes communicate with their neighbors using finite sets of locally shared variables. A node can read its own variables and those of its neighbors, but can only write to its own variables. Each node operates according to its local program. A distributed algorithm \(\mathcal A\) is defined as a collection of n programs, each operating on a single node. The state of a node in \({\mathcal A}\) is defined by the values of its local variables and is represented using an abstract Coq datatype State. This datatype is implemented as a record containing the values of the program variables. A node p can access the states of its neighbors using the corresponding channels: we call this the local configuration of p, and model it as a function typed (Local_Env := Channel \(\rightarrow \) option State) which returns the current state of a neighbor, given the name of the corresponding channel (or \(\bot \) for an invalid name). The program of each node p in \(\mathcal A\) consists of a finite set of guarded actions: \( \langle guard \rangle \ \hookrightarrow \ \langle statement \rangle \). The guard is a Boolean expression involving variables of p and its neighbors. The statement updates some variables of p. An action can be executed only if its guard evaluates to true; in this case, the action is said to be enabled. A node is said to be enabled if at least one of its actions is enabled. The local program at node p is modeled by a function run of type (list Channel \(\rightarrow \) (Channel \(\rightarrow \) Channel) \(\rightarrow \) State \(\rightarrow \) Local_Env \(\rightarrow \) option State). This function accesses the local topology and states around p: it takes as first two arguments \(\mathcal {N}_{p}\) and \(\rho _p\); it then takes as inputs the current state of p and its current local configuration. The returned value is the next state of node p if p is enabled, \(\bot \) otherwise. run provides a functional view of the algorithm: it includes the whole set of possible actions, but returns a single result; this model is thus restricted to deterministic algorithms.
A configuration is defined as an instance of the states of all nodes in the system, i.e., a function with type (Env := Node \(\rightarrow \) State). For a given node p and configuration g, the term (g p) represents the state of p in configuration g. Thanks to this encoding, we easily obtain the local configuration (type Local_Env) of node p by composing g and peer as a function (local_env g p) which returns (g p’) when (peer p c) returns Some p’, and \(\bot \) otherwise. Hence, the execution of the algorithm on node p in current configuration g is obtained by: (run \(\mathcal {N}_\mathtt{p}\) \(\rho _\mathtt{p}\) (g p) (local_env g p)). In configuration g, if there exist some enabled nodes, a daemon selects a non-empty set of them; every chosen node atomically executes its algorithm, leading to a new configuration g’. The transition from g to g’ is called a step. To model steps in Coq, we use functions with type (Diff := Node \(\rightarrow \) option State). We simply call difference a variable d of type Diff. A difference contains the updated states of the nodes that actually execute some action during the step, and maps any other node to \(\bot \). We define the predicate valid_diff that qualifies the current configuration and a difference expressing the result of a step by some enabled processes. It holds when at least one enabled node actually moves and all updates in the difference correspond to the execution of the algorithm by enabled processes, namely, run. The next configuration, g’, is then obtained applying function (diff_eval d g) such that: \(\forall \) p, (g’ p) = (d p) if (d p) \(\ne \bot \), and (g’ p) = (g p) otherwise.
Steps induce a binary relation \(\mapsto \) over configurations defined in Coq by the relation Step: (Step g2 g1) expresses that g1 \(\mapsto \) g2 (meaning that g1 \(\mapsto \) g2 is actually a valid step), i.e., there exists some valid difference d for g1 (valid_diff g1 d) and g2 is equal to (diff_eval d g1). An execution of \(\mathcal A\) is a sequence of configurations g \({}_0\) g \({}_1\) \(\ldots \) g \({}_i\) \(\ldots \) such that g \(_{i-1}\) \(\mapsto \) g \({}_i\) for all \(i>0\). Executions may be finite or infinite and are modeled in Coq with a type and a predicate:

where (Fst e) returns the first configuration of e. The keyword CoInductive generates a greatest fixed point capturing potentially infinite constructions.Footnote 2 Thus, variable e of type Exec actually represents an (valid) execution of \(\mathcal A\) if (valid_exec e) holds, i.e., if each pair of consecutive configurations g1, g2 in e satisfies (Step g2 g1).
Maximal executions are either infinite, or end at a terminal configuration in which no action of \({\mathcal A}\) is enabled at any node. Terminal configurations are detected in Coq using the proposition (terminal g), for a configuration g, which holds when every node computes run from g and returns \(\bot \). This predicate is decidable since we assume that the set of nodes is finite. A maximal execution is described by the coinductive proposition:

As explained before, each step from a configuration to another is driven by a daemon. In our case study, we assume that the daemon is distributed and unfair. Distributed means that while the configuration is not terminal, the daemon should select at least one enabled node, maybe more. Unfair means that there is no fairness constraint, i.e., the daemon might never select an enabled node unless it is the only one enabled. The propositions valid_diff, Step and henceforth valid_exec are sufficient to handle the distributed unfair daemon.
We allow a part of a node state to be read-only: this is modeled with type ROState and by the projection function (RO_part: State \(\rightarrow \) ROState) which typically represents a subset of the variables handled in the State of the node. We add the property RO_stable to express the fact that those variables are actually read-only, namely no execution of run can change their values. From the assumption RO_stable, we show that any property defined on the read-only variables of a configuration is indeed preserved during steps. The introduction of Read-Only variables has been motivated by the fact that we want to encompass the diversity of anonymity levels from the distributed computing literature, e.g., fully anonymous, semi-anonymous, rooted, fully identified networks, etc. By default (with empty RO_part), our Coq model defines fully anonymous network thanks to the distinction between nodes (type Node) and channels (type Channel). We enriched our model to reflect other assumptions, e.g., fully identified networks. We define predicate Assume which constrains read-only variables of a configuration (in the case of the fully identified nodes assumption, it expresses uniqueness of identifiers). It will be assumed at each initial configuration and, by RO_stable it will remain true all along any execution.
Setoids. When using Coq function types to represent configurations and differences, we need to state pointwise function equality, which equates functions having equal values (extensional equality). The Coq default equality is inadequate for functions since it asserts equality of implementations (intensional equality). So, instead we chose to use the setoid paradigm: we endow every base type with an equivalence relation. Consequently, every function type is endowed with a partial equivalence relation (i.e., symmetric and transitive) which states that, given equivalent inputs, the outputs of two equivalent functions are equivalent. However, we also need reflexivity to reason, i.e., functions equivalent to themselves. Such functions are called compatible: they return equivalent results when executed with equivalent parameters. In all the framework, we assume compatible configurations only. We also prove compatibility for every function and predicate defined in the sequel. Additionally, we assume that equivalence relations on base types are decidable.
3 Self-Stabilization and Silence
We now express self-stabilization [12] in the locally shared memory model with composite atomicity using Coq properties. Let \(\mathcal A\) be a distributed algorithm. Let  be a predicate on executions (type (Exec \(\rightarrow \) Prop)). \(\mathcal A\) is self-stabilizing w.r.t. specification
be a predicate on executions (type (Exec \(\rightarrow \) Prop)). \(\mathcal A\) is self-stabilizing w.r.t. specification  (predicate (self_stab
(predicate (self_stab  )) if there exists a predicate
)) if there exists a predicate  on configurations (type (Env \(\rightarrow \) Prop)) such that:
on configurations (type (Env \(\rightarrow \) Prop)) such that:
-
\(\mathcal A\) converges to
 , i.e., every maximal execution contains a configuration which satisfies
, i.e., every maximal execution contains a configuration which satisfies  :
: 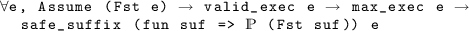
(safe_suffix S e) inductively checks that e contains a suffix that satisfies S;
-
 is closed under \(\mathcal A\), i.e., for each possible step g \(\mapsto \) g’, (
is closed under \(\mathcal A\), i.e., for each possible step g \(\mapsto \) g’, (  g) implies (
g) implies (  g’): \(\forall \) g1 g2, Assume g1 \(\rightarrow \)
g’): \(\forall \) g1 g2, Assume g1 \(\rightarrow \)  g1 \(\rightarrow \) Step g2 g1 \(\rightarrow \)
g1 \(\rightarrow \) Step g2 g1 \(\rightarrow \)  g2; and
g2; and -
\(\mathcal A\) meets
 from
from  , i.e., every maximal execution, starting from configurations which satisfy
, i.e., every maximal execution, starting from configurations which satisfy  , satisfies
, satisfies  :
: 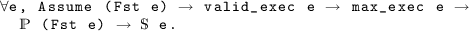
The configurations which satisfy the predicate  are said to be legitimate.
are said to be legitimate.
An algorithm is silent if the communication between the nodes is fixed from some point of the execution [13]. This latter definition can be transposed in the locally shared memory model by \(\mathcal A\) is silent if all its executions are finite:

By definition, maximal executions of a silent and self-stabilizing algorithm w.r.t some specification  end in configurations which are usually used as legitimate configurations, i.e., satisfying
end in configurations which are usually used as legitimate configurations, i.e., satisfying  . In this case,
. In this case,  only allows executions made of a single configuration which must be legitimate;
only allows executions made of a single configuration which must be legitimate;  is then noted
is then noted  . To prove that \(\mathcal A\) is both silent and self-stabilizing w.r.t.
. To prove that \(\mathcal A\) is both silent and self-stabilizing w.r.t.  , we use a common sufficient condition which requires to prove that:
, we use a common sufficient condition which requires to prove that:
-
all executions of \(\mathcal A\) are finite:
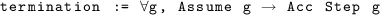
-
and all terminal configurations of \(\mathcal A\) satisfy
 :
: 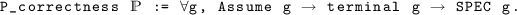
The inductive proposition Acc is taken from Library Coq.Init.Wf which provides tools on well-founded inductions. Predicate (Acc Step g) means that any descending chain from g is finite. The sufficient condition, used to prove that an algorithm is both silent and self-stabilizing, is then:

4 General Tools for Proving Termination
Usual termination proofs are based on some global potential built from local ones. For example, local potentials can be integers and the global potential can be the sum of them. In this case, the argument for termination may be, for example, the fact that the global potential is lower bounded and strictly decreases at each step of the algorithm. Global potential decrease is due to the modification of local states at some nodes, however studying aggregators such as sums may hide scenarios, making the proof more complex. Instead, we build here a global potential as the multiset containing the local potential of each node and provide a sufficient condition for termination on this multiset. Our method is based on two criteria that are sufficient to meet the conditions for using the Dershowitz-Manna well-founded ordering on multisets [11]. Given those criteria, we can show that the multiset of (local) potentials globally decreases at each step. For multisets and Dershowitz-Manna order, we used results from Library CoLoR [2].
Steps. One difficulty we faced, when trying to apply this technique straightly, is that we cannot always define the local potential function at a node without assuming some properties on its local state, and so on the associated configuration. Thus, we had to assume the existence of some stable set of configurations in which the local potential function can be defined. When necessary, we use our technique to prove termination of a subrelation of the relation Step, provided that the algorithm has been initialized in the required stable set of configurations. This point is modeled by a predicate on configurations, (safe: Env \(\rightarrow \) Prop), and a type safeEnv := { g | safe g } which represents the set of safe configurations into which we restrict the termination proof. Precisely, safeEnv is a type whose values are ordered pairs containing a term g and a proof of (safe g). Safe configurations should be stable, i.e., it is assumed that no step can exit from the set. The relation for which termination will be proven is then defined by safeStep sg2 sg1 := Step (getEnv sg2) (getEnv sg1) where getEnv accesses the actual configuration (of type Env).
Potential. We assume that within safe configurations, each node can be endowed with a potential value obtained using function pot: safeEnv \(\rightarrow \) Node \(\rightarrow \) Mnat. Notice that Mnat simply represents natural numbersFootnote 3 encoded using the type from Library CoLoR.MultisetNat [2]; it is equipped with the usual equivalence relation, noted \(=_\mathtt{P}\), and the usual well-founded order on natural numbers, noted \(<_\mathtt{P}\).
Multiset Ordering. We recall that a multiset of elements in the setoid P endowed with its equivalence relation \(=_P\), is defined as a set containing finite numbers of occurrences (w.r.t. \(=_P\)) of elements of P. Such a multiset is usually formally defined as a multiplicity function \(m: P\rightarrow \mathbb {N}_{\ge 1}\) which maps any element to its number of occurrences in the multiset. We focus here on finite multisets, namely, multisets whose multiplicity function has finite support. Now, we assume that P is also ordered using relation \(<_P\), compatible with \(=_P\). We use the Dershowitz-Manna order on finite multisets [11] defined as follows: the multiset N is smaller than the multiset M, noted \(N \prec M\), if and only if there are three multisets X, Y and Z such that \(X \ne \emptyset \wedge M = Z+X \wedge N = Z+Y \wedge \forall y \in Y, \exists x \in X, y <_{P} x\), where ‘\(+\)’ between multisets means adding multiplicities. Informally, to obtain a multiset N smaller than M, we may remove from M all elements of X and then add all elements of Y. Elements in Z are the ones that are present in both M and N. It is required that at least one element is removed (\(X\ne \emptyset \)) and each element that is added must be smaller (w.r.t. \(<_P\)) than some removed element. It has been shown that if \(<_P\) is a well-founded order, then so is the corresponding order \(\prec \).
In our context, we consider finite multisets over Pot, (i.e., \(=_P\) is \(=_\mathtt{P}\) and \(<_P\) stands for \(<_\mathtt{P}\)). We have chosen to model them as lists of elements of Pot and we build the potential of a configuration as the multiset of the potentials of all nodes, namely a multiset of (local) potentials of a configuration sg is defined by

where all_nodes is the list of all nodes in the network (see Sect. 2) and (List.map f l) is the standard operation that returns the list made of each elements of l on which f has been applied. The corresponding Dershowitz-Manna order is defined using the library CoLoR [2]. The library also contains the proof that (well_founded \(<_\mathtt{P}\) ) \(\rightarrow \) (well_founded \(\prec \) ) ((well_founded R := \(\forall \) a, Acc R a) is taken from standard Coq Library Coq.Init.Wf, as Acc). Using this latter result and the standard result which proves (well_founded \(<_\mathtt{P}\) ), we easily deduce (well_founded \(\prec \) ).
Termination Theorem. Proving the termination of an algorithm then consists in showing that for any safe step of the algorithm, the corresponding global potential decreases w.r.t. the Dershowitz-Manna order \(\prec \), namely:

We establish a sufficient condition made of two criteria on node potentials which validates safe_incl. The Local criterion finds for any node p whose potential has increased, a witness node p’ whose potential has decreased from a value that is even higher than the new potential of p:

Global criterion exhibits, at any step, a node whose potential has changed:

Assuming both hypothesis, we are able to prove safe_incl as follows: we define Z as the multiset of local potentials which did not change, and X (resp. Y) as the complement of Z in the multiset of local potentials (Pot sg1) (resp. (Pot sg2)). Global criterion is used to show that \(X\ne \emptyset \), and local criterion is used to show that \(\forall y \in Y, \exists x \in X, y <_\mathtt{P} x\). Since any relation included in a well-founded order is also well-founded, we get that relation safeStep is well-founded. Finally, since we know that property safe is stable (from stable_safe), we get ( \(\forall \) g, safe g \(\rightarrow \) Acc Step g) which proves that the algorithm terminates from any safe configuration.
5 Case Study
We have certified a non trivial part of the silent self-stabilizing algorithm proposed in [8]. Given a non-negative integer k, this algorithm builds a k-clustering of a bidirectional connected network \(G= (V, E)\) containing at most \(\lfloor \frac{n-1}{k+1} \rfloor + 1\) k-clusters, where n is the number of nodes. A k-cluster of G is a set \(C \subseteq V\), together with a designated node \({\textit{Clusterhead}}(C) \in C\), such that each member of C is within distance k of \({\textit{Clusterhead}}(C)\).Footnote 4 A k -clustering is then a partition of V into distinct k-clusters. The k-clustering problem is related to the notion of k -hop dominating set since the set of clusterheads of any k-clustering is a k-hop dominating set, i.e., a subset D of V such that every node is within distance k from at least one node of D.
The algorithm proposed in [8] is actually a hierarchical collateral composition [9] of two silent self-stabilizing sub-algorithms: the former builds a rooted spanning tree, the latter is a k-clustering construction which stabilizes once a rooted spanning tree is available in the network. The crucial part of the second sub-algorithm consists in computing, in a self-stabilizing and silent way, a k-hop dominating set D of size at most \(\lfloor \frac{n-1}{k+1} \rfloor + 1\) in an arbitrary rooted spanning tree. D will designate the set of clusterheads in the computed k-clustering. This task is performed using the 1-rule Algorithm \(\mathcal {D}({k})\), whose code is given in Algorithm 1.

We have used our framework to encode \(\mathcal {D}({k})\), its assumptions, its specification, and to build a certified proof which shows that \(\mathcal {D}({k})\) is silent and self-stabilizing for building a k-hop dominating set of at most \(\lfloor \frac{n-1}{k+1} \rfloor + 1\) nodes in any bidirectional network equipped with a rooted spanning tree.
Local States. We denote the spanning tree and its root by T and \(\textit{r}\), respectively. In \(\mathcal {D}({k})\), the knowledge of T is locally distributed at each node p using the constant input \(\mathtt {Par}({p})\) \(\in \mathcal {N}_{p} \cup \{\perp \}\). When \(p \ne \textit{r}\), \(\mathtt {Par}({p})\) \(\in \mathcal {N}_{p}\) and designates its parent in the tree. Otherwise, p is the root and \(\mathtt {Par}({p}) = \perp \). Then, each node p maintains a single variable: \(p.\alpha \), an integer in range \(\{0, ..., 2k\}\). We have instantiated the Coq State of a node as a record containing fields (Par: option Channel) and ( \(\alpha \) : Z). (Par p) stands for \(\mathtt {Par}({p})\) and is the unique read-only variable for p. Moreover, ( \(\alpha \) p) stands for \(p.\alpha \) and is taken in Z (integers). We chose to encode every number in the algorithm as integer in Z, since some of them may be negative (see \({\textit{MaxAShort}}\)) and computations use minus (see \({\textit{Alpha}}\)). Furthermore, we have proven \(p.\alpha \) is in range \(\{0, ..., 2k\}\) after p participates in any step and also when the system is in a terminal configuration.
Spanning Tree. We express the assumption about the spanning tree using predicate (span_tree \(\textit{r}\) Par). This predicate checks that the graph T induced by Par is a subgraph of G which actually encodes a spanning tree rooted at \(\textit{r}\) by the conjunction of
-
\(\textit{r}\) is the unique node such that \(\mathtt {Par}({\textit{r}}) = \perp \),
-
\(\mathtt {Par}({p})\), for every non-root node p, is an existing channel outgoing from p,
-
T contains no loop.
From the last point, we show that, since the number of nodes is finite, the relation extracted from Par between nodes and their parents (resp. children) in T is well-founded. We call this result WF_par (resp. WF_child) and express it using well_founded.
We expressed the assumptions on the network G, i.e., in any configuration g, G is bidirectional and a rooted spanning tree is available in G (n.b., this latter also implies that G is connected), in the predicate Assume:

Specification. The goal of \(\mathcal {D}({k})\) is to compute an output predicate \({\textit{kDominator}}(p)\) for every node p (see Algorithm 1 for its definition) in such way that the system converges to a terminal configuration in which the set \(Dom= \{p \in V\ |\ {\textit{kDominator}}(p) \}\) defines a k-hop dominating set of T (and so of G). We consider any positive parameter k, i.e., k is taken in Z (as for other numbers) and is assumed to be positive. We define the expected specification using the predicate  on configurations, where
on configurations, where  holds in configuration g if and only if the set \(Dom= \{p \in V\ |\ {\textit{kDominator}}(p) \}\) is a k-hop dominating set of T:
holds in configuration g if and only if the set \(Dom= \{p \in V\ |\ {\textit{kDominator}}(p) \}\) is a k-hop dominating set of T:

where predicate is_path detects if the list of nodes path actually represents a path in the tree T between the nodes kdom and p, and length computes the length of the path.
\(\mathcal {D}({k})\) in Coq. We translate the unique rule of \(\mathcal {D}({k})\) into the type Algorithm. Every predicate and macro of Algorithm 1 is directly encoded in Coq: the translation is quasi-syntactic (see Library KDomSet_algo in the online browsing) and provides a definition of run. The definition of \(\mathcal {D}({k})\), of type Algorithm, comes with a proof that run is compatible, as a composition of compatible functions, and also with a straightforward proof of RO_stable which asserts that the read-only part of the state, Par, is constant during steps, when applying run.
Overview of \(\mathcal {D}({k})\). Algorithm \(\mathcal {D}({k})\), whose code is given in Algorithm 1, computes a k-hop dominating set of T (and so of G), noted \(Dom\), using the variable \(\alpha \) at each node. Precisely, \(Dom\) is defined as the set of nodes p such that \({\textit{kDominator}}(p)\) holds, i.e., where \(p.\alpha = k\), or \(p.\alpha < k\) and \(p = r\). \(Dom\) is constructed in a bottom-up fashion starting from the leaves of T. The goal of variable \(p.\alpha \) at each node p is twofold. First, it allows to determine a path of length at most k from p to a particular node q of \(Dom\) which acts as a witness for guaranteeing the k-hop domination of \(Dom\). Consequently, q will be denoted as \(W\!itness(p)\) in the following. Second, once correctly evaluated, the value \(p.\alpha \) is equal to \(\Vert p,x\Vert \), where x is the furthest node in T(p), the subtree of T rooted at p, that has the same witness as p.
We divide processes into short and tall according to the value of their \(\alpha \)-variable: If p satisfies \({\textit{IsShort}}(p)\), i.e., \(p.\alpha < k\), then p is said to be short; otherwise, p satisfies \({\textit{IsTall}}(p)\) and is said to be tall. In a terminal configuration, the meaning of \(p.\alpha \) depends on whether p is short or tall.
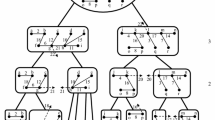
If p is short, we have two cases: \(p\ne \textit{r}\) or \(p = \textit{r}\). In the former case, \(W\!itness(p) \in Dom\) is outside of T(p), that is, the path from p to \(W\!itness(p)\) goes through the parent link of p in the tree, and the distance from p to \(W\!itness(p)\) is at most \(k-p.\alpha \). See, for example, in Configuration (I) of Fig. 1, \(k=2\) and \(j.\alpha = 0\) mean that \(W\!itness(j)\) is at most at distance \(k-0 = 2\), now its witness e is at distance 2. In the latter case, p (\(= \textit{r}\)) may not be k-hop dominated by any process of \(Dom\) inside its subtree and, by definition, there is no process outside its subtree, indeed \(T(p) = T\), see the root a in Configuration (I) of Fig. 1. Thus, p must be placed in \(Dom\).
If p is tall, there is a process q at \(p.\alpha -k\) hops below p such that \(q.\alpha =k\). So, \(q \in Dom\) and p is k-hop dominated by q. Hence, \(W\!itness(p) = q\). The path from p to \(W\!itness(p)\) goes through a tall child with minimum \(\alpha \)-value. See, for example, in Configuration (I) of Fig. 1, \(k = 2\) and \(c.\alpha = 4\) mean that \(W\!itness(c)\), here e, is \(4-k = 2\) hops below c. Note that, if \(p.\alpha = k\), then \(p.\alpha -k=0\), that is, \(p = q = W\!itness(p)\) and p belongs to \(Dom\).
Two examples of 2-clustering computed by \(\mathcal {D}({2})\) are given in Fig. 1. In Fig. 1.(I), the root is a short process, consequently it belongs to \(Dom\). In Fig. 1.(II), the root is a tall process, consequently it does not belong to \(Dom\).
Two examples of 2-hop dominating sets computed by \(\mathcal {D}({2})\). We only draw the spanning tree, other edges are omitted. The root of each tree is the rightmost node. \(\alpha \)-values are given inside the nodes. Bold circles represent members of \(Dom\). Arrows represent the path from nodes to their associated witnesses.
6 Self-Stabilization of \(\mathcal {D}({k})\)
According to the sufficient condition (Lemma silent_self_stab) given in Sect. 3, we prove the self-stabilization of \(\mathcal {D}({k})\) in two steps: termination in Subsect. 6.1 and partial correctness in Subsect. 6.2.
6.1 Termination of \(\mathcal {D}({k})\).
We use the general result from Sect. 4 to prove termination of \(\mathcal {D}({k})\), expressed as follows:

First, we assume sym_net and that the root node \(\textit{r}\) exists. We instantiate safe as every configuration in which read-only variables Par satisfy (span_tree \(\textit{r}\) Par). Notice that the assumption on the existence of the spanning tree T rooted at \(\textit{r}\) is mandatory, since, as we will see below, the local potentials we use in our proof are based on the depth of nodes in T. Finally, note that it is easy to prove that safe is stable since it only depends on read-only variables.
Potential. We define the depth of a node as the distance between the node and the root \(\textit{r}\) in the spanning tree T. Let sg be a safe configuration and p be a node. (depth sg p) is 1 (natural number, type nat) if p is the root \(\textit{r}\), and (1 + (depth sg q)) where q the parent of p in T otherwise. This definition relies on structural induction on (WF_par n). We define the potential (pot sg p) of node p in safe configuration sg as 0 if p is not enabled in sg, and (depth sg p) otherwise.
Local Criterion. Let sg1 and sg2 be two safe configurations such that (safeStep sg2 sg1). Consider a node p whose potential increases during the step, i.e., such that (pot sg1 p) \(<_\mathtt{P}\) (pot sg2 p). This means, from definition of pot, that p is disabled at sg1 (potential is 0) and becomes enabled at sg2 (potential equals (depth sg2 p)>0). To show the local criterion, we exhibit a down-path in the tree T from p to some leaf that contains a node q enabled in sg1 which becomes disabled in the next configuration, sg2. We prove the result in two steps. First, we necessarily exhibit a child of node p, child, which executes its algorithm during the step. As second step, we prove Lemma moving_node_has_disabled_desc, which states that when the node child moves, it is down-linked in T to a node (maybe the node itself) which was enabled and becomes disabled during the step. This result is proven by induction on (WF_child child), i.e., on the down-paths from child in T.
Global Criterion. Global criterion requires to find a node whose potential differs between sg1 and sg2. We show that there is a node p with potential (depth sg1 p) in sg1 (>0, by definition), and potential 0 in sg2. Namely, p is enabled in sg1, but disabled in sg2. The proof uses the fact that at least one node has moved during the step. Then, we reuse Lemma moving_node_has_disabled_desc to show that any node that participates to the step has a descendant (on a given down-path of T) which is enabled in sg1, but disabled in sg2.
Termination. Theorem k_dom_set_terminates follows directly from local and global criteria.
6.2 Partial Correctness of \(\mathcal {D}({k})\)
The proof of partial correctness consists in showing that predicate  holds in any terminal configuration satisfying Assume
\(_\mathtt{kdom}\):
holds in any terminal configuration satisfying Assume
\(_\mathtt{kdom}\):

From definition of  , we need to check the existence of a path in G between any node p and any node kdom \(\in Dom\), such that this path is of length at most k. To achieve this property, the algorithm builds tree paths of particular shape: those paths use edges of T in both direct sense (from a node to its parent) and reverse sense (from a node to one of its children). Precisely, these edges are defined using relation is_kDom_edge, which depends on \(\alpha \)-values: for any short node s, we select the edge linking s to its parent in T (using Par); while for any tall node t which is not in \(Dom\), we select an edge linking t to a child c such that \(c.\alpha = t.\alpha -1\). The relation is_kDom_edge defines a subgraph of G called kdom-graph. So, to show Theorem kdom_at_terminal, it is sufficient prove that for any configuration g such that (Assume
\(_\mathtt{kdom}\) g) and (terminal g), we have:
, we need to check the existence of a path in G between any node p and any node kdom \(\in Dom\), such that this path is of length at most k. To achieve this property, the algorithm builds tree paths of particular shape: those paths use edges of T in both direct sense (from a node to its parent) and reverse sense (from a node to one of its children). Precisely, these edges are defined using relation is_kDom_edge, which depends on \(\alpha \)-values: for any short node s, we select the edge linking s to its parent in T (using Par); while for any tall node t which is not in \(Dom\), we select an edge linking t to a child c such that \(c.\alpha = t.\alpha -1\). The relation is_kDom_edge defines a subgraph of G called kdom-graph. So, to show Theorem kdom_at_terminal, it is sufficient prove that for any configuration g such that (Assume
\(_\mathtt{kdom}\) g) and (terminal g), we have:

where is_kDom_path checks that its parameter path is a path on the kdom-graph between kdom and p.
The rest of the analysis is conducted assuming a terminal configuration g such that (Assume \(_\mathtt{kdom}\) g) holds. We first prove that any node p satisfying \(p.\alpha > 0\) has a child q such that \(p.\alpha = q.\alpha + 1\) (the proof is simply a case analysis on \({\textit{MaxAShort}}(q) + {\textit{MinATall}}(q) \le 2 k - 2\)). Then, the proof is split into two cases, depending on whether the node is tall or short. We prove, for every tall (resp. short) node p and every \(i\in \mathbb {N}\), that when \(p.\alpha = k + i\) (resp. \(k - i\)), there exists a witness node q for which \({\textit{kDominator}}\) holds and a path, of length at most i, from p to q in kdom-graph. In both cases, the proof is conducted by induction on i.
Conclusion. Using Lemma silent_self_stab, we obtain that \(\mathcal {D}({k})\) is a silent self-stabilizing algorithm for  :
:

7 Quantitative Properties
In addition to partial correctness, we have shown that the k-hop dominating \(Dom\) set built by \(\mathcal {D}({k})\) satisfies \(|Dom| \le \lfloor \frac{n-1}{k+1} \rfloor + 1\), where n is the number of nodes. Precisely, we have formally proven the equivalent property which states that \((n-1) \ge (k+1)(|Dom|-1)\). Intuitively, this means that at least all but one element of \(Dom\) have been chosen as witness by at least \(k+1\) distinct nodes each.
Counting Elements in Sets. We have set up a library dealing with cardinality of sets in general, and then finite sets. The library contains basic properties about set operations such as cardinality of Cartesian product, disjoint union, subset inclusion, etc. We also proved in Coq the existence of finite cardinality for finite sets using lists. Those proofs have been conducted using standard techniques.
Proving Counting for \(\mathcal {D}({k})\). First, we assume a terminal configuration g. Using above results about the number of elements in the list all_nodes, we show the existence of the natural number n, i.e., the number of nodes. Similarly, the existence of the natural number \(|Dom|\) is obtained using the list all_nodes restricted to nodes p such that ( \({\textit{kDominator}}\) (g p) = true).
Then, we define as regular head each node of \(Dom\) such that \(\alpha = k\). By definition the set of regular heads is included in \(Dom\). Again, we prove the existence of the natural number rh which represents the number of regular heads in g.
Next, we define a regular node as a node which designates a regular head as witness. We prove the existence of the natural number rn which is the number of regular nodes in g. We prove that for each regular head h, for any \(0\le i \le k\), there is a regular node \(p_i\) such that \(\alpha =i\) which designates h as witness in g. This implies that there is a path of length \(k+1\) in the kdom-graph linking \(p_0\) to h. We then group each regular head together with the regular nodes that designate it as witness: each group contains at least \(k+1\) regular nodes. Thus, \(rn \ge (k+1)rh\).
Now, we have two cases. If the root is tall in g (i.e., \(\textit{r}.\alpha \ge k\)), then \(rh = |Dom|\) and \(rn = n\). Otherwise, the root is short in g, and \(Dom\) contains both the regular heads and the root (which is not regular in this case). Thus, \(|Dom| = rh + 1\) and, similarly, the set of nodes contains at least regular nodes plus the root, so \(rn \le n-1\). Hence, in either case, \((n-1) \ge (k+1)(|Dom|-1)\) holds in g.
8 Conclusion
We proposed a general framework to build certified proofs of self-stabilizing algorithms. To achieve our goals, we developed, in particular, general tools about potential functions, which are commonly used in termination proofs of self-stabilizing algorithms. We also proposed a library dealing with cardinality of sets. We use this latter to show a quantitative property on the output of our case-study algorithm.
In future works, we expect to certify more complex self-stabilizing algorithms. Such algorithms are usually designed by composing more basic blocks. In this line of thought, we envision to certify general theorems related to classic composition techniques such as collateral or fair compositions.
Finally, we expect to use our experience on quantitative properties to tackle the certification of time complexity of stabilizing algorithms, a.k.a. the stabilization time.
Notes
- 1.
Option type is used for partial functions which, by convention, return (Some __) when defined, and None otherwise (denoted by \(\bot \) in this paper).
- 2.
As opposed to this, the keyword Inductive only captures finite constructions.
- 3.
Natural numbers cover many cases and we expect the same results when further extending to other types of potential.
- 4.
the distance \(\Vert p, q\Vert \) between two nodes p and q is the length of a shortest path from p to q in G.
References
Ben-Othman, J., Bessaoud, K., Bui, A., Pilard, L.: Self-stabilizing algorithm for efficient topology control in wireless sensor networks. J. Comput. Sci. 4(4), 199–208 (2013)
Blanqui, F., Koprowski, A.: CoLoR: a coq library on well-founded rewrite relations and its application to the automated verification of termination certificates. Math. Struct. Comput. Sci. 21(4), 827–859 (2011)
Caron, E., Chuffart, F., Tedeschi, C.: When self-stabilization meets real platforms: an experimental study of a peer-to-peer service discovery system. future gener. comput. syst. 29(6), 1533–1543 (2013)
Chen, M., Monin, J.F.: Formal verification of netlog protocols. In: TASE (2012)
Chen, N., Yu, H., Huang, S.: A self-stabilizing algorithm for constructing spanning trees. Inf. Process. Lett. 39, 147–151 (1991)
Courtieu, P.: Proving self-stabilization with a proof assistant. In: IPDPS (2002)
Courtieu, P., Rieg, L., Tixeuil, S., Urbain, X.: Impossibility of gathering, a certification. Inf. Process. Lett. 115(3), 447–452 (2015)
Datta, A.K., Larmore, L.L., Devismes, S., Heurtefeux, K., Rivierre, Y.: Competitive self-stabilizing k-clustering. In: ICDCS (2012)
Datta, A.K., Larmore, L.L., Devismes, S., Heurtefeux, K., Rivierre, Y.: Self-stabilizing small k-dominating sets. IJNC 3(1), 116–136 (2013)
Deng, Y., Monin, J.F.: Verifying self-stabilizing population protocols with Coq. In: TASE (2009)
Dershowitz, N., Manna, Z.: Proving termination with multiset orderings. Commun. ACM 22(8), 465–476 (1979)
Dijkstra, E.W.: Self-stabilizing systems in spite of distributed control. Commun. ACM 17, 643–644 (1974)
Dolev, S., Gouda, M.G., Schneider, M.: Memory requirements for silent stabilization. In: PODC, pp. 27–34 (1996)
Ghosh, S.: An alternative solution to a problem on self-stabilization. ACM Trans. Program. Lang. Syst. 15(4), 735–742 (1993)
Huang, S., Chen, N.: Self-stabilizing depth-first token circulation on networks. Distrib. Comput. 7(1), 61–66 (1993)
Küfner, P., Nestmann, U., Rickmann, C.: Formal verification of distributed algorithms. In: Baeten, J.C.M., Ball, T., de Boer, F.S. (eds.) TCS 2012. LNCS, vol. 7604, pp. 209–224. Springer, Heidelberg (2012)
Kulkarni, S.S., Rushby, J.M., Shankar, N.: A case-study in component-based mechanical verification of fault-tolerant programs. In: WSS, pp. 33–40 (1999)
Lamport, L.: How to write a 21st century proof. J. fixed point theory appl. 11(1), 43–63 (2012)
The Coq Development Team: The Coq Proof Assistant, Reference Manual. http://coq.inria.fr/refman/
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 IFIP International Federation for Information Processing
About this paper
Cite this paper
Altisen, K., Corbineau, P., Devismes, S. (2016). A Framework for Certified Self-Stabilization. In: Albert, E., Lanese, I. (eds) Formal Techniques for Distributed Objects, Components, and Systems. FORTE 2016. Lecture Notes in Computer Science(), vol 9688. Springer, Cham. https://doi.org/10.1007/978-3-319-39570-8_3
Download citation
DOI: https://doi.org/10.1007/978-3-319-39570-8_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-39569-2
Online ISBN: 978-3-319-39570-8
eBook Packages: Computer ScienceComputer Science (R0)




 , i.e., every maximal execution contains a configuration which satisfies
, i.e., every maximal execution contains a configuration which satisfies  :
: 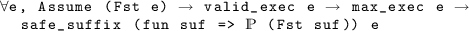
 is closed under
is closed under 



 from
from  , i.e., every maximal execution, starting from configurations which satisfy
, i.e., every maximal execution, starting from configurations which satisfy  , satisfies
, satisfies  :
: 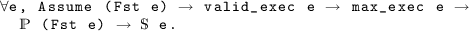
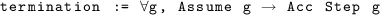
 :
: