Fuzzy Logic Control of a Humanoid Robot on Unstable Terrain

Abstract

This paper describes a novel system for enabling a humanoid robot to balance on highly dynamic terrain using fuzzy logic. We evaluate this system by programming Jimmy, a small, humanoid DARwIn-OP robot, to balance on a bongo board – a simple apparatus consisting of a deck resting on a free-rolling wheel – using our novel fuzzy logic system and a PID controller based on our previous work (Baltes et al. [1]). Both control algorithms are tested using two different control policies: “do the shake,” wherein the robot attempts to keep the bongo board’s deck level by CoM manipulation; and “let’s sway,” wherein the robot pumps its legs up and down at regular intervals in an attempt to induce a state of dynamic stability to the system. Our experiments show that fuzzy logic control is equally capable to PID control for controlling a bongo board system.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

In this paper we present a fuzzy logic control system for controlling a humanoid robot standing on a bongo board. This is a continuation of our previously-published research [1] into active balancing on highly-dynamic surfaces using Jimmy¹, a DARwIn-OP humanoid robot.

For humanoid robots to be useful in the broadest possible applications they must be able to traverse all manner of terrain without falling. While recent developments in hardware and software have seen humanoid robots improve dramatically in capabilities when traversing mostly-level ground with good traction – e.g. between 2009 and 2013 the world record for the HuroCup sprint event² has improved from 01:07.50 to 00:25.50 [2] – the ability to traverse arbitrary terrain with unknown traction remains beyond the state-of-the-art.

In order to analyse the problems of active balancing on unknown and unstable terrain we selected the bongo board, a simple apparatus consisting of a deck with a single free-rolling wheel positioned below it, as a sample problem. A humanoid robot stands on top of the board and must control their CoM in such a way as to keep the bongo board’s wheel centred and prevent the ends of the bongo board from striking the ground. Figure 1 shows a robot on the bongo board.

Fig. 1.

Jimmy standing on a bongo board. (Baltes et al. [1])

The remainder of this paper is organised as follows: Sect. 2 presents an analysis of the bongo board and how it relates to the well-known inverted pendulum problem. Here we also discuss our previous research using PID control to balance the bongo board. Section 3 describes a fuzzy logic system for controlling a humanoid robot on a bongo board directly inspired by a solution for the inverted pendulum problem. We summarise our experimental procedure and perform a quantitative analysis of the performance of the fuzzy logic controller compared to our previous PID-based solution in Sect. 4. Finally we discuss practical applications of this research and provide avenues of future research in Sect. 5.

2 Analysis and Related Work

This section provides a brief analysis of the cart-and-rod problem and how it relates to the bongo board. The development of a Fuzzy Logic system for controlling a cart-and-rod inverted pendulum is summarised. Finally we discuss our earlier work in controlling a humanoid robot on a bongo board, including a Proportional-Integral-Derivative (PID) controller-based system by Baltes et al. [1].

2.1 Analysis of the Inverted Pendulum

The inverted pendulum problem is a well-known problem in control theory wherein a mass m is placed at the top of a rigid rod of length l. The other end of the rod is connected to a fulcrum inside a powered cart. The goal of the system is to control the forward velocity of the cart in such a way as to keep the mass and rod upright.

Figure 2 shows the classic cart-and-rod inverted pendulum problem and the forces acting on the system. Gravity, g, pulls down on the mass, applying torque $\tau$ at the fulcrum. The cart accelerates at a(t), bringing the fulcrum towards the mass and applying torque to counteract $\tau$.

Fig. 2.

The cart-and-rod inverted pendulum problem. A mass m is placed on a rod of length l anchored to a fulcrum inside a mobile cart. Gravity g acts on the mass, applying torque $\tau$ and pulling the mass down. The cart accelerates at a rate of a(t) to keep the fulcrum positioned below the mass and keep the rod in an upright position.

Many solutions for the inverted pendulum problem have been demonstrated including PID controllers [3], reinforcement learning [4, 5], and fuzzy logic [6, 7].

2.2 Fuzzy Logic Control for Inverted Pendula

Yamakawa demonstrated that a simple set of fuzzy implications could be used to balance a cart-and-rod inverted pendulum [7]. In his implementation the cart is powered by a simple electric motor, with the speed $\dot{y}$ determined by the voltage supplied to the motor. His fuzzy rules take the inclination, $\theta$, and angular velocity, $\dot{\theta }$, of the pendulum as inputs and outputs the horizontal velocity of the cart, $\dot{y}$, as shown in Algorithm 1. Yamakawa’s implementation defines seven fuzzy input and output sets: Positive Large (PL), Positive Medium (PM), Positive Small (PS), Near-Zero (ZR), Negative Small (NS), Negative Medium (NM), and Negative Large (NL). Rules are not defined for states where the system is highly unstable (e.g. $\theta$ and $\dot{\theta }$ are both positive-large). Because the goal of the fuzzy control system is to keep the cart-and-rod in a relatively stable state with $\theta$ and $\dot{\theta }$ being small we can make the assumption that the system is working correctly when implementing these rules. If the system is in a relatively unstable state then the control system has already failed its stated purpose. Therefore Yamakawa’s rules do not define any behaviour for situations when the rod is severely inclined (e.g. $\theta$ is NL) or when the rod is falling quicky (e.g. $\dot{\theta }$ is PL).

2.3 Analysis of the Bongo Board

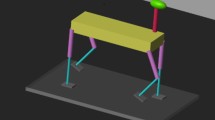
The bongo board can be seen as a variation of the cart-and-rod problem, only instead of the cart controlling the motion of the mass above the cart the rider controls the motion of the deck and wheel below them. A bongo board system is shown in Fig. 3, illustrating the major variables at work in the system.

Fig. 3.

An idealised bongo board in an unstable position with the rider. The rider’s torso is offset horizontally by $x_{torso}$ and vertically by $y_{torso}$ with respect to the midpoint between the robot’s feet. The legs have been adjusted to lengths $y_{R}$ and $y_{L}$ for the right and left legs respectively. $\phi _{r}$ gives the inclination of the rider due to the difference in heights of the legs. The arms have been set to angles $\theta _{R}$ and $\theta _{L}$ with respect to the right and left shoulders. The robot’s CoM, m, is offset from the torso because of the arm positions. $\theta$ denotes the inclination of m with respect to the line drawn from the midpoint between the robot’s feet. $\theta _{m}$ denotes the angle between m and the point of contact between the deck and the wheel. The distance from this point of contact and m is given by l. The deck is inclined by $\phi$ from the horizontal. (Baltes et al. [1])

The rider is assumed to have five degrees of freedom they can use to exert forces on the system: the angle of each shoulder in the frontal plane ($\theta _{L}$ and $\theta _{R}$ for the left and right shoulders respectively), the lateral and vertical offsets of the torso ($x_{torso}$ and $y_{torso}$ respectively), and the angle of inclination of the torso relative to the deck ($\phi _{r}$). Humans observed balancing on a bongo board tend to rely on lower-spine and hip mobility to control $\phi _{r}$. Many humanoid robots lack this level of torso flexibility, but may independently control the length of each leg by extending or contracting the knee to control $\phi _{r}$ [1].

Unlike the cart-and-rod inverted pendulum, the bongo board does not have a fixed fulcrum; the point of contact between the deck and the wheel translates along the deck as the wheel rolls from side-to-side and as the deck rotates around the periphery of the wheel. This means that, in the absence of forces exerted by the rider, two events will occur:

• 1. the deck will rotate under the effect of gravity, following the same principle as the falling mass in the cart-and-rod problem; and

• 2. the deck will roll downhill along the wheel, mimicking the effect of a mass sliding down an inclined plane.

Figure 4 shows a simplified bongo board in an unstable position. The passive rider (i.e. a rider exerting no forces on the system) has been replaced with a point-mass positioned at height l above the deck. As gravity pulls the mass down the deck rotates around the wheel with torque $\tau$. This rotation causes lateral force $F_{\alpha }$ as the falling mass forces the pivot-point to translate. Finally, because the deck is inclined gravity will pull the entire deck-rider assembly downhill with force $F_{\theta }$. The equations for $\tau$, $F_{\alpha }$, and $F_{\theta }$ are given below:

Fig. 4.

An idealised bongo board in an unstable position. $\theta$ shows the rider’s inclination relative to the deck, while $\theta _{m}$ shows the rider’s inclination relative to the point of contact between the wheel and the deck. $\theta _{r}$ gives the rider’s torso’s absolute inclination. The mass, m lies at height l above the deck. As the bongo board falls the mass rotates downward applying force $F_{\alpha }$ to the system, while the entire mass-rod-deck assembly slides downhill, applying $F_{\theta }$ to the system. $l'$ gives the distance from the point of contact between the wheel and the deck to the rider’s CoM.

$$\begin{aligned} \tau = gml'\sin \theta _{m} \end{aligned}$$

(1)

$$\begin{aligned} F_{\alpha } = ml(\ddot{\theta }_{m}\cos \theta _{m} - \dot{\theta }_{m}^{2}\sin \theta _{m}) \end{aligned}$$

(2)

$$\begin{aligned} F_{\theta } = mg\cos \theta _{m} \end{aligned}$$

(3)

By rotating the arms in the frontal plane, shifting the torso’s CoM, and inclining the torso relative to the deck the rider exerts several forces and moments on the system that counteract $\tau$, $F_{\alpha }$, and $F_{\theta }$.

2.4 Control Systems for the Bongo Board

Because of the complex nature of the bongo board relatively few practical implementations capable of balancing the system exist. Anderson and Hodgins [8] demonstrated that it is possible for a small humanoid robot to balance on a deck attached to a fixed pivot point using an adaptive torque-based approach. McGrath et al. [9] showed that active balancing and correction for inclination with a small humanoid robot using gyroscope feedback was possible. Other work in the area of balancing in highly-dynamic environments are primarily theoretical [10, 11]. While push-recovery strategies, such as Pratt et al.’s work [12], are useful for traversing unstable terrain, they rely on the ground providing a consistent normal force to arrest the robot’s movement. Because the bongo board’s deck is unsupported, except for the area in contact with the wheel, foot-placement strategies alone are insufficient for keeping the bongo board system stable.

Baltes et al. [1] demonstrated the first practical implementation of a humanoid robot capable of balancing on a bongo board. Their implementation uses PID controllers to adjust five degrees of freedom: the angle of each shoulder in the frontal plane, the vertical and horizontal positions of the torso’s CoM relative to the deck, and the inclination of the robot’s torso. Figure 5 shows how the robot’s CoM is controlled; by extending or contracting the legs the CoM is moved vertically; by adjusting the lengths of the legs and rotating the hips and ankles in the frontal plane the CoM can be moved horizontally; and by contracting one leg while extending the other the robot can incline its entire torso to the left or right.

Fig. 5.

Diagrams showing how the rider in the neutral position (extreme left) and how it uses the joints in the legs and hips to raise/lower its CoM (centre-left), shift its CoM side-to-side (centre-right), and incline its torso (extreme right).

Baltes et al. [1] propose three different control policies, dubbed “stiff upper lip,” “do the shake,” and “let’s sway,” each using a slightly different set of control laws and motions. The “stiff upper lip” policy was determined to be ineffective, but “do the shake” and “let’s sway” were both able to control the bongo board for short periods of time.

Baltes et al.’s control policies use PD controllers to control the robot’s arm and torso rotation. In Eqs. 4 and 5 the terms $K_{a_{p}}$ and $K_{a_{d}}$ refer to the P- and D-gains used to control the arms, while $K_{t_{p}}$ and $K_{t_{d}}$ refer to the P- and D-gains used to control the inclination of the torso. All gains were manually tuned.

The “do the shake” policy consists of two PD controllers that independently control the robot’s torso inclination and arm rotation. To compensate for sensor latency a linear predictive sensor model [13] to extrapolate the robot’s current state based on previous sensor readings. If the predicted inclination and angular velocity are small then the torso inclination is left alone and the arms are spun to make small corrections. If the predicted inclination or angular velocity is large the arms and torso inclination are both used to correct the robot’s motion. The control law used for the “do the shake” policy is given in Eq. 4.

$$\begin{aligned} \begin{array}{r} \theta _{torso}' = predicted(\theta _{torso},\dot{\theta }_{torso}) \\ d_{arms} = K_{a_{p}}\theta _{torso}' + K_{a_{d}}\dot{\theta }_{torso}' \\ \theta _{torso} = K_{t_{p}}\theta _{torso}' + K_{t_{d}}\dot{\theta }_{torso}'\\ \end{array} \end{aligned}$$

(4)

The “let’s sway” policy was largely identical to “do the shake” save for the addition of a regular oscillation to the robot’s motion; the legs continuously pump up and down in an attempt to induce a state of dynamic stability to the system. The control law for the “let’s sway” policy is given in Eq. 5.

$$\begin{aligned} \begin{array}{r} \theta _{torso}' = predicted(\theta _{torso},\dot{\theta }_{torso}) \\ \theta _{desired} = \sin (\omega t) \\ d_{arms} = K_{a_{p}}(\theta _{torso}'-\theta _{desired}) + K_{a_{d}}(\dot{\theta }_{torso}'-\dot{\theta }_{desired}) \\ \theta _{torso} = K_{t_{p}}(\theta _{torso}-\theta _{desired})' + K_{t_{d}}(\dot{\theta }_{torso}'-\dot{\theta }_{desired})\\ \end{array} \end{aligned}$$

(5)

Based on the angular velocity and inclination of the robot’s torso as recorded during several trials using all three control policies and through qualitative observations Baltes et al. concluded that the introduction of a regular oscillation from the “let’s sway” policy improved the robot’s overall stability, albeit not in a statistically significant way.

3 Fuzzy Rules for the Bongo Board

Based on Yamakawa’s rules for the cart-and-rod inverted pendulum and Baltes et al.’s PID-based system for controlling the motion of a bongo board we define a set of rules to control the five degrees of freedom that the bongo board’s rider uses:

• $\theta$, the angle from the deck to the rider’s centre of mass;

• $x_{torso}$, the lateral offset of the rider’s torso;

• $y_{torso}$, the vertical offset of the rider’s torso;

• $\theta _{L}$, the angle of the rider’s left shoulder; and

• $\theta _{R}$, the angle of the rider’s right shoulder.

As with Yamakawa’s rules, we define our rules such that the rate of change of each degree of freedom is output. For simplicity we control the angular velocity of both arms simultaneously. Therefore the fuzzy rules specify the angular velocity of both arms as a single output. The fuzzy rules defined for balancing the bongo board are shown in Algorithm 2, using the same abbreviations described in Sect. 2.2.

The fuzzy rules use the inclination and angular velocity of the bongo board’s deck, $\phi$ and $\dot{\phi }$ respectively, as inputs. Given knowledge of the robot’s torso’s inclination and angular velocity and the current positions of the joints in robot’s legs the inclination and angular velocity of the deck can be trivially calculated.

The fuzzy rules output the desired angular velocity of the arms ($\dot{\theta }_{arm}$) and the torso ($\dot{\theta }$) as well as the linear velocities of the rider’s CoM along the x-axis (parallel to the deck of the bongo board) and y-axis (perpendicular to the deck of the bongo board).

We set the PS, NS, PM, and NM thresholds for $\phi$ and $\dot{\phi }$ based on the data recorded during our initial research with PID controllers [1]. The thresholds for the output variables ($\dot{\theta }_{arm}$, $\dot{x}$, $\dot{y}$, and $\dot{\theta }$) were determined experimentally by placing the robot on the bongo board and observing its behaviour, increasing or decreasing each threshold based on the robot’s performance and the sensor data recorded. In all cases the ZR threshold was left at zero.

These rules specify that when the deck is inclined one direction, but the angular velocity is in the opposite direction the system should produce near-zero outputs; when the bongo board is either in a stable position, or is self-stabilizing (i.e. rotating in such a way that the deck becomes more level) the system should allow this process to continue uninterrupted. The vertical and horizontal torso offsets are only used when the system is highly unstable; these DOFs are used only as a last-resort to stabilise the system when arm motion and torso inclination prove insufficient.

4 Evaluation

To evaluate the performance of the fuzzy logic controller compared to Baltes et al.’s PID-based system we perform five 30-second trials using the PID and fuzzy logic controllers using both the “let’s sway” and “do the shake” control policies. Due to the low success rate of the “stiff upper lip” policy reported by Baltes et al. [1] we omit this control policy from our experiment. These trials are performed using a physical robot standing on a wooden bongo board, as shown in Fig. 1. During the trials the robot operates on battery power with no external cables (e.g. power, ethernet) connected. A human operator is present to reset the apparatus should the bongo board fall and the robot is unable to autonomously right the board.

During each trial the robot records the angular velocity and inclination of the torso, as well as the positions of each joint. From these data we can calculate the angular velocity and inclination of the bongo board’s deck.

Table 1 shows the angular velocity and inclination of the robot’s torso ($\theta$, $\dot{\theta }$) and of the deck ($\phi$,$\dot{\phi }$) across all trials.

Table 1. Minimum, maximum, and average deck inclination and difference in inclination from the previous tick. Measurements are in $^{\circ }$ and $^\circ$/tick (1 tick $\approx$ 8 ms).

4.1 Comparison of Control Policies

Both the “do the shake” and “let’s sway” policies exhibited similar performance regardless of the control algorithm used. The “do the shake” policy performed best when used with the fuzzy logic controller, while the “let’s sway” policy performed better with the PID controller. The differences in performance were slight and are not statistically significant.

As observed by Baltes et al., the “let’s Sway” policy did successfully maintain a lower average angular velocity in the robot’s torso [1]. The difference was very small; the difference in average torso velocities $4.00597\times 10^{-5}$ deg./s. The “let’s sway” policy does not appear to offer any significant benefits to balancing, but is not detrimental either.

The “do the shake” policy used with the fuzzy logic controller maintained the lowest average deck inclination with the smallest standard deviation of all experiments. Additionally, this combination of control algorithm and control policy had the lowest recorded average $\dot{\phi }$. These findings are mirrored in the average torso inclination and angular velocity, indicating that the “do the shake” policy may be preferable over the “let’s sway” policy.

4.2 Comparison of Control Algorithms

Both the fuzzy logic and PID controllers were successfully able to control the motion of the bongo board and maintain a stable position for short periods of time. Qualitatively the fuzzy logic controller appeared to maintain a stable position for longer continuous periods of time, but was unable to automatically recover; when using the PID controller if either end of the deck struck the ground the robot would react very strongly, autonomously bouncing the deck back to a horizontal position. The fuzzy logic controller did not exhibit this self-recovery property.

The fuzzy logic controller’s inability to self-recover after the deck struck the ground is primarily attributable to the fact that the rules are written with the assumption that the system is relatively stable and $\phi$ and $\dot{\phi }$ are small. When the deck strikes the ground the system undergoes extreme deceleration, sometimes exceeding 1g. This large change in velocity requires a correspondingly large output, which is unaccounted for in the fuzzy rule-set. The PID controller in contrast has no strict upper bound on the magnitude of its output; the large deceleration due to the deck-strike is passed directly into the PID controller, which in turn produces a very strong response as its output. The introduction of additional rules to the fuzzy rule-set to specifically address the large changes in velocity experienced during a deck-strike may allow the fuzzy logic controller to self-recover in a similar fashion as the PID controller.

The fuzzy logic controller, when used with the “do the shake” policy maintained the lowest average deck inclination with the lowest standard deviation, indicating that overall the fuzzy logic controller was slightly more stable than the PID controller. This improvement is not statistically significant, but does indicate that, like the cart-and-rod inverted pendulum, the bongo board can be controlled by both PID control and fuzzy logic.

Fig. 6.

A humanoid robot equipped with skis demonstrating alpine skiing. We use the “do the shake” policy to control the robot’s pitch and roll while skiing. (Winnipeg Free Press [16])

5 Conclusions and Future Work

This research has shown that two well-known solutions to the inverted pendulum problem – PID control and fuzzy logic – are both well-suited to the bongo board. Furthermore we have shown that the introduction of a rhythmic oscillation to the bongo board system, while not detrimental, has little benefit to the stability of the bongo board.

This research has numerous possible applications to humanoid robotics. Active balancing on unstable terrain will be an essential skill for humanoid robots to be useful in arbitrary environments. Examples of such environments include loose rubble, which may suddenly slip or give-way underfoot; ice or wet linoleum, which offers minimal traction; and deep carpet or foam, which compresses underfoot and provides uneven support.

Iverach-Brereton et al. demonstrated a simple shuffling gait for ice skating [14, 15], but could not sustain a glide phase due in part to the difficulty in balancing on a single skate blade. The use a PID or fuzzy logic controller to control the robot’s lateral balance may allow the robot to balance for longer periods on a single skate, allowing for a more sustained glide phase.

The bongo board is fundamentally, like balancing on a skate blade, is a largely two-dimensional problem; the skate blade, like the bongo board, provides adequate support for the robot to remain stable along the front-back axis. Balancing along the left-right axis only requires control over movement in the frontal plane. The wobble board – an apparatus consisting of a circular deck and a free-rolling, spherical fulcrum below it – conversely requires control over translation and rotation in the frontal, sagittal, and transversal planes due to the spherical motion allowed by the fulcrum. Implementing a solution for the wobble board remains part of our ongoing research.

We have recently begun research into alpine skiing using a humanoid robot, shown in Fig. 6. Balancing on skis while going downhill requires control over rotation and translation in the frontal and sagittal planes, but does not require control over rotation in the transversal plane; the length of the skis prevents the robot from twisting in an uncontrolled fashion. To ensure that the robot’s skis remain in contact with the hill regardless of inclination while simultaneously keeping the robot’s torso vertical we implemented a controller using the “do the shake” policy to control the robot’s motions in the frontal and sagittal planes. A video demonstrating this automatic correction for slope can be seen here: https://youtu.be/XU17sbItYxI.

Our work on alpine skiing demonstrates that the bongo board solutions presented here are applicable to more practical problems of balancing on varied terrain, as well as balancing in higher-dimensional problems than the more traditional bongo board.