1 Introduction

Symbolic Trajectory Evaluation (STE) is a model checking technique that grew out of multi-valued logic simulation on the one hand, and symbolic simulation on the other hand [2]. Among various formal verification techniques in use today, STE comes closest to functional simulation and is among the most successful formal verifiation techniques used in the industry. In STE, specifications take the form of symbolic trajectory formulas that mix Boolean expressions and the temporal next-time operator. The Boolean expressions provide a convenient means of describing different operating conditions in a circuit in a compact form. By allowing only the most elementary of temporal operators, the class of properties that can be expressed is fairly restricted as compared to other temporal logics (see [4] for a nice survey). Nonetheless, experience has shown that many important aspects of synchronous digital systems at various levels of abstraction can be captured using this restricted logic. For example, it is quite adequate for expressing many of the subtleties of system operation, including clocking schemas, pipelining control, as well as complex data computations [7, 8, 12].

In return for the restricted expressiveness of STE specifications, the STE model checking algorithm provides siginificant computational efficiency. As a result, STE can be applied to much larger designs than any other model checking technique. For example, STE is routinely used in the industry today to carry out complete formal input-output verification of designs with several hundred thousand latches [7, 8]. Unfortunately, this still falls short of providing an automated technique for formally verifying modern system-on-chip designs, and there is clearly a need to scale up the capacity of STE even further.

The first approach that was pursued in this direction was structural decomposition. In this approach, the user must break down a verification task into smaller sub-tasks, each involving a distinct STE run. After this, a deductive system can be used to reason about the collections of STE runs and verify that they together imply the desired property of the overall design [6]. In theory, structural decomposition allows verification of arbitrarily complex designs. However, in practice, the difficulty and tedium of breaking down a property into small enough sub-properties that can be verified with an STE engine limits the usefulness of this approach significantly. In addition, managing the structural decomposition in the face of rapidly changing RTL limits the applicability of structural decomposition even further.

A different approach to increase the scale of designs that can be verified is to use aggressive abstraction beyond what is provided automatically by current STE implementations. If we ensure that our abstract model satisfies the requirements of the general theory of STE, then a property that is verified on the abstract model holds on the original model as well. Although the general theory of STE allows a very general circuit model [11], all STE implementations so far have used a three-valued circuit model. Thus, every bit-level signal is allowed to have one of three values: 0, 1 or X, where X represents “either 0 or 1”. This limits the amount of abstraction that can be achieved. The main contribution of this paper is to show how much more abstract lattices can be derived automatically from RTL descriptions, and how the general theory of STE can be instantiated with these lattices to give a practical word-level STE engine that provides significant gains in capacity and efficiency on a set of benchmarks.

Operationally, word-level STE bears similarities with word-level bounded model checking (BMC). However, there are important differences, the most significant one being the use of X-based abstractions on slices of words, called atoms, in word-level STE. This allows a wide range of abstraction possibilities, including a combination of user-specified and automatic abstractions – often a necessity for complex verification tasks. Our preliminary experimental results indicate that by carefully using X-based abstractions in word-level STE, it is indeed possible to strike a good balance between accuracy (cautious propagation of X) and performance (liberal propagation of X).

The remainder of the paper is organized as follows. We discuss how words in an RTL design can be split into atoms in Sect. 2. Atoms form the basis of abstracting groups of bits. In Sect. 3, we elaborate on the lattice of values that this abstraction generates, and Sect. 4 presents a new way of encoding values of atoms in this lattice. We also discuss how to symbolically simulate RTL operators and compute least upper bounds using this encoding. Section 5 presents an instantiation of the general theory of STE using the above lattice, and discusses an implementation. Experimental results on a set of RTL benchmarks are presented in Sect. 6, and we conclude in Sect. 7.

2 Atomizing Words

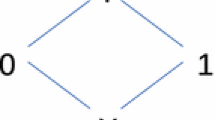
In bit-level STE [2, 12], every variable is allowed to take values from \(\{0, 1, X\}\), where X denotes “either 0 or 1”. The ordering of information in the values 0, 1 and X is shown in the lattice in Fig. 1, where a value lower in the order has “less information” than one higher up in the order. The element \(\top \) is added to complete the lattice, and represents an unachievable over-constrained value. Tools that implement bit-level STE usually use dual-rail encoding to reason about ternary values of variables. In dual-rail encoding, every bit-level variable v is encoded using two binary variables \(v_0\) and \(v_1\). Intuitively, \(v_i\) indicates whether v can take the value i, for i in \(\{0, 1\}\). Thus, 0, 1 and X are encoded by the valuations (0, 1), (1, 0) and (1, 1), respectively, of \((v_0, v_1)\). By convention, \((v_0, v_1) = (0, 0)\) denotes \(\top \). An undesired consequence of dual-rail encoding is the doubling of binary variables in the encoded system. This can pose serious scalability issues when verifying designs with wide datapaths, large memories, etc. Attempts to scale STE to large designs must therefore raise the level of abstraction beyond that of individual bits.

Fig. 1.
figure 1

Ternary lattice

Full size image

In principle, one could go to the other extreme, and run STE at the level of words as defined in the RTL design. This requires defining a lattice of values of words, and instantiating the general theory of STE [11] with this lattice. The difficulty with this approach lies in implementing it in practice. The lattice of values of an m-bit word, where each bit in the word can take values in \(\{0, 1, X\}\), is of size at least \(3^m\). Symbolically representing values from such a large lattice and reasoning about them is likely to incur overheads similar to that incurred in bit-level STE. Therefore, STE at the level of words (as defined in the RTL design) does not appear to be a practical proposition for scaling.

The idea of splitting words into sub-words for the purpose of simplifying analysis is not new (see e.g. [5]). An aggressive approach to splitting (an extreme example being bit-blasting) can lead to proliferation of narrow sub-words, making our technique vulnerable to the same scalability problems that arise with dual-rail encoding. Therefore, we adopt a more controlled approach to splitting. Specifically, we wish to split words in such a way that we can speak of an entire sub-word having the value X without having to worry about which individual bits in the sub-word have the value X. Towards this end, we partition every word in an RTL design into sub-words, which we henceforth call atoms, such that every RTL statement that reads or updates a word either does so for all bits in an atom, or for no bit in an atom. In other words, no RTL statement (except the few discussed at the end of this section) reads or updates an atom partially.

The above discussion leads to a fairly straightforward algorithm for identifying atoms in an RTL design. We refer the reader to the full version of the paper [3] for details of our atomization technique, and illustrate it on a simple example below. Figure 2(a) shows a System-Verilog code fragment, and Fig. 2(b) shows an atomization of words, where the solid vertical bars represent the boundaries of atoms. Note that every System-Verilog statement in Fig. 2(a) either reads or writes all bits in an atom, or no bit in an atom. Since we wish to reason at the granularity of atoms, we must interpret word-level reads and writes in terms of the corresponding atom-level reads and writes. This can be done either by modifying the RTL, or by taking appropriate care when symbolically simulating the RTL. For simplicity of presentation, we show in Fig. 2(c) how the code fragment in Fig. 2(b) would appear if we were to use only the atoms identified in Fig. 2(b). Note that no statement in the modified RTL updates or reads a slice of an atom. However, a statement may be required to read a slice of the result obtained by applying an RTL operator to atoms (see, for example, Fig. 2(c) where we read a slice of the result obtained by adding concatenated atoms). In our implementation, we do not modify the RTL. Instead, we symbolically simulate the original RTL, but generate the expressions for various atoms that would result from simulating the modified RTL.

Fig. 2.
figure 2

Illustrating atomization

Full size image

Once the boundaries of all atoms are determined, we choose to disregard values of atoms in which some bits are set to X, and the others are set to 0 or 1. This choice is justified since all bits in an atom are read or written together. Thus, either all bits in an atom are considered to have values in \(\{0, 1\}\), or all of them are considered to have the value X. This implies that values of an m-bit atom can be encoded using \(m+1\) bits, instead of using 2m bits as in dual-rail encoding. Specifically, we can associate an additional “invalid” bit with every m-bit atom. Whenever the “invalid” bit is set, all bits in the atom are assumed to have the value X. Otherwise, all bits are assumed to have values in \(\{0, 1\}\). We show later in Sects. 4.1 and 4.2 how the value and invalid bit of an atom can be recursively computed from the values and invalid bits of the atoms on which it depends.

Memories and arrays in an RTL design are usually indexed by variables instead of by constants. This makes it difficult to atomize memories and arrays statically, and we do not atomize them. Similarly, if a design has a logical shift operation, where the shift length is specified by a variable, it is difficult to statically identify subwords that are not split by the shift operation. We ignore all such RTL operations during atomizaion, and instead use extensional arrays [13] to model and reason about them. Section 4.2 briefly discusses the modeling of memory/array reads and writes in this manner. A more detailed description is available in the full version of the paper [3].

3 Lattice of Atom Values

Recall that the primary motivation for atomizing words is to identify the right granularity at which an entire sub-word (atom) can be assigned the value X without worrying about which bits in the sub-word have the value X. Therefore, an m-bit atom a takes values from the set \(\{\overbrace{0\cdots 00}^\text {m bits}, \;\ldots \; \overbrace{1\cdots 11}^\text {m bits}, \mathbf {X}\}\), where \(\mathbf {X}\) is a single abstract value that denotes an assignment of X to at least one bit of a. Note the conspicuous absence of values like \(0X1\cdots 0\) in the above set. Figure 3(a) shows the lattice of values for a 3-bit atom, ordered by information content. The \(\top \) element is added to complete the lattice, and represents an unachievable over-constrained value. Figure 3(b) shows the lattice of values of the same atom if we allow each bit to take values in \(\{0, 1, X\}\). Clearly, the lattice in Fig. 3(a) is shallower and sparser than that in Fig. 3(b).

Fig. 3.
figure 3

Atom-level and bit-level lattices

Full size image

Consider an m-bit word w that has been partitioned into non-overlapping atoms of widths \(m_1, \ldots m_r\), where \(\sum _{j=1}^r m_j = m\). The lattice of values of w is given by the product of r lattices, each corresponding to the values of an atom of w. For convenience of representation, we simplify the product lattice by collapsing all values that have at least one atom set to \(\top \) (and therefore represent unachievable over-constrained values), to a single \(\top \) element. It can be verified that the height of the product lattice (after the above simplification) is given by \(r+1\), the total number of elements in it is given by \(\prod _{j=1}^r \big (2^{m_j} + 1\big ) + 1\) and the number of elements at level i from the bottom is given by \(\left( {\begin{array}{c}m\\ i\end{array}}\right) \prod _{j=1}^i 2^{m_j}\), where \(0 < i \le r\). It is not hard to see from these expressions that atomization using few wide atoms (i.e., small values of r and large values of \(m_j\)) gives shallow and sparse lattices compared to atomization using many narrow atoms (i.e., large values of r and small values of \(m_j\)). The special case of a bit-blasted lattice (see Fig. 3(b)) is obtained when \(r = m\) and \(m_j = 1\) for every \(j \in \{1, \ldots r\}\).

Using a sparse lattice is advantageous in symbolic reasoning since we need to encode a small set of values. Using a shallow lattice helps in converging fast when computing least upper bounds – an operation that is crucially needed when performing symbolic trajectory evaluation. However, making the lattice of values sparse and shallow comes at the cost of losing precision of reasoning. By atomizing words based on their actual usage in an RTL design, and by abstracting values of atoms wherein some bits are set to X and the others are set to 0 or 1, we strike a balance between depth and density of the lattice of values on one hand, and precision of reasoning on the other.

4 Symbolic Simulation with Invalid-Bit Encoding

As mentioned earlier, an m-bit atom can be encoded with \(m+1\) bits by associating an “invalid bit” with the atom. For notational convenience, we use \({\mathsf {val}}(a)\) to denote the value of the m bits constituting atom a, and \({\mathsf {inv}}(a)\) to denote the value of its invalid bit. Thus, an m-bit atom a is encoded as a pair \(({\mathsf {val}}(a), {\mathsf {inv}}(a))\), where \({\mathsf {val}}(a)\) is a bit-vector of width m, and \({\mathsf {inv}}(a)\) is of \(\mathsf {Boolean}\) type. Given \(({\mathsf {val}}(a), {\mathsf {inv}}(a))\), the value of a is given by \({\mathsf {ite}}({\mathsf {inv}}(a), \mathbf {X}, {\mathsf {val}}(a))\), where “\({\mathsf {ite}}\)” denotes the usual “if-then-else” operator. For clarity of exposition, we call this encoding “invalid-bit encoding”. Note that invalid-bit encoding differs from dual-rail encoding even when \(m=1\). Specifically, if a 1-bit atom a has the value X, we can use either \((0, \mathsf {true})\) or \((1, \mathsf {true})\) for \(({\mathsf {val}}(a), {\mathsf {inv}}(a))\) in invalid-bit encoding. In contrast, there is a single value, namely \((a_0, a_1) = (1,1)\), that encodes the value X of a in dual-rail encoding. We will see in Sect. 4.2 how this degree of freedom in invalid-bit encoding of X can be exploited to simplify the symbolic simulation of word-level operations on invalid-bit-encoded operands, and also to simplify the computation of least upper bounds.

Symbolic simulation is a key component of symbolic trajectory evaluation. In order to symbolically simulate an RTL design in which every atom is invalid-bit encoded, we must first determine the semantics of word-level RTL operators with respect to invalid-bit encoding. Towards this end, we describe below a generic technique for computing the value component of the invalid-bit encoding of the result of applying a word-level RTL operator. Subsequently, we discuss how the invalid-bit component of the encoding is computed.

4.1 Symbolically Simulating Values

Let \({\mathsf {op}}\) be a word-level RTL operator of arity k, and let res be the result of applying \({\mathsf {op}}\) on \(v_1, v_2, \ldots v_k\), i.e., \(res = {\mathsf {op}}(v_1, v_2, \ldots v_k)\). For each i in \(\{1, \ldots k\}\), suppose the bit-width of operand \(v_i\) is \(m_i\), and suppose the bit-width of res is \(m_{res}\). We assume that each operand is invalid-bit encoded, and we are interested in computing the invalid-bit encoding of a specified slice of the result, say res[q : p], where \(0 \le p \le q \le m_{res} - 1\). Let \(\langle {\mathsf {op}} \rangle : \{0, 1\}^{m_1} \times \cdots \times \{0, 1\}^{m_k} \rightarrow \{0, 1\}^{m_{res}}\) denote the RTL semantics of \({\mathsf {op}}\). For example, if \({\mathsf {op}}\) denotes 32-bit unsigned addition, then \(\langle {\mathsf {op}} \rangle \) is the function that takes two 32-bit operands and returns their 32-bit unsigned sum. The following lemma states that \({\mathsf {val}}(res[q:p])\) can be computed if we know \(\langle {\mathsf {op}} \rangle \) and \({\mathsf {val}}(v_i)\), for every \(i \in \{1, \ldots k\}\). Significantly, we do not need \({\mathsf {inv}}(v_i)\) for any \(i \in \{1, \ldots k\}\) to compute \({\mathsf {val}}(res[q:p])\).

Lemma 1

Let \(v = \big (\langle {\mathsf {op}} \rangle ({\mathsf {val}}(v_1), {\mathsf {val}}(v_2), \ldots {\mathsf {val}}(v_k))\big )[q:p]\). Then \({\mathsf {val}}(res[q:p])\) is given by v, where \(res = {\mathsf {op}}(v_1, v_2, \ldots v_k)\).

The proof of Lemma 1, given in [3], exploits the observation that if \({\mathsf {inv}}(res[q:p])\) is \(\mathsf {true}\), then the value of \({\mathsf {val}}(res[q:p])\) does not matter. Lemma 1 tells us that when computing \({\mathsf {val}}(res[q:p])\), we can effectively assume that invalid-bit encoding is not used. This simplifies symbolic simulation with invalid-bit encoding significantly. Note that this simplification would not have been possible had we not had the freedom to ignore \({\mathsf {val}}(res[q:p])\) when \({\mathsf {inv}}(res[q:p])\) is \(\mathsf {true}\).

4.2 Symbolically Simulating Invalid Bits

We now turn to computing \({\mathsf {inv}}(res[q:p])\). Unfortunately, computing \({\mathsf {inv}}(res[q:p])\) precisely is difficult and involves operator-specific functions that are often complicated. We therefore choose to approximate \({\mathsf {inv}}(res[q:p])\) in a sound manner with functions that are relatively easy to compute. Specifically, we allow \({\mathsf {inv}}(res[q:p])\) to evaluate to \(\mathsf {true}\) (denoting \(res[q:p] = \mathbf {X}\)) even in cases where a careful calculation would have shown that \({\mathsf {op}}(v_1, v_2, \ldots v_k)\) is not \(\mathbf {X}\). However, we never set \({\mathsf {inv}}(res[q:p])\) to \(\mathsf {false}\) if any bit in res[q : p] can take the value X in a bit-blasted evaluation of res. Striking a fine balance between the precision and computational efficiency of the sound approximations is key to building a practically useful symbolic simulator using invalid-bit encoding. Our experience indicates that simple and sound approximations of \({\mathsf {inv}}(res[q:p])\) can often be carefully chosen to serve our purpose. While we have derived templates for approximating \({\mathsf {inv}}(res[q:p])\) for res obtained by applying all word-level RTL operators that appear in our benchmarks, we cannot present all of them in detail here due to space constraints. We present below a discussion of how \({\mathsf {inv}}(res[q:p])\) is approximated for a subset of important RTL operators. Importantly, we use a recursive formulation for computing \({\mathsf {inv}}(res[q:p])\). This allows us to recursively compute invalid bits of atoms obtained by applying complex sequences of word-level operations to a base set of atoms.

Word-Level Addition: Let \(+_m\) denote an m-bit addition operator. Thus, if a and b are m-bit operands, \(a +_mb\) generates an m-bit sum and a 1-bit carry. Let the carry generated after adding the least significant r bits of the operands be denoted \(carry_r\). We discuss below how to compute sound approximations of \({\mathsf {inv}}(sum[q:p])\) and \({\mathsf {inv}}(carry_r)\), where \(0 \le p \le q \le m-1\) and \(1 \le r \le m\).

It is easy to see that the value of sum[q : p] is completely determined by a[q : p], b[q : p] and \(carry_p\). Therefore, we can approximate \({\mathsf {inv}}(sum[q:p])\) as follows: \({\mathsf {inv}}(sum[q:p])\! = \! {\mathsf {inv}}(a[q:p]) \vee {\mathsf {inv}}(b[q:p]) \vee {\mathsf {inv}}(carry_p)\).

To see why the above approximation is sound, note that if all of \({\mathsf {inv}}(a[q:p])\), \({\mathsf {inv}}(b[q:p])\) and \({\mathsf {inv}}(carry_p)\) are \(\mathsf {false}\), then a[q : p], b[q : p] and \(carry_p\) must have non-\(\mathbf {X}\) values. Hence, there is no uncertainty in the value of sum[q : p] and \({\mathsf {inv}}(sum[q:p]) = \mathsf {false}\). On the other hand, if any of \({\mathsf {inv}}(a[q:p]\), \({\mathsf {inv}}(b[q:p])\) or \({\mathsf {inv}}(carry_p)\) is \(\mathsf {true}\), there is uncertainty in the value of sum[q : p].

The computation of \({\mathsf {inv}}(carry_p)\) (or \({\mathsf {inv}}(carry_r)\)) is interesting, and deserves special attention. We identify three cases below, and argue that \({\mathsf {inv}}(carry_p)\) is \(\mathsf {false}\) in each of these cases. In the following, \(\mathbf {0}\) denotes the p-bit constant \(00\cdots 0\).

  1. 1.

    If \(\big ({\mathsf {inv}}(a[p-1:0]) \vee {\mathsf {inv}}(b[p-1:0])\big ) = \mathsf {false}\), then both \({\mathsf {inv}}(a[p-1:0])\) and \({\mathsf {inv}}(b[p-1:0])\) must be \(\mathsf {false}\). Therefore, there is no uncertainty in the values of either \(a[p-1:0]\) or \(b[p-1:0]\), and \({\mathsf {inv}}(carry_p) = \mathsf {false}\).

  2. 2.

    If \(\big (\lnot {\mathsf {inv}}(a[p-1:0]) \wedge ({\mathsf {val}}(a[p-1:0]) = \mathbf {0})\big )=\mathsf {true}\), then the least significant p bits of \({\mathsf {val}}(a)\) are all 0. Regardless of \({\mathsf {val}}(b)\), it is easy to see that in this case, \({\mathsf {val}}(carry_p) = 0\) and \({\mathsf {inv}}(carry_p) = \mathsf {false}\).

  3. 3.

    This is the symmetric counterpart of the case above, i.e., \(\big (\lnot {\mathsf {inv}}(b[p-1:0]) \wedge ({\mathsf {val}}(b[p-1:0]) = \mathbf {0})\big )=\mathsf {true}\).

We now approximate \({\mathsf {inv}}(carry_p)\) by combining the conditions corresponding to the three cases above. In other words,

Word-Level Division: Let \(\div _m\) denote an m-bit division operator. This is among the most complicated word-level RTL operators for which we have derived an approximation of the invalid bit. If a and b are m-bit operands, \(a \div _m b\) generates an m-bit quotient, say quot, and an m-bit remainder, say rem. We wish to compute \({\mathsf {inv}}(quot[q:p])\) and \({\mathsf {inv}}(rem[q:p])\), where \(0 \le p \le q \le m-1\). We assume that if \({\mathsf {inv}}(b)\) is \(\mathsf {false}\), then \({\mathsf {val}} \ne 0\); the case of \(a \div _m b\) with \(({\mathsf {val}}(b), {\mathsf {inv}}(b)) = (0, \mathsf {false})\) leads to a “divide-by-zero” exception, and is assumed to be handled separately.

The following expressions give sound approximations for \({\mathsf {inv}}(quot[q:p])\) and \({\mathsf {inv}}(rem[q:p])\). In these expressions, we assume that i is a non-negative integer such that \(2^i \le {\mathsf {val}}(b) < 2^{i+1}\). We defer the argument for soundness of these approximations to the full version of the paper [3], for lack of space.

$$\begin{aligned} {\mathsf {inv}}(quot[q:p])= & {} {\mathsf {ite}}({\mathsf {inv}}(b), \,temp_1, \, temp_2), \text { where } \\ temp_1= & {} {\mathsf {inv}}(a) \,\vee \, ({\mathsf {val}}(a[m-1:p]) \ne \mathbf {0}) \text { and }\\ temp_2= & {} {\mathsf {ite}}({\mathsf {val}}(b) = 2^i, \,temp_3, \,(i < p) \,\vee \, {\mathsf {inv}}(a[m-1:p])), \text { where } \\ temp_3= & {} (p+i \le m-1) \,\wedge \, {\mathsf {inv}}(a[\min (q+i,m-1):p+i])) \\ {\mathsf {inv}}(rem[q:p])\!= & {} \!{\mathsf {inv}}(b) \,\vee \, {\mathsf {ite}}({\mathsf {val}}(b) = 2^i, (i > p) \wedge {\mathsf {inv}}(a[\min (q, i-1):p]), i \ge p) \end{aligned}$$

Note that the constraint \(2^i \le {\mathsf {val}}(b) < 2^{i+1}\) in the above formulation refers to a fresh variable i that does not appear in the RTL. We will see later in Sect. 5 that a word-level STE problem is solved by generating a set of word-level constraints, every satisfying assignment of which gives a counter-example to the verification problem. We add constraints like \(2^i \le {\mathsf {val}}(b) < 2^{i+1}\) in the above formulation, to the set of word-level constraints generated for an STE problem. This ensures that every assignment of i in a counterexample satisfies the required constraints on i.

If-then-else: Consider a conditional assignment statement “if (BoolExpr) then x = Exp1; else x = Exp2;”. Symbolically simulating this statement gives \(x = {\mathsf {ite}}(\mathsf {BoolExpr}, \mathsf {Exp1}, \mathsf {Exp2})\). The following gives a sound approximation of \({\mathsf {inv}}(x[q:p])\); the proof of soundness is given in the full version of the paper [3].

$$\begin{aligned} {\mathsf {inv}}(x[q:p])= & {} {\mathsf {ite}}({\mathsf {inv}}(\mathsf {BoolExpr}), \, temp_1, \, temp_2), \text { where } \\ temp_1= & {} {\mathsf {inv}}(\mathsf {Exp1}[q:p])\,\vee \,{\mathsf {inv}}(\mathsf {Exp2}[q:p])\,\vee \, ({\mathsf {val}}(\mathsf {Exp1}[q:p]) \ne {\mathsf {val}}(\mathsf {Exp2}[q:p])) \\ temp_2= & {} {\mathsf {ite}}({\mathsf {val}}(\mathsf {BoolExpr}), \,{\mathsf {inv}}(\mathsf {Exp1}[q:p]), {\mathsf {inv}}(\mathsf {Exp2}[q:p])) \end{aligned}$$

Bit-Wise Logical Operations: Let \(\lnot _m\) and \(\wedge _m\) denote bit-wise negation and conjunction operators respectively, for m-bit words. If a, b, c and d are m-bit words such that \(c = \lnot _m a\) and \(d = a \wedge _m b\), it is easy to see that the following give sound approximations of \({\mathsf {inv}}(c)\) and \({\mathsf {inv}}(d)\).

$$\begin{aligned} {\mathsf {inv}}(c[q:p])= & {} {\mathsf {inv}}(a[q:p]) \\ {\mathsf {inv}}(d[q:p])= & {} \big ({\mathsf {inv}}(a[q:p]) \vee {\mathsf {inv}}(b[q:p])\big ) \,\wedge \big ({\mathsf {inv}}(a[q:p]) \vee ({\mathsf {val}}(a[q:p]) \ne \mathbf {0})\big )\,\wedge \,\\&\big ({\mathsf {inv}}(b[q:p]) \vee ({\mathsf {val}}(b[q:p]) \ne \mathbf {0})\big ) \end{aligned}$$

The invalid bits of other bit-wise logical operators (like disjunction, xor, nor, nand, etc.) can be obtained by first expressing them in terms of \(\lnot _m\) and \(\wedge _m\) and then using the above approximations.

Memory/Array Reads and Updates: Let \(\mathsf {A}\) be a 1-dimensional array, \(\mathsf {i}\) be an index expression, and \(\mathsf {x}\) be a variable and \(\mathsf {Exp}\) be an expression of the base type of A. For notational convenience, we will use \(\mathsf {A}\) to refer to both the array, and the (array-typed) expression for the value of the array. On symbolically simulating the RTL statement “x = A[i];”, we update the value of \(\mathsf {x}\) to \({\mathsf {read}}(\mathsf {A}, \mathsf {i})\), where the \({\mathsf {read}}\) operator is as in the extensional theory of arrays (see [13] for details). Similarly, on symbolically simulating the RTL statement “A[i] = Exp”, we update the value of array \(\mathsf {A}\) to \({\mathsf {update}}(\mathsf {A}_{\text {orig}}, \mathsf {i}, \mathsf {Exp})\), where \(\mathsf {A}_{\text {orig}}\) is the (array-typed) expression for \(\mathsf {A}\) prior to simulating the statement, and the \({\mathsf {update}}\) operator is as in the extensional theory of arrays.

Since the expression for a variable or array obtained by symbolic simulation may now have \({\mathsf {read}}\) and/or \({\mathsf {update}}\) operators, we must find ways to compute sound approximations of the invalid bit for expressions of the form \({\mathsf {read}}(\mathsf {A}, \mathsf {i})[q:p]\). Note that since \(\mathsf {A}\) is an array, the symbolic expression for \(\mathsf {A}\) is either (i) \(\mathsf {A}_{\text {init}}\), i.e. the initial value of \(\mathsf {A}\) at the start of symbolic simulation, or (ii) \({\mathsf {update}}(\mathsf {A}', \mathsf {i}', \mathsf {Exp}')\) for some expressions \(\mathsf {A}'\), \(\mathsf {i}'\) and \(\mathsf {Exp}'\), where \(\mathsf {A}'\) has the same array-type as \(\mathsf {A}\), \(\mathsf {i}'\) has an index type, and \(\mathsf {Exp}'\) has the base type of \(\mathsf {A}\). For simplicity of exposition, we assume that all arrays are either completely initialized or completely uninitialized at the start of symbolic simulation. The invalid bit of \({\mathsf {read}}(\mathsf {A}, \mathsf {i})[q:p]\) in case (i) is then easily seen to be \({\mathsf {true}}\) if \(\mathsf {A}_{\text {init}}\) denotes an uninitialized array, and \({\mathsf {false}}\) otherwise. In case (ii), let v denote \({\mathsf {read}}(\mathsf {A}, \mathsf {i})\). The invalid bit of v[q : p] can then be approximated as:

$$\begin{aligned} {\mathsf {inv}}(v[q:p])= & {} {\mathsf {inv}}(\mathsf {i}) \vee {\mathsf {inv}}(\mathsf {i}')\vee {\mathsf {ite}}\left( {\mathsf {val}}(\mathsf {i}) = {\mathsf {val}}(\mathsf {i}'), {\mathsf {inv}}(\mathsf {Exp}'[q:p]), temp\right) , \text { where} \\ temp= & {} {\mathsf {inv}}({\mathsf {read}}(\mathsf {A}', \mathsf {i})[q:p]). \end{aligned}$$

We defer the argument for soundness of the above approximation to the full version of the paper [3].

4.3 Computing Least Upper Bounds

Let \(a = ({\mathsf {val}}(a), {\mathsf {inv}}(a))\) and \(b = ({\mathsf {val}}(b), {\mathsf {inv}}(b))\) be invalid-bit encoded elements in the lattice of values for an m-bit atom. We define \(c = lub(a, b)\) as follows.

  1. (a)

    If \((\lnot {\mathsf {inv}}(a) \wedge \lnot {\mathsf {inv}}(b) \wedge ({\mathsf {val}}(a) \ne {\mathsf {val}}(b))\), then \(c = \top \).

  2. (b)

    Otherwise, \({\mathsf {inv}}(c) = {\mathsf {inv}}(a) \wedge {\mathsf {inv}}(b)\) and \({\mathsf {val}}(c) = {\mathsf {ite}}({\mathsf {inv}}(a), \,{\mathsf {val}}(b), \,{\mathsf {val}}(a))\) (or equivalently \({\mathsf {val}}(c) = {\mathsf {ite}}({\mathsf {inv}}(b), \,{\mathsf {val}}(a), \,{\mathsf {val}}(b))\)).

Note the freedom in defining \({\mathsf {val}}(c)\) in case (b) above. This freedom comes from the observation that if \({\mathsf {inv}}(c) = \mathsf {true}\), the value of \({\mathsf {val}}(c)\) is irrelevant. Furthermore, if the condition in case (a) is not satisfied and if both \({\mathsf {inv}}(a)\) and \({\mathsf {inv}}(b)\) are \(\mathsf {false}\), then \({\mathsf {val}}(a) = {\mathsf {val}}(b)\). This allows us to simplify the expression for \({\mathsf {val}}(c)\) on-the-fly by replacing it with \({\mathsf {val}}(b)\), if needed.

5 Word-Level STE

In this section, we briefly review the general theory of STE [11] instantiated to the lattice of values of atoms. An RTL design C consists of inputs, outputs and internal words. We treat bit-level signals as 1-bit words, and uniformly talk of words. Every input, output and internal word is assumed to be atomized as described in Sect. 2. Every atom of bit-width m takes values from the set \(\{\mathbf {0} \ldots \mathbf {2^m-1}, \mathbf {X}\}\), where constant bit-vectors have been represented by their integer values. The values themselves are ordered in a lattice as discussed in Sect. 3. Let \(\le _m\) denote the ordering relation and \(\sqcup _m\) denote the lub operator in the lattice of values for an m-bit atom. The lattice of values for a word is the product of lattices corresponding to every atom in the word. Let \(\mathcal {{A}}\) denote the collection of all atoms in the design, and let \(\mathcal {{D}}\) denote the collection of values of all atoms in \(\mathcal {{A}}\). A state of the design is a mapping \(s: \mathcal {{A}} \rightarrow \mathcal {{D}} \cup {\top }\) such that if \(a \in \mathcal {{A}}\) is an m-bit atom, then s(a) is a value in the set \(\{\mathbf {0}, \ldots \mathbf {2^m-1}, \mathbf {X}, \top \}\). Let \(\mathcal {{S}}\) denote the set of all states of the design, and let \((\mathcal {{S}}, \sqsubseteq , \sqcup )\) be a lattice that is isomorphic to the product of lattices corresponding to the atoms in \(\mathcal {{A}}\).

Given a design C, let \({\mathsf {Tr}}_C: \mathcal {{S}} \rightarrow \mathcal {{S}}\) define the transition function of C. Thus, given a state s of C at time t, the next state of the design at time \(t+1\) is given by \({\mathsf {Tr}}_C(s)\). To model the behavior of a design over time, we define a sequence of states as a mapping \(\sigma : \mathbb {N} \rightarrow \mathcal {{S}}\), where \(\mathbb {N}\) denotes the set of natural numbers. A trajectory for a design C is a sequence \(\sigma \) such that for all \(t \in \mathbb {N}\), \({\mathsf {Tr}}_C(\sigma (t)) \sqsubseteq \sigma (t+1)\). Given two sequences \(\sigma _1\) and \(\sigma _2\), we abuse notation and say that \(\sigma _1 \sqsubseteq \sigma _2\) iff for every \(t \in \mathbb {N}\), \(\sigma _1(t) \sqsubseteq \sigma _2(t)\).

The general trajectory evaluation logic of Seger and Bryant [11] can be instantiated to words as follows. A trajectory formula is a formula generated by the grammar \(\varphi \) : := \(\mathsf {a}\) is \(\mathsf {val}\) \(\mid \) \(\varphi \) and \(\varphi \) \(\mid \) \(P \rightarrow \varphi \) \(\mid \) \(N \varphi \), where \(\mathsf {a}\) is an atom of C, \(\mathsf {val}\) is a non-X, non-\(\top \) value in the lattice of values for \(\mathsf {a}\), and P is a quantifier-free formula in the theory of bit-vectors. Formulas like P in the grammar above are also called guards in STE parlance.

We use Seger et al’s [2, 12] definitions for the defining sequence of a trajectory formula \(\psi \) given the assignment \(\phi \), denoted \([\psi ]^\phi \), and for the defining trajectory of \(\psi \) with respect to a design C, denoted \([\![\psi ]\!]_C^\phi \). Details of these definitions may be found in the full version of the paper [3]. In symbolic trajectory evaluation, we are given an antecedent \(\mathsf {Ant}\) and a consequent \(\mathsf {Cons}\) in trajectory evaluation logic. We are also given a quantifier-free formula \(\mathsf {Constr}\) in the theory of bit-vectors with free variables that appear in the guards of \(\mathsf {Ant}\) and/or \(\mathsf {Cons}\). We wish to determine if for every assignment \(\phi \) that satisfies \(\mathsf {Constr}\), we have \([\mathsf {Cons}]^\phi \sqsubseteq [\![\mathsf {Ant}]\!]_C^\phi \).

5.1 Implementation

We have developed a tool called \(\mathsf {STEWord}\) that uses symbolic simulation with invalid-bit encoding and SMT solving to perform STE. Each antecedent and consequent tuple has the format (g, a, vexpr, start, end), where g is a guard, a is the name of an atom in the design under verification, vexpr is a symbolic expression over constants and guard variables that specifies the value of a, and start and end denote time points such that \(end \ge start + 1\).

An antecedent tuple \((g, a, vexpr, t_1, t_2)\) specifies that given an assignment \(\phi \) of guard variables, if \(\phi \models g\), then atom a is assigned the value of expression vexpr, evaluated on \(\phi \), for all time points in \(\{t_1, \ldots t_2 - 1\}\). If, however, \(\phi \not \models g\), atom a is assigned the value \(\mathbf {X}\) for all time points in \(\{t_1, \ldots t_2-1\}\). If a is an input atom, the antecedent tuple effectively specifies how it is driven from time \(t_1\) through \(t_2-1\). Using invalid-bit encoding, the above semantics is easily implemented by setting \({\mathsf {inv}}(a)\) to \(\lnot g\) and \({\mathsf {val}}(a)\) to vexpr from time \(t_1\) through \(t_2-1\). If a is an internal atom, the defining trajectory requires us to compute the lub of the value driven by the circuit on a and the value specified by the antecedent for a, at every time point in \(\{t_1, \ldots t_2-1\}\). The value driven by the circuit on a at any time is computed by symbolic simulation using invalid-bit encoding, as explained in Sects. 4.1 and 4.2. The value driven by the antecedent can also be invalid-bit encoded, as described above. Therefore, the lub can be computed as described in Sect. 4.3. If the lub is not \(\top \), \({\mathsf {val}}(a)\) and \({\mathsf {inv}}(a)\) can be set to the value and invalid-bit, respectively, of the lub. In practice, we assume that the lub is not \(\top \) and proceed as above. The conditions under which the lub evaluates to \(\top \) are collected separately, as described below. The values of all internal atoms that are not specified in any antecedent tuple are obtained by symbolically simulating the circuit using invalid-bit encoding.

If the lub computed above evaluates to \(\top \), we must set atom a to an unachievable over-constrained value. This is called antecedent failure in STE parlance. In our implementation, we collect the constraints (formulas representing the condition for case (a) in Sect. 4.3) under which antecedent failure occurs for every antecedent tuple in a set \(\mathsf {AntFail}\). Depending on the mode of verification, we do one of the following:

  • If the disjunction of formulas in \(\mathsf {AntFail}\) is satisfiable, we conclude that there is an assignment of guard variables that leads to an antecedent failure. This can then be viewed as a failed run of verification.

  • We may also wish to check if \([\mathsf {Cons}]^\phi \sqsubseteq [\![\mathsf {Ant}]\!]_C^\phi \) only for assignments \(\phi \) that do not satisfy any formula in \({\mathsf {AntFail}}\). In this case, we conjoin the negation of every formula in \({\mathsf {AntFail}}\) to obtain a formula, say \({\mathsf {NoAntFail}}\), that defines all assignments \(\phi \) of interest.

A consequent tuple \((g, a, vexpr, t_1, t_2)\) specifies that given an assignment \(\phi \) of guard variables, if \(\phi \models g\), then atom a must have its invalid bit set to \({\mathsf {false}}\) and value set to vexpr, (evaluated on \(\phi \)) for all time points in \(\{t_1, \ldots t_2 - 1\}\). If \(\phi \not \models g\), a consequent tuple imposes no requirement on the value of atom a. Suppose that at time t, a consequent tuple specifies a guard g and a value expression vexpr for an atom a. Suppose further that \(({\mathsf {val}}(a), {\mathsf {inv}}(a))\) gives the invalid-bit encoded value of this atom at time t, as obtained from symbolic simulation. Checking whether \([\mathsf {Cons}]^\phi (t)(a) \sqsubseteq [\![\mathsf {Ant}]\!]_C^\phi (t)(a)\) for all assignments \(\phi \) reduces to checking the validity of the formula \(\big (g \rightarrow (\lnot {\mathsf {inv}}(a) \wedge (vexpr = {\mathsf {val}}(a))) \big )\). Let us call this formula \(OK_{a, t}\). Let \(\mathcal {{T}}\) denote the set of all time points specified in all consequent tuples, and let \(\mathcal {{A}}\) denote the set of all atoms of the design. The overall verification goal then reduces to checking the validity of the formula \(OK \,\triangleq \,\bigwedge _{t \in \mathcal {{T}},\;a \in \mathcal {{A}}} OK_{a,t}\). If we wish to focus only on assignments \(\phi \) that do not cause any antecedent failure, our verification goal is modified to check the validity of \({\mathsf {NoAntFail}} \rightarrow OK\). In our implementation, we use \(\mathsf {Boolector}\) [1], a state-of-the-art solver for bit-vectors and the extensional theory of arrays, to check the validity (or satisfiability) of all verification formulas (or their negations) generated by \(\mathsf {STEWord}\).

6 Experiments

We used \(\mathsf {STEWord}\) to verify properties of a set of System-Verilog word-level benchmark designs. Bit-level STE tools are often known to require user-guidance with respect to problem decomposition and variable ordering (for BDD based tools), when verifying properties of designs with moderate to wide datapaths. Similarly, BMC tools need to introduce a fresh variable for each input in each time frame when the value of the input is unspecified. Our benchmarks were intended to stress bit-level STE tools, and included designs with control and datapath logic, where the width of the datapath was parameterized. Our benchmarks were also intended to stress BMC tools by providing relatively long sequences of inputs that could either be X or a specified symbolic value, depending on a symbolic condition. In each case, we verified properties that were satisfied by the system and those that were not. For comparative evaluation, we implemented word-level bounded model checking as an additional feature of \(\mathsf {STEWord}\) itself. Below, we first give a brief description of each design, followed by a discussion of our experiments.

Design 1: Our first design was a three-stage pipelined circuit that reads four pairs of k-bit words in each cycle, computed the absolute difference of each pair, and then added the absolute differences with a current running sum. Alternatively, if a reset signal was asserted, the pipeline stage that stored the sum was reset to the all-zero value, and the addition of absolute differences of pairs of inputs started afresh from the next cycle. In order to reduce the stage delays in the pipeline, the running sum was stored in a redundant format and carry-save-adders were used to perform all additions/subtractions. Only in the final stage was the non-redundant result computed. In addition, the design made extensive use of clock gating to reduce its dynamic power consumption – a characteristic of most modern designs that significantly complicates formal verification. Because of the non-trivial control and clock gating, the STE verification required a simple datapath invariant. Furthermore, in order to reduce the complexity in specifying the correctness, we broke down the overall verification goal into six properties, and verified these properties using multiple datapath widths.

Design 2: Our second design was a pipelined serial multiplier that reads two k-bit inputs serially from a single k-bit input port, multiplied them and made the result available on a 2k-bit wide output port in the cycle after the second input was read. The entire multiplication cycle was then re-started afresh. By asserting and de-asserting special input flags, the control logic allowed the circuit to wait indefinitely between reading its first and second inputs, and also between reading its second input and making the result available. We verified several properties of this circuit, including checking whether the result computed was indeed the product of two values read from the inputs, whether the inputs and results were correctly stored in intermediate pipeline stages for various sequences of asserting and de-asserting of the input flags, etc. In each case, we tried the verification runs using different values of the bit-width k.

Design 3: Our third design was an implementation of the first stage in a typical digital camera pipeline. The design is fed the output of a single CCD/CMOS sensor array whose pixels have different color filters in front of them in a Bayer mosaic pattern [9]. The design takes these values and performs a “de-mosaicing” of the image, which basically uses a fairly sophisticated interpolation technique (including edge detection) to estimate the missing color values. The challenge here was not only verifying the computation, which entailed adding a fairly large number of scaled inputs, but also verifying that the correct pixel values were used. In fact, most non-STE based formal verification engines will encounter difficulty with this design since the final result depends on several hundreds of 8-bit quantities.

Design 4: Our fourth design was a more general version of Design 3, that takes as input a stream of values from a single sensor with a mosaic filter having alternating colors, and produces an interpolated red, green and blue stream as output. Here, we verified 36 different locations on the screen, which translates to 36 different locations in the input stream. Analyzing this example with BMC requires providing new inputs every cycle for over 200 cycles, leading to a blow-up in the number of variables used.

For each benchmark design, we experimented with a bug-free version, and with several buggy versions. For bit-level verification, we used both a BDD-based STE tool [12] and propositional SAT based STE tool [10]; specifically, the tool \(\mathsf {Forte}\) was used for bit-level STE. We also ran word-level BMC to verify the same properties.

In all our benchmarks, we found that \(\mathsf {Forte}\) and \(\mathsf {STEWord}\) successfully verified the properties within a few seconds when the bitwidth was small (8 bits). However, the running time of \(\mathsf {Forte}\) increased significantly with increasing bit-width, and for bit-widths of 16 and above, \(\mathsf {Forte}\) could not verify the properties without serious user intervention. In contrast, \(\mathsf {STEWord}\) required practically the same time to verify properties of circuits with wide datapaths, as was needed to verify properties of the same circuits with narrower datapaths, and required no user intervention. In fact, the word-level SMT constraints generated for a circuit with a narrow datapath were almost identical to those generated for the same circuit with a wider datapath, except for the bit-widths of atoms. This is not surprising, since once atomization is done, symbolic simulation is agnostic to the widths of various atoms. An advanced SMT solver like Boolector is often able to exploit the word-level structure of the final set of constraints and solve it without resorting to bit-blasting.

The BMC experiments involved adding a fresh variable in each time frame when the value of an input was not specified or conditionally specified. This resulted in a significant blow-up in the number of additional variables, especially when we had long sequences of conditionally driven inputs. This in turn adversely affected SMT-solving time, causing BMC to timeout in some cases.

To illustrate how the verification effort with \(\mathsf {STEWord}\) compared with the effort required to verify the same property with a bit-level BDD- or SAT-based STE tool, and with word-level BMC, we present a sampling of our observations in Table 1, where no user intervention was allowed for any tool. Here “-” indicates more than 2 hours of running time, and all times are on an Intel Xeon 3GHz CPU, using a single core. In the column labeled “Benchmark”, Designi-Pj corresponds to verifying property j (from a list of properties) on Design i. The column labeled “Word-level latches (# bits)” gives the number of word-level latches and the total number of bits in those latches for a given benchmark. The column labeled “Cycles of Simulation” gives the total number of time-frames for which STE and BMC was run. The column labeled “Atom Size (largest)” gives the largest size of an atom after our atomization step. Clearly, atomization did not bit-blast all words, allowing us to reason at the granularity of multi-bit atoms in \(\mathsf {STEWord}\).

Table 1. Comparing verification effort (time) with \(\mathsf {STEWord}\), \(\mathsf {Forte}\) and BMC
Full size table

Our experiments indicate that when a property is not satisfied by a circuit, Boolector finds a counterexample quickly due to powerful search heuristics implemented in modern SMT solvers. BDD-based bit-level STE engines are, however, likely to suffer from BDD size explosion in such cases, especially when the bit-widths are large. In cases where there are long sequences of conditionally driven inputs (e.g., design 4) BMC performs worse compared to \(\mathsf {STEWord}\), presumably beacause of the added complexity of solving constraints with significantly larger number of variables. In other cases, the performance of BMC is comparable to that of \(\mathsf {STEWord}\). An important observation is that the abstractions introduced by atomization and by approximations of invalid-bit expressions do not cause \(\mathsf {STEWord}\) to produce conservative results in any of our experiments. Thus, \(\mathsf {STEWord}\) strikes a good balance between accuracy and performance. Another interesting observation is that for correct designs and properties, SMT solvers (all we tried) sometimes fail to verify the correctness (by proving unsatisfiability of a formula). This points to the need for further developments in SMT solving, particularly for proving unsatisfiability of complex formulas. Overall, our experiments, though limited, show that word-level STE can be beneficial compared to both bit-level STE and word-level BMC in real-life verification problems.

We are currently unable to make the binaries or source of \(\mathsf {STEWord}\) publicly available due to a part of the code being proprietary. A web-based interface to \(\mathsf {STEWord}\), along with a usage document and the benchmarks reported in this paper, is available at http://www.cfdvs.iitb.ac.in/WSTE/.

7 Conclusion

Increasing the level of abstraction from bits to words is a promising approach to scaling STE to large designs with wide datapaths. In this paper, we proposed a methodology and presented a tool to achieve this automatically. Our approach lends itself to a counterexample guided abstraction refinement (CEGAR) framework, where refinement corresponds to reducing the conservativeness in invalid-bit expressions, and to splitting existing atoms into finer bit-slices. We intend to build a CEGAR-style word-level STE tool as part of future work.