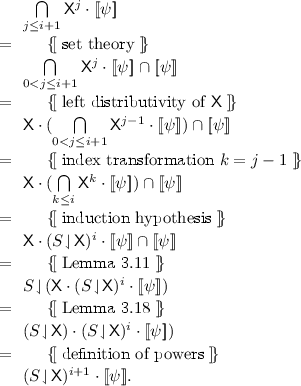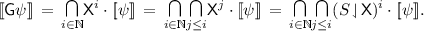Abstract
Concurrent Kleene Algebras (CKAs) serve to describe general concurrent systems in a unified way at an abstract algebraic level. Recently, a graph-based model for CKA has been defined in which the incoming and outgoing edges of a graph define its input/output interface. The present paper provides a simplification and a significant extension of the original model to cover notions of states, predicates and assertions in the vein of algebraic treatments using modal semirings. Moreover, it uses the extension to set up a variant of the temporal logic \(\mathsf {CTL}^*\) for the interface model.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Also called monotone or isotone.
References
Back, R., von Wright, J.: Refinement Calculus - A Systematic Introduction. Graduate Texts in Computer Science. Springer, New York (1998)
de Bakker, J., Meertens, L.: On the completeness of the inductive assertion method. J. Comput. Syst. Sci. 11(3), 323–357 (1975)
Blikle, A.: A comparative review of some program verification methods. In: Gruska, J. (ed.) Mathematical Foundations of Computer Science 1977. LNCS, vol. 53, pp. 17–33. Springer, Heidelberg (1977)
Brink, C., Rewitzky, I.: A Paradigm for Program Semantics: Power Structures and Duality. CSLI Publications, Stanford (2001)
Conway, J.: Regular Algebra and Finite Machines. Chapman and Hall, London (1971)
Dang, H.H., Möller, B.: Concurrency and local reasoning under reverse exchange. Sci. Comput. Prog. 85(Part B), 204–223 (2013)
Dang, H., Glück, R., Möller, B., Roocks, P., Zelend, A.: Exploring modal worlds. J. Log. Algebr. Meth. Program. 83(2), 135–153 (2014)
Desharnais, J., Möller, B., Struth, G.: Modal Kleene algebra and applications - a survey. J. Relational Methods Comput. Sci. 1, 93–131 (2004)
Desharnais, J., Möller, B., Struth, G.: Kleene algebra with domain. ACM Trans. Comput. Log. 7(4), 798–833 (2006)
Desharnais, J., Möller, B.: Characterizing determinacy in Kleene algebras. Inf. Sci. 139(3–4), 253–273 (2001)
Dijkstra, R.M.: Computation calculus bridging a formalization gap. Sci. Comput. Program. 37, 3–36 (2000)
Emerson, E.A.: Temporal and modal logic. In: van Leeuwen, J. (ed.) Handbook of Theoretical Computer Science. Formal Models and Semantics (B), vol. B, pp. 995–1072. Elsevier, Amsterdam (1990)
Frias, M.F., Pombo, C.L.: Interpretability of first-order linear temporal logics in fork algebras. J. Log. Algebr. Program. 66(2), 161–184 (2006)
Gischer, J.L.: The equational theory of pomsets. Theoret. Comput. Sci. 61(2–3), 199–224 (1988)
Hoare, T., Möller, B., Struth, G., Wehrman, I.: Concurrent Kleene algebra and its foundations. J. Log. Algebr. Program. 80(6), 266–296 (2011)
Hoare, T., van Staden, S.: The laws of programming unify process calculi. Sci. Comput. Program. 85, 102–114 (2014)
Hoare, T., van Staden, S., Möller, B., Struth, G., Villard, J., Zhu, H., O’Hearn, P.: Developments in concurrent Kleene algebra. In: Höfner, P., Jipsen, P., Kahl, W., Müller, M.E. (eds.) RAMiCS 2014. LNCS, vol. 8428, pp. 1–18. Springer, Heidelberg (2014)
Hoare, T., van Staden, S., Möller, B., Struth, G., Villard, J., Zhu, H., O’Hearn, P.: Developments in concurrent Kleene algebra. In: Höfner, P., Jipsen, P., Kahl, W., Müller, M.E. (eds.) RAMiCS 2014. LNCS, vol. 8428, pp. 1–18. Springer, Heidelberg (2014)
Jipsen, P.: Concurrent Kleene algebra with tests. In: Höfner, P., Jipsen, P., Kahl, W., Müller, M.E. (eds.) RAMiCS 2014. LNCS, vol. 8428, pp. 37–48. Springer, Heidelberg (2014)
von Karger, B.: Temporal algebra. Math. Struct. Comput. Sci. 8(3), 277–320 (1998)
von Karger, B., Berghammer, R.: A relational model for temporal logic. Logic J. IGPL 6(2), 157–173 (1998)
Main, M.: A powerdomain primer – a tutorial for the Bulletin of the EATCS 33. Technical report, CU-CS-375-87 (1987). Paper 360, University Colorado at Boulder, Department of Computer Science (1987). http://scholar.colorado.edu/csci_techreports/360
Möller, B., Höfner, P., Struth, G.: Quantales and temporal logics. In: Johnson, M., Vene, V. (eds.) AMAST 2006. LNCS, vol. 4019, pp. 263–277. Springer, Heidelberg (2006)
O’Hearn, P.W., Reynolds, J.C., Yang, H.: Separation and information hiding. ACM Trans. Program. Lang. Syst. 31(3), 1–50 (2009)
Rosenthal, K.: Quantales and Their Applications, Pitman Research Notes in Mathematics Series, vol. 234. Longman Scientific and Technical, Harlow (1990)
Schmidt, G.: Programme als partielle Graphen. TU Munich, FB Mathematik. Habilitation Thesis (1977)
Schmidt, G., Ströhlein, T.: Relations and Graphs: Discrete Mathematics for Computer Scientists. Springer, Heidelberg (1993)
Solin, K., von Wright, J.: Enabledness and termination in refinement algebra. Sci. Comput. Program. 74(8), 654–668 (2009)
Tarlecki, A.: A language of specified programs. Sci. Comput. Program. 5(1), 59–81 (1985)
Wehrman, I., Hoare, C.A.R., O’Hearn, P.W.: Graphical models of separation logic. Inf. Process. Lett. 109(17), 1001–1004 (2009)
Winskel, G.: On powerdomains and modality. Theor. Comput. Sci. 36, 127–137 (1985)
Zhou, C., Hoare, C.A.R., Ravn, A.P.: A calculus of durations. Inf. Process. Lett. 40(5), 269–276 (1991)
Acknowledgments
We are grateful to Jules Desharnais, Peter Höfner, Martin E. Müller, Patrick Roocks, Stephan van Staden and the anonymous referees for thorough proofreading and valuable comments.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendix: Deferred Proofs
Appendix: Deferred Proofs
Proof of Lemma 3.5.
We only show Part 1, since Part 2 is analogous. First,

We simplify the first two summands; the other two are analogous. For summand number one we have

For summand number two we have

Altogether, the claim is shown. \(\square \)
Proof of Theorem 3.6.
First we observe that \((\mathsf {G},|)\) is an aggregation algebra in the sense of [15] and \(\mathrm{CS}\) and \(\mathrm{CC}(G,G') {\,=_{ df}\, }\mathsf{TRUE}\) can be viewed as independence relations with \(\mathrm{CS}\subseteq \mathrm{CC}\). With this, the claim follows from Lemmas 3.4 and 3.5 and Proposition 3.6 of [15] if we can show that the restricting predicates \(\mathrm{CS}\) and \(\mathrm{CC}\) are bilinear, i.e., satisfy.
and the analogous property for \(\mathrm{CC}\), and \(\mathrm{CC}\) is symmetric. For \(\mathrm{CC}\) both claims are trivial. To show (11), we exploit that the definition of \(\mathrm{CS}\) is symmetric in both arguments, so that it suffices to consider the first argument.

Proof of Lemma 3.18.
By the definitions of; and  their result, and its interfaces, coincides with that of parallel composition whenever it is defined.
their result, and its interfaces, coincides with that of parallel composition whenever it is defined.
We start by showing the first equation. By the above remark and Lemma 3.5,

For the second summand we calculate

Concerning the first summand we have

Therefore the first summand reduces to \({ in}(G)\), as required.
The equation \({ in}(G) = { in}(G \!\downharpoonright \!{ in}(G'))\) is immediate, since the definition of \(\downharpoonright \) and \({ in}(G') = { out}(G)\) entail \(G \!\downharpoonright \!{ in}(G') = G\).
The equations for \({ out}\) are proved completely symmetrically.
Now we can show associativity of  . Assume graphlets \(G,G,G''\). If any of them is \(\Box \) then the associativity equation is immediate from the definition of
. Assume graphlets \(G,G,G''\). If any of them is \(\Box \) then the associativity equation is immediate from the definition of  . Otherwise we only need to check the case where \({ in}(G') = { out}(G)\) and \({ in}(G'') = { out}(G')\) so that both
. Otherwise we only need to check the case where \({ in}(G') = { out}(G)\) and \({ in}(G'') = { out}(G')\) so that both  and
and  are defined. By the just proved equations for \({ in}\) and \({ out}\) then also
are defined. By the just proved equations for \({ in}\) and \({ out}\) then also  and
and  , so that also
, so that also  and
and  are defined; by definition of
are defined; by definition of  and associativity of ; they coincide.
and associativity of ; they coincide.
Next, by the definition of the restriction operators, \(G \!\downharpoonright \!C\) and \(C \!\downharpoonleft \!G'\) are defined iff \({ out}(G) \subseteq C\) and \({ in}(G') \subseteq C\). In that case \(G \!\downharpoonright \!C = G\) and \(C \!\downharpoonleft \!G' = G'\) and therefore

Finally, the last two claims are immediate from the definition of restriction and the first two claims. \(\square \)
Proof of Lemma 3.24.
We only show the first equation, since the second is analogous. By the definition of \(\mathbin {|||}\) and Lemma 3.5 we have
The first summand reduces to \({ in}(G)\) if we can show \({ in}(G) \subseteq \overline{E'} \mathbin {\!\times \!}E\), equivalently, \({ in}(G) \cap \overline{\overline{E'} \mathbin {\!\times \!}E} = \emptyset \). We calculate,

Symmetrically, the second summand reduces to \({ in}(G')\). \(\square \)
Proof of Theorem 4.6.
-
1.

-
2.
We show by induction on \(i\) that \( \bigcap \limits _{j \le i} \mathsf {X}^j \cdot {[\![\psi ]\!]} = (S \!\downharpoonleft \!\mathsf {X})^i \cdot {[\![\psi ]\!]}\). The base case \(i=0\) is trivial. The induction step proceeds as follows:
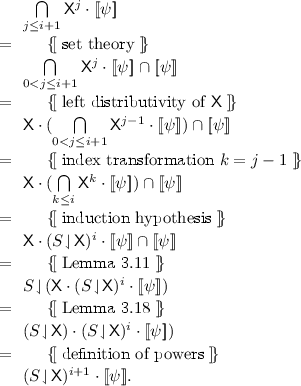
By this,
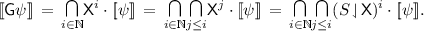
An easy induction shows \((S \!\downharpoonleft \!\mathsf {X})^\omega \subseteq (S \!\downharpoonleft \!\mathsf {X})^i \cdot {[\![\psi ]\!]}\) for all \(i\) and hence \((S \!\downharpoonleft \!\mathsf {X})^\omega \subseteq {[\![\mathsf {G}\psi ]\!]}\). For the reverse inclusion it suffices to show that \({[\![\mathsf {G}\psi ]\!]} \,=\, (S \!\downharpoonleft \!\mathsf {X}) \cdot {[\![\mathsf {G}\psi ]\!]}\). Indeed,

\(\square \)
Rights and permissions
Copyright information
© 2015 Springer International Publishing Switzerland
About this paper
Cite this paper
Möller, B., Hoare, T. (2015). Exploring an Interface Model for CKA. In: Hinze, R., Voigtländer, J. (eds) Mathematics of Program Construction. MPC 2015. Lecture Notes in Computer Science(), vol 9129. Springer, Cham. https://doi.org/10.1007/978-3-319-19797-5_1
Download citation
DOI: https://doi.org/10.1007/978-3-319-19797-5_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-19796-8
Online ISBN: 978-3-319-19797-5
eBook Packages: Computer ScienceComputer Science (R0)