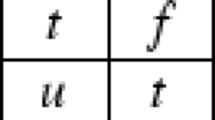What William of Ockham and Luis de Molina Would have said to Nuel Belnap: A Discussion of Some Arguments Against “The Thin Red Line”

Abstract

According to A. N. Prior the use of temporal logic makes it possible to obtain a clear understanding of the consequences of accepting the doctrines of indeterminism and free choice. Nuel Belnap is one of the most important writers who have contributed to the further exploration of the tense-logical systems as seen in the tradition after Prior. In some of his early papers Prior suggested the idea of the true future. Obviously, this idea corresponds to an important notion defended by classical writers such as William of Ockham and Luis de Molina. Belnap and others have considered this traditional idea introducing the term, “the thin red line” (TRL), arguing that this idea is rather problematic. In this paper I argue that it is possible to respond to the challenges from Belnap and others in a reasonable manner. It is demonstrated that it is in fact possible to establish a consistent TRL theory. In fact, it turns out that there several such theories which may all be said to support the classical idea of a true future defended by Ockham and Molina.

The Prior Collection at Bodleian Library in Oxford contains a few letters from Nuel Belnap to A. N. Prior and a few letters from Prior in reply—all from the period from 1960 to 1962. From the content of these letters it is evident that the two scholars shared a deep interest in philosophical logic. They both greatly appreciated the beauty of logical structures; in particular, they were interested in modal logic. For a new edition of his Formal logic Prior wanted to include some biographical data of some of the logicians he quoted in the book, and in a letter he asked Belnap to help him providing some data for that purpose. Prior received the data from Belnap, and in reply he wrote dated 28 March, 1960, he stated: “1930 seems to have been a good year for modal logic—you, Smiley, Lemmon, Jonathan Bennett ...”.

Clearly, modal logic attracted several brilliant young logicians during the 1950s and the 1960s. Prior, himself, had worked a lot with modal logic during the 1950s. More and more, these activities came to be combined with his interest in temporal logic and in the discussions regarding determinism and indeterminism. One of his main interests had to do with the Master Argument of Diodorus Cronus and the search for the so-called Diodorean modality (Prior 1955). It was well-known that Diodorus had formulated his argument about 300 BC in order to demonstrate that the world is deterministic, and to argue for a reductive account of modal notions to temporal notions; specifically that possibility should be conceived as “what is or what is going to be” (Øhrstrøm and Hasle 1995, p. 15 ff; Øhrstrøm and Hasle 2006). To Prior this gave rise to three interesting questions:

• 1. What is the formal structure of the modal logic in which possibility is defined in the Diodorean way, on the assumption that time is a linear and discrete sequence of instants?

• 2. How can a formal and valid version the Master Argument of Diodorus be formulated?

• 3. How can indeterminism be defended (in terms of tense-logical systems consistent with the assumption of free choice) against the valid versions of the Diodorean argument and similar arguments?

Prior worked intensively with these and similar questions from 1953 to his death in 1969. In doing so he found it most useful to study the theories of temporal logic. According to Prior the use of temporal logic would make it possible to obtain a better understanding of the consequences of accepting the idea of free choice. In particular, he also realized that the notion of branching time could be most helpful in this respect.

Question 1 above was fully answered during Prior’s lifetime. In fact, Prior dedicated a complete chapter of his Past, Present and Future to this problem and its solution (see Prior 1967, p. 20 ff.). As we shall see, the study of this question actually led to the construction of the first branching time models. Prior’s work with question 2 led him to the formulation of a reconstruction of the Master Argument (see Prior 1967, p. 32 ff.). Working with question 3, Prior developed some very important systems of temporal logic consistent with the assumption of free choice. In this chapter we shall mainly comment on his Ockhamistic system.

When Prior died in 1969 many additional problems regarding temporal logic and indeterminism had been discovered. Since then several logicians and philosophers have continued Prior’s line of thinking. Clearly, Nuel Belnap is one of the most important writers who have contributed to the further exploration of tense-logical approach to the study of indeterminism and free action.

Much of Nuel Belnap’s work has been carried out within a Priorean tradition. As we shall see Belnap has elaborated the Priorean view that, although we may formulate a so-called prima facie kind truth of contingent futures, such statements cannot be what Belnap has called “settled true”. Belnap has described this inspiration from Arthur Prior in the following way:

Although I suppose it is unscholarly, I have always thought that what I formulate using “settled” is indeed what he “meant”, and what he “would have said” had he been aware of the mischief that could, alas, be caused by not making “settled” explicit. [Personal communication, 31 Oct., 2009].

Branching time

In his book Time and Modality (1957), Prior suggested that the modal logic of the Diodorean concept of possibility (and time) is simply the modal system, S4. One of the first readers to react on Prior’s book, was Saul Kripke who was only 17 years old when he wrote the following to Prior:

I have been reading your book Time and Modality with considerable interest. The interpretations and discussions of modality contained in your lectures are indeed very fruitful and interesting. There is, however an error in the book which ought to be pointed out, if you have not learned of it already [Letter from Saul Kripke to A. N. Prior, dated Sept. 3, 1958, The Prior Collection, Bodleian Library, Oxford; see Ploug and Øhrstrøm 2011].

Young Saul Kripke then continued his letter by explaining that the formula,

$$\begin{aligned} \square {\lozenge p ~\vee }~\square \lozenge \!\!\sim \!\!{p} \end{aligned}$$

can be verified using Prior’s representation of Diodorean time as discrete sequences, but that this formula can be shown not to be provable in S4. In this way Kripke made an important contribution to the search for an axiomatic system corresponding to the Diodorean notion of modality. This research engaged several researchers in the late 1950s and the early 1960s. (See Prior 1967, p. 176). Even more important was the following passage from Saul Kripke’s letter in which he suggested how the semantics of S4 could be visualized. Kripke’s formulation of this very original idea in the letter makes it reasonable to classify the occurrence of this letter as one of the most important events in the history of logic during the twentieth century. Kripke wrote:

I have in fact obtained this infinite matrix on the basis of my own investigations on semantical completeness theorems for quantified extensions of S4 (with or without the Barcan axiom). However, I shall present it here from the point of view of your “tensed” interpretation. (I myself was working with ordinary modal logic.) The matrix seems related to the “indeterminism” discussed in your last chapters, although it probably cannot be identified with it. Now in an indetermined system, we perhaps should not regard time as a linear series, as you have done. Given the present moment, there are several possibilities for what the next moment may be like—and for each possible next moment, there are several possibilities for the next moment after that. Thus the situation takes the form, not of a linear sequence, but of a “tree” (Fig. 1):

Saul Kripke explains this branching time model in the following way:

The point 0 (or origin) is the present, and the points 1, 2, and 3 (of rank 2) are the possibilities for the next moment. If the point 1 actually does come to pass, 4, 5, and 6 are its possible successors, and so on. The whole tree then represents the entire set of possibilities for present and future; and every point determines a subtree consisting of its own present and future. Now if we let a tree sequence attach not three (as above) but a denumerable infinity of points to every point on the tree, we have a characteristic matrix for S4. An element of the matrix is a tree, with either 1 or 3 occupying each point; the designated tree contains only l’s. If all points on the proper ‘subtree’ determined by a point on the tree p are 1’s, the corresponding point on Lp is a 1; otherwise, it is a 3. (In other words, a proposition is considered “necessary” if and only if it is and definitely always will be the case.) [Letter from Saul Kripke to A.N. Prior, dated Sept. 3, 1958, The Prior Collection, Bodleian Library, Oxford]; (see Ploug and Øhrstrøm 2011).

Here ‘1’ stands for ‘true’ or ‘true proposition’, and ‘3’ stands for ‘false’ or ‘false proposition’. ‘L’ stands for the necessity operator.

Fig. 1

The branching time model suggested by Saul Kripke

In this way Saul Kripke argued that S4 corresponds to a branching time system combined with the Diodorean notion of temporal modality. This is the first ever presentation of branching time as a logical system. This was clearly recognised by Prior, who in his book Past, Present and Future discussed what he called “Kripke’s branching time matrix for S4” (Prior 1967, p. 27). However, there are some obvious shortcomings of Kripke’s semantics for predictions, i.e. that ‘it will be p’ and ‘it is possible that it will be that p’ are indistinguishable because Kripke keeps the semantic clause from linear time. This observation may have been an important part of Prior’s motivation in his further development of branching time models.

Prior seems to have hesitated a bit in embracing the idea of branching time. This probably has to do with the so-called ‘B-like’ properties of the system (mainly the properties of the before-after relation). Prior clearly wanted a so-called A-theoretic approach to time (i.e. a view of time based on the tenses: past, present and future). On the other hand, he found that the crucial A-theoretical notion of free choice could be represented in terms of branching time in a very clear and convincing manner. In his later further elaboration of branching time Nuel Belnap strongly emphasized the possibility of explaining what indeterminism is using this approach to time. Belnap and Green stated:

Branching time is not itself an indeterministic theory; instead, it says what indeterminism is, and it says what determinism is, but branching time does not choose between them (Belnap and Green 1994, p. 370).

When it comes to branching time, Belnap takes a clear stand. He argues that what he calls “Our World” can in fact be conceived as a branching time system, (see Belnap and Green 1994, pp. 370, 371 and 386). According to Belnap it is essential that the choices are real, i.e., that the world contains what he calls real possibility. For this reason, he argues that one should reject the idea suggested by David Lewis, according to which the possibilities should be seen as parallel lines (and not as branching lines). According to Belnap, such a view is misleading because it does not represent the possibilities available to the free agents as belonging to reality (see Belnap 2007).

In his further development of the idea of branching time, Prior found great inspiration in the study of medieval philosophy. In particular, he found the works of William of Ockham (c. 1285–1347) interesting. The central theme in the medieval discussions regarding temporal logic was the apparent conflict between the doctrines of divine foreknowledge and human freedom. Can man be free if God already now knows with certainty what the person in question is going to choose? Ockham wrote a famous book, Tractatus de praedestinatione et de futuris contingentibus, on the subject, which exists in a modern translation and edition by Marilyn McCord Adams and Norman Kretzmann [1969]. In the book Ockham asserted that God knows all future contingents, but he also maintained that human beings can freely choose between alternative possibilities. He argued that the doctrines of divine foreknowledge and human freedom are in fact compatible.

Prior’s study of Ockham’s writings was a great inspiration when he formulated his formal ideas on branching time. Clearly, it should be kept in mind that Ockham himself had no formal language at his disposal. Prior had to transform Ockham’s ideas into a modern context. Alex Malpass has edited the hitherto unpublished paper by Prior, Postulate Sets for Tense Logic [Forthcoming], which is kept in the Prior Collection at the Bodleian Library in Oxford. This paper was written and circulated in the mid-60s, and is probably a draft of Prior (1966) paper Postulates for Tense Logic and chapter VII.4 of Past, Present and Future (1967). The paper is the earliest known example of Prior’s attempts at formulating a branching theory of his own. In the paper Prior presents what he calls “an Occamist model”, which he used to formulate an account of the future tense that was more acceptable to Ockham’s philosophical views on future contingents than Kripke’s simple semantics. (In his early writing Prior seems to have used the spelling ‘Occam’, whereas he used ‘Ockham’ in his later writings.)

In these models the course of time (in a rather broad sense of this phrase) is represented by a line which, as it moves from left to right (past to future), continually divides into branches, so that from any given point on the diagram there is a unique route backwards (to the left; to the past) but a variety of routes forwards (to the right; to the future). In each model there is a single designated point, representing the actual present moment; and in an Occamist model there is a single designated line (taking one only of the possible forward routes at each fork), which might be picked out in red, representing the actual course of events (Prior 2014).

In his 1966 paper, Prior suggested two versions of the Occamist model, O and O$'$. In both of them he assumed a designated route. He wrote:

In each O and O$'$ model there is a single designated route from left to right, taking one direction only at each fork. This represents the actual course of events (1966, p. 157).

This idea of the true future as a single designated line is an idea which is now seen as rather controversial within the discussion of branching time models. Prior made a formal distinction between A-variables which stand for “those propositions which it is now beyond our power to make true or false” (so-called) and other propositional variables. Using this distinction and the notion of branching time, Prior showed how actual assignments of truth values at a point in the model and various so-called prima facie assignments could be introduced. He presented the first three steps in the procedure in the following way:

• (1) Each A-variable is arbitrarily assigned an actual truth-value at each point, and this is its only prima facie assignment at that point.

• (2) A prima facie assignment to Fn$\varvec{\Phi }$ at a point x will give it the value assigned to $\varvec{\Phi }$ at the distance n along some path to the right of x (where the diagram forks within this distance, Fn$\varvec{\Phi }$ will have a number of different prima facie assignments at x).

• (3) An actual assignment to Fn$\varvec{\Phi }$ at x gives it the value of $\varvec{\Phi }$ at the distance n to the right along the designated line.

In the paper, Prior illustrates his definitions by the following simple model:

It should be noted that Prior in his book Past, Present and Future dropped the use of the idea of “an actual assignment” and concentrated on a definition of the Ockhamistic model in terms prima facie assignments only, although no surviving explanation from Prior exists which explains why he dropped the notion. As I have argued in [1981], William of Ockham would not be an Ockhamist in this Priorean sense. However, the theorems of the two Priorean and Ockham-like systems will be the same, and the Ockhamist system defined in Past, Present and Future is certainly interesting (see Reynolds 2003).

Prior’s Ockhamistic system suggested in Prior (1967, p. 126 ff). may be presented in terms of the following recursive definition (see Øhrstrøm and Hasle 2011):

(a)	Ock(m, c, p) $=$ 1	iff	TRUE(p, m) $=$ 1, where p is any propositional constant.
(b)	Ock(m, c, p $\wedge$ q) $=$ 1	iff	both Ock(m, c, p) $=$ 1 and Ock(m, c, q) $=$ 1
(c)	Ock(m, c,$\sim$ p) $=$ 1	iff	not Ock(m, c, p) $=$ 1
(d)	Ock(m, c, Fp) $=$ 1	iff	Ock($m^\prime , c, p$) $=$ 1 for some $m^{\prime }\;{\in }\; c$ with $m < m^ \prime$
(e)	Ock(m, c, Pp) $=$ 1	iff	Ock($m^\prime , c, p$ ) $=$ 1 for some $m^{\prime }\;{\in }\;c$ with $m^ \prime < m$
(f)	Ock($m, c, \lozenge p$) $=$ 1	iff	Ock($m, c^\prime ,p$) $=$ 1 for some $c^{\prime }\;{\in }\;{C}$(m)

Here TRUE is a function, which gives a truth-value (0 or 1) for any propositional constant at any moment m in the branching time structure, (TIME, $\le$). What Prior called lines or routes, i.e. the maximal linearly ordered subsets in (TIME, $\le$), are often now called chronicles. We shall use this term in the following. C(m) is defined as the set of chronicles through the moment of time m, i.e., $C (m) = \{c \in C {\vert } m \in {c}\}$, where C is the set of all chronicles in (TIME, $\le$).

Strictly speaking, (a)–(f) only explain when Ock has the value 1 (‘true’). It should be added, that the value is 0 (‘false’), if it does not follow from the recursive definition above that is 1.

Ock $(m,c,p) = 1$ can be read ‘p is true at m in the chronicle c’. A formula p is said to be Ockham-valid if and only if Ock $(m,c,p) = 1$ for any t in any c in any branching time structure, (TIME, $\le$) and any valuation function TRUE. Here C should not be taken as an independent parameter. Furthermore, it should be noted that relative to a single chronicle, (a)–(e) are exactly the same definitions as those used in linear tense-logic (i.e. the tense-logic which follows if (TIME,$\le$) is a linear structure).

We define the dual operators, H, G, and $\square$ in the usual manner as ${\sim }P{\sim },{\sim }F{\sim }$, and ${\sim }{\lozenge }{\sim }$ respectively.

Obviously, there is no designated line (Thin Red Line) in Prior’s Ockhamistic system from Past, Present and Future, as there were in the two earlier versions of the system mentioned above. If we wish to have such a feature, it has to be added explicitly.

In their 1994 paper, Belnap and Green introduced the term “the Thin Red Line” with reference to an idea very much similar to Prior’s “designated line, picked out in red”. The term suggested by Belnap and Green was not inspired by Prior’s earlier notion. (Belnap apparently never received a copy of Prior’s Postulate Sets for Tense Logic, and he was not aware of Prior’s use of the expression [Personal communication, 25 April, 2012].)

Belnap’s and Green’s term was inspired by a report from the Crimean War in The London Times: “The Russians dashed on towards that thin red-line streak tipped with a line of steel.” It has even been suggested that the thin red line should in fact be conceived as infrared indicating “that the Thin Red Line does not imply that mortals are capable of seeing the future” (Belnap et al. 2001, p. 139).

Belnap and his co-workers have presented several arguments against the idea of “the thin red line” and the use of this idea in branching time semantics. In the following, we shall consider some of these arguments and discuss to what extent the idea can be defended. I shall refer to William of Ockham as a main spokesman for the view that the thin red line is important for the proper understanding of temporal reality. In addition I shall refer to the works of Luis de Molina (1535–1600), who much later than Ockham defended an even more elaborated version of the notion of “the thin red line” (see Craig 1988, p. 175). In both cases the notion was presented in terms of the Christian doctrine of divine foreknowledge. It should, however, be pointed out that this view does not have to be linked to a theological framework. Everything which will be said in favour of the idea of the thin red line can be translated into a secular language.

1 There is No Truth Concerning Future Contingents

Nuel Belnap has maintained that “the Thin Red Line” is in no way part of the real world. Before a free choice the alternative possibilities are equally real. There is no designated future if the choice is free. Nobody could know what is going to be freely chosen before the choice has actually been made. In his own words:

There is no real choice without the reality of alternative possible choices facing the agent. Each of these possibilities is, before the moment of choice, as real as any other. It is true and important that at most one of these possibilities will be realized. It is equally true and equally important that none of these possibilities is a ghostly image of some specially distinguished one among them that some philosopher might label “the actual choice”. This form of actualism is a bad idea (Belnap 2001, p. 2).

It seems that Belnap assumes that “a ghostly image” of “the actual choice” is needed in order to make it true that a certain free agent is going to carry out a certain act. However, as Trenton Merricks (2007) has argued the need for truth-makers in order to establish the truth of propositions can certainly be questioned. As Merricks has shown we may alternative hold that being true is a primitive monadic property (2007: 170 ff.) It is, on the other hand, probably true that medieval logicians would have a view closer to what Belnap is criticising as their metaphysical reasoning for believing in “the thin red line”.

It is not difficult to imagine how William of Ockham would have replied to Belnap’s criticism. He would probably have pointed out that Belnap’s position should be accepted as long as we are dealing with human cognition alone. However, there might be a deeper structure in reality which is not directly accessible to the human mind, but which nevertheless is useful for a deeper understanding of natural language and common sense reasoning. As a believer, Ockham stated his view referring to divine foreknowledge. He willingly admitted that this idea is very hard to understand for a human being. However, he attempted to clarify the issue as much as possible. Ockham stated:

... the divine essence is an intuitive cognition that is so perfect, so clear, that it is an evident cognition of all things past and future, so that it knows which part of a contradiction [involving such things] is true and which part is false (Ockham 1969, p.50).

Ockham had to admit that much of this cannot be stated in a very clear manner. In fact, he maintained that it is impossible to express clearly the way in which God knows future contingents. He also had to conclude that in general the divine knowledge about the contingent future is inaccessible. God is able to communicate the truth about the future to us, but if God reveals the truth about the future by means of unconditional statements, the future statements cannot be contingent anymore. Hence, God’s unconditional foreknowledge regarding future contingents is in principle not revealed, whereas conditionals can be communicated to the prophets. Even so, that part of divine foreknowledge about future contingents which is not revealed must also be considered as true according to Ockham.

Ockham was aware that the concept of communication was essential to this discussion—especially, of course, the communication coming from God to human beings. He claimed that God can communicate the truth about the future to us. Nevertheless, according to Ockham divine knowledge regarding future contingents does not imply that they are necessary. As an example Ockham considered the prophecy of Jonah: “Yet forty days, and Nineveh shall be overthrown” [The Book of Jonah ch. 3 v. 4]. This prophecy was a communication from God about the future. Therefore, it might seem to follow that when this prophecy had been proclaimed the future destruction of Nineveh would be necessary. But Ockham did not accept that. Instead, he made room for human freedom in the face of true prophecies by assuming that “all prophecies about future contingents were conditionals” (Ockham 1969, p. 44). So according to Ockham we must understand the prophecy of Jonah as presupposing the condition “unless the citizens of Nineveh repent”. Obviously, this is in fact exactly how the citizens of Nineveh understood the statement of Jonah!

Ockham realised that the revelation of the future by means of an unconditional statement, communicated from God to the prophet, is incompatible with the contingency of the prophecy. If God reveals the future by means of unconditional statements, then the future is inevitable, since the divine revelation must be true. Such possible restrictions on the use of divine communication (revelation) must be taken into consideration, if the belief in divine foreknowledge is to be compatible with the belief in the freedom of human actions.

When translated into a secular language this means that if there is a designated future, which is invisible to human agents, it will not destroy their freedom of choice. In terms of Belnap’s notions: If the thin red line is in fact part of reality, then it has to be “infrared” in the sense that it is undetectably to human beings, given that free choice is also part of reality. However, this is not surprising. There are many aspects of reality which we are ready to accept although they are even in principle not verifiable. One such aspect is in fact free choice itself and its rooting the human mind!

2 A Thin Red Line Theory is Insufficient as a Background for a Proper Understanding of the Structure of Tenses in Natural Language

The typical argument given in favour of the assumption of a designated future is that we may in this way deal better with natural language and common sense reasoning. However, it has been argued that this assumption is quite insufficient as a background for a satisfactory model fit for dealing with the logic of tenses in natural language. The Thin Red Line is supposed to help, but perhaps it does not.

Nuel Belnap and Mitchell Green have given a very nice example in support of this criticism of a “Thin Red Line” theory:

The coin will come up heads. It is possible, though that it will come up tails, and then later it will come up tails again (though at this moment it could come up heads), and then, inevitably, still later it will come up tails yet again (Belnap and Green 1994, p. 379).

Clearly, this example calls for the use of so-called embedded tenses. It is not sufficient to be able to refer to what is actually going to be the case, but we should also be able to discuss what in alternative (counterfactual) situations would have been going to happen. A designated future, it seems, is not enough.

Belnap and Green’s statement may be represented in terms of tense logic with $\tau$ representing tails and $\eta$ heads, respectively:

$$\begin{aligned} F(1)\eta \wedge \lozenge F(1)(\tau \wedge \lozenge F(1)\eta \wedge F(1)(\tau \wedge \square F(1) \tau )) \end{aligned}$$

The problem for a Thin Red Line theory in evaluating this proposition is how to understand the embedded occurrences of the F-operator. One way to do this is by using the following branching time structure, which has been enriched with arrows indicating not only a single designated future, but actually a designated future at every branching point in the system (Fig. 2):

Fig. 2

A branching time model representing an example suggested by Nuel Belnap and Mitchell Green

The example shows that if the model is taken seriously, then there must be a function TRL, which gives the true future for any moment of time, m. More precisely, TRL(m) yields the linear past as well as the true future of m, extended to a maximal set. In this way, TRL(m) will for any moment of time, m, be a chronicle within the branching time system.

It is very likely that William of Ockham would have accepted the points made by Belnap and Green regarding embedded tenses. When analysing the features of the Ockhamistic model, it becomes evident that within the model there must be a true future, not only in every actual situation or instant, but also in every possible situation. This was at least realised by Luis de Molina, who worked some centuries after Ockham, but still very much in the same scholastic tradition. Molina’s special contribution is the idea of (God’s) middle knowledge, “by which, in virtue of the most profound and inscrutable comprehension of each free will, He saw in His own essence what each such will would do with its innate freedom were it to be placed in this or that or indeed in infinitely many orders of things — even though it would really be able, if it so willed, to do the opposite” (quoted from Craig 1988, p. 175). Craig goes on to explain it as follows: “... whereas by His natural knowledge God knows that, say, Peter when placed in a certain set of circumstances could either betray Christ or not betray Christ, being free to do either under identical circumstances, by His middle knowledge God knows what Peter would do if placed under those circumstances” (Craig 1988, p. 175). Craig has argued that such counterfactuals of freedom can be true even if there is nothing to make it true and no grounding of such truth. On the contrary, the truth of counterfactuals of freedom might be taken as indicating the theories of truth-makers and grounding should be rejected. (See Craig 2001, Merricks 2007, 146 ff.)

Using Prior’s notion of branching time it might be extended and represented by a diagram such as the following where the idea of the true future (including the idea of ‘middle knowledge’) is indicated by the use of arrows showing the true or selected courses of events (Fig. 3).

Fig. 3

A representation of the Ockhamistic/Molinistic model in terms of Prior’s notion of branching time

The wisdom obtained from the critical points made by Belnap and Green suggests that a Thin Red Line theory based on a single designated line will be insufficient. If such a theory is possible, it has to include a unique true future at any point in the model although there may be several possible futures at each point in the model. The conclusion is that in the search for a Thin Red Line theory, one should look for a theory based on a TRL-function from temporal moments to histories in the model. We shall call such a theory “a TRL theory”.

3 An Obvious Requirement Regarding Iterative Tenses Makes TRL Theories Problematic

Belnap and Green (1994) have argued that any serious TRL theory should imply the validity of the following fundamental relation regarding iterative tenses.

$$\begin{aligned} \mathrm{{(T1)}} PPq&\supset Pq \\ \mathrm{{(T2)}} FFq&\supset Fq \end{aligned}$$

From an intuitive point of view the validity of (T1-2) appears to be rather obvious. T1 says that if it was that it was that q, then it was that q, etc. This understanding of the iterated tenses seems straight forward given the way the tenses are used in natural language and in common sense reasoning. In a similar way, several other basic expressions have to come out as valid in general, if the theory in question is to be accepted. One other obvious proposition which should be valid in general is

$$\begin{aligned} \mathrm{{(M1)}} Fq \supset \lozenge Fq \end{aligned}$$

If it will be that q, then it is possible that it will be that q. There can be no doubt that William of Ockham would have understood this type of requirement. After all, he also wanted to formulate a logical theory in accordance with natural language and common sense reasoning.

In their 1994 paper Belnap and Green suggested that the TRL-function in a TRL theory in order to lead to the general validity of expressions like (T1-2) and (M1) satisfy the following conditions:

$$\begin{aligned}&\mathrm{{(TRL1)}}\;m \in TRL(m) \\&\mathrm{{(TRL2)}}\;m_{1} < m_{2} \supset TRL(m_{1}) = TRL(m_{2}) \end{aligned}$$

However, as Belnap and Green have correctly pointed out the acceptance of the combination of (TRL1) and (TRL2) entails a rejection of the very idea of branching time. The reason is that if (TRL1) and (TRL2) are both accepted, it follows from $m_{1} < m_{2}$ that $m_{2} \in TRL(m_{1})$, i.e. that all moments of time after $m_{1}$ would have to belong to the thin red line through $m_{1}$, which means that there will in fact be no branching at all.

This seems to give rise to a problem for the TRL theory. However, it turns out that there is in fact no need to accept (TRL2), which seems to be too strong a requirement. Rather than (TRL2), the weaker condition (TRL2$^\prime )$ can be employed:

$$\begin{aligned} (\mathrm{{TRL}}2^ \prime ) (m_{1} < m_{2} \wedge m_{2} \in TRL(m_{1}))\supset TRL(m_{1}) =TRL(m_{2}) \end{aligned}$$

This weaker requirement appears to be much more natural in relation to the basic idea of TRL-theory. Belnap has later accepted that (TRL2$^\prime )$ is a relevant alternative to (TRL2) ([Personal correspondence, 1 Aug. 1996] and Belnap et al. 2001, p. 169).

Following Prior’s ideas in Postulate Sets for Tense Logic extended to a TRL-model we can formulate the following truth condition for the future operator:

• (i) Fq is true a moment m iff there is a moment of time, $m' \in TRL\mathrm{(}m\mathrm{)}$, such that $m< m'$ and q is true at $m'$.

In the same way it is possible to define what it means for a proposition, Pq, to be true at the moment m, taking TRL(m) as the designated line.

Given these truth conditions it is easily seen that (T1-2) are valid in general. In addition (M1) will be valid in general, if we accept the following truth condition:

• (ii) $\lozenge Fq$ is true a moment $m$ iff there is a moment of time, $m'$, and a chronicle, c, such that $m \in c, m' \in c, m < m'$ and q is true at $m'$.

4 TRL Theories Lead to Problematic Evaluations at Counterfactual Moments of Time

Belnap and Green (1994) have argued that in addition to (T1-2) any serious TRL theory should imply the general validity of expressions like

$$\begin{aligned} \mathrm{{(T3)}} ~ q \supset P(x)F(x)q \end{aligned}$$

where P(x) stands for “it was the case x time units ago” and F(x) stands for “it is going to be the case in x time units”. (T3) should be true not only at moments belonging to the history which is actually taking place, but also at counterfactual moments.

Again, following a tradition from medieval logic, it seems reasonable to require that statements like (T3) are true even at counterfactual moments of time. Logicians like William of Ockham would be very likely to have accepted that (T3) should be valid in general.

However, this will be difficult to maintain (T3) as valid within a TRL-theory if we assume a rigorous notion of compositionality for the evaluation of truth values. Consider, for instance, a branching time model, which can be illustrated in the following way:

Given this TRL model we may ask whether $q\supset P(x)F(x)q$ is true at $m_{2}$. As indicated above q is true at $m_{2}$. However, assuming a rigorous notion of compositionality P(x)F(x)q is false at $m_{2}$, since F(x)q appears to false at $m_{3}$.

However, alternatively one may insist that any evaluation of a truth value at moment of time, m, should be carried out as if TRL(m) were the designated line (“The Thin Red Line”). This means that truth of a position, p, at a moment of time, m, may simply be defined in term of the truth-function in Prior’s Ockhamistic system in the following way:

$$\begin{aligned} \mathrm{{true}}_\mathrm{{T}}(p, m) = Ock(m,{TRL(m)},{p}) \end{aligned}$$

If this is accepted no iteration of the tense operators, P and F, will get us off the designated chronicle when calculating the truth value of a proposition at m. Using this approach to the evaluation of counterfactual truth-values, we will in the above case find that the implication, $q{\supset }P(x)F(x)q,$ is in fact true at $m_{2}$. This is so, because the evaluation is carried out only referring to $TRL(m_{2})$.

Taking this rather simple approach we end up with a logical system with exactly the same theorems as in Priorean Ockhamism, including (T3). This is what we might call the simple Ockhamistic answer to the Belnap-Green challenge.

However, it might be objected that if we were to assume a designated chronicle as a background for the evaluation of the truth-value of a tense-logical proposition it ought to be $TRL(m_{1})$ (i.e. the actual history) and not an alternative history such as $TRL(m_{2} )$. This objection appears to be based on the view, that any counterfactual statement in principle has made as seen from the actual world. When we are claiming that something like (T3) might be true even at a counterfactual moment of time, ${m}_{2}$, what we mean is that at the present moment of time, ${m}_{1}$, it is true for any numbers x and y that

$$\begin{aligned} P(y) \lozenge F(y)(q \supset P(x)F(x)q) \end{aligned}$$

In fact, the claim that (T3) holds in general, means that the implication mentioned in (T3) would have been true no matter what had happened in the past i.e. even if alternative past possibilities had been actualized. This means that at the present time, $m_{1}$, the following is true for arbitrary positive numbers z, y and x:

$$\begin{aligned} P(z) \square F(y)(q \supset P(x)F(x)q) \end{aligned}$$

According to this approach, we suggest that the truth-value of a tense-logical expression at a moment of time, m, should be evaluated as in Prior’s paper mentioned above using the branching time and taking TRL(m) to be the designated (red) line. In order to deal with the modal operators in a precise manner, we need a truth condition for the modal operators which more general than (ii) in Sect. 3. We may consider the following Ockhamistic truth condition:

• (iii) $\lozenge p$ is true at the moment of time, m, relative to a chronicle c iff there is a chronicle, $c'$, through m, such that p is true at m relative to a $c'$, which is understood as the chronicle that should be used in the further evaluation.

However, it may be objected that in such a model the TRL-function has really no role to play in the semantics, in the sense that the properties of the TRL-function does not influence which propositions are valid in general and which are invalid. However, as pointed out in Braüner et al. (2000), Øhrstrøm (2009), it is in fact possible to create an alternative system, in which the TRL-function plays such a role. This may be done using the following Ockhamistic truth condition:

• (iv) $\lozenge p$ is true at the moment of time, m, relative to a chronicle, c, iff there is a chronicle, $c'$, belonging to $C_{T} (m),$ such that p is true at m relative to a $c'$, which is understood as the chronicle that should be used in the further evaluation,

where

$$ \begin{aligned} C_{T}(m) = \{ c {\vert } {m} \in {c} ~ \& ~{TRL}({ m^ \prime )}={c}, \text {for any}~ {m}^\prime ~ \in {c}~\mathrm{{with}}~ {m} < {m}^ \prime \} \end{aligned}$$

Note that $C(m)$ is a subset of all chronicles through m. With this definition any history used in evaluation of the proposition ${ \lozenge } p$ at a moment $m$, can be conceived as a $TRL(m^\prime )$, where $m^\prime$ is a moment immediately after m.

As argued in Braüner et al. (2000), Øhrstrøm (2009) this alternative definition leads to a slightly different semantics, according which e.g. the proposition, $F(x) \lozenge F(y)p \supset \lozenge F(y)F(y)p$, will not be valid in general. This means that in this system something which is not yet possible may become possible, i.e. new possibilities may turn up! However, it should be emphasized there is not absolute need to go for a system like this, but the existence of this alternative system at least shows that simple TRL-system mentioned above it not the only possible and that it is possible to define a semantic system in which the TRL-function plays a significant role in the semantics.

5 Conclusion

As argued above, it is possible to respond to the Belnap-Green challenge in a reasonable manner. One solution is the simple Ockhamistic answer. A slightly more sophisticated solution has been suggested in Braüner et al. (2000). There are other interesting solutions such as the one suggested by Malpass and Wawer (2012), where there is a single designated line and a supervaluational account of counterfactual future contingents is given.

Playing with a title of Dummett (The logical basis of metaphysics, 1991), Nuel Belnap wrote:

If you wish to learn the “metaphysical basis of logic” according to some logician, studying the inductive account of the language is useful, but it is crucial to understand his or her explanations of the parameters that are at bottom of the entire enterprise (Belnap 2007, p. 97).

No doubt, William of Ockham would have agreed. He wanted to study the tenses as they are used in natural language and in common sense reasoning. But he certainly wanted to do so based on what he believed to be the fundamental features of our world. A very important feature of the world according to Ockham’s view is that exactly one of the many possible ways, in which the world may develop, is the true one. He would insist that we have to develop our logical theories taking this important fact into account. And even more important we have to carry out this task in a logically consistent manner. For this reason William of Ockham would clearly also have appreciated the challenges formulated by Nuel Belnap and his co-workers, since these thoughtful comments have been a great help to anyone who wants to establish a consistent theory of what Belnap and Green have called “the thin red line”.