A Theory of Possible Ancestry in the Style of Nuel Belnap’s Branching Space-Time

Abstract

We present a general theory of possible ancestry that is a case of modal ersatzism because we do not take possibilities in terms of offspring as given, but construct them from objects of another kind. Our construction resembles Nuel Belnap’s theory of branching space-time insofar as we also carve all possibilities from a single pre-existing structure. According to the basic theory of possible ancestry, there is a discrete partially ordered set called a structure of possibilia, any subset of which is called admissible iff it is downward closed under the ordering relation. A structure of possibilia is meant to model possible living beings standing in the relation of possible ancestry, and the admissible sets are meant to model possible scenarios. Thus the Kripkean intuition of the necessity of (ancestral) origin is incorporated at the very core of our theory. In order to obtain a more general formulation of our theory which allows numerous specifications that might be useful in concrete biological modeling, we single out two places in our framework where further requirements can be implemented: Global requirements will put further constraints on the ordering relation; local requirements will put further constraints on admissibility. To make our theory applicable in an indeterminist world, we use admissible sets to construct the (possible) moments and (possible) histories of a branching time structure. We then show how the problem of ontological competition can be solved by adding an incompatibility partition to a structure of possibilia, and conclude with some remarks about how this addition might provide a clue for developing a variant of the theory of branching space-time that can account for the trousers worlds of general relativity.

This postscript and the family of theories it describes grew from discussions between Niko Strobach and Martin Pleitz about earlier drafts of Strobach’s paper “In Retrospect”. It was written jointly but with somewhat diverging motivations, with Strobach having a special interest in the question of ontological competition and the clue it provides for a general relativity friendly variant of BST and Pleitz having a special interest in the most general form of a theory of possible ancestry and the constructions that allow to answer the question of embeddability. We are grateful to the participants of the discussion during the WIRP II workshop at GAP 8 in Konstanz in September 2012, in particular to Peter Fritz and Thomas Müller.

1 Ersatzism of Belnapian Elegance

The aim of this postscript is to present a theory of possible ancestry that emulates the elegance of Nuel Belnap’s theory of branching space-time (BST), and in particular of the modal side of BST ¹. To bring out what is particularly elegant about it, let us have a look at how other theories of modality model possibilities. It is most common to model a possibility as a possible world, viewing the collection of all possible worlds as modal space, which is structured by the relation of accessibility that holds between worlds. Modal primitivism takes a possible world as a given object, irreducible to anything else. Modal ersatzism reduces each possible world to a construction from objects of a different kind, typically to a maximally consistent set of sentences or to a maximally coherent collection of states of affairs.² On this basis, both primitivism and ersatzism of the typical kind form modal space by knitting together their respective modal components by adding the relation of accessibility to the collection of possible worlds. BST, in contrast, gives a picture of much more cohesion and unity. Far from constructing modal space by knitting together possibilities, which (for typical ersatzism) are themselves the result of pasting together some of a plurality of modal atoms, it carves possibilities out from a single pre-existing structure, Our World. This is so because what corresponds naturally to possible worlds in the BST framework are histories, and these are just subsets of Our World that are defined by recourse to the inner structure of Our World (its ordering relation) alone. So BST, though of course also a case of modal ersatzism, is ersatzism of an untypically elegant kind.

The theory of possible ancestry sketched in Strobach’s “In Retrospect” is like primitivism and like typical ersatzism insofar it also knits together possibilities to form modal space. Hence we will here dub it “TPA$^\mathrm{{knit}}$”. What we want to achieve in this sequel to Strobach’s paper is to find a theory of possible ancestry such that there is some obvious one-to-one correspondence of some of its elements to the possibilities of TPA$^\mathrm{{knit}}$, but which is closer to Belnap’s BST insofar as it is based on carving out possibilities rather than knitting them together. (To make this contrast explicit, we will sometimes call our theory of possible ancestry “TPA$^\mathrm{{carve}}$”, but usually we will stick to the shorter “TPA”.) The results will not quite be Belnap-style BST structures, but nearly so, and they will give a flexible framework for biological modeling.

2 The Basic Theory of Possible Ancestry

We start out by giving a basic variant of a theory of possible ancestry, which will suffice to explain some core notions and our main idea. The basic theory is as follows.

A structure of possibilia is an ordered pair $\langle \mathrm{{D}},\prec \rangle$, where D is a non-empty set of objects and $\prec$ is a relation on D. Nothing is required of D; in particular, D may be infinite. The relation $\prec$ is required to be irreflexive, anti-symmetric (and hence will be asymmetric),³ and transitive, so that it is a partial strong order on D (hence the notation, “$\prec$”), and to be discrete. Nothing else is required of $\prec$; in particular, $\prec$ need not be connected and $\prec$ (when viewed as a graph) may contain both upward and downward branches and may thus be unlike the tree structure of branching time. Furthermore, some subsets of D are singled out as admissible, a set being admissible just in case it is downward closed under the relation $\prec$.

Formally⁴: (Irreflexivity) $\lnot (\mathrm{{x}} \prec \mathrm{{x}})$.

(Anti-Symmetry) $\mathrm{{x}} \ne \mathrm{{y}}\wedge \mathrm{{x}} \prec \mathrm{{y}} \rightarrow \lnot (\mathrm{{y}} \prec \mathrm{{x}})$.

(Transitivity) $\mathrm{{x}} \prec \mathrm{{y}} \wedge \mathrm{{y}} \prec \mathrm{{z}} \rightarrow \mathrm{{x}} \prec \mathrm{{z}}$.

(Discreteness)⁵ $\mathrm{{x}} \prec \mathrm{{y}} \rightarrow \varvec{\exists } \mathrm{{z}} (\mathrm{{x}} \preccurlyeq \mathrm{{z}} \wedge \mathrm{{z}} \prec \mathrm{{y}} \wedge \varvec{\forall }\mathrm{{w}} (\mathrm{{x}} \preccurlyeq \mathrm{{w}} \wedge \mathrm{{w}} \prec \mathrm{{y}} \rightarrow \mathrm{{w}} \preccurlyeq \mathrm{{z}})) \wedge \varvec{\exists } \mathrm{{z}}{\text {'}} (\mathrm{{x}} \prec \mathrm{{z}}{\text {'}} \wedge \mathrm{{z}}{\text {'}} \preccurlyeq \mathrm{{y}} \wedge \varvec{\forall }\mathrm{{w}} (\mathrm{{x}} \prec \mathrm{{w}} \wedge \mathrm{{w}} \preccurlyeq \mathrm{{y}} \rightarrow \mathrm{{z}}' \preccurlyeq \mathrm{{w}}))$.

(Def. Closure) A set $\mathrm{{M}}\subseteq \mathrm{{D}}$ is downward closed iff $\mathrm{{x}} \in \mathrm{{M}} \wedge \mathrm{{y}} \prec \mathrm{{x}} \rightarrow \mathrm{{y}} \in \mathrm{{M}}$.

(Def. Admissibility) A set $\mathrm{{M}}\subseteq \mathrm{{D}}$ is admissible iff M is downward closed.

The intended material interpretation of our formal ontology of a structure of possibilia and its admissible sets is as follows. The elements of the domain D represent possible living beings. The relation $\prec$ on D is represents possible ancestry, i.e., $\mathrm{{x}} \prec \mathrm{{y}}$ if and only if x is a possible ancestor of y (or, equivalently, y is a possible descendant of x). The admissible sets represent ancestral possibilities—alternatives in terms of offspring.⁶

In the light of this interpretation, we can explain our choice of requirements. Partly, the reasons for the requirements on the relation of possible ancestry mirror those for the corresponding requirements of (actual) ancestry made in Strobach’s “In Retrospect”. This is so for (Irreflexivity), (Transitivity), and (Discreteness). No being can be its own ancestor. If a first being can be an ancestor of a second, and the second being can be an ancestor of a third, then the first can be an ancestor of the third. And in view of our understanding of the ordering relation as one of possible ancestry, it just makes no sense to allow dense patches in the structure of possibilia, to say nothing of continuous ones.

The motivation of (Closure) and, as it will turn out, also of (Anti-Symmetry), is more substantial. We want our theory of possible ancestry to respect the Kripkean claim of the necessity of (ancestral) origin: Any possible being has each one of its possible ancestors of necessity—a being with distinct ancestors just would be a distinct being. Therefore any possibility must be downward closed, i.e., for any being that it contains it must also contain each one of the possible ancestors of that being. In other words, possibly being an ancestor entails being an ancestor, so that in many situations we may abridge talk about possible ancestry to talk about ancestry.⁷

It turns out that the Kripkean claim also motivates (Anti-Symmetry). If ancestral origin were contingent, we might well have two distinct possible living beings A and B such that in one possibility being A is an ancestor of being B and in another possibility being B is an ancestor of being A. But because of the explication of the Kripkean claim in terms of (Closure), and in view of (Transitivity), A and B would be their own ancestors in each one of the two possibilities of this scenario, which obviously conflicts with (Irreflexivity). So, reflecting on the inadmissibility of such circular relations of ancestry as those between A and B lets us note that incorporating the relation of possible ancestry on the level of possibilia already does quite much to commit us to a Kripkean doctrine of the necessity of ancestral origin. Or, what probably amounts to the same thing, an incorporation of the relation of possible ancestry on the level of possibilia and a restriction of ancestral relations within each possibility like (Closure) make sense only when they are implemented together.

Note that, according to the above definition, the empty set is admissible. This will be technically convenient later on,⁸ and it can also be motivated intuitively. For is it not possible that there is no (and there never has been any) living being at all? A similar claim that involved a truly unrestricted quantifier (i.e., that it is possible that there is nothing at all) might well be contentious. But in the case of the present framework, the intuitive background story has other entities—e.g., atoms, chemical compounds, water, air, and the planet Earth—besides the possible living beings modeled by the elements of the domain D. Clearly an entirely uninhabited Earth is possible relative to some moments in time (especially in the far past), and we can even imagine entire possible histories in which live never evolves.⁹

With our basic theory, we have already achieved some similarity to Belnap’s BST. This becomes evident by contrasting the present TPA$^\mathrm{{carve}}$ to the TPA$^\mathrm{{knit}}$ of Strobach’s paper. While the latter starts out with given possibilities, each with its own relation of ancestry, which have to be made to match each other by certain requirements on those relations to enable the next step of knitting them together, the former needs no corresponding requirements because possibilities are carved out of a single pre-existing object, the structure of possibilia.

However, we yet have no natural one-to-one correspondence between the possibilities of TPA$^\mathrm{{carve}}$ and the possibilities of TPA$^\mathrm{{knit}}$. This is so because our basic theory leaves out many of the requirements, especially of cardinality and connectedness, which are implemented in TPA$^\mathrm{{knit}}$ (which it in turn had inherited from the non-modal formal theory of ancestry, FTA). So, although we already have captured a few basic metaphysical intuitions, there is still some way to go for our TPA$^\mathrm{{carve}}$ to model the biological realm in a satisfactory way.

3 The General Form of a Theory of Possible Ancestry and Some Specific Theories

In order to do some biological modeling, we will now leave behind the basic theory of possible ancestry and move on to a plurality of specific theories of possible ancestry. We will start with what is common to them all, with the general form of a theory of possible ancestry. Going specific means adding details to the structure of possibilia and the possibilities it contains. We do this by adding requirements to the basic theory. The general form of a theory of possible ancestry tells us that there are two different places in the theory where we can implement the extra requirements.

The general formulation of a theory TPA$^\mathrm{{carve}}$ is as follows. A structure of possibilia is a domain ordered by an asymmetrical, transitive, and discrete relation such that the domain and the relation satisfy some additional theory-specific requirement $\varGamma$ (gamma for “global”), e.g., of cardinality or connectedness. An admissible set is a downward closed subset of the domain such that the set together with the ordering relation satisfy some additional theory-specific requirement $\varLambda$ (lambda for “local”), e.g., again, of cardinality or connectedness.

Formally:

(Irreflexivity), (Anti-Symmetry), (Transitivity), & (Discreteness)¹⁰

(Gamma) $\langle \mathrm{{D}}, \prec \rangle$ satisfies the additional requirement $\Gamma$.

(Def. Admissibility) A set $\mathrm{{M}} \subseteq \mathrm{{D}}$ is admissible iff M is downward closed and $\langle \mathrm{{M}}, \prec \rangle$ satisfies the additional requirement $\Lambda$.

To see how this general framework can be used we will look at some examples of specific theories that can be obtained by choosing particular sentences $\Gamma$ and $\Lambda$.

First, the trivial example. The basic theory is that special case where for $\Gamma$ and $\Lambda$ we insert some tautologies into the general form, i.e., where further constraints are put neither on the structure of possibilia nor on the admissible sets.

Next, the example of a direct counterpart of the theory $\mathrm{TPA}^\mathrm{{knit}}$, called simply “TPA” in Sect. 3.2 of “In Retrospect”. Its axiom TPA 1 corresponds to the framework delivered already by our basic theory, but it does its work on a more specific structure of possibilia, which can be obtained by putting the conjunction of all the BTA postulates from Sect. 2.2 of “In Retrospect” in the place of $\Gamma$. The possible strengthened theories discussed by Strobach in Sect. 3.2 can be obtained by adding U as a further conjunct of $\Gamma$ and adding TPA 2 or TPA 2* as a further conjunct of $\Lambda$. Thus we have found a natural one-to-one correspondence between the possibilities of TPA$^\mathrm{{carve}}$ and the possibilities of TPA$^\mathrm{{knit}}$ (which our basic theory could not yet deliver): Each one of the pairs $\langle \mathrm{{D}}_\mathrm{{{P}}},<_\mathrm{{{P}}}\rangle$ of TPA$^\mathrm{{knit}}$ corresponds to an admissible set of the present specific variant of TPA$^\mathrm{{carve}}$, because, when the domain of TPA$\mathrm{^{carve}}$ is taken to be a superset of the union of all the $\mathrm{{D}}_\mathrm{{{P}}}$, each relation $<_\mathrm{{{P}}}$ need only be taken as the restriction of the relation $\prec$ of TPA$^\mathrm{{carve}}$ to the admissible set corresponding to $\mathrm{{D}}_\mathrm{{P}}$, and everything will fall into place nicely.

As our next family of examples, we have some specific theories that share the following characteristic with the above direct counterpart of the theory TPA$^\mathrm{{knit}}$: Each one of the possibilities they deliver satisfies all the postulates of the non-modal basic theory of ancestry (BTA) of Sect. 2.2 of “In Retrospect”. We have constructed the direct counterpart by putting all the BTA postulates into the slot held open by “$\Gamma$” in the general form of a theory of possible ancestry. It is interesting to see what happens when we move some of them over to the slot “$\Lambda$”, that is, when we understand them not as global but as local requirements. The results are impressive in the case of constraints of cardinality, where it arguably makes much biological sense, too.

Using the cardinality constraints¹¹ as conjuncts not of $\Gamma$ but of $\Lambda$ will allow the structure of possibilia to have an infinite domain because it moves the requirements of finiteness into the admissible sets. For example, any possible being in each possibility has only finitely many direct descendants, but it may nevertheless stand in the relation of direct possible ancestry to infinitely many possible beings. Here is a reason why we should not demand that some ancestor has only finitely many possible descendants. While a living being cannot actually reproduce infinitely often within a given amount of time and cannot actually leave infinitely many direct descendants, it may well do so possibly in the following sense: While no infinite branching within the same alternative is possible, the same parents may have an infinity of different possible children. (The more strongly we understand the metaphysical principle of the necessity of origin, the more plausible this gets. For according to a very strict reading of that principle, even offspring from the same sperm and egg would be a different individual if both had met a second earlier, or half a second, or a quarter of a second etc. Maybe this reading of the principle is too strict to be credible.¹² Still, we do not take it to be to the disadvantage of our framework that it can model the consequences of the strict reading.)

Another class of examples shows again how sensitive the general form of a theory is to choices whether a certain constraint is implemented in a global or a local way. When we put a constraint of connectedness (like postulate U) into the place of $\Gamma$, we get a much more severe restriction on our frame of possibilia than when we put it into the place of $\Lambda$. In the former case, all possible living beings are connected, whereas in the latter case, only the living beings of each possibility are connected, which would allow for the possibility of an entirely disjoint alternative to the actual development of life even in the face of the intuition of the unity of life and its deictic component that motivates postulate U.¹³ Something similar can be said about the postulates about starting points and endpoints.¹⁴

There are also some specific theories that do not result from recombining the BTA postulates, but can be obtained easily from the general form by some small additions to the language of TPA. If we add species predicates (“... is a horse”, “... is a dog”), we can formulate postulates that state the impossibility of interbreeding, and put species-specific upper limits on the number of direct ancestors a being can have (the number being two for mammals and one for cells that reproduce by fission), and so on. Thus a whole wealth of distinctions becomes available. For instance, although prima facie it is natural to give a rigid interpretation to all species predicates, they arguably can also be construed as flaccid.¹⁵ But then it may come about that some given individuals that belong to distinct species in some possibilities belong to the same species in other possibilities.

The preceding examples should be enough to show that in its general form our theory of possible ancestry allows to do some realistic biological modeling. We want to close this section with a remark about the way in which we have split up general principles and specific constraints by using some postulates, like the transitivity of possible ancestry and the downward closure of ancestral possibilities, to formulate the general form and others, like those of cardinality and connectedness, to formulate specific requirements of a global or local sort. What is behind this way of splitting up postulates is a conviction about how to draw the line between metaphysical and empirical inquiry. The postulates enshrined in the general form of all our theories of possible ancestry are motivated by metaphysical principles, first and foremost Kripke’s claim about the necessity of ancestral origin. In contrast, all the optional specific postulates—of cardinality, connectedness, the existence of starting points and endpoints, and all species-relative constraints—are in principle open to empirical revision.¹⁶ To see the metaphysical character of Kripke’s claim, just try to devise an experiment (or, more generally, try to come up with any empirical consideration) that would make it possible to falsify it! It nevertheless is fitting that Kripke’s claim and the other motivations behind the general form are incorporated at the core of a biological theory because these are metaphysical facts about the subject matter of biology.

Now, after we have given our theory a lot of flexibility, which will allow it to model quite a large part of biological reality, we should investigate how it relates to the picture of branching time, which after all has provided the intuitive background all along.

4 The Question of Embeddability: States, Moments, and Histories

Belnap developed BST as a formal framework to model an indeterminist world, making a significant step toward accommodating modern physics by adding resources to model spatial variation to the branching time framework of Kripke and Prior. The intuitive interpretation of our theory of possible ancestry presupposes a similar intuition of indeterminism.¹⁷ Hence the question arises of how its ontology can be embedded in a branching time structure.

The task is not trivial, because typically neither a structure of possibilia nor any of its restrictions to an admissible set will have the requisite property of having no downward branches. A typical family tree is not a tree in the branching-time sense, and the same goes for any typical structure of possibilia. (If fission were the only means of reproduction, a structure of possibilia need indeed not have downward branches. But they will appear as soon as there can be reproductive acts that require more than one participant.)

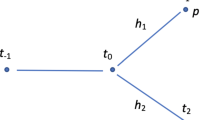
So, how can we construct a branching time structure from the means at our disposal? Here, the admissible sets clearly play a central role. We will motivate our construction by a look at how the possibilities they model correspond to elements of the branching time structure that is implicit in our intended interpretation. Facing the future, it is obvious that from the possibility modeled by an admissible set there typically will sprout many different historical paths towards later possible situations, depending on which possible children (modeled by direct descendants in terms of $\prec$) of some of the inhabitants of that possibility come into existence. Facing the past, we encounter a small surprise because there may also be a plurality of paths branches leading up to the possibility modeled by an admissible set. E.g., towards the admissible set containing Eve, Adam, and their two sons Abel and Cain, there is one path via the admissible set {Eve, Adam, Abel} and a second path via the admissible set {Eve, Adam, Cain}, because the corresponding structure of possibilia does not determine whether Cain or Abel was born first. As the structure of admissible sets as ordered by inclusion may have downward branches, chains of admissible sets are unfit to model (possible) histories or parts thereof, and our admissible sets turn out to be too coarse-grained to correspond to the nodes of a branching time tree, which we might call (possible) moments.

Nonetheless, it should also be evident from the biblical examples that there is a close connection between admissible sets and moments. We can understand an admissible set as the (possible) state the world is in at some a moment, a state that in many cases will be shared by a plurality of distinct moments. This observation puts us in a position to construct (possible) moments and (possible) histories. We will say that a moment is individuated not only by its state, but also by the chain of states that it is reached by. In our example we can thus pry apart the moment where Eve, Adam, Abel, and Cain belong to the state and Abel is firstborn and the distinct moment where the same family of four belongs to the state but Cain is firstborn. Here is our construction:

A set of elements from D is a (possible) state iff it is an admissible set.

Note that {} is a state; we call it the empty state. The set of all states is partially ordered by inclusion, with the empty state being smaller than all other states.

A set of states is a (possible) moment iff it is a maximal chain¹⁸ in the set of all states as ordered by inclusion from the empty state {} to some state.

Note that {{}} is a moment. The set of all moments is partially ordered by inclusion, which plays the role that the relation of accessibility has in a branching time structure. As it precedes all other moments in terms of this relation, {{}} may aptly be called the first moment.

A set of moments is a (possible) history iff it is a maximal chain in the set of all moments as ordered by inclusion from the first moment {{}} to some moment.

Note that {{{}}} is a history—it accounts for the possibility that live evolves never. All histories overlap—in fact their union forms a tree-like structure with a single root in the first moment. Thus we have found a way of embedding our ancestral alternatives in the tree structure of indeterminist time.

***

By now we have come as near in our analogy to the structure of BST as we will get. In the next section we will deal with a phenomenon that resists treatment in this framework.

5 Ontological Competition

In the past sections we have looked at structures of possibilia mainly under the aspect of co-possibility, investigating possible collections of possible beings that can (or even must) be grouped together. We now turn to the contradictory aspect of incompatibility.

Let us have a look at three examples from the realm that is to provide the material interpretation to our formal theory, which we will consider as test cases for its power to model phenomena of incompatibility.

• (Example 1) A human couple, Elizabeth and Peter, actually have a lot of children and they could have had even more children, or a distinct lot of possible children, or another lot, or ... However, there clearly is an upper limit to the number of children they could have had, determined (roughly speaking) by the minimum length of a pregnancy and the maximum duration a woman can bear children. So, the number of the possible children of Elizabeth and Peter exceeds the upper limit of children they could have had by far. Any collection of possible children of a number that exceeds this upper limit is not compatible.

• (Example 2) Two possible mammals, A and B, are such that they not only have the same ancestors but result from the very same sperm and egg, while their dates of conception are a few seconds apart. For the scope of this example we understand beings of the kind of A and B to be individuated by their time of conception (among other things). Hence we must see A and B as incompatible individuals.

• (Example 3) A cell of a kind that reproduces by fission actually splits into the two daughter cells $\mathrm{{D}}_{1}$ and $\mathrm{{D}}_{2}$, but it could have split in a different way (e.g., distributing its material in a different way) that would have led to the two possible daughter cells $\mathrm{{E}}_{1}$ and $\mathrm{{E}}_{2}$. But every cell can split only once—though its daughter cells may split in turn, it is no longer there to split up again. Hence $\mathrm{{D}}_{1}$ is incompatible with $\mathrm{{E}}_{1},\mathrm{{D}}_{1}$ is incompatible with $\mathrm{{E}}_{2}$, and so on. In fact, as there plausibly are many possibilities for a cell to split up, there will be a large plurality of incompatible pairs of possible daughter cells for each cell.

These examples illustrate three general observations that are relevant to the task of modeling phenomena of incompatibility. Firstly, incompatibility need not be a two-place relation. It may well be that each two of the many possible children of Elizabeth and Peter of (Example 1) are compatible, but clearly no collection of a hundred of them is a population of any possibility.¹⁹ Robert Brandom makes a corresponding observation with respect to sentences or claims: “the claim that the piece of fruit in my hand is a blackberry is incompatible with the two claims that it is red and that it is ripe, though not with either of them individually—in keeping with the childhood slogan that blackberries are red when they’re green.”²⁰

Secondly, incompatibility comes in two flavors, extrinsic and intrinsic. The decisive question is this: Is the incompatibility due to some external factor or is it founded in the possible objects themselves? A clear case of extrinsic incompatibility is provided by (Example 1), because there is nothing in the possible children themselves that explains their joint incompatibility, which rather rests on those external factors determining the maximum number of children a woman can bear. A clear case of intrinsic incompatibility can be found in (Example 3), because it is due to the very nature of some possible daughter cells that they are not possible siblings and hence are incompatible. (Example 2) might be less easy to classify, but the strict reading of the principle of the necessity of origin we adopt for its scope would tip the scales in favor of construing the time of conception as an internal factor, because of its individuating force.

Thirdly, all three examples taken together provide ample evidence for the importance of the metaphysical phenomenon of ontological competition: Some possible individuals can come to be only by cutting off the chance of existence for others (of course, they do not literally struggle). We think that this phenomenon has not received the attention it deserves. So, let us get on with modeling it in our formal ontology!

Extrinsic incompatibility is easily accommodated in the general framework laid out in Sect. 3, at least if we decide to invest species membership into a model. We need only add to $\Lambda$ a species-relative cardinality constraint on the number of direct descendants of any pair of possible parents, and there will be only possibilities that conform to the intuitions behind (Example 1).

With intrinsic incompatibility, however, we reach the limits of what our theory of possible ancestry in its current state can achieve. There just is no natural way to model those cases of incompatibility that are due to the nature of the incompatible possibilia themselves by any general statements that act as constraints on either the global or the local level.²¹ In the scenario of (Example 3), what leads to the incompatibility of the possible cells $\mathrm{{D}}_{1}$ or $\mathrm{{E}}_{1}$ is no property that they might share with some other possible cells, but their individual nature.

How are we to enhance our theory of possible ancestry to give it the power to model intrinsic incompatibility?

There is the somewhat brutal way of adding an arbitrary filter that admits only some of our admissible sets: To the structure of possibilia $\langle \mathrm{{D}}, \prec \rangle$ and the admissible sets defined in terms of it we add P, which is a subset of the set of admissible sets. No element of P may contain any collection of possibilia that according to our intended interpretation are intrinsically incompatible. We obtain the theory TPA$^\mathrm{{carve+filter}}$ from TPA$^\mathrm{{{carve}}}$ by adding to the requirement $\Lambda$ the postulate that a set is only admissible if it is an element of P. In the terms of Sect. 1, any such theory would be a hybrid between elegant ersatzism (“carve”) and primitivism (“filter”). By taking the brutal way we thus would be in danger of losing something of what we have gained so far.

We are optimistic that there also is a somewhat more subtle way.²² Inspired by the work of Brandom in incompatibility semantics, we add to our framework an incompatibility partition INC. It is a subset of the powerset of the domain D and satisfies the single postulate of persistence: Any superset of a set in INC is also in INC. The intuitive reason for the property of persistence is that you just cannot remove an incompatibility between some objects by adding further objects.²³ Now we add the local requirement that no subset of an admissible set may be in INC. What we thus acquire is a tool to model intrinsic incompatibility— but a tool that had to be added to our structure of possibilia because we have found no way of carving it from it.

6 Back To Branching Space-Time: General Relativity

We have moved some distance away from the structures of BST that inspired our theory of possible ancestry in the beginning. But in fact, apart from its intended literal interpretation, this postscript might be read as a little parable on a certain aspect of BST. Investing a suitable incompatibility partition for possible point events may be one way to solve the problem posed to BST by the so-called trousers worlds of general relativity theory (GTR).²⁴

Belnap’s theory BST reduces the incompatibility of two possible point events to their not having a common upper bound. But there is a price to be paid for this elegance, because due to this reduction BST cannot distinguish between the basic scenario of indeterminism, where a history after some time branches into two histories, and what happens in the single history of a trousers world of GTR, where (roughly speaking) a connected space after some time splits up into two disconnected spaces.²⁵So one might add another primitive to the theory, an incompatibility partition INC. Now the required distinctions can be made:

A collection of possible point events is incompatible iff the set formed by them is in INC.

A collection of possible point events is merely spatially disconnected (towards the future) iff the set formed by them has no upper bound but is not in INC.²⁶

We have, however, to tread very carefully. For note that Belnap’s reduction of incompatibility to being without an upper bound is reached via his definition of a history: In BST, first a history is defined as a maximally directed set—a set such that each two of its elements have an upper bound in it—and then compatibility is defined as belonging to a single history. To implement our idea for a solution of the trousers world problem we thus have to change the definition of a history. Upward directedness will no longer do because a history that is a trousers world for some of its points does not include an upper bound. On this approach, a new definition of “history” would resemble the one we have given for admissible sets in the context of the theory of possible ancestry:

A subset of Our World is a history iff it is downward closed with respect to the causal order and none of its subsets is in INC.

We conjecture that with an incompatibility partition as a new primitive and this revised definition of a history, a theory can be constructed in a way similar to BST that has a broader range of application when it comes to GTR. This would be a comparatively simple approach, though it admittedly lacks the elegance of the original BST style of dealing with histories. Perhaps, one day, the approach might turn out useful for discrete models of space-time which take quantum gravity into account. But as our proposal for a solution to the trousers world problem does not consist merely in an addition to Belnap’s theory, but in changing one of its most basic ingredients, there remains much work to be done in the future.