Abstract
Guarded Kleene Algebra with Tests (GKAT) is a fragment of Kleene Algebra with Tests (KAT) that was recently introduced to reason efficiently about imperative programs. In contrast to KAT, GKAT does not have an algebraic axiomatization, but relies on an analogue of Salomaa’s axiomatization of Kleene Algebra. In this paper, we present an algebraic axiomatization and prove two completeness results for a large fragment of GKAT consisting of skip-free programs.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Kleene algebra with tests (KAT) [26] is a logic for reasoning about semantics and equivalence of simple imperative programs. It extends Kleene Algebra (KA) with Boolean control flow, which enables encoding of conditionals and while loops.
KAT has been applied to verification tasks. For example, it was used in proof-carrying Java programs [24], in compiler optimization [28], and file systems [8]. More recently, KAT was used for reasoning about packet-switched networks, serving as a core to NetKAT [4] and Probabilistic NetKAT [12, 43].
The success of KAT in networking is partly due to its dual nature: it can be used to both specify and verify network properties. Moreover, the implementations of NetKAT and ProbNetKAT were surprisingly competitive with state-of-the-art tools [13, 44]. Part of the surprise with the efficiency of these implementations is that the decision problem for equivalence in both KAT and NetKAT is PSPACE-complete [29, 4]. Further investigations [42] revealed that the tasks performed in NetKAT only make use of a fragment of KAT. It turns out that the difficulty of deciding equivalence in KAT can largely be attributed to the non-deterministic nature of KAT programs. If one restricts to KAT programs that operate deterministically with respect to Boolean control flow, the associated decision problem is almost linear. This fragment of KAT was first identified in [30] and further explored as guarded Kleene algebra with tests (GKAT) [42].
The study in [42] proved that the decision problem for GKAT programs is almost linear, and proposed an axiomatization of equivalence. However, the axiomatization suffered from a serious drawback: it included a powerful uniqueness of solutions axiom (UA), which greatly encumbers algebraic reasoning in practice. In order to use (UA) to show that a pair of programs are equivalent, one needs to find a system of equations that they both satisfy. Even more worryingly, the axiomatization contained a fixed-point axiom with a side condition reminiscent of Salomaa’s axiomatization for regular expressions, which is known to be non-algebraic and impair the use of the axiomatic reasoning in context (as substitution of atomic programs is not sound anymore). The authors of [42] left as open questions whether (UA) can be derived from the other GKAT axioms and whether the non-algebraic side condition can be removed. Despite the attention GKAT has received in recent literature [40, 48, 41], these questions remain open.
In the present work, we offer a partial answer to the questions posed in [42]. We show that proving the validity of an equivalence in GKAT does not require (UA) if the pair of programs in question are of a particular form, what we call skip-free. This fragment of GKAT is expressive enough to capture a large class of programs, and it also provides a better basis for algebraic reasoning: we show that the side condition of the fixed-point axiom can be removed. Our inspiration to look at this fragment came from recent work of Grabmayer and Fokkink’s on the axiomatization of 1-free star expressions modulo bisimulation [15, 14], an important stepping stone to solving a decades-open problem posed by Milner [33].
In a nutshell, our contribution is to identify a large fragment of GKAT, what we call the skip-free fragment, that admits an algebraic axiomatization. We axiomatize both bisimilarity and language semantics and provide two completeness proofs. The first proves completeness of skip-free GKAT modulo bisimulation [40], via a reduction to completeness of Grabmayer and Fokkink’s system [15]. The second proves completeness of skip-free GKAT w.r.t. language semantics via a reduction to skip-free GKAT modulo bisimulation. We also show that equivalence proofs of skip-free GKAT expressions (for both semantics) embed in full GKAT.
The next section contains an introduction to GKAT and an overview of the open problems we tackle in the technical sections of the paper.
2 Overview
In this section we provide an overview of our results. We start with a motivating example of two imperative programs to discuss program equivalence as a verification technology. We then show how GKAT can be used to solve this problem and explore the open questions that we tackle in this paper.
Equivalence for Verification. In the game Fizz! Buzz! [36], players sit in a circle taking turns counting up from one. Instead of saying any number that is a multiple of \(3\), players must say “fizz”, and multiples of \(5\) are replaced with “buzz”. If the number is a multiple both \(3\) and \(5\), the player must say “fizz buzz”.
Imagine you are asked in a job interview to write a program that prints out the first \(100\) rounds of a perfect game of Fizz! Buzz!. You write the function
 as given in Figure 1(i). Thinking about the interview later that day, you look up a solution, and you find
as given in Figure 1(i). Thinking about the interview later that day, you look up a solution, and you find
 , depicted in Figure 1(ii). You suspect that
, depicted in Figure 1(ii). You suspect that
 should do the same thing as
should do the same thing as
 , and after thinking it over for a few minutes, you realize your program could be transformed into the reference solution by a series of transformations that do not change its semantics:
, and after thinking it over for a few minutes, you realize your program could be transformed into the reference solution by a series of transformations that do not change its semantics:
-
1.
Place the common action
 at the end of the loop.
at the end of the loop. -
2.
Replace
 with
with
 and swap
and swap
 with
with
 .
. -
3.
Merge the nested branches of
 and
and
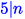 into one.
into one.
Feeling somewhat more reassured, you ponder the three steps above. It seems like their validity is independent of the actual tests and actions performed by the code; for example, swapping the branches of an if - then - else - block while negating the test should be valid under any circumstances. This raises the question: is there a family of primitive transformations that can be used to derive valid ways of rearranging imperative programs? Furthermore, is there an algorithm to decide whether two programs are equivalent under these laws?
Enter \(\boldsymbol{\textsf{GKAT}}\). Guarded Kleene Algebra with Tests (GKAT) [42] has been proposed as a way of answering the questions above. Expressions in the language of GKAT model skeletons of imperative programs, where the exact meaning of tests and actions is abstracted. The laws of GKAT correspond to program transformations that are valid regardless of the semantics of tests and actions.
Formally, GKAT expressions are captured by a two-level grammar, generated by a finite set of tests T and a finite set of actions \(\varSigma \), as follows:
\(\textsf{BExp}\) is the set of Boolean expressions, built from 0 (
 ), 1 (
), 1 (
 ), and primitive tests from T, and composed using \(\vee \) (
), and primitive tests from T, and composed using \(\vee \) (
 ), \(\wedge \) (
), \(\wedge \) (
 ) and
) and
 (
(
 ). \(\textsf{GExp}\) is the set of GKAT expressions, built from tests (assert statements) and primitive actions \(p \in \varSigma \). Here, \(e +_b f\) is a condensed way of writing
). \(\textsf{GExp}\) is the set of GKAT expressions, built from tests (assert statements) and primitive actions \(p \in \varSigma \). Here, \(e +_b f\) is a condensed way of writing
 , and \(e^{(b)}\) is shorthand for
, and \(e^{(b)}\) is shorthand for
 ; the operator \(\cdot \) models sequential composition. By convention, the sequence operator \(\cdot \) takes precedence over the operator \(+_b\).
; the operator \(\cdot \) models sequential composition. By convention, the sequence operator \(\cdot \) takes precedence over the operator \(+_b\).
Example 2.1
Abbreviating statements of the form
 by simply writing
by simply writing
 , Figure 1(i) can be rendered as the GKAT expression
, Figure 1(i) can be rendered as the GKAT expression

Similarly, the program in Figure 1(ii) gives the GKAT expression

Semantics. A moment ago, we stated that GKAT equivalences are intended to witness program equivalence, regardless of how primitive tests and actions are interpreted. We make this more precise by recalling the relational semantics of GKAT programs [42].Footnote 1 The intuition behind this semantics is that if the possible states of the machine being programmed are modelled by some set S, then tests are predicates on S (comprised of all states where the test succeeds), and actions are relations on S (encoding the changes in state affected by the action).
Definition 2.2
([42]). A (relational) interpretation is a triple \(\sigma = (S, \textsf{eval}, \textsf{sat})\) where S is a set, \(\textsf{eval}: \varSigma \rightarrow \mathcal {P}(S \times S)\) and \(\textsf{sat}: T \rightarrow \mathcal {P}(S)\). Each relational interpretation \(\sigma \) gives rise to a semantics \(\llbracket -\rrbracket _\sigma : \textsf{GExp}\rightarrow \mathcal {P}(S \times S)\), as follows:
Here we use \(\circ \) for relation composition and \({}^*\) for reflexive transitive closure.
Remark 2.3
If \(\textsf{eval}(p)\) is a partial function for every \(p \in \varSigma \), then so is \(\llbracket e\rrbracket _\sigma \) for each e. The above therefore also yields a semantics in terms of partial functions.
The relation \(\llbracket e\rrbracket _\sigma \) contains the possible pairs of start and end states of the program e. For instance, the input-output relation of \(\llbracket e +_b f\rrbracket \) consists of the pairs in \(\llbracket e\rrbracket _\sigma \) (resp. \(\llbracket f\rrbracket _\sigma \)) where the start state satisfies b (resp. violates b).
Example 2.4
We could model the states of the machine running Fizz! Buzz! as pairs \((m, \ell )\), where m is the current value of the counter n, and \(\ell \) is a list of words printed so far; the accompanying maps \(\textsf{sat}\) and \(\textsf{eval}\) are given by:

For instance, the interpretation of
 connects states of the form \((m, \ell )\) to states of the form \((m + 1, \ell )\)—incrementing the counter by one, and leaving the output unchanged. Similarly,
connects states of the form \((m, \ell )\) to states of the form \((m + 1, \ell )\)—incrementing the counter by one, and leaving the output unchanged. Similarly,
 statements append the given string to the output.
statements append the given string to the output.
On the one hand, this parameterized semantics shows that programs in the GKAT syntax can be given a semantics that corresponds to the intended meaning of their actions and tests. On the other hand, it allows us to quantify over all possible interpretations, and thus abstract from the meaning of the primitives.
As it happens, two expressions have the same relational semantics under any interpretation if and only if they have the same language semantics [42], i.e., in terms of languages of guarded strings as used in KAT [26]. Since equivalence under the language semantics is efficiently decidable [42], so is equivalence under all relational interpretations. The decision procedure in [42] uses bisimulation and known results from automata theory. These techniques are good for mechanization but hide the algebraic structure of programs that plays. To expose this, algebraic laws of GKAT program equivalence were studied.
Program transformations. GKAT programs are (generalized) regular expressions, which are intuitive to reason about and for which many syntactic equivalences are known and explored. In [42], a set of sound axioms \(e \equiv f\) such that \(\llbracket e\rrbracket _\sigma = \llbracket f\rrbracket _\sigma \) for all \(\sigma \) was proposed, and it was shown that these can be used to prove a number of useful facts about programs. For instance, the following two equivalences are axioms of GKAT:

The first of these says that common code at the tail end of branches can be factored out, while the second says that the code in branches of a conditional can be swapped, as long as we negate the test. Returning to our running example, if we apply the first law to (1) three times (once for each guarded choice),

Finally, we can apply \((e +_b f) +_c (g +_b h) \equiv e +_{b \wedge c} (f +_c (g +_b h))\), which is provable from the axioms of GKAT, to transform (3) into (2).
Being able to transform one GKAT program into another using the axioms of GKAT is useful, but the question arises: do the axioms capture all equivalences that hold? More specifically, are the axioms of GKAT powerful enough to prove that \(e \equiv f\) whenever \(\llbracket e\rrbracket _\sigma = \llbracket f\rrbracket _\sigma \) holds for all \(\sigma \)?
In [42], a partial answer to the above question is provided: if we extend the laws of GKAT with the uniqueness axiom (UA), then the resulting set of axioms is sound and complete w.r.t. the language semantics. The problem with this is that (UA) is not really a single axiom, but rather an axiom scheme, which makes both its presentation and application somewhat unwieldy.
To properly introduce (UA), we need the following notion.
Definition 2.5
A left-affine system is defined by expressions \(e_{11}, \dots , e_{nn} \in \textsf{GExp}\) and \(f_1, \dots , f_n \in \textsf{GExp}\), along with tests \(b_{11}, \dots , b_{nn} \in \textsf{BExp}\). A sequence of expressions \(s_1, \dots , s_n \in \textsf{GExp}\) is said to be a solution to this system if
Here, the operations \(+_{b_{ij}}\) associate to the right.
A left-affine system is called guarded if no \(e_{ij}\) that appears in the system successfully terminates after reading an atomic test. In other words, each coefficient denotes a productive program, meaning it must execute some action before successfully terminating—we refer to Section 7.3 for more details.
Stated fully, (UA) says that if expressions \(s_1, \dots , s_n\) and \(t_1, \dots , t_n\) are solutions to the same guarded left-affine system, then \(s_i \equiv t_i\) for \(1 \le i \le n\).
On top of the infinitary nature of (UA), the side condition demanding guardedness prevents purely algebraic reasoning: replacing action symbols in a valid GKAT equation with arbitrary GKAT expressions might yield an invalid equation! The situation is analogous to the empty word property used by Salomaa [38] to axiomatize equivalence of regular expressions. The side condition of guardedness appearing in (UA) is inherited from another axiom of GKAT, the fixed-point axiom, which in essence is the unary version of this axiom scheme and explicitly defines the solution of one guarded left-affine equation as a while loop.
Remark 2.6
Part of the problem of the uniqueness axiom is that the case for general n does not seem to follow easily from the case where \(n = 1\). The problem here is that, unlike the analogous situation for Kleene algebra, there is no general method to transform a left-affine system with \(n+1\) unknowns into one with n unknowns [30], even if this is possible in certain cases [42].
The open questions. We are motivated by two open questions from [42]:
-
First, can the uniqueness axiom be eliminated? The other axioms of GKAT contain the instantiation of (UA) for \(n = 1\), which has so far been sufficient in all handwritten proofs of equivalence that we know. Yet (UA) seems to be necessary in both known completeness proofs.
-
Second, can we eliminate the guardedness side condition? Kozen [25] showed that Salomaa’s axiomatization is subsumed by a set of axioms that together imply existence and uniqueness of least solutions to systems of equations, but this approach has not yet borne fruit in GKAT.
This paper. Our main contribution is to show that, in a particular fragment of GKAT, both questions can be answered in the positive (see Figure 2).
Axioms for language semantics skip-free GKAT (in addition to Boolean algebra axioms for tests, see Fig. 3). If the axiom marked \(\dagger \) is omitted the above axiomatize a finer semantics, bisimilarity.
In Section 3, we present what we call the skip-free fragment of GKAT, consisting of programs that do not contain assert statements in the body (other than
 ); in other words, Boolean statements are restricted to control statements. For this fragment, we show that the axiom scheme (UA) can be avoided entirely. In fact, this is true for language semantics (as first introduced in [42]) as well as for the bisimulation semantics of [40].
); in other words, Boolean statements are restricted to control statements. For this fragment, we show that the axiom scheme (UA) can be avoided entirely. In fact, this is true for language semantics (as first introduced in [42]) as well as for the bisimulation semantics of [40].
In Section 4, we provide a bridge to a recent result in process algebra. In the 80s, Milner offered an alternative interpretation of regular expressions [33], as what he called star behaviours. Based on work of Salomaa from the 1960s [38], Milner proposed a sound axiomatization of the algebra of star behaviours, but left completeness an open problem. After 38 years, it was recently solved by Clemens Grabmayer [14] following up on his joint work with Wan Fokkink showing that a suitable restriction of Milner’s axioms is complete for the one-free fragment of regular expressions modulo bisimulation [15]. We leverage their work with an interesting embedding of skip-free GKAT into the one-free regular expressions.
This leads to two completeness results. In Section 5, we start by focusing on the bisimulation semantics of the skip-free fragment, and then in Section 6 expand our argument to its language semantics. More precisely, we first provide a reduction of the completeness of skip-free GKAT up to bisimulation to the completeness of Grabmayer and Fokkink’s 1-free regular expressions modulo bisimulation [15]. We then provide a reduction of the completeness of skip-free GKAT modulo language semantics to the completeness of skip-free GKAT modulo bisimulation via a technique inspired by the tree pruning approach of [40].
Finally, in Section 7, we connect our semantics of skip-free GKAT expressions to the established semantics of full GKAT. We also connect the syntactic proofs between skip-free GKAT expressions in both our axiomatization and the existing one. In conjunction with the results of Sections 5 and 6, the results in Section 7 make a significant step towards answering the question of whether the axioms of GKAT give a complete description of program equivalence, in the positive.
Proofs appear in the full version [22].
3 Introducing Skip-free GKAT
The axiom scheme (UA) can be avoided entirely in a certain fragment of GKAT, both for determining bisimilarity and language equivalence. In this section, we give a formal description of the expressions in this fragment and their semantics.
Skip-free expressions. The fragment of GKAT in focus is the one that excludes sub-programs that may accept immediately, without performing any action. Since these programs can be “skipped” under certain conditions, we call the fragment that avoids them skip-free. Among others, it prohibits sub-programs of the form
 for
for
 , but also
, but also
 , which is equivalent to
, which is equivalent to
 .
.
Definition 3.1
Given a set \(\varSigma \) of atomic actions, the set \(\textsf{GExp}^-\) of skip-free GKAT expressions is given by the grammar
where \(b\) ranges over the Boolean algebra expressions \(\textsf{BExp}\).
Unlike full GKAT, in skip-free GKAT the loop construct is treated as a binary operation, analogous to Kleene’s original star operation [23], which was also binary. This helps us avoid loops of the form \(e^{(b)}\), which can be skipped when b does not hold. The expression \(e_1 ^{(b)} e_2\) corresponds to \(e_1 ^{(b)} \cdot e_2\) in GKAT.
Example 3.2
Using the same notational shorthand as in Example 2.1, the block of code in Figure 1(ii) can be cast as the skip-free GKAT expression

Note how we use a skip-free loop of the form \(e_1 {\mathbin {^{(b)}}} e_2\) instead of the looping construct \(e_1^{(b)}\) before concatenating with \(e_2\), as was done for GKAT.
3.1 Skip-free Semantics
There are three natural ways to interpret skip-free GKAT expressions: as automata, as behaviours, and as languages.Footnote 2 After a short note on Boolean algebra, we shall begin with the automaton interpretation, also known as the small-step semantics, from which the other two can be derived.
The axioms of Boolean algebra [18].
Boolean algebra. To properly present our automata, we need to introduce one more notion. Boolean expressions \(\textsf{BExp}\) are a syntax for elements of a Boolean algebra, an algebraic structure satisfying the equations in Fig. 3. When a Boolean algebra is freely generated from a finite set of basic tests (T in the case of \(\textsf{BExp}\)), it has a finite set \(\textsf{At}\) of nonzero minimal elements called atoms. Atoms are in one-to-one correspondence with sets of tests, and the Boolean algebra is isomorphic to \(\mathcal P(\textsf{At})\), the sets of subsets of \(\textsf{At}\), equipped with \({\vee } = {\cup }\), \({\wedge } = {\cap }\), and \(\overline{(-)} = \textsf{At}\setminus (-)\). In the context of programming, one can think of an atom as a complete description of the machine state, saying which tests are true and which are false. We will denote atoms by the Greek letters \(\alpha \) and \(\beta \), sometimes with indices. Given a Boolean expression \(b\in \textsf{BExp}\) and an atom \(\alpha \in \textsf{At}\) we say that \(\alpha \) entails b, written \(\alpha \le b\), whenever \(\overline{\alpha }\vee b = 1\), or equivalently \(\alpha \vee b = b\).
Automata. Throughout the paper, we use the notation \(\bullet + S\) where S is a set and \(\bullet \) is a symbol to denote the disjoint union (coproduct) of \(\{ \bullet \}\) and S.
The small-step semantics of a skip-free GKAT expression uses a special type of deterministic automaton. A skip-free automaton is a pair (X, h), where X is a set of states and \(h:X \rightarrow (\bot + \varSigma \times (\checkmark + X))^\textsf{At}\) is a transition structure. At every \(x \in X\) and for any \(\alpha \in \textsf{At}\), one of three things can happen:
-
1.
\(h(x)(\alpha ) = (p, y)\), which we write as
 , means the state x under \(\alpha \) makes a transition to a new state y, after performing the action p;
, means the state x under \(\alpha \) makes a transition to a new state y, after performing the action p; -
2.
\(h(x)(\alpha ) = (p, \checkmark )\), which we write
 , means the state x under \(\alpha \) successfully terminates with action p;
, means the state x under \(\alpha \) successfully terminates with action p; -
3.
\(h(x)(\alpha ) = \bot \), which we write \(x \downarrow \alpha \), means the state x under \(\alpha \) terminates with failure. Often we will leave these outputs implicit.
Definition 3.3
(Automaton of expressions). We equip the set \(\textsf{GExp}^-\) of all skip-free GKAT expressions with an automaton structure \((\textsf{GExp}^-, \partial )\) given in Fig. 4, representing step-by-step execution. Given \(e \in \textsf{GExp}^-\), we denote the set of states reachable from \(e\) by \(\langle e\rangle \) and call this the small-step semantics of \(e\).
The small-step semantics of skip-free GKAT expressions is inspired by Brzozowski’s derivatives [7], which provide an automata-theoretic description of the step-by-step execution of a regular expression. Our first lemma tells us that, like regular expressions, skip-free GKAT expressions correspond to finite automata.
Lemma 3.4
For any \(e \in \textsf{GExp}^-\), \(\langle e\rangle \) has finitely many states.
Example 3.5
The automaton that arises from the program
 is below, with
is below, with
 . The expression \(e\) is the same as in Example 3.2, \(e_1\) is the same as e but without the action
. The expression \(e\) is the same as in Example 3.2, \(e_1\) is the same as e but without the action
 in front, and
in front, and
 . We also adopt the convention of writing
. We also adopt the convention of writing
 where \(b \in \textsf{BExp}\) to represent all transitions
where \(b \in \textsf{BExp}\) to represent all transitions
 where \(\alpha \le b\).
where \(\alpha \le b\).

The automaton interpretation of a skip-free GKAT expression (its small-step semantics) provides an intuitive visual depiction of the details of its execution. This is a useful view on the operational semantics of expressions, but sometimes one might want to have a more precise description of the global behaviour of the program. The remaining two interpretations of skip-free GKAT expressions aim to capture two denotational semantics of expressions: one finer, bisimilarity, that makes a distinction on the branching created by how its states respond to atomic tests, which actions can be performed, and when successful termination and crashes occur; another coarser, language semantics, that assigns a language of traces to each expression capturing all sequences of actions that lead to successful termination. The key difference between these two semantics is their ability to distinguish programs that crash early in the execution versus programs that crash later—this is evident in the axiomatizations of both semantics. We start by presenting the language semantics as this is the more traditional one associated with GKAT (and regular) expressions.
Language semantics. Formally, a (skip-free) guarded trace is a nonempty string of the form \(\alpha _1p_1 \cdots \alpha _n p_n\), where each \(\alpha _i \in \textsf{At}\) and \(p_i \in \varSigma \). Intuitively, each \(\alpha _i\) captures the state of program variables needed to execute program action \(p_i\) and the execution of each \(p_i\) except the last yields a new program state \(\alpha _{i+1}\). A skip-free guarded language is a set of guarded traces.
Skip-free guarded languages should be thought of as sets of strings denoting successfully terminating computations.
Definition 3.6
(Language acceptance). In a skip-free automaton \((X, h)\) with a state \(x \in X\), the language accepted by \(x\) is the skip-free guarded language

If \((X, h)\) is clear from context, we will simply write \(\mathcal {L}(x)\) instead of \(\mathcal {L}(x, (X, h))\). If \(\mathcal {L}(x) = \mathcal {L}(y)\), we write \(x \sim _\mathcal {L}y\) and say that \(x\) and \(y\) are language equivalent.
Each skip-free GKAT expression is a state in the automaton of expressions (Definition 3.3) and therefore accepts a language. The language accepted by a skip-free GKAT expression is the set of successful runs of the program it denotes. Analogously to \(\textsf {GKAT} \), we can describe this language inductively.
Lemma 3.7
Given an expression \(e\in \textsf{GExp}^-\), the language accepted by e in \((\textsf{GExp}^-, \partial )\), i.e., \(\mathcal {L}(e) = \mathcal {L}(e, (\textsf{GExp}^-, \partial ))\) can be characterized as follows:
Here, we write \(b L = \{\alpha p w \in L \mid \alpha \le b\}\) and \(L_1 \cdot L_2 = \{ wx : w \in L_1, x \in L_2 \} \), while \(L^0 = \{ \epsilon \}\) (where \(\epsilon \) denotes the empty word) and \(L^{n+1} = L \cdot L^n\).
Lemma 3.7 provides a way of computing the language of an expression e without having to generate the automaton for e.
Bisimulation semantics. Another, finer, notion of equivalence that we can associate with skip-free automata is bisimilarity.
Definition 3.8
Given skip-free automata \((X, h)\) and \((Y, k)\), a bisimulation is a relation \(R \subseteq X \times Y\) such that for any \(x \mathrel {R} y\), \(\alpha \in \textsf{At}\) and \(p \in \varSigma \):
-
1.
\(x \downarrow \alpha \) if and only if \(y \downarrow \alpha \),
-
2.
 if and only if
if and only if
 , and
, and -
3.
for any \(x' \mathrel {R} y'\),
 if and only if
if and only if
 .
.
We call \(x\) and \(y\) bisimilar if \(x \mathrel {R} y\) for some bisimulation R and write
 .
.
In a fixed skip-free automaton \((X, h)\), we define
 to be the largest bisimulation, called bisimilarity. This is an equivalence relation and a bisimulation.Footnote 3 The bisimilarity equivalence class of a state is often called its behaviour.
to be the largest bisimulation, called bisimilarity. This is an equivalence relation and a bisimulation.Footnote 3 The bisimilarity equivalence class of a state is often called its behaviour.
Example 3.9
In the automaton below, \(x_1\) and \(x_2\) are bisimilar. This is witnessed by the bisimulation \(\{(x_1, x_2), (x_2, x_2)\}\).

We can also use bisimulations to witness language equivalence.
Lemma 3.10
Let \(e_1, e_2 \in \textsf{GExp}^-\). If
 , then \(\mathcal {L}(e_1) = \mathcal {L}(e_2)\).
, then \(\mathcal {L}(e_1) = \mathcal {L}(e_2)\).
The converse of Lemma 3.10 is not true. Consider, for example, the program \(p^{(1)}q\) that repeats the atomic action \(p \in \varSigma \) indefinitely, never reaching \(q\). Since
we know that \(p^{(1)}q \sim _\mathcal {L}0\). But \(p^{(1)}q\) and \(0\) are not bisimilar, since Fig. 4 tells us that
 and \(0 \downarrow \alpha \), which together refute Definition 3.8.1.
and \(0 \downarrow \alpha \), which together refute Definition 3.8.1.
3.2 Axioms
Next, we give an inference system for bisimilarity and language equivalence consisting of equations and equational inference rules. The axioms of skip-free GKAT are given in Fig. 2. They include the equation (\(\dagger \)), which says that early deadlock is the same as late deadlock. This is sound with respect to the language interpretation, meaning that (\(\dagger \)) is true if \(x\) is replaced with a skip-free guarded language, but it is not sound with respect to the bisimulation semantics. For example, the expressions \(p \cdot 0\) and \(0\) are not bisimilar for any \(p \in \varSigma \). Interestingly, this is the only axiomatic difference between bisimilarity and language equivalence.
Remark 3.11
The underlying logical structure of our inference systems is equational logic [5], meaning that provable equivalence is an equivalence relation that is preserved by the algebraic operations.
Given expressions \(e_1, e_2 \in \textsf{GExp}^-\), we write \(e_1 \equiv _\dagger e_2\) and say that \(e_1\) and \(e_2\) are \(\equiv _\dagger \)-equivalent if the equation \(e_1 = e_2\) can be derived from the axioms in Fig. 2 without the axiom marked (\(\dagger \)). We write \(e_1 \equiv e_2\) and say that \(e_1\) and \(e_2\) are \(\equiv \)-equivalent if \(e_1 = e_2\) can be derived from the whole set of axioms in Fig. 2.
The axioms in Fig. 2 are sound with respect to the respective semantics they axiomatize. The only axiom that is not sound w.r.t. bisimilarity is \(x\cdot 0\equiv 0\), as this would relate automata with different behaviours (x may permit some action to be performed, and this is observable in the bisimulation).
Theorem 3.12
(Soundness). For any \(e_1, e_2 \in \textsf{GExp}^-\),
-
1.
If \(e_1 \equiv _\dagger e_2\), then
 .
. -
2.
If \(e_1 \equiv e_2\), then \(e_1 \sim _\mathcal {L}e_2\).
We consider the next two results, which are jointly converse to Theorem 3.12, to be the main theorems of this paper. They state that the axioms in Fig. 2 are complete for bisimilarity and language equivalence respectively, i.e., they describe a complete set of program transformations for skip-free GKAT.
Theorem 3.13
(Completeness I). If
 , then \(e_1 \equiv _\dagger e_2\).
, then \(e_1 \equiv _\dagger e_2\).
Theorem 3.14
(Completeness II). If \(e_1 \sim _\mathcal {L}e_2\), then \(e_1 \equiv e_2\).
We prove Theorem 3.13 in Section 5 by drawing a formal analogy between skip-free GKAT and a recent study of regular expressions in the context of process algebra [15]. We include a short overview of this recent work in the next section.
We delay the proof of Theorem 3.14 to Section 6, which uses a separate technique based on the pruning method introduced in [40].
4 1-free Star Expressions
Regular expressions were introduced by Kleene [23] as a syntax for the algebra of regular events. Milner offered an alternative interpretation of regular expressions [33], as what he called star behaviours. Based on work of Salomaa [38], Milner proposed a sound axiomatization of the algebra of star behaviours, but left completeness an open problem. After nearly 40 years of active research from the process algebra community, a solution was finally found by Grabmayer [14].
A few years before this result, Grabmayer and Fokkink proved that a suitable restriction of Milner’s axioms gives a complete inference system for the behaviour interpretation of a fragment of regular expressions, called the one-free fragment [15]. In this section, we give a quick overview of Grabmayer and Fokkink’s one-free fragment [15], slightly adapted to use an alphabet that will be suitable to later use in one of the completeness proofs of skip-free GKAT.
Syntax. In the process algebra literature [33, 15, 14], regular expressions generated by a fixed alphabet \(A\) are called star expressions, and denote labelled transition systems (LTSs) with labels drawn from \(A\). As was mentioned in Section 3, skip-free automata can be seen as certain LTSs where the labels are atomic test/atomic action pairs. In Section 5, we encode skip-free GKAT expressions as one-free regular expressions and skip-free automata as LTSs with labels drawn from \(\textsf{At}\cdot \varSigma \). We instantiate the construction from [15] of the set of star expressions generated by the label set \(\textsf{At}\cdot \varSigma \).
Definition 4.1
The set \(\textsf{StExp}\) of one-free star expressions is given by
Semantics. The semantics of \(\textsf{StExp}\) is now an instance of the labelled transition systems that originally appeared in [15], with atomic test/atomic action pairs as labels and a (synthetic) output state \(\checkmark \) denoting successful termination.
For the rest of this paper, we call a pair (S, t) a labelled transition system when S is a set of states and \(t:S \rightarrow \mathcal P(\textsf{At}\cdot \varSigma \times (\checkmark + S))\) is a transition structure. We write
 if \((\alpha p, y) \in t(x)\) and
if \((\alpha p, y) \in t(x)\) and
 if \((\alpha p, \checkmark ) \in t(x)\).
if \((\alpha p, \checkmark ) \in t(x)\).
The set \(\textsf{StExp}\) can be given the structure of a labelled transition system \((\textsf{StExp}, \tau )\), defined in Fig. 5. If \(r \in \textsf{StExp}\), we write \(\langle r\rangle \) for the transition system obtained by restricting \(\tau \) to the one-free star expressions reachable from \(r\) and call \(\langle r \rangle \) the small-step semantics of \(r\).
The bisimulation interpretation of one-free star expressions is subtler than the bisimulation interpretation of skip-free GKAT expressions. The issue is that labelled transition systems (LTSs) are nondeterministic in general: it is possible for an LTS to have both a
 and a
and a
 transition for \(p \ne q\) or \(y \ne z\). The appropriate notion of bisimilarity for LTSs can be given as follows.
transition for \(p \ne q\) or \(y \ne z\). The appropriate notion of bisimilarity for LTSs can be given as follows.
Definition 4.2
Given labelled transition systems \((S, t)\) and \((T, u)\), a bisimulation between them is a relation \(R \subseteq S \times T\) s.t. for any \(x \mathrel {R} y\) and \(\alpha p \in \textsf{At}\cdot \varSigma \),
-
1.
 if and only if
if and only if
 ,
, -
2.
if
 , then there exist \(x' \mathrel {R} y'\) such that
, then there exist \(x' \mathrel {R} y'\) such that
 , and
, and -
3.
if
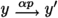 , then there exist \(x' \mathrel {R} y'\) such that
, then there exist \(x' \mathrel {R} y'\) such that
 .
.
As before, we denote the largest bisimulation by
 . We call \(x\) and \(y\) bisimilar and write
. We call \(x\) and \(y\) bisimilar and write
 if \(x \mathrel {R} y\) for some bisimulation R.
if \(x \mathrel {R} y\) for some bisimulation R.
The following closure properties of bisimulations of LTSs are useful later. They also imply that bisimilarity is an equivalence relation. Like in the skip-free case, the bisimilarity equivalence class of a state is called its behaviour.
Lemma 4.3
Let \((S, t)\), \((T, u)\), and \((U, v)\) be labelled transition systems. Furthermore, let \(R_1, R_2 \subseteq S \times T\) and \(R_3 \subseteq T \times U\) be bisimulations. Then \(R_1 ^{op} = \{(y, x) \mid x \mathrel {R_1} y\}\), \(R_1 \cup R_2\) and \(R_1 \circ R_3\) are bisimulations.
Axiomatization. We follow [15], where it was shown that the axiomatization found in Fig. 6 is complete with respect to bisimilarity for one-free star expressions. Given a pair \(r_1, r_2 \in \textsf{StExp}\), we write \(r_1 \equiv _* r_2\) and say that \(r_1\) and \(r_2\) are \(\equiv _*\)-equivalent if the equation \(r_1 = r_2\) can be derived from the axioms in Fig. 6.
The following result is crucial to the next section, where we prove that the axioms of \(\equiv _\dagger \) are complete with respect to bisimilarity in skip-free GKAT.
Theorem 4.4
([15, Theorem. 7.1]).
 if and only if \(r_1 \equiv _* r_2\).
if and only if \(r_1 \equiv _* r_2\).
5 Completeness for Skip-free Bisimulation GKAT
This section is dedicated to the proof of our first completeness result, Theorem 3.13, which says that the axioms of Fig. 2 (excluding \(\dagger \)) are complete with respect to bisimilarity in skip-free GKAT. Our proof strategy is a reduction of our completeness result to the completeness result for \(\textsf{StExp}\) (Theorem 4.4).
The key objects of interest in the reduction are a pair of translations: one translation turns skip-free GKAT expressions into one-free star expressions and maintains bisimilarity, and the other translation turns (certain) one-free star expressions into skip-free GKAT expressions and maintains provable bisimilarity.
We first discuss the translation between automata and labelled transition systems, which preserves and reflects bisimilarity. We then introduce the syntactic translations and present the completeness proof.
5.1 Transforming skip-free automata to labelled transition systems
We can easily transform a skip-free automaton into an LTS by essentially turning
 transitions into
transitions into
 transitions. This can be formalized, as follows.
transitions. This can be formalized, as follows.
Definition 5.1
Given a set \(X\), we define \(\textsf{grph}_X : (\bot + \varSigma \times (\checkmark + X))^\textsf{At}\rightarrow \mathcal P(\textsf{At}\cdot \varSigma \times (\checkmark + X)) \) to be \( \textsf{grph}_X(\theta ) = \{(\alpha p, x) \mid \theta (\alpha ) = (p, x)\} \). Given a skip-free automaton \((X, h)\), we define \(\textsf{grph}_*(X, h) = {(X, \textsf{grph}_X \circ h)}\)
The function \(\textsf{grph}_X\) is injective: as its name suggests, \(\textsf{grph}_X(\theta )\) is essentially the graph of \(\theta \) when viewed as a partial function from \(\textsf{At}\) to \({\varSigma \times (\checkmark + X)}\). This implies that the transformation \(\textsf{grph}_*\) of skip-free automata into LTSs preserves and reflects bisimilarity.
Lemma 5.2
Let \(x, y \in X\), and \((X, h)\) be a skip-free automaton. Then
 in \((X, h)\) if and only if
in \((X, h)\) if and only if
 in \(\textsf{grph}_*(X, h)\).
in \(\textsf{grph}_*(X, h)\).
Leading up to the proof of Theorem 3.13, we also need to undo the effect of \(\textsf{grph}_*\) on skip-free automata with a transformation that takes every LTS of the form \(\textsf{grph}_*(X, h)\) to its underlying skip-free automaton \((X, h)\).
The LTSs that can be written in the form \(\textsf{grph}_*(X, h)\) for some skip-free automaton \((X, h)\) can be described as follows. Call a set \(U \in \mathcal {P}(\textsf{At}\cdot \varSigma \times (\checkmark + X))\) graph-like if whenever \((\alpha p, x)\in U\) and \((\alpha q, y) \in U\), then \(p = q\) and \(x = y\). An LTS \((S, t)\) is deterministic if \(t(s)\) is graph-like for every \(s \in S\).
Lemma 5.3
An LTS \((S, t)\) is deterministic if and only if \((S, t) = \textsf{grph}_*(X, h)\) for some skip-free automaton \((X, h)\).
Remark 5.4
As mentioned in (See footnote 3), there is a coalgebraic outlook in many of the technical details in the present paper. For the interested reader, \(\textsf{grph}\) and \(\textsf{func}\) are actually natural transformations between the functors whose coalgebras correspond to skip-free automata and labelled transitions, and are furthermore inverse to one another. This implies that \(\textsf{grph}_*\) and \(\textsf{func}_*\) witness an isomorphism between the categories of skip-free automata and deterministic LTSs.
5.2 Translating Syntax
We can mimic the transformation of skip-free automata into deterministic labelled transition systems and vice-versa by a pair of syntactic translations going back and forth between skip-free GKAT expressions and certain one-free star expressions. Similar to how only some labelled transition systems can be turned into skip-free automata, only some one-free star expressions have corresponding skip-free GKAT expressions—the deterministic ones.
The definition of deterministic expressions requires the following notation: given a test \(b \in \textsf{BExp}\), we define \(b\cdot r\) inductively on \(r \in \textsf{StExp}\) as follows:
for any \(\alpha p \in \textsf{At}\cdot \varSigma \) and \(r_1,r_2 \in \textsf{StExp}\).
Definition 5.5
The set of deterministic one-free star expressions is the smallest subset \(\textsf{Det}\subseteq \textsf{StExp}\) such that \(0 \in \textsf{Det}\) and \(\alpha p \in \textsf{Det}\) for any \(\alpha \in \textsf{At}\) and \(p \in \varSigma \), and for any \(r_1, r_2 \in \textsf{Det}\), and \(b \in \textsf{BExp}\), \(b\cdot r_1 + \bar{b} \cdot r_2, r_1r_2\), and \((b \cdot r_1)*(\bar{b} \cdot r_2) \in \textsf{Det}\).
From \(\textsf{GExp}^-\) to \(\textsf{Det}\). We can now present the translations of skip-free expressions to deterministic one-free star expressions.
Definition 5.6
We define the translation function \({\text {gtr}}: \textsf{GExp}^- \rightarrow \textsf{Det}\) by
for any \(b \in \textsf{BExp}\), \(p \in \varSigma \), \(e_1,e_2 \in \textsf{GExp}\).
Remark 5.7
In Definition 5.6, we make use of a generalized sum \(\sum _{\alpha \in \textsf{At}}\). Technically, this requires we fix an enumeration of \(\textsf{At}\) ahead of time, say \(\textsf{At}= \{\alpha _1, \dots , \alpha _{n}\}\), at which point we can define \(\sum _{\alpha \in \textsf{At}} r_\alpha = r_{\alpha _1} + \cdots + r_{\alpha _n}\). Of course, \(+\) is commutative and associative up to \(\equiv _*\), so the actual ordering of this sum does not matter as far as equivalence is concerned.
The most prescient feature of this translation is that it respects bisimilarity.
Lemma 5.8
The graph of the translation function \({\text {gtr}}\) is a bisimulation of labelled transition systems between \(\textsf{grph}_*(\textsf{GExp}^-, \partial )\) and \((\textsf{StExp}, \tau )\). Consequently, if
 in \(\textsf{grph}_*(\textsf{GExp}^-, \partial )\), then
in \(\textsf{grph}_*(\textsf{GExp}^-, \partial )\), then
 in \((\textsf{StExp}, \tau )\).
in \((\textsf{StExp}, \tau )\).
From \(\textsf{Det}\) to \(\textsf{GExp}^-\). We would now like to define a back translation function \({\text {rtg}}: \textsf{Det}\rightarrow \textsf{GExp}^-\) by induction on its argument. Looking at Definition 5.5, one might be tempted to write \({\text {rtg}}(b \cdot r_1 + \bar{b} \cdot r_2) = {\text {rtg}}(r_1) +_b {\text {rtg}}(r_2)\), but the fact of the matter is that it is possible for there to be distinct \(b,c \in \textsf{BExp}\) such that \(b \cdot r_1 + \bar{b} \cdot r_2 = c \cdot r_1 + \bar{c} \cdot r_2\), even when b and c have different atoms.
Definition 5.9
Say that \(r_1, r_2 \in \textsf{StExp}\) are separated by \(b \in \textsf{BExp}\) if \(r_1 = b\cdot r_1\) and \(r_2 = \bar{b} \cdot r_2\). If such a \(b\) exists we say that \(r_1\) and \(r_2\) are separated.
Another way to define \(\textsf{Det}\) is therefore to say that \(\textsf{Det}\) is the smallest subset of \(\textsf{StExp}\) containing \(0\) and \(\textsf{At}\cdot \varSigma \) that is closed under sequential composition and closed under unions and stars of separated one-free star expressions.
Suppose \(r_1\) and \(r_2\) are separated by both \(b\) and \(c\). Then one can prove that \((b \vee c)r_1 \equiv _* br_1 + cr_1 \equiv _* r_1\) and \(\overline{(b \vee c)}r_2 = (\bar{b} \wedge \bar{c})r_2 \equiv _* \bar{b}(\bar{c} r_2) \equiv _* r_2\), so \(r_1\) and \(r_2\) are separated by \(b \vee c\) as well. Since there are only finitely many Boolean expressions up to equivalence, there is a maximal (weakest) test \(b(r_1,r_2) \in \textsf{BExp}\) such that \(r_1\) and \(r_2\) are separated by \(b(r_1, r_2)\).
Definition 5.10
The back translation \({\text {rtg}}: \textsf{Det}\rightarrow \textsf{GExp}^-\) is defined by
for any \(r_1,r_2 \in \textsf{StExp}\). In the union and star cases, we may use that \(r_1\) and \(r_2\) are separated (by definition of \(\textsf{Det}\)), so that \(b(r_1, r_2)\) is well-defined.
The most prescient property of \({\text {rtg}}\) is that it preserves provable equivalence.
Lemma 5.11
Let \(r_1, r_2 \in \textsf{Det}\). If \(r_1 \equiv _* r_2\), then \({\text {rtg}}(r_1) \equiv _\dagger {\text {rtg}}(r_2)\).
The last fact needed in the proof of completeness is that, up to provable equivalence, every skip-free GKAT expression is equivalent to its back-translation.
Lemma 5.12
For any \(e \in \textsf{GExp}^-\), \(e \equiv _\dagger {\text {rtg}}({\text {gtr}}(e))\).
We are now ready to prove Theorem 3.13, that provable bisimilarity is complete with respect to behavioural equivalence in skip-free GKAT.
Theorem
3.13
(Completeness I).
If
 , then
\(e_1 \equiv _\dagger e_2\)
.
, then
\(e_1 \equiv _\dagger e_2\)
.
Proof
Let \(e_1,e_2 \in \textsf{GExp}\) be a bisimilar pair of skip-free GKAT expressions. By Lemma 5.2, \(e_1\) and \(e_2\) are bisimilar in \(\textsf{grph}_*(\textsf{GExp}^-, \partial )\). By Lemmas 5.8 and 4.3, the translation \({\text {gtr}}: \textsf{grph}_*(\textsf{GExp}^-, \partial ) \rightarrow (\textsf{StExp}, \tau )\) preserves bisimilarity, so \({\text {gtr}}(e_1)\) and \({\text {gtr}}(e_2)\) are bisimilar in \((\textsf{StExp}, \tau )\) as well. By Theorem 4.4, \({\text {gtr}}(e_1) \equiv _* {\text {gtr}}(e_2)\). Therefore, by Lemma 5.11, \({\text {rtg}}({\text {gtr}}(e_1)) \equiv _\dagger {\text {rtg}}({\text {gtr}}(e_2))\). Finally, by Lemma 5.12, we have \( e_1 \equiv _\dagger {\text {rtg}}({\text {gtr}}(e_1)) \equiv _\dagger {\text {rtg}}({\text {gtr}}(e_2)) \equiv _\dagger e_2 \).
6 Completeness for Skip-free GKAT
The previous section establishes that \(\equiv _\dagger \)-equivalence coincides with bisimilarity for skip-free GKAT expressions by reducing the completeness problem of skip-free GKAT up to bisimilarity to a solved completeness problem, namely that of one-free star expressions up to bisimilarity. In this section we prove a completeness result for skip-free GKAT up to language equivalence. We show this can be achieved by reducing it to the completeness problem of skip-free GKAT up to bisimilarity, which we just solved in the previous section.
Despite bisimilarity being a less traditional equivalence in the context of Kleene algebra, this reduction simplifies the completeness proof greatly, and justifies the study of bisimilarity in the pursuit of completeness for GKAT.
The axiom \(x \cdot 0 = 0\) (which is the only difference between skip-free GKAT up to language equivalence and skip-free GKAT up to bisimilarity) indicates that the only semantic difference between bisimilarity and language equivalence in skip-free GKAT is early termination. This motivates our reduction to skip-free GKAT up to bisimilarity below, which involves reducing each skip-free expression to an expression representing only the successfully terminating branches of execution.
Now let us turn to the formal proof of Theorem 3.14, which says that if \(e, f \in \textsf{GExp}^-\) are such that \(\mathcal {L}(e) = \mathcal {L}(f)\), then \(e \equiv f\). In a nutshell, our strategy is to produce two terms \(\lfloor e\rfloor , \lfloor f\rfloor \in \textsf{GExp}^-\) such that \(e \equiv \lfloor e\rfloor \), \(f \equiv \lfloor f\rfloor \) and
 in \((\textsf{GExp}^-, \partial )\). The latter property tells us that \(\lfloor e\rfloor \equiv _\dagger \lfloor f\rfloor \) by Theorem 3.13, which allows us to conclude \(e \equiv f\). The expression \(\lfloor e\rfloor \) can be thought of as the early termination version of \(e\), obtained by pruning the branches of its execution that cannot end in successful termination.
in \((\textsf{GExp}^-, \partial )\). The latter property tells us that \(\lfloor e\rfloor \equiv _\dagger \lfloor f\rfloor \) by Theorem 3.13, which allows us to conclude \(e \equiv f\). The expression \(\lfloor e\rfloor \) can be thought of as the early termination version of \(e\), obtained by pruning the branches of its execution that cannot end in successful termination.
To properly define the transformation \(\lfloor -\rfloor \) on expressions, we need the notion of a dead state in a skip-free automaton, analogous to a similar notion from [42].
Definition 6.1
Let (X, h) be a skip-free automaton. The set D(X, h) is the largest subset of X such for all \(x \in D(X, h)\) and \(\alpha \in \textsf{At}\), either \(h(x)(\alpha ) = \bot \) or \(h(x)(\alpha ) \in \varSigma \times D(X,h)\). When \(x \in D(X, h)\), x is dead; otherwise, it is live.
In the sequel, we say \(e \in \textsf{GExp}^-\) is dead when e is a dead state in \((\textsf{GExp}^-, \partial )\), i.e., when \(e \in D(\textsf{GExp}^-, \partial )\). Whether e is dead can be determined by a simple depth-first search, since e can reach only finitely many expressions by \(\partial \). The axioms of skip-free GKAT can also tell when a skip-free expression is dead.
Lemma 6.2
Let \(e \in \textsf{GExp}\). If e is dead, then \(e \equiv 0\).
We are now ready to define \(\lfloor -\rfloor \), the transformation on expressions promised above. The intuition here is to prune the dead subterms of e by recursive descent; whenever we find a part that will inevitably lead to an expression that is never going to lead to acceptance, we set it to 0.
Definition 6.3
Let \(e \in \textsf{GExp}^-\) and \(a \in \textsf{BExp}\). In the sequel we use ae as a shorthand for \(e +_a 0\). We furthermore define \(\lfloor e\rfloor \) inductively, as follows

The transformation defined above yields a term that is \(\equiv \)-equivalent to e, provided that we include the early termination axiom \(e \cdot 0 \equiv 0\). The proof is a simple induction on e, using Lemma 6.2.
Lemma 6.4
For any \(e \in \textsf{GExp}^-\), \(e \equiv \lfloor e\rfloor \).
It remains to show that if \(\mathcal {L}(e) = \mathcal {L}(f)\), then \(\lfloor e\rfloor \) and \(\lfloor f\rfloor \) are bisimilar. To this end, we need to relate the language semantics of e and f to their behaviour. As a first step, we note that behaviour that never leads to acceptance can be pruned from a skip-free automaton by removing transitions into dead states.
Definition 6.5
Let (X, h) be a skip-free automaton. Define \(\lfloor h\rfloor : X \rightarrow GX\) by
Moreover, language equivalence of two states in a skip-free automaton implies bisimilarity of those states, but only in the pruned version of that skip-free automaton. The proof works by showing that the relation on X that connects states with the same language is, in fact, a bisimulation in \((X, \lfloor h\rfloor )\).
Lemma 6.6
Let (X, h) be a skip-free automaton and \(x,y \in X\). We have

The final intermediate property relates the behaviour of to states in the pruned skip-free automaton of expressions to the syntactic skip-free automaton.
Lemma 6.7
The graph \(\{(e, \lfloor e\rfloor ) \mid e \in \textsf{GExp}^-\}\) of \(\lfloor -\rfloor \) is a bisimulation of skip-free automata between \((\textsf{GExp}^-, \lfloor \partial \rfloor )\) and \((\textsf{GExp}^-, \partial )\).
We now have all the ingredients necessary to prove Theorem 3.14.
Theorem 3.14 (Completeness II). If \(e_1 \sim _\mathcal {L}e_2\) , then \(e_1 \equiv e_2\) .
Proof
If \(e_1 \sim _\mathcal {L}e_2\), then by definition \(\mathcal {L}(e_1) = \mathcal {L}(e_2)\). By Lemma 6.6,
 in \((\textsf{GExp}^-, \lfloor \partial \rfloor )\), which by Lemma 6.7 implies that
in \((\textsf{GExp}^-, \lfloor \partial \rfloor )\), which by Lemma 6.7 implies that
 in \((\textsf{GExp}^-, \partial )\). From Theorem 3.13 we know that \(\lfloor e_1\rfloor \equiv _\dagger \lfloor e_2\rfloor \), and therefore \(e_1 \equiv e_2\) by Lemma 6.4.
in \((\textsf{GExp}^-, \partial )\). From Theorem 3.13 we know that \(\lfloor e_1\rfloor \equiv _\dagger \lfloor e_2\rfloor \), and therefore \(e_1 \equiv e_2\) by Lemma 6.4.
7 Relation to GKAT
So far we have seen the technical development of skip-free GKAT without much reference to the original development of GKAT as it was presented in [42] and [40]. In this section, we make the case that the semantics of skip-free GKAT is merely a simplified version of the semantics of GKAT, and that the two agree on which expressions are equivalent after embedding skip-free GKAT into GKAT. More precisely, we identify the bisimulation and language semantics of skip-free GKAT given in Section 3 with instances of the existing bisimulation [40] and language [42] semantics of GKAT proper. The main takeaway is that two skip-free GKAT expressions are equivalent in our semantics precisely when they are equivalent when interpreted as proper GKAT expressions in the existing semantics.
7.1 Bisimulation semantics
To connect the bisimulation semantics of skip-free GKAT to GKAT at large, we start by recalling the latter. To do this, we need to define \(\textsf {GKAT} \) automata.
Definition 7.1
A (GKAT) automaton is a pair (X, d) such that X is a set and \(d: X \rightarrow (\bot + \checkmark + \varSigma \times X)^\textsf{At}\) is a function called the transition function. We write
 to denote \(d(x)(\alpha ) = (p, y)\), \(x \Rightarrow \alpha \) to denote \(d(x)(\alpha ) = \checkmark \), and \(x\downarrow \alpha \) if \(d(x)(\alpha )\) is undefined.
to denote \(d(x)(\alpha ) = (p, y)\), \(x \Rightarrow \alpha \) to denote \(d(x)(\alpha ) = \checkmark \), and \(x\downarrow \alpha \) if \(d(x)(\alpha )\) is undefined.
Automata can be equipped with their own notion of bisimulation.Footnote 4
Definition 7.2
Given automata (X, h) and (Y, k), a bisimulation between them is a relation \(R \subseteq X \times Y\) such that if \(x \mathrel {R} y\), \(\alpha \in \textsf{At}\) and \(p \in \varSigma \),:
-
1.
if \(h(x)(\alpha ) = \bot \), then \(k(y)(\alpha ) = \bot \); and
-
2.
if \(h(x)(\alpha ) = \checkmark \), then \(k(y)(\alpha ) = \checkmark \); and
-
3.
if \(h(x)(\alpha ) = (p, x')\), then \(k(y)(\alpha ) = (p, y')\) such that \(x' \mathrel {R} y'\).
We call x and \(y\) bisimilar and write
 if \(x \mathrel {R} y\) for some bisimulation \(R\).
if \(x \mathrel {R} y\) for some bisimulation \(R\).
Remark 7.3
The properties listed above are implications, but it is not hard to show that if all three properties hold for R, then so do all of their symmetric counterparts. For instance, if \(k(y)(\alpha ) = (p, y')\), then certainly \(h(x)(\alpha )\) must be of the form \((q, x')\), which then implies that \(q = p\) while \(x' \mathrel {R} y'\).
Two GKAT expressions are bisimilar when they are bisimilar as states in the syntactic automaton [40], \((\textsf{GExp}, \delta )\), summarised in Fig. 7.
Remark 7.4
The definition of \(\delta \) given above diverges slightly from the definition in [40]. Fortunately, this does not make a difference in terms of the bisimulation semantics: two expressions are bisimilar in \((\textsf{GExp}, \delta )\) if and only if they are bisimilar in the original semantics. The full version [22] contains a detailed account.
There is a fairly easy way to convert a skip-free automaton into a \(\textsf {GKAT} \) automaton: simply reroute all accepting transitions into a new state \(\top \), that accepts immediately, and leave the other transitions the same.
Definition 7.5
Given a skip-free automaton (X, d), we define the automaton \(\textsf{embed}(X, d) = (X + \top , \tilde{d})\), where \(\tilde{d}\) is defined by
We can show that two states are bisimilar in a skip-free automaton if and only if these same states are bisimilar in the corresponding \(\textsf {GKAT} \) automaton.
Lemma 7.6
Let (X, d) be a skip-free automaton, and let \(x, y \in X\).

The syntactic skip-free automaton \((\textsf{GExp}^-, \partial )\) can of course be converted to a \(\textsf {GKAT} \) automaton in this way. It turns out that there is a very natural way of correlating this automaton to the syntactic \(\textsf {GKAT} \) automaton \((\textsf{GExp}, \delta )\).
Lemma 7.7
The relation \(\{ (e, e) : e \in \textsf{GExp}^- \} \cup \{ (\top , 1) \}\) is a bisimulation between \(\textsf{embed}(\textsf{GExp}^-, \partial )\) and \((\textsf{GExp}, \delta )\).
We now have everything to relate the bisimulation semantics of skip-free GKAT expressions to the bisimulation semantics of GKAT expressions at large.
Lemma 7.8
Let \(e, f \in \textsf{GExp}^-\). The following holds:

Proof
We derive using Lemmas 7.6 and 7.7, as follows: since the graph of \(\textsf{embed}\) is a bisimulation,
 in \((\textsf{GExp}^-, \partial )\) iff
in \((\textsf{GExp}^-, \partial )\) iff
 in \(\textsf{embed}(\textsf{GExp}^-, \partial )\) if and only if
in \(\textsf{embed}(\textsf{GExp}^-, \partial )\) if and only if
 in \((\textsf{GExp}, \delta )\). In the last step, we use the fact that if R is a bisimulation (of automata) between (X, h) and (Y, k), and S is a bisimulation between (Y, k) and \((Z, \ell )\), then \(R \circ S\) is a bisimulation between (X, h) and \((Z, \ell )\).
in \((\textsf{GExp}, \delta )\). In the last step, we use the fact that if R is a bisimulation (of automata) between (X, h) and (Y, k), and S is a bisimulation between (Y, k) and \((Z, \ell )\), then \(R \circ S\) is a bisimulation between (X, h) and \((Z, \ell )\).
7.2 Language semantics
We now recall the language semantics of GKAT, which is defined in terms of guarded strings [29], i.e., words in the set \(\textsf{At}\cdot (\varSigma \cdot \textsf{At})^*\), where atoms and actions alternate. In GKAT, successful termination occurs with a trailing associated test, representing the state of the machine at termination. In an execution of the sequential composition of two programs \(e \cdot f\), the test trailing the execution of \(e\) needs to match up with an input test compatible with \(f\), otherwise the program crashes at the end of executing \(e\). The following operations on languages of guarded strings record this behaviour by matching the ends of traces on the left with the beginnings of traces on the right.
Definition 7.9
For \(L, K \subseteq At \cdot (\varSigma \cdot \textsf{At})^*\), define \( L \diamond K = \{ w\alpha {}x : w\alpha \in L, \alpha {}x \in K \} \) and \( L^{(*)} = \bigcup _{n \in \mathbb {N}} L^{(n)} \), where \(L^{(n)}\) is defined inductively by setting \(L^{(0)} = \textsf{At}\) and \(L^{(n+1)} = L \diamond L^{(n)}\).
The language semantics of a GKAT expression is now defined in terms of the composition operators above, as follows.
Definition 7.10
We define \(\widehat{\mathcal {L}}: \textsf{GExp}\rightarrow \mathcal {P}(\textsf{At}\cdot (\varSigma \cdot \textsf{At})^*)\) inductively, as follows:

This semantics is connected to the relational semantics from Definition 2.2:
Theorem 7.11
([42]). For \(e, f \in \textsf{GExp}\), we have \(\widehat{\mathcal {L}}(e) = \widehat{\mathcal {L}}(f)\) if and only if \(\llbracket e\rrbracket _\sigma = \llbracket f\rrbracket _\sigma \) for all relational interpretations \(\sigma \)
Moreover, since skip-free GKAT expressions are also GKAT expressions, this means that we now have two language interpretations of the former, given by \(\widehat{\mathcal {L}}\) and \(\mathcal {L}\). Fortunately, one can easily be expressed in terms of the other.
Lemma 7.12
For \(e \in \textsf{GExp}^-\), it holds that \(\widehat{\mathcal {L}}(e) = \mathcal {L}(e) \cdot \textsf{At}\).
As an easy consequence of the above, we find that the two semantics must identify the same skip-free GKAT-expressions.
Lemma 7.13
For \(e, f \in \textsf{GExp}^-\), we have \(\mathcal {L}(e) = \mathcal {L}(f)\) iff \(\widehat{\mathcal {L}}(e) = \widehat{\mathcal {L}}(f)\).
By Theorem 3.14, these properties imply that \(\equiv \) also axiomatizes relational equivalence of skip-free GKAT-expressions, as a result.
Corollary 7.14
Let \(e, f \in \textsf{GExp}^-\), we have \(e \equiv f\) if and only if \(\llbracket e\rrbracket _\sigma = \llbracket f\rrbracket _\sigma \) for all relational interpretations \(\sigma \).
7.3 Equivalences
Finally, we relate equivalences as proved for skip-free GKAT expressions to those provable for GKAT expressions, showing that proofs of equivalence for skip-free GKAT expressions can be replayed in the larger calculus, without (UA).
The axioms of GKAT as presented in [42, 40] are provided in Figure 8. We write \(e \approx _\dagger f\) when \(e = f\) is derivable from the axioms in Figure 8 with the exception of (\(\dagger \)), and \(e \approx f\) when \(e = f\) is derivable from the full set.
The last axiom of GKAT is not really a single axiom, but rather an axiom scheme, parameterized by the function \(E: \textsf{GExp}\rightarrow \textsf{BExp}\) defined as follows:
The function E models the analogue of Salomaa’s empty word property [38]: we say e is guarded when E(b) is equivalent to 0 by to the laws of Boolean algebra. Notice that as GKAT expressions, skip-free GKAT expressions are always guarded.
Since skip-free GKAT expressions are also GKAT expressions, we have four notions of equivalence for GKAT expressions: as skip-free expressions or GKAT expressions in general, either with or without (\(\dagger \)). These are related as follows.
Theorem 7.15
Let \(e, f \in \textsf{GExp}^-\). Then (1) \(e \approx _\dagger f\) if and only if \(e \equiv _\dagger f\), and (2) \(e \approx f\) if and only if \(e \equiv f\).
Proof
For the forward direction of (1), we note that if \(e \approx _\dagger f\), then
 in \((\textsf{GExp}, \delta )\) by Theorem 3.12. By Lemma 7.8,
in \((\textsf{GExp}, \delta )\) by Theorem 3.12. By Lemma 7.8,
 in \((\textsf{GExp}^-, \delta )\) and therefore \(e \equiv _\dagger f\) by Theorem 3.13. Conversely, note that any proof of \(e = f\) by the axioms of Figure 2 can be replayed using the rules from Figure 8. In particular, the guardedness condition required for the last skip-free GKAT axiom using the last GKAT axiom is always true, because \(E(g) \approx _\dagger 0\) for any \(g \in \textsf{GExp}^-\).
in \((\textsf{GExp}^-, \delta )\) and therefore \(e \equiv _\dagger f\) by Theorem 3.13. Conversely, note that any proof of \(e = f\) by the axioms of Figure 2 can be replayed using the rules from Figure 8. In particular, the guardedness condition required for the last skip-free GKAT axiom using the last GKAT axiom is always true, because \(E(g) \approx _\dagger 0\) for any \(g \in \textsf{GExp}^-\).
The proof of the second claim is similar, but uses Theorem 3.13 instead.
8 Related Work
This paper fits into a larger research program focused on understanding the logical and algebraic content of programming. Kleene’s paper introducing the algebra of regular languages [23] was a foundational contribution to this research program, containing an algebraic account of mechanical programming and some of its sound equational laws. The paper also contained an interesting completeness problem: give a complete description of the equations satisfied by the algebra of regular languages. Salomaa was the first to provide a sound and complete axiomatization of language equivalence for regular expressions [38].
The axiomatization in op. cit. included an inference rule with a side condition that prevented it from being algebraic in the sense that the validity of an equation is not preserved when substituting letters for arbitrary regular expressions. Nevertheless, this inspired axiomatizations of several variations and extensions of Kleene algebra [46, 42, 41], as well as Milner’s axiomatization of the algebra of star behaviours [33]. The side condition introduced by Salomaa is often called the empty word property, an early version of a concept from process theory called guardednessFootnote 5 that is also fundamental to the theory of iteration [6].
Our axiomatization of skip-free GKAT is algebraic due to the lack of a guardedness side-condition (it is an equational Horn theory [32]). This is particularly desirable because it allows for an abundance of other models of the axioms. Kozen proposed an algebraic axiomatization of Kleene algebra that is sound and complete for language equivalence [25], which has become the basis for a number of axiomatizations of other Kleene algebra variants [13, 19, 20, 47] including Kleene algebra with tests [26]. KAT also has a plethora of relational models, which are desirable for reasons we hinted at in Section 2.
GKAT is a fragment of KAT that was first identified in [30]. It was later given a sound and complete axiomatization in [42], although the axiomatization is neither algebraic nor finite (it includes (UA), an axiom scheme that stands for infinitely many axioms). It was later shown that dropping \(x\cdot 0 = 0\) (called (S3) in [42]) from this axiomatization gives a sound and complete axiomatization of bisimilarity [40]. The inspiration for our pruning technique is also in [40], where a reduction of the language equivalence case to the bisimilarity case is discussed.
Despite the existence of an algebraic axiomatization of language equivalence in KAT, GKAT has resisted algebraic axiomatization so far. Skip-free GKAT happens to be a fragment of GKAT in which every expression is guarded, thus eliminating the need for the side condition in Fig. 8 and allowing for an algebraic axiomatization. An inequational axiomatization resembling that of KAT might be gleaned from the recent preprint [39], but we have not investigated this carefully. The GKAT axioms for bisimilarity of ground terms can also likely be obtained from the small-step semantics of GKAT using [1, 2, 3], but unfortunately this does not appear to help with the larger completeness problem.
The idea of reducing one completeness problem in Kleene algebra to another is common in Kleene algebra; for instance, it is behind the completeness proof of KAT [29]. Cohen also reduced weak Kleene algebra as an axiomatization of star expressions up to simulation to monodic trees [10], whose completeness was conjectured by Takai and Furusawa [45]. Grabmayer’s solution to the completeness problem of regular expressions modulo bisimulation [14] can also be seen as a reduction to the one-free case [15], since his crystallization procedure produces an automaton that can be solved using the technique found in op. cit. Other instances of reductions include [9, 4, 11, 47, 19, 21, 31, 35, 27]. Recent work has started to study reductions and their compositionality properties [11, 20, 34].
9 Discussion
We continue the study of efficient fragments of Kleene Algebra with Tests (KAT) initiated in [42], where the authors introduced Guarded Kleene Algebra with Tests (GKAT) and provided an efficient decision procedure for equivalence. They also proposed a candidate axiomatization, but left open two questions.
-
The first question concerned the existence of an algebraic axiomatization, which is an axiomatization that is closed under substitution—i.e., where one can prove properties about a certain program p and then use p as a variable in the context of a larger program, being able to substitute as needed. This is essential to enable compositional analysis.
-
The second question left open in [42] was whether an axiomatization that did not require an axiom scheme was possible. Having a completeness proof that does not require an axiom scheme to reason about mutually dependent loops is again essential for scalability: we should be able to axiomatize single loops and generalize this behaviour to multiple, potentially, nested loops.
In this paper, we identified a large fragment of GKAT, which we call skip-free GKAT (\(\textsf {GKAT} ^-\)), that can be axiomatized algebraically without relying on an axiom scheme. We show how the axiomatization works well for two types of equivalence: bisimilarity and language equivalence, by proving completeness results for both semantics. Having the two semantics is interesting from a verification point of view as it gives access to different levels of precision when analyzing program behaviour, but also enables a layered approach to the completeness proofs.
We provide a reduction of the completeness proof for language semantics to the one for bisimilarity. Moreover, the latter is connected to a recently solved [14] problem proposed by Milner. This approach enabled two things: it breaks down the completeness proofs and reuses some of the techniques while also highlighting the exact difference between the two equivalences (captured by the axiom \(e\cdot 0\equiv 0\) which does not hold for bisimilarity). We also showed that proofs of equivalence in skip-free GKAT transfer without any loss to proofs of equivalence in GKAT.
There are several directions for future work. The bridge between process algebra and Kleene algebra has not been exploited to its full potential. The fact that we could reuse results by Grabmayer and Fokkink [14, 15] was a major step towards completeness. An independent proof would have been much more complex and very likely required the development of technical tools resembling those in [14, 15]. We hope the results in this paper can be taken further and more results can be exchanged between the two communities to solve open problems.
The completeness problem for full GKAT remains open, but our completeness results for skip-free GKAT are encouraging. We believe they show a path towards studying whether an algebraic axiomatization can be devised or a negative result can be proved. A first step in exploring a completeness result would be to try extending Grabmayer’s completeness result [14] to a setting with output variables—this is a non-trivial exploration, but we are hopeful will yield new tools for completeness. As mentioned in the introduction, NetKAT [4] (and its probabilistic variants [12, 43]) have been one of the most successful extensions of KAT. We believe the step from skip-free GKAT to a skip-free guarded version of NetKAT is also a worthwhile exploration. Following [16], we hope to be able to explore these extensions in a modular and parametric way.
Change history
08 June 2023
A correction has been published.
Notes
- 1.
A probabilistic semantics in terms of sub-Markov kernels is also possible [42].
- 2.
- 3.
This follows directly from seeing skip-free automata as a special type of coalgebra and the fact that the functor involved preserves weak pullbacks [37]. In fact, coalgebra has been an indispensable tool in the production of the current paper, guiding us to the correct definitions and simplifying many of the proofs.
- 4.
- 5.
This is a different use of the word “guarded” than in “guarded Kleene algebra with tests”. In the context of process theory, a recursive specification is guarded if every of its function calls occurs within the scope of an operation.
References
Aceto, L.: Deriving complete inference systems for a class of GSOS languages generation regular behaviours. In: CONCUR. pp. 449–464 (1994). https://doi.org/10.1007/978-3-540-48654-1_33
Aceto, L., Caltais, G., Goriac, E., Ingólfsdóttir, A.: Axiomatizing GSOS with predicates. In: SOS. pp. 1–15 (2011). https://doi.org/10.4204/EPTCS.62.1
Aceto, L., Caltais, G., Goriac, E., Ingólfsdóttir, A.: PREG axiomatizer - A ground bisimilarity checker for GSOS with predicates. In: CALCO. pp. 378–385 (2011). https://doi.org/10.1007/978-3-642-22944-2_27
Anderson, C.J., Foster, N., Guha, A., Jeannin, J.B., Kozen, D., Schlesinger, C., Walker, D.: NetKAT: semantic foundations for networks. In: POPL. pp. 113–126 (2014). https://doi.org/10.1145/2535838.2535862
Birkhoff, G.: On the structure of abstract algebras. Mathematical Proceedings of the Cambridge Philosophical Society 31(4), 433–454 (1935). https://doi.org/10.1017/S0305004100013463
Bloom, S.L., Ésik, Z.: Iteration Theories - The Equational Logic of Iterative Processes. EATCS Monographs on Theoretical Computer Science, Springer (1993). https://doi.org/10.1007/978-3-642-78034-9
Brzozowski, J.A.: Derivatives of regular expressions. J. ACM 11(4), 481–494 (1964). https://doi.org/10.1145/321239.321249
Chajed, T., Tassarotti, J., Kaashoek, M.F., Zeldovich, N.: Argosy: verifying layered storage systems with recovery refinement. In: PLDI. pp. 1054–1068 (2019). https://doi.org/10.1145/3314221.3314585
Cohen, E.: Hypotheses in Kleene algebra. Tech. rep., Bellcore (1994)
Cohen, E.: Weak Kleene algebra is sound and (possibly) complete for simulation (2009). https://doi.org/10.48550/arXiv.0910.1028
Doumane, A., Kuperberg, D., Pous, D., Pradic, P.: Kleene algebra with hypotheses. In: FOSSACS. pp. 207–223 (2019). https://doi.org/10.1007/978-3-030-17127-8_12
Foster, N., Kozen, D., Mamouras, K., Reitblatt, M., Silva, A.: Probabilistic NetKAT. In: ESOP. pp. 282–309 (2016). https://doi.org/10.1007/978-3-662-49498-1_12
Foster, N., Kozen, D., Milano, M., Silva, A., Thompson, L.: A coalgebraic decision procedure for NetKAT. In: POPL. pp. 343–355 (2015). https://doi.org/10.1145/2676726.2677011
Grabmayer, C.: Milner’s proof system for regular expressions modulo bisimilarity is complete: Crystallization: Near-collapsing process graph interpretations of regular expressions. In: LICS. pp. 34:1–34:13 (2022). https://doi.org/10.1145/3531130.3532430
Grabmayer, C., Fokkink, W.J.: A complete proof system for 1-free regular expressions modulo bisimilarity. In: LICS. pp. 465–478 (2020). https://doi.org/10.1145/3373718.3394744
Greenberg, M., Beckett, R., Campbell, E.H.: Kleene algebra modulo theories: a framework for concrete KATs. In: PLDI. pp. 594–608 (2022). https://doi.org/10.1145/3519939.3523722
Gumm, H.P.: Functors for coalgebras. Algebra Universalis 45 (11 1998). https://doi.org/10.1007/s00012-001-8156-x
Huntington, E.V.: Sets of independent postulates for the algebra of logic. Transactions of the American Mathematical Society 5(3), 288–309 (1904). https://doi.org/10.1090/S0002-9947-1904-1500675-4
Kappé, T., Brunet, P., Rot, J., Silva, A., Wagemaker, J., Zanasi, F.: Kleene algebra with observations. In: CONCUR. pp. 41:1–41:16 (2019). https://doi.org/10.4230/LIPIcs.CONCUR.2019.41
Kappé, T., Brunet, P., Silva, A., Wagemaker, J., Zanasi, F.: Concurrent Kleene algebra with observations: From hypotheses to completeness. In: FOSSACS. pp. 381–400 (2020). https://doi.org/10.1007/978-3-030-45231-5_20
Kappé, T., Brunet, P., Silva, A., Zanasi, F.: Concurrent Kleene algebra: Free model and completeness. In: ESOP. pp. 856–882 (2018). https://doi.org/10.1007/978-3-319-89884-1_30
Kappé, T., Schmid, T., Silva, A.: A complete inference system for skip-free guarded Kleene algebra with tests (2023). https://doi.org/10.48550/arXiv.2301.11301
Kleene, S.C.: Representation of events in nerve nets and finite automata. Automata studies 34, 3–41 (1956)
Kot, L., Kozen, D.: Kleene algebra and bytecode verification. Electron. Notes Theor. Comput. Sci. 141(1), 221–236 (2005). https://doi.org/10.1016/j.entcs.2005.02.028
Kozen, D.: A completeness theorem for Kleene algebras and the algebra of regular events. Inf. Comput. 110(2), 366–390 (1994). https://doi.org/10.1006/inco.1994.1037
Kozen, D.: Kleene algebra with tests and commutativity conditions. In: TACAS. pp. 14–33 (1996). https://doi.org/10.1007/3-540-61042-1_35
Kozen, D., Mamouras, K.: Kleene algebra with equations. In: ICALP. pp. 280–292 (2014). https://doi.org/10.1007/978-3-662-43951-7_24
Kozen, D., Patron, M.: Certification of compiler optimizations using Kleene algebra with tests. In: CL. pp. 568–582 (2000). https://doi.org/10.1007/3-540-44957-4_38
Kozen, D., Smith, F.: Kleene algebra with tests: Completeness and decidability. In: CSL. pp. 244–259 (1996). https://doi.org/10.1007/3-540-63172-0_43
Kozen, D., Tseng, W.D.: The Böhm-Jacopini theorem is false, propositionally. In: MPC. pp. 177–192 (2008). https://doi.org/10.1007/978-3-540-70594-9_11
Laurence, M.R., Struth, G.: Completeness theorems for pomset languages and concurrent Kleene algebras (2017). https://doi.org/10.48550/arXiv.1705.05896
Makowsky, J.A.: Why Horn formulas matter in computer science: Initial structures and generic examples. J. Comput. Syst. Sci. 34(2/3), 266–292 (1987). https://doi.org/10.1016/0022-0000(87)90027-4
Milner, R.: A complete inference system for a class of regular behaviours. J. Comput. Syst. Sci. 28(3), 439–466 (1984). https://doi.org/10.1016/0022-0000(84)90023-0
Pous, D., Rot, J., Wagemaker, J.: On tools for completeness of Kleene algebra with hypotheses. In: RAMICS. pp. 378–395 (2021). https://doi.org/10.1007/978-3-030-88701-8_23
Pous, D., Wagemaker, J.: Completeness theorems for Kleene algebra with top. In: CONCUR. pp. 26:1–26:18 (2022). https://doi.org/10.4230/LIPIcs.CONCUR.2022.26
Rees, J.: Fizz Buzz: 101 Spoken Numeracy Games. Learning Development Aids (2002)
Rutten, J.J.M.M.: Universal coalgebra: a theory of systems. Theor. Comput. Sci. 249(1), 3–80 (2000). https://doi.org/10.1016/S0304-3975(00)00056-6
Salomaa, A.: Two complete axiom systems for the algebra of regular events. J. ACM 13(1), 158–169 (1966). https://doi.org/10.1145/321312.321326
Schmid, T.: A (co)algebraic framework for ordered processes (2022). https://doi.org/10.48550/arXiv.2209.00634
Schmid, T., Kappé, T., Kozen, D., Silva, A.: Guarded Kleene algebra with tests: Coequations, coinduction, and completeness. In: ICALP. pp. 142:1–142:14 (2021). https://doi.org/10.4230/LIPIcs.ICALP.2021.142
Schmid, T., Rozowski, W., Silva, A., Rot, J.: Processes parametrised by an algebraic theory. In: ICALP. pp. 132:1–132:20 (2022). https://doi.org/10.4230/LIPIcs.ICALP.2022.132
Smolka, S., Foster, N., Hsu, J., Kappé, T., Kozen, D., Silva, A.: Guarded Kleene algebra with tests: verification of uninterpreted programs in nearly linear time. In: POPL. pp. 61:1–61:28 (2020). https://doi.org/10.1145/3371129
Smolka, S., Kumar, P., Foster, N., Kozen, D., Silva, A.: Cantor meets Scott: semantic foundations for probabilistic networks. In: POPL. pp. 557–571 (2017). https://doi.org/10.1145/3009837.3009843
Smolka, S., Kumar, P., Kahn, D.M., Foster, N., Hsu, J., Kozen, D., Silva, A.: Scalable verification of probabilistic networks. In: PLDI. pp. 190–203 (2019). https://doi.org/10.1145/3314221.3314639
Takai, T., Furusawa, H.: Monodic tree Kleene algebra. In: RelMICS/AKA. pp. 402–416 (2006). https://doi.org/10.1007/11828563_27
Wagemaker, J., Bonsangue, M.M., Kappé, T., Rot, J., Silva, A.: Completeness and incompleteness of synchronous Kleene algebra. In: MPC. pp. 385–413 (2019). https://doi.org/10.1007/978-3-030-33636-3_14
Wagemaker, J., Brunet, P., Docherty, S., Kappé, T., Rot, J., Silva, A.: Partially observable concurrent Kleene algebra. In: CONCUR. pp. 20:1–20:22 (2020). https://doi.org/10.4230/LIPIcs.CONCUR.2020.20
Zetzsche, S., Silva, A., Sammartino, M.: Guarded Kleene algebra with tests: Automata learning (2022). https://doi.org/10.48550/arXiv.2204.14153
Acknowledgements
A. Silva and T. Schmid were partially funded by ERC grant Autoprobe (grant agreement 101002697). T. Kappé was supported by the EU’s Horizon 2020 research and innovation programme under Marie Skłodowska-Curie grant agreement No. 101027412 (VERLAN).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2023 The Author(s)
About this paper
Cite this paper
Kappé, T., Schmid, T., Silva, A. (2023). A Complete Inference System for Skip-free Guarded Kleene Algebra with Tests. In: Wies, T. (eds) Programming Languages and Systems. ESOP 2023. Lecture Notes in Computer Science, vol 13990. Springer, Cham. https://doi.org/10.1007/978-3-031-30044-8_12
Download citation
DOI: https://doi.org/10.1007/978-3-031-30044-8_12
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-30043-1
Online ISBN: 978-3-031-30044-8
eBook Packages: Computer ScienceComputer Science (R0)






 at the end of the loop.
at the end of the loop. with
with
 and swap
and swap
 with
with
 .
. and
and
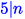 into one.
into one.

 , means the state x under
, means the state x under  , means the state x under
, means the state x under 
 if and only if
if and only if
 , and
, and if and only if
if and only if
 .
. .
.
 if and only if
if and only if
 ,
, , then there exist
, then there exist  , and
, and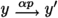 , then there exist
, then there exist  .
.

 is
is 
