Preprocessing of Propagation Redundant Clauses

Abstract

The propagation redundant (PR) proof system generalizes the resolution and resolution asymmetric tautology proof systems used by conflict-driven clause learning (CDCL) solvers. PR allows short proofs of unsatisfiability for some problems that are difficult for CDCL solvers. Previous attempts to automate PR clause learning used hand-crafted heuristics that work well on some highly-structured problems. For example, the solver SaDiCaL incorporates PR clause learning into the CDCL loop, but it cannot compete with modern CDCL solvers due to its fragile heuristics. We present PReLearn, a preprocessing technique that learns short PR clauses. Adding these clauses to a formula reduces the search space that the solver must explore. By performing PR clause learning as a preprocessing stage, PR clauses can be found efficiently without sacrificing the robustness of modern CDCL solvers. On a large portion of SAT competition benchmarks we found that preprocessing with PReLearn improves solver performance. In addition, there were several satisfiable and unsatisfiable formulas that could only be solved after preprocessing with PReLearn. PReLearn supports proof logging, giving a high level of confidence in the results.

The authors are supported by the NSF under grant CCF-2108521.

1 Introduction

Conflict-driven clause learning (CDCL) [27] is the standard paradigm for solving the satisfiability problem (SAT) in propositional logic. CDCL solvers learn clauses implied through resolution inferences. Additionally, all competitive CDCL solvers use pre- and in-processing techniques captured by the resolution asymmetric tautology (RAT) proof system [21]. As examples, the well-studied pigeonhole and mutilated chessboard problems are challenging benchmarks with exponentially-sized resolution proofs [1, 12]. It is possible to construct small hand-crafted proofs for the pigeonhole problem using extended resolution (ER) [8], a proof system that allows the introduction of new variables [32]. ER can be expressed in RAT but has proved difficult to automate due to the large search space. Even with modern inprocessing techniques, many CDCL solvers struggle on these seemingly simple problems. The propagation redundant (PR) proof system allows short proofs for these problems [14, 15], and unlike in ER, no new variables are required. This makes PR an attractive candidate for automation.

At a high level, CDCL solvers make decisions that typically yield an unsatisfiable branch of a problem. The clause that prunes the unsatisfiable branch from the search space is learned, and the solver continues by searching another branch. PR extends this paradigm by allowing more aggressive pruning. In the PR proof system a branch can be pruned as long as there exists another branch that is at least as satisfiable. As an example, consider the mutilated chessboard. The mutilated chessboard problem involves finding a covering of $2 \times 1$ dominos on an $n \times n$ chessboard with two opposite corners removed (see Section 5.4). Given two horizontally oriented dominoes covering a $2 \times 2$ square, two vertically oriented dominos could cover the same $2 \times 2$ square. For any solution that uses the dominos in the horizontal orientation, replacing them with the dominos in the vertical orientation would also be a solution. The second orientation is as satisfiable as the first, and so the first can be pruned from the search space. Even though the number of possible solutions may be reduced, the pruning is satisfiability preserving. This is a powerful form of reasoning that can efficiently remove many symmetries from the mutilated chessboard, making the problem much easier to solve [15].

The satisfaction-driven clause learning (SDCL) solver SaDiCaL [16] incorporates PR clause learning into the CDCL loop. SaDiCaL implements hand-crafted decision heuristics that exploit the canonical structure of the pigeonhole and mutilated chessboard problems to find short proofs. However, SaDiCaL’s performance deteriorates under slight variations to the problems including different constraint encodings [7]. The heuristics were developed from a few well-understood problems and do not generalize to other problem classes. Further, the heuristics for PR clause learning are likely ill-suited for CDCL, making the solver less robust.

In this paper, we present PReLearn, a preprocessing technique for learning PR clauses. PReLearn alternates between finding and learning PR clauses. We develop multiple heuristics for finding PR clauses and multiple configurations for learning some subset of the found PR clauses. As PR clauses are learned we use failed literal probing [11] to find unit clauses implied by the formula. The preprocessing is made efficient by taking advantage of the inner/outer solver framework in SaDiCaL. The learned PR clauses are added to the original formula, aggressively pruning the search space in an effort to guide CDCL solvers to short proofs. With this method PR clauses can be learned without altering the complex heuristics that make CDCL solvers robust. PReLearn focuses on finding short PR clauses and failed literals to effectively reduce the search space. This is done with general heuristics that work across a wide range of problems.

Most SAT solvers support logging proofs of unsatisfiability for independent checking [17, 20, 33]. This has proved valuable for verifying solutions independent of a (potentially buggy) solver. Modern SAT solvers log proofs in the DRAT proof system (RAT [21] with deletions). DRAT captures all widely used pre- and in-processing techniques including bounded variable elimination [10], bounded variable addition [26], and extended learning [4, 32]. DRAT can express the common symmetry-breaking techniques, but it is complicated [13]. PR can compactly express some symmetry-breaking techniques [14, 15], yielding short proofs that can be checked by the proof checker DPR-trim [16]. PR gives a framework for strong symmetry-breaking inferences and also maintains the highly desirable ability to independently verify proofs.

The contributions of this paper include: (1) giving a high-level algorithm for extracting PR clauses, (2) implementing several heuristics for finding and learning PR clauses, (3) evaluating the effectiveness of different heuristic configurations, and (4) assessing the impact of PReLearn on solver performance. PReLearn improves the performance of the CDCL solver Kissat on a quarter of the satisfiable and unsatisfiable competition benchmarks we considered. The improvement is significant for a number of instances that can only be solved by Kissat after preprocessing. Most of them come from hard combinatorial problems with small formulas. In addition, PReLearn directly produces refutation proofs for the mutilated chessboard problem containing only unit and binary PR clauses.

2 Preliminaries

We consider propositional formulas in conjunctive normal form (CNF). A CNF formula $\psi$ is a conjunction of clauses where each clause is a disjunction of literals. A literal l is either a variable x (positive literal) or a negated variable $\overline{x}$ (negative literal). For a set of literals L the formula $\psi (L)$ is the clauses $\{C \in \psi \; | \; C \cap L \ne \emptyset \}$.

An assignment is a mapping from variables to truth values 1 (true) and 0 (false). An assignment is total if it assigns every variable to a value, and partial if it assigns a subset of variables to values. The set of variables occurring in a formula, assignment, or clause is given by $\mathsf {var}(\psi )$, $\mathsf {var}(\alpha )$, or $\mathsf {var}(C)$. For a literal l, $\mathsf {var}(l)$ is a variable.

An assignment $\alpha$ satisfies a positive (negative) literal l if $\alpha$ maps $\mathsf {var}(l)$ to true ($\alpha$ maps $\mathsf {var}(l)$ to false, respectively), and falsifies it if $\alpha$ maps $\mathsf {var}(l)$ to false ($\alpha$ maps $\mathsf {var}(l)$ to true, respectively). We write a finite partial assignment as the set of literals it satisfies. An assignment satisfies a clause if the clause contains a literal satisfied by the assignment. An assignment satisfies a formula if every clause in the formula is satisfied by the assignment. A formula is satisfiable if there exists a satisfying assignment, and unsatisfiable otherwise. Two formula are logically equivalent if they share the same set of satisfying assignments. Two formulas are satisfiability equivalent if they are either both satisfiable or both unsatisfiable.

If an assignment $\alpha$ satisfies a clause C we define $C {\left| _{\alpha }\right. } = \top$, otherwise $C {\left| _{\alpha }\right. }$ represents the clause C with the literals falsified by $\alpha$ removed. The empty clause is denoted by $\bot$. The formula $\psi$ reduced by an assignment $\alpha$ is given by $\psi {\left| _{\alpha }\right. } = \{ C {\left| _{\alpha }\right. } \; | \; C \in \psi \; \text {and} \; C {\left| _{\alpha }\right. } \ne \top \}$. Given an assignment $\alpha = l_{1}\dots l_{n}$, $C = ( \overline{l}_{1} \vee \dots \vee \overline{l}_{n})$ is the clause that blocks $\alpha$. The assignment blocked by a clause is the negation of the literals in the clause. The literals touched by an assignment is defined by $\mathsf {touched}_{\alpha } (C) = \{ l \; | \; l \in C \; \text {and} \; \mathsf {var}(l) \in \mathsf {var}(\alpha ) \}$ for a clause. For a formula $\psi$, $\mathsf {touched}_{\alpha } (\psi )$ is the union of touched variables for each clause in $\psi$. A unit is a clause containing a single literal. The unit clause rule takes the assignment $\alpha$ of all units in a formula $\psi$ and generates $\psi {\left| _{\alpha }\right. }$. Iteratively applying the unit clause rule until fixpoint is referred to as unit propagation. In cases where unit propagation yields $\bot$ we say it derived a conflict. A formula $\psi$ implies a formula $\psi '$, denoted $\psi \models \psi '$, if every assignment satisfying $\psi$ satisfies $\psi '$. By $\psi \vdash _{1} \psi '$ we denote that for every clause $C \in \psi '$, applying unit propagation to the assignment blocked by C in $\psi$ derives a conflict. If unit propagation derives a conflict on the formula $\psi \cup \{\{l\}\}$, we say l is a failed literal and the unit $\overline{l}$ is logically implied by the formula. Failed literal probing [11] is the process of successively assigning literals to check if units are implied by the formula. In its simplest form, probing involves assigning a literal l and learning the unit $\overline{l}$ if unit propagation derives a conflict, otherwise l is unassigned and the next literal is checked.

To evaluate the satisfiability of a formula, a CDCL solver [27] iteratively performs the following operations: First, the solver performs unit propagation, then tests for a conflict. Unit propagation is made efficient with two-literal watch pointers [28]. If there is no conflict and all variables are assigned, the formula is satisfiable. Otherwise, the solver chooses an unassigned variable through a variable decision heuristic [6, 25], assigns a truth value to it, and performs unit propagation. If, however, there is a conflict, the solver performs conflict analysis potentially learning a short clause. In case this clause is the empty clause, the formula is unsatisfiable.

3 The PR Proof System

A clause C is redundant w.r.t. a formula $\psi$ if $\psi$ and $\psi \cup \{C\}$ are satisfiability equivalent. The clause sequence $\psi , C_{1}, C_{2} , \dots , C_{n}$ is a clausal proof of $C_{n}$ if each clause $C_{i} \; (1 \le i \le n)$ is redundant w.r.t. $\psi \cup \{ C_{1}, C_{2} , \dots , C_{i-1}\}$. The proof is a refutation of $\psi$ if $C_{n}$ is $\bot$. Clausal proof systems may also allow deletion. In a refutation proof clauses can be deleted freely because the deletion cannot make a formula less satisfiable.

Clausal proof systems are distinguished by the kinds of redundant clauses they allow to be added. The standard SAT solving paradigm CDCL learns clauses implied through resolution. These clauses are logically implied by the formula, and fall under the reverse unit propagation (RUP) proof system. The Resolution Asymmetric Tautology (RAT) proof system generalizes RUP. All commonly used inprocessing techniques emit DRAT proofs. The propagation redundant (PR) proof system generalizes RAT by allowing the pruning of branches without loss of satisfaction.

Let C be a clause in the formula $\psi$ and $\alpha$ the assignment blocked by C. Then C is PR w.r.t. $\psi$ if and only if there exists an assignment $\omega$ such that $\psi {\left| _{\alpha }\right. } \; \vdash _{1} \psi {\left| _{\omega }\right. }$ and $\omega$ satisfies C. Intuitively, this allows inferences that block a partial assignment $\alpha$ as long as another assignment $\omega$ is as satisfiable. This means every assignment containing $\alpha$ that satisfies $\psi$ can be transformed to an assignment containing $\omega$ that satisfies $\psi$.

Clausal proofs systems must be checkable in polynomial time to be useful in practice. RUP and RAT are efficiently checkable due to unit propagation. In general, determining if a clause is PR is an NP-complete problem [18]. However, a PR proof is checkable in polynomial time if the witness assignments $\omega$ are included. A clausal proof with witnesses will look like $\psi , (C_{1},\omega _{1}), (C_{2},\omega _{2}) , \dots , (C_{n},\omega _{n})$. The proof checker DPR-trim can efficiently check PR proofs that include witnesses. Further, DPR-trim can emit proofs in the LPR format. They can be validated by the formally-verified checker Cake-LPR [31], which was used to validate results in recent SAT competitions.

4 Pruning Predicates and SaDiCaL

Determining if a clause is PR is NP-complete and can naturally be formulated in SAT. Given a clause C and formula $\psi$, a pruning predicate is a formula such that if it is satisfiable, the clause C is redundant w.r.t. $\psi$. SaDiCaL uses two pruning predicates to determine if a clause is PR: positive reduct and filtered positive reduct. If either predicate is satisfiable, the satisfying assignment serves as the witness showing the clause is PR.

Given a formula $\psi$ and assignment $\alpha$, the positive reduct is the formula $G \wedge C$ where C is the clause that blocks $\alpha$ and $G = \{ \mathsf {touched}_{\alpha } (D) \; | \; D \in \psi \; \text {and} \; \; D {\left| _{\alpha }\right. } = \top \}$. If the positive reduct is satisfiable, the clause C is PR w.r.t. $\psi$. The positive reduct is satisfiable iff the clause blocked by $\alpha$ is a set-blocked clause [23].

Given a formula $\psi$ and assignment $\alpha$, the filtered positive reduct is the formula $G \wedge C$ where C is the clause that blocks $\alpha$ and $G = \{ \mathsf {touched}_{\alpha } (D) \; | \; D \in \psi \; \text {and} \; D {\left| _{\alpha }\right. } \; \nvdash _{1} \mathsf {touched}_{\alpha } (D) \}$. If the filtered positive reduct is satisfiable, the clause C is PR w.r.t. $\psi$. The filtered positive reduct is a subset of the positive reduct and is satisfiable iff the clause blocked by $\alpha$ is a set-propagation redundant clause [14]. Example 1 shows a formula for which the positive and filtered positive reducts are different, and only the filtered positive reduct is satisfiable.

Example 1

Given the formula $( x_{1} \vee x_{2}) \wedge ( \overline{x}_{1} \vee x_{2} )$, the positive reduct with $\alpha = x_{1}$ is $( x_{1}) \wedge ( \overline{x}_{1} )$, which is unsatisfiable. The clause $( x_{1})$ can be filtered, giving the filtered positive reduct $( \overline{x}_{1} )$, which is satisfiable.

SaDiCaL [16] uses satisfaction-driven clause learning (SDCL) that extends CDCL by learning PR clauses [18] based on (filtered) positive reducts. SaDiCaL uses an inner/outer solver framework. The outer solver attempts to solve the SAT problem with SDCL. SDCL diverges from the basic CDCL loop when unit propagation after a decision does not derive a conflict. In this case a reduct is generated using the current assignment, and the inner solver attempts to solve the reduct using CDCL. If the reduct is satisfiable, the PR clause blocking the current assignment is learned, and the SDCL loop continues. The PR clause can be simplified by removing all non-decision variables from the assignment. SaDiCaL emits PR proofs by logging the satisfying assignment of the reduct as the witness, and these proofs are verified with DPR-trim. The key to SaDiCaL finding good PR clauses leading to short proofs is the decision heuristic, because variable selection builds the candidate PR clauses. Hand-crafted decision heuristics enable SaDiCaL to find short proofs on pigeonhole and mutilated chessboard problems. However, these heuristics differ significantly from the score-based heuristics in most CDCL solvers. Our experiences with SaCiDaL suggest that improving the heuristics for SDCL reduces the performance of CDCL and the other way around. This may explain why SaDiCaL performs worse than standard CDCL solvers on the majority of the SAT competition benchmarks. While SaDiCaL integrates finding PR clauses of arbitrary size in the main search loop, our tool focuses on learning short PR clauses as a preprocessing step. This allows us to develop good heuristics for PR learning without compromising the main search loop.

5 Extracting PR Clauses

The goal of PReLearn is to find useful PR clauses that improve the performance of CDCL solvers on both satisfiable and unsatisfiable instances. Figure 1 shows how a SAT problem is solved using PReLearn. For some preset time limit, PR clauses are found and then added to the original formula. Interleaved in this process is failed literal probing to check if unit clauses can be learned. When the preprocessing stage ends, the new formula that includes learned PR clauses is solved by a CDCL solver. If the formula is satisfiable, the solver will produce a satisfying assignment. If the formula is unsatisfiable, a refutation proof of the original formula can be computed by combining the satisfaction preserving proof from PReLearn and the refutation proof emitted by the CDCL solver. The complete proof can be verified with DPR-trim.

Fig. 1.

Solving a formula with PReLearn and a CDCL solver.

PReLearn alternates between finding PR clauses and learning PR clauses. Candidate PR clauses are found by iterating over each variable in the formula, and for each variable constructing clauses that include that variable. To determine if a clause is PR, the positive reduct generated by that clause is solved. It can be costly to generate and solve many positive reducts, so heuristics are used to find candidate clauses that are more likely to be PR. It is possible to find multiple PR clauses that conflict with each other. PR clauses are conflicting if adding one of the PR clauses to the formula makes the other no longer PR. Learning PR clauses involves selecting PR clauses that are nonconflicting. The selection may maximize the number of PR clauses learned or optimize for some other metric. Adding PR clauses and units derived from probing may cause new clauses to become PR, so the entire process is iterated multiple times.

5.1 Finding PR Clauses

PR clauses are found by constructing a set of candidate clauses and solving the positive reduct generated by each clause. In SaDiCaL the candidates are the clauses blocking the partial assignment of the solver after each decision in the SDCL loop that does not derive a conflict. In effect, candidates are constructed using the solver’s variable decision heuristic. We take a more general approach, constructing sets of candidates for each variable based on unit propagation and the partial assignment’s $\mathsf {neighbors}$.

For a variable x, $\mathsf {neighbors}(x)$ denotes the set of variables occurring in clauses containing literal x or $\overline{x}$, excluding variable x. For a partial assignment $\alpha$, $\mathsf {neighbors}(\alpha )$ denotes $\bigcup _{x \in \mathsf {var}(\alpha )} \mathsf {neighbors}(x) \setminus \mathsf {var}(\alpha )$. Candidate clauses for a literal l are generated in the following way:

• Let $\alpha$ be the partial assignment found by unit propagation starting with the assignment that makes l true.

• Generate the candidate PR clauses $\{ (\overline{l} \vee y), (\overline{l} \vee \overline{y}) \; | \; y \in \mathsf {neighbors}(\alpha ) \}$.

Example 2 shows how candidate binary clauses are constructed using both polarities of an initial variable x. In Example 3 the depth is expanded to reach more variables and create larger sets of candidate clauses. The depth parameter is used in Section 5.4.

Example 2

Consider the following formula: $( x_{1} \vee \overline{x}_{2} ) \wedge ( \overline{x}_{1} \vee x_{3} ) \wedge ( x_{1} \vee x_{4} \vee x_{5} ) \wedge ( x_{2} \vee x_{6} \vee x_{7} ) \wedge ( x_{3} \vee x_{7} \vee x_{8} ) \wedge ( x_{8} \vee x_{9} )$,

Case 1: We start with $\mathsf {var}(x_{1}) = 1$ and perform unit propagation resulting in $\alpha = \{x_{1} x_{3}\}$. Observe that $\mathsf {neighbors}(\alpha ) = \{x_{2}, x_{4}, x_{5}, x_{7}, x_{8} \}$. The generated candidate clauses are $(\overline{x}_{1} \vee x_{2}), (\overline{x}_{1} \vee \overline{x}_{2}), (\overline{x}_{1} \vee x_{4}), (\overline{x}_{1} \vee \overline{x}_{4}), \dots ,(\overline{x}_{1} \vee x_{8}), (\overline{x}_{1} \vee \overline{x}_{8})$.

Case 2: We start with $\mathsf {var}(x_{1}) = 0$ and perform unit propagation resulting in $\alpha = \{\overline{x}_{1} \overline{x}_{2}\}$. Observe that $\mathsf {neighbors}(\alpha ) = \{x_{3}, x_{4}, x_{5}, x_{6}, x_{7} \}$. The generated candidate clauses are $(x_{1} \vee x_{3}), (x_{1} \vee \overline{x}_{3}), (x_{1} \vee x_{4}),(x_{1} \vee \overline{x}_{4}), \dots ,(x_{1} \vee x_{7}), (x_{1} \vee \overline{x}_{7})$.

Example 3

Take the formula from Example 2 and assignment of $\mathsf {var}(x_{1}) = 1$ as in case 1. The set of candidate clauses can be expanded by also considering the unassigned neighbors of the variables in $\mathsf {neighbors}(\alpha )$. For example, $\mathsf {neighbors}(x_{8}) = \{x_{3}, x_{7}, x_{9}\}$, of which $x_{9}$ is new and unassigned. This adds $(\overline{x}_{1} \vee x_{9})$ and $(\overline{x}_{1} \vee \overline{x}_{9})$ to the set of candidate clauses. This can be iterated by including $\mathsf {neighbors}$ of new unassigned variables from the prior step.

We consider both polarities when constructing candidates for a variable. After all candidates for a variable are constructed, the positive reduct for each candidate is generated and solved in order. Note that propagated literals appearing in the partial assignment do not appear in the PR clause. The satisfying assignment is stored as the witness and the PR clause may be learned immediately depending on the learning configuration.

This process is naturally extended to ternary clauses. The binary candidates are generated, and for each candidate $(x \vee y )$, x and y are assigned to false in the first step. The variables $z \in \mathsf {neighbors}(\alpha )$ yield clauses $( x \vee y \vee z)$ and $( x \vee y \vee \overline{z})$. This approach can generate many candidate ternary clauses depending on the connectivity of the formula since each candidate binary clause is expanded. A filtering operation would be useful to avoid the blow-up in number of candidates. There are likely diminishing returns when searching for larger PR clauses because (1) there are more possible candidates, (2) the positive reducts are likely larger, and (3) each clause blocks less of the search space. We consider only unit and binary candidate clauses in our main evaluation.

Ideally, we should construct candidate clauses that are likely PR to reduce the number of failed reducts generated. Note, the (filtered) positive reduct can only be satisfiable if given the partial assignment there exists a reduced, satisfied clause. By focusing on neighbors, we guarantee that such a clause exists. The reduced heuristic in SaDiCaL finds variables in all reduced but unsatisfied clauses. The idea behind this heuristic is to direct the assignment towards conditional autarkies that imply a satisfiable positive reduct [18]. The $\mathsf {neighbors}$ approach generalizes this to variables in all reduced clauses whether or not they are unsatisfied. A comparison can be found in our repository.

5.2 Learning PR Clauses

Given multiple clauses that are PR w.r.t. the same formula, it is possible that some of the clauses conflict with each other and cannot be learned simultaneously. Example 4 shows how learning one PR clause may invalidate the witness of another PR clause. It may be that a different witness exists, but finding it requires regenerating the positive reduct to include the learned PR clause and solving it. The simplest way to avoid conflicting PR clause is to learn PR clauses as they are found. When a reduct is satisfiable, the PR clauses is added to the formula and logged with its witness in the proof. Then subsequent reducts will be generated from the formula including all added PR clauses. Therefore, a satisfiable reduct ensures a PR clause can be learned.

Alternatively, clauses can be found in batches, then a subset of nonconflicting clauses can be learned. The set of conflicts between PR clauses can be computed in polynomial time. For each pair of PR clauses C and D, if the assignment that generated the pruning predicate for D touches C and C is not satisfied by the witness of D, then C conflicts with D. In some cases reordering the two PR clauses may avoid a conflict. In Example 4 learning the second clause would not affect the validity of the first clauses’ witness. Once the conflicts are known, clauses can be learned based on some heuristic ordering. Batch learning configurations are discussed more in the following section.

Example 4

Assume the following clause witness pairs are valid in a formula $\psi$: $\{( x_{1} \vee x_{2} \vee x_{3} ), x_{1} \overline{x}_{2} \overline{x}_{3} \}$, and $\{( x_{1} \vee \overline{x}_{2} \vee x_{4} ), \overline{x}_{1}\overline{x}_2 x_{4}\}$. The first clause conflicts with the second. If the first clause is added to $\psi$, the clause $( x_{1} \vee x_{2} )$ would be in the positive reduct for the second clause, but it is not satisfied by the witness of the second clause.

5.3 Additional Configurations

The sections above describe the PReLearn configuration used in the main evaluation, i.e., finding candidate PR clauses with the $\mathsf {neighbors}$ heuristic and learning clauses instantly as the positive reducts are solved. In this section we present several additional configurations. The time-constrained reader may skip ahead to Section 5.4 for the presentation of our main results.

In batch learning a set of PR clauses are found in batches then learned. Learning as many nonconflicting clauses as possible coincides with the maximum independent set problem. This problem is NP-Hard. We approximate the solution by adding the clause causing the fewest conflicts with unblocked clauses. When a clause is added, the clauses it blocks are removed from the batch and conflict counts are recalculated Alternatively, clauses can be added in a random order. Random ordering requires less computation at the cost of potentially fewer learned PR clauses.

The $\mathsf {neighbors}$ heuristic for constructing candidate clauses can be modified to include a depth parameter. $\mathsf {neighbors}(i)$ indicates the number of iterations expanding the variables. For example, $\mathsf {neighbors}(2)$ expands on the variables in $\mathsf {neighbors}(1)$, seen in Example 3. We also implement the $\mathsf {reduced}$ heuristic, shown in Example 5. Detailed evaluations and comparisons can be found in our repository. In general, we found that the additional configurations did not improve on our main configuration. More work needs to be done to determine when and how to apply these additional configurations.

Example 5

Given the set of clauses $( x_{1} \vee x_{2} \vee x_{3} ) \wedge ( \overline{x}_{1} \vee x_{3} \vee x_{4} ) \wedge ( x_{3} \vee x_{5} )$, and initial assignment $\alpha = x_{1}$, only the second clause is reduced and not satisfied, giving $\mathsf {reduced}(\alpha ) = \{ x_{3}, x_{4} \}$ and candidate clauses $(\overline{x}_{1} \vee x_{3} )$, $(\overline{x}_{1} \vee x_{4} )$, $(\overline{x}_{1} \vee \overline{x}_{3} )$, $(\overline{x}_{1} \vee \overline{x}_{4} )$.

5.4 Implementation

PReLearn was implemented using the inner/outer-solver framework in SaDiCaL. The inner solver acts the same as in SaDiCaL, solving pruning predicates using CDCL. The outer solver is not used for SDCL, but the SDCL data-structures are used to find and learn PR clauses. The outer solver is initialized with the original formula and maintains the list of variables, clauses, and watch pointers. By default, the outer solver has no variables assigned other than learned units. When finding candidates, the variables in the partial clause are assigned in the outer solver. Unit propagation makes it possible to find all reduced clauses in the formula with a single pass. This is necessary for constructing the positive reduct. After a candidate clause has been assigned and the positive reduct solved, the variables are unassigned. This returns the outer solver to the top-level before examining the next candidate. When a PR clause is learned, it is added to the formula along with its watch pointers. Additionally, failed literals are found if assigning a variable at the top-level causes a conflict through unit propagation. The negation of a failed literal is a unit that can be added to the formula.

In a single iteration each variable in the formula is processed in a breadth-first search (BFS) starting from the first variable in the numbering. When a variable is encountered it is first checked whether either assignment of the variable is a failed literal or a unit PR clause. If not, binary candidates are generated based on the selected heuristic and PR clauses are learned based on the learning configuration. Variables are added to the frontier of the BFS as they are encountered during candidate clause generation, but they are not repeated. Optionally, after all variables have been encountered the BFS restarts, now constructing ternary candidates. The repetition continues to the desired clause length. Then another iteration begins again with binary clauses. Running PReLearn multiple times is important because adding PR clauses in one iteration may allow additional clauses to be added in the next.

Fig. 2.

Occurrences of two horizontal dominoes may be replaced by two vertical dominos in a solution. Similarly, occurrences of a horizontal domino atop two vertical dominos can be replaced by shifting the horizontal domino down.

6 Mutilated Chessboard

The mutilated chessboard is an $n \times n$ grid of alternating black and white squares with two opposite corners removed. The problem is whether or not the the board can be covered with $2 \times 1$ dominoes. This can be encoded in CNF by using variables to represent domino placements on the board. At-most-one constraints (using the pairwise encodings) say only one domino can cover each square, and at-least-one constraints (using a disjunction) say some domino must cover each square.

In recent SAT competitions, no proof-generating SAT solver could deal with instances larger than $N = 18$. In ongoing work, we found refutation proofs that contain only units and binary PR clauses for some boards of size $N \le 30$. PReLearn can be modified to automatically find proofs of this type. Running iterations of PReLearn until saturation, meaning no new binary PR clauses or units can be found, yields some set of units and binary PR clauses. Removing the binary PR clauses from the formula and rerunning PReLearn will yield additional units and a new set of binary PR clauses. Repeating the process of removing binary PR clauses and keeping units will eventually derive the empty clause for this problem. Figure 3 gives detailed values for $N=20$. Within each execution (red dotted lines) there are at most 10 iterations (red tick markers), and each iteration learns some set of binary PR clauses (red). Some executions saturate binary PR clauses before the tenth iteration and exit early. At the end of each execution the binary PR clauses are deleted, but the units (blue) are kept for the following execution. A complete DPR proof (PR with deletion) can be constructed by adding deletion information for the binary PR clauses removed between each execution when concatenating the PReLearn proofs. The approach works for mutilated chess because in each execution there are many binary PR clauses that can be learned and will lead to units, but they are mutually exclusive and cannot be learned simultaneously. Further, adding units allows new binary PR clauses to be learned in following executions.

Fig. 3.

Unit and binary PR clauses learned each execution (red-dotted line) until a contradiction was found. Markers on binary PR lines represent an iteration within an execution.

Table 1. Statistics running multiple executions of PReLearn on the mutilated chessboard problem with the configurations described below. Total units includes failed literals and learned PR units. The average units and average binary PR clauses learned during each execution (Exe.) are shown as well.

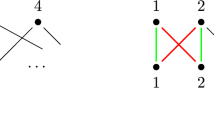
Table 1 shows the statistics for PReLearn. Achieving these results required some modifications to the configuration of PReLearn. First, notice in Figure 2 the PR clauses that can be learned involve blocking one domino orientation that can be replaced by a symmetric orientation. To optimize for these types of PR clauses, we only constructed candidates where the first literal was negative. The $\mathsf {neighbors}$ heuristic had to be increased to a depth of 6, meaning more candidates were generated for each variable. Intuitively, the proof is constructed by adding binary PR clauses in order to find negative units (dominos that cannot be placed) around the borders of the board. Following iterations build more units inwards, until a point is reached where units cover almost the entire board. This forces an impossible domino placement leading to a contradiction. Complete proofs using only units and binary PR clauses were found for boards up to size $N=24$ within 5, 000 seconds. We verified all proofs using DPR-trim. The mutilated chessboard has a high degree of symmetry and structure, making it suitable for this approach. For most problems it is not expected that multiple executions while keeping learned units will find new PR clauses.

Experiments were done with several configurations (see Section 5.3) to find the best results. We found that increasing the depth of $\mathsf {neighbors}$ was necessary for larger boards including $N = 24$. Increasing the depth allows more binary PR clauses to be found, at the cost of generating more reducts. This is necessary to find units. The $\mathsf {reduced}$ heuristic (a subset of $\mathsf {neighbors}$) did not yield complete proofs. We also tried incrementing the depth after each execution starting with 1 and reseting at 9. In this approach, the execution times for depth greater than 6 were larger but did not yield more unit clauses on average. We attempted batch learning on every 500 found clauses using either random or the sorted heuristic. In each batch many of the 500 PR clauses blocked each other because many conflicting PR clauses can be found on a small set of variables in mutilated chess. The PR clauses that were blocked would be found again in following iterations, leading to more reducts generated and solved. This caused much longer execution times. Adding PR clauses instantly is a good configuration for reducing execution time when there are many conflicting clauses. However, for some less symmetric problems it may be worth the tradeoff to learn the clauses in batches, because learning a few bad PR clauses may disrupt the subsequent iterations.

7 SAT Competition Benchmarks

We evaluated PReLearn on previous SAT competition formulas. Formulas from the ’13, ’15, ’16, ’19, ’20, and ’21 SAT competitions’ main tracks were grouped by size. 0-10k contains the 323 formulas with less than 10, 000 clauses and 10k-50k contains the 348 formulas with between 10, 000 and 50, 000 clauses. In general, short PR proofs have been found for hard combinatorial problems typically having few clauses (0-10k). These include the pigeonhole and mutilated chessboard problems, some of which appear in 0-10k benchmarks. The PR clauses that can be derived for these formulas are intuitive and almost always beneficial to solvers. Less is known about the impact of PR clauses on larger formulas, motivating our separation of test sets by size. The repository containing the preprocessing tool, experiment configurations, and experiment data can be found at https://github.com/jreeves3/PReLearn.

We ran our experiments on StarExec [30]. The specs for the compute nodes can be found online.¹ The compute nodes that ran our experiments were Intel Xeon E5 cores with 2.4 GHz, and all experiments ran with 64 GB of memory and a 5, 000 second timeout. We run PReLearn for 50 iterations over 100 seconds, exiting early if no new PR clauses were found in an iteration.

PReLearn was executed as a stand-alone program, producing a derivation proof and a modified CNF. For experiments, the CDCL solver Kissat [5] was called once on the original formula and once on the modified CNF. Kissat was selected because of its high-rankings in previous SAT competitions, but we expect the results to generalize to other CDCL SAT solvers.

Derivation proofs from PReLearn were verified in all solved instances using the independent proof checker DPR-trim using a forward check. This can be extended to complete proofs in the following way. In the unsatisfiable case the proof for the learned PR clauses is concatenated to the proof traced by Kissat, and the complete proof is verified against the original formula. In the satisfiable case the partial proof for the learned PR clauses is verified using a forward check in DPR-trim, and the satisfying assignment found by Kissat is verified by the StarExec post-processing tool. Due to resource limitations, we verified a subset of complete proofs in DPR-trim. This is more costly because it involves running Kissat with proof logging, then running DPR-trim on the complete proof.

Table 2. Fraction of benchmarks where PR clauses were learned, average runtime of PReLearn, generated positive reducts and satisfiable positive reducts (PR clauses learned), and number of failed literals found.

Table 3. Number of total solved instances and exclusive solved instances running Kissat with and without PReLearn. Number of improved instances running Kissat with PReLearn. PReLearn execution times were included in total execution times.

Table 2 shows the cumulative statistics for running PReLearn on the benchmark sets. Note the number of satisfiable reducts is the number of learned PR clauses, because PR clauses are learned immediately after the reduct is solved. These include both unit and binary PR clauses. A very small percentage of generated reducts is satisfiable, and subsequently learned. This is less important for small formulas when reducts can be computed quickly and there are fewer candidates to consider. However, for the 10k-50k formulas the average runtime more than triples but the number of generated reducts less than doubles. PR clauses are found in about two thirds of the formulas, showing our approach generalizes beyond the canonical problems for which we knew PR clauses existed. Expanding the exploration and increasing the time limit did not help to find PR clauses in the remaining one third.

Table 3 gives a high-level picture of PReLearn’s impact on Kissat. PReLearn significantly improves performance on 0-10k SAT and UNSAT benchmarks. These contain the hard combinatorial problems including pigeonhole that PReLearn was expected to perform well on. There were 4 additional SAT formulas solved with PReLearn that Kissat alone could not solve. This shows that PReLearn impacts not only hard unsatisfiable problems but satisfiable problems as well. On the other hand, the addition of PR clauses makes some problems more difficult. This is clear with the 10k-50k results, where 5 benchmarks are solved exclusively with PReLearn and 7 are solved exclusively without. Additionally, PReLearn improved Kissat’s performance on 102 of 671 or approx. $15\%$ of benchmarks. This is a large portion of benchmarks, both SAT and UNSAT, for which PReLearn is helpful.

Fig. 4.

Execution times w/ and w/o PReLearn on 0-10k (top) and 10k-50k (bottom) benchmarks. The left-hand point of each segment shows the time for the SAT solver alone; the right-hand point indicates the combined time for preprocessing and solving.

Figure 4 gives a more detailed picture on the impact of PReLearn per benchmark. In the scatter plot the left-hand end of each line indicates the Kissat execution time, while the length of the line indicates the PReLearn execution time, and so the right-hand end gives the total time for PReLearn plus Kissat. Lines that cross the diagonal indicate that the preprocessing improved Kissat’s performance but ran for longer than the improvement. PReLearn improved performance for points above the diagonal. Points on the dotted-lines (timeout) are solved by one configuration and not the other.

The top plot gives the results for the 0-10k formulas, with many points on the top timeout line as expected. These are the hard combinatorial problems that can only be solved with PReLearn. In general, the unsatisfiable formulas benefit more than the satisfiable formulas. PR clauses can reduce the number of solutions in a formula and this may explain the negative impact on many satisfiable formulas. However, there are still some satisfiable formulas that are only solved with PReLearn.

In the bottom plot, formulas that take a long time to solve (above the diagonal in the upper right-hand corner) are helped more by PReLearn. In the bottom half of the plot, many lines cross the diagonal meaning the addition of PR clauses provided a negligible benefit. For this set there are more satisfiable formulas for which PReLearn is helpful.

The results in Figure 4 are encouraging, with many formulas significantly benefitting from PReLearn. PReLearn improves the performance on both SAT and UNSAT formulas of varying size and difficulty. In addition, lines that cross the diagonal imply that improving the runtime efficiency of PReLearn alone would produce more improved instances. For future work, it would be beneficial to classify formulas before running PReLearn. There may exist general properties of a formula that signal when PReLearn will be useful and when PReLearn will be harmful to a CDCL solver. For instance, a formula’s community structure [2] may help focus the search to parts of the formula where PR clauses are beneficial.

Table 4. Some formulas solved by Kissat exclusively with PReLearn (top) and some formulas solved exclusively without PReLearn (bottom). (*) solved without Kissat. Clauses include PR clauses and failed literals learned.

7.1 Benchmark Families

In this section we analyze benchmark families that PReLearn had the greatest positive (negative) effect on, found in Table 4. Studying the formulas PReLearn works well on may reveal better heuristics for finding good PR clauses.

It has been shown that PR works well for hard combinatorial problems based on perfect matchings [14, 15]. The perfect matching benchmarks (randomG) [7] are a generalization of the pigeonhole (php) and mutilated chessboard problems with varying at-most-one encodings and edge densities. The binary PR clauses can be intuitively understood as blocking two edges from the perfect matching if there exists two other edges that match the same nodes. These benchmarks are relatively small but extremely hard for CDCL solvers. Symmetry-breaking with PR clauses greatly reduces the search space and leads Kissat to a short proof of unsatisfiability. PReLearn also benefits other hard combinatorial problems that use pseudo-Boolean constraints. The pseudo-Boolean (Pb-chnl) [24] benchmarks are based on at-most-one constraints (using the pairwise encoding) and at-least-one constraints. These formulas have a similar graphical structure to the perfect matching benchmarks. Binary PR clauses block two edges when another set of edges exists that are incident to the same nodes.

For the other two benchmark families that benefited from PReLearn, the intuition behind PR learning is less clear. The fixed-shape random formulas (fsf) [29] are parameterized non-clausal random formulas built from hyper-clauses. The SAT encoding makes use of the Plaisted-Greenbaum transformation, introducing circuit-like structure to the problem. The superpermutation problem (sp) [22] asks whether a sequence of digits 1–n of length l can contain every permutation of [1, n] as a subsequence, and the optimization variant asks for the smallest such l given n. The sequence of l digits is encoded directly and passed through a multi-layered circuit that checks for the existence of each individual permutation. Digits use the binary (bin) or unary (una) encoding, are strict stri if clauses constrain digit bits to valid encodings and nonstrict nons otherwise, and flat if the circuit is a large AND or tree for prefix recognizing nested circuits. The formulas given ask to find a prefix of a superpermutation for $n=5$ or length 26 with 19 permutations. The check for 19 permutations was encoded as cardinality constraints in a pseudo-Boolean instance, then converted back to SAT. Each individual permutation is checked by duplicating circuits at each possible starting position of the permutation in l. PR clauses may be pruning certain starting positions for some permutations or affecting the pseudo-Boolean constraints. This cannot be determined without a deeper knowledge of the benchmark generator.

The relativized pigeonhole problem (rphp) [3] involves placing k pigeons in $k-1$ holes with n nesting places. This problem has polynomial hardness for resolution, unlike the exponential hardness of the classical pigeonhole problem. The symmetry-breaking preprocessor BreakID [9] generates symmetry-breaking formulas for rphp that are easy for a CDCL solver. PReLearn can learn many PR clauses but the formula does not become easier. Note PReLearn can solve the php with $n=12$ in a second.

One problem is clause and variable permuting (a.k.a. shuffling). The mutilated chessboard problem can still be solved by PReLearn after permuting variables and clauses. The pigeonhole problem can be solved after permuting clauses but not after permuting variable names. In PReLearn, PR candidates are sorted by variable name independent of clause ordering, but when the variable names change the order of learned clauses changes. In the mutilated chessboard problem there is local structure, so similar PR clauses are learned under variable renaming. In the pigeonhole problem there is global structure, so a variable renaming can significantly change the binary PR clauses learned and cause earlier saturation with far fewer units.

Another problem is that the addition of PR clauses can change the existing structure of a formula and negatively affect CDCL heuristics. The Pythagorean Triples Problem (Ptn) [19] asks whether monochromatic solutions of the equation $a^{2} + b^{2} = c^{2}$ can be avoided. The formulas encode numbers $\{1, \dots , 7824\}$, for which a valid 2-coloring is possible. In the namings, the N in bN denotes the number of backbone literals added to the formula. A backbone literal is a literal assigned true in every solution. Adding more than 20 backbone literals makes the problem easy. For each formula Kissat can find a satisfying assignment, but timeouts with the addition of PR clauses. For one instance, adding only 39 PR clauses will lead to a timeout. In some hard SAT and UNSAT problems solvers require some amount of luck and adding a few clauses or shuffling a formula can cause a CDCL solver’s performance to sharply decrease. The Pythagorean Triples problem was originally solved with a local search solver, and local search still performs well after adding PR clauses.

In a straight-forward way, one can avoid the negative effects of adding harmful PR clauses by running two solvers in parallel: one with PReLearn and one without. This fits with the portfolio approach for solving SAT problems.

8 Conclusion and Future Work

In this paper we presented PReLearn, a tool built from the SaDiCaL framework that learns PR clauses in a preprocessing stage. We developed several heuristics for finding PR clauses and multiple configurations for clause learning. In the evaluation we found that PReLearn improves the performance of the CDCL solver Kissat on many benchmarks from past SAT competitions.

For future work, quantifying the usefulness of each PR clause in relation to guiding the CDCL solver may lead to better learning heuristics. This is a difficult task that likely requires problem specific information. Separately, failed clause caching can improve performance by remembering and avoiding candidate clauses that fail with unsatisfiable reducts in multiple iterations. This would be most beneficial for problems like the mutilated chessboard that have many conflicting PR clauses. Lastly, incorporating PReLearn during in-processing may allow for more PR clauses to be learned. This could be implemented with the inner/outer solver framework but would require a significantly narrowed search. CDCL learns many clauses during execution and it would be infeasible to examine binary PR clauses across the entire formula.