Abstract
This paper contains a Schur analytic approach to a truncated matricial moment problem of Hamburger type, which is studied in the most general case. It is shown that a Schur type algorithm constructed by the authors for a related moment problem can be suitably modified to obtain a full description of the solution set with the aid of a linear fractional transformation with polynomial generating matrix-valued function. The main feature of our Schur type algorithm consists of an appropriate synthesis of two different versions of types of algorithms, namely on the one side an algebraic one working for sequences of complex matrices and on the other side a function theoretic one applied to special classes of holomorphic matrix functions.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
References
V.M. Adamyan, I.M. Tkachenko, Solution of the truncated matrix Hamburger moment problem according to M. G. Krein, in Operator Theory and Related Topics, vol. II (Odessa, 1997). Operator Theory Advance Application, vol. 118 (Birkhäuser, Basel, 2000), pp. 33–51
V.A. Bolotnikov, On degenerate Hamburger moment problem and extensions of nonnegative Hankel block matrices. Integr. Equ. Oper. Theory 25(3), 253–276 (1996)
V.A. Bolotnikov, On Degenerate Hamburger Moment Problem and Extensions of Positive Semidefinite Hankel Block Matrices (2008). arXiv:0812.4567 [math.CA]
G.N. Chen, Y.J. Hu, The truncated Hamburger matrix moment problems in the nondegenerate and degenerate cases, and matrix continued fractions. Linear Algebra Appl. 277(1–3), 199–236 (1998)
G.N. Chen, Y.J. Hu, A unified treatment for the matrix Stieltjes moment problem in both nondegenerate and degenerate cases. J. Math. Anal. Appl. 254(1), 23–34 (2001)
A.E. Choque Rivero, Yu.M. Dyukarev, B. Fritzsche, B. Kirstein, A truncated matricial moment problem on a finite interval, in Interpolation, Schur Functions and Moment Problems. Operator Theory Advance Application, vol. 165 (Birkhäuser, Basel, 2006), pp. 121–173
V.A. Derkach, S. Hassi, H. de Snoo, Truncated moment problems in the class of generalized Nevanlinna functions. Math. Nachr. 285(14–15), 1741–1769 (2012)
V.K. Dubovoj, B. Fritzsche, B. Kirstein, Matricial version of the classical Schur problem, in Teubner-Texte zur Mathematik [Teubner Texts in Mathematics], vol. 129 (B. G. Teubner Verlagsgesellschaft mbH, Stuttgart, 1992). With German, French and Russian summaries
H. Dym, On Hermitian block Hankel matrices, matrix polynomials, the Hamburger moment problem, interpolation and maximum entropy. Integr. Equ. Oper. Theory 12(6), 757–812 (1989)
Y.M. Dyukarev, B. Fritzsche, B. Kirstein, C. Mädler, H.C. Thiele, On distinguished solutions of truncated matricial Hamburger moment problems. Complex Anal. Oper. Theory 3(4), 759–834 (2009)
B. Fritzsche, B. Kirstein, C. Mädler, On Hankel nonnegative definite sequences, the canonical Hankel parametrization, and orthogonal matrix polynomials. Complex Anal. Oper. Theory 5(2), 447–511 (2011)
B. Fritzsche, B. Kirstein, C. Mädler, On matrix-valued Herglotz-Nevanlinna functions with an emphasis on particular subclasses. Math. Nachr. 285(14–15), 1770–1790 (2012)
B. Fritzsche, B. Kirstein, C. Mädler, T. Schwarz, On a Schur-type algorithm for sequences of complex p × q-matrices and its interrelations with the canonical Hankel parametrization, in Interpolation, Schur Functions and Moment Problems. II. Operator Theory Advance Application, vol. 226 (Birkhäuser/Springer, Basel, 2012), pp. 117–192
B. Fritzsche, B. Kirstein, C. Mädler, T. Schwarz, On the concept of invertibility for sequences of complex p × q-matrices and its application to holomorphic p × q-matrix-valued functions, in Interpolation, Schur Functions and Moment Problems. II. Operator Theory Advance Application, vol. 226 (Birkhäuser/Springer, Basel, 2012), pp. 9–56
B. Fritzsche, B. Kirstein, C. Mädler, On a simultaneous approach to the even and odd truncated matricial Hamburger moment problems, in Recent Advances in Inverse Scattering, Schur Analysis and Stochastic Processes. Operator Theory Advance Application, vol. 244 (Birkhäuser/Springer, Cham, 2015), pp. 181–285
B. Fritzsche, B. Kirstein, C. Mädler, On a simultaneous approach to the even and odd truncated matricial Stieltjes moment problem I: An α-Schur-Stieltjes-type algorithm for sequences of complex matrices. Linear Algebra Appl. 521, 142–216 (2017)
B. Fritzsche, B. Kirstein, C. Mädler, On a simultaneous approach to the even and odd truncated matricial Stieltjes moment problem II: an α-Schur–Stieltjes-type algorithm for sequences of holomorphic matrix-valued functions. Linear Algebra Appl. 520, 335–398 (2017)
B. Fritzsche, B. Kirstein, C. Mädler, On the structure of Hausdorff moment sequences of complex matrices, in Advances in Complex Analysis and Operator Theory. Trends Mathematical (Birkhäuser/Springer, Cham, 2017), pp. 165–217
B. Fritzsche, B. Kirstein, C. Mädler, An application of the Schur complement to truncated matricial power moment problems, in Operator Theory, Analysis and the State Space Approach Operator Theory Advance Application, vol. 271 (Birkhäuser/Springer, Cham, 2018), pp. 215–238
B. Fritzsche, B. Kirstein, C. Mädler, T. Schröder, On the truncated matricial Stieltjes moment problem
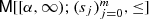 . Linear Algebra Appl. 544, 30–114 (2018)
. Linear Algebra Appl. 544, 30–114 (2018)B. Fritzsche, B. Kirstein, C. Mädler, Matricial canonical moments and parametrization of matricial Hausdorff moment sequences. Complex Anal. Oper. Theory 13(5), 2123–2169 (2019)
B. Fritzsche, B. Kirstein, C. Mädler, A closer look at the solution set of the truncated matricial moment problem
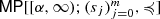 , in Function Theory, Operator Theory, Schur Analysis and System Theory—A Volume in Honor of V. E. Katsnelson, ed. by D. Alpay, B. Fritzsche, B. Kirstein. Operator Theory Advance Application, vol. 280 (Springer, Switzerland, 2020), pp. 387–492
, in Function Theory, Operator Theory, Schur Analysis and System Theory—A Volume in Honor of V. E. Katsnelson, ed. by D. Alpay, B. Fritzsche, B. Kirstein. Operator Theory Advance Application, vol. 280 (Springer, Switzerland, 2020), pp. 387–492B. Fritzsche, B. Kirstein, C. Mädler, Schur analysis of matricial Hausdorff moment sequences. Linear Algebra Appl. 590, 133–209 (2020)
B. Fritzsche, B. Kirstein, C. Mädler, A Schur–Nevanlinna type algorithm for the truncated matricial Hausdorff moment problem. Complex Anal. Oper. Theory. 15(2), 1–129 (2021)
F. Gesztesy, E.R. Tsekanovskii, On matrix-valued Herglotz functions. Math. Nachr. 218, 61–138 (2000)
I.S. Kats, On Hilbert spaces generated by monotone Hermitian matrix-functions. Har’kov Gos. Univ. Uč. Zap. 34 = Zap. Mat. Otd. Fiz.-Mat. Fak. i Har’kov. Mat. Obšč. (4) 22, 95–113 (1950/1951)
I.V. Kovalishina, Analytic theory of a class of interpolation problems. Izv. Akad. Nauk SSSR Ser. Mat. 47(3), 455–497 (1983)
C. Mädler, Behandlung finiter matrizieller Potenzmomentenprobleme mittels Algorithmen vom Schur-Nevanlinna-Typ. Habilitationsschrift (Universität Leipzig, Leipzig, 2017)
R. Nevanlinna, Asymptotische Entwicklungen beschränkter Funktionen und das Stieltjessche Momentenproblem. Ann. Acad. Sci. Fenn. Ser. A 18, 53 (1922)
V.P. Potapov, Linear-fractional transformations of matrices, in Studies in the Theory of Operators and their Applications (Russian), vol. 177, ed. by V.A. Marchenko (“Naukova Dumka”, Kiev, 1979), pp. 75–97
M. Rosenberg, The square-integrability of matrix-valued functions with respect to a non-negative Hermitian measure. Duke Math. J. 31, 291–298 (1964)
H.C. Thiele, Einige Klassen holomorpher Matrixfunktionen und zugehörige Integraldarstellungen. Diplomarbeit (Universität Leipzig, Leipzig, 2002)
H.C. Thiele, Beiträge zu matriziellen Potenzmomentenproblemen. Dissertation (Universität Leipzig, Leipzig, 2006)
J. Weidmann, Lineare Operatoren in Hilberträumen (B. G. Teubner, Stuttgart, 1976). Mathematische Leitfäden
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
Appendix A Some Particular Facts on Matrix Theory
Remark A.1
Let  and let
and let  be such that
be such that  . Then
. Then  and
and  .
.
For each  , there exists a unique matrix X such that the four equations AXA = A, XAX = X,
, there exists a unique matrix X such that the four equations AXA = A, XAX = X,  , and (XA)∗ = XA hold true. This particular matrix X is said to be the Moore–Penrose inverse of A and one writes
, and (XA)∗ = XA hold true. This particular matrix X is said to be the Moore–Penrose inverse of A and one writes  for this matrix X. In particular, if A is a non-singular complex q × q matrix, then
for this matrix X. In particular, if A is a non-singular complex q × q matrix, then  . It seems to be useful stating some basic results on Moore–Penrose inverses of complex matrices.
. It seems to be useful stating some basic results on Moore–Penrose inverses of complex matrices.
Remark A.2
If  , then
, then  .
.
Lemma A.3 (see e. g. [8, Lem. 1.1.9])
Let
 and let
and let
be the block representation of E with p × p block a. Then the matrix E is non-negative Hermitian if and only if the four conditions ,
,  , c = b
∗
, and
, c = b
∗
, and are fulfilled.
are fulfilled.
A complex p × q matrix K is called contractive in case ∥K∥S ≤ 1.
Remark A.4
Let  . Using Lemma A.3 (see also, e. g., [8, Thm. 1.1.2]), easily one can see that the matrix K is contractive if and only if the matrix I
q − K
∗
K is non-negative Hermitian.
. Using Lemma A.3 (see also, e. g., [8, Thm. 1.1.2]), easily one can see that the matrix K is contractive if and only if the matrix I
q − K
∗
K is non-negative Hermitian.
Remark A.5
Let \(\widetilde {J}_{q}\) be given by (4.1). Let  be such that
be such that

In view of

then  . In particular,
. In particular,  if and only if
if and only if  .
.
Remark A.6
Let  be such that (A.2) and
be such that (A.2) and  hold true. In view of Remark A.5, then
hold true. In view of Remark A.5, then  . Because of
. Because of  and Remark A.4, moreover, the matrix
and Remark A.4, moreover, the matrix  is contractive.
is contractive.
Remark A.7
Let C be a contractive complex q × q matrix. Let  and
and  . Because of
. Because of

then  . Regarding Remark 4.1 and that C is contractive, furthermore
. Regarding Remark 4.1 and that C is contractive, furthermore

Clearly,  .
.
We will write  for the (left) Euclidean inner product in
for the (left) Euclidean inner product in  , i. e., for all
, i. e., for all  , let
, let  . If
. If  is a non-empty subset of
is a non-empty subset of  , then the set
, then the set  of all
of all  which fulfil
which fulfil  for all
for all  is a subspace of
is a subspace of  and is called (left) orthogonal complement of
and is called (left) orthogonal complement of  . If
. If  and
and  are subspaces of
are subspaces of  such that
such that  for every choice of u in
for every choice of u in  and w in
and w in  , then
, then  and
and  is said to be the orthogonal sum of
is said to be the orthogonal sum of  and
and  . If
. If  is a subspace of
is a subspace of  , then there exists exactly one matrix
, then there exists exactly one matrix  such that both
such that both  and
and  are fulfilled for each
are fulfilled for each  . This matrix
. This matrix  is called the orthoprojection matrix onto
is called the orthoprojection matrix onto  . In particular,
. In particular,  for all
for all  . A complex q × q matrix P is said to be an orthogonal projection matrix, if there exists a subspace
. A complex q × q matrix P is said to be an orthogonal projection matrix, if there exists a subspace  of
of  such that
such that  .
.
Proposition A.8
Let . Then P is an orthogonal projection matrix if and only if P
2 = P and P
∗ = P hold true.
. Then P is an orthogonal projection matrix if and only if P
2 = P and P
∗ = P hold true.
For a detailed proof of Proposition A.8, see, e. g., [34, Satz 2.54].
Remark A.9
If  is a subspace of
is a subspace of  , then
, then  .
.
Lemma A.10
Let
 and let
and let
 be a sequence of linear subspaces of
be a sequence of linear subspaces of
 such that
such that

holds true. For all
 , let
, let
 and let
and let
 . Then
. Then
Proof
From (A.3) and a well-known result on orthoprojection matrices (see, e. g., [34, Satz 4.31]) we get that  holds true for all
holds true for all  . Moreover, (A.3) and a further well-known result on orthoprojection matrices (see, e. g., [34, Satz 4.30(c)]) deliver the equations
. Moreover, (A.3) and a further well-known result on orthoprojection matrices (see, e. g., [34, Satz 4.30(c)]) deliver the equations  for all
for all  and the representation
and the representation  as orthogonal sum. Therefore, using the Kronecker delta δ
jk, it is readily checked that (P
j − P
j−1)(P
k − P
k−1) = δ
jk(P
j − P
j−1) for all
as orthogonal sum. Therefore, using the Kronecker delta δ
jk, it is readily checked that (P
j − P
j−1)(P
k − P
k−1) = δ
jk(P
j − P
j−1) for all  and, consequently,
and, consequently,
□
Remark A.11
Let  be a subspace of
be a subspace of  with dimension
with dimension  . Let u
1, u
2, …, u
d be an orthonormal basis of
. Let u
1, u
2, …, u
d be an orthonormal basis of  and let
and let  . Then
. Then  .
.
Remark A.12
For each  , the equations
, the equations  as well as
as well as  hold true.
hold true.
Remark A.13
If  , then
, then  and
and  .
.
Lemma A.14
Let
 . Then:
. Then:
-
(a)
Let
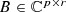 . Then
. Then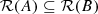 if and only if
if and only if .
. -
(b)
Let
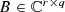 . Then
. Then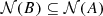 if and only if
if and only if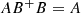 .
.
Remark A.15
Let  be such that
be such that  fulfils 1 ≤ r ≤ q − 1. Let u
1, u
2, …, u
q be an orthonormal basis of
fulfils 1 ≤ r ≤ q − 1. Let u
1, u
2, …, u
q be an orthonormal basis of  such that u
1, u
2, …, u
r is a basis of
such that u
1, u
2, …, u
r is a basis of  , let
, let  , and let
, and let  . For every choice of
. For every choice of  , then
, then  and
and  .
.
Lemma A.16
Let , let
, let be such that U
∗
U = I
r
, and let
be such that U
∗
U = I
r
, and let . Then the matrices
. Then the matrices and
and fulfil
fulfil and
and as well as\(B^* A=U\widetilde {B}^*\widetilde {A}U^*\)
. In particular,
as well as\(B^* A=U\widetilde {B}^*\widetilde {A}U^*\)
. In particular, if and only if
if and only if .
.
Proof
Clearly,  . Moreover, we have \(A^* A=U\widetilde {A}^* U^* U\widetilde {A}U^*=U\widetilde {A}^*\widetilde {A}U^*\). Obviously,
. Moreover, we have \(A^* A=U\widetilde {A}^* U^* U\widetilde {A}U^*=U\widetilde {A}^*\widetilde {A}U^*\). Obviously,  . Taking additionally into account Proposition A.8, we consequently obtain
. Taking additionally into account Proposition A.8, we consequently obtain

as well as

It remains to show that  is fulfilled. In view of (A.4), we have
is fulfilled. In view of (A.4), we have

If r = q, then U is unitary and, therefore,  and the assertion follows from (A.5). Let r < q and
and the assertion follows from (A.5). Let r < q and  . Then there is
. Then there is  such that
such that  is a unitary q × q matrix. In particular,
is a unitary q × q matrix. In particular,
hold true. Using U
∗
U = I
r and Remarks A.11 and A.9, then  and
and  follow. Additionally using (A.5) and (A.6), we obtain
follow. Additionally using (A.5) and (A.6), we obtain

□
Lemma A.17
Let be such that
be such that fulfils r ≥ 1. Let u
1, u
2, …, u
rbe an orthonormal basis of
fulfils r ≥ 1. Let u
1, u
2, …, u
rbe an orthonormal basis of and let
and let . Furthermore, let P and Q be complex q × q matrices such that
. Furthermore, let P and Q be complex q × q matrices such that as well as
as well as and
and hold true. Then the matrix
hold true. Then the matrix is non-singular and the matrices
is non-singular and the matrices and
and fulfil
fulfil and ψ
∗
ϕ = (B
−1
U)∗(Q
∗
P)(B
−1
U). Furthermore, the matrices
and ψ
∗
ϕ = (B
−1
U)∗(Q
∗
P)(B
−1
U). Furthermore, the matrices and
and fulfil the following statements:
fulfil the following statements:
-
(a)
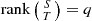 and\(\det (S^* S+T^* T)=\det (\phi ^*\phi +\psi ^*\psi )\).
and\(\det (S^* S+T^* T)=\det (\phi ^*\phi +\psi ^*\psi )\). -
(b)
T ∗ S = B −∗(Q ∗ P)B −1.
-
(c)
S = PB −1and T = QB −1as well as
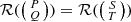 .
.
Proof
The idea of the proof is taken from [2, Lem. 4.3]. We only consider the case r < q. Let  . Then there is
. Then there is  such that
such that  is a unitary q × q matrix. In particular, (A.6) holds true. Using Remark 4.1, we get
is a unitary q × q matrix. In particular, (A.6) holds true. Using Remark 4.1, we get  . Set
. Set  , then Remark A.6 shows that \(\det B\neq 0\) and that
, then Remark A.6 shows that \(\det B\neq 0\) and that  is contractive. Since W is unitary, then the matrix
is contractive. Since W is unitary, then the matrix  is contractive as well. Moreover, we have
is contractive as well. Moreover, we have

Obviously,  and B + A = 2Q are true and, consequently,
and B + A = 2Q are true and, consequently,

follow. According to Remark A.11, we have  . Thus,
. Thus,  yields UU
∗
P = P. Therefore, (A.7) and (A.6) imply
yields UU
∗
P = P. Therefore, (A.7) and (A.6) imply  , i. e., V
∗
C = V
∗. Considering (A.6), then the lower blocks of K read V
∗
CU = V
∗
U = 0d×r and V
∗
CV = V
∗
V = I
d which is, in particular, unitary. Consequently, K admits the block representation
, i. e., V
∗
C = V
∗. Considering (A.6), then the lower blocks of K read V
∗
CU = V
∗
U = 0d×r and V
∗
CV = V
∗
V = I
d which is, in particular, unitary. Consequently, K admits the block representation

and, therefore,

Due to (A.7), we infer
and
In view of (A.6) and  and using Remark A.9, we have
and using Remark A.9, we have  . Consequently, PB
−1 = S and QB
−1 = T hold true which proves (c) and
. Consequently, PB
−1 = S and QB
−1 = T hold true which proves (c) and  . Assertion (b) immediately follows from (c). Using U
∗
U = I
r and
. Assertion (b) immediately follows from (c). Using U
∗
U = I
r and  , the application of Lemma A.16 yields \(\det (S^* S+T^* T)=\det (\phi ^*\phi +\psi ^*\psi )\) and
, the application of Lemma A.16 yields \(\det (S^* S+T^* T)=\det (\phi ^*\phi +\psi ^*\psi )\) and  . Moreover, considering that T
∗
S = U(ψ
∗
ϕ)U
∗ holds true, finally we obtain
. Moreover, considering that T
∗
S = U(ψ
∗
ϕ)U
∗ holds true, finally we obtain
which completes the proof. □
Appendix B Some Facts on the Integration Theory of Non-negative Hermitian Measures
In this section, we present basic facts regarding the integration theory with respect to non-negative Hermitian measures. Throughout the section, let  . We write
. We write  denoting the σ-algebra of all Borel subsets of
denoting the σ-algebra of all Borel subsets of  . Let Ω be a non-empty set and let
. Let Ω be a non-empty set and let  be a σ-algebra on Ω. Consider a measure ν on the measurable space
be a σ-algebra on Ω. Consider a measure ν on the measurable space  . We use
. We use  to denote the set of all
to denote the set of all  -
- -measurable functions
-measurable functions  such that
such that  . We will write
. We will write  for the σ-algebra of all Borel subsets of
for the σ-algebra of all Borel subsets of  . An
. An  -
- -measurable function
-measurable function  is said to be integrable with respect to ν if
is said to be integrable with respect to ν if  belongs to
belongs to  , i. e. all entries f
jk belong to the class
, i. e. all entries f
jk belong to the class  . In this case, let
. In this case, let

A matrix-valued function μ the domain of which is  and the values of which belong to the set
and the values of which belong to the set  of all non-negative Hermitian complex q × q matrices is called non-negative Hermitian q × q measure on
of all non-negative Hermitian complex q × q matrices is called non-negative Hermitian q × q measure on  if it is σ-additive, i. e., if μ fulfils
if it is σ-additive, i. e., if μ fulfils  for each sequence
for each sequence  of pairwise disjoint sets belonging to
of pairwise disjoint sets belonging to  . By
. By  we denote the set of all non-negative Hermitian q × q measures on
we denote the set of all non-negative Hermitian q × q measures on  , i. e., the set of all σ-additive mappings
, i. e., the set of all σ-additive mappings  . Let
. Let  . For each
. For each  and for each
and for each  , the function μ
jk describes a complex measure on
, the function μ
jk describes a complex measure on  and the variation ν
jk of μ
jk is a finite measure on
and the variation ν
jk of μ
jk is a finite measure on  . Especially, μ
11, μ
22, …, μ
qq and the so-called trace measure
. Especially, μ
11, μ
22, …, μ
qq and the so-called trace measure  of μ are finite measures on
of μ are finite measures on  . For each function f belonging to
. For each function f belonging to  we use the notation
we use the notation

For this integral, we write  as well.
as well.
Lemma B.1
Let
 be a measurable space, let
be a measurable space, let
 , and let
, and let
 be an
be an
 -
-
 -measurable mapping. Using standard arguments of measure and integration theory, easily one can see that the following statements are equivalent:
-measurable mapping. Using standard arguments of measure and integration theory, easily one can see that the following statements are equivalent:
-
(i)
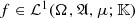 .
. -
(ii)
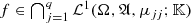 .
. -
(iii)
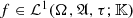 , where τ is the trace measure of μ.
, where τ is the trace measure of μ.
-
(iv)
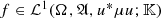 for each
for each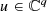 .
.
Now we turn our attention to an other integral based on investigations by I. S. Kats [26] and M. Rosenberg [31]. Let  be a measurable space and let
be a measurable space and let  . Then, for every choice of j and k in
. Then, for every choice of j and k in  , the complex measure μ
jk is absolutely continuous with respect to the trace measure τ of μ. If ν describes an arbitrary measure on
, the complex measure μ
jk is absolutely continuous with respect to the trace measure τ of μ. If ν describes an arbitrary measure on  such that, for all
such that, for all  , the complex measure μ
jk is absolutely continuous with respect to ν, we say that μ is absolutely continuous with respect to ν and the matrix-valued function
, the complex measure μ
jk is absolutely continuous with respect to ν, we say that μ is absolutely continuous with respect to ν and the matrix-valued function  built by the corresponding Radon–Nikodym derivatives of μ
jk with respect to ν is said to be a version of the Radon–Nikodym derivative of μ with respect to ν and is well defined up to sets of zero ν-measure. An ordered pair
built by the corresponding Radon–Nikodym derivatives of μ
jk with respect to ν is said to be a version of the Radon–Nikodym derivative of μ with respect to ν and is well defined up to sets of zero ν-measure. An ordered pair  consisting of an
consisting of an  -
- -measurable function
-measurable function  and an
and an  -
- -measurable function
-measurable function  is said to be left-integrable with respect to μ if \(\Phi \mu _{\tau }^{\prime }\Psi ^*\) belongs to
is said to be left-integrable with respect to μ if \(\Phi \mu _{\tau }^{\prime }\Psi ^*\) belongs to  . In this case the integral
. In this case the integral

is (well) defined and we also write  for this integral.
for this integral.
Appendix C Linear Fractional Transformations of Matrices
In this appendix we summarize some basic facts on linear fractional transformations of matrices. Our considerations modify results due to V. P. Potapov [30], stated in [20].
Remark C.1
Let  and
and  . Then easily one can check that the following statements are equivalent (see, e. g., [20, Lem. D.2]):
. Then easily one can check that the following statements are equivalent (see, e. g., [20, Lem. D.2]):
-
(i)
The set
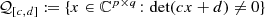 is non-empty.
is non-empty. -
(ii)
The set
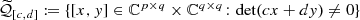 is non-empty.
is non-empty. -
(iii)
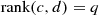 .
.
Notation C.2
Let  and let (A.1) be the block representation of E with p × p block a. If
and let (A.1) be the block representation of E with p × p block a. If  , then the linear fractional transformations
, then the linear fractional transformations  and
and  are defined by
are defined by

Proposition C.3
Let
 and let
and let

be the block representations of E
1and E
2with p × p blocks a
1and a
2
. Let and let (A.1) be the block representation of E with p × p block a. Suppose that
and let (A.1) be the block representation of E with p × p block a. Suppose that and
and hold true. Let
hold true. Let . Then
. Then . Furthermore, if
. Furthermore, if , then
, then for all
for all .
.
A detailed proof of Proposition C.3 is given, e. g., in [20, Prop. D.4]. Note that the conditions  and
and  do not imply
do not imply  (see [20, Example D.6]).
(see [20, Example D.6]).
Rights and permissions
Copyright information
© 2021 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this chapter
Cite this chapter
Fritzsche, B., Kirstein, B., Kley, S., Mädler, C. (2021). Parametrization of the Solution Set of a Matricial Truncated Hamburger Moment Problem by a Schur Type Algorithm. In: Alpay, D., Peretz, R., Shoikhet, D., Vajiac, M.B. (eds) New Directions in Function Theory: From Complex to Hypercomplex to Non-Commutative. Operator Theory: Advances and Applications(), vol 286. Birkhäuser, Cham. https://doi.org/10.1007/978-3-030-76473-9_9
Download citation
DOI: https://doi.org/10.1007/978-3-030-76473-9_9
Published:
Publisher Name: Birkhäuser, Cham
Print ISBN: 978-3-030-76472-2
Online ISBN: 978-3-030-76473-9
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


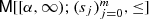 . Linear Algebra Appl. 544, 30–114 (2018)
. Linear Algebra Appl. 544, 30–114 (2018)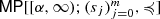 , in Function Theory, Operator Theory, Schur Analysis and System Theory—A Volume in Honor of V. E. Katsnelson, ed. by D. Alpay, B. Fritzsche, B. Kirstein. Operator Theory Advance Application, vol. 280 (Springer, Switzerland, 2020), pp. 387–492
, in Function Theory, Operator Theory, Schur Analysis and System Theory—A Volume in Honor of V. E. Katsnelson, ed. by D. Alpay, B. Fritzsche, B. Kirstein. Operator Theory Advance Application, vol. 280 (Springer, Switzerland, 2020), pp. 387–492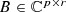 . Then
. Then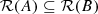 if and only if
if and only if .
.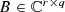 . Then
. Then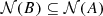 if and only if
if and only if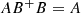 .
.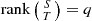 and
and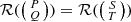 .
.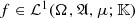 .
.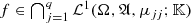 .
.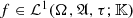 , where τ is the trace measure of μ.
, where τ is the trace measure of μ.
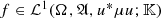 for each
for each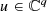 .
.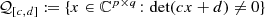 is non-empty.
is non-empty.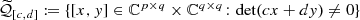 is non-empty.
is non-empty.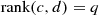 .
.