Abstract
Modern attribute-based anonymous credential (ABC) systems benefit from special encodings that yield expressive and highly efficient show proofs on logical statements. The technique was first proposed by Camenisch and Groß, who constructed an SRSA-based ABC system with prime-encoded attributes that offers efficient AND, OR and NOT proofs. While other ABC frameworks have adopted constructions in the same vein, the Camenisch-Groß ABC has been the most expressive and asymptotically most efficient proof system to date, even if it was constrained by the requirement of a trusted message-space setup and an inherent restriction to finite-set attributes encoded as primes. In this paper, combining a new set commitment scheme and an SDH-based signature scheme, we present a provably secure ABC system that supports show proofs for complex statements. This construction is not only more expressive than existing approaches, but it is also highly efficient under unrestricted attribute space due to its ECC protocols only requiring a constant number of bilinear pairings by the verifier; none by the prover. Furthermore, we introduce strong security models for impersonation and unlinkability under adaptive active and concurrent attacks to allow for the expressiveness of our ABC as well as for a systematic comparison to existing schemes. Given this foundation, we are the first to comprehensively formally prove the security of an ABC with expressive show proofs. Specifically, building upon the q-(co-)SDH assumption, we prove the security against impersonation with a tight reduction. Besides the set commitment scheme, which may be of independent interest, our security models can serve as a foundation for the design of future ABC systems.
This work was supported in part by the European Research Council Starting Grant “Confidentiality-Preserving Security Assurance (CASCAde)” under Grant GA n\(^{\circ }\)716980.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
An anonymous attribute-based credential (ABC) system allows a user to obtain credentials, that is, certified attribute set A from issuers and to anonymously prove the possession of these credentials as well as properties of A. Anonymous credentials were first proposed by Chaum [25] but it does not draw much attention until Brands [12] constructed a pragmatic single-show ABC system and Camenisch and Lysyanskaya (CL) [21] presented a practical multi-show ABC system. CL-ABC system uses the signer’s signature on a committed, and therefore blinded, attribute as the user credential. The proof of possession of a valid credential is a zero-knowledge proof of knowledge on the validity of the signature and the wellformedness of the commitment. This commit-and-sign technique has been employed by ABC systems from RSA-based signature scheme [22] and pairing-based signature schemes [4, 5, 7, 9, 15, 19, 20, 23, 24, 42] on blocks of messages in which the i-th attribute is fixed as the exponent to the i-th base. Therefore, the show proofs have a computational complexity linear to the number of attributes in the credential, in terms of the modular exponentiations and scalar multiplications, respectively.
In contrast to the technique above which is termed as traditional encoding by Camenisch and Groß [17, 18], they suggested a prime encoding for the SRSA-CL signature scheme [22] to offer show proofs on AND, OR and NOT statements with constant complexity for the prime-encoded attributes. Specifically, the Camenisch-Groß (CG) construction separates the unrestricted attribute space \(\mathcal {S}\) into string attributes space and finite-set attributes space such that \(\mathcal {S}=\mathcal {S}_S\cup \mathcal {S}_F\). The CG encoding uses a product of prime numbers to represent a finite-set attribute set \(A_F\in \mathcal {S}_F\) in a single exponent, a technique subsequently applied to graphs as complex data structures [32, 33]. Prime encoding results in highly efficient show proofs: each execution only requires a constant number of modular exponentiations. However, the construction constrains \(\mathcal {S}_F\) to a set of pre-certified prime numbers and increases the public key sizeFootnote 1. Furthermore, the security of the CG ABC system was only established on the properties of its show proofs and not formally on the overall properties of the ABC system. Despite these drawbacks, to the best of our knowledge, CG ABC system [18, 32] is the only ABC system in the standard model that has show proof for AND, OR, and NOT statements with constant complexity.
Related Works. The SDH-CL signature scheme [19, 23, 44] is a popular candidate for the ABC system based on the traditional encoding. It is also referred as the BBS+ signature scheme [1, 4, 5, 11, 45, 48] or the Okamoto signature scheme [2, 39]. Au et al. [4] and Akagi et al. [2] constructed provably secure ABC systems on this foundation while Camenisch et al. [19] integrated a pairing-based accumulator to yield an ABC system that supports revocation. Later, Sudarsono et al. [45] applied the accumulator on \(\mathcal {S}_F\) as in prime encoding and showed that the resulting ABC system can support show proofs for AND and OR statements with constant complexity. Yet, the accumulator requires a large public key size: \(|\mathcal {S}_F|\) finite-set attributes plus the corresponding \(|\mathcal {S}_F|\) signatures. Inspired by the concept of attribute-based signature, Zhang and Feng [48] solved the large public key problem, while additionally supporting threshold statements (ANY) in show proofs, at the cost of having the credential size linear to \(|A_F|\). Comparing the traditional encoding-based ABC systems to the accumulator-based ABC systems, the latter require more bilinear pairing operations in the show proofs, and having either large public key or credential sizes.
There were some attempts to apply Camenisch et al.’s accumulator [19] and its variants on P-signatures [35], LRSW-CL signature [34] and structure preserving signatures [6, 40, 43] to support complex non-interactive zero-knowledge (NIZK) show proofs. Among all, Sadiah et al.’s ABC system [43] offers the most expressive show proofs. Considering only \(\mathcal {S}=\mathcal {S}_F\), their ABC system allows constant-size and constant-complexity NIZK show proofs for monotone formulas at the cost of issuing \(|\mathcal {P}(A_F)|\) credentials to every user where \(\mathcal {P}(A_F)\) is the power set of the user attribute set \(A_F\). Instead of performing this expensive process during the issuing protocol, Okishima and Nakanishi’s ABC system [40] generates \(\mathcal {P}(S_F)\) during key generation and inflates the public key size with \(|\mathcal {P}(S_F)|\) signatures to enable constant-size non-interactive witness-indistinguishable (NIWI) show proofs for conjunctive composite formulas. There are also ABC systems [7, 9] that were built on Pointcheval and Sanders’ signature [41]. The ABC system proposed by Bemmann et al. [7] combines both traditional encoding and accumulator [38] to support monotone formulas under the non-interactive proof of partial knowledge protocol [3]. Although it has significantly shorter credential and supports unrestricted attribute space compared to that of Sadiah et al.’s [43], its show proofs complexity is linear to the number of literals in the monotone formula.
The findings on the use of accumulator in constructing ABC system correspond to the observations in the ABC transformation framework proposed by Camenisch et al. [16]. They discovered that the CL signatures are not able to achieve constant-size NIZK show proofs without random oracle. The framework takes in a structure-preserving signature scheme and a vector commitment scheme to produce an UC-secure ABC system. Their instantiation supports constant-size NIZK show proofs on subset statements and provably secure under the common reference string model. Using the similar ingredients, Fuchsbauer et al. [31] constructed an ABC system that offers constant-size NIZK show proofs on subset statement. The security models in the two works, however, are not designed to cover expressive show proofs. Other frameworks [9, 20] that formalized the commit-and-sign technique and even those [7, 40, 43] support show proofs on complex statements also fall short in this aspect.
Research Gap. Existing constructions yield considerable restrictions when expressive show proofs are concerned: The SRSA-based CG scheme [17] as well as accumulator-based schemes [6, 34, 35, 40, 43, 45] constrain the attribute space to finite-set attributes (\(A_F\in \mathcal {S}_F\)) and require a trusted setup that inflates either the public-key size or the credential size. Their expressiveness and the computational complexity are no better than the pairing-based constructions [2, 4, 7, 31, 48] and the general ABC frameworks [9, 16, 20] alike, when only string attributes \((A_S\in \mathcal {S}_S)\) are considered. Expressive proofs for large attribute set are desirable in privacy-preserving applications such as direct anonymous attestation [13, 14, 26,27,28,29]. Also, we observe a need for a systematic canonicalization of security models for all mentioned schemes. In short, an ideal ABC system should have:
-
1.
strong security assurance, and
-
2.
appropriate public key size, and
-
3.
expressive show proofs with low complexity regardless of the attribute space.
Our Contribution. We present a perfectly hiding and computationally binding set commitment scheme, called MoniPoly, which supports set membership proofs and disjointness proofs on the committed messages. Following the commit-and-sign methodology, we combine the MoniPoly commitment scheme tracing back to Kate et al.’s work [36] with SDH-based Camenisch-Lysyanskaya signature scheme [23, 44] to present an efficient ABC system that support expressive show proofs for AND, OR and k-out-of-n threshold (ANY) clauses as well as their respective complements (NAND, NOR and NANY). Our ABC system is the most efficient construction for the unrestricted attribute space to-date. And it is at least as expressive as the existing constructions specially crafted for the restricted attribute space.
To the best of our knowledge, neither the constructions nor security models of existing ABC systems allow for complex interactive show proofs. As an immediate contribution, we rigorously define the necessary and stronger security notions for ABC systems. Our notions for security of impersonation resilience and unlinkability under adaptive active and concurrent attacks are stronger than those of the state-of-the-art ABC systems [16, 20, 31, 40]. We prove the security of our construction with respect to the security against impersonation and linkability in the standard model, especially offering a tight reduction for impersonation resilience under the q-(co-)SDH assumption.
Organization. We organize the paper as follows. In Sect. 2, we briefly introduce the underlying SDH-based CL signature scheme. In Sect. 3, we present the MoniPoly commitment scheme. We present our ABC system which is a combination of the MoniPoly commitment scheme with SDH-based CL signatures [23, 44] in Sect. 4. Section 5 offers an evaluation of the MoniPoly ABC in terms of security properties, expressivity as well as computational complexity in comparison to other schemes in the field.
2 Preliminaries
The MoniPoly commitment and ABC schemes are based on standard mathematical foundations in elliptic curves and bilinear maps as well as notions on signature schemes and proof systems. Readers may refer to the full version [46] for this information.
2.1 The SDH-Based CL Signature Scheme
Camenisch and Lysyanskaya [23] introduced a technique to construct secure pairing-based signature schemes which support signing on committed messages. They also showed that their technique can extract an efficient SDH-based signature scheme from Boneh et al.’s group signature [11] scheme but no security proof was provided. This scheme was later proven to be seuf-cma-secure with a tight reduction [44] to the SDH assumption in the standard model. We describe the SDH-CL signature scheme [19, 23, 44] as follows:
KeyGen(\(1^k)\): Construct three cyclic groups \(\mathbb {G} _1,\mathbb {G} _2,\mathbb {G} _T\) of order p based on an elliptic curve whose bilinear pairing is \(\mathsf {e}:\mathbb {G} _1\times \mathbb {G} _2 \rightarrow \mathbb {G} _T\). Select random generators \(a,b,c \in \mathbb {G} _1\), \(g_2\in \mathbb {G} _2\) and a secret value  . Output the public key \(pk=(\mathsf {e},\mathbb {G} _1,\mathbb {G} _2,\mathbb {G} _T,p,a,b,c,g_2,X=g_2^x)\) and the secret key \(sk=x\).
. Output the public key \(pk=(\mathsf {e},\mathbb {G} _1,\mathbb {G} _2,\mathbb {G} _T,p,a,b,c,g_2,X=g_2^x)\) and the secret key \(sk=x\).
Sign(m, pk, sk): On input m, choose the random values  to compute \(v=(a^mb^sc)^{\frac{1}{x+t}}\). In the unlikely case in which \(x+t=0 \mod p\) occurs, reselect a random t. Output the signature as \(sig = (t,s,v)\).
to compute \(v=(a^mb^sc)^{\frac{1}{x+t}}\). In the unlikely case in which \(x+t=0 \mod p\) occurs, reselect a random t. Output the signature as \(sig = (t,s,v)\).
Verify(m, sig, pk): Given \(sig = (t,s,v)\), output 1 if the equation:
holds and output 0 otherwise.
Theorem 1
[44] SDH-based CL signature scheme is seuf-cma-secure in the standard model if the Strong Diffie-Hellman problem is \((t_{\mathsf {sdh}},\varepsilon _{\mathsf {sdh}})\)-hard.
3 MoniPoly Set Commitment Scheme
The key idea of set commitment scheme traces back to the polynomial commitment scheme [36] which can commit to a polynomial and support opening at indexes of the polynomial. Inheriting this nature, our MoniPoly set commitment scheme and similar ones [16, 31] transform a message  into \((x'+m)\) where
into \((x'+m)\) where  is not known to the user and multiple messages form a monic polynomial \(f(x')=\prod _{i=1}^n(x'+m_i)\). This monic polynomial, in turn, can be rewritten as \(f(x')=\sum _{i=0}^n\mathsf {m}_ix'^i\). Its coefficients
is not known to the user and multiple messages form a monic polynomial \(f(x')=\prod _{i=1}^n(x'+m_i)\). This monic polynomial, in turn, can be rewritten as \(f(x')=\sum _{i=0}^n\mathsf {m}_ix'^i\). Its coefficients  can be efficiently computed, for instance, using the encoding algorithm
can be efficiently computed, for instance, using the encoding algorithm  described in the full version [46].
described in the full version [46].
Our commitment scheme’s unique property is that it treats the opening value as one of the roots in the monic polynomial. Hence, the name MoniPoly. Folding the opening value into the monic polynomial yields compelling advantages, especially, enabling a greater design space for presentation proofs.
While related schemes [16, 31, 36] realize subset opening, our scheme supports the opening of intersection sets and difference sets, in addition. Thus, MoniPoly is more expressive. Furthermore, the presentation proofs created on MoniPoly are more efficient than other commitment-based frameworks. Finally, treating the opening value as a root of the monic polynomial yields a scheme that is closely aligned with well-established commitment scheme paradigms, which, in turn, fits into a range of popular signature schemes and enables signing committed messages.
3.1 Interface
We define the MoniPoly set commitment scheme as the following algorithms:
-
1.
Setup\((1^k,n)\rightarrow (pk,sk)\). A pair of public and secret keys (pk, sk) are generated by a trusted authority based on the security parameter input \(1^k\). The message domain \(\mathcal {D}\) is defined and \(n-1\) is the maximum messages allowed. If n is fixed, sk is not required in the rest of the scheme.
-
2.
Commit\((pk,A,o)\rightarrow (C)\). On the input of pk, a message set \(A\in \mathcal {D}^{n-1}\) and a random opening value \(o\in \mathcal {D}\), output the commitment C.
-
3.
Open\((pk,C,A,o)\rightarrow b\). Return \(b=1\) if C is a valid commitment to A with the opening value o under pk, and return \(b=0\) otherwise.
-
4.
OpenIntersection\((pk,C,A,o,(A',l))\rightarrow (I,W) \text{ or }\perp \). If \(|A'\cap A|\ge l\) holds, return an intersection set \(I =A'\cap A\) of length l with the corresponding witness W, and return an error \(\perp \) otherwise.
-
5.
VerifyIntersection\((pk,C,(I,W),(A',l))\rightarrow b\). Return \(b=1\) if W is a witness for S being the intersection set of length l for \(A'\) and the set committed to in C, and return \(b=0\) otherwise.
-
6.
OpenDifference\((pk,C,A,o,(A',\bar{l}))\rightarrow (D,W)\). If \(|A'-A|\ge \bar{l}\) holds, return the difference set \(D =A'-A\) of length \(\bar{l}\) with the corresponding witness W, and return \(\perp \) otherwise.
-
7.
VerifyDifference\((pk,C,(D,W),(A',\bar{l}))\rightarrow b\). Return \(b=1\) if W is the witness for D being the difference set of length \(\bar{l}\) for \(A'\) and the set committed to in C, and return \(b=0\) otherwise.
3.2 Security Requirements
Definition 1
A set commitment scheme is perfectly hiding if every commitment \(C=\mathsf {Commit}(pk,A,o)\) is uniformly distributed such that there exists an \(o'\ne o\) for all \(A'\ne A\) where \(\mathsf {Open}(pk,C,A',o')=1\).
Definition 2
An adversary \(\mathcal {A}\) is said to \((t_{\mathsf {bind}},\varepsilon _\mathsf {bind})\)-break the binding security of a set commitment scheme if \(\mathcal {A}\) runs in time at most \(t_{\mathsf {bind}}\) and furthermore:
for a negligible probability \(\varepsilon _\mathsf {bind}\) and any two pairs \((A_1,o_1),(A_2,o_2)\) output by \(\mathcal {A}\). We say that a set commitment scheme is \((t_{\mathsf {bind}},\varepsilon _\mathsf {bind})\)-secure wrt. binding if no adversary \((t_{\mathsf {bind}},\varepsilon _\mathsf {bind})\)-breaks the binding security of the set commitment scheme.
3.3 Construction
We describe the MoniPoly commitment scheme as follows:
Setup\((1^k)\). Construct three cyclic groups \(\mathbb {G} _1,\mathbb {G} _2,\mathbb {G} _T\) of order p based on an elliptic curve whose bilinear pairing is \(e:\mathbb {G} _1\times \mathbb {G} _2 \rightarrow \mathbb {G} _T\). Select random generators \(a\in \mathbb {G} _1\), \(g_2\in \mathbb {G} _2\) and a secret values  . Compute the values \(a_0=a,a_1=a^{x'},\ldots ,a_{n}=a^{x'^{n}},X_0=g_2,X_1=g_2^{x'},\ldots ,X_{n}=g_2^{x'^{n}}\) to output the public key \(pk=(\mathsf {e},\mathbb {G} _1,\mathbb {G} _2,\mathbb {G} _T,p,\{a_i,X_i\}_{0\le i \le n })\) and the secret key \(sk=(x')\). Note that sk can be discarded by the authority if the parameter n is fixed.
. Compute the values \(a_0=a,a_1=a^{x'},\ldots ,a_{n}=a^{x'^{n}},X_0=g_2,X_1=g_2^{x'},\ldots ,X_{n}=g_2^{x'^{n}}\) to output the public key \(pk=(\mathsf {e},\mathbb {G} _1,\mathbb {G} _2,\mathbb {G} _T,p,\{a_i,X_i\}_{0\le i \le n })\) and the secret key \(sk=(x')\). Note that sk can be discarded by the authority if the parameter n is fixed.
Commit(pk, A, o). Taking as input a message set  and the random opening value
and the random opening value  , output the commitment as
, output the commitment as
where \(\{\mathsf {m}_j\}=\mathsf {MPEncode}(A\cup \{o\})\).
Open(pk, C, A, o). Return 1 if \(C=\prod _{j=0}^{n}a_j^{\mathsf {m}_j}\) holds where \(\{\mathsf {m}_j\}=\mathsf {MPEncode}(A\cup \{o\})\) and return 0 otherwise.
OpenIntersection\((pk,C,A,o,(A',l))\). If \(|A'\cap A|\ge l\) holds, return an intersection set \(I =A'\cap A\) of length l and a witness such that:
where \(\{\mathsf {w}_{j}\}=\mathsf {MPEncode}((A\cup \{o\})-I)\). Otherwise, return a null value \(\perp \). The correctness can be verified as follows:
VerifyIntersection\((pk,C,I,W,(A',l))\). Return 1 if
holds and return 0 otherwise, where \(\{\mathsf {i}_{j}\}=\mathsf {MPEncode}(I)\), \(\{\mathsf {m}_{1,j}\}=\mathsf {MPEncode}(A')\) and \(\{\mathsf {m}_{2,j}\}=\mathsf {MPEncode}(A'-I)\). The correctness is as follows:
OpenDifference\((pk,C,A,o,(A',\bar{l}))\). If \(|A'\cap A|\ge \bar{l}\) holds, return a difference set \(D =A'- A\) of length \(\bar{l}\) and the witness \((W=\prod _{j=0}^{n-\bar{l}} a_j^{\mathsf {w}_{j}},\{\mathsf {r}_{j}\}_{j=0}^{\bar{l}-1})\). The values \((\{\mathsf {w}_{j}\},\{\mathsf {r}_{j}\})=\mathsf {MPEncode}(A)/\mathsf {MPEncode}(D)\) are computed using expanded synthetic division such that \(\{\mathsf {w}_{j}\}\) are the coefficients of quotient \(q(x')\) and \(\{\mathsf {r}_{j}\}\) are the coefficients of remainder \(r(x')\). Specifically, let the polynomial divisor be \(d(x')=\sum _j^{\bar{l}}\mathsf {d}_jx'^j\) where \(\{\mathsf {d}_j\}=\mathsf {MPEncode}(D)\), the monic polynomial \(f(x')\) in the commitment \(C=a_0^{f(x')}\) can be rewritten as \(f(x')=d(x')q(x')+r(x')\). Note that \(\prod _{j=0}^{\bar{l}-1} a_j^{\mathsf {r}_{j}}\ne 1_{\mathbb {G} _1}\) whenever \(d(x')\) cannot divide \(f(x')\), i.e., the sets A and D are disjoint. The correctness can be verified from the following:
VerifyDifference\((pk,C,D,(W,\{\mathsf {r}_{j}\}_{j=0}^{\bar{l}-1}),(A',\bar{l}))\). Return 1, if the following holds:
and return 0 otherwise, where \(\{\mathsf {d}_{j}\}=\mathsf {MPEncode}(D)\), \(\{\mathsf {m}_{1,j}\}=\mathsf {MPEncode}(A')\) and \(\{\mathsf {m}_{2,j}\}=\mathsf {MPEncode}(A'-D)\). The correctness is as follows:
Remark 1
In the security analysis of MoniPoly, we will take a different approach compared to the previous constructions [16, 31, 36]. We consider the perfectly hiding property and the conventional computational binding property [30] that only requires an adversary cannot present two pairs \((A_1,o_1)\) and \((A_2,o_2)\) such that \(\mathsf {Commit}(pk,A_1,o_1)=\mathsf {Commit}(pk,A_2,o_2)\). We will show in Section 3.4 that this conventional binding property is a superset of formers’ subset binding properties.
3.4 Security Analysis
Theorem 2
The MoniPoly commitment scheme is perfectly hiding.
Proof
Given a commitment \(C=a_0^{(x'+o)\prod _{j=1}^{n-1}(x'+m_j)}\), there are  possible pairs of \(((m_1',\ldots ,m_{n-1}'),o')\ne ((m_1,\ldots ,m_{n-1}),o)\) which can result in the same C. Furthermore, for every committed message set \(\{m_1,\ldots ,m_{n-1}\}\), there is a unique o such that:
possible pairs of \(((m_1',\ldots ,m_{n-1}'),o')\ne ((m_1,\ldots ,m_{n-1}),o)\) which can result in the same C. Furthermore, for every committed message set \(\{m_1,\ldots ,m_{n-1}\}\), there is a unique o such that:
Since o is chosen independently of the committed messages \(\{m_1,\ldots ,m_{n-1}\}\), the latter are perfectly hidden. \(\square \)
The following theorem considers an adversary which breaks the binding property by finding two different message sets A and \(A^*\) which can be of different lengths such that \(|A|\ge |A^*|\). The proof is in the full version [46].
Theorem 3
The MoniPoly commitment scheme is \((t_{\mathsf {bind}},\varepsilon _\mathsf {bind})\)-secure wrt. the binding security if the co-SDH problem is \((t_{\mathsf {cosdh}},\varepsilon _\mathsf {cosdh})\)-hard such that:
where T(n) is the time for dominant group operations in \(\mathbb {G} _1\) to extract a co-SDH solution where n is the total of committed messages plus the opening value.
4 Attribute-Based Anonymous Credential System
Before presenting the formal definition of ABC system, we briefly define the attribute set A and the access policy \(\phi \) in our proposed ABC system which are closely related to MoniPoly’s opening algorithms. Informally, we view a relation between two attribute sets as a clause. Clauses can be accumulated using the logical \(\wedge \) operator in building the composite statement for an access policy.
Attribute. We view a descriptive attribute set \(A=\{m_1,\ldots ,m_n\}\) as a user’s identity. To be precise, an attribute m is an attribute-value pair in the format attribute=value and A is a set of attributes. For instance, the identity of a user can be described as: \(A=\{``\mathsf {gender=male}'',``\mathsf {name=bob}",``\mathsf {ID=123456}",``\mathsf {role=}\) \(\mathsf {manager}",``\mathsf {branch=Y}"\}\).
Access Policy. An access policy \(\phi \) as defined by the BNF grammar in Table 1 expresses the relationship between two attribute sets A and \(A'\). An access policy \(\phi \) is formed by an attribute set A as well as a statement \(\mathsf {stmt}\) that specifies the relation between A and \(A'\). We have some additional rules for the \(\phi \) where we require \(|A|=n>1\) and \(|A'|\le n\). Besides, in the special case of \(|A'|=1\), the connective must be either AND or NAND. An access policy \(\phi \) outputs 1 if the underlying statement is evaluated to true and outputs 0 otherwise. Taking the attribute set A above as an example, we have \(\phi _{\mathsf {stmt}}(A)=\phi _{\mathsf {AND}(A_1')\wedge \mathsf {OR}(A_2')}(A)=1\) for the attribute sets \(A_1'=\{``\mathsf {role=manager}"\}\) and \(A_2'=\{``\mathsf {branch=X}",``\mathsf {branch=Y}",``\mathsf {branch=Z}"\}\). Note that the attribute set \(A'\) has been implicitly defined by \(\mathsf {stmt}\) and we simply write \(\phi _{\mathsf {stmt}}\) in the subsequent sections when the reference to the attribute set \(A'\) is clear.
4.1 Interface
We define an attribute-based anonymous credential system by five algorithms \(\mathsf {ABC}=\{\mathsf {KeyGen}, \mathsf {Obtain}, \mathsf {Issue}, \mathsf {Prove}, \mathsf {Verify}\}\) as follows:
-
1.
\(\mathsf {KeyGen}(1^k,1^n)\rightarrow (pk,sk)\): This algorithm is executed by the issuer. On the input of the security parameter k and the attributes upper bound n, it generates a key pair (pk, sk).
-
2.
\((\mathsf {Obtain}(pk,A), \mathsf {Issue}(pk,sk))\rightarrow (cred \text{ or }\perp )\): These two algorithms form the credential issuing protocol. The first algorithm is executed by the user with the input of the issuer’s public key pk and an attribute set A. The second algorithm is executed by the issuer and takes as input the issuer’s public key pk and secret key sk. At the end of the protocol, Obtain outputs a valid credential cred produced by Issue or a null value \(\perp \) otherwise.
-
3.
\((\mathsf {Prove}(pk,cred,\phi _{\mathsf {stmt}}),\mathsf {Verify}(pk,\phi _{\mathsf {stmt}}))\rightarrow b\): These two algorithms form the credential presentation protocol. The second algorithm is executed by the credential verifier which takes as input the issuer’s public key pk and has the right to decide the access policy \(\phi _{\mathsf {stmt}}\). The first algorithm is executed by the credential prover which takes as input the issuer’s public key pk, user’s credential cred and an access policy \(\phi _{\mathsf {stmt}}\) such that \(\phi _{\mathsf {stmt}}(A)=1\). If \(\phi _{\mathsf {stmt}}(A)=0\), the credential holder aborts and Verify outputs \(b=0\). If \(\phi =\bot \), prover and verifier complete a proof of possession which proves the validity of credential only instead of a show proof which additionally proves the relation between A and \(A'\). At the end of the protocol, Verify outputs \(b=1\) if it accepts prover and outputs \(b=0\) otherwise.
In the following, we define the key security requirements for an anonymous credential system in the form of impersonation resilience and unlinkability.
4.2 Security Requirements
4.2.1 Impersonation Resilience
The security goal of an ABC system requires that it is infeasible for an adversary to get accepted by the verifier in the show proof. The security against impersonation under active and concurrent attacks is described in the following game between an adversary \(\mathcal {A}\) and a challenger \(\mathcal {C}\).
Game 1 (\(\mathsf {imp-aca}(\mathcal {A}, \mathcal {C})\))
-
1.
Setup: \(\mathcal {C}\) runs \(\mathsf {KeyGen}(1^k,1^n)\) and sends pk to \(\mathcal {A}\).
-
2.
Phase 1: \(\mathcal {A}\) is able to issue concurrent queries to the Obtain, Prove and Verify oracles where he plays the role of user, prover and verifier, respectively, on any attribute set \(A_i\) of his choice in the i-th query. \(\mathcal {A}\) can also issue queries to the IssueTranscript oracle which takes in \(A_i\) and returns the corresponding transcripts of issuing protocol.
-
3.
Challenge: \(\mathcal {A}\) outputs the challenge attribute set \(A^*\) and its corresponding access policy \(\phi _{\mathsf {stmt}}^*\) such that \(\phi _{\mathsf {stmt}}^*(A_i)=0\) and \(\phi _{\mathsf {stmt}}^*(A^*)=1\) for every \(A_i\) queried to the Obtain oracle during Phase 1.
-
4.
Phase 2: \(\mathcal {A}\) can continue to query the oracles as in Phase 1 with the restriction that it cannot query an attribute set \(A_i\) to Obtain such that \(\phi _{\mathsf {stmt}}^*(A_i)=1\).
-
5.
Impersonate: \(\mathcal {A}\) completes a show proof as the prover with \(\mathcal {C}\) as the verifier for the access policy \(\phi _{\mathsf {stmt}}^*(A^*)=1\). \(\mathcal {A}\) wins the game if \(\mathcal {C}\) outputs 1.
Definition 3
An adversary \(\mathcal {A}\) is said to \((t_{\mathsf {imp}},\varepsilon _\mathsf {imp})\)-break the imp-aca security of an ABC system if \(\mathcal {A}\) runs in time at most \(t_{\mathsf {imp}}\) and wins in Game 1 such that:
for a negligible probability \(\varepsilon _\mathsf {imp}\). We say that an ABC system is imp-aca-secure if no adversary \((t_{\mathsf {imp}},\varepsilon _\mathsf {imp})\)-wins Game 1.
Note that we reserve the term unforgeability of the signature scheme in contrast to some contributions in the literature [2, 9, 16, 20, 31, 42]. One can view our impersonation resilience notion as the stronger version of the misauthentication resistance from the ABC systems with expressive show proofs [6, 40, 43] which does not cover the active and concurrent adversary besides disallowing adaptive queries. We also introduce a new oracle, namely, \(\mathsf {IssueTranscript}\) that covers the passive adversary for the issuing protocol. This makes our security definition more comprehensive than that by related works [9, 16, 20, 31].
4.2.2 Unlinkability
Unlinkability requires that an adversary cannot link the attributes or instances among the issuing protocols and the presentation protocols. We consider two types of unlinkability notions, namely, full attribute unlinkability and full protocol unlinkability. We require that an adversary, after being involved in the generation of a list of credentials, cannot differentiate the sequence of two attribute sets in the full attribute unlinkability. The security model for full attribute unlinkability under active and concurrent attacks (aunl-aca) is defined as a game between an adversary \(\mathcal {A}\) and a challenger \(\mathcal {C}\).
Game 2 (\(\mathsf {aunl-aca}(\mathcal {A}, \mathcal {C})\))
-
1.
Setup: \(\mathcal {C}\) runs \(\mathsf {KeyGen}\) and sends pk, sk to \(\mathcal {A}\).
-
2.
Phase 1: \(\mathcal {A}\) is able to issue concurrent queries to the Obtain, Issue, Prove and Verify oracles where he plays the role of user, issuer, prover and verifier, respectively, on any attribute set \(A_i\) of his choice in the i-th query. \(\mathcal {A}\) can also issue queries to an additional oracle, namely, Corrupt which takes in a transcript of issuing protocol or show proofs whose user or prover, respectively, is \(\mathcal {C}\) and returns the entire internal state, including the random seed used by \(\mathcal {C}\) in the transcript.
-
3.
Challenge: \(\mathcal {A}\) decides the two equal-length, non-empty attribute sets \(A_0,A_1\) and the access policy \(\phi _{\mathsf {stmt}}^*\) which he wishes to challenge such that \(\phi _{\mathsf {stmt}}^*(A_0)=\phi _{\mathsf {stmt}}^*(A_1)=1\). \(\mathcal {A}\) is allowed to select \(A_0,A_1\) from the existing queries to Obtain in Phase 1. \(\mathcal {C}\) responds by randomly choosing a challenge bit \(b\in \{0,1\}\) and interacts as the user with \(\mathcal {A}\) as the issuer to complete the protocols:
$$\begin{aligned} (\mathsf {Obtain}(pk,A_{b}), \mathsf {Issue}(pk,sk))\rightarrow cred_{b},\\ (\mathsf {Obtain}(pk,A_{1-b}), \mathsf {Issue}(pk,sk))\rightarrow cred_{1-b}. \end{aligned}$$Subsequently, \(\mathcal {C}\) interacts as the prover with \(\mathcal {A}\) as the verifier for polynomially many times as requested by \(\mathcal {A}\) to complete the protocols in the same order:
$$\begin{aligned} (\mathsf {Prove}(pk,cred_{b},\phi _{\mathsf {stmt}}^*),\mathsf {Verify}(pk,\phi _{\mathsf {stmt}}^*))\rightarrow 1,\\ (\mathsf {Prove}(pk,cred_{1-b},\phi _{\mathsf {stmt}}^*),\mathsf {Verify}(pk,\phi _{\mathsf {stmt}}^*))\rightarrow 1. \end{aligned}$$ -
4.
Phase 2: \(\mathcal {A}\) can continue to query the oracles as in Phase 1 except querying the transcripts of the challenged issuing and show proofs to Corrupt.
-
5.
Guess: \(\mathcal {A}\) outputs a guess \(b'\) and wins the game if \(b'=b\).
Definition 4
An adversary \(\mathcal {A}\) is said to \((t_{\mathsf {aunl}},\varepsilon _\mathsf {aunl})\)-break the aunl-aca-security of an ABC system if \(\mathcal {A}\) runs in time at most \(t_{\mathsf {aunl}}\) and wins in Game 2 such that:
for a negligible probability \(\varepsilon _\mathsf {aunl}\). We say that an ABC system is aunl-aca-secure if no adversary \((t_{\mathsf {aunl}},\varepsilon _\mathsf {aunl})\)-wins Game 2.
Our full attribute unlinkability is more generic than that in Camenisch et al.’s ABC transformation frameworks [16] where we assume the challenged attribute sets \(A_0,A_1\) are not equivalent such that \(A_0\ne A_1\). Besides, unlike Ringers et al.’s unlinkability notion [42], ours covers both issuing and show proofs as in Camenisch et al.’s privacy notions [20], though the latter does not have a Corrupt oracle while the former does.
On the other hand, as far as we know, the full protocol unlinkability has not been considered before. This notion requires that an adversary, after being involved in the generation of a list of credentials, cannot link an instance of issuing protocol and an instance of a show proof that are under the same credential. The full protocol unlinkability under active and concurrent attacks (punl-aca) is defined as a game between an adversary \(\mathcal {A}\) and a challenger \(\mathcal {C}\):
Game 3 (\(\mathsf {punl-aca}(\mathcal {A}, \mathcal {C})\)).
-
1.
Setup: Same to that of Game 2.
-
2.
Phase 1: Same to that of Game 2.
-
3.
Challenge: \(\mathcal {A}\) decides the two equal-length, non-empty attribute sets \(A_0,A_1\) and the access policy \(\phi _{\mathsf {stmt}}^*\) which he wishes to challenge such that \(\phi _{\mathsf {stmt}}^*(A_0)=\phi _{\mathsf {stmt}}^*(A_1)=1\). \(\mathcal {A}\) is allowed to select \(A_0,A_1\) from the existing queries to Obtain in Phase 1. \(\mathcal {C}\) responds by randomly choosing two challenge bits \(b_1,b_2\in \{0,1\}\) and interacts as the user with \(\mathcal {A}\) as the issuer to complete the protocols in the order
$$\begin{aligned} (\mathsf {Obtain}(pk,A_{b_1}), \mathsf {Issue}(pk,sk))\rightarrow cred_{b_1},\\ (\mathsf {Obtain}(pk,A_{1-b_1}), \mathsf {Issue}(pk,sk))\rightarrow cred_{1-b_1}. \end{aligned}$$Subsequently, \(\mathcal {C}\) interacts as the prover with \(\mathcal {A}\) as the verifier for polynomially many times as requested by \(\mathcal {A}\) to complete the protocols in the order
$$\begin{aligned} (\mathsf {Prove}(pk,cred_{b_2},\phi _{\mathsf {stmt}}^*),\mathsf {Verify}(pk,\phi _{\mathsf {stmt}}^*))\rightarrow 1,\\ (\mathsf {Prove}(pk,cred_{1-b_2},\phi _{\mathsf {stmt}}^*),\mathsf {Verify}(pk,\phi _{\mathsf {stmt}}^*))\rightarrow 1. \end{aligned}$$ -
4.
Phase 2: Same to that of full attribute unlinkability game.
-
5.
Guess: \(\mathcal {A}\) outputs a guessed pair of issuing protocol transcript \(\pi _{(O,I)}\) and show proof transcript \(\pi _{(P,V)}\) and wins the game if the pair is under the same credential such that \(cred_{\pi _{(O,I)}}=cred_{\pi _{(P,V)}}\).
Definition 5
An adversary \(\mathcal {A}\) is said to \((t_{\mathsf {punl}},\varepsilon _\mathsf {punl})\)-break the punl-aca-security of an ABC system if \(\mathcal {A}\) runs in time at most \(t_{\mathsf {punl}}\) and wins in Game 3 such that:
for a negligible probability \(\varepsilon _\mathsf {punl}\). We say that an ABC system is punl-aca-secure if no adversary \((t_{\mathsf {punl}},\varepsilon _\mathsf {punl})\)-wins Game 3.
For the completeness of the security notion, we define a security notion weaker than unlinkability, namely, full anonymity in the full version [46] and show that Fuchsbauer et al.’s ABC system [31] cannot achieve this weaker security notion. Furthermore, we prove that the full attribute unlinkability implies full anonymity in an ABC system but the opposite does not hold. We also show that there is no reduction between full attribute unlinkability and full protocol unlinkability. Therefore, we only prove the security against the full attribute unlinkability and the full protocol unlinkability for our proposed ABC system.
4.3 Construction
Concisely, a user credential cred is an SDH-CL signature sig on the MoniPoly commitment C of his attribute set A. Next, the show proofs of our ABC system is proving the validity of sig and C such that:
where \(\mathsf { Pred }=\{\mathsf {Intersection,Difference}\}\). The commitment verification algorithms are the main ingredient that form the access policy for our ABC system. We describe the proposed ABC system as follows:
\(\mathsf {KeyGen}(1^k)\): Construct three cyclic groups \(\mathbb {G} _1,\mathbb {G} _2,\mathbb {G} _T\) of order p based on an elliptic curve whose bilinear pairing is \(e:\mathbb {G} _1\times \mathbb {G} _2 \rightarrow \mathbb {G} _T\). Select random generators \(a,b,c\in \mathbb {G} _1\), \(g_2\in \mathbb {G} _2\) and two secret values  . Compute the values \(a_0=a,a_1=a^{x'},\ldots ,a_n=a^{x'^{n}},X=g_2^x, X_0=g_2,X_1=g_2^{x'},\ldots ,X_n=g_2^{x'^n}\) to output the public key \(pk=(\mathsf {e},\mathbb {G} _1,\mathbb {G} _2,\mathbb {G} _T,p,b,c,\{a_i,X_i\}_{0\le i \le n},X)\) and the secret key \(sk=(x,x')\).
. Compute the values \(a_0=a,a_1=a^{x'},\ldots ,a_n=a^{x'^{n}},X=g_2^x, X_0=g_2,X_1=g_2^{x'},\ldots ,X_n=g_2^{x'^n}\) to output the public key \(pk=(\mathsf {e},\mathbb {G} _1,\mathbb {G} _2,\mathbb {G} _T,p,b,c,\{a_i,X_i\}_{0\le i \le n},X)\) and the secret key \(sk=(x,x')\).
\((\mathsf {Obtain}(pk,A), \mathsf {Issue}(pk,sk))\): User interacts with verifier as follows to generate a user credential cred on an attribute set \(A=\{m_1,\ldots ,m_{n-1}\}\).
-
1.
User chooses a random opening value
 to compute \(C=\prod _{j=0}^na_j^{\mathsf {m}_j}=\mathsf {Commit}(pk,A,o)\). Subsequently, user selects random
to compute \(C=\prod _{j=0}^na_j^{\mathsf {m}_j}=\mathsf {Commit}(pk,A,o)\). Subsequently, user selects random 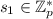 to initialize the issuing protocol by completing the protocol with the issuer: $$\begin{aligned} PK\bigg \{(\alpha _0,\ldots ,\alpha _n,\sigma ):M=\prod _{j=0}^na_j^{\alpha _j}b^{\sigma }\bigg \} \end{aligned}$$
to initialize the issuing protocol by completing the protocol with the issuer: $$\begin{aligned} PK\bigg \{(\alpha _0,\ldots ,\alpha _n,\sigma ):M=\prod _{j=0}^na_j^{\alpha _j}b^{\sigma }\bigg \} \end{aligned}$$where \(\sigma =s_1\) and \(\{\alpha _0,\ldots ,\alpha _n\}=\{\mathsf {m}_0,\ldots ,\mathsf {m}_n\}\).
-
2.
Issuer proceeds to the next step if the protocol is verified. Else, issuer outputs \(\perp \) and stops.
-
3.
Issuer generates the SDH-CL signature for M as \(sig=(t,s_2,v=(Mb^{s_2}c)^{1/(x+t)})\).
-
4.
If sig is not a valid signature on \(A\cup \{o\}\), user outputs \(\perp \) and stops. Else, user outputs the credential as \(cred=(t,s,v,A=A\cup \{o\})\) where:
$$\begin{aligned} s&=s_1+s_2, v=\left( a_0^{\prod _{j=1}^{n}(x'+m_{j})}b^sc\right) ^{1/(x+t)}. \end{aligned}$$
4.3.1 Proof of Possession
This protocol proves the ownership of a valid credential cred and the wellformedness of the committed attribute set \(A=\{m_1,\ldots ,m_n\}\) without disclosing any attribute. The Prove and Verify algorithms interact as follows.
\((\mathsf {Prove}(pk,cred,\bot ),\mathsf {Verify}(pk,\bot ))\):
-
1.
Verifier requests for a proof of possessions protocol by sending an empty access policy \(\phi =\bot \).
-
2.
Prover chooses random
 to randomize the credential as \(cred'=(t'=ty,s'=sr^2,v'=v^{r^2y^{-1}})\).
to randomize the credential as \(cred'=(t'=ty,s'=sr^2,v'=v^{r^2y^{-1}})\). -
3.
Setting \(v',W=\prod _{j=0}^{n-1}a_j^{\mathsf {w}_j'}\) as the public input where \(\{\mathsf {w}_j'\}_{0\le j \le n-1}=r\times \mathsf {MPEncode}(A-\{o\})\), prover runs the zero-knowledge protocol below with the verifier:
$$\begin{aligned} PK\bigg \{(\rho ,\tau ,\gamma ,\alpha _0,\alpha _1,\sigma ):&\mathsf {e}(C^{\rho }b^{\sigma }c^{\rho }v'^{-\tau },X_0)=\mathsf {e}(v'^{\gamma },X)~\wedge \\&\mathsf {e}(C^{\rho },X_0)=\mathsf {e}(W,X_1^{\alpha _1}X_0^{\alpha _0})\bigg \} \end{aligned}$$where \(\rho =r^2,\tau =t',\gamma =y,\{\alpha _j\}=r\times \mathsf {MPEncode}(\{o\}),\sigma =s'\). The protocol above can be compressed as:
$$\begin{aligned} PK\bigg \{(\rho ,\tau ,\gamma ,\alpha _0,\alpha _1,\sigma ):\mathsf {e}(W,X_1^{\alpha _1}X_0^{\alpha _0})\mathsf {e}\left( b^{\sigma }c^{\rho }v'^{-\tau },X_0\right) =\mathsf {e}(v'^{\gamma },X)\bigg \} \end{aligned}$$to realize a more efficient proof.
-
4.
Verifier outputs 1 if the protocol is verified and 0 otherwise.
4.3.2 Show Proofs
A show proof proves the relation between the attribute set A in cred and the queried set \(A'\) chosen by the verifier. Using the same compression technique from the proof of possession, we describe the single clause show proofs by the following presentation protocols.
 . This protocol allows prover to disclose an attribute set \(A'=\{m_1,\ldots ,m_k\}\subseteq A\) upon the request from verifier and proves that his credential cred contains \(A'\). The showing protocol for AND proof is as follows.
. This protocol allows prover to disclose an attribute set \(A'=\{m_1,\ldots ,m_k\}\subseteq A\) upon the request from verifier and proves that his credential cred contains \(A'\). The showing protocol for AND proof is as follows.
\((\mathsf {Prove}(pk,cred,\phi _{\mathsf {AND}(A')}),\mathsf {Verify}(pk,\phi _{\mathsf {AND}(A')}))\):
-
1.
Verifier requests an AND proof for the attribute set \(A'=\{m_1,\ldots ,m_k\}\).
-
2.
If \(A'\not \subseteq A\), prover aborts and the verifier outputs 0.
-
3.
Else, prover chooses random
 to randomize the credential as \(cred'=(t'=ty,s'=sr,v'=v^{ry^{-1}}, \{\mathsf {w}_j'\}_{0\le j \le n-k}=r\times \mathsf {MPEncode}(A- A'))\).
to randomize the credential as \(cred'=(t'=ty,s'=sr,v'=v^{ry^{-1}}, \{\mathsf {w}_j'\}_{0\le j \le n-k}=r\times \mathsf {MPEncode}(A- A'))\). -
4.
Setting \(v',W=\prod _{j=0}^{n-k} a_j^{\mathsf {w}_j'}\) as the public input, prover runs the zero-knowledge protocol below with the verifier:
$$\begin{aligned} PK\bigg \{(\rho ,\tau ,\gamma ,\sigma ):\mathsf {e}\left( W,\prod _{j=0}^{k} X_j^{\mathsf {m}_j}\right) \mathsf {e}(b^{\sigma }c^{\rho }v'^{-\tau },X_0)=\mathsf {e}(v'^{\gamma },X)\bigg \} \end{aligned}$$where \(\prod _{j=0}^{k} X_j^{\mathsf {m}_j}\) and \(\{\mathsf {m}_j\}=\mathsf {MPEncode}(A')\) are computed by the verifier and \(\rho =r,\tau =t',\gamma =y,\sigma =s'\).
-
5.
Verifier outputs 1 if the protocol is verified and 0 otherwise.
 . This is the show proof for the threshold statement, and it is an OR proof when the threshold is equal to one. Consider the scenario where the prover is given an attribute set \(A'=\{m_1,\ldots ,m_k\}\) and he needs to prove that he has l attributes \(\{m_j\}_{1\le j\le l}\in (A'\cap A)\) without the verifier knowing which attributes he is proving. The showing protocol for the ANY statement is as follows.
. This is the show proof for the threshold statement, and it is an OR proof when the threshold is equal to one. Consider the scenario where the prover is given an attribute set \(A'=\{m_1,\ldots ,m_k\}\) and he needs to prove that he has l attributes \(\{m_j\}_{1\le j\le l}\in (A'\cap A)\) without the verifier knowing which attributes he is proving. The showing protocol for the ANY statement is as follows.
\((\mathsf {Prove}(pk,cred,\phi _{\mathsf {ANY}(l,A')}),\mathsf {Verify}(pk,\phi _{\mathsf {ANY}(l,A')}))\):
-
1.
Verifier requests an \(\mathsf {ANY}(l,A')\) proof for the attribute set \(A'=\{m_1,\ldots ,m_k\}\).
-
2.
Prover randomly selects l-attribute intersection set \(I\subseteq (A'\cap A)\). If no such I can be formed, the prover aborts and the verifier outputs 0.
-
3.
Else, prover chooses random
 to randomize the credential as \(cred'=(t'=ty,s'=sr^2,v'=v^{r^2y^{-1}},\{\mathsf {w}_j'\}_{0\le j \le n-l}=r\times \mathsf {MPEncode}(A- I))\).
to randomize the credential as \(cred'=(t'=ty,s'=sr^2,v'=v^{r^2y^{-1}},\{\mathsf {w}_j'\}_{0\le j \le n-l}=r\times \mathsf {MPEncode}(A- I))\). -
4.
Setting \(v',W=\prod _{j=0}^{n-l} a_j^{\mathsf {w}_j'},W'=\left( \prod _{j=0}^{k-l}a_j^{\mathsf {m}_{2,j}}\right) ^{r^{-1}}\) as the public input where \(\{\mathsf {m}_{2,j}\}_{0\le j\le k-l}=\mathsf {MPEncode}(A'- I)\), prover runs the zero-knowledge protocol below with the verifier:
$$\begin{aligned} PK\bigg \{&(\rho ,\tau ,\gamma ,\iota _0,\ldots ,\iota _{l},\sigma ):\\&\mathsf {e}\left( W'W,\prod _{j=0}^{l} X_j^{\iota _j}\right) \mathsf {e}\left( \prod _{j=0}^{k}a_j^{-\mathsf {m}_{1,j}}b^{\sigma }c^{\rho }v'^{-\tau },X_0\right) =\mathsf {e}(v'^{\gamma },X)\bigg \} \end{aligned}$$where \(\prod _{j=0}^{k} a_j^{-\mathsf {m}_{1,j}}\) and \(\{\mathsf {m}_{1,j}\}_{0\le j\le k}=\mathsf {MPEncode}(A')\) are computed by the verifier and \(\rho =r^2,\tau =t',\gamma =y,\{\iota _j\}_{0\le j \le l}=r\times \mathsf {MPEncode}(I),\sigma =s'\).
-
5.
Verifier outputs 1 if the protocol is verified and 0 otherwise.
 . This is the showing protocol for the NAND statement which allows a prover to show that an attribute set \(A'=\{m_1,\ldots ,m_k\}\) is disjoint with the set A in his credential. Note that it is a NOT proof when \(|A'|=1\). The showing protocol on the NAND statement is as below.
. This is the showing protocol for the NAND statement which allows a prover to show that an attribute set \(A'=\{m_1,\ldots ,m_k\}\) is disjoint with the set A in his credential. Note that it is a NOT proof when \(|A'|=1\). The showing protocol on the NAND statement is as below.
\((\mathsf {Prove}(pk,cred,\phi _{\mathsf {NAND}(A')}),\mathsf {Verify}(pk,\phi _{\mathsf {NAND}(A')}))\):
-
1.
Verifier requests a NAND proof for the attribute set \(A'=\{m_1,\ldots ,m_k\}\).
-
2.
If \(|A'- A|< k\), prover aborts and the verifier outputs 0.
-
3.
Else, prover chooses random
 to randomize the credential as \(cred'=(t'=ty,s'=sr,v'=v^{ry^{-1}},\{\mathsf {w}_{j}'=r\mathsf {w}_{j}\}_{0\le j \le n-k},\{\mathsf {r}_{j}'=r\mathsf {r}_{j}\}_{0\le j \le k-1})\) where \((\{\mathsf {w}_{j}\}_{0\le j \le n-k},\{\mathsf {r}_{j}\}_{0\le j \le k-1})=\mathsf {MPEncode}(A)/\mathsf {MPEncode}(A')\).
to randomize the credential as \(cred'=(t'=ty,s'=sr,v'=v^{ry^{-1}},\{\mathsf {w}_{j}'=r\mathsf {w}_{j}\}_{0\le j \le n-k},\{\mathsf {r}_{j}'=r\mathsf {r}_{j}\}_{0\le j \le k-1})\) where \((\{\mathsf {w}_{j}\}_{0\le j \le n-k},\{\mathsf {r}_{j}\}_{0\le j \le k-1})=\mathsf {MPEncode}(A)/\mathsf {MPEncode}(A')\). -
4.
Setting \(v',W=\prod _{j=0}^{n-k} a_j^{\mathsf {w}_{j}'}\) as the public input, prover runs the zero-knowledge protocol with the verifier:
$$\begin{aligned} PK\bigg \{&(\rho ,\tau ,\gamma ,\mu _0,\ldots ,\mu _{k-1},\sigma ): \prod _{j=0}^{k-1}a_j^{\mu _j}\ne \mathbb {G} _1 \wedge \\&\mathsf {e}\left( W,\prod _{j=0}^{k} X_j^{\mathsf {m}_j}\right) \mathsf {e}\left( \prod _{j=0}^{k-1}a_j^{\mu _j} b^{\sigma }c^{\rho }v'^{-\tau },X_0\right) =\mathsf {e}(v'^{\gamma },X)\bigg \} \end{aligned}$$where \(\prod _{j=0}^{k} X_j^{\mathsf {m}_j}\) and \(\{\mathsf {m}_j\}=\mathsf {MPEncode}(A')\) are computed by the verifier and \(\{\mu _j\}=\{\mathsf {r}_j'\},\rho =r,\tau =t',\gamma =y,\sigma =s'\).
-
5.
Verifier outputs 1 if the protocol is verified and 0 otherwise.
 . This is the showing protocol for the negated threshold statement. Consider the scenario where the prover is given an attribute set \(A'=\{m_1,\ldots ,m_k\}\) and he needs to prove that an l-attribute set \(D\subseteq (A'-A)\) are not in the credential without the verifier knowing which attributes he is proving. The showing protocol on the NANY statement is as below.
. This is the showing protocol for the negated threshold statement. Consider the scenario where the prover is given an attribute set \(A'=\{m_1,\ldots ,m_k\}\) and he needs to prove that an l-attribute set \(D\subseteq (A'-A)\) are not in the credential without the verifier knowing which attributes he is proving. The showing protocol on the NANY statement is as below.
\((\mathsf {Prove}(pk,cred,\phi _{\mathsf {NANY}(\bar{l},A')}),\mathsf {Verify}(pk,\phi _{\mathsf {NANY}(\bar{l},A')}))\):
-
1.
Verifier requests a NANY proof for the attributes \(A'=\{m_1,\ldots ,m_k\}\).
-
2.
Prover randomly selects an \(\bar{l}\)-attribute difference set \(D\in (A'-A)\). If no such D can be formed, prover aborts and the verifier outputs 0.
-
3.
Else, prover chooses random
 to randomize the credential as \(cred'=(t'=ty,s'=sr^2,v'=v^{r^2y^{-1}},\{\mathsf {w}_{j}'=r\mathsf {w}_{j}\}_{0\le j \le n-\bar{l}},\{\mathsf {r}_{j}'=r^2\mathsf {w}_{j}\}_{0\le j\le \bar{l}-1})\) where \((\{\mathsf {w}_{j}\}_{0\le j \le n-\bar{l}},\{\mathsf {r}_{j}\}_{0\le j\le \bar{l}-1})=\mathsf {MPEncode}(A)/\mathsf {MPEncode}(D)\).
to randomize the credential as \(cred'=(t'=ty,s'=sr^2,v'=v^{r^2y^{-1}},\{\mathsf {w}_{j}'=r\mathsf {w}_{j}\}_{0\le j \le n-\bar{l}},\{\mathsf {r}_{j}'=r^2\mathsf {w}_{j}\}_{0\le j\le \bar{l}-1})\) where \((\{\mathsf {w}_{j}\}_{0\le j \le n-\bar{l}},\{\mathsf {r}_{j}\}_{0\le j\le \bar{l}-1})=\mathsf {MPEncode}(A)/\mathsf {MPEncode}(D)\). -
4.
Setting \(v',W=\prod _{j=0}^{n-\bar{l}} a_j^{\mathsf {w}_{j}'},W'=\left( \prod _{j=0}^{k-\bar{l}}a_j^{\mathsf {m}_{2,j}}\right) ^{r^{-1}}\) as the public input where \(\{\mathsf {m}_{2,j}\}_{0\le j\le k-\bar{l}}=\mathsf {MPEncode}(A'-D)\), prover runs the zero-knowledge protocol with the verifier:
$$\begin{aligned} PK\bigg \{&(\rho ,\tau ,\gamma ,\delta _0,\ldots ,\delta _{\bar{l}},\mu _0,\ldots ,\mu _{\bar{l}-1},\sigma ): \prod _{j=0}^{\bar{l}-1}a_j^{\mu _j}\ne \mathbb {G} _1 \wedge \\&\mathsf {e}\left( W'W,\prod _{j=0}^{\bar{l}} X_j^{\delta _j}\right) \mathsf {e}\left( \prod _{j=0}^{k}a_j^{-\mathsf {m}_{1,j}}\prod _{j=0}^{\bar{l}-1}a_j^{\mu _j} b^{\sigma }c^{\rho }v'^{-\tau },X_0\right) =\mathsf {e}(v'^{\gamma },X) \bigg \} \end{aligned}$$where \(\prod _{j=0}^{k} a_j^{-\mathsf {m}_{1,j}}\) and \(\{\mathsf {m}_{1,j}\}_{0\le j\le k}=\mathsf {MPEncode}(A')\) are computed by the verifier and \(\{\mu _j\}=\{\mathsf {r}_j'\},\rho =r^2,\tau =t',\gamma =y,\{\delta _j\}_{0\le j \le \bar{l}}=r\times \mathsf {MPEncode}(D),\sigma =s'\).
-
5.
Verifier outputs 1 if the protocol is verified and 0 otherwise.
4.4 Efficiently Enabling Composite Statements
Composite statements, such as, composed of multiple high-level conjunctions, can be realized with MoniPoly efficiently. For that, we propose an efficient strategy instead of naively repeating the show proofs multiple times for an access policy with a composite statement.
The prover runs a proof of possession protocol followed by a proof to show that the committed attributes from every clause in the composite statement is part of the committed attributes in the credential. For instance, given the composite statement \(\mathsf {stmt}=\mathsf {AND}(A_1') \wedge \mathsf {ANY}(l,A_2')\) where \(k_1=|A_1'|, k_2=|A_2'|\), a prover can run the showing protocol as follows. Let \(W_{A_1'}=\prod _{j=0}^{n-k_1} a_j^{\mathsf {w}_{A_1',j}'},W_{A_2'}=\prod _{j=0}^{n-l} a_j^{\mathsf {w}_{A_2',j}'},W_{A_2'}'=\prod _{j=0}^{k_2-l} a_j^{\mathsf {m}_{A_2',2,j}'}\) where \(\{\mathsf {w}_{A_1',j}'\}_{0\le j \le n-k_1}=r^2\times \mathsf {MPEncode}(A- A'_1)\), \(\{\mathsf {w}_{A_2',j}'\}_{0\le j \le n-l}=r\times \mathsf {MPEncode}(A- I)\), \(\{\mathsf {m}_{A_2',2,j}'\}_{0\le j \le k_{2-l}}=r^{-1}\times \mathsf {MPEncode}(A_2'- I)\) for a randomly selected  . Setting \(v',W_{A_1'},W_{A_2'},W_{A_1'}'\) as public inputs, the prover runs the showing protocol on \(\phi _{\mathsf {stmt}}\) as follows:
. Setting \(v',W_{A_1'},W_{A_2'},W_{A_1'}'\) as public inputs, the prover runs the showing protocol on \(\phi _{\mathsf {stmt}}\) as follows:
where \(\prod _{j=0}^{k_1} X_j^{\mathsf {m}_{A_1',j}},\prod _{j=0}^{k_2}a_j^{\mathsf {m}_{A_2',2,j}},\{\mathsf {m}_{A_1',1,j}\}_{0\le j \le k_1}=\mathsf {MPEncode}(A_1'),\{\mathsf {m}_{A_2',1,j}\}_{0\le j \le k_2}=\mathsf {MPEncode}(A_2')\) are computed by the verifier and \(\rho =r^2,\tau =t',\gamma =y,\{\iota _j\}_{0\le j \le l}=r\times \mathsf {MPEncode}(I),\sigma =s'\). It is thus obvious that for any composite statement of k clauses, we can run the protocol above in a similar way using \(k+2\) pairings. In precise, the \(k+1\) pairings on the left-hand side correspond to the k clauses and a credential. Lastly, the corresponding credential elements in the pairings at the left-hand side and right-hand side are brought up to the power of k, respectively. Note that the complexity of \(k+2\) parings does not change even when negation clauses are involved.
4.5 Security Analysis
4.5.1 Impersonation Resilience
We establish the security of the MoniPoly ABC system by constructing a reduction to the (co-)SDH problem. To achieve tight security reduction, we make use of Multi-Instance Reset Lemma [37] as the knowledge extractor which requires the adversary \(\mathcal {A}\) to run N parallel instances of impersonation under active and concurrent attacks. The challenger \(\mathcal {C}\) can fulfill this requirement by simulating the \(N-1\) instances from its given SDH instance which is random self-reducible [10]. Since this is obvious, we describe only the simulation for a single instance of impersonation under active and concurrent attacks in the security proofs.
Theorem 4
If an adversary \(\mathcal {A}\) \((t_{\mathsf {imp}},\varepsilon _\mathsf {imp})\)-breaks the imp-aca-security of the proposed anonymous credential system, then there exists an algorithm \(\mathcal {C}\) which \((t_{\mathsf {cosdh}},\varepsilon _\mathsf {cosdh})\)-breaks the co-SDH problem such that:
or an algorithm \(\mathcal {C}\) which \((t_{\mathsf {sdh}},\varepsilon _\mathsf {sdh})\)-breaks the SDH problem such that:
where N is the total adversary instance, \(q=Q_{(O,I)}+Q_{(P,V)}\) is the total query made to the \(\mathsf {Obtain}\) and \(\mathsf {Verify}\) oracles, while \(T(q^2)\) is the time parameterized by q to setup the simulation environment and to extract the SDH solution. Consider the dominant time elements \(t_{\mathsf {imp}}\) and \(t_{\mathsf {sdh}}\) only, we have:
Let \(N=(\varepsilon _\mathsf {imp}-\frac{1+(q-1)!/p^{q-2}}{p})^{-1}\), we get \(\varepsilon _{\mathsf {sdh}}\ge (1-e^{-1})^2\ge 1/3\) and the success ratio is:
which gives a tight reduction.
To modularize the proof for Theorem 4, we categorize the way an adversary impersonates in Table 2. This is like the approach in the tight reduction proof for the SDH-CL signature scheme proposed by Schäge [44]. Subsequently, we differentiate \(\mathcal {A}\) into \(\mathcal {A}=\{\mathcal {A}_{bind},\mathcal {A}_1,\mathcal {A}_2,\mathcal {A}_3\}\) corresponding to four different simulation strategies by \(\mathcal {C}\). We omit the proof for the binding property of MoniPoly commitment scheme \(\mathcal {A}_{bind}\) which has been described in Theorem 3 and can be trivially applied here.
In each of the simulation strategy, we consider only the success probability of breaking the SDH problem which is weaker than the DLOG problem such that \(\varepsilon _{\mathsf {sdh}}\ge \varepsilon _{\mathsf {dlog}}\). Let \(M^*=\prod _{j=1}^n(x'+m_j^*)\) and \(M_i=\prod _{j=1}^n(x'+m_{i,j})\) where \(A^*=\{m_j^*\}\) and \(A_i=\{m_j\}\), respectively, the DLOG problem can be solved whenever the forgery \(v^*\) produced by \(\mathcal {A}\) equals to a \(v_i\) which has been generated by \(\mathcal {C}\) such that:
which leads to:
where \(\mathcal {C}\) can solve the SDH problem using x. Following the equation, the Type 14 impersonation \((A^*,v^*,s^*)=(A_i,v_i,s_i)\) will not happen as it causes a division by zero. On the other hand, Type 16 represents the impersonation using the uncorrupted cred generated by \(\mathcal {C}\) when it answers \(\mathcal {A}\)’s \(\mathsf {IssueTranscript}\) queries or \(\mathsf {Verify}\) queries. If \(\mathcal {A}\)’s view is independent of \(\mathcal {C}\)’s choice of \((t_i,s_i)\), we have \((t^*,s^*)\ne (t_i,s_i)\) with probability \(1-1/p\). This causes Type 16 impersonation to happen with a negligible probability of 1/p at which point our simulation fails.
We present Lemmas 1, 2 and 3 corresponding to the adversaries \(\mathcal {A}_1,\) \(\mathcal {A}_2\) and \(\mathcal {A}_3\) as follows. The proofs for the lemmas are in the full version [46].
Lemma 1
If an adversary \(\mathcal {A}_1\) \((t_{\mathsf {imp}},\varepsilon _\mathsf {imp})\)-breaks the imp-aca-security of the proposed anonymous credential system, then there exists an algorithm \(\mathcal {C}\) which \((t_{\mathsf {sdh}},\varepsilon _\mathsf {sdh})\)-solves the SDH problem such that:
where N is the total of adversary instances, \(q=Q_{(O,I)}+Q_{(P,V)}\) is the number of queries made to the \(\mathsf {Obtain}\) and \(\mathsf {Verify}\) oracles, while \(T(q^2)\) is the time parameterized by q to setup the simulation environment and to extract the SDH solution.
Lemma 2
If an adversary \(\mathcal {A}_2\) \((t_{\mathsf {imp}},\varepsilon _\mathsf {imp})\)-breaks the imp-aca-security of the proposed anonymous credential system, then there exists an algorithm \(\mathcal {C}\) which \((t_{\mathsf {sdh}},\varepsilon _\mathsf {sdh})\)-solves the SDH problem such that:
where N is the total of adversary instances, \(q=Q_{(O,I)}+Q_{(P,V)}\) is the number of queries made to the \(\mathsf {Obtain}\) and \(\mathsf {Verify}\) oracles, while \(T(q^2)\) is the time parameterized by q to setup the simulation environment and to extract the SDH solution.
Lemma 3
If an adversary \(\mathcal {A}_3\) \((t_{\mathsf {imp}},\varepsilon _\mathsf {imp})\)-breaks the imp-aca-security of the proposed anonymous credential system, then there exists an algorithm \(\mathcal {C}\) which \((t_{\mathsf {sdh}},\varepsilon _\mathsf {sdh})\)-solves the SDH problem such that:
where N is the total of adversary instances, \(q=Q_{(O,I)}+Q_{(P,V)}\) is the number of queries made to the \(\mathsf {Obtain}\) and \(\mathsf {Verify}\) oracles, while \(T(q^2)\) is the time parameterized by q to setup the simulation environment and to extract the SDH solution.
Combining Theorem 3, Lemmas 1, 2, and 3 gives Theorem 4 as required.
4.5.2 Unlinkability
Next, we prove the unlinkability of the proposed ABC system. It is sufficient to show that the witnesses, the committed attributes and the randomized credential in the issuing protocol and presentation protocol, respectively, are perfectly hiding. Then, we demonstrate that every instance of the protocols is uniformly distributed due to the random self-reducibility property. This implies that even when \(\mathcal {A}\) is given access to the Obtain, Issue, Prove, Verify and Corrupt oracles, it does not has advantage in guessing the challenged attribute sets. The proofs for Lemma 5 and 7 are in the full version [46].
Lemma 4
The committed attributes and the corresponding witness in the issuing protocol of the ABC system are perfectly hiding.
Proof
By Theorem 2, the MoniPoly commitment \(C=\prod _{j=0}^{n}a_j^{\mathsf {m}_{j}}\) in the issuing protocol is perfectly hiding. Subsequently, the value \(M=Cb^{s_1}\) is a Pedersen commitment which is also perfectly hiding. The same reasoning is applicable on the commitment value in the zero-knowledge protocol \(R=\prod _{j=0}^{n}a_j^{\tilde{\mathsf {m}}_{j}}b^{\tilde{s}_{1}}\) which has the same structure as that of M. \(\square \)
Lemma 5
The initialization of the issuing protocol in the ABC system has random self-reducibility.
Lemma 6
The randomized credential in the presentation protocol of the ABC system are perfectly hiding.
Proof
Given a user’s randomized credential \(v'=v^{ry^{-1}}\) in the show proof, there are  possible pairs of \((r',y')\ne (r,y)\) which can result in the same \(v'\). Besides, for each r, there is a unique y such that:
possible pairs of \((r',y')\ne (r,y)\) which can result in the same \(v'\). Besides, for each r, there is a unique y such that:
Since r, y are chosen independently from each other, and of the credential element v, the latter is perfectly hidden. The same reasoning applies on the randomized credential \(v'=v^{r^2y^{-1}}\). \(\square \)
Lemma 7
The presentation protocol of the ABC system offers random self-reducibility.
Theorem 5
If the initialization of the issuing protocol and the presentation protocol have random self-reducibility, and their witnesses, committed attributes as well as the randomized credential are perfectly hiding, the ABC system is aunl-aca-secure.
Using the similar approach, we show that the security of full protocol unlinkability also holds for the proposed ABC system.
Theorem 6
If the initialization of the issuing protocol and the presentation protocol have random self-reducibility, and their witnesses, committed attributes as well as randomized credential are perfectly hiding, the ABC system is punl-aca-secure.
5 Evaluation
5.1 Security
We offer a general overview of security properties in comparison with other schemes here and offer the tightness analysis of our own scheme in the full version [46].
We summarize the security properties of ABC systems in either SDH or alternative paradigms in Table 3. The table shows that the relevant schemes vary significantly in their fulfilled security requirements. MoniPoly is the only ABC system that achieves the full range of security requirements. At the same time, it is proven secure in the standard model with a tight security reduction.
5.2 Expressivity and Computational Complexity
In Table 4, we compare the MoniPoly ABC system to relevant popular ABC systems with respect to their realized show proofs and asymptotic computational complexities. Table 4 is normalized in that it considers only the asymptotic complexity for the most expensive operations (e.g., the scalar multiplication, modular exponentiation, or pairing).
5.2.1 Expressivity over Unrestricted Attribute Space
The MoniPoly ABC system is the first scheme that can efficiently support all logical statements in the show proofs regardless of the types of attribute space (cf. Table 4). That is, MoniPoly operates on arbitrary attributes while offering a wide range of statements in its expressiveness.
We note that the traditional encoding can achieve the same expressiveness, in principle, in an unrestricted attribute space \(\mathcal {S}\) as well as string attribute space \(\mathcal {S}_S\). However, traditional encoding will yield inefficient proofs.
5.2.2 Expressivity over Finite-Set Attribute Space
Let us now consider the comparison with schemes with only finite-set attribute space \(\mathcal {S}_F\). Most of the accumulator-based ABC systems [43, 45] are restricted to finite-set attributes only. While MoniPoly supports negation statements in terms of expressivity, their show proofs do not. The restriction to finite-set attributes and monotone (non-negative) formula affords them a low asymptotic complexity in show proofs. However, their setup and issuing protocols are prohibitively expensive with exponential computational and space complexity (\(O(2^{n_F})\) [40] and \(O(2^{\sqrt{n_F}})\) [43]), in turn, restricting the number of attributes that can be feasibly encoded.
The latest ABC system in this line of work [40] proposes a workaround on the negated forms of attributes separately. In this scheme, each of its show proof has O(L) complexity where L is the maximum number of \(\wedge \) operators permitted in a composite conjunctive formulae. Moreover, the additional negated finite-set attributes double the credential size and the already massive public key size.
5.2.3 Comparison to Commitment-Based Schemes
MoniPoly bears similarities in terms of computational and communication complexity to other commitment-based ABC systems [16, 31]. Although MoniPoly does not have constant asymptotic complexity, the verifier is required to compute only three pairings for a single-clause show proof. This makes our scheme the most efficient construction of its kind in this comparison. At the same time, apart from having constant-size AND proof similarly to the relevant commitment-based schemes [16, 31], MoniPoly has constant-size possession proof.
5.2.4 Parametric Complexity Analysis
We estimate the computational complexity of the schemes listed in Table 4 and present in Fig. 1 the complexity for each ABC system at 128-bit security level. While schemes especially crafted for a restricted finite-set attribute space are the fastest schemes in the field, Monipoly is the most efficient ABC system based on commitment schemes and outperforms most schemes in the field, overall. If strength in terms of security properties is a prerequisite, our ABC system outperforms all listed in Table 4 while having efficient constant size show proofs.
This estimation is based on the following relative computation costs in equivalents of scalar multiplications in \(\mathbb {G} _1\):
-
BLS-12 curve at 128-bit security: for a scalar multiplication in \(\mathbb {G} _2\), an exponentiation in \(\mathbb {G} _T\) and a pairing, respectively, is about the same as computing 2, 6 and 9 scalar multiplications (\(M_1\)) in \(\mathbb {G} _1\). The modular exponentiation of RSA-3072 on the other hand is equivalent to \(5M_1\).
We also assume the computational cost in Type-1 pairing friendly curve is equivalent to that of Type-3 as well as \(L=1\) and \(N=1\). The details of the estimation can be found in the full version [46].
Notes
- 1.
If the prime numbers are not pre-certified by a signature each, the show proofs have to include expensive interval proofs.
References
Abe, M., Fuchsbauer, G., Groth, J., Haralambiev, K., Ohkubo, M.: Structure-preserving signatures and commitments to group elements. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 209–236. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14623-7_12
Akagi, N., Manabe, Y., Okamoto, T.: An efficient anonymous credential system. In: Tsudik, G. (ed.) FC 2008. LNCS, vol. 5143, pp. 272–286. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85230-8_25
Anada, H., Arita, S., Sakurai, K.: Attribute-based two-tier signatures: definition and construction. In: Kwon, S., Yun, A. (eds.) ICISC 2015. LNCS, vol. 9558, pp. 36–49. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-30840-1_3
Au, M.H., Susilo, W., Mu, Y.: Constant-size dynamic k-TAA. In: De Prisco, R., Yung, M. (eds.) SCN 2006. LNCS, vol. 4116, pp. 111–125. Springer, Heidelberg (2006). https://doi.org/10.1007/11832072_8
Barki, A., Brunet, S., Desmoulins, N., Traoré, J.: Improved algebraic MACs and practical keyed-verification anonymous credentials. In: Avanzi, R., Heys, H. (eds.) SAC 2016. LNCS, vol. 10532, pp. 360–380. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-69453-5_20
Begum, N., Nakanishi, T., Funabiki, N.: Efficient proofs for CNF formulas on attributes in pairing-based anonymous credential system. In: Kwon, T., Lee, M.-K., Kwon, D. (eds.) ICISC 2012. LNCS, vol. 7839, pp. 495–509. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-37682-5_35
Bemmann, K., Blömer, J., Bobolz, J., Bröcher, H., et al.: Fully-featured anonymous credentials with reputation system. In: Proceedings of the 13th International Conference on Availability, Reliability and Security, ARES 2018, pp. 42:1–42:10. ACM (2018)
Blömer, J., Bobolz, J.: Delegatable attribute-based anonymous credentials from dynamically malleable signatures. In: Preneel, B., Vercauteren, F. (eds.) ACNS 2018. LNCS, vol. 10892, pp. 221–239. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-93387-0_12
Blömer, J., Bobolz, J., Diemert, D., Eidens, F.: Updatable anonymous credentials and applications to incentive systems. In: Proceedings of the 2019 ACM SIGSAC Conference on Computer and Communications Security, CCS 2019, pp. 1671–1685. Association for Computing Machinery (2019)
Boneh, D., Boyen, X.: Short signatures without random oracles and the SDH assumption in bilinear groups. J. Cryptology 21(2), 149–177 (2008)
Boneh, D., Boyen, X., Shacham, H.: Short group signatures. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 41–55. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-28628-8_3
Brands, S.A.: Rethinking Public Key Infrastructures and Digital Certificates: Building in Privacy. MIT Press, Cambridge (2000)
Brickell, E., Li, J.: Enhanced privacy id from bilinear pairing for hardware authentication and attestation. In: 2010 IEEE Second International Conference on Social Computing, pp. 768–775, August 2010
Brickell, E., Li, J.: A pairing-based DAA scheme further reducing TPM resources. In: Acquisti, A., Smith, S.W., Sadeghi, A.-R. (eds.) Trust 2010. LNCS, vol. 6101, pp. 181–195. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13869-0_12
Camenisch, J., Drijvers, M., Dzurenda, P., Hajny, J.: Fast keyed-verification anonymous credentials on standard smart cards. In: Dhillon, G., Karlsson, F., Hedström, K., Zúquete, A. (eds.) SEC 2019. IAICT, vol. 562, pp. 286–298. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-22312-0_20
Camenisch, J., Dubovitskaya, M., Haralambiev, K., Kohlweiss, M.: Composable and modular anonymous credentials: definitions and practical constructions. In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015. LNCS, vol. 9453, pp. 262–288. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48800-3_11
Camenisch, J., Groß, T.: Efficient attributes for anonymous credentials. In: Proceedings of the 15th ACM Conference on Computer and Communications Security, pp. 345–356. ACM (2008)
Camenisch, J., Groß, T.: Efficient attributes for anonymous credentials. ACM Trans. Inf. Syst. Secur. 15(1), 4:1–4:30 (2012)
Camenisch, J., Kohlweiss, M., Soriente, C.: An accumulator based on bilinear maps and efficient revocation for anonymous credentials. In: Jarecki, S., Tsudik, G. (eds.) PKC 2009. LNCS, vol. 5443, pp. 481–500. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-00468-1_27
Camenisch, J., Krenn, S., Lehmann, A., Mikkelsen, G.L., Neven, G., Pedersen, M.Ø.: Formal treatment of privacy-enhancing credential systems. In: Dunkelman, O., Keliher, L. (eds.) SAC 2015. LNCS, vol. 9566, pp. 3–24. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-31301-6_1
Camenisch, J., Lysyanskaya, A.: An efficient system for non-transferable anonymous credentials with optional anonymity revocation. In: Pfitzmann, B. (ed.) EUROCRYPT 2001. LNCS, vol. 2045, pp. 93–118. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44987-6_7
Camenisch, J., Lysyanskaya, A.: A signature scheme with efficient protocols. In: Cimato, S., Persiano, G., Galdi, C. (eds.) SCN 2002. LNCS, vol. 2576, pp. 268–289. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-36413-7_20
Camenisch, J., Lysyanskaya, A.: Signature schemes and anonymous credentials from bilinear maps. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 56–72. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-28628-8_4
Chase, M., Meiklejohn, S., Zaverucha, G.: Algebraic macs and keyed-verification anonymous credentials. In: Proceedings of the 2014 ACM SIGSAC Conference on Computer and Communications Security, CCS 2014, pp. 1205–1216. ACM (2014)
Chaum, D.: Security without identification: transaction systems to make big brother obsolete. Commun. ACM 28(10), 1030–1044 (1985)
Chen, L.: A DAA scheme requiring less TPM resources. In: Bao, F., Yung, M., Lin, D., Jing, J. (eds.) Inscrypt 2009. LNCS, vol. 6151, pp. 350–365. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-16342-5_26
Chen, L., Li, J.: Flexible and scalable digital signatures in TPM 2.0. In: Proceedings of the Conference on Computer & Communications Security (CCS), CCS 2013, pp. 37–48. ACM (2013)
Chen, X., Feng, D.: Direct anonymous attestation for next generation TPM (2008)
Chu, X., Yu, Q.: A new efficient property-based attestation protocol based on elliptic curves. In: 2012 IEEE 11th International Conference on Trust, Security and Privacy in Computing and Communications, pp. 730–736, June 2012
Damgård, I.: Commitment schemes and zero-knowledge protocols. In: Damgård, I.B. (ed.) EEF School 1998. LNCS, vol. 1561, pp. 63–86. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48969-X_3
Fuchsbauer, G., Hanser, C., Slamanig, D.: Structure-preserving signatures on equivalence classes and constant-size anonymous credentials. J. Cryptology 32(2), 498–546 (2019)
Groß, T.: Signatures and efficient proofs on committed graphs and NP-statements. In: Böhme, R., Okamoto, T. (eds.) FC 2015. LNCS, vol. 8975, pp. 293–314. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-47854-7_18
Groß, T.R.: Efficient certification and zero-knowledge proofs of knowledge on infrastructure topology graphs. In: Proceedings of the 6th Edition of the ACM Workshop on Cloud Computing Security, CCSW 2014, pp. 69–80. Association for Computing Machinery, New York (2014)
Guo, N., Gao, T., Wang, J.: Privacy-preserving and efficient attributes proof based on selective aggregate CL-signature scheme. Int. J. Comput. Math. 93(2), 273–288 (2016)
Izabachène, M., Libert, B., Vergnaud, D.: Block-wise P-signatures and non-interactive anonymous credentials with efficient attributes. In: Chen, L. (ed.) IMACC 2011. LNCS, vol. 7089, pp. 431–450. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-25516-8_26
Kate, A., Zaverucha, G.M., Goldberg, I.: Constant-size commitments to polynomials and their applications. In: Abe, M. (ed.) ASIACRYPT 2010. LNCS, vol. 6477, pp. 177–194. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-17373-8_11
Kiltz, E., Masny, D., Pan, J.: Optimal security proofs for signatures from identification schemes. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9815, pp. 33–61. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53008-5_2
Nguyen, L.: Accumulators from bilinear pairings and applications. In: Menezes, A. (ed.) CT-RSA 2005. LNCS, vol. 3376, pp. 275–292. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-30574-3_19
Okamoto, T.: Efficient blind and partially blind signatures without random Oracles. In: Halevi, S., Rabin, T. (eds.) TCC 2006. LNCS, vol. 3876, pp. 80–99. Springer, Heidelberg (2006). https://doi.org/10.1007/11681878_5
Okishima, R., Nakanishi, T.: An anonymous credential system with constant-size attribute proofs for CNF formulas with negations. In: Attrapadung, N., Yagi, T. (eds.) IWSEC 2019. LNCS, vol. 11689, pp. 89–106. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26834-3_6
Pointcheval, D., Sanders, O.: Short randomizable signatures. In: Sako, K. (ed.) CT-RSA 2016. LNCS, vol. 9610, pp. 111–126. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-29485-8_7
Ringers, S., Verheul, E., Hoepman, J.-H.: An efficient self-blindable attribute-based credential scheme. In: Kiayias, A. (ed.) FC 2017. LNCS, vol. 10322, pp. 3–20. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70972-7_1
Sadiah, S., Nakanishi, T., Begum, N., Funabiki, N.: Accumulator for monotone formulas and its application to anonymous credential system. J. Inf. Process. 25, 949–961 (2017)
Schäge, S.: Tight proofs for signature schemes without random Oracles. In: Paterson, K.G. (ed.) EUROCRYPT 2011. LNCS, vol. 6632, pp. 189–206. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-20465-4_12
Sudarsono, A., Nakanishi, T., Funabiki, N.: Efficient proofs of attributes in pairing-based anonymous credential system. In: Fischer-Hübner, S., Hopper, N. (eds.) PETS 2011. LNCS, vol. 6794, pp. 246–263. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22263-4_14
Tan, S.-Y., Groß, T.: Monipoly–an expressive \(q\)-SDH-based anonymous attribute-based credential system [extended version]. Cryptology ePrint Archive Report 2020/587 (ia.cr/2020/587), IACR, May 2020
Tsang, P.P., Au, M.H., Kapadia, A., Smith, S.W.: Blacklistable anonymous credentials: blocking misbehaving users without TTPS. In: Proceedings of the 14th ACM Conference on Computer and Communications Security, CCS 207, pp. 72–81. ACM (2007)
Zhang, Y., Feng, D.: Efficient attribute proofs in anonymous credential using attribute-based cryptography. In: Chim, T.W., Yuen, T.H. (eds.) ICICS 2012. LNCS, vol. 7618, pp. 408–415. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-34129-8_39
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 International Association for Cryptologic Research
About this paper
Cite this paper
Tan, SY., Groß, T. (2020). MoniPoly—An Expressive q-SDH-Based Anonymous Attribute-Based Credential System. In: Moriai, S., Wang, H. (eds) Advances in Cryptology – ASIACRYPT 2020. ASIACRYPT 2020. Lecture Notes in Computer Science(), vol 12493. Springer, Cham. https://doi.org/10.1007/978-3-030-64840-4_17
Download citation
DOI: https://doi.org/10.1007/978-3-030-64840-4_17
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-64839-8
Online ISBN: 978-3-030-64840-4
eBook Packages: Computer ScienceComputer Science (R0)



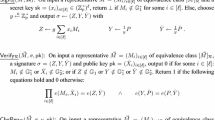

 to compute
to compute 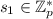 to initialize the issuing protocol by completing the protocol with the issuer:
to initialize the issuing protocol by completing the protocol with the issuer:  to randomize the credential as
to randomize the credential as  to randomize the credential as
to randomize the credential as  to randomize the credential as
to randomize the credential as  to randomize the credential as
to randomize the credential as  to randomize the credential as
to randomize the credential as 
