Abstract
The share size of general secret-sharing schemes is poorly understood. The gap between the best known upper bound on the total share size per party of \(2^{0.64n}\) (Applebaum et al., STOC 2020) and the best known lower bound of \(\varOmega (n/\log n)\) (Csirmaz, J. of Cryptology 1997) is huge (where n is the number of parties in the scheme). To gain some understanding on this problem, we study the share size of secret-sharing schemes of almost all access structures, i.e., of almost all collections of authorized sets. This is motivated by the fact that in complexity, many times almost all objects are hardest (e.g., most Boolean functions require exponential size circuits). All previous constructions of secret-sharing schemes were for the worst access structures (i.e., all access structures) or for specific families of access structures.
We prove upper bounds on the share size for almost all access structures. We combine results on almost all monotone Boolean functions (Korshunov, Probl. Kibern. 1981) and a construction of (Liu and Vaikuntanathan, STOC 2018) and conclude that almost all access structures have a secret-sharing scheme with share size \(2^{\tilde{O}(\sqrt{n})}\).
We also study graph secret-sharing schemes. In these schemes, the parties are vertices of a graph and a set can reconstruct the secret if and only if it contains an edge. Again, for this family there is a huge gap between the upper bounds – \(O(n/\log n)\) (Erdös and Pyber, Discrete Mathematics 1997) – and the lower bounds – \(\varOmega (\log n)\) (van Dijk, Des. Codes Crypto. 1995). We show that for almost all graphs, the share size of each party is \(n^{o(1)}\). This result is achieved by using robust 2-server conditional disclosure of secrets protocols, a new primitive introduced and constructed in (Applebaum et al., STOC 2020), and the fact that the size of the maximal independent set in a random graph is small. Finally, using robust conditional disclosure of secrets protocols, we improve the total share size for all very dense graphs.
A. Beimel—This work was done while visiting Georgetown University, supported by NSF grant no. 1565387, TWC: Large: Collaborative: Computing Over Distributed Sensitive Data and also supported by ERC grant 742754 (project NTSC), by ISF grant 152/17, and by a grant from the Cyber Security Research Center at Ben-Gurion University of the Negev.
O. Farràs—This work is supported by grant 2017 SGR 705 from the Government of Catalonia and grant RTI2018-095094-B-C21 “CONSENT” from the Spanish Government.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
A dealer wants to store a string of secret information (a.k.a. a secret) on a set of computers such that only some pre-defined subsets of the computers can reconstruct the information. We will refer to the computers as the parties, their number as n, and the collection of authorized sets that can reconstruct the secret as an access structure. To achieve this goal the dealer uses a secret-sharing scheme – a randomized function that is applied to the secret and produces n strings, called shares. The dealer gives the i-th share to the i-th party, and any authorized set of parties can reconstruct the secret from its shares. Nowadays, secret-sharing schemes are used as a building box in many cryptographic tasks (see, e.g., [10, 13]). We consider schemes where unauthorized sets of parties gain absolutely no information on the secret from their shares, i.e., the security is information theoretic. We will mainly try to reduce the sizes of the shares given to the parties. To understand why minimizing the share size is important, let us consider the original secret-sharing schemes of [44] for an arbitrary access structure; in these schemes the size of each share is greater than \(2^n\), making them impractical when, for example, \(n=100\). Even in the most efficient scheme known today, the share size is \(2^{0.64n}\) [5] (improving on [4, 48]).
We ask the question if the above share size can be reduced for almost all access structures. One motivation for this question is that in complexity theory, almost all Boolean functions are often the hardest functions. For example, Shannon [58] showed that almost all Boolean functions require circuits of size \(2^{\varOmega (n)}\), this lower bound applies also to other models, e.g., formulas. Furthermore, almost all monotone Boolean functions require monotone circuits and monotone formulas of size \(2^{\varOmega (n)}\). Dealing with properties of almost all objects is a common theme in combinatorics, e.g., properties of almost all graphs. A famous example states that the size of the maximum independent set (and clique) of almost all n-vertex graphs is approximately \(2\log n\) [43]; we use this property in our constructions. Using a result on almost all monotone Boolean functions [47], we show that almost all access structures can be realized by a secret-sharing scheme with maximum share size \(2^{\tilde{O}(\sqrt{n})}\).
In this paper, we also study graph secret-sharing schemes. In a secret-sharing scheme realizing a graph G, the parties are vertices of the graph G and a set can reconstruct the secret if and only if it contains an edge. The naive scheme to realize a graph is to share the secret independently for each edge; this result implies a share of size O(n) per party. A better scheme with share size \(O(n/\log n)\) per party is implied by a result of Erdös and Pyber [38]. Graph secret-sharing schemes were studied in many previous works. One motivation for studying graph secret-sharing schemes is that they are simpler than secret-sharing schemes for general access structures and phenomena proved for graph secret-sharing schemes were later generalized to general access structures (e.g., Blundo et al. [26] proved that in any non-ideal access structure the share size of at least one party is at least 1.5 times the size of the secret, a result that was later proved for every access structure [51]). Another motivation is that, by [54, Section 6.3.1], for every \(0<c < 1/2\) any graph secret-sharing scheme with share size \(O(n^c)\) per party implies a secret-sharing scheme for any access structure with share size \(2^{(0.5+c/2+o(1))n}\); thus, major improvement in the share size for all graphs will result in improved schemes for all access structures. However, in spite of the recent improvements in the share size for general access structures [4, 5, 48] and for specific families of access structures (e.g., forbidden graphs [18, 41, 49] and uniform access structures [2, 4, 19]), no such improvement was achieved for schemes for graphs. We show that almost all graphs can be realized by a secret-sharing scheme with share size \(n^{o(1)}\) per party.
1.1 Previous Results
We next describe the most relevant previous results. We refer the reader to Fig. 1 for a description of the maximum share size in previous constructions and our constructions.
Measures of Share Size. The size of a share is simply the length of the string representing it. For a secret-sharing scheme, two measures of for the share size were considered: (1) the maximum share size, i.e., the maximum over all parties in the scheme of the size of the share of the party, (2) the total share size, i.e., the sum over all parties in the scheme of the size of the share of the party. For a given scheme, the maximum share size is bounded from above by the total share size, which is bounded from above by n times the maximum share size. The distinction between these two measures is important for graph secret-sharing schemes, and there might be trade-offs between optimizing one measure and optimizing the other. On the other hand, the share size in the secret-sharing schemes considered in this paper for general access structures is larger than \(2^{\sqrt{n}}\), thus for these schemes the distinction between the measures is less important.
We will also consider the normalized total (respectively, maximum) share size, i.e., the ratio between the sum of the share sizes (respectively, maximum share size) and the size of the secret. This normalized maximum share size (also known as information ratio) is similar in spirit to measures considered in information theory and it is interesting since the length of each share is at least the length of the secret [46]. In this work, we will consider the normalized share size for two regimes: (1) Moderately short secrets of size \(\tilde{O}(n)\), and (2) Following [2, 3], we also consider exponentially long secrets of size \(2^{n^2}\). The latter size is not reasonable, however, these schemes may lead to schemes with the same share size for shorter secrets and they provide barriers for proving lower bounds via information inequalities.
Bounds on the Share Size. Secret-sharing schemes were introduced by Blakely [24] and Shamir [57] for the threshold case and by Ito, Saito, and Nishizeki [44] for the general case. In the original secret-sharing schemes for arbitrary access structures of Ito et al. [44] the maximum share size is \(2^{n-1}\). Additional constructions of secret-sharing schemes followed, e.g., [22, 23, 29, 45, 59]. For specific access structures, the share size in these schemes is less than the share size in the scheme of [44]; however, the share size in the above schemes for arbitrary access structures is \(2^{n-o(n)}\). In a recent breakthrough work, Liu, and Vaikuntanathan [48] (using results of [50]) constructed a secret-sharing scheme for arbitrary access structures with share size \(2^{0.944n}\) and a linear secret-sharing scheme with share size \(2^{0.999n}\). Applebaum et al. [5] (using results of [4, 50]) improved these results, constructing a secret-sharing schemes for arbitrary access structures with share size \(2^{0.637n}\) and a linear secret-sharing scheme with share size \(2^{0.762n}\). It is an important open problem if the share size can be improved to \(2^{o(n)}\) (or even smaller). Lower bounds for secret-sharing were proven in, e.g., [25, 30, 33, 34, 37]. These lower bounds are very far from the upper bounds – the best lower bound is \(\varOmega (n^2/\log n)\) for the normalized total share size for an explicit access structure (proven by Csirmaz [33]).
For graph secret-sharing schemes there is also a big gap between the upper bounds and lower bounds. Erdös and Pyber [38] have proved that every graph can be partitioned into complete bipartite graphs such that each vertex is contained in at most \(O(n/\log n)\) complete bipartite graphs. Blundo et al. [25] observed that this implies that the normalized maximum share size of realizing every n-vertex graph is \(O(n/\log n)\) (for secrets of size \(\log n\)). Van Dijk [37] proved a lower bound of \(\varOmega (\log n)\) on the normalized maximum share size of realizing an explicit n-vertex graph. Csirmaz [35] extended this lower bound to the n-vertex Boolean cube. He observed that a lower bound of \(\varOmega (\log n)\) on a specific graph implies a lower bound of \(\varOmega (\log \log n)\) for almost all graphs (as almost all n-vertex graphs contain a copy of every \(\log n\)-vertex graph [28]). Furthermore, Csirmaz asked if for almost every graph there is a scheme with normalized maximum share size \(o(n/\log n)\). We answer this question affirmatively by showing for almost all graphs a secret-sharing scheme with maximum share size \(n^{o(1)}\).
Linear Secret-Sharing Schemes. Linear secret-sharing schemes, introduced by [29, 45], are schemes in which the random string is a vector of elements over some finite field \(\mathbb {F}_q\), the domain of secrets is also \(\mathbb {F}_q\), and the shares are computed as a linear map over \(\mathbb {F}_q\). Many known schemes are linear, e.g., [22, 24, 57] and the schemes for graphs implied by [38]. They are equivalent to a linear-algebraic model of computation called monotone span programs [45]. Linear secret-sharing schemes are useful as they are homomorphic: given shares of two secrets \(s,s'\), each party can locally add its shares and obtain a share of \(s+s'\). For many applications of secret sharing, linearity is essential, e.g., [8, 32, 61], hence, constructing linear secret-sharing schemes is important. The size of the shares in the best known linear secret-sharing scheme is \(2^{0.76n}\) [5] (improving upon [48]). Pitassi and Robere [55] proved an exponential lower bound of \(2^{cn}\log q\) on the share in linear secret-sharing schemes over \(\mathbb {F}_q\) for an explicit access structure of (where \(0< c<1/2\) is a constant). Babai et al. [9] proved a lower bound of \(2^{n/2-o(n)}\sqrt{\log q}\) on the share in linear secret-sharing schemes over \(\mathbb {F}_q\) for almost all access structures.
Multi-linear secret-sharing schemes, introduced by [23], are a generalization of linear secret-sharing schemes in which the domain of secrets is \(\mathbb {F}^\ell _q\) for some integer \(\ell \). In [2, 5], such schemes improve the normalized maximum share size compared to the linear secret-sharing schemes constructed in those papers (i.e., the multi-linear schemes share a longer secret while using the same share size as the linear schemes). Beimel et al. [11] proved that every lower bound proved for linear secret-sharing schemes using the Gal-Pudlák criteria [40] also applies to multi-linear secret-sharing schemes. In particular, this implies that the \(n^{\varOmega (\log n)}\) lower bound of [9] for the normalized maximum share size for an explicit access structure and the \(\varOmega (\sqrt{n})\) lower bound of [17] for the normalized maximum share size for an explicit graph access structure hold also for multi-linear secret-sharing schemes. We note that it is not clear if multi-linear secret-sharing schemes can replace linear secret-sharing schemes in many applications, e.g., in the MPC protocols of [32] that are secure against general adversarial structures.
Conditional Disclosure of Secrets (CDS) Protocols [42]. A CDS protocol for a Boolean function f involves k servers and a referee. Each server holds a common secret s, a common random string r, and a private input \(x_i\); using these r, s, and \(x_i\) the i-th server computes one message (without seeing any other input or message) and sends it to the referee. The referee, knowing the inputs \(x_1,\dots ,x_k\) and the messages, should be able to compute s iff \(f(x_1,\dots ,x_k)=1\). CDS protocols were used in many cryptographic applications, such as symmetric private information retrieval protocols [42], attribute based encryption [8, 41, 61], priced oblivious transfer [1], and secret-sharing schemes [4, 5, 48]. Applebaum et al. [5] defined robust CDS protocols (see Definition 2.10) and used them to construct secret-sharing schemes for arbitrary access structures. We use robust CDS protocols to construct schemes for almost all graphs and for all very dense graphs.
The original construction of k-server CDS protocols for general k-input functions, presented in [42], has message size \(O(N^k)\) (where N is the input domain size of each server). This construction is linear. Recently, better constructions of CDS protocols for general functions have been presented. Beimel et al. [18] have shown a non-linear 2-server CDS protocol with message size \(O(N^{1/2})\) and Gay et al. [41] constructed a linear 2-server CDS protocol with the same message size. Then, Liu et al. [49] have designed a 2-server non-linear CDS protocol with message size \(2^{O(\sqrt{\log N \log \log N})}\) and Liu et al. [50] have constructed a k-server CDS protocol with message size \(2^{\tilde{O}(\sqrt{k \log N})}\). Beimel and Peter [20] and Liu et al. [50] have constructed a linear CDS protocol with message size \(O(N^{(k-1)/2})\); by [20], this bound is optimal for linear CDS protocols (up to a factor of k). Applebaum and Arkis [2] (improving on Applebaum et al. [3]) have showed that there is a CDS protocol with long secrets – of size \(\varTheta (2^{N^k})\) – in which the message size is 4 times the secret size. Lower bounds on the message size in CDS protocols and in linear CDS protocols have been proven in [3, 6, 7, 41].
Forbidden Graph Access Structures. In a forbidden-graph secret-sharing scheme for a graph G, introduced by Sun and Shieh [60], the parties are the vertices of the graph G and a set is authorized if it is an edge or its size is at least 3. A forbidden-graph secret-sharing scheme for a graph G is not harder than a graph secret-sharing realizing G: Given a secret-sharing scheme realizing a graph, one can construct a forbidden-graph secret-sharing scheme for G by giving a share of the graph secret-sharing scheme and a share of a 3-out-of-n threshold secret-sharing schemes. Furthermore, forbidden graph secret-sharing schemes are closely related to 2-server CDS protocols: Beimel et al. [18] have described a transformation from a CDS protocol for a function describing the graph G to a forbidden graph secret-sharing scheme for G in which the maximum share size of the scheme is \(O(\log n)\) times the message size of the CDS protocol. Furthermore, by [2, 18], if we consider secrets of size at least \(O(\log ^2 n)\), then there is a transformation in which the normalized maximum share size is a constant times the message size of the CDS protocol. As a result, we get that every forbidden graph G can be realized by a secret-sharing with maximum share size \(n^{o(1)}\) (using the CDS protocol of [49]), by a linear secret-sharing scheme over \(\mathbb {F}_q\) with maximum share size \(\tilde{O}(\sqrt{n}\log q)\) for every prime power q (using the CDS protocol of [41]), and a multi-linear secret-sharing scheme with normalized maximum share size O(1) for secrets of length \(2^{n^2}\) [2]. We nearly match these bounds for graph access structures for almost all graphs.
1.2 Our Results and Techniques
We next describe the results we achieve in this paper. We again refer the reader to Fig. 1 for a description of the maximum share size in previous constructions and our constructions.
Almost All Access Structures. We prove upper bounds on the share size for almost all access structures, namely almost all access structures have a secret-sharing scheme with share size \(2^{\tilde{O}(\sqrt{n})}\), a linear secret-sharing scheme with share size \(2^{n/2+o(n)}\), and a multi-linear secret-sharing scheme with maximum share size \(\tilde{O}(\log n)\) for secrets of size \(2^{n^2}\). Our linear secret-sharing scheme for almost all access structures are optimal (up to a factor of \(2^{o(n)}\)) for a one-bit secret (by a lower bound of Babai et al. [9]).
The construction for almost all access structures is a simple combination of previous results. The first result, proved by Korshunov [47] in 1981, is that in almost all access structures with n parties all minimum authorized sets are of size between \(n/2-1\) and \(n/2+2\), i.e., all sets of size at most \(n/2-2\) are unauthorized and all sets of size at least \(n/2+3\) are authorized. The second result we use, proved by Liu and Vaikuntanathan [48], is that such access structures can be realized by secret-sharing schemes with share size as above. These results are presented in Sect. 3.
We also prove lower bounds on the normalized share size in linear secret-sharing schemes for almost all access structures. Rónyai et al. [56] proved that for every finite field \(\mathbb {F}_q\) for almost all access structures the normalized share size of linear secret-sharing schemes over \(\mathbb {F}_q\) realizing the access structure is at least \(\varOmega (2^{n/3-o(n)})\). The result of Rónyai et al. [56] does not rule-out the possibility that for every access structures there exists some finite field \(\mathbb {F}_q\) (possibly with a large q) such that the access structure can be realized by a linear secret-sharing schemes over \(\mathbb {F}_q\) with small normalized share size. This could be plausible since we know that there are access structures that can be realized by an efficient linear secret-sharing scheme over one field, but require large shares in any linear secret-sharing scheme over fields with a different characteristic [21, 55]. Pitassi and Robere [55] proved that there exists an explicit access structure for which this is not true, i.e., there exists a constant \(c>0\) such that in any linear secret-sharing scheme realizing it the normalized share size is \(2^{cn}\). In Theorem 3.10, we prove that this is not true for almost all access structures, namely, for almost every access structure the normalized share size in any linear secret-sharing scheme realizing the access structure is \(\varOmega (2^{n/3-o(n)})\). Our proof uses a fairly recent result on the number of representable matroids [53].
(G, t)-Graph Secret-Sharing Schemes and Robust CDS. We define a hierarchy of access structures between forbidden graph access structures and graph access structures. In a (G, t)-secret-sharing scheme, every set containing an edge is authorized and, in addition, every set of size \(t+1\) is authorized. In other words, the unauthorized sets are independent sets in G of size at most t. We show that (G, t)-secret-sharing schemes are equivalent to 2-server t-robust CDS protocols. As a result, using the robust CDS protocols of [5], we get efficient (G, t)-secret-sharing schemes, e.g., schemes with maximum share size \(n^{o(1)}t\). These results are presented in Sect. 4. We note that, for an arbitrary graph G, our (G, n)-secret-sharing scheme, which is a graph secret-sharing scheme realizing G, the share size does not improve upon the scheme of [38].
Almost All Graph Secret-Sharing Schemes. We show that for almost all graphs, there exists a secret-sharing scheme with maximum share size \(n^{o(1)}\), a linear secret-sharing scheme with normalized maximum share size \(\tilde{O}(\sqrt{n})\) (for moderately short secrets), and a multi-linear secret-sharing scheme with normalized maximum share size \(\tilde{O}(\log {n})\) for exponentially long secrets. By [11, 17], there exists a graph such that in every multi-linear secret-sharing scheme realizing the graph the normalized maximum share size is \(\varOmega (\sqrt{n})\), thus, we get a separation for multi-linear secret-sharing schemes between the normalized maximum share size for almost all graphs and the maximum share size of the worst graph. These results are presented in Sect. 5.
To construct our scheme for almost all graphs, we use the fact that if the size of every independent set in a graph G is at most t, then a (G, t)-secret-sharing scheme is a graph secret-sharing scheme realizing G. Our construction follows from the fact that for almost every graph, the size of the maximal independent set in a random graph is \(O(\log n)\) [43].
We also consider the maximum share size of random n-vertex graphs drawn from the Erdös-Rényi [39] distribution \(\mathscr {G}(n,p)\), that is, each pair of vertices is independently connected by an edge with probability p. For example, \(\mathscr {G}(n,1/2)\) is the uniform distribution over the n-vertex graphs. On one hand, with probability nearly 1 the size of the maximum independent set in a graph drawn from \(\mathscr {G}(n,p)\) is at most \(O(\frac{1}{p} \log n)\), thus, using (G, t)-secret-sharing schemes with \(t=O(\frac{1}{p} \log n)\), we realize a graph in \(\mathscr {G}(n,p)\) with normalized maximum share size \(n^{o(1)}/p\). On the other hand, with probability nearly 1 the degree of all vertices in the graph drawn from \(\mathscr {G}(n,p)\) is O(pn), thus, it can be realized by the trivial secret-sharing scheme with maximum share size O(pn). Combining these two schemes, the hardest distribution in our construction is \(\mathscr {G}(n,1/\sqrt{n})\) for which the normalized maximum share size is \(\sqrt{n}\). We do not know if there is a better secret-sharing scheme for graphs drawn from \(\mathscr {G}(n,1/\sqrt{n})\) or this distribution really requires shares of size \(n^{\varOmega (1)}\).
Dense Graph Secret-Sharing Schemes. Following [14], we study graph secret-sharing schemes for very dense graphs, i.e., graphs with at least \(\left( {\begin{array}{c}n\\ 2\end{array}}\right) -n^{1+\beta }\) edges for some constant \(\beta \). For these graphs, Beimel et al. [14] have constructed a linear secret-sharing scheme with maximum share size \(\tilde{O}(n^{1/2+\beta /2})\) and another linear secret-sharing scheme with total share size \(\tilde{O}(n^{5/4+3\beta /4})\). We improve on the latter result and show that all very dense graphs can be realized by a secret-sharing scheme with normalized total share size of \(n^{1+\beta +o(1)}\) for moderately short secrets of size \(\tilde{O}(n)\). To put this result in perspective, this total share size matches (up to a factor of \(n^{o(1)}\)) to the total share size of the naive secret-sharing scheme for sparse graphs with \(n^{1+\beta }\) edges. These schemes are presented in Sect. 6.
We next describe the high-level ideas of our construction realizing a graph G with at least \(\left( {\begin{array}{c}n\\ 2\end{array}}\right) -n^{1+\beta }\) edges. If every vertex in G has degree at least \(n-n^{\beta }\), then the size of every independent set in G is at most \(n^{\beta }+1\), and we can use a \((G,n^{\beta }+1)\)-secret-sharing schemes, resulting in normalized total share size \(O(n^{1+\beta +o(1)})\). While in a graph with at least \(\left( {\begin{array}{c}n\\ 2\end{array}}\right) -n^{1+\beta }\) edges the average degree is at least \(n-O(n^\beta )\), the graph can contain vertices whose degree is small. To overcome this problem, we use an idea of [14]. We consider the set of vertices A whose degree is smallest in G and execute a secret-sharing scheme realizing the graph restricted to this set (denoted \(G'\)). We choose the size of this set such that: (1) the size of the set is small, thus, the total share size in realizing \(G'\) is small, and (2) the degree of the each vertex not in A is big, thus, we can realize the graph without the edges between vertices in A by a (G, t)-secret-sharing scheme for a relatively small t. We apply the above construction iteratively to get our scheme.
Hypergraph Secret-Sharing Schemes. A secret-sharing realizes a hypergraph H if the parties of the scheme are the vertices of H and a set of parties can reconstruct the secret if and only if it contains a hyperedge. In this work, we construct schemes for k-hypergraphs, that is, hypergraphs whose hyperedges are all of size k. The access structures of these schemes are also called k-homogeneous. The best secret-sharing scheme for k-hypergraphs known to date is the original scheme of [44], which have maximum share size \(O(\left( {\begin{array}{c}n\\ k-1\end{array}}\right) )\). Extending the results explained above, we show a connection between k-hypergraph secret-sharing schemes and k-server t-robust CDS protocols. For any constant k, we show that for almost every k-hypergraph there exists a secret-sharing scheme with maximum share size is \(n^{o(1)}\), a linear secret-sharing scheme with normalized maximum share size \(\tilde{O}(n^{(k-1)/2})\), and a multi-linear secret-sharing scheme with normalized maximum share size \(\tilde{O}(\log ^{k-1}{n})\) for exponentially long secrets. These schemes are presented in the full version of this paper [13].
Interpretation of Our Results. In this work we have shown that for almost all access structures there exist secret-sharing schemes that are more efficient than the known secret-sharing schemes for the worst access structures. Similarly, we have constructed for almost every graph G a secret-sharing schemes realizing G that are more efficient than the known secret-sharing schemes realizing the worst graph. One possible conclusion from this result is that in secret-sharing schemes almost all access structures might not be the hardest access structures. Another possible interpretation is that our results may be generalized to all access structures. We note that in one case we know that the former interpretation is true: there is a graph for which the normalized maximum share size for multi-linear schemes is at least \(\varOmega (\sqrt{n})\) (for every size of secrets) [11, 17], while we show an upper bound for almost all graphs of \(\tilde{O}(\log n)\) (for long secrets).
Open Problems. Can the normalized share size of almost all access structures can be improved? We do not have any non-trivial lower-bound on the normalized share size for them. Recall that an access structure is n/2-uniform if all sets of size less than n/2 are unauthorized, all sets of size greater than n/2 are authorized, and sets of size exactly n/2 can be either authorized or unauthorized. By [4] (using results of [2]), every n/2-uniform access structure can be realized by a scheme with normalized maximum share size \(O(n^2)\) (with exponentially long secrets). Since almost all access structures somewhat resemble uniform access structures (see Theorem 3.2), one can hope that almost every access structure can be realized by a scheme with polynomial normalized share size.
Another research problem is to study the complexity of almost all functions for other primitives with information-theoretic security, for example, private simultaneous messages (PSM) protocols, MPC protocols, MPC protocols with constant number of rounds, and private information retrieval (PIR) protocols for almost all databases. For all these primitives there is a huge gap between the known upper bounds and lower bounds on the message size. Are there more efficient protocols for any of these primitives for almost all functions than the protocols for all functions?
2 Preliminaries
In the section, we present the preliminary results needed for this work. First, we define secret-sharing schemes, linear secret-sharing schemes, graph secret-sharing schemes, and homogeneous access structures. Second, we define conditional disclosure of secrets (CDS) protocols, and robust CDS protocols. We also present several CDS and robust CDS protocols from [2, 20, 49, 50] that are used in this work. Finally, we present a short introduction to random graphs and random access structures.
Secret-Sharing Schemes. We present the definition of secret-sharing scheme as given in [12, 31]. For more information about this definition and secret-sharing in general, see [10].
Definition 2.1
(Access Structures). Let \(P=\left\{ P_1,\dots ,P_n \right\} \) be a set of parties. A collection \(\varGamma \subseteq 2^P\) is monotone if \(B \in \varGamma \) and \(B \subseteq C\) imply that \(C \in \varGamma \). An access structure is a monotone collection \(\varGamma \subseteq 2^P\) of non-empty subsets of \(P\). Sets in \(\varGamma \) are called authorized, and sets not in \(\varGamma \) are called forbidden.
Definition 2.2
(Secret-Sharing Schemes). A secret-sharing scheme \(\varPi \) with domain of secrets S, such that \(|S| \ge 2\), is a mapping from \(S\times R\), where R is some finite set called the set of random strings, to a set of n-tuples \(S_1\times S_2 \times \dots \times S_{n}\), where \(S_j\) is called the domain of shares of \(P_j\). A dealer distributes a secret \(s \in S\) according to \(\varPi \) by first sampling a random string \(r \in R\) with uniform distribution, computing a vector of shares \(\varPi (s,r)=(s_1,\ldots ,s_{n})\), and privately communicating each share \(s_j\) to party \(P_j\). For a set \(A \subseteq P\), we denote \(\varPi _A(s,r)\) as the restriction of \(\varPi (s,r)\) to its A-entries (i.e., the shares of the parties in A).
A secret-sharing scheme \(\varPi \) with domain of secrets S realizes an access structure \(\varGamma \) if the following two requirements hold:
Correctness. The secret s can be reconstructed by any authorized set of parties. That is, for any set \(B=\left\{ P_{i_1},\dots ,P_{i_{|B|}} \right\} \in \varGamma \) there exists a reconstruction function \(\mathrm{Recon}_B:S_{i_1} \times \cdots \times S_{i_{|B|}} \rightarrow S\) such that \(\mathrm{Recon}_B\left( \varPi _B(s,r)\right) =s\) for every secret \(s \in S\) and every random string \(r \in R\).
Privacy. Any forbidden set cannot learn anything about the secret from its shares. Formally, for any set \(T=\left\{ P_{i_1},\dots ,P_{i_{|T|}} \right\} \notin \varGamma \) and every pair of secrets \(s,s' \in S\), the distributions \(\varPi _T(s,r)\) and \(\varPi _T(s',r)\) are identical, where the distributions are over the choice of r from R at random with uniform distribution.
Given a secret-sharing scheme \(\varPi \), define the size of the secret as \(\log |S|\), the share size of party \(P_j\) as \(\log |S_j|\), the maximum share size as \(\max _{1\le j \le n} \left\{ \log |S_j| \right\} \), and the total share size as \(\sum _{j=1}^n \log |S_j|\).
A secret-sharing scheme is multi-linear if the mapping that the dealer uses to generate the shares given to the parties is linear, as we formalize at the following definition.
Definition 2.3
(Multi-linear and Linear Secret-Sharing Schemes). Let \(\varPi \) be a secret-sharing scheme with domain of secrets S. We say that \(\varPi \) is a multi-linear secret-sharing scheme over a finite field \(\mathbb {F}\) if there are integers \(\ell _d,\ell _r,\ell _1,\dots ,\ell _n\) such that \(S=\mathbb {F}^{\ell _d}\), \(R=\mathbb {F}^{\ell _r}\), \(S_1=\mathbb {F}^{\ell _1},\ldots ,S_{n}=\mathbb {F}^{\ell _n}\), and the mapping \(\varPi \) is a linear mapping over \(\mathbb {F}\) from \(\mathbb {F}^{\ell _d+\ell _r}\) to \(\mathbb {F}^{\ell _1+\cdots +\ell _n}\). We say that a scheme is linear over \(\mathbb {F}\) if \(S=\mathbb {F}\) (i.e., when \(\ell _d=1\)).
Definition 2.4
(Graph secret-sharing schemes). Let \(G=(V, E)\) be an undirected graph with \(|V|=n\); for simplicity we assume that \(E\ne \emptyset \). We define \(\varGamma _G\) as the access structure whose minimal authorized subsets are the edges in G, that is, the unauthorized sets are independent sets in the graph. A secret-sharing scheme realizing an access structure \(\varGamma _{G}\) is said to be a secret-sharing scheme realizing the graph G and is called a graph secret-sharing schemes.
These schemes are one of the main topics in this work. In this paper, we study very dense graphs, graphs with at least \(\left( {\begin{array}{c}n\\ 2\end{array}}\right) -n^{1+\beta }\) edges for some \(0\le \beta <1\).
We also study k-homogeneous access structures, which are access structures whose minimal authorized subsets are of the size k. For example, graph access structures are 2-homogeneous access structures. For \(k>2\), it is convenient to define k-homogeneous access structures from hypergraphs. A hypergraph is a pair \(H=(V,E)\) where V is a set of vertices and \(E\subseteq 2^V\setminus \{\emptyset \}\) is the set of hyperedges. A hypergraph is k-uniform if \(|e|=k\) for every \(e\in E\). A k-uniform hypergraph is complete if \(E=\left( {\begin{array}{c}V\\ k\end{array}}\right) =\{e\subseteq V\, :\, |e|=k\}\). Observe that there is a one-to-one correspondence between uniform hypergraphs and homogeneous access structures, and that complete uniform hypergraphs correspond to threshold access structures. Given a hypergraph \(H=(V,E)\), we define \(\varGamma _H\) as the access structure whose minimal authorized sets are the hyperedges of H.
We contrast homogeneous access structures with uniform access structures (studied, e.g., in [2, 4, 19, 60]). A k-uniform access structures is also described by a k-uniform hyper-graph and its authorized sets are all the hyper-edges and all sets of size at least \(k+1\). Thus, k-homogeneous access structures are harder to realize as they might contain forbidden sets of size much larger than k.Footnote 1
Conditional Disclosure of Secrets. We define k-server conditional disclosure of secrets protocols, originally defined in [42].
Definition 2.5
(Conditional Disclosure of Secrets Protocols). Let \(f: X_1 \times \cdots \times X_k \rightarrow \{0,1\}\) be a k-input function. A k-server CDS protocol \(\mathcal {P}\) for f with domain of secrets S consists of:
-
1.
A finite domain of common random strings R, and k finite message domains \(M_1,\ldots ,M_k\),
-
2.
Deterministic message computation functions
 , where
, where  for every \(i \in [k]\) (we also say that
for every \(i \in [k]\) (we also say that  is the message sent by the i-th server to the referee), and
is the message sent by the i-th server to the referee), and -
3.
A deterministic reconstruction function
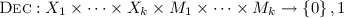 .
.
We denote  . We say that a CDS protocol \(\mathcal {P}\) is a CDS protocol for a function f if the following two requirements hold:
. We say that a CDS protocol \(\mathcal {P}\) is a CDS protocol for a function f if the following two requirements hold:
Correctness. For any input \((x_1, \dots , x_k) \in X_1 \times \cdots \times X_k\) for which \(f(x_1, \dots , x_k)=1\), every secret \(s \in S\), and every common random string \(r \in R\),

Privacy. For any input \(x=(x_1, \dots , x_k) \in X_1 \times \cdots \times X_k\) for which \(f(x_1, \dots , x_k)=0\) and for every pair of secrets \(s,s'\), the distributions  and
and  are identical, where the distributions are over the choice of r from R at random with uniform distribution.
are identical, where the distributions are over the choice of r from R at random with uniform distribution.
The message size of a CDS protocol \(\mathcal {P}\) is defined as the size of largest message sent by the servers, i.e., \(\max _{1 \le i \le k} \left\{ \log |M_i| \right\} \).
Next, we present the properties of three CDS protocols that are used in this work. The CDS protocol presented in Theorem 2.6 has linear properties: the messages are generated from the secret and the randomness with linear mappings. Theorem 2.6 is a particular case of Theorem 6 of [2], while Theorem 2.7 is from [49].
Theorem 2.6
([2]). For any 2-input function \(f:[n]\times [n]\rightarrow \{0,1\}\) there is a 2-server CDS protocol in which, for sufficiently large secrets, i.e., secrets of size \(2^{n^2}\), each server communicates at most 3 bits per each bit of the secret.
Theorem 2.7
([49]). For any 2-input function \(f:[n]\times [n]\rightarrow \{0,1\}\) there is a 2-server CDS protocol with a one bit secret and message size \(n^{O(\sqrt{ \log \log n/\log n})}=n^{o(1)}\).
Theorem 2.8
([50]). For any k-input functions \(f:[n]^k\rightarrow \{0,1\}\) there is a k-server CDS protocol with a one bit secret and message size \(n^{O(\sqrt{k/\log n}\log (k\log n))}\).
Robust Conditional Disclosure of Secrets. In a recent work [5], Applebaum et al. define a stronger notion of CDS protocols that is useful for constructing secret-sharing schemes. In a k-server CDS protocol, we assume that each server sends one message to the referee. Therefore, the referee only has access to k messages. In a robust k-server CDS protocol, we consider the case that the referee can have access to more than one message from some servers (generated with the same common random string), and privacy is guaranteed even if an adversary sees a bounded number of messages from each server.
Definition 2.9
(Zero sets). Let \(f: X_1 \times \cdots \times X_k \rightarrow \{0,1\}\) be a k-input function. We say that a set of inputs \(Z \subseteq X_1\times \cdots \times X_k\) is a zero set of f if \(f(x)=0\) for every \(x \in Z\). For sets \(Z_1,\dots ,Z_k\), we denote  , and
, and

Definition 2.10
(Robust conditional disclosure of secrets (RCDS) protocols). Let \(\mathcal {P}\) be a k-server CDS protocol for a k-input function \(f:X_1\times \cdots \times X_k \rightarrow \left\{ 0,1 \right\} \) and \(Z=Z_1\times \cdots \times Z_k\subseteq X_1\times \cdots \times X_k\) be a zero set of f. We say that \(\mathcal {P}\) is robust for the set Z if for every pair of secrets \(s,s' \in S\), it holds that  and
and  are identically distributed. Let \(t_1,\ldots ,t_k\) be integers. We say that \(\mathcal {P}\) is a \((t_1,\ldots ,t_k)\)-robust CDS protocol if it is robust for every zero set \(Z_1\times \cdots \times Z_k\) such that \(|Z_i|\le t_i\) for every \(i\in [k]\) and it is a t-robust CDS protocol if it is \((t,\dots ,t)\)-robust.
are identically distributed. Let \(t_1,\ldots ,t_k\) be integers. We say that \(\mathcal {P}\) is a \((t_1,\ldots ,t_k)\)-robust CDS protocol if it is robust for every zero set \(Z_1\times \cdots \times Z_k\) such that \(|Z_i|\le t_i\) for every \(i\in [k]\) and it is a t-robust CDS protocol if it is \((t,\dots ,t)\)-robust.
In this work we use several constructions of robust CDS protocols presented in [4], which are based on non-robust CDS protocols. Theorem 2.11 presents linear and multi-linear robust CDS protocols in which the underlying CDS protocol is from [41]. Then, Theorem 2.12 presents a generic transformation from non-robust CDS protocols to robust CDS protocols. In this transformation, if the original CDS is linear, then the resulting robust CDS is multi-linear.
Theorem 2.11
([5, Theorem D.5]). Let \(f : [N]\times [N]\rightarrow \{0, 1\}\) be a function. Then, for every finite field \(\mathbb {F}_q\) and every integer \(t\le N/(2\log ^2 N)\), there is a linear 2-server (t, N)-robust CDS protocol for f with one element secrets in which the message size is \(O((t\log ^2 t+\sqrt{N})t\log t\log ^2 N\log q).\) Furthermore, there is \(p_0\) such that for every prime-power \(q>p_0\) there is a multi-linear 2-server (t, N)-robust CDS protocol for f over \(\mathbb {F}_q\) with secrets of size \(\varTheta (t^2\log q \log t \log ^3 N)\) in which the normalized message size is \(O(t \log ^2 t + \sqrt{N}).\)
Theorem 2.12
([5, Theorem E.2]). Let \(f: [N]^k\rightarrow \{0,1\}\) be a k-input function, for some integer \(k > 1\), and \(t\le \min \{kN/2,2^{\sqrt{N/k}}\}\) be an integer. Assume that for some integer \(m\ge 1\), there is a k-server CDS protocol \(\mathcal {P}\) for f with secrets of size m in which the message size is c(N, m). Then, there is a k-server t-robust CDS protocol for f with secrets of size m in which the message size is \(O\left( c(N, m) k^{3k-1}2^kt^k\log ^{2k-1} t \log ^2(N)\right) .\) If \(\mathcal {P}\) is a linear protocol over \(\mathbb {F}_{2^m}\), then the resulting protocol is also linear. Furthermore, there is a k-server t-robust CDS protocol for f with secrets of size \(\varTheta (mk^2t \log t \log ^2(N))\) in which the normalized message size is \(O\left( \frac{c(N, m)}{m}k^{3k-3}2^{k}t^{k-1}\cdot \log ^{2k-2}t\right) .\)
Random Graphs and Access Structures. In this work, we use several results on random graphs to construct secret-sharing schemes for almost all graphs with improved share size. First, we present the Erdös-Rényi model for random graphs [39]. For an introduction to this topic see, e.g., [27].
Let \(\mathscr {G}_n\) be the family of graphs with the vertex set \(V=\{1,\ldots ,n\}\). Given \(0< p < 1\), the model \(\mathscr {G}(n,p)\) is a probability distribution over \(\mathscr {G}_n\) in which each edge is chosen independently with probability p, that is, if G is a graph with m edges, then \(\Pr [\{G\}]=p^m(1-p)^{\left( {\begin{array}{c}n\\ 2\end{array}}\right) -m}.\) Note that when \(p=1/2\), any two graphs are equiprobable.
We say that almost every graph in \(\mathscr {G}(n,p)\) has a certain property Q if \(\Pr [Q]\rightarrow 1\) as \(n\rightarrow \infty \). For \(p=1/2\), saying that almost every graph in \(\mathscr {G}(n,p)\) has a certain property Q is equivalent to saying that the number of graphs in \(\mathscr {G}_n\) satisfying Q divided by \(|\mathscr {G}_n|\) tends to 1 as \(n\rightarrow \infty \). In this case, we will say that almost all graphs satisfy Q.
Analogously, we will use the same expression for any family of access structures \(F_n\). We say that almost all access structures in \(F_n\) satisfy Q if the number of access structures in \(F_n\) satisfying Q divided by \(|F_n|\) tends to 1 as \(n\rightarrow \infty \). In particular, we study the family of homogeneous access structures and the family of all access structures.
Next, we present some properties of the maximum independent sets of graphs in \(\mathscr {G}(n,p)\). Lemma 2.13 was presented by Grimmett and McDiarmid in [43]. Several subsequent results gave more accurate bound on the size of maximum independent sets, but it is enough for our purposes. In Lemma 2.14 we give bounds to the maximum independent sets in \(\mathscr {G}(n,p)\) for non-constant p. In Lemma 2.15 and Lemma 2.16 we present further properties of almost all graphs. The proofs of Lemmas 2.14 and 2.15 are in the full version of this paper [13].
Lemma 2.13
([43]). Let \(0<p<1\) be a constant. Then the size of a maximum independent set in almost every graph in \(\mathscr {G}(n,p)\) is smaller than \(2\log n/\log (\frac{1}{1-p})+o(\log n)\).
As a consequence of Lemma 2.13, the size of a maximum independent set in almost every graph in \(\mathscr {G}_n\) is smaller than \((2+o(1))\log n\).
Lemma 2.14
The size of a maximum independent set in almost every graph in \(\mathscr {G}(n,p)\) is \(O(\frac{\log n}{p})\) if \(1/n \le p \le 1/2\), and \(1+\frac{2+o(1)}{\alpha }\) if \(p=1-n^{-\alpha }\) for some \(1/\log n\le \alpha \le 1\).
With a similar proof, we can also show that for every \(0\le \beta \le 1-\frac{1}{\log n}\), almost all graph with \(n^{1+\beta }\) edges have maximal independent sets of size at most \(O(n^{1-\beta }\log n)\), and almost all graphs with \(\left( {\begin{array}{c}n\\ 2\end{array}}\right) -n^{1+\beta }\) have maximal independent sets of size at most \(1+\frac{2+o(1)}{1-\beta }\).
Lemma 2.15
Almost all graphs in \(\mathscr {G}(n,p)\) with \(p=\omega (\log n/n)\) have degree at most 2pn.
Lemma 2.16
([28, Theorem 1]). Almost every graph with \(n=\lceil r^2 2^{r/2}\rceil \) vertices contains every graph of r vertices as an induced subgraph.
3 Secret-Sharing Schemes for Almost All Access Structures
This section is dedicated to the study of general access structures. Combining results on monotone Boolean functions by Korshunov [47] and secret-sharing schemes from [2, 48], we obtain secret-sharing schemes for almost all access structures. Then, we present lower bounds on the maximum share size for almost all access structures.
3.1 Upper Bounds for Almost All Access Structures
First, we define the family of slice access structures. These access structures have a special role in the general constructions presented in [4, 5, 48]. In Theorem 3.2, we present a family of slice access structures that contains almost all access structures. It is direct consequence of the results in [47] for monotone Boolean functions (also presented in [62, p. 99]).
Definition 3.1
Let a, b be two integers satisfying \(1\le a<b\le n\). We define \(S_{a,b}\) as the family of access structures \(\varGamma \) satisfying that, for every \(A\subseteq P\): if \(|A|> b\), then \(A\in \varGamma \), and if \(|A|< a\), then \(A\notin \varGamma \).
Theorem 3.2
([47]). Let \(\ell =\lfloor n/2 \rfloor \). Almost all access structures (i.e., monotone collections of sets) are in \(S_{\ell -1,\ell +1}\) if n is even, and in \(S_{\ell -1,\ell +2}\) if n is odd.
Theorem 3.3
Almost all access structures can be realized by the following secret-sharing schemes.
-
1.
A secret-sharing scheme with maximum share size \(2^{O(\sqrt{n}\log n)}\).
-
2.
A linear secret-sharing scheme with maximum share size \(2^{n/2+o(n)}\).
-
3.
A multi-linear secret-sharing scheme with normalized maximum share size \(2^{O(\sqrt{n\log n})}\) for secrets of size \(2^{n^2}\).
Proof
By Theorem 3.2, constructing secret-sharing schemes for access structures in \(S_{\ell -1,\ell +2}\) suffices for constructing secret-sharing schemes for almost all access structures.
Assume that for every k-input function \(f : [N]^k\rightarrow \{0,1\}\) and secret of size m there is a k-server CDS protocol for f in which the message size is c(N, m). By [48], for every k there is a secret-sharing scheme for \(\varGamma \in S_{a,b}\) with maximum share size at most
for \(N=\left( {\begin{array}{c}n/k\\ a/k\end{array}}\right) \). In our case, \(a=\lfloor \frac{n}{2}\rfloor -1\) and \(b=\lfloor \frac{n}{2}\rfloor +2\). Choosing \(k=\sqrt{\frac{n}{\log n}}\), we have
Taking the k-server CDS protocol with message size \(c(N, m)=2^{O(\sqrt{\log N}\log \log N}\le 2^{O(\sqrt{n}\log n)}\) from [50], we get the first secret-sharing scheme. If we take the linear k-server CDS protocol from [20, 50] with message size \(O(N^{(k-1)/2})\le 2^{n/2+o(n)}\), we get the second secret-sharing scheme. The third secret-sharing scheme is obtained by using the k-server CDS protocol with message size \(c(N, m)\le 4m\) from [2]. \(\square \)
As a consequence of this result, Hypotheses 1 and 3 in [2] are true for almost all access structures:
Hypothesis 3.4
(SS is short). Every access structure over n parties is realizable with small information ratio (say \(2^{o(n)}\)).
Hypothesis 3.5
(SS is amortizable). For every access structure over n parties, and every sufficiently long secret s, there exists a secret-sharing scheme with small information ratio (e.g., sub-exponential in n).
3.2 Almost All Access Structures Require Long Shares in Linear Secret-Sharing Schemes
Rónyai et al. [56] proved that for every finite field \(\mathbb {F}_q\) for almost every access structure \(\varGamma \) the normalized total share size of linear secret-sharing schemes over \(\mathbb {F}_q\) realizing \(\varGamma \) is at least \(2^{n/3-o(n)}\). We reverse the order of quantifiers and prove that for almost every access structure \(\varGamma \), for every finite field \(\mathbb {F}_q\) the normalized total share size of linear secret-sharing schemes over \(\mathbb {F}_q\) realizing \(\varGamma \) is at least \(2^{n/3-o(n)}\).
The rest of the section is organized as follows. We start by defining monotone span program and representable matroids; these notions are used to prove the lower bounds. Thereafter, we prove our new lower bound on the normalized total share size of linear secret-sharing schemes. More details about these results can be found in [13].
Definitions. A linear secret-sharing scheme with total share size m can be described by a matrix M with m rows such that the shares are computed by multiplying M by a vector whose first coordinate is the secret s and the other coordinates are random field elements. It is convenient to describe a linear secret-sharing scheme by a monotone span program, a computational model introduced by Karchmer and Wigderson [45]. The reader is referred to [10] for more background on monotone span programs and their connections to secret sharing.
Definition 3.6
(Monotone Span Program [45]). A monotone span program is a triple \(\mathcal {M}=(\mathbb {F}, M, \rho )\), where \(\mathbb {F}\) is a field, M is an \(d\times b\) matrix over \(\mathbb {F}\), and \(\rho : \left\{ 1,\dots ,d \right\} \rightarrow \left\{ p_1,\dots ,p_n \right\} \) labels each row of M by a party.Footnote 2 The size of \(\mathcal {M}\) is the number of rows of M (i.e., \(d\)). For any set \(A \subseteq \left\{ p_1,\dots ,p_n \right\} \), let \(M_A\) denote the sub-matrix obtained by restricting M to the rows labeled by parties in A. We say that \(\mathcal {M}\) accepts B if the rows of \(M_B\) span the vector \(\mathbf {e}_1=(1,0,\ldots ,0)\). We say that \(\mathcal {M}\) accepts an access structure \(\varGamma \) if \(\mathcal {M}\) accepts a set B if and only if \(B \in \varGamma \).
Theorem 3.7
([45]). There exists a linear secret-sharing scheme over \(\mathbb {F}_q\) realizing an access structure \(\varGamma \) with secrets of size \(\log q\) and total share size \(d\log q\) if and only if there exists a monotone span program \(\mathcal {M}=(\mathbb {F}_q, M, \rho )\) accepting the access structure \(\varGamma \) such that M is an \(d\times d\) matrix.
We next define representable matroids and quote the result of [53]. For our proof, we do not need the definition of matroids; we note that they are an axiomatic abstraction of linear independency.
Definition 3.8
A matroid representable over a field \(\mathbb {F}\) is a pair (A, r), where A is a finite set, called a ground set, and \(r:2^A \rightarrow \left\{ 0,1,\dots ,|A| \right\} \) is a function, called a rank function, such that there are vectors \(\left\{ v_a \right\} _{a \in A}\) in \(\mathbb {F}^{|A|}\) for which for every \(B \subseteq A\)
where \(\mathrm{rank}(V)\) is the linear-algebraic rank of vectors, i.e., the maximum number of linearly independent vectors in V. A representable matroid is a matroid representable over some field.
Theorem 3.9
([53]). For every \(d \ge 12\), there are at most \(2^{d^{3}/4}\) representable matroids with ground set [d].
The following theorem generalize the lower bounds of [9, 56].
Theorem 3.10
For almost every access structure \(\varGamma \) with n parties the following property holds: For every prime-power q, the normalized total share size in every linear secret-sharing scheme realizing \(\varGamma \) over the field \(\mathbb {F}_q\) is at least \(2^{n/3-o(n)}\).
Proof
The proof is similar to the proof of [9], with a more complex upper bound on the number of access structure that can be realized with a monotone span program of size \( d\).
Fix some labeling function \(\rho _0:[d] \rightarrow \left\{ p_1,\dots ,p_n \right\} \) and assume that there is a monotone span program \(\mathcal {M}=(\mathbb {F}_q, M, \rho _0)\) accepting an access structure \(\varGamma \) where M is matrix over some field \(\mathbb {F}_q\) of size \(d\times d\). Let \(M_i\) be the i-th row of M and \(M_0=\mathbf {e}_1\) and define a representable matroid with a ground set \(A=\left\{ 0,\dots ,d \right\} \) and a rank function \(r(B)=\mathrm{rank}\left\{ M_i:i\in B \right\} \). We next show that the rank function r together with \(\rho _0\) determines the access structure \(\varGamma \) accepted by \(\mathcal {M}\). Indeed, \(B \in \varGamma \) if and only if \(\mathbf {e}_1 \in \mathrm{span}\left\{ M_i:p_{\rho _0(i)} \in B \right\} \) if and only if
if and only if \(r(\left\{ i:p_{\rho _0(i)} \in B \right\} = r(\left\{ i:p_{\rho _0(i)} \in B \right\} \cup \left\{ 0 \right\} ). \) Thus, the number of access structures that can be realized by a linear scheme with normalized total share size is upper-bounded by the number of labeling functions \(\rho \) times the number of representable matroids with ground set \(\left\{ 0,\dots ,d \right\} \), i.e., by \(n^d \times 2^{(d+1)^3/4} \le 2^{d^3/2}\). To conclude, for \(d=2^{n/3}/n^{1/6}\), almost all access structures do not have a linear secret-sharing scheme with normalized total share size smaller than d. \(\square \)
A Lower Bound on the Share Size in Linear Secret-Sharing Schemes with a One Bit Secret. Finally, for a one-bit secret, we obtain in Theorem 3.11 a lower bound of \(2^{n/2-o(n)}\) on the total share size of linear secret-sharing schemes over any field realizing almost all access structures, even if the secret is a bit. Notice that this lower bound is on the total share size (and not on the normalized total share size). When we share a bit using a linear secret-sharing scheme over \(\mathbb {F}_q\) for \(q >2\), we only use the scheme to share the secrets \(0,1\in \mathbb {F}_q\). Since we are proving a lower bound the total share size, assuming that the secret is a bit only makes the result stronger.
The constant in the exponent in Theorem 3.11 is 1/2 (compared to a constant 1/3 in Theorem 3.10), matching the construction of linear secret-sharing schemes for almost all access structures in Theorem 3.3 (up to lower order terms). This theorem is a special case of [4, Theorem 5.5], however, the proof of this special case is simpler.
Theorem 3.11
For almost every access structure \(\varGamma \) with n parties the following property holds: For every prime-power q, the total share size in every linear secret-sharing scheme over \(\mathbb {F}_q\) realizing \(\varGamma \) with a one bit secret is at least \(2^{n/2-o(n)}\).
Proof
There are at most \(n^dq^{d^2}\) monotone span programs of size \(d\) over \(\mathbb {F}_q\) (as there are \(q^{d^2}\) matrices and n ways to label each row by a party). For \(d> \log n\), \(n^dq^{d^2} < q^{2d^2}\). The total share size in the linear secret-sharing scheme constructed from such monotone span program is \(D=d\log q\). Thus, the number of linear secret-sharing schemes over \(\mathbb {F}_q\) with total share size \(D\) is at most \(q^{2(D/\log q)^2} < 2^{2D^2}\). Furthermore, when \(q > 2^D\), the share size of each party is at least \(\log q > D\) as each share contains at least on element from \(\mathbb {F}_q\). Thus, the number of linear secret-sharing schemes with total share size \(D\) is at most
Taking \(D=0.4\cdot 2^{n/2-0.25\log n}\), the number of access structures that have a linear secret-sharing scheme over any field with total share size at most D is less than \(2^{3\cdot 0.16 \cdot 2^n/\sqrt{n}}\), i.e., almost all access structures require total share size larger than D in all linear secret-sharing schemes. \(\square \)
4 \(\varvec{(G,t)}\)-Secret-Sharing Schemes
In this section, we present a new family of schemes that we call (G, t)-secret-sharing schemes. We show that there is a close bi-directional connection between these schemes and 2-server robust CDS protocols, generalizing the connection between (non-robust) CDS protocols and forbidden graphs secret-sharing schemes. These schemes will be later used to construct graph secret-sharing schemes.
4.1 The Definition of \(\varvec{(G,t)}\)-Secret-Sharing Schemes
Definition 4.1
Let \(G=(V, E)\) be an undirected graph with \(|V|=n\) such that \(E\ne \emptyset \) and let \(\varGamma _G\) be the graph access structure determined by G (that is, each edge is a minimal authorized set and each independent set is forbidden). For any \(0\le t\le n-1\), define \(\varGamma _t\) as the t-out-of-n threshold access structure on V (that is, \(\varGamma _t=\{A\subseteq X: |A|\ge t\}\)) and define the access structure \(\varGamma _{G,t}\) on V as \(\varGamma _{G,t}=\varGamma _G\cup \varGamma _{t+1}.\) We say a secret-sharing scheme is a (G, t)-secret-sharing scheme if it realizes the access structure \(\varGamma _{G,t}\).
Next, we present some properties of these schemes. If \(\varPi \) is a (G, t)-secret-sharing scheme, then all subsets containing edges are authorized, independent subsets of G of size at most t are forbidden, and subsets of size greater than t are authorized. If \(t=2\), then \(\varGamma _{G,t}\) is a forbidden graph access structure determined by a graph G (for an introduction to these access structures, see [16], for example). If the size of a largest independent set of G is \(\mu \), then every subset of size \(\mu +1\) is authorized in \(\varGamma _G\). Therefore, \(\varGamma _{G,t}=\varGamma _G\) for every \(t\ge \mu \). In particular, \(\varGamma _{G,n-1}=\varGamma _G\) for every graph G.
4.2 \(\varvec{(G,t)}\)-Secret-Sharing Schemes from Robust CDS Protocols
We now present constructions of (G, t)-secret-sharing schemes. First, we present a transformation from robust CDS protocols to (G, t)-secret-sharing schemes. Then, using the robust CDS schemes presented in Sect. 2, we provide explicit (G, t)-secret-sharing schemes.
Lemma 4.2
Let \(G=(V,E)\) be a graph with \(|V|=n\), and let \(0<t<n\). If there exists a 2-server t-robust CDS protocol with secrets of size m and messages of size c(N, m) for functions \(f:[n]^2\rightarrow \left\{ 0,1 \right\} \), then there is a (G, t)-secret-sharing scheme with secrets of size m and shares of size \(2\cdot c(N, m)+\max \left\{ m,O(\log n) \right\} \). Moreover, if CDS protocol is linear, then the secret-sharing scheme is also linear.
Proof
We construct the (G, t)-secret-sharing scheme using the scheme in Fig. 2. Next we prove the correctness and privacy properties.
Correctness: Let \(A\subseteq [n]\) be a minimal authorized subset in \(\varGamma _{G,t}\). Then A is either in E or A is of size \(t+1\). If \(A=\{i,j\}\) is in E, then \(f(i,j)=1\), i.e., the message of Alice (the first server) on i and the message of Bob (the second server) on j determines s, so the pair \(\{i,j\}\) can recover s. If \(|A|=t+1\), then A can recover s using the \((t+1)\)-out-of-n secret-sharing scheme.
Privacy: Let A be a maximal forbidden subset. Then A does not contain any edge in E and \(|A|\le t\). The shares received from the threshold secret-sharing scheme do not provide any information about s. Now we analyze the information provided by the messages of \(\mathcal {P}\). The parties in A receive Alice’s messages for A and Bob’s messages for A. Observe that the set \(A\times A\) does not contain edges of G, thus, \(A\times A\) is a zero-set of f and the t-robustness of \(\mathcal {P}\) guarantees the privacy of the scheme.
The maximum share size of the resulting scheme is twice the message size of \(\mathcal {P}\) plus the share size of the \((t+1)\)-out-of-n secret-sharing scheme.
If \(\mathcal {P}\) is a linear protocol over \(\mathbb {F}_q\), we can choose a Shamir \((t+1)\)-out-of-n secret-sharing scheme over a finite field \(\mathbb {F}_{q^{\ell }}\) with \(q^{\ell }>n\). Since this scheme is also linear over \(\mathbb {F}_q\), the resulting secret-sharing scheme is also linear over \(\mathbb {F}_q\). \(\square \)
In Lemma 4.2, we showed a way to construct (G, t)-secret-sharing schemes from t-robust CDS protocols. Conversely, we can also construct robust CDS protocols from (G, t)-secret-sharing schemes, as shown in Lemma 4.3.
Lemma 4.3
Let \(f:[n]\times [n]\rightarrow \{0,1\}\) be a function and let \(0<t<n\). Define \(G=(([n]\times \left\{ 1 \right\} )\cup ([n] \times \left\{ 2 \right\} ),E)\) as the bipartite graph with \(E=\{((i,1),(j,2)): i \in [n], j \in [n], f(i,j)=1\}\). If there exists a (G, 2t)-secret-sharing scheme with secrets of size m and maximum share size c(2n, m), then there exists a 2-server t-robust CDS protocol for f with message size c(2n, m).
Proof
Let \(\varPi \) be a (G, 2t)-secret-sharing scheme. We define a 2-server t-robust CDS protocol \(\mathcal {P}\) for f as follows. The message spaces \(M_1\) and \(M_2\) of the servers are the spaces of shares of parties \([n]\times \left\{ 1 \right\} \) and \([n]\times \left\{ 2 \right\} \), respectively. The common randomness r is the randomness of the dealer in \(\varPi \). The function \(\text{ Enc}_i(j,s,r)\) for \(i \in \left\{ 1,2 \right\} \) outputs the share of party (j, i) with the secret s and randomness r, and \(\text{ Dec }\) is the reconstruction function of \(\varPi \).
The correctness of \(\mathcal {P}\) is guaranteed because every pair in E is authorized in \(\varPi \). The t-robustness of \(\mathcal {P}\) is guaranteed because every zero-set \(Z_1\times Z_2\) where \(|Z_1|,|Z_2| \le t\) corresponds to an independent set \((Z_1 \times \left\{ 1 \right\} ) \cup (Z_2 \times \left\{ 2 \right\} )\) of size at most 2t in G, thus the messages of the inputs in \(Z_1 \cup Z_2\) are shares of a forbidden set in \(\varPi \). \(\square \)
Now that we showed the connection between (G, t)-secret-sharing schemes from t-robust CDS protocols, we present (G, t)-secret-sharing schemes that use Theorems 2.12 and 2.11.
Lemma 4.4
Let \(G=(V,E)\) be a graph with \(|V|=n\), and let \(1\le t< n/2\). If there exist a 2-server CDS protocol with message size c(N, m) for functions with domain size n and secrets of size m, then there exists a (G, t)-secret-sharing scheme with maximum share size \(O(t^2\log ^3t\log ^2n \cdot c(N, m)),\) and a (G, t)-secret-sharing scheme with secrets of size \(\varTheta (mt\log t\log ^2 n)\) and normalized maximum share size \(O(t\log ^2 t\cdot c(N, m)/m).\)
Proof
Theorem 2.12 guarantees that there exists a 2-server t-robust CDS protocol with message size \(\ell (n)=O(t^2 c(N, m)\log ^3t\log ^2n),\) and a 2-server t-robust CDS protocol with secrets of size \(m'=\varTheta (mt\log t\log ^2n)\) with normalized message size \(\ell (n)/m'=O(t\log ^2 t \cdot c(N, m)/m).\) Using these 2-server t-robust CDS protocols and Lemma 4.2 we obtain the lemma. \(\square \)
We conclude this section presenting different (G, t)-secret-sharing schemes that are obtained from robust CDS schemes applying Lemma 4.2 and Lemma 4.4.
Theorem 4.5
Let \(G=(V,E)\) be a graph with \(|V|=n\) and let \(1<t<n\).
-
1.
There exists a (G, t)-secret-sharing scheme with moderately-short secrets of size \(O(t \log ^3 n)\), normalized maximum share size
$$\begin{aligned} n^{O(\sqrt{\log \log n/\log n})}t \log ^2 n=n^{o(1)}t \log ^2 n, \end{aligned}$$and normalized total share size \(n^{1+O(\sqrt{\log \log n/\log n})}t \log ^2 n=n^{1+o(1)}t \log ^2 n\);
-
2.
For every prime power q, there exists a linear (G, t)-secret-sharing scheme over \(\mathbb {F}_q\) with and maximum share size \(O\left( (t \log ^2 t + \sqrt{n})t\log t\log ^2 n\log q\right) ;\)
-
3.
There exists an integer \(p_0\) such that for every prime power \(q>p_0\), there exists a multi-linear (G, t)-secret-sharing scheme over \(\mathbb {F}_q\) with moderately-short secrets of size \(\varTheta (t^2 \log t \log ^2 n \log n \log q)\) and normalized maximum share size \(O(t \log ^2 t + \sqrt{n})\);
-
4.
There exists a multi-linear (G, t)-secret-sharing scheme over \(\mathbb {F}_2\) with secrets of size \(2^{n^2}\) and normalized maximum share size \(O(t\log ^2 t)\).
Proof
Scheme 1: By Theorem 2.7, for any function \(f:[n]^2\rightarrow \left\{ 0,1 \right\} \) there exists a 2-server CDS protocol with secret of size \(m=1\) and messages size \(c(n, 1) =n^{O(\sqrt{\log \log n / \log n})}\). Applying Theorem 2.12 with the CDS protocol from Theorem 2.7 results in a 2-server t-robust CDS protocol with secrets of size \(O(t\log t \log ^2 n)=O(t \log ^3 n)\), message size \(O(n^{O(\sqrt{\log \log n/ \log n})}t^2 \log ^5 t)\), and normalized message size \(O(n^{O(\sqrt{\log \log n/\log n})}t \log ^2 t).\) By Lemma 4.2, there is a (G, t)-secret-sharing with secrets of size \(O(t \log ^3 n)\) and maximum share size \(O(n^{O(\sqrt{\log \log n /\log n})}t^2 \log ^5 t)\), thus with normalized maximum share size \(O(n^{O(\sqrt{\log \log n/\log n})}t \log ^2 n)\) and with normalized total share size \(O(n^{1+O(\sqrt{\log \log n/\log n})}t \log ^2 n)\).
Scheme 2: Theorem 2.11 guarantees that for \(t\le n/(2\log ^2 n)\) there exists a linear 2-server t-robust CDS protocol over \(\mathbb {F}_q\) with message size \(O\left( (t \log ^2 t + \sqrt{n})t\log t\log ^2 n\log q\right) \). Thus, by Lemma 4.2 there is a (G, t)-secret-sharing scheme where the maximum share size is the above message size. For \(t> n/(2\log ^2 n)\), the upper bound also holds because there is always a linear (G, t)-secret-sharing with maximum share size \(O(n/\log n)\) [38].
Scheme 3: Theorem 2.11 also guarantees, for a large enough q, a 2-server (t, n)-robust CDS protocol with secrets of size \(\varTheta ( t^2 \log t \log ^2 n \log q)\) and normalized message size \(O(t \log ^2 t + \sqrt{n})\). Again, we construct the desired (G, t)-secret-sharing with from the robust CDS protocol applying Lemma 4.2.
Scheme 4: By Theorem 2.6, there exists a multi-linear CDS protocol over \(\mathbb {F}_2\) with normalized message size \(c(N, m)/m=3\) for secrets of size \(2^{n^2}\). Applying Lemma 4.4, we obtain a multi-linear (G, t)-secret-sharing over \(\mathbb {F}_2\) with normalized maximum share size \(O(t \log ^2 t \cdot c(N, m)/m)=O(t \log ^2 t)\). \(\square \)
5 Secret-Sharing Schemes for Almost All Graphs
In this section we study the maximum share size of secret-sharing schemes for almost all graphs and for almost all graphs in \(\mathscr {G}(n,p)\) for different values of p. The previous and new results for almost all graphs are summarized in Fig. 1, while the results for \(\mathscr {G}(n,p)\) are summarized in Fig. 4.
Schemes presented in this section rely on the properties of almost all graphs shown in the end of Sect. 2, and use the (G, t)-secret-sharing schemes presented in Sect. 4. In order to understand the share size of secret-sharing schemes for almost all graphs, we provide lower bounds for them in Theorems 5.5 and 5.7.
5.1 Schemes for Almost All Graphs
As a consequence of Lemma 2.13, the size of every independent set in almost every graph in \(\mathscr {G}_n\) is \(O(\log n)\). We observed in Sect. 4 that a (G, t)-secret-sharing scheme is also a secret-sharing scheme realizing G when t is bigger than the size of a largest independent set of G. Hence, we consider the four constructions presented in Theorem 4.5 for \(t=O(\log n)\). In Theorem 5.1 we present the resulting schemes.
Theorem 5.1
Almost all graphs with n vertices can be realized by the following schemes.
-
1.
A secret-sharing scheme with maximum share size \(n^{O(\sqrt{\log \log n/\log n})}=n^{o(1)}\),
-
2.
A linear secret-sharing scheme over \(\mathbb {F}_q\) with maximum share size \(\tilde{O}(\sqrt{n}\log q)\) for every prime power q,
-
3.
A multi-linear secret-sharing scheme over \(\mathbb {F}_q\) with normalized maximum share size \(O(\sqrt{n})\) and moderately-short secrets of size \(\varTheta (\log q \log ^3 n \log \log n)\) for a large enough q, and
-
4.
A multi-linear secret-sharing scheme over \(\mathbb {F}_2\) with normalized maximum share size \(O\left( \log n (\log \log n)^2\right) \) for secrets of size \(2^{n^2}\).
5.2 Secret-Sharing Schemes for \(\varvec{\mathscr {G}(n,p)}\)
In order to study properties of sparse graphs, we study \(\mathscr {G}(n,n^{-\alpha })\) for a constant \(0<\alpha <1\). Almost all graphs in \(G(n,n^{-\alpha })\) have maximal independent sets of size at most \(t=O(n^{\alpha }\log n)\). Following the procedure we developed in the previous section, we can construct secret-sharing schemes for almost all graphs in \(G(n,n^{-\alpha })\) using Theorem 4.5. Similar bounds can be obtained for linear schemes and multi-linear schemes. They are presented in Fig. 4.
Theorem 5.2
Let \(0<\alpha <1\) be a constant. Almost every graph in \(\mathscr {G}(n,n^{-\alpha })\) can be realized by a secret-sharing scheme with normalized maximum share size \(n^{\min (\alpha ,1-\alpha )+o(1)}\) and secret of size \(\tilde{O}(\sqrt{n})\).
Proof
We present two schemes \(\varPi _1\) and \(\varPi _2\) for almost all graphs in \(\mathscr {G}(n,n^{-\alpha })\). The scheme \(\varPi _1\) consists on sharing the secret for each edge independently. By Lemma 2.15, almost every graph in \(\mathscr {G}(n,n^{-\alpha })\) has maximum degree of at most \(2n^{1-\alpha }\). Therefore, the maximum share size of \(\varPi _1\) is \(2n^{1-\alpha }\) for almost all graphs in \(\mathscr {G}(n,n^{-\alpha })\).
The second scheme \(\varPi _2\) is obtained from Theorem 4.5. For almost every graph in \(\mathscr {G}(n,n^{-\alpha })\) the size of a maximum independent set is \(O(n^\alpha \log n)\) (by Lemma 2.14). Thus, we let \(\varPi _2\) be the \((G,O(n^\alpha \log n))\)-secret-sharing scheme of Theorem 4.5 with secret of size \(\varTheta (t \log ^3 n)=\varTheta (n^\alpha \log ^4 n )\) and normalized maximum share size \(O(n^{o(1)}t\log ^2 n)=O(n^{\alpha +o(1)}\log ^3 n)=n^{\alpha +o(1)}\).
Therefore, almost every graph in \(\mathscr {G}(n,n^{-\alpha })\) can be realized by a secret-sharing scheme with normalized maximum share size \(\min (2n^{1-\alpha },n^{\alpha +o(1)})\le n^{\min (1-\alpha ,\alpha )+o(1)}\). \(\square \)
For \(\alpha \le 1/2\), the best choice is \(\varPi _1\), and for \(\alpha >1/2\), the best choice is \(\varPi _2\). For \(\alpha =1/2\), the normalized maximum share size of almost all graphs in \(\mathscr {G}(n,n^{-\alpha })\) in our scheme is \(O(\sqrt{n})\). This is the constant \(\alpha \) that gives the worst upper bound on the normalized maximum share size of secret-sharing schemes for \(\mathscr {G}(n,n^{-\alpha })\).
Finally, we study properties of very dense graphs by analyzing \(\mathscr {G}(n,1-n^{-\alpha })\) for a constant \(0<\alpha <1\). By Lemma 2.14, the size of a maximum independent set for almost all graphs in \(\mathscr {G}(n,1-n^{-\alpha })\) is constant. As we saw above, graphs with small independent sets admit more efficient schemes. In Theorem 5.4 we present secret-sharing schemes for almost all graphs in \(\mathscr {G}(n,1-n^{-\alpha })\). Two of the schemes we present in Theorem 5.4 follow quite easily from our previous results. In contrast, the linear scheme we construct in Theorem 5.4 does not follow from previous results on robust CDS protocols. Rather, it follows from the following theorem of [16] on the total share size for forbidden graph secret sharing schemes and the techniques of [5].
Theorem 5.3
([16, Theorem 6]). Let \(G=(V,E)\) graph with n vertices and at least \(\left( {\begin{array}{c}n\\ 2\end{array}}\right) -n^{1+\beta }\) edges, for some \( 0 \le \beta < 1\). Then for every prime-power \(q >n\) there is a linear (G, 2)-secret-sharing scheme over \(\mathbb {F}_q\) that with total share size \(\tilde{O}(n^{1+\beta /2}\log q)\).
Theorem 5.4
Let \(0\le \beta <1\) be a constant. Almost all graphs in \(\mathscr {G}(n,1-n^{\beta -1})\) can be realized by a secret-sharing scheme with maximum share size \(n^{o(1)}\), a linear secret-sharing scheme over \(\mathbb {F}_q\) with total share size \(\tilde{O}(n^{1+\beta /2}\log q)\) for every prime-power \(q > n\), and a multi-linear secret-sharing scheme over \(\mathbb {F}_2\) with exponentially long secrets of size \(2^{n^2}\) and normalized maximum share size O(1).
Proof
By Lemma 2.14, the size of a maximum independent set for almost all graphs in \(\mathscr {G}(n,1-n^{-\alpha })\) is some constant c. The non-linear secret-sharing scheme and the secret-sharing scheme with long secrets are obtained by applying Theorem 4.5 with \(t=O(1)\).
To construct the linear secret-sharing scheme we note that the maximum degree of almost every graph G in \(\mathscr {G}(n,1-n^{\beta -1})\) is at least \(n-2n ^{\beta }\) (by Lemma 2.15 applied to \(\overline{G}\)), thus the number of edges in G is at least \(\left( {\begin{array}{c}n\\ 2\end{array}}\right) -n^{1+\beta }\). The linear scheme is derived by using the technique of [5] to transform the (G, 2)-secret-sharing scheme from Theorem 5.3 to a (G, c)-secret-sharing scheme: Let \(\mathcal {H}=\left\{ h_i:[n]\rightarrow [c^2]: 1 \le i \le \ell \right\} \) be a family of perfect hash functions,Footnote 3 where \(|\mathcal {H}|=\ell =O(\log n)\). The (G, c)-secret-sharing scheme, denoted \(\varPi \), is as follows:
-
Input: a secret \(s \in \mathbb {F}_q\).
-
Choose \(\ell -1\) random elements \(s_1,\ldots ,s_{\ell -1}\) from \(\mathbb {F}_q\) and let \(s_\ell =s-(s_1+\cdots +s_{\ell -1})\).
-
For every \(i \in \left\{ 1,\dots ,\ell \right\} \) and every \(a,b \in \left\{ 1,\dots ,c^2 \right\} \), independently share \(s_i\) using the (G, 2)-secret-sharing scheme and give the share of vertex v to v if and only if \(h_i(v)\in \left\{ a,b \right\} \).
For the correctness of the scheme \(\varPi \), let (u, v) be an edge in G (i.e., an authorized set). For every i, the parties u, v can reconstruct \(s_i\) from the scheme for \(a=h(u),b=h(v)\). For the privacy of \(\varPi \), let B be an independent set in G (i.e., a forbidden set). By Lemma 2.14, we can assume that the size of B is at most c, thus, there exists a hash function \(h_i \in \mathcal {H}\) such that \(h_i(u) \ne h_i(v)\) for every distinct \(u,v \in B\). Therefore, in any sharing of \(s_i\) for some values a, b the parties in B hold at most 2 shares, and these shares are of a forbidden set. The privacy of the (G, 2)-secret-sharing scheme implies that the parties in B do not get any information on \(s_i\) from this execution. Since all executions of the (G, 2)-secret-sharing scheme are executed with an independent random string, the parties in B do not get any information on \(s_i\) from the shares of \(\varPi \), hence they get no information on s. Note that the total share size in \(\varPi \) is \(O(\log n)\) times the total share size of the (G, 2)-secret-sharing scheme. \(\square \)
5.3 Lower Bounds for the Share Size for Almost All Graphs
Next, we present lower bounds for the maximum share size of secret-sharing schemes for almost all graphs. This question was first addressed by Csirmaz in [35], where he proved a lower bound which we include in Theorem 5.5.
Theorem 5.5
For almost every graph G, the normalized maximum share size of every secret-sharing scheme realizing G is \(\varOmega (\log \log n)\), and the normalized maximum share size of every multi-linear secret-sharing scheme realizing G is \(\varOmega (\log ^{1/2} n)\).
Proof
(Sketch). Both bounds are a consequence of Lemma 2.16 (which says that almost all n-vertex graphs contain all graphs of size \(\log n\) as an induced graph), taking different graphs with \(\log n\) vertices. The first bound was proved by Csirmaz in [35], taking the family of hypercube graphs (or the graphs of [37]). The second bound is a consequence of the results in [11, 17]. The complete proof is in the full version of this paper [13]. \(\square \)
Remark 5.6
Lemma 2.16 provides a connection between the maximum share size of schemes for every graph access structure with \(r=\log n\) vertices and the maximum share size of schemes for almost all graph access structures with n vertices. In Theorem 5.5 we used it in one direction, but it could also be used in the converse direction. For instance: if there exist secret-sharing schemes for almost all n-vertex graphs with (normalized) maximum share size \(\ll \frac{\log n}{\log \log n}\), then there exist secret-sharing schemes realizing every r-vertex graph with (normalized) maximum share size \(\ll r/\log r\), which is currently the best upper bound [38].
In Theorem 5.7, we quote a lower bound on the maximum share size for linear graph secret-sharing schemes, proved in [15, 52]. Notice, however, that this bound does not grow as a function of the size of the secrets.
Theorem 5.7
([15, 52]). For almost every graph G, the maximum share size of every linear secret-sharing scheme realizing G is \(\varOmega (\sqrt{n})\).
6 Secret-Sharing Schemes for Very Dense Graphs
In this section we study secret-sharing schemes for very dense graphs, i.e., graphs with n vertices and at least \(\left( {\begin{array}{c}n\\ 2\end{array}}\right) -n^{1+\beta }\) edges for some \(0\le \beta <1\). This problem was originally studied in [14], and the best previously known upper bounds on the maximum share size and the total share size are presented in Theorems 6.1 and 6.2.
Theorem 6.1
([14]). Let \(G=(V,E)\) be a graph with \(|V|=n\) and \(|E|\ge \left( {\begin{array}{c}n\\ 2\end{array}}\right) -n^{1+\beta }\) for some \(0\le \beta <1\). Then, there exists a linear secret-sharing scheme realizing G with maximum share size \(\tilde{O}(n^{1/2+\beta /2})\), total share size \(\tilde{O}(n^{3/2+\beta /2})\), and secret of size \(O(\log n)\).
The above theorem hides poly-logarithmic factors in the share size. It was also shown in [14] that these poly-logarithmic factors can be avoided if we consider multi-linear secret-sharing schemes and normalized share size: for the graphs considered in Theorem 6.1, there exists a multi-linear secret-sharing scheme with normalized maximum share size \(O(n^{1/2+\beta /2})\) and secret of size \(O(\log ^2 n)\).
In [14], there is another secret-sharing construction for very dense graphs, presented in Theorem 6.2. The total share size of this scheme is smaller than the one in Theorem 6.1, but the maximum share size may be larger.
Theorem 6.2
([14]). Let \(G=(V,E)\) be a graph with \(|V|=n\) and \(|E|\ge \left( {\begin{array}{c}n\\ 2\end{array}}\right) -n^{1+\beta }\) for some \(0\le \beta <1\). There exists a linear secret-sharing scheme realizing G with total share size \(\tilde{O}(n^{5/4+3\beta /4})\).
As an observation, notice that as a direct implication of the results in previous sections we can construct a scheme whose maximum share size is similar to the maximum share size as in the scheme of Theorem 6.2 (see the full version of this paper [13]).
We use (G, t)-secret-sharing schemes, described in the Sect. 4, to construct secret-sharing schemes for all very dense graphs. Our main result for dense graphs is Theorem 6.4, where we show that graphs with at least \(\left( {\begin{array}{c}n\\ 2\end{array}}\right) -n^{1+\beta }\) edges admit secret-sharing schemes with normalized total share size \(n^{1+\beta +o(1)}\). This result nearly matches the best total share size for sparse graphs with at most \(n^{1+\beta }\) edges (for which we share the secret independently for each edge). The construction follows the ideas described in the introduction.
In Fig. 3, we present a secret-sharing scheme \(\varPi _{\mathrm{dense}}\) realizing very dense graphs. In Theorem 6.4, we use \(\varPi _{\mathrm{dense}}\) recursively to obtain our improved secret-sharing scheme for dense graphs. The proofs of Lemma 6.3 and Theorem 6.4 are presented in the full version of this paper [13].
Total share size for different families of graphs and constant \(0<\beta <1\). Note that almost all graphs in \(\mathscr {G}(n,n^{\beta -1})\) and in \(\mathscr {G}(n,1-n^{\beta -1})\) have \(\varTheta (n^{1+\beta })\) and \(\left( {\begin{array}{c}n\\ 2\end{array}}\right) -\varTheta (n^{1+\beta })\) edges, respectively.
Lemma 6.3
Let \(G=(V,E)\) be a graph with \(|V|=n\) and \(|E|\ge \left( {\begin{array}{c}n\\ 2\end{array}}\right) -n^{1+\beta }\) for some \(0\le \beta <1\). The scheme described in Fig. 3 is a secret-sharing scheme realizing G.
Theorem 6.4
Let \(G=(V,E)\) be a graph with \(|V|=n\) and \(|E|\ge \left( {\begin{array}{c}n\\ 2\end{array}}\right) -n^{1+\beta }\) for some \(0\le \beta <1\). Then G can be realized by a secret-sharing schemes with secrets of size \(O(n \log ^3 n)\) and normalized total share size \(n^{1+\beta +o(1)}.\)
Remark 6.5
In Theorem 6.4, we combine the secret-sharing scheme for very dense graphs in Theorem 6.1 with several instances of the first scheme of Theorem 4.5. Instead, if we replace the former by the fourth scheme of Theorem 4.5, we obtain a multi-linear secret-sharing scheme with secrets of exponential size and normalized total share size \(\tilde{O}(n^{1+\beta })\) for exponentially long secrets.
In Fig. 4, we summarize the current bounds on the total share size for graphs with at most \(n^{1+\beta }\) edges, graphs with at least \(\left( {\begin{array}{c}n\\ 2\end{array}}\right) -n^{1+\beta }\) edges, \(\mathscr {G}(n,n^{\beta -1})\), and \(\mathscr {G}(n,1-n^{\beta -1})\), for constant \(0<\beta <1\). Additional remarks and observations are presented in the full version of this paper [13].
Notes
- 1.
For example, given a secret-sharing realizing the k-homogeneous access structures of a hyper-graph H, we can realize the k-uniform access structures of H by additionally sharing the secret in a \((k+1)\)-out-of-k secret-sharing scheme.
- 2.
For simplicity, in this paper we label a row by a party \(p_j\) rather than by a variable \(x_j\) as done in [45].
- 3.
A family \(\mathcal {H}\) is a family of perfect hash functions for sets of size at most c if for every \(B \subset \left\{ 1,\dots ,n \right\} \) such that \(|B| \le c\), there exists a function \(h \in \mathcal {H}\) such that h is one-to-one on B, that is, \(h(u) \ne h(v)\) for every distinct \(u,v \in B\). By a standard probabilistic argument, such family of size \(O(c \log n)\) exists. For a constant c, the size of the family is \(O(\log n)\).
References
Aiello, B., Ishai, Y., Reingold, O.: Priced oblivious transfer: how to sell digital goods. In: Pfitzmann, B. (ed.) EUROCRYPT 2001. LNCS, vol. 2045, pp. 119–135. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44987-6_8
Applebaum, B., Arkis, B.: On the power of amortization in secret sharing: d-uniform secret sharing and CDS with constant information rate. In: Beimel, A., Dziembowski, S. (eds.) TCC 2018. LNCS, vol. 11239, pp. 317–344. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03807-6_12
Applebaum, B., Arkis, B., Raykov, P., Vasudevan, P.N.: Conditional disclosure of secrets: amplification, closure, amortization, lower-bounds, and separations. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10401, pp. 727–757. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_24
Applebaum, B., Beimel, A., Farràs, O., Nir, O., Peter, N.: Secret-sharing schemes for general and uniform access structures. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019. LNCS, vol. 11478, pp. 441–471. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17659-4_15
Applebaum, B., Beimel, A., Nir, O., Peter, N.: Better secret sharing via robust conditional disclosure of secrets. In: Proceedings of the 52th ACM Symposium on the Theory of Computing, pp. 280–293 (2020)
Applebaum, B., Holenstein, T., Mishra, M., Shayevitz, O.: The communication complexity of private simultaneous messages, revisited. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10821, pp. 261–286. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78375-8_9
Applebaum, B., Vasudevan, P.N.: Placing conditional disclosure of secrets in the communication complexity universe. In: 10th ITCS, pp. 4:1–4:14 (2019)
Attrapadung, N.: Dual system encryption via doubly selective security: framework, fully secure functional encryption for regular languages, and more. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 557–577. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_31
Babai, L., Gál, A., Wigderson, A.: Superpolynomial lower bounds for monotone span programs. Combinatorica 19(3), 301–319 (1999)
Beimel, A.: Secret-sharing schemes: a survey. In: Chee, Y.W., et al. (eds.) IWCC 2011. LNCS, vol. 6639, pp. 11–46. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-20901-7_2
Beimel, A., Ben-Efraim, A., Padró, C., Tyomkin, I.: Multi-linear secret-sharing schemes. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 394–418. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54242-8_17
Beimel, A., Chor, B.: Universally ideal secret sharing schemes. IEEE Trans. Inf. Theory 40(3), 786–794 (1994)
Beimel, A., Farràs, O.: The share size of secret-sharing schemes for almost all access structures and graphs. IACR Cryptology ePrint Archive 2020, 664 (2020)
Beimel, A., Farràs, O., Mintz, Y.: Secret-sharing schemes for very dense graphs. J. Cryptol. 29(2), 336–362 (2016)
Beimel, A., Farràs, O., Mintz, Y., Peter, N.: Linear secret-sharing schemes for forbidden graph access structures. Technical report 2017/940, IACR Cryptology ePrint Archive (2017). Full version of [16]
Beimel, A., Farràs, O., Mintz, Y., Peter, N.: Linear secret-sharing schemes for forbidden graph access structures. In: Kalai, Y., Reyzin, L. (eds.) TCC 2017. LNCS, vol. 10678, pp. 394–423. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70503-3_13
Beimel, A., Gál, A., Paterson, M.: Lower bounds for monotone span programs. Comput. Complex. 6(1), 29–45 (1997)
Beimel, A., Ishai, Y., Kumaresan, R., Kushilevitz, E.: On the cryptographic complexity of the worst functions. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 317–342. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54242-8_14
Beimel, A., Kushilevitz, E., Nissim, P.: The complexity of multiparty PSM protocols and related models. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10821, pp. 287–318. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78375-8_10
Beimel, A., Peter, N.: Optimal linear multiparty conditional disclosure of secrets protocols. In: Peyrin, T., Galbraith, S. (eds.) ASIACRYPT 2018. LNCS, vol. 11274, pp. 332–362. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03332-3_13
Beimel, A., Weinreb, E.: Separating the power of monotone span programs over different fields. SIAM J. Comput. 34(5), 1196–1215 (2005)
Benaloh, J., Leichter, J.: Generalized secret sharing and monotone functions. In: Goldwasser, S. (ed.) CRYPTO 1988. LNCS, vol. 403, pp. 27–35. Springer, New York (1990). https://doi.org/10.1007/0-387-34799-2_3
Bertilsson, M., Ingemarsson, I.: A construction of practical secret sharing schemes using linear block codes. In: Seberry, J., Zheng, Y. (eds.) AUSCRYPT 1992. LNCS, vol. 718, pp. 67–79. Springer, Heidelberg (1993). https://doi.org/10.1007/3-540-57220-1_53
Blakley, G.R.: Safeguarding cryptographic keys. In: Proceedings of the 1979 AFIPS National Computer Conference. AFIPS Conference Proceedings, vol. 48, pp. 313–317 (1979)
Blundo, C., De Santis, A., Gargano, L., Vaccaro, U.: On the information rate of secret sharing schemes. Theoret. Comput. Sci. 154(2), 283–306 (1996)
Blundo, C., Santis, A.D., Gaggia, A.G., Vaccaro, U.: New bounds on the information rate of secret sharing schemes. IEEE Trans. Inf. Theory 41(2), 549–553 (1995)
Bollobás, B.: Random Graphs, 2nd edn. Cambridge University Press, Cambridge (2001)
Bollobás, B., Thomason, A.: Graphs which contain all small graphs. Eur. J. Combin. 2(1), 13–15 (1981)
Brickell, E.F.: Some ideal secret sharing schemes. J. Combin. Math. Combin. Comput. 6, 105–113 (1989)
Capocelli, R.M., De Santis, A., Gargano, L., Vaccaro, U.: On the size of shares for secret sharing schemes. J. Cryptol. 6(3), 157–168 (1993)
Chor, B., Kushilevitz, E.: Secret sharing over infinite domains. J. Cryptol. 6(2), 87–96 (1993)
Cramer, R., Damgård, I., Maurer, U.: General secure multi-party computation from any linear secret-sharing scheme. In: Preneel, B. (ed.) EUROCRYPT 2000. LNCS, vol. 1807, pp. 316–334. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-45539-6_22
Csirmaz, L.: The dealer’s random bits in perfect secret sharing schemes. Studia Sci. Math. Hungar. 32(3–4), 429–437 (1996)
Csirmaz, L.: The size of a share must be large. J. Cryptol. 10(4), 223–231 (1997)
Csirmaz, L.: Secret sharing schemes on graphs. Technical report 2005/059, Cryptology ePrint Archive (2005). eprint.iacr.org/
Csirmaz, L.: An impossibility result on graph secret sharing. Des. Codes Cryptogr. 53(3), 195–209 (2009)
van Dijk, M.: On the information rate of perfect secret sharing schemes. Des. Codes Cryptogr. 6(2), 143–169 (1995)
Erdös, P., Pyber, L.: Covering a graph by complete bipartite graphs. Discrete Math. 170(1–3), 249–251 (1997)
Erdös, P., Rényi, A.: On random graphs. I. Publ. Math. Debrecen 6, 290–297 (1959)
Gál, A., Pudlák, P.: Monotone complexity and the rank of matrices. Inf. Process. Lett. 87, 321–326 (2003)
Gay, R., Kerenidis, I., Wee, H.: Communication complexity of conditional disclosure of secrets and attribute-based encryption. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9216, pp. 485–502. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48000-7_24
Gertner, Y., Ishai, Y., Kushilevitz, E., Malkin, T.: Protecting data privacy in private information retrieval schemes. J. Comput. Syst. Sci. 60(3), 592–629 (2000)
Grimmett, G.R., McDiarmid, C.J.H.: On colouring random graphs. Math. Proc. Cambridge Philos. Soc. 77(2), 313–324 (1975)
Ito, M., Saito, A., Nishizeki, T.: Secret sharing schemes realizing general access structure. In: GLOBECOM 1987, pp. 99–102 (1987). Journal version: Multiple assignment scheme for sharing secret. J. Cryptol. 6(1), 15–20 (1993)
Karchmer, M., Wigderson, A.: On span programs. In: 8th Structure in Complexity Theory, pp. 102–111 (1993)
Karnin, E.D., Greene, J.W., Hellman, M.E.: On secret sharing systems. IEEE Trans. Inf. Theory 29(1), 35–41 (1983)
Korshunov, A.D.: On the number of monotone Boolean functions. Probl. Kibern 38, 5–108 (1981)
Liu, T., Vaikuntanathan, V.: Breaking the circuit-size barrier in secret sharing. In: 50th STOC, pp. 699–708 (2018)
Liu, T., Vaikuntanathan, V., Wee, H.: Conditional disclosure of secrets via non-linear reconstruction. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10401, pp. 758–790. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_25
Liu, T., Vaikuntanathan, V., Wee, H.: Towards breaking the exponential barrier for general secret sharing. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10820, pp. 567–596. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78381-9_21
Martí-Farré, J., Padró, C.: On secret sharing schemes, matroids and polymatroids. J. Math. Cryptol. 4(2), 95–120 (2010)
Mintz, Y.: Information ratios of graph secret-sharing schemes. Master’s thesis, Department of Computer Science, Ben Gurion University (2012)
Nelson, P.: Almost all matroids are non-representable. Bull. Lond. Math. Soc. 50(2), 245–248 (2018)
Peter, N.: Secret-sharing schemes and conditional disclosure of secrets protocols. Ph.D. thesis, Ben-Gurion University of the Negev (2020). http://aranne5.bgu.ac.il/others/PeterNaty19903.pdf
Pitassi, T., Robere, R.: Lifting Nullstellensatz to monotone span programs over any field. In: 50th STOC, pp. 1207–1219 (2018)
Rónyai, L., Babai, L., Ganapathy, M.K.: On the number of zero-patterns of a sequence of polynomials. J. AMS 14(3), 717–735 (2001)
Shamir, A.: How to share a secret. Commun. ACM 22, 612–613 (1979)
Shannon, C.E.: The synthesis of two-terminal switching circuits. Bell Syst. Tech. J. 28(1), 59–98 (1949)
Simmons, G.J.: How to (really) share a secret. In: Goldwasser, S. (ed.) CRYPTO 1988. LNCS, vol. 403, pp. 390–448. Springer, New York (1990). https://doi.org/10.1007/0-387-34799-2_30
Sun, H.M., Shieh, S.P.: Secret sharing in graph-based prohibited structures. In: INFOCOM 1997, pp. 718–724 (1997)
Wee, H.: Dual system encryption via predicate encodings. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 616–637. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54242-8_26
Wegener, I.: The Complexity of Boolean Functions. Wiley-Teubner Series in Computer Science. B. G. Teubner and John Wiley, Chichester (1987)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 International Association for Cryptologic Research
About this paper
Cite this paper
Beimel, A., Farràs, O. (2020). The Share Size of Secret-Sharing Schemes for Almost All Access Structures and Graphs. In: Pass, R., Pietrzak, K. (eds) Theory of Cryptography. TCC 2020. Lecture Notes in Computer Science(), vol 12552. Springer, Cham. https://doi.org/10.1007/978-3-030-64381-2_18
Download citation
DOI: https://doi.org/10.1007/978-3-030-64381-2_18
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-64380-5
Online ISBN: 978-3-030-64381-2
eBook Packages: Computer ScienceComputer Science (R0)






 , where
, where  for every
for every  is the message sent by the i-th server to the referee), and
is the message sent by the i-th server to the referee), and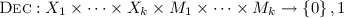 .
.


