Abstract
In this paper, we present a relating semantics in order to investigate the connexive logic. We remind Barbershop paradox noted by Lewis Carroll in 1894. Next we apply the relating semantics to investigate this paradox in detail and to show its relation to the connexive logic.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Sextus attributed the first interpretation to Filon, and second one to Diodorus. Historians recognized them as Filon from Megara and his master Diodorus Cronos; see [13], fn. 4—about interrelations between the two interpretations, see e.g. [28], ch. 4, Sect. 1, [20], ch. 3, Sect. 3. Sextus left unattributed connexive and emphatic interpretations, however, one can figure out that the third approach comes from Chrysippus and the fourth one was defended by the Peripatetic School, see [20], p. 129. We employ the term “emphatic” as Sextus uses the word
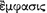 in the sense that “in that implication we emphasise in consequent what is expressed in antecedent”. Let us add that “Outline of Pyrrhonism” successively lived until two full English translations: Robert Gregg Bury’s dated 1933 (see [8]) and Beson Mates’ dated 1996 (see [29]). Moreover, a long passage devoted to the four conditionals interpretation appears in English in Kneales, [20], p. 129.
in the sense that “in that implication we emphasise in consequent what is expressed in antecedent”. Let us add that “Outline of Pyrrhonism” successively lived until two full English translations: Robert Gregg Bury’s dated 1933 (see [8]) and Beson Mates’ dated 1996 (see [29]). Moreover, a long passage devoted to the four conditionals interpretation appears in English in Kneales, [20], p. 129. - 2.
Translation: Beson Mates 1996, see. previous footnote. Earlier in the paper dated 1961 (see [28], pp. 47–48) Mates uses “holds” instead of “sound” and “incompatible” instead of “inconsistent”. In logical literature one could find Kneales translation: “And those who introduce the notion of connection say that a conditional is sound when the contradictory of its consequent is incompatible with its antecedent”. In Bury’s translation it looks as follows: “And those who introduce ‘connexion’ or ‘coherence’ assert that it is a valid hypothetical syllogism whenever the opposite of its consequent contradicts its antecedent clause”.
- 3.
One should emphasise that in the subject literature Philo’s approach evokes a some interpretational problems, whilst Diodorean and even more Chrysippian approaches are interpreted in many different ways. For example, Daniel Bonevac and Josh Dever ([4], p. 179) interpret the first three approaches in the following way, considering the fourth one as unclear. Philo: \(A\rightarrow B\) iff \(\sim \!\!(A\,\wedge \sim \!\! B)\), Diodorus: \(A\rightarrow B\) iff it is always the case that \(\sim \!\!(A\,\wedge \sim \!\! B)\), Chrysippus: \(A\rightarrow B\) iff it is necessary that \(\sim \!\!(A\,\wedge \sim \!\! B)\). Accordingly, one can recognize that the strict implication is expressed by Chrysippian, and not Diodoren approach. However Bonevac and Josh interpretation pass over an important relation between the antecedent and consequent (
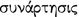 ) which allows us to consider it doubtful.
) which allows us to consider it doubtful. - 4.
“Lives of the Eminent Philosophers” VII, 73, trans. Pamela Mensch, [24]. Classical XX-century translation by Robert Drew Hicks in 1925 (see [23]): “A hypothetical proposition is therefore true, if the contradictory of its conclusion is incompatible with its premiss, e.g. ‘If it is day, it is light.’ This is true. For the statement ‘It is not light,’ contradicting the conclusion, is incompatible with the premiss ‘It is day.’ On the other hand, a hypothetical proposition is false, if the contradictory of its conclusion does not conflict with the premiss, e.g. ‘If it is day, Dion is walking.’ For the statement ‘Dion is not walking’ does not conflict with the premiss ‘It is day.”’ On whether Diogenes really characterizes here the third type of conditional discussed by Sextus, see [28], pp. 48–49. Let us also note, that the very sentences employed by Diogenes as example of true conditional occur in writings by many ancient authors discussing implication and argumentation.
- 5.
- 6.
[3], p. 286 (bk II, chap. vi, Sect. 1, lines 1–3). The notation adapted to the present paper.
- 7.
In our times, the propositional forms and inference schemes postulated by Boethius were analysed by Karl Dürr (see [7]). This author tries to find the conditional being sound independently if interpreted as material or strict implication. The author’s conclusion is that in both interpretations the formula corresponding to the above inference schema is not a tautology—more strictly, it is not provable neither in the system of Principia Mathematica nor in S2. He did not take account of the possibility of connexive interpretation.
- 8.
Boethian Thesis in the form of negation of conjunction is sometimes called Abelard’s Principle or Strawson’s Thesis, in turn connexive theses used by Aristotle as well as by Boethius are called Aristotelian, see [12], pp. 346–347.
- 9.
- 10.
- 11.
Where A is a contingent truth and \(B\rightarrow C\) a logical truth, see [30], p. 427.
- 12.
Classical conditions could be here replaced by non-classical interpretations i.e. intuitionistic, paraconsistent etc., see [21], pp. 27–28. However, this remains out of the scope of this paper.
- 13.
This classification is not disjoint. A lot depends on theoretical settles. For example, indexicals come within a contextual interpretation. However it could also come under pragmatic or semantic interpretation depending on how to make a demarcation line between semantics and pragmatics. In turn, temporal or causal interpretation could also mean some type of contextual interpretation.
- 14.
See e.g. [37], p. 176 and: Preface to special issue of Philosophical Studies: 36(2), 1979. In Preface one can find a list of seminar participants. One emphasizes there, among others, Robert Goldblatt contribution to constructing proofs of metatheorems of this logic, David Lewis’ proposal to give ‘A is related to B’ a meaning ‘A and B share some common subject-matter’, see [38], p. 39. In 80s. Lewis developes the issue of a “subject-matter” independent from relating logic, see e.g. [25].
- 15.
- 16.
Bertrand Russell in the second edition of The Principles of Mathematics wrote: “The principle that false propositions imply all propositions solves Lewis Carroll’s paradox [...] The assertion made in that paradox is that, if p, q, r be propositions, and q implies r, while p implies that q implies not-r, then p must be false, on the supposed ground that ‘q implies r’ and ‘q implies not-r’ are incompatible. But in virtue of our definition of negation, if q be false, both these implications will hold: the two together, in fact, whatever proposition r may be, are equivalent to not-q. Thus the only inference warranted by Lewis Carroll’s premisses is that if p be true, q must be false, i.e. that p implies not-q; and this is the conclusion, oddly enough, which common sense would have drawn in the particular case which he discusses”, [35], fn. on p. 18.
References
Angell, R. B. (1962). A propositional logic with subjunctive conditionals. Journal of Symbolic Logic, 27(3), 327–343.
Aristotle (1989). Prior analytics. Robert Smith (trans.). Indianapolis, Cambridge: Hackett Publishing Company.
Boethius, A. M. S. (1969). De hypotheticis syllogismis. Edited, commented and translated by Luca Libertello, Brescia: Paideia.
Bonevac, D., & Dever, J. (2012). A history of the connectives. In D. M. Gabbay et al. (Eds.), Handbook of the history of logic. Volume 11: Logic: A history of its central concepts (pp. 175–233). Amsterdam: Elsevier.
Cantwell, J. (2008). The logic of conditional negation. Notre Dame Journal of Formal Logic, 49(3), 245–260.
Carroll, L. (1894). A logical paradox. Mind, 3(11), 436–438.
Dürr, K. (1951). The propositional logic of Boethius. Amsterdam: North-Holland.
Empiricus, S. (1933). Outline of pyrrhonism. Robert G. Bury (trans.). Cambridge, MA: Harvard University Press.
Empiricus, S. (1935). Against the logicians. Robert G. Bury (trans.). Cambridge, MA: Harvard University Press.
Epstein, R. L. (1979). Relatedness and implication. Philosophical Studies, 36, 137–173.
Epstein, R. L. (1990). The semantic foundations of logic. Vol. 1: Propositional logics. Dordrecht: Kluwer Academic Publishers.
Estrada-González, L., & Ramírez-Cámara, E. (2016). A comparison of connexive logics. The IfCoLog Journal of Logics and their Applications, 3(3), 341–355.
Hurst, M. (1935). Implication in the fourth century B.C. Mind, 176(44), 484–495.
Jarmużek, T. (2020). Relating semantics as fine-grained semantics for intensional propositional logics. In A. Giordani, J. Malinowski (Eds.), Logic in high definition, trends in logical semantics (this volume). Berlin: Springer.
Jarmużek, T., & Kaczkowski, B. J. (2014). On some logic with a relation imposed on formulae: Tableau system F. Bulletin of the Section of Logic, 43(1/2), 53–72.
Jarmużek, T., & Klonowski, M. Some intensional logics defined by relating semantics and tableau systems. In A. Giordani, J. Malinowski (Eds.), Logic in high definition, trends in logical semantics (this volume). Berlin: Springer.
Jarmużek, T., & Malinowski, J. (2019). Boolean connexive logics: Semantics and tableau approach. Logic and Logical Philosophy, 28(3), 427–448.
Jarmużek, T. & Malinowski, J. (2019). Modal Boolean connexive logics: Semantics and tableau approach. Bulletin of the Section of Logic, 48(3), 215–245.
Kapsner, A. (2012). Strong connexivity. Thought: A Journal of Philosophy 1(2): 141–145.
Kneale, W., & Kneale, M. (1962). The development of logic. London: Duckworth.
Krajewski, S. (1982). On relatedness logic of Richard L. Epstein. Bulletin of the Section of Logic, 11(1–2), 24–28.
Krajewski, S. (1986). Relatedness logic. Reports on Mathematical Logic, 20, 7–14.
Laertius, D. (1925). Lives of eminent philosophers. Robert D. Hicks (trans.). Cambridge, MA: Harvard University Press,
Laertius, D. (2018). Lives of the eminent philosophers. Pamela Mensch (trans.). In J. Miller (Ed.). Oxford: Oxford University Press.
Lewis, D. (1988). Relevant implication. Theoria, 54(3), 161–174.
Łukasiewicz, J. (1957). Aristotle’s syllogistic from the standpoint of modern formal logic (2nd ed.). Oxford: Clarendon Press.
Malinowski, J. (2019). Barbershop paradox and connexive implication. Ruch Filozoficzny (Philosophical Movement), 75(2), 109–115.
Mates, B. (1961). Stoic logic. Berkeley and Los Angeles: University of California Press.
Mates, B. (1996). The skeptic way: Sextus empiricus’s outlines of pyrrhonism. Oxford: Oxford University Press.
McCall, S. (2012). A history of connexivity. In D. M. Gabbay et al. (Eds.), Handbook of the history of logic. Volume 11: Logic: A history of its central concepts (pp. 415–449). Amsterdam: Elsevier.
Moktefi, A. (2008). Lewis Carroll’s logic. In D. M. Gabbay, J. Woods (Eds.), Handbook of the history of logic. Volume 4: British logic in the nineteenth century (pp. 457–505). Amsterdam: North-Holland.
Mortensen, C. (1984). Aristotle’s thesis in consistent and inconsistent logics. Studia Logica, 43(1–2), 107–116.
Nelson, E. J. (1930). Intensional relations. Mind, 156(39), 440–453.
Rahman, S. (2012). Hugh MacColl and George Boole on hypotheticals. In J. Gasser (Ed.), A Boole anthology. Recent and classical studies in the logic of George Boole (pp. 287–310). Amsterdam: Elsevier.
Russell, B. (1938). The principles of mathematics (2nd ed.). New York: W.W. Norton & Company.
Walton, D. N. (1979). Philosophical basis of relatedness logic. Philosophical Studies, 36(2), 115–136.
Walton, D. N. (1979). Relatedness in intensional action chains. Philosophical Studies, 36(2), 175–223.
Walton, D. N. (1982). Topical relevance in argumentation. Philadelphia: John Benjamins.
Walton, D. N. (2004). Relevance in argumentation. London: Lawrence Erlbaum Associates.
Wansing, H. (2016). Connexive logic. In E. N. Zalta (Ed.), The stanford encyclopedia of philosophy. https://plato.stanford.edu/archives/spr2016/entries/logic-connexive/.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 The Editor(s) (if applicable) and The Author(s), under exclusive license to Springer Nature Switzerland AG
About this chapter
Cite this chapter
Malinowski, J., Palczewski, R. (2021). Relating Semantics for Connexive Logic. In: Giordani, A., Malinowski, J. (eds) Logic in High Definition. Trends in Logic, vol 56. Springer, Cham. https://doi.org/10.1007/978-3-030-53487-5_4
Download citation
DOI: https://doi.org/10.1007/978-3-030-53487-5_4
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-53486-8
Online ISBN: 978-3-030-53487-5
eBook Packages: Religion and PhilosophyPhilosophy and Religion (R0)


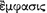 in the sense that “in that implication we emphasise in consequent what is expressed in antecedent”. Let us add that “Outline of Pyrrhonism” successively lived until two full English translations: Robert Gregg Bury’s dated 1933 (see [
in the sense that “in that implication we emphasise in consequent what is expressed in antecedent”. Let us add that “Outline of Pyrrhonism” successively lived until two full English translations: Robert Gregg Bury’s dated 1933 (see [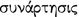 ) which allows us to consider it doubtful.
) which allows us to consider it doubtful.