Abstract
Relating logics are examples of non-classical logics that make it possible to seriously consider various non-logical relationships that occur between sentences. The main idea behind such logics is that logical values is not the only thing that matters when we consider truth conditions for formulas built by propositional connectives. What should be considered as another important factor is a content relationship or some other relations, such as causality and temporal successions which hold between sentences or between the states of affairs that are usually expressed by means of those sentences. Hence, the factor is in fact intensional. In the article, we analyze relating logics and make a philosophical introduction to this subject; we introduce a relating language and its general semantic framework. It is a short introduction to the field of relating logics. Next, we describe some special cases of relating logics from a semantic point of view, and finally, as a decision procedure we introduce adequate tableau systems for those logics.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Epstein in [3, pp. 61–84, 115–143] considers relating connectives on the grounds of the following logics: relatedness logics \(\mathrm {S}\) and \(\mathrm {R}\), dependence logics \(\mathrm {D}\), \(\mathrm {dD}\), \(\mathrm {Eq}\) and \(\mathrm {DPC}\).
- 2.
More about the ideas of relating semantics (generalizations, historical issues, applications etc.) can be read in [9].
- 3.
The letter
 in notation of relating connectives comes from the Polish words ‘
in notation of relating connectives comes from the Polish words ‘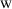 iązać’ (verb) and ‘
iązać’ (verb) and ‘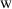 iążący’ (adjective) which might be translated as ‘relate’ and ‘relating’.
iążący’ (adjective) which might be translated as ‘relate’ and ‘relating’. - 4.
It is possible to express in the considered language purely intensional functors. For instance, we can examine a functor defined in the following way
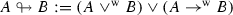 . We can easily check that
. We can easily check that 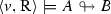 iff
iff 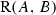 . Let us also notice that it is possible to consider unary relating functors. For instance, a kind of a relating negation (the relating counterpart of Boolean negation) could be defined as
. Let us also notice that it is possible to consider unary relating functors. For instance, a kind of a relating negation (the relating counterpart of Boolean negation) could be defined as 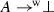 , where \(\perp \) is interpreted in the standard way. These issues, however, require a separate analysis that goes beyond the scope of this article.
, where \(\perp \) is interpreted in the standard way. These issues, however, require a separate analysis that goes beyond the scope of this article. - 5.
Surely, if \(\mathbf {Q}= \emptyset \), then \(\models _{\mathbf {Q}}A\) and \(\varSigma \models _{\mathbf {Q}}A\), for all \(\varSigma \cup \{A\} \subseteq \mathsf {For}\). But we would not like to discuss the trivial logic here. The very similar situation is in Definition 5.
- 6.
The name of logic \(\mathrm {W}\) comes from the Polish words ‘
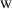 iązać’ (verb) and ‘
iązać’ (verb) and ‘ iążący’ (adjective) which might be translated as ‘relate’ and ‘relating’ (cf. footnote 3).
iążący’ (adjective) which might be translated as ‘relate’ and ‘relating’ (cf. footnote 3). - 7.
We write ‘heuristically’, since precise definitions of these distinctions have not been worked out yet.
References
Blackburn, P., de Rijke, M., & Venema, Y. (2001). Modal logic. Cambridge: Cambridge University Press.
Epstein, R. L. (1979). Relatedness and implication. Philosophical Studies, 36, 137–173.
Epstein, R. L. (with the assistance and collaboration of: W. A. Carnielli, I. M. L. D’Ottaviano, S. Krajewski, R. D. Maddux). (1990). The semantic foundations of logic. Volume 1: Propositional logics. Dordrecht: Springer Science+Business Media.
Jarmużek, T. (2013). Tableau metatheorem for modal logics. In R. Ciuni, H. Wansing, C. Willkommen (Eds.), Recent trends in philosphical logic (Vol. 41, pp. 103–126). Trends in logic. Berlin: Springer.
Jarmużek, T., & Kaczkowski, B. (2014). On some logic with a relation imposed on formulae: Tableau system \(\cal{F}\). Bulletin of the Section of Logic, 43(1/2), 53–72.
Jarmużek, T., & Klonowski, M. (2020). On logic of strictly-deontic modalities. Logic and Logical Philosophy, 29(3), 335–380.
Jarmużek, T., & Malinowski, J. (2019). Boolean connexive logics: Semantics and tableau approach. Logic and Logical Philosophy, 28(3), 427–448.
Jarmużek, T., & Malinowski, J. (2019). Modal Boolean connexive logics: Semantics and tableau approach. Bulletin of the Section of Logic, 48(3), 213–243.
Jarmużek, T. (2020). Relating semantics as fine-grained semantics for intensional logics. In A. Giordani, J. Malinowski (Eds.), Logic in High Definition. Trends in Logical Semantics (this volume). Berlin: Springer, (pp. 13–30) (2020), 335–380.
Klonowski, M. (2018). Post’s completeness theorem for symmetric relatedness logic S. Bulletin of the Section of Logic, 47(3), 201–215.
Krajewski, S. (1982). On relatedness logic of Richard L. Epstein. Bulletin of the Section of Logic, 11(1/2), 24–30.
Malinowski, J. (2019). Barbershop paradox and connexive implication. Ruch Filozoficzny (Philosophical Movement), 75(2), 107–114.
Malinowski, J., & Palczewski R. (2020). Relating semantics for connexive logics. In A. Giordani, J. Malinowski (Eds.), Logic in High Definition. Trends in Logical Semantics (pp. 49–65). Berlin: Springer.
Paoli, F. (1993). Semantics for first degree relatedness logic. Reports on Mathematical Logic, 27, 81–94.
Paoli, F. (1996). S is constructively complete. Reports on Mathematical Logic, 30, 31–47.
Paoli, F. (2007). Tautological entailments and their rivals. In J. Y. Béziau, W. Carnielli, & D. Gabbay (Eds.), Handbook of paraconsistency (pp. 153–175). London: College Publications.
Scheffler, U. (1993). On the logic of event causation. Logic and Logical Philosophy, 1, 129–155.
Walton, D. (1979). Philosophical basis of relatedness logic. Philosophical Studies, 36, 115–136.
Acknowledgements
The research of Tomasz Jarmużek presented in the following article was financed by the National Science Centre, Poland, grant No.: UMO-2015/19/B/HS1/02478. While the research of Mateusz Klonowski presented in the following article was financed by the National Science Centre, Poland, grant No.: UMO-2015/19/N/HS1/02401. The authors also would like to thank the anonymous referee for all his remarks and interesting suggestions.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 The Editor(s) (if applicable) and The Author(s), under exclusive license to Springer Nature Switzerland AG
About this chapter
Cite this chapter
Jarmużek, T., Klonowski, M. (2021). Some Intensional Logics Defined by Relating Semantics and Tableau Systems. In: Giordani, A., Malinowski, J. (eds) Logic in High Definition. Trends in Logic, vol 56. Springer, Cham. https://doi.org/10.1007/978-3-030-53487-5_3
Download citation
DOI: https://doi.org/10.1007/978-3-030-53487-5_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-53486-8
Online ISBN: 978-3-030-53487-5
eBook Packages: Religion and PhilosophyPhilosophy and Religion (R0)


 in notation of relating connectives comes from the Polish words ‘
in notation of relating connectives comes from the Polish words ‘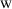 iązać’ (verb) and ‘
iązać’ (verb) and ‘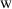 iążący’ (adjective) which might be translated as ‘relate’ and ‘relating’.
iążący’ (adjective) which might be translated as ‘relate’ and ‘relating’.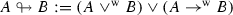 . We can easily check that
. We can easily check that 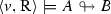 iff
iff 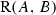 . Let us also notice that it is possible to consider unary relating functors. For instance, a kind of a relating negation (the relating counterpart of Boolean negation) could be defined as
. Let us also notice that it is possible to consider unary relating functors. For instance, a kind of a relating negation (the relating counterpart of Boolean negation) could be defined as 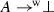 , where
, where 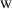 iązać’ (verb) and ‘
iązać’ (verb) and ‘ iążący’ (adjective) which might be translated as ‘relate’ and ‘relating’ (cf. footnote 3).
iążący’ (adjective) which might be translated as ‘relate’ and ‘relating’ (cf. footnote 3).