Abstract
Some aggregation functions that are not necessarily associative, namely overlap and grouping functions, have called the attention of many researchers in the recent past. This is probably due to the fact that they are a richer class of operators whenever one compares with other classes of aggregation functions, such as t-norms and t-conorms, respectively. In the present work we introduce a more general proposal for disjunctive n-ary aggregation functions entitled general grouping functions, in order to be used in problems that admit n dimensional inputs in a more flexible manner, allowing their application in different contexts. We present some new interesting results, like the characterization of that operator and also provide different construction methods.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
- Grouping functions
- n-dimensional grouping functions
- General grouping functions
- General overlap functions
1 Introduction
Overlap functions are a kind of aggregation functions [3] that are not required to be associative, and they were introduced by Bustince et al. in [4] to measure the degree of overlapping between two classes or objects. Grouping functions are the dual notion of overlap functions. They were introduced by Bustince et al. [5] in order to express the measure of the amount of evidence in favor of either of two alternatives when performing pairwise comparisons [1] in decision making based on fuzzy preference relations [6]. They have also been used as the disjunction operator in some important problems, such as image thresholding [17] and the construction of a class of implication functions for the generation of fuzzy subsethood and entropy measures [13].
Overlap and grouping functions have been largely studied since they are richer than t-norms and t-conorms [18], respectively. Regarding, for instance, some properties like idempotency, homogeneity, and, mainly, the self-closeness feature with respect to the convex sum and the aggregation by generalized composition of overlap/grouping functions [7, 8, 10, 12]. For example, there is just one idempotent t-conorm (namely, the maximum t-conorm) and two homogeneous t-conorms (namely, the maximum and the probabilistic sum of t-conorms). On the contrary, there are uncountable numbers of idempotent, as well as homogenous, grouping functions [2, 11]. For comparisons among properties of grouping functions and t-conorms, see [2, 5, 17]
However, grouping functions are bivariate functions. Since they may be non associative, they can only be applied in bi-dimensional problems (that is, when just two classes or objects are considered). In order to solve this drawback, Gómez et al. [16] introduced the concept of n-dimensional grouping functions, with an application to fuzzy community detection.
Recently, De Miguel et al. [20] introduced general overlap functions, by relaxing some boundary conditions, in order to apply to an n-ary problem, namely, fuzzy rule based classification systems, more specifically, in the determination of the matching degree in the fuzzy reasoning method. Then, inspired on the paper by De Miguel et al. [20], the objective of this present paper is to introduce the concept of general grouping functions, providing their characterization and different construction methods. The aim is to define the theoretical basis of a tool that can be used to express the measure of the amount of evidence in favor of one of multiple alternatives when performing n-ary comparisons in multi-criteria decision making based on n-ary fuzzy heterogeneous, incomplete preference relations [14, 19, 26], which we let for future work.
The paper is organized as follows. Section 2 presents some preliminary concepts. In Sect. 3, we define general grouping functions, studying some properties. In Sect. 4, we study the characterization of general grouping functions, providing some construction methods. Section 5 is the Conclusion.
2 Preliminary Concepts
In this section, we highlight some relevant concepts used in this work.
Definition 1
A function \(N:[0,1] \rightarrow [0,1]\) is a fuzzy negation if it holds: (N1) N is antitonic, i.e. \( N(x) \le N(y) \) whenever \(y \le x \) and (N2) \(N(0) = 1 \) and \( N(1) = 0 \).
Definition 2
[3] An n-ary aggregation function is a mapping \(A :[0,1]^{n} \rightarrow [0,1]\) satisfying: (A1) \(A(0, \ldots , 0) = 0\) and \(A(1, \ldots , 1) = 1\); (A2) increasingness: for each \(i \in \{1,\ldots , n \}\), if \(x_i \le y\) then \(A(x_1,\ldots , x_{n})\le A(x_1, \ldots ,x_{i-1}, y, x_{i+1},\ldots , x_{n}).\)
Definition 3
An n-ary aggregation function \(A :[0, 1]^n \rightarrow [0, 1]\) is called conjunctive if, for any  , it holds that
, it holds that  . And A is called disjunctive if, for any
. And A is called disjunctive if, for any  , it holds that
, it holds that  .
.
Definition 4
[4] A binary function \(O :[0,1]^2 \rightarrow [0,1]\) is said to be an overlap function if it satisfies the following conditions, for all \(x, y, z \in [0,1]\):
- (O1):
-
\(O(x,y) = O(y,x)\);
- (O2):
-
\(O(x,y) = 0\) if and only if \(x = 0\) or \(y = 0\);
- (O3):
-
\(O(x,y) = 1\) if and only if \(x = y = 1\);
- (O4):
-
if \( x\le y\) then \(O(x,z) \le O(y, z)\);
- (O5):
-
O is continuous;
Definition 5
[5] A binary function \(G :[0,1]^2 \rightarrow [0,1]\) is said to be a grouping function if it satisfies the following conditions, for all \(x, y, z \in [0,1]\):
- (G1):
-
\(G(x,y) = G(y,x)\);
- (G2):
-
\(G(x,y) = 0\) if and only if \(x = y = 0\);
- (G3):
-
\(G(x,y) = 1\) if and only if \(x = 1\) or \( y = 1\);
- (G4):
-
If \( x\le y\) then \(G(x,z) \le G(y, z)\);
- (G5):
-
G is continuous;
For all properties and related concepts on overlap functions and grouping functions, see [2, 5, 7, 9, 10, 21, 23,24,25].
Definition 6
[22] A function \(G :[0,1]^2 \rightarrow [0,1]\) is a 0-grouping function if the second condition in Definition 5 is replaced by: (\(G2'\)) If \(x = y = 0\) then \(G(x,y)=0\). Analogously, a function \(G:[0,1]^2 \rightarrow [0,1]\) is a 1-grouping function if the third condition in Definition 5 is replaced by: (\(G3'\)) If \(x = 1\) or \(y = 1\) then \(G(x,y)=1\).
Both notions were extended in several ways and some of them are presented in the following definitions.
Definition 7
[15] An n-ary function \(\mathcal {G} :[0,1]^n \rightarrow [0,1]\) is called an n-dimensional grouping function if for all  :
:
-
1.
\(\mathcal {G}\) is commutative;
-
2.
 if and only if \(x_i=0\), for all \(i=1,\ldots ,n\);
if and only if \(x_i=0\), for all \(i=1,\ldots ,n\); -
3.
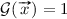 if and only if there exists \(i \in \{1,\ldots ,n\}\) with \(x_i=1\);
if and only if there exists \(i \in \{1,\ldots ,n\}\) with \(x_i=1\); -
4.
\(\mathcal {G}\) is increasing;
-
5.
\(\mathcal {G}\) is continuous.
Definition 8
[20] A function \( \mathcal {GO}:[0,1]^n \rightarrow [0,1]\) is said to be a general overlap function if it satisfies the following conditions, for all  :
:
- (\(\mathcal {GO}1\)):
-
\(\mathcal {GO}\) is commutative;
- (\(\mathcal {GO}2\)):
-
If
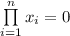 then
then  ;
; - (\(\mathcal {GO}3\)):
-
If
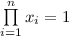 then
then  ;
; - (\(\mathcal {GO}4\)):
-
\(\mathcal {GO}\) is increasing;
- (\(\mathcal {GO}5\)):
-
\(\mathcal {GO}\) is continuous.
3 General Grouping Functions
Following the ideas given in [20], we can also generalize the idea of general grouping functions as follows.
Definition 9
A function \( \mathcal {GG}:[0,1]^n \rightarrow [0,1]\) is called a general grouping function if the following conditions hold, for all  :
:
- (\(\mathcal {GG}1\)):
-
\(\mathcal {GG}\) is commutative;
- (\(\mathcal {GG}2\)):
-
If
 then
then 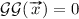 ;
; - (\(\mathcal {GG}3\)):
-
If there exists \(i \in \{1,\ldots ,n\}\) such that \(x_i = 1\) then
 ;
; - (\(\mathcal {GG}4\)):
-
\(\mathcal {GG}\) is increasing;
- (\(\mathcal {GG}5\)):
-
\(\mathcal {GG}\) is continuous.
Note that (\(\mathcal {GG}2\)) is the same of saying that 0 is an anhilator of the general grouping function \(\mathcal {GG}\).
Proposition 1
If \(\mathcal {G}:[0,1]^n \rightarrow [0,1]\) is an n-dimensional grouping function, then \(\mathcal {G}\) is also a general grouping function.
Proof
Straighforward. \(\square \)
From this proposition, we can conclude that the concept of general grouping functions is a generalization of n-dimensional grouping functions, which on its turn is a generalization of the concepts of 0-grouping functions and 1-grouping functions.
Example 1
-
1.
Every grouping function \(G:[0,1]^2 \rightarrow [0,1]\) is a general grouping function, but the converse does not hold.
-
2.
The function \(\mathcal {GG}(x,y)=\min \{1,2 - (1-x)^2- (1-y)^2\}\) is a general grouping function, but it is not a bidimensional grouping function, since \(\mathcal {GG}(0.5,0.5)=1\).
-
3.
Consider \(G(x,y)=\max \{1-(1-x)^p,1-(1-y)^p\}\), for \(p>0\) and \(S_{\mathfrak {L}}(x,y)=\min \{1,x+y\}\). Then, the function \(\mathcal {GG}^{S_{\mathfrak {L}}} (x,y)=G (x,y) {S_{\mathfrak {L}}} (x,y)\) is a general grouping function.
-
4.
Take any grouping function G, and a continuous t-conorm S. Then, the generalization of the previous item is the binary general grouping function given by: \(\mathcal {GG}(x,y)=G (x,y) S(x,y)\)
-
5.
Other examples are:
$$\begin{aligned} Prod\_S\_Luk (x_1, \ldots , x_n)= & {} \left( 1- \prod _{i=1}^{n}{(1- x_i)} \right) * \left( \min \left\{ \sum _{i=1}^{n}{x_i}, 1\right\} \right) \\ GM\_S\_Luk(x_1, \ldots , x_n)= & {} \left( 1 - \root n \of {\prod _{i=1}^{n}{(1-x_i)}} \right) *\left( \min \left\{ \sum _{i=1}^{n}{x_i}, 1\right\} \right) .\end{aligned}$$
The generalization of the third item of Example 1 can be seen as follows.
Proposition 2
Take any grouping function G, and any t-conorm S. Then, the binary general grouping function given by: \(\mathcal {GG}(x,y)=G (x,y) S(x,y)\).
Proposition 3
Let \(F:[0,1]^{n} \rightarrow [0,1]\) be a commutative and continuous aggregation function. Then the following statements hold:
-
(i) If F is disjunctive, then F is a general grouping function.
-
(ii) If F is conjunctive, then F is neither a general grouping function nor an n-dimensional grouping function.
Proof
Consider a commutative and continuous aggregation function \(F :[0,1]^{n} \rightarrow [0,1]\). It follows that:
(i) Since F is commutative (\(\mathcal {GG}1\)), continuous (\(\mathcal {GG}5\)) and clearly increasing (\(\mathcal {GG}4\)), then it remains to prove the following:
(\(\mathcal {GG}2\)) Suppose that  . Then, since F is an aggregation function, it holds that \(F(0, \ldots , 0) =0\).
. Then, since F is an aggregation function, it holds that \(F(0, \ldots , 0) =0\).
(\(\mathcal {GG}3\)) Suppose that, for some  , there exists \(i \in \{1, \ldots , n\}\) such that \(x_i =1\). Then, since F is disjunctive, then
, there exists \(i \in \{1, \ldots , n\}\) such that \(x_i =1\). Then, since F is disjunctive, then  which means that
which means that  .
.
(ii) Suppose that F is a conjunctive aggregation function and it is either a general grouping function or an n-dimensional grouping function. Then, by either (\(\mathcal {GG}3\)) or (\(\mathcal {G}3\)), if for some  , there exists \(i \in \{1, \ldots , n\}\) such that \(x_i =1\), then
, there exists \(i \in \{1, \ldots , n\}\) such that \(x_i =1\), then  . Take
. Take  , it follows that \(F(1, 0 \ldots , 0) = 1 = \max \{1, 0 \ldots , 0\} \not \le 0 = \min \{1, 0 \ldots , 0\}\), which is a contradiction with the conjunctive property. Thus, one concludes that F is neither a general grouping function nor an n-dimensional grouping function. \(\square \)
, it follows that \(F(1, 0 \ldots , 0) = 1 = \max \{1, 0 \ldots , 0\} \not \le 0 = \min \{1, 0 \ldots , 0\}\), which is a contradiction with the conjunctive property. Thus, one concludes that F is neither a general grouping function nor an n-dimensional grouping function. \(\square \)
We say that an element \(a\in [0,1]\) is a neutral element of \(\mathcal {GG}\) if for each \(x\in [0,1]\), \(\mathcal {GG}(x,\underbrace{a,\ldots ,a}_{(n-1)})=x\).
Proposition 4
Let \(\mathcal {GG} :[0,1]^n \rightarrow [0,1] \) be a general grouping function with a neutral element \(a\in [0,1]\). Then, \(a=0\) if and only if \(\mathcal {GG}\) satisfies, for all  , the following condition:
, the following condition:
- \((\mathcal {GG}2')\):
-
If
 , then
, then  .
.
Proof
(\(\Rightarrow \)) Suppose that (i) the neutral element of \(\mathcal {GG}\) is \(a=0\) and (ii) \(\mathcal {GG}(x_1,\ldots ,x_n) =0\). Then, by (i), one has that, for each \(x_1 \in [0,1]\), it holds that \(x_1 =\mathcal {GG}(x_1,0\ldots ,0)\). By (ii) and since \(\mathcal {GG}\) is increasing, it follows that
Similarly, one shows that \(x_2,\ldots ,x_n=0\), that is  .
.
(\(\Leftarrow \)) Suppose that \(\mathcal {GG}\) satisfies \((\mathcal {GG}2')\) and that \(\mathcal {GG}(x_1,\ldots ,x_n)=0\), for \((x_1,\ldots ,x_n) \in [0,1]^n\). Then, by \((\mathcal {GG}2')\), it holds that  . Since a is the neutral element of \(\mathcal {GG}\), one has that \(\mathcal {GG}(0,a, \ldots , a)=0\), which means that \(a=0\), by \((\mathcal {GG}2')\). \(\square \)
. Since a is the neutral element of \(\mathcal {GG}\), one has that \(\mathcal {GG}(0,a, \ldots , a)=0\), which means that \(a=0\), by \((\mathcal {GG}2')\). \(\square \)
Remark 1
Observe that the result stated by Proposition 4 does not mean that when a general grouping function has a neutral element, then it is necessarily equal to 0. In fact, for each \(a \in (0,1)\), the function \(\mathcal {GG} :[0,1]^n \rightarrow [0,1]\), for all  , defined by:
, defined by:

is a general grouping function with a as neutral element.
Proposition 5
If 0 is the neutral element of a general grouping function \(\mathcal {GG} :[0,1]^n \rightarrow [0,1]\) and \(\mathcal {GG}\) is idempotent, then \(\mathcal {GG}\) is the maximum.
Proof
Since \(\mathcal {GG}\) is idempotent and increasing in each argument, then one has that for all  : (1)
: (1)  . Then we have that
. Then we have that  for some \(k=1,\ldots ,n\); so we have \(x_k = \mathcal {GG}(0,\ldots ,x_k, \ldots ,0) \le \mathcal {GG}(x_1,\ldots , x_k, \ldots ,x_n)\) and then (2)
for some \(k=1,\ldots ,n\); so we have \(x_k = \mathcal {GG}(0,\ldots ,x_k, \ldots ,0) \le \mathcal {GG}(x_1,\ldots , x_k, \ldots ,x_n)\) and then (2)  . So, from (1) and (2) one has that
. So, from (1) and (2) one has that  , for each
, for each  . \(\square \)
. \(\square \)
3.1 General Grouping Functions on Lattices
Following a similar procedure described in [20] for general overlap functions on lattices, it is possible to characterize general grouping functions. In order to do that, first we introduce some properties and notations.
Let us denote by \(\mathfrak {G}^n\) the set of all general grouping functions. Define the ordering relation \(\le _{\mathfrak {G}^n}\,\in \,\mathfrak {G}^n \times \mathfrak {G}^n\), for all \(\mathcal {GG}_1, \mathcal {GG}_2 \in \mathfrak {G}^n\) by:

The supremum and infimum of two arbitrary general grouping functions \(\mathcal {GG}_1, \mathcal {GG}_2 \in \mathfrak {G}^n\) are, respectively, the general grouping functions \(\mathcal {GG}_1 \vee \mathcal {GG}_2, \mathcal {GG}_1 \wedge \mathcal {GG}_2 \in \mathfrak {G}^n\), defined, for all  by:
by:  and
and  .
.
The following result is immediate:
Theorem 1
The ordered set \((\mathfrak {G}^n,\le _{\mathfrak {G}^n})\) is a lattice.
Remark 2
Note that the supremum of the lattice \((\mathfrak {G}^n,\le _{\mathfrak {G}^n})\) is given, for all  , by:
, by:

On the other hand, the infimum of \((\mathfrak {G}^n,\le _{\mathfrak {G}^n})\) is given, for all  , by:
, by:

However, neither \(GG_{\sup }\) nor \(GG_{\inf }\) are general grouping functions, since they are not continuous. Thus, in the lattice \((\mathfrak {G}^n,\le _{\mathfrak {G}^n})\) there is no bottom neither top elements. Then, similarly to general overlap functions, the lattice (\( \mathfrak {G}^n, \le _{\mathfrak {G}^n}\)) is not complete.
4 Characterization of General Grouping Functions and Construction Methods
In this section we provide a characterization and some constructions methods for general grouping functions.
Theorem 2
The mapping \( \mathcal {GG}:\ [0,1]^n \rightarrow [0,1]\) is a general grouping function if and only if

for some \(f,h:[0,1]^n \rightarrow [0,1]\) the following properties hold, for all  :
:
- (i):
-
f and h are commutative;
- (ii):
-
f is increasing and h is decreasing.
- (iii):
-
If
 , then
, then 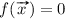 .
. - (iv):
-
If there exists \(i\in \{1, \ldots , n\}\) such that \(x_i = 1\), then
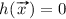 .
. - (v):
-
f and h are continuous.
- (vi):
-
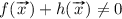 for any
for any 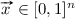 .
.
Proof
It follows that:
(\(\Rightarrow \)) Suppose that \(\mathcal {GG}\) is a general grouping function, and take  and
and  . Then one always have
. Then one always have  , and so Equation (1) is well defined. Also, conditions (i)–(v) trivially hold.
, and so Equation (1) is well defined. Also, conditions (i)–(v) trivially hold.
(\(\Leftarrow \)) Consider \(f,h:[0,1]^n \rightarrow [0,1]\) satisfying conditions (i)–(v). We will show that \(\mathcal {GG}\) defined according to Eq. (1) is a general grouping function. It is immediate that \( \mathcal {GG}\) is commutative (\(\mathcal {GG}1\)) and continuous (\(\mathcal {GG}5\)). To prove (\(\mathcal {GG}2\)), notice that if  then
then  and thus
and thus  . Now, let us prove that (\(\mathcal {GG}3\)) holds. For that, observe that if there exists \(i\in \{1, \ldots , n\}\) such that \(x_i = 1\), then
. Now, let us prove that (\(\mathcal {GG}3\)) holds. For that, observe that if there exists \(i\in \{1, \ldots , n\}\) such that \(x_i = 1\), then  , and, thus, it is immediate that
, and, thus, it is immediate that  . The proof of (\(\mathcal {GG}4\)) is similar to [20, Theorem 3]. \(\square \)
. The proof of (\(\mathcal {GG}4\)) is similar to [20, Theorem 3]. \(\square \)
Example 2
Observe that Theorem 2 provides a method for constructing general grouping functions. For example, take the maximum powered by p, defined by:

with \(p >0\). So, if we take the function \(T{\max }^{p}_{\alpha }:[0,1]^n \rightarrow [0,1]\), called \(\alpha \)-truncated maximum powered by p, given, for all  and \(\alpha \in (0,1)\), by:
and \(\alpha \in (0,1)\), by:

then it is clear that \(T{\max }^{p}_{\alpha }\) is not continuous. However, one can consider the function \(CT{\max }^{p}_{\alpha ,\epsilon } :[0,1]^n \rightarrow [0,1]\), called the continuous truncated maximum powered by p, for all  , \(\alpha \in [0,1]\) and \(\epsilon \in (0,\alpha ]\), which is defined by:
, \(\alpha \in [0,1]\) and \(\epsilon \in (0,\alpha ]\), which is defined by:

Observe that taking \(f=CT{\max }^{p}_{\alpha ,\epsilon }\), then f satisfies conditions (i)–(iii) and (v) in Theorem 2. Now, take  , which satisfies conditions (i)–(ii) and (iv)–(v) required in Theorem 2. Thus, this assures that
, which satisfies conditions (i)–(ii) and (iv)–(v) required in Theorem 2. Thus, this assures that

is a general grouping function.
Remark 3
Observe that the maximum powered by p is an n-dimensional grouping function [15] and that \(CT{\max }^{p}_{\alpha ,\epsilon }\) is a general grouping function. However, \(CT{\max }^{p}_{\alpha ,\epsilon }\) is not an n-dimensional grouping function, for \(\alpha -\epsilon >0\), since \(CT{\max }^{p}_{\alpha ,\epsilon }(\alpha -\epsilon ,\ldots ,\alpha -\epsilon )=0\).
Corollary 1
Consider the functions \(f,h:[0,1]^n \rightarrow [0,1]\) and let \(\mathcal {GG}:[0,1]^n \rightarrow [0,1]\) be a general grouping function constructed according to Theorem 2, and taking into account functions f and h. Then \( \mathcal {GG}\) is idempotent if and only if, for all \(x \in [0,1)\), it holds that:
Proof
(\(\Rightarrow \)) If \(\mathcal {GG}\) is idempotent, then by Theorem 2 it holds that:
It follows that: \(f(x,\ldots ,x)= x(f(x,\ldots ,x)+h(x,\ldots ,x))\)
(\(\Leftarrow \)) It is immediate. \(\square \)
Example 3
Take the function \(\alpha \beta \)-truncated maximum powered by p, \(T{\max }^{p}_{\alpha \beta }: [0,1]^n \rightarrow [0,1]\), for all  ; \(\alpha ,\beta \in (0,1)\) and \(\alpha < \beta \), defined by:
; \(\alpha ,\beta \in (0,1)\) and \(\alpha < \beta \), defined by:

It is clear that \(T{\max }^{p}_{\alpha \beta }\) is not continuous. However, we can define its continuous version, \(CT{\max }^{p}_{\alpha \beta ,\epsilon \delta }:[0,1]^n \rightarrow [0,1]\), for all  ; \(\alpha \in [0,1)\); \(\beta ,\epsilon ,\delta \in (0,1]\); \(\alpha +\epsilon , \beta -\delta \in (0,1)\) and \(\alpha +\epsilon < \beta -\delta \), as follows:
; \(\alpha \in [0,1)\); \(\beta ,\epsilon ,\delta \in (0,1]\); \(\alpha +\epsilon , \beta -\delta \in (0,1)\) and \(\alpha +\epsilon < \beta -\delta \), as follows:

Observe that \(CT{\max }^{p}_{\alpha \beta ,\epsilon \delta }\) satisfies conditions \((\mathcal {GG}1)\)-\((\mathcal {GG}5)\) from Definition 9, and then it is a general grouping function. But, whenever \(\alpha \ne 0\) or \(\beta \ne 1\), then \(CT{\max }^{p}_{\alpha \beta ,\epsilon \delta }\) is not an n-dimensional grouping function, once \(CT{\max }^{p}_{\alpha \beta ,\epsilon \delta }( \alpha -\epsilon , \ldots ,\alpha -\epsilon )=0\), for \(\alpha -\epsilon > 0\), because \(\max ^p(\alpha -\epsilon , \ldots ,\alpha -\epsilon )=\alpha -\epsilon < \alpha \).
The following Theorem generalizes Example 3 providing a construction method for general grouping functions from truncated n-dimensional grouping functions.
Theorem 3
Consider \(\alpha \in [0,1)\); \(\beta ,\epsilon ,\delta \in (0,1]\); \(\alpha +\epsilon , \beta -\delta \in (0,1)\) and \(\alpha < \beta \), \(\alpha +\epsilon < \beta -\delta \). Let \(\mathcal {G}\) be an n-dimensional grouping function, whose \(\alpha \beta \)-truncated version is defined, for all  , by:
, by:

Then, the continuous version of \(T{\mathcal {G}}_{\alpha \beta }\), for all  , is given by:
, is given by:

and it is a general grouping function. Besides that, whenever \(\alpha = 0\) and \(\beta =1\), then \(CT{\mathcal {G}}_{\alpha \beta ,\epsilon \delta }\) is an n-dimensional grouping function.
The following proposition shows a construction method of general grouping functions that generalizes Example 1(4).
Proposition 6
Let \(\mathcal {G}:[0,1]^n \rightarrow [0,1]\) be an n-dimensional grouping function and let \(F:[0,1]^n \rightarrow [0,1]\) be a commutative and continuous aggregation function such that, for all  , if there exists \( i\in \{1,\ldots ,n\}\) such that \(x_i=1\), then
, if there exists \( i\in \{1,\ldots ,n\}\) such that \(x_i=1\), then  . Then
. Then  is a general grouping function.
is a general grouping function.
Proof
It is immediate that \(\mathcal {GG}_{\mathcal {G}F}\) is well defined, (\(\mathcal {GG}1\)) commutative, (\(\mathcal {GG}4\)) increasing and (\(\mathcal {GG}5\)) continuous, since \(\mathcal {G}\), F and the product operation are commutative, increasing and continuous. To prove (\(\mathcal {GG}2\)), whenever  , then by (\(\mathcal {G}2\)), it holds that
, then by (\(\mathcal {G}2\)), it holds that  , and, thus,
, and, thus,  For (\(\mathcal {GG}3\)), whenever there exists \(i\in \{1, \ldots , n\}\) such that \(x_i = 1\), then, by (\(\mathcal {G}3\)), one has that
For (\(\mathcal {GG}3\)), whenever there exists \(i\in \{1, \ldots , n\}\) such that \(x_i = 1\), then, by (\(\mathcal {G}3\)), one has that  , and, by the property of F, it holds that
, and, by the property of F, it holds that  . It follows that:
. It follows that:  . \(\square \)
. \(\square \)
The following result is immediate.
Corollary 2
Let \(\mathcal {GH} :[0,1]^n \rightarrow [0,1]\) be a general grouping function and let \(F :[0,1] \rightarrow [0,1]\) be a commutative and continuous aggregation function such that, for all  , if there exists \( i\in \{1,\ldots ,n\}\) such that \(x_i=1\), then
, if there exists \( i\in \{1,\ldots ,n\}\) such that \(x_i=1\), then  . Then
. Then  is a general grouping function.
is a general grouping function.
Note that \(\mathfrak {G}^n\) is closed with respect to some aggregation functions, as stated by the following results, which provide construction methods of general grouping functions.
Theorem 4
Consider \(M :\ [0,1]^2 \rightarrow [0,1] \). For any \(\mathcal {GG}_1, \mathcal {GG}_2 \in \mathfrak {G}^n\), define the mapping \(M_{\mathcal {GG}_1,\mathcal {GG}_2}:[0,1]^n \rightarrow [0,1]\), for all  , by:
, by:

Then, \(M_{\mathcal {GG}_1,\mathcal {GG}_2} \in \mathfrak {G}^n \) if and only if M is a continuous aggregation function.
Proof
It follows that:
(\(\Rightarrow \)) Suppose that \(M_{\mathcal {GG}_1,\mathcal {GG}_2} \in \mathfrak {G}^n \). Then it is immediate that M is continuous and increasing (A2). Now consider  and suppose that
and suppose that  . Then, by (\(\mathcal {GG}2\)), one has that:
. Then, by (\(\mathcal {GG}2\)), one has that:  and
and  . Thus, it holds that \(M(0,0)=0\). Now, consider
. Thus, it holds that \(M(0,0)=0\). Now, consider  , such that there exists \(i\in \{1, \ldots , n\}\) such that \(x_i=1\). Then, by (\(\mathcal {GG}3\)), one has that:
, such that there exists \(i\in \{1, \ldots , n\}\) such that \(x_i=1\). Then, by (\(\mathcal {GG}3\)), one has that:  and
and  Therefore, it holds that \(M(1,1)=1\). This proves that M also satisfies (A1), and, thus, M is a continuous aggregation function.
Therefore, it holds that \(M(1,1)=1\). This proves that M also satisfies (A1), and, thus, M is a continuous aggregation function.
(\(\Leftarrow \)) Suppose that M is a continuous aggregation function. Then it is immediate that \(M_{\mathcal {GG}_1,\mathcal {GG}_2}\) is (\(\mathcal {GG}1\)) commutative, (\(\mathcal {GG}4\)) increasing and (\(\mathcal {GG}5\)) continuous. For (\(\mathcal {GG}2\)), consider  such that
such that  . Then, by (\(\mathcal {GG}2\)), one has that
. Then, by (\(\mathcal {GG}2\)), one has that  . It follows that:
. It follows that:  , by (A1), since M is an aggregation function. Finally, for (\(\mathcal {GG}3\)) consider that there exists \(i \in \{1, \ldots ,n\}\) such that \(x_i=1\) for some
, by (A1), since M is an aggregation function. Finally, for (\(\mathcal {GG}3\)) consider that there exists \(i \in \{1, \ldots ,n\}\) such that \(x_i=1\) for some  . Then, it holds that
. Then, it holds that  . It follows that:
. It follows that:  , by (A1), since M is an aggregation function. This proves that \(M_{\mathcal {GG}_1,\mathcal {GG}_2} \in \mathfrak {G}^n \). \(\square \)
, by (A1), since M is an aggregation function. This proves that \(M_{\mathcal {GG}_1,\mathcal {GG}_2} \in \mathfrak {G}^n \). \(\square \)
Example 4
In the sense of Theorem 4, \(\mathfrak {G}^n\) is closed under any bidimensional overlap functions, grouping functions and continuous t-norms and t-conorms [18].
Corollary 3
Consider \(M:[0,1]^2 \rightarrow [0,1] \). For any n-dimensional grouping functions \(\mathcal {G}_1, \mathcal {G}_2:[0,1]^n \rightarrow [0,1] \), define the mapping \(M_{\mathcal {G}_1,\mathcal {G}_2}:[0,1]^n \rightarrow [0,1]\), for all  , by:
, by:

Then, \(M_{\mathcal {G}_1,\mathcal {G}_2} \in \mathfrak {G}^n \) if and only if M is a continuous aggregation function.
Proof
It follows from Theorem 4, since any n-dimensional grouping function is a general grouping function. \(\square \)
Theorem 4 can be easily extended for n-ary functions \(M^n:[0,1]^n \rightarrow [0,1]\):
Theorem 5
Consider \(M^n:[0,1]^n \rightarrow [0,1]\). For any \(\mathcal {GG}_1, \ldots , \mathcal {GG}_n \in \mathfrak {G}^n\), define the mapping \(M_{\mathcal {GG}_1,\ldots ,\mathcal {GG}_n}: [0,1]^n \rightarrow [0,1]\), for all  , by:
, by:

Then, \(M_{\mathcal {GG}_1,\ldots ,\mathcal {GG}_n} \in \mathfrak {G}^n \) if and only if \(M^n: [0,1]^n \rightarrow [0,1]\) is a continuous n-ary aggregation function.
Proof
Analogous to the proof of Theorem 4. \(\square \)
This result can be extended for n-dimensional grouping functions.
Corollary 4
Consider \(M^n:[0,1]^n \rightarrow [0,1]\) and fr any n-dimensional grouping functions \(\mathcal {G}_1, \ldots , \mathcal {G}_n\) define the mapping \(M_{\mathcal {G}_1,\ldots ,\mathcal {G}_n}:[0,1]^n \rightarrow [0,1]\), for all  , by:
, by:

Then, \(M_{\mathcal {G}_1,\ldots ,\mathcal {G}_n}\) is a general grouping function if and only if \(M^n:[0,1]^n \rightarrow [0,1]\) is a continuous n-ary aggregation function.
Corollary 5
Let \(\mathcal {GG}_1, \ldots , \mathcal {GG}_m:[0,1]^n \rightarrow [0,1]\) be general grouping functions and consider weights \(w_{1}, \ldots , w_{m} \in [0,1]\) such that  . Then the convex sum
. Then the convex sum  is also a general grouping function.
is also a general grouping function.
Proof
Since the weighted sum is a continuous commutative n-ary aggregation function, the result follows from Theorem 5. \(\square \)
It is possible to obtain general grouping functions from the generalized composition of general grouping functions and aggregation functions satisfying specific conditions:
Theorem 6
Let \(\mathcal {GG}_2:[0,1]^n \rightarrow [0,1]\) be a general grouping function and let the n-ary aggregation functions \(A_1, \ldots , A_n:[0,1]^n \rightarrow [0,1]\) be continuous, commutative and disjunctive. Then, the function \(\mathcal {GG}_1:[0,1]^n \rightarrow [0,1]\) defined, for all  , by:
, by:  is a general grouping function.
is a general grouping function.
Proof
Since \(\mathcal {GG}_2\), \(A_1, \ldots ,A_n\) are commutative, increasing and continuous functions, then \(\mathcal {GG}_1\) satisfies conditions (\(\mathcal {GG}1\)), (\(\mathcal {GG}4\)) and (\(\mathcal {GG}5\)). So, it remains to prove:
(\(\mathcal {GG}2\)) Let  be such that \(\sum \limits _{i=1}^n x_i =0\). Then, since \(A_1\) is disjunctive, we have that
be such that \(\sum \limits _{i=1}^n x_i =0\). Then, since \(A_1\) is disjunctive, we have that  , that is
, that is  . Equivalently, one obtains
. Equivalently, one obtains  . Thus, since \(\mathcal {GG}_2\) is a general grouping function, one has that
. Thus, since \(\mathcal {GG}_2\) is a general grouping function, one has that 
(\(\mathcal {GG}3\)) Suppose that, for some  , there exists \(i \in \{1, \ldots , n \}\) such that \(x_i =1\). So, since \(A_1\) is disjunctive then
, there exists \(i \in \{1, \ldots , n \}\) such that \(x_i =1\). So, since \(A_1\) is disjunctive then  , that is
, that is  . Since \(\mathcal {GG}_2\) is a general grouping function, it follows that
. Since \(\mathcal {GG}_2\) is a general grouping function, it follows that  . \(\square \)
. \(\square \)
Next proposition uses the n-duality property.
Proposition 7
Consider a continuous fuzzy negation \(N :[0,1] \rightarrow [0,1]\) and a general overlap function \(\mathcal {GO}:[0,1]^n \rightarrow [0,1]\), then for all  :
:

is a general grouping function. Reciprocally, if \(\mathcal {GG} :[0,1]^n \rightarrow [0,1]\) is a general grouping function, then for all  :
:

is a general overlap function.
Proof
Since we have a continuous fuzzy negation and bearing in mind that general overlap functions and general grouping functions are commutative, increasing and continuous functions according to Definition 8 and Definition 9, respectively, then \(\mathcal {GO}\) and \(\mathcal {GG}\) satisfy conditions \((\mathcal {GO}1),(\mathcal {GG}1)\); \((\mathcal {GO}4),(\mathcal {GG}4)\) and \((\mathcal {GO}5),(\mathcal {GG}5)\). So, it remains to prove:
\((\mathcal {GG}2)\) For Eq. (4), take \(x_i = 0\), for all \(i \in \{1,\ldots ,n\}\). Therefore,

\((\mathcal {GG}3)\) If there exists a \(x_i = 1\), for some \(i \in \{1,\ldots ,n\}\), then

\((\mathcal {GO}2)\) Similarly, for Eq. (5), take a \(x_i = 0\) for some \(i \in \{1,\ldots ,n\}\). So,

\((\mathcal {GO}3)\) Now, consider that \(x_i = 1\), for all \(i \in \{1,\ldots ,n\}\). Then,

\(\square \)
5 Conclusions
In this paper, we first introduced the concept of general grouping functions and studied some of their properties. Then we provided a characterization of general grouping functions and some construction methods.
The theoretical developments presented here allow for a more flexible approach when dealing with decision making problems with multiple alternatives. Immediate future work is concerned with the development of an application in multi-criteria decision making based on n-ary fuzzy heterogeneous, incomplete preference relations.
References
Barzilai, J.: Consistency measures for pairwise comparison matrices. J. Multi-Criteria Decis. Anal. 7(3), 123–132 (1998). https://doi.org/doi.org/10.1002/(SICI)1099-1360(199805)7:3%3C123::AID-MCDA181%3E3.0.CO;2-8
Bedregal, B.C., Dimuro, G.P., Bustince, H., Barrenechea, E.: New results on overlap and grouping functions. Inf. Sci. 249, 148–170 (2013). https://doi.org/10.1016/j.ins.2013.05.004
Beliakov, G., Pradera, A., Calvo, T.: Aggregation Functions: A Guide for Practitioners. Springer, Berlin (2007). https://doi.org/10.1007/978-3-540-73721-6
Bustince, H., Fernandez, J., Mesiar, R., Montero, J., Orduna, R.: Nonlinear analysis: theory, overlap functions. Methods Appl. 72(3–4), 1488–1499 (2010)
Bustince, H., Pagola, M., Mesiar, R., Hüllermeier, E., Herrera, F.: Grouping, overlaps, and generalized bientropic functions for fuzzy modeling of pairwise comparisons. IEEE Trans. Fuzzy Syst. 20(3), 405–415 (2012). https://doi.org/10.1109/TFUZZ.2011.2173581
Chiclana, F., Herrera, F., Herrera-Viedma, E.: Integrating multiplicative preference relations in a multipurpose decision-making model based on fuzzy preference relations. Fuzzy Sets Syst. 122(2), 277–291 (2001). https://doi.org/10.1016/S0165-0114(00)00004-X
Dimuro, G.P., Bedregal, B.: Archimedean overlap functions: the ordinal sum and the cancellation, idempotency and limiting properties. Fuzzy Sets Syst. 252, 39–54 (2014). https://doi.org/10.1016/j.fss.2014.04.008
Dimuro, G.P., Bedregal, B.: On residual implications derived from overlap functions. Inf. Sci. 312, 78–88 (2015). https://doi.org/10.1016/j.ins.2015.03.049
Dimuro, G.P., Bedregal, B., Bustince, H., Mesiar, R., Asiain, M.J.: On additive generators of grouping functions. In: Laurent, A., Strauss, O., Bouchon-Meunier, B., Yager, R.R. (eds.) IPMU 2014. CCIS, vol. 444, pp. 252–261. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-08852-5_26
Dimuro, G.P., Bedregal, B., Fernandez, J., Sesma-Sara, M., Pintor, J.M., Bustince, H.: The law of O-conditionality for fuzzy implications constructed from overlap and grouping functions. Int. J. Approximate Reasoning 105, 27–48 (2019). https://doi.org/10.1016/j.ijar.2018.11.006
Dimuro, G.P., Bedregal, B., Santiago, R.H.N.: On \((G, N)\)-implications derived from grouping functions. Inf. Sci. 279, 1–17 (2014). https://doi.org/10.1016/j.ins.2014.04.021
Dimuro, G.P., Bedregal, B., Bustince, H., Asiáin, M.J., Mesiar, R.: On additive generators of overlap functions. Fuzzy Sets Syst. 287, 76–96 (2016). https://doi.org/10.1016/j.fss.2015.02.008. Theme: Aggregation Operations
Dimuro, G.P., Bedregal, B., Bustince, H., Jurio, A., Baczyński, M., Miś, K.: QL-operations and QL-implication functions constructed from tuples \((O, G, N)\) and the generation of fuzzy subsethood and entropy measures. Int. J. Approximate Reasoning 82, 170–192 (2017). https://doi.org/10.1016/j.ijar.2016.12.013
Fodor, J., Roubens, M.: Fuzzy Preference Modelling and Multicriteria Decision Support. Kluwer Academic Publisher, Dordrecht (1994)
Gómez, D., Rodríguez, J.T., Montero, J., Bustince, H., Barrenechea, E.: n-Dimensional overlap functions. Fuzzy Sets Syst. 287, 57–75 (2016). https://doi.org/10.1016/j.fss.2014.11.023. Theme: Aggregation Operations
Gómez, D., Rodríguez, J.T., Montero, J., Yáñez, J.: Fuzzy community detection based on grouping and overlapping functions. In: 2015 Conference of the International Fuzzy Systems Association and the European Society for Fuzzy Logic and Technology (IFSA-EUSFLAT-15). Atlantis Press, Paris (2015). https://doi.org/10.2991/ifsa-eusflat-15.2015.215
Jurio, A., Bustince, H., Pagola, M., Pradera, A., Yager, R.: Some properties of overlap and grouping functions and their application to image thresholding. Fuzzy Sets Syst. 229, 69–90 (2013). https://doi.org/10.1016/j.fss.2012.12.009
Klement, E., Mesiar, R., Pap, E.: Triangular Norms, Trends in Logic - Studia Logica Library, vol. 8. Kluwer Academic Publishers, Dordrecht (2000)
Lourenzutti, R., Krohling, R.A., Reformat, M.Z.: Choquet based topsis and todim for dynamic and heterogeneous decision making with criteria interaction. Inf. Sci. 408, 41–69 (2017). https://doi.org/10.1016/j.ins.2017.04.037
Miguel, L.D., et al.: General overlap functions. Fuzzy Sets Syst. 372, 81–96 (2019). https://doi.org/10.1016/j.fss.2018.08.003. Theme: Aggregation Operations
Qiao, J., Hu, B.Q.: On the distributive laws of fuzzy implication functions over additively generated overlap and grouping functions. IEEE Tran. Fuzzy Syst. 26(4), 2421–2433 (2018). https://doi.org/10.1109/TFUZZ.2017.2776861
Qiao, J., Hu, B.Q.: On interval additive generators of interval overlap functions and interval grouping functions. Fuzzy Sets Syst. 323, 19–55 (2017). https://doi.org/10.1016/j.fss.2017.03.007
Qiao, J., Hu, B.Q.: On the migrativity of uninorms and nullnorms over overlap and grouping functions. Fuzzy Sets Syst. 346, 1–54 (2018). https://doi.org/10.1016/j.fss.2017.11.012
Qiao, J., Hu, B.Q.: On generalized migrativity property for overlap functions. Fuzzy Sets Syst. 357, 91–116 (2019). https://doi.org/10.1016/j.fss.2018.01.007
Qiao, J., Hu, B.Q.: On homogeneous, quasi-homogeneous and pseudo-homogeneous overlap and grouping functions. Fuzzy Sets Syst. 357, 58–90 (2019). https://doi.org/10.1016/j.fss.2018.06.001. Theme: Aggregation Functions
Ureña, R., Chiclana, F., Morente-Molinera, J., Herrera-Viedma, E.: Managing incomplete preference relations in decision making: a review and future trends. Inf. Sci. 302, 14–32 (2015). https://doi.org/10.1016/j.ins.2014.12.061
Acknowledgments
Supported by CNPq (233950/2014-1, 307781/2016-0, 301618/2019-4), FAPERGS (17/2551 - 0000872-3, 19/2551 - 0001279-9, 19/ 2551 - 0001660-3), PNPD/CAPES (464880 /2019-00) and the Spanish Ministry of Science and Technology (PC093 - 094TFIPDL, TIN2016-81731-REDT, TIN2016-77356-P (AEI/FEDER, UE)).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Santos, H. et al. (2020). General Grouping Functions. In: Lesot, MJ., et al. Information Processing and Management of Uncertainty in Knowledge-Based Systems. IPMU 2020. Communications in Computer and Information Science, vol 1238. Springer, Cham. https://doi.org/10.1007/978-3-030-50143-3_38
Download citation
DOI: https://doi.org/10.1007/978-3-030-50143-3_38
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-50142-6
Online ISBN: 978-3-030-50143-3
eBook Packages: Computer ScienceComputer Science (R0)





 if and only if
if and only if 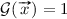 if and only if there exists
if and only if there exists 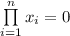 then
then  ;
;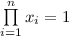 then
then  ;
; then
then 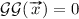 ;
; ;
; , then
, then  .
. , then
, then 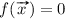 .
.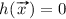 .
.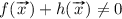 for any
for any 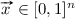 .
.