Abstract
We show that chosen plaintext attacks (CPA) security is equivalent to chosen ciphertext attacks (CCA) security for key-dependent message (KDM) security. Concretely, we show how to construct a public-key encryption (PKE) scheme that is KDM-CCA secure with respect to all functions computable by circuits of a-priori bounded size, based only on a PKE scheme that is KDM-CPA secure with respect to projection functions. Our construction works for KDM security in the single user setting.
Our main result is achieved by combining the following two steps. First, we observe that by combining the results and techniques from the recent works by Lombardi et al. (CRYPTO 2019), and by Kitagawa et al. (CRYPTO 2019), we can construct a reusable designated-verifier non-interactive zero-knowledge (DV-NIZK) argument system based on an IND-CPA secure PKE scheme and a secret-key encryption (SKE) scheme satisfying one-time KDM security with respect to projection functions. This observation leads to the first reusable DV-NIZK argument system under the learning-parity-with-noise (LPN) assumption. Then, as the second and main technical step, we show a generic construction of a KDM-CCA secure PKE scheme using an IND-CPA secure PKE scheme, a reusable DV-NIZK argument system, and an SKE scheme satisfying one-time KDM security with respect to projection functions. Since the classical Naor-Yung paradigm (STOC 1990) with a DV-NIZK argument system does not work for proving KDM security, we propose a new construction methodology to achieve this generic construction.
Moreover, we show how to extend our generic construction and achieve KDM-CCA security in the multi-user setting, by additionally requiring the underlying SKE scheme in our generic construction to satisfy a weak form of KDM security against related-key attacks (RKA-KDM security) instead of one-time KDM security. From this extension, we obtain the first KDM-CCA secure PKE schemes in the multi-user setting under the CDH or LPN assumption.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
- Public-key encryption
- Key-dependent message security
- Chosen ciphertext security
- Designated-verifier non-interactive zero-knowledge argument
1 Introduction
1.1 Background
The most basic security notion for public-key encryption (PKE) is indistinguishability against chosen plaintext attacks (IND-CPA security) [26]. Intuitively, IND-CPA security guarantees that an adversary can obtain no information about a message from its encryption, except for its length. However, in practice, PKE schemes should satisfy the stronger notion of indistinguishability against chosen ciphertext attacks (IND-CCA security) [37, 38]. IND-CCA security implies non-malleability [7, 20], and provides security guarantees against active adversaries [9].
Since IND-CCA security is stronger than IND-CPA security, the existence of IND-CCA secure PKE implies that of IND-CPA secure one. However, the implication of the opposite direction is not known. While a partial negative result was shown by Gertner, Malkin, and Myers [25], the question whether an IND-CCA secure PKE scheme can be constructed from an IND-CPA secure one has still been standing as a major open question in cryptography from both the theoretical and practical points of view.
In the literature, a number of efforts have been made for (implicitly or explicitly) tackling the problem. Among them, we highlight the two very recent works that make solid progress. Koppula and Waters [33] showed that an IND-CCA secure PKE scheme can be constructed from an IND-CPA secure one by using a pseudorandom generator (PRG) satisfying a special security notion. This additional primitive is called a hinting PRG. Subsequently, Kitagawa, Matsuda, and Tanaka [30] showed that a transformation from an IND-CPA secure PKE scheme to an IND-CCA secure one is also possible by using a secret-key encryption (SKE) scheme satisfying one-time key-dependent message security [8] instead of a hinting PRG.
We further study the question of CPA security vs CCA security. Many previous works focusing on this question sought an additional assumption that bridges IND-CPA security and IND-CCA security. In this work, we tackle the question from a somewhat different angle. Concretely, we aim at finding a security notion under which CPA security and CCA security are equivalent. As far as we know, such an equivalence is not known for any security notion for PKE schemes (e.g., leakage resilience, key-dependent message security, and selective opening security). Finding such a security notion is an important question in the theoretical study of public-key cryptography. Moreover, we believe that clarifying for what types of notions CPA security and CCA security are equivalent potentially gives us new insights for the major open question on the equivalence between IND-CPA security and IND-CCA security.
Based on the above motivation, in this work, we study the equivalence of CPA security and CCA security for key-dependent message (KDM) security [8]. Informally, KDM security guarantees that an encryption scheme can securely encrypt messages that depend on its own secret key. We can see some connections between IND-CCA security and KDM-CPA security from several previous results [27, 30, 36], and thus KDM security can be considered as one of the best candidates for which CPA security and CCA security could be shown equivalent. Moreover, KDM security is important and interesting enough to be studied in its own right since it has found a number of applications in both theoretical and practical studies in cryptography, e.g., anonymous credentials [15], formal methods [1], hard-disc encryption [10], fully homomorphic encryption [24], non-interactive zero-knowledge proofs [16, 17], and homomorphic secret-sharing [11].
1.2 Our Results
As noted above, we study the equivalence between CPA security and CCA security for KDM security. Then, we obtain the following main theorem.
Theorem 1 (Informal)
Assume that there exists a KDM-CPA secure PKE scheme. Then, there exists a KDM-CCA secure PKE scheme.
We show this theorem for KDM-CPA security and KDM-CCA security in the single user setting. The underlying scheme needs to be KDM-CPA secure with respect to functions called projection functions ( secure). The family of projection functions is one of the simplest classes of functions, and KDM security with respect to this function class has been widely studied [5, 10, 12, 13, 22]. The resulting scheme is KDM-CCA secure with respect to all functions computable by circuits of a-priori bounded size. The achieved security notion is the CCA-analogue of the notion called bounded KDM security by Barak, Haitner, Hofheinz, and Ishai [6].
secure). The family of projection functions is one of the simplest classes of functions, and KDM security with respect to this function class has been widely studied [5, 10, 12, 13, 22]. The resulting scheme is KDM-CCA secure with respect to all functions computable by circuits of a-priori bounded size. The achieved security notion is the CCA-analogue of the notion called bounded KDM security by Barak, Haitner, Hofheinz, and Ishai [6].
We obtain Theorem 1 by combining the following two steps.
Reusable DV-NIZK Based on One-Time KDM Secure SKE. A designated-verifier non-interactive zero-knowledge (DV-NIZK) argument system is a relaxation of a standard NIZK argument system in the common reference string model (CRS-NIZK, for short), and allows a verifier to have its own public/secret key pair; The public key is used to generate a proof non-interactively, which can be verified by using the corresponding secret key. A DV-NIZK argument system is said to be reusable if its soundness (resp. zero-knowledge property) is maintained even if an adversary can make multiple verification (resp. proving) queries. It was recently shown by Lombardi, Quach, Rothblum, Wichs, and Wu [34] that a reusable DV-NIZK argument system can be constructed from the combination of an IND-CPA secure PKE scheme and a hinting PRG introduced by Koppula and Waters [33].
As the first step for Theorem 1, we observe that we can construct a reusable DV-NIZK argument system based on an IND-CPA secure PKE scheme and an SKE scheme that is one-time KDM secure with respect to projection functions (one-time \(\mathcal {P}\)-KDM secure), by combining the results and techniques from the recent works by Lombardi et al. [34] and Kitagawa et al. [30].
In fact, this is somewhat obvious from the results [30, 34] and not our main contribution. However, this observation leads to the following interesting implications. A one-time \(\mathcal {P}\)-KDM secure SKE scheme can be constructed based on the polynomial hardness of the constant-noise learning-parity-with-noise (LPN) assumption [5]. Moreover, we can construct an IND-CPA secure PKE scheme based on the polynomial hardness of the low-noise LPN assumption [2] or the sub-exponential hardness of the constant-noise LPN assumption [41]. Thus, combined together, our observation leads to the first reusable DV-NIZK argument system based on either the polynomial hardness of the low-noise LPN assumption or the sub-exponential hardness of the constant-noise LPN assumption.
We note that the exact same observation (i.e. a reusable DV-NIZK argument system based on IND-CPA secure PKE and one-time \(\mathcal {P}\)-KDM secure SKE, and the LPN-based instantiation) was very recently made independently and concurrently by Lombardi et al. [35].
Generic Construction of KDM-CCA Secure PKE Using Reusable DV-NIZK. Then, as the second and main technical step for Theorem 1, we show a generic construction of KDM-CCA secure PKE based on the following five building blocks: an IND-CPA secure PKE scheme, an IND-CCA secure PKE scheme, a one-time \(\mathcal {P}\)-KDM secure SKE scheme, a garbling scheme, and a reusable DV-NIZK argument system.
In the first step above, we show how to construct a reusable DV-NIZK argument system from an IND-CPA secure PKE scheme and a one-time \(\mathcal {P}\)-KDM secure SKE scheme. Also, IND-CCA secure PKE can be constructed from the same building blocks [30]. Moreover, a garbling scheme can be constructed from one-way functions [40], which is in turn implied by other building blocks. Therefore, through our generic construction, we can construct a KDM-CCA secure PKE scheme based on an IND-CPA secure PKE scheme and a one-time \(\mathcal {P}\)-KDM secure SKE scheme. Since both of the underlying primitives are implied by  secure PKE, we obtain Theorem 1.
secure PKE, we obtain Theorem 1.
We highlight that our construction can “amplify” KDM security in terms of not only the class of functions (from projection functions to circuits of a-priori bounded size) but also the number of KDM-encryption queries allowed for an adversary. Specifically, among the building blocks, the only “KDM-secure” component is the one-time \(\mathcal {P}\)-KDM secure SKE scheme, while our construction achieves the standard many-time KDM-CCA security. For more details, see Sect. 2.3.
One might think that if we can use a reusable DV-NIZK argument system, a KDM-CPA secure PKE scheme can easily be transformed into a KDM-CCA secure one by the Naor-Yung paradigm [37]. In fact, if the goal is to achieve an IND-CCA secure PKE scheme, then it is possible to replace a CRS-NIZK argument system in the Naor-Yung paradigm with a reusable DV-NIZK argument system. Furthermore, Camenisch, Chandran, and Shoup [14] showed that (a slight variant of) the Naor-Yung paradigm with a CRS-NIZK argument system can be used to transform a KDM-CPA secure PKE scheme into a KDM-CCA secure one. Unfortunately, however, things are not so easy if we aim at achieving KDM-CCA security using a reusable DV-NIZK argument system via the Naor-Yung paradigm (or its existing variants). The main cause of difficulty is that if we apply the standard Naor-Yung paradigm using a DV-NIZK argument system, the secret verification key of the DV-NIZK argument system is included in the secret key of the resulting scheme, and a circularity involving a DV-NIZK argument system occurs in the KDM-CCA security game. Our main technical contribution is circumventing this difficulty. We will detail the difficulty as well as our techniques in Sect. 2.
KDM-CCA Security in the Multi-user Setting Based on New Assumptions. Although our main focus in this work is on showing that KDM-CPA security and KDM-CCA security are equivalent, through the above results, we obtain the first KDM-CCA secure PKE schemes based on the computational Diffie-Hellman (CDH) assumption and the LPN assumption, since KDM-CPA secure PKE schemes can be constructed under these assumptions [13, 21, 22]. These schemes satisfy only KDM-CCA security in the single user setting, since so does our generic construction, as noted earlier.
We then show how to extend our generic construction and achieve a PKE scheme satisfying KDM-CCA security in the multi-user setting under the CDH and LPN assumptions. This is done by requiring the underlying SKE scheme in our generic construction to satisfy a variant of KDM security against related-key attacks (RKA-KDM security) [4], instead of one-time KDM security. (We also require a mild property that a secret key is a uniformly distributed random string.) An SKE scheme satisfying our definition of RKA-KDM security can be constructed based on the (polynomial hardness of) constant-noise LPN assumption [4]. Moreover, we show how to construct an SKE scheme satisfying our RKA-KDM security notion based on hash encryption [13, 22], which in turn can be based on the CDH assumption. This construction is an extension of a KDM-CPA secure PKE scheme based on batch encryption proposed by Brakerski, Lombardi, Segev, and Vaikuntanathan [13].
Due to the space constraint, we omit the construction of an RKA-KDM secure SKE scheme using a hash encryption scheme from the proceedings version. For the construction, see the full version.
1.3 Related Work
Generic Constructions for KDM-CCA Secure PKE. To the best of our knowledge, the only existing generic methods for constructing KDM-CCA secure PKE, are the works by Camenisch, Chandran, and Shoup [14], by Galindo, Herrantz, and Villar [23], and by Kitagawa and Tanaka [31]. Camenisch et al. [14] showed how to construct a KDM-CCA secure PKE scheme from a KDM-CPA secure PKE scheme, an IND-CCA secure PKE scheme, and a CRS-NIZK proof (or argument) system. (We will touch it in Sect. 2.) Galindo et al. [23] showed how to construct a KDM-CCA secure PKE scheme from an identity-based encryption scheme which satisfies so-called master-key-dependent message security, via the transformation by Canetti, Halevi, and Katz [18]. However, the only known instantiation of Galindo et al.’s method can achieve security against adversaries that make an a-priori bounded number of master-key-KDM-encryption queries, which is translated to KDM-CCA security against adversaries that make an a-priori bounded number of KDM-encryption queries. Kitagawa and Tanaka [31] showed how to construct a KDM-CCA secure PKE scheme based on a hash proof system [19] satisfying some homomorphic property. It is not obvious how to modify the methods of [23, 31] to achieve a generic construction of a KDM-CCA secure PKE scheme starting from a KDM-CPA secure one.
2 Technical Overview
In this section, we provide a technical overview of our main results. As mentioned in the introduction and will be detailed in Sect. 4, we can observe from the previous results [30, 34] that a reusable DV-NIZK argument system can be constructed based on the combination of an IND-CPA secure PKE scheme and a one-time KDM secure SKE scheme. Thus, in this overview, we mainly focus on the generic construction of a PKE scheme that is KDM-CCA secure in the single user setting using a reusable DV-NIZK argument system. (From here on, we drop “reusable”.) We also briefly explain how to extend it into the multi-user setting by using RKA-KDM secure SKE. We start with why we cannot achieve such a generic construction by using the standard Naor-Yung paradigm [37].
2.1 Naor-Yung Paradigm with DV-NIZK Fails for KDM
Camenisch, Chandran, and Shoup [14] showed that the Naor-Yung paradigm with a CRS-NIZK argument system goes through for KDM security. We first review their construction, and then explain the problems that arise when replacing the underlying CRS-NIZK argument system with a DV-NIZK argument system.
KDM-CCA PKE by Camenisch et al. [14]. The construction uses a KDM-CPA secure PKE scheme \(\mathsf {PKE}\), an IND-CCA secure PKE scheme \(\mathsf {PKE}'\), and a CRS-NIZK argument system \(\mathsf {NIZK}\).Footnote 1 Using these building blocks, we construct \(\mathsf {PKE_{NY}}\) as follows. A public key of \(\mathsf {PKE_{NY}}\) consists of \((\mathsf {pk},\mathsf {pk}_{\mathsf {cca}},\mathsf {crs})\), where \(\mathsf {pk}\) and \(\mathsf {pk}_{\mathsf {cca}}\) are public keys of \(\mathsf {PKE}\) and \(\mathsf {PKE}'\), respectively, and \(\mathsf {crs}\) is a CRS of \(\mathsf {NIZK}\). The corresponding secret key is \(\mathsf {sk}\) corresponding to \(\mathsf {pk}\). The secret key \(\mathsf {sk}_{\mathsf {cca}}\) corresponding to \(\mathsf {pk}_{\mathsf {cca}}\) is discarded and used only in the security proof. When encrypting a message m, \(\mathsf {PKE_{NY}}\) generates a ciphertext of the form
where \(\mathsf {Enc}\) and \(\mathsf {Enc}'\) denote the encryption algorithms of \(\mathsf {PKE}\) and \(\mathsf {PKE}'\), respectively, and \(\pi \) is a proof of \(\mathsf {NIZK}\) proving that \(\mathsf {ct}\) and \(\mathsf {ct}_{\mathsf {cca}}\) encrypt the same message, generated by using m and random coins used to generate \(\mathsf {ct}\) and \(\mathsf {ct}_{\mathsf {cca}}\) as a witness. When decrypting the ciphertext, we first check whether the proof \(\pi \) is accepted or not. If \(\pi \) is accepted, we decrypt \(\mathsf {ct}\) by using \(\mathsf {sk}\), and recover m.
Camenisch et al. showed that \(\mathsf {PKE_{NY}}\) is KDM-CCA secure for a function class \(\mathcal {F}\) with respect to which the underlying PKE scheme \(\mathsf {PKE}\) satisfies KDM-CPA security.Footnote 2
Circularity Involving DV-NIZK. We now explain why the above construction technique by Camenisch et al. does not work if we use a DV-NIZK argument system instead of a CRS-NIZK argument system.
If we use a DV-NIZK argument system \(\mathsf {DVNIZK}\) instead of \(\mathsf {NIZK}\) as a building block of \(\mathsf {PKE_{NY}}\), then we need a secret key \(\mathsf {sk}_{\mathsf {dv}}\) of \(\mathsf {DVNIZK}\) to verify a proof contained in a ciphertext when decrypting the ciphertext. Thus, we have to include \(\mathsf {sk}_{\mathsf {dv}}\) into the secret key of \(\mathsf {PKE_{NY}}\).
In this case, an encryption of a message of the form \(f(\mathsf {sk}\Vert \mathsf {sk}_{\mathsf {dv}})\) is given to an adversary in the KDM-CCA security game, where f is a function chosen by the adversary as a KDM-encryption query. Then, there is a circularity problem involving not only encryption schemes but also \(\mathsf {DVNIZK}\), since when encrypting a message \(f(\mathsf {sk}\Vert \mathsf {sk}_{\mathsf {dv}})\), a proof of \(\mathsf {DVNIZK}\) is generated to guarantee that encryptions of its own secret key \(\mathsf {sk}_{\mathsf {dv}}\) are well-formed. Even if such a circularity exists, we can use the zero-knowledge property of \(\mathsf {DVNIZK}\) in the security proof since a reduction algorithm attacking the zero-knowledge property is given a secret verification key \(\mathsf {sk}_{\mathsf {dv}}\) and thus can handle such a circularity. However, we cannot use its soundness property in the security proof unless we solve the circularity, because a secret verification key \(\mathsf {sk}_{\mathsf {dv}}\) is not directly given to an adversary attacking the soundness of \(\mathsf {DVNIZK}\).
Due to this circularity problem involving a DV-NIZK argument system, it seems difficult to achieve a KDM-CCA secure PKE scheme using a DV-NIZK variant of the Naor-Yung paradigm.
2.2 How to Solve the Circularity Problem Involving DV-NIZK?
The circularity problem involving a DV-NIZK argument system of \(\mathsf {PKE_{NY}}\) occurs because in the security game, a message depending on \(\mathsf {sk}_{\mathsf {dv}}\) is encrypted by encryption schemes the validity of whose ciphertexts is proved by the DV-NIZK argument system. In order to solve this circularity problem, we have to design a scheme so that it has an indirection that a message is not directly encrypted by encryption schemes related to a DV-NIZK argument system.
The most standard way to add such an indirection to encryption schemes would be to use the hybrid encryption methodology. However, it is difficult to use the hybrid encryption methodology to construct a KDM-CCA secure scheme, since it leads to a dead-lock in the sense that the key encapsulation mechanism and data encapsulation mechanism could encrypt each other’s secret key in the presence of key-dependent messages.
Thus, we use a different technique. We use a garbling scheme [40] to realize the indirection that a message is not directly encrypted by encryption schemes related to a DV-NIZK argument system.Footnote 3 Concretely, when encrypting a message m, we first garble a circuit into which m is hardwired. Then, we encrypt each of the labels generated together with the garbled circuit by a PKE scheme, and then generate a proof proving that the encryptions of the labels are well-formed by using a DV-NIZK argument system.
In order to realize the above idea using a garbling scheme, we use a one-time KDM secure SKE scheme at the key generation to encrypt (and add to a public key) secret key components of the building block PKE schemes. With the help of a one-time KDM secure SKE scheme, a garbling scheme makes it possible to simulate an encryption of the secret key without directly using the secret key itself, and we can prove the (multi-time) KDM security of the resulting scheme, which has the indirection.
Below, we first show the KDM-CPA variant of our construction without using a DV-NIZK argument system. Then, we show how to extend it into a KDM-CCA secure one.
2.3 KDM-CPA Variant of Our Construction
In the following, we show how to construct a KDM-CPA secure PKE scheme \(\mathsf {PKE}_{\mathsf {kdm}}^*\) from a garbling scheme, a one-time KDM secure SKE scheme \(\mathsf {SKE}\), and \(\mathrm{{IND}}\text {-}\mathrm{{CPA}}\) secure PKE schemes \(\mathsf {PKE}\) and \(\mathsf {PKE}'\).
Construction Using Garbled Circuits. The key generation algorithm generates a key pair \((\mathsf {PK},\mathsf {SK})\) of \(\mathsf {PKE}_{\mathsf {kdm}}^*\) as follows. It first generates a secret key \(s = (s_1, \dots , s_{\ell _{\mathsf {s}}}) \in \{0,1\}^{\ell _{\mathsf {s}}}\) of \(\mathsf {SKE}\). Next, it generates a key pair \((\mathsf {pk}',\mathsf {sk}')\) of \(\mathsf {PKE}'\) and \(2{\ell _{\mathsf {s}}}\) key pairs \((\mathsf {pk}_{j,\alpha },\mathsf {sk}_{j,\alpha })_{j\in [{\ell _{\mathsf {s}}}],\alpha \in \{0,1\}}\) of \(\mathsf {PKE}\). Then, it encrypts \({\ell _{\mathsf {s}}}+1\) secret keys \(\mathsf {sk}'\) and \((\mathsf {sk}_{j,s_j})_{j\in [{\ell _{\mathsf {s}}}]}\) into \(\mathsf {ct}_{\mathsf {ske}}\) by \(\mathsf {SKE}\) under the key s. The public-key \(\mathsf {PK}\) consists of \(2{\ell _{\mathsf {s}}}+1\) public keys \(\mathsf {pk}'\) and \((\mathsf {pk}_{j,\alpha })_{j\in [{\ell _{\mathsf {s}}}],\alpha \in \{0,1\}}\), and \(\mathsf {ct}_{\mathsf {ske}}\). The corresponding secret key \(\mathsf {SK}\) is just s. Namely, \(\mathsf {PK}\) and \(\mathsf {SK}\) are of the form
respectively, where \(\mathsf {E}_s(\cdot )\) denotes the encryption algorithm of \(\mathsf {SKE}\) using the key s.
When encrypting a message m under \(\mathsf {PK}\), \(\mathsf {PKE}_{\mathsf {kdm}}^*\) first garbles a constant circuit \(\mathsf {Q}\) that has m hardwired and outputs it for any input of length \({\ell _{\mathsf {s}}}\).Footnote 4 This results in a single garbled circuit \(\widetilde{\mathsf {Q}}\) and \(2{\ell _{\mathsf {s}}}\) labels \((\mathsf {lab}_{j,\alpha })_{j\in [{\ell _{\mathsf {s}}}],\alpha \in \{0,1\}}\). Then, the encryption algorithm encrypts “0-labels” \(\mathsf {lab}_{j,0}\) into \(\mathsf {ct}_{j,\alpha }\) by \(\mathsf {pk}_{j,\alpha }\) for every \(j\in [{\ell _{\mathsf {s}}}]\) and \(\alpha \in \{0,1\}\). It finally encrypts \(\widetilde{\mathsf {Q}}\) and those encrypted labels \((\mathsf {ct}_{j,\alpha })_{j,\alpha }\) using \(\mathsf {pk}'\). The resulting ciphertext \(\mathsf {CT}\) is of the form
where \(\mathsf {Enc}\) and \(\mathsf {Enc}'\) are the encryption algorithms of \(\mathsf {PKE}\) and \(\mathsf {PKE}'\), respectively. We stress that for every \(j\in [n]\), the same label \(\mathsf {lab}_{j,0}\) is encrypted under both \(\mathsf {pk}_{j,0}\) and \(\mathsf {pk}_{j,1}\).
When decrypting the ciphertext \(\mathsf {CT}\) using the secret key \(\mathsf {SK}=s\), we first retrieve the secret keys \(\mathsf {sk}'\) and \((\mathsf {sk}_{j,s_j})_{j\in [{\ell _{\mathsf {s}}}]}\) from \(\mathsf {ct}_{\mathsf {ske}}\) contained in \(\mathsf {PK}\). Then, using \(\mathsf {sk}'\), we recover \(\widetilde{\mathsf {Q}}\) and \((\mathsf {ct}_{j,\alpha })_{j\in [{\ell _{\mathsf {s}}}],\alpha \in \{0,1\}}\). Moreover, we recover the “0-label” \(\mathsf {lab}_{j,0}\) from \(\mathsf {ct}_{j,s_j}\) using \(\mathsf {sk}_{j,s_j}\) for every \(j\in [{\ell _{\mathsf {s}}}]\). Finally, we evaluate the recovered garbled circuit \(\widetilde{\mathsf {Q}}\) with these \({\ell _{\mathsf {s}}}\) “0-labels” by the evaluation algorithm of the garbling scheme. This results in m, since given \(0^{{\ell _{\mathsf {s}}}}\), \(\mathsf {Q}\) outputs m.
Overview of the Security Proof of \(\mathsf {PKE}_{\mathsf {kdm}}^*\). We explain how we prove the KDM-CPA security in the single user setting of \(\mathsf {PKE}_{\mathsf {kdm}}^*\). Specifically, we explain that no adversary \(\mathcal {A}\) can guess the challenge bit b with probability significantly greater than 1/2 given an encryption of \(f_b(\mathsf {SK})=f_b(s)\), when \(\mathcal {A}\) queries two functions \((f_0,f_1)\) as a KDM-encryption query.Footnote 5
In this construction, the secret keys of \(\mathsf {PKE}\) corresponding to s, namely \((\mathsf {sk}_{j,s_j})_{j\in [{\ell _{\mathsf {s}}}]}\), are encrypted in \(\mathsf {ct}_{\mathsf {ske}}\), but the rest of the secret keys \((\mathsf {sk}_{j,1 \oplus s_j})_{j\in [{\ell _{\mathsf {s}}}]}\) are hidden from \(\mathcal {A}\)’s view. Thus, in the security proof, we can always use the IND-CPA security of \(\mathsf {PKE}\) under the public keys \((\mathsf {pk}_{j,1 \oplus s_j})_{j\in [{\ell _{\mathsf {s}}}]}\). By combining the IND-CPA security of \(\mathsf {PKE}\) under these keys with the security of the garbling scheme, we can change the security game so that the encryption of \(f_b(s)\) given to \(\mathcal {A}\) can be simulated without using s, without being noticed by \(\mathcal {A}\). Concretely, in the modified security game, an encryption of \(f_b(s)\) is generated as follows. We first generate \(\widetilde{\mathsf {Q}}\) and \((\mathsf {lab}_{j,\alpha })_{j\in [{\ell _{\mathsf {s}}}],\alpha \in \{0,1\}}\) by garbling a circuit computing \(f_b\), instead of a constant circuit \(\mathsf {Q}\) in which \(f_b(s)\) is hardwired. Then, we encrypt \(\mathsf {lab}_{j,\alpha }\) into \(\mathsf {ct}_{j,\alpha }\) by \(\mathsf {pk}_{j,\alpha }\) for every \(j\in [{\ell _{\mathsf {s}}}]\) and \(\alpha \in \{0,1\}\). Finally, we encrypt \(\widetilde{\mathsf {Q}}\) and those encrypted labels \((\mathsf {ct}_{j,\alpha })_{j,\alpha }\) using \(\mathsf {pk}'\), and obtain \(\mathsf {CT}=\mathsf {Enc}_{\mathsf {pk}'}(\widetilde{\mathsf {Q}},(\mathsf {ct}_{j,0},\mathsf {ct}_{j,1})_{j\in [{\ell _{\mathsf {s}}}]})\). We see that we now do not need s to generate \(\mathsf {CT}\). The explanation so far in fact works even when \(\mathcal {A}\) makes multiple KDM-encryption queries.
After the above change, a ciphertext \(\mathsf {CT}\) given to \(\mathcal {A}\) does not have any information of s, and thus we can use the one-time KDM security of \(\mathsf {SKE}\). Although the message \((\mathsf {sk}', (\mathsf {sk}_{j,s_j})_{j\in [{\ell _{\mathsf {s}}}]})\) encrypted in \(\mathsf {ct}_{\mathsf {ske}}\) depends on the secret key s, by relying on the one-time KDM security of \(\mathsf {SKE}\), we can further change the security game so that \(\mathsf {ct}_{\mathsf {ske}}\) is generated as an encryption of some constant message such as the all-zero string. Then, since \(\mathsf {sk}'\) is now hidden from \(\mathcal {A}\)’s view, we can argue that \(\mathcal {A}\)’s advantage in the final game is essentially 1/2 based on the IND-CPA security of \(\mathsf {PKE}'\). This completes the proof for the KDM-CPA security of \(\mathsf {PKE}_{\mathsf {kdm}}^*\).
Features of \(\mathsf {PKE}_{\mathsf {kdm}}^*\). This KDM-CPA secure construction \(\mathsf {PKE}_{\mathsf {kdm}}^*\) has some nice properties. First, all of the building blocks are implied by KDM-CPA secure PKE. (Recall that a garbling scheme can be realized from one-way functions [40].) Moreover, through this construction, we can transform a one-time KDM-CPA secure scheme into a (multi-time) KDM-CPA secure PKE scheme. Also, the resulting scheme satisfies KDM-CPA security with respect to all functions computable by circuits of a-priori bounded size even though the underlying KDM-CPA secure scheme needs to satisfy a much weaker form of KDM-CPA security. Concretely, the underlying scheme needs to be only KDM-CPA secure with respect to projection functions, since the encrypted message \((\mathsf {sk}', (\mathsf {sk}_{j,s_j})_{j\in [{\ell _{\mathsf {s}}}]})\) can be seen as an output of a function \(g(x_1, \dots , x_{\ell _{\mathsf {s}}})=(\mathsf {sk}', (\mathsf {sk}_{j,x_j})_{j\in [{\ell _{\mathsf {s}}}]})\), which can be described as a projection function of an input \(x = (x_1,\dots ,x_{{\ell _{\mathsf {s}}}}) \in \{0,1\}^{{\ell _{\mathsf {s}}}}\) that has \((\mathsf {sk}', (\mathsf {sk}_{j,\alpha })_{j\in [{\ell _{\mathsf {s}}}],\alpha \in \{0,1\}})\) hardwired. From these facts, in the single user setting, the construction \(\mathsf {PKE}_{\mathsf {kdm}}^*\) in fact improves the previous amplification methods for KDM-CPA secure schemes [3, 22, 32]. In addition, most importantly, \(\mathsf {PKE}_{\mathsf {kdm}}^*\) can be easily extended into a KDM-CCA secure one by using a DV-NIZK argument system.
2.4 KDM-CCA Secure PKE Using DV-NIZK
We extend \(\mathsf {PKE}_{\mathsf {kdm}}^*\) into a KDM-CCA secure PKE scheme \(\mathsf {PKE}_{\mathsf {kdm}}\) by the following two steps.
First, we use a DV-NIZK argument system \(\mathsf {DVNIZK}\) for proving that encrypted labels are well-formed. Concretely, we use it in the following manner. When generating a key pair \((\mathsf {PK},\mathsf {SK})\) of \(\mathsf {PKE}_{\mathsf {kdm}}\), we additionally generate a key pair \((\mathsf {pk}_{\mathsf {dv}},\mathsf {sk}_{\mathsf {dv}})\) of \(\mathsf {DVNIZK}\), and add \(\mathsf {pk}_{\mathsf {dv}}\) to \(\mathsf {PK}\). Moreover, we encrypt \(\mathsf {sk}_{\mathsf {dv}}\) into \(\mathsf {ct}_{\mathsf {ske}}\) together with \((\mathsf {sk}',(\mathsf {sk}_{j,s_j})_{j\in [{\ell _{\mathsf {s}}}]})\) by using s. Namely, \(\mathsf {PK}\) is of the form
The secret key \(\mathsf {SK}\) is still only \(s = (s_1,\dots , s_{{\ell _{\mathsf {s}}}}) \in \{0,1\}^{{\ell _{\mathsf {s}}}}\). When encrypting a message m, we first generate \(\widetilde{\mathsf {Q}}\) and \((\mathsf {ct}_{j,0},\mathsf {ct}_{j,1})_{j\in [{\ell _{\mathsf {s}}}]}\) in the same way as \(\mathsf {PKE}_{\mathsf {kdm}}^*\). Then, using \(\mathsf {pk}_{\mathsf {dv}}\), we generate a proof \(\pi \) of \(\mathsf {DVNIZK}\) proving that \(\mathsf {ct}_{j,0}\) and \(\mathsf {ct}_{j,1}\) encrypt the same message for every \(j\in [{\ell _{\mathsf {s}}}]\), by using \(\mathsf {lab}_{j,0}\) and random coins used to generate \(\mathsf {ct}_{j,0}\) and \(\mathsf {ct}_{j,1}\) as a witness.
Next, in order to make the entire part of the ciphertext non-malleable, we require that \(\mathsf {PKE}'\) satisfy IND-CCA security instead of IND-CPA security, and encrypt \(\widetilde{\mathsf {Q}}\), the encrypted labels \((\mathsf {ct}_{j,0},\mathsf {ct}_{j,1})_{j\in [{\ell _{\mathsf {s}}}]}\), and the proof \(\pi \), using \(\mathsf {pk}'\) of \(\mathsf {PKE}'\). Therefore, the resulting ciphertext \(\mathsf {CT}\) is of the form
We perform the decryption of this ciphertext in the same way as before, except that we additionally check whether \(\pi \) is accepted or not by using \(\mathsf {sk}_{\mathsf {dv}}\) retrieved from \(\mathsf {ct}_{\mathsf {ske}}\), and if it is not accepted, the ciphertext is rejected.
As mentioned earlier (and will be detailed in Sect. 4), by combining the techniques from the two recent results [30, 34], a DV-NIZK argument system can be based on the same building blocks. Moreover, an IND-CCA secure PKE scheme can also be based on the same building blocks [30]. Thus, similarly to \(\mathsf {PKE}_{\mathsf {kdm}}^*\), all the building blocks of \(\mathsf {PKE}_{\mathsf {kdm}}\) can be based on the combination of an IND-CPA secure PKE scheme and a one-time KDM secure SKE scheme, which are in turn both implied by a KDM-CPA secure PKE scheme.
Overview of the Security Proof of \(\mathsf {PKE}_{\mathsf {kdm}}\). At first glance, the circularity involving \(\mathsf {DVNIZK}\) occurs when encrypting a key-dependent message \(f(\mathsf {SK})=f(s)=\mathsf {sk}_{\mathsf {dv}}\) by \(\mathsf {PKE}_{\mathsf {kdm}}\), where f is a function that, given s as input, retrieves \(\mathsf {sk}_{\mathsf {dv}}\) from \(\mathsf {ct}_{\mathsf {ske}}\) by using s and outputs \(\mathsf {sk}_{\mathsf {dv}}\). This is because \(\mathsf {DVNIZK}\) is used to generate a proof that proves \(\mathsf {ct}_{j,0}\) and \(\mathsf {ct}_{j,1}\) encrypt the same label, and the labels may contain some information of the key-dependent message f(s) since it is generated by garbling a constant circuit \(\mathsf {Q}\) into which f(s) is hardwired. However, due to the indirection that \(\mathsf {sk}_{\mathsf {dv}}\) is not encrypted by encryption schemes the validity of whose ciphertexts is proved by the DV-NIZK argument system, we can solve the circularity and prove the KDM-CCA security of \(\mathsf {PKE}_{\mathsf {kdm}}\) by adding some modifications to the proof for the KDM-CPA security of \(\mathsf {PKE}_{\mathsf {kdm}}^*\) explained in the previous section.
First of all, the zero-knowledge property of \(\mathsf {DVNIZK}\) allows us to change the security game so that we use the simulator for the zero-knowledge property to generate the DV-NIZK key pair \((\mathsf {pk}_{\mathsf {dv}}, \mathsf {sk}_{\mathsf {dv}})\) at the key generation, and we use the simulator also for generating a fake proof \(\pi \) in a ciphertext when responding to KDM-encryption queries. Then, similarly to what we do in the proof for \(\mathsf {PKE}_{\mathsf {kdm}}^*\), we can change the security game so that we do not need s for responding to KDM-encryption queries by using the security of the garbling scheme and the IND-CPA security of \(\mathsf {PKE}\) under public keys \((\mathsf {pk}_{j,1 \oplus s_j})_{j\in [{\ell _{\mathsf {s}}}]}\). However, differently from the proof for the KDM-CPA security of \(\mathsf {PKE}_{\mathsf {kdm}}^*\), we cannot use the one-time KDM security of \(\mathsf {SKE}\) immediately after this change. This is because we still need s for responding to decryption queries. More specifically, when responding to a decryption query, we have to decrypt the “\(s_j\)-side” ciphertext \(\mathsf {ct}_{j,s_j}\) of \(\mathsf {PKE}\) using \(\mathsf {sk}_{j,s_j}\) for every \(j\in [{\ell _{\mathsf {s}}}]\) to recover the labels of a garbled circuit.Footnote 6 Thus, before using the one-time KDM security of \(\mathsf {SKE}\), we change the security game so that we do not need s to respond to decryption queries by relying on the soundness of \(\mathsf {DVNIZK}\).
Concretely, we change the security game so that when responding to a decryption query \(\mathsf {CT}\), we always decrypt the “0-side” ciphertext \(\mathsf {ct}_{j,0}\) of \(\mathsf {PKE}\) using \(\mathsf {sk}_{j,0}\) for every \(j\in [{\ell _{\mathsf {s}}}]\). Although we cannot justify this change based solely on the soundness of \(\mathsf {DVNIZK}\), we can justify it by combining the soundness and zero-knowledge property of \(\mathsf {DVNIZK}\), the one-time KDM security of \(\mathsf {SKE}\), and the IND-CCA security of \(\mathsf {PKE}'\) using a deferred analysis technique. This technique of justifying changes for decryption queries using the deferred analysis originates in the context of expanding the message space of IND-CCA secure PKE schemes [28], and was already shown to be useful in the context of KDM-CCA security [29, 31]. In fact, the indirection explained so far makes it possible to use the deferred analysis technique.
Once we change how decryption queries are answered in this way, we can complete the remaining part of the proof based on the one-time KDM security of \(\mathsf {SKE}\) and the IND-CCA security of \(\mathsf {PKE}'\) similarly to the proof for the KDM-CPA security of \(\mathsf {PKE}_{\mathsf {kdm}}^*\).
Is It Essential to Encrypt \(\mathsf {sk}_{\mathsf {dv}}\) into \(\mathsf {ct}_{\mathsf {ske}}\)? It is not essential to maintain \(\mathsf {sk}_{\mathsf {dv}}\) (and \(\mathsf {sk}'\)) in the encrypted form \(\mathsf {ct}_{\mathsf {ske}}\) by the key s and make \(\mathsf {SK}\) consist only of s. In fact, we can consider a variant of \(\mathsf {PKE}_{\mathsf {kdm}}\) such that we set \(\mathsf {SK}:=(s,\mathsf {sk}_{\mathsf {dv}},\mathsf {sk}')\). In this case, we use \(2\cdot {\ell _{\mathsf {\mathsf {SK}}}}=2\cdot (\left| s\right| +\left| \mathsf {sk}_{\mathsf {dv}}\right| +\left| \mathsf {sk}'\right| )\) key pairs of \(\mathsf {PKE}\), and we generate \(\mathsf {ct}_{\mathsf {ske}}\) as an encryption of \((\mathsf {sk}_{j,\mathsf {SK}_j})_{j\in [{\ell _{\mathsf {\mathsf {SK}}}}]}\) by s, where \(\mathsf {SK}_j\) is the j-th bit of \(\mathsf {SK}\) for every \(j\in [{\ell _{\mathsf {\mathsf {SK}}}}]\). Even if we adopt such a construction, we can realize an indirection that is sufficient to use the deferred analysis technique, and we can prove its KDM-CCA security similarly to the above.
The security proof for \(\mathsf {PKE}_{\mathsf {kdm}}\) is simpler than that for the above variant. Moreover, as we will explain below, we need to encrypt \(\mathsf {sk}_{\mathsf {dv}}\) and \(\mathsf {sk}'\) and make \(\mathsf {SK}=s\) when considering KDM-CCA security in the multi-user setting. For these reasons, we adopt the current construction of \(\mathsf {PKE}_{\mathsf {kdm}}\).
2.5 Extension to KDM-CCA Security in the Multi-user Setting
We finally explain how to extend the above construction \(\mathsf {PKE}_{\mathsf {kdm}}\) into a scheme that is KDM-CCA secure in the multi-user setting. In fact, we need not change the construction at all. The only difference is that we require a weak variant of RKA-KDM security [4] for the underlying SKE scheme \(\mathsf {SKE}\), instead of one-time KDM security. We also require a mild property that a secret key is uniformly distributed over the secret key space \(\{0,1\}^{{\ell _{\mathsf {s}}}}\).
Informally, an SKE scheme is said to be RKA-KDM secure if no adversary can guess the challenge bit b with probability significantly greater than 1/2 given an encryption of \(f_b(s)\) under the key \(s\oplus \varDelta \in \{0,1\}^{{\ell _{\mathsf {s}}}}\) when it queries two functions \((f_0,f_1)\) and a key shift \(\varDelta \in \{0,1\}^{{\ell _{\mathsf {s}}}}\) as an RKA-KDM-encryption query. For our purpose, we need a much weaker form of RKA-KDM security where all key shifts are not chosen by an adversary, but generated uniformly at random in advance by the challenger. We call our RKA-KDM security passive RKA-KDM security. For its formal definition, see Definition 3 in Sect. 3.
In the security proof of the KDM-CCA security in the multi-user setting of \(\mathsf {PKE}_{\mathsf {kdm}}\), there exist n key pairs of \(\mathsf {PKE}_{\mathsf {kdm}}\) for some polynomial n of the security parameter. As the first step of the proof, we change the security game so that n secret keys \(s^1,\dots ,s^n\) of \(\mathsf {PKE}_{\mathsf {kdm}}\) are generated by first generating a single source key s and n key shifts \((\varDelta ^i)_{i\in [n]}\) and then setting \(s^i:=s\oplus \varDelta ^i\) for every \(i\in [n]\). This does not at all change the distribution of the keys due to the requirement on \(\mathsf {SKE}\) that a secret key is distributed uniformly in the secret key space \(\{0,1\}^{{\ell _{\mathsf {s}}}}\). We next change the security game so that for every \({i^*}\in [n]\), an encryption of \(f_b(s^1 \Vert \dots \Vert s^n)\) under the \({i^*}\)-th key can be simulated from \(f_b\) and n key shifts \((\varDelta ^i)_{i\in [n]}\) and not the source key s, where \(({i^*},f_0,f_1)\) is a KDM-encryption query made by an adversary. This is possible by garbling a circuit into which \(f_b\), \({i^*}\), and \((\varDelta ^i)_{i\in [n]}\) are hardwired,Footnote 7 while we just directly garble \(f_b\) in the proof for the single user security. Then, we can complete the rest of the security proof in the same way as the proof of the single user security except that we use the (passive) RKA-KDM security instead of one-time KDM security.
Differently from the single user case, it is critical that \(\mathsf {sk}_{\mathsf {dv}}\) and \(\mathsf {sk}'\) are encrypted into \(\mathsf {ct}_{\mathsf {ske}}\), and \(\mathsf {SK}\) consists only of s. If \(\mathsf {SK}\) is of the form \((s,\mathsf {sk}_{\mathsf {dv}},\mathsf {sk}')\), it is not clear how we control the multiple secret keys even if \(\mathsf {SKE}\) is RKA-KDM secure.
KDM-CCA Secure PKE from New Assumptions. An SKE scheme satisfying our definition of RKA-KDM security can be constructed based on the LPN assumption [4]. Moreover, we show how to construct an SKE scheme satisfying our RKA-KDM security definition based on hash encryption [13, 22] which in turn can be based on the CDH assumption. The construction is an extension of that of a KDM-CPA secure PKE scheme based on batch encryption proposed by Brakerski et al. [13]. For the details of the construction and its security proof, see the full version.
In addition to RKA-KDM secure SKE schemes, all other building blocks of our construction can be obtained based on the LPN and CDH assumptions via KDM-CPA secure PKE schemes. Through our generic construction, we obtain the first PKE schemes that are KDM-CCA secure in the multi-user setting based on the LPN and CDH assumptions. Previously to our work, KDM-CCA secure PKE schemes even in the single user setting based on these assumptions were not known.
2.6 On the Connections with the Techniques by Barak et al. [6]
The idea of garbling a constant circuit used in this overview was previously used by Barak et al. [6] in which they constructed a PKE scheme that is KDM-CPA secure with respect to functions computable by circuits of a-priori bounded size (i.e. bounded-KDM-CPA security). They used the technique of garbling a constant circuit together with a primitive that they call targeted encryption, which is a special form of PKE and whose syntactical and security requirements have some similarities with hash encryption [22]. In fact, the KDM-CPA variant of our construction \(\mathsf {PKE}_{\mathsf {kdm}}^*\) explained in Sect. 2.3 can be described by using the abstraction of targeted encryption in which the targeted encryption scheme is constructed from an IND-CPA secure PKE scheme and a one-time KDM secure SKE scheme.Footnote 8
We note that although we can use the abstraction of targeted encryption for the KDM-CPA variant of our construction, it seems difficult to use it for our main construction of a KDM-CCA secure PKE scheme. The problem is that if we use the abstraction of targeted encryption, we have to prove the well-formedness of ciphertexts of the targeted encryption scheme by using the DV-NIZK argument system. As explained in Sect. 2.5, in the security proof of our KDM-CCA secure PKE scheme, we have to change the security game so that when responding to a decryption query, we recover all labels from “0-side” ciphertexts \((\mathsf {ct}_{j,0})_{j \in [\ell _s]}\) of the underlying IND-CPA secure PKE scheme (instead of “\(s_i\)-side” ciphertexts \((\mathsf {ct}_{j, s_i})_{j \in [\ell _s]}\)). This key-switching step is not compatible with the syntax of targeted encryption, and it seems difficult to use a targeted encryption scheme in a black-box way.
3 Preliminaries
In this section, we review basic notation and the definitions of cryptographic primitives used in the paper.
3.1 Notations
\(\mathbb {N}\) denotes the set of natural numbers, and for \(n \in \mathbb {N}\), we define \([n]:=\{1, \ldots , n\}\). For a discrete finite set S, |S| denotes its size, and \(x \xleftarrow {\mathsf {r}}S\) denotes choosing an element x uniformly at random from S. For strings x and y, \(x \Vert y\) denotes their concatenation. For a (probabilistic) algorithm or a function \(\mathsf {A}\), \(y \leftarrow \mathsf {A}(x)\) denotes assigning to y the output of \(\mathsf {A}\) on input x, and if we need to specify a randomness r used in \(\mathsf {A}\), we denote \(y \leftarrow \mathsf {A}(x;r)\) (in which case the computation of \(\mathsf {A}\) is understood as deterministic on input x and r). \(\lambda \) always denotes a security parameter. PPT stands for probabilistic polynomial time. A function \(f(\lambda )\) is said to be negligible if \(f(\lambda )\) tends to 0 faster than \(\lambda ^{-c}\) for every constant \(c>0\). We write \(f(\lambda ) = \mathsf{negl}(\lambda )\) to mean that \(f(\lambda )\) is a negligible function.
3.2 Public-Key Encryption
A public-key encryption (PKE) scheme \(\mathsf {PKE}\) is a three tuple \((\mathsf {KG}, \mathsf {Enc}, \mathsf {Dec})\) of PPT algorithms. The key generation algorithm \(\mathsf {KG}\), given a security parameter \(1^\lambda \) as input, outputs a public key \(\mathsf {pk}\) and a secret key \(\mathsf {sk}\). The encryption algorithm \(\mathsf {Enc}\), given a public key \(\mathsf {pk}\) and a message m as input, outputs a ciphertext \(\mathsf {ct}\). The (deterministic) decryption algorithm \(\mathsf {Dec}\), given a public key \(\mathsf {pk}\), a secret key \(\mathsf {sk}\), and a ciphertext \(\mathsf {ct}\) as input, outputs a message m (which could be the special symbol \(\bot \) indicating that \(\mathsf {ct}\) is invalid). As correctness, we require \(\mathsf {Dec}(\mathsf {sk}, \mathsf {Enc}(\mathsf {pk}, m)) = m\) for all \(\lambda \in \mathbb {N}\), all \((\mathsf {pk}, \mathsf {sk})\leftarrow \mathsf {KG}(1^\lambda )\), and all m.
Security Notions for PKE. Next, we review the definitions of key-dependent message security against chosen plaintext attacks/chosen ciphertext attacks (KDM-CPA/CCA security). Note that IND-CPA/CCA security are covered as their special cases.
Definition 1
(KDM-CCA/KDM-CPA Security). Let \(\mathsf {PKE}\) be a PKE scheme whose secret key and message spaces are \(\mathcal {SK}\) and \(\mathcal {M}\), respectively. Let \({n} \in \mathbb {N}\), and let \(\mathcal {F}\) be a function family with domain \(\mathcal {SK}^{{n}}\) and range \(\mathcal {M}\). Consider the following \({\mathcal {F}}\text {-}\mathrm{{KDM}}^{({n})}\text {-}\mathrm{{CCA}}\) game between a challenger and an adversary \(\mathcal {A}\).
-
1.
First, the challenger chooses a challenge bit \(b \xleftarrow {\mathsf {r}}\{0,1\}\). Next, the challenger generates \({n}\) key pairs \(\left( \mathsf {pk}^i,\mathsf {sk}^i\right) \leftarrow \mathsf {KG}(1^{\lambda })\left( i\in [{n}]\right) \). Then, the challenger sets \(\mathbf {sk}:=\left( \mathsf {sk}^1, \ldots , \mathsf {sk}^{n}\right) \) and sends \(\left( \mathsf {pk}^1, \ldots , \mathsf {pk}^{n}\right) \) to \(\mathcal {A}\). Finally, the challenger prepares an empty list \(L_\mathsf {kdm}\).
-
2.
\(\mathcal {A}\) may adaptively make the following queries.
-
KDM-encryption queries: \(\mathcal {A}\) sends \((j, f_0,f_1)\in [{n}] \times \mathcal {F}^2\) to the challenger. The challenger returns \(\mathsf {ct}\leftarrow \mathsf {Enc}(\mathsf {pk}^j, f_b(\mathbf {sk}))\) to \(\mathcal {A}\). Finally, the challenger adds \((j, \mathsf {ct})\) to \(L_\mathsf {kdm}\).
-
Decryption queries: \(\mathcal {A}\) sends \((j, \mathsf {ct})\) to the challenger. If \((j, \mathsf {ct})\in L_\mathsf {kdm}\), then the challenger returns \(\bot \) to \(\mathcal {A}\). Otherwise, the challenger returns \(m\leftarrow \mathsf {Dec}(\mathsf {pk}^j,\mathsf {sk}^j,\mathsf {ct})\) to \(\mathcal {A}\).
-
-
3.
\(\mathcal {A}\) outputs \(b' \in \{0,1\}\).
We say that \(\mathsf {PKE}\) is \({\mathcal {F}}\text {-}\mathrm{{KDM}}^{({n})}\text {-}\mathrm{{CCA}}\) secure if for all PPT adversaries \(\mathcal {A}\), we have \(\mathsf {Adv}_{\mathsf {PKE}, \mathcal {F},\mathcal {A},{n}}^{\mathsf {kdmcpa}}(\lambda ) := 2 \cdot \left| \Pr [b=b'] - 1/2\right| = \mathsf{negl}(\lambda )\).
\({\mathcal {F}}\text {-}\mathrm{{KDM}}^{({n})}\text {-}\mathrm{{CPA}}\) security is defined similarly, using the \({\mathcal {F}}\text {-}\mathrm{{KDM}}^{(n)}\text {-}\mathrm{{CPA}}\) game where an adversary \(\mathcal {A}\) is not allowed to make decryption queries.
The above definition is slightly different from the standard definition where an adversary is required to distinguish encryptions of \(f(\mathsf {sk}^1,\dots ,\mathsf {sk}^n)\) from encryptions of some fixed message. However, the two definitions are equivalent if the function class \(\mathcal {F}\) contains a constant function, which is the case for the function families used in this paper (see below). This formalization is easier to work with for security proofs.
Function Families. In this paper, we will deal with the following function families for KDM security of PKE:
-
\(\mathcal {P}\) (Projection functions): A function is said to be a projection function if each of its output bits depends on at most a single bit of its input. We denote by \(\mathcal {P}\) the family of projection functions.
-
\(\mathcal {B}_{\mathsf {size}}\) (Circuits of a-priori bounded size \(\mathsf {size}\)): We denote by \(\mathcal {B}_{\mathsf {size}}\), where \(\mathsf {size}= \mathsf {size}(\lambda )\) is a polynomial, the function family such that each member in \(\mathcal {B}_{\mathsf {size}}\) can be described by a circuit of size \(\mathsf {size}\).
-
\(\mathcal {C}\) (Constant functions): We denote by \(\mathcal {C}\) the set of all constant functions. Note that \({\mathcal {C}}\text {-}\mathrm{{KDM}}\text {-}\mathrm{{CCA}}\) (resp.
 ) security is equivalent to IND-CCA (resp. IND-CPA) security.
) security is equivalent to IND-CCA (resp. IND-CPA) security.
3.3 Secret-Key Encryption
A secret-key encryption (SKE) scheme \(\mathsf {SKE}\) is a three tuple \((\mathsf {K}, \mathsf {E}, \mathsf {D})\) of PPT algorithms. The key generation algorithm \(\mathsf {K}\), given a security parameter \(1^\lambda \) as input, outputs a key s. The encryption algorithm \(\mathsf {E}\), given a key s and a message m as input, outputs a ciphertext \(\mathsf {ct}\). The (deterministic) decryption algorithm \(\mathsf {D}\), given a key s and a ciphertext \(\mathsf {ct}\) as input, outputs a message m (which could be the special symbol \(\bot \) indicating that \(\mathsf {ct}\) is invalid). As correctness, we require \(\mathsf {D}(s, \mathsf {E}(s, m)) = m\) for all \(\lambda \in \mathbb {N}\), all keys s output by \(\mathsf {K}(1^\lambda )\), and all m.
Security Notions for SKE. In this paper, we will deal with two types of security notions for SKE: one-time KDM security and passive RKA-KDM security. We review the definitions below.
One-time KDM security is a weak form of KDM-CPA security in which an adversary is allowed to make only a single KDM-encryption query.
Definition 2 (One-Time KDM Security)
Let \(\mathsf {SKE}= (\mathsf {K}, \mathsf {E}, \mathsf {D})\) be an SKE scheme whose key and message spaces are \(\mathcal {K}\) and \(\mathcal {M}\), respectively. Let \(\mathcal {F}\) be a function family with domain \(\mathcal {K}\) and range \(\mathcal {M}\). Consider the following one-time \(\mathcal {F}\)-KDM game between a challenger and an adversary \(\mathcal {A}\).
-
1.
First, the challenger chooses a challenge bit \(b \xleftarrow {\mathsf {r}}\{0,1\}\). Next, the challenger generates a secret key \(s \leftarrow \mathsf {K}(1^\lambda )\) and sends \(1^\lambda \) to \(\mathcal {A}\).
-
2.
\(\mathcal {A}\) sends a function \(f\in \mathcal {F}\) as a single KDM-encryption query to the challenger. If \(b=1\), the challenger returns \(\mathsf {ct}\leftarrow \mathsf {E}(s,f(s))\) to \(\mathcal {A}\); Otherwise, the challenger returns \(\mathsf {ct}\leftarrow \mathsf {E}(s,0^{|f(\cdot )|})\) to \(\mathcal {A}\). (Note that this step is done only once.)
-
3.
\(\mathcal {A}\) outputs \(b' \in \{0,1\}\).
We say that \(\mathsf {SKE}\) is one-time \(\mathcal {F}\)-KDM secure if for all PPT adversaries \(\mathcal {A}\), we have \(\mathsf {Adv}_{\mathsf {SKE}, \mathcal {F},\mathcal {A}}^{\mathsf {otkdm}}(\lambda ) := 2 \cdot \left| \Pr [b=b']-1/2\right| = \mathsf{negl}(\lambda )\).
Remark 1 (On the Message Space of One-Time KDM Secure SKE)
Unlike ordinary IND-CPA secure encryption schemes, extending the message space of KDM secure encryption schemes is in general not easy. Fortunately, however, things are easy for \(\mathcal {P}\)-KDM security. We can extend the message space of a one-time \(\mathcal {P}\)-KDM secure SKE scheme as much as we want, if the size of the message space of the SKE scheme is already sufficiently large. Specifically, we can show that if there exists a one-time \(\mathcal {P}\)-KDM secure SKE scheme whose secret key and message spaces are \(\{0,1\}^{\ell _{\mathsf {}}}\) and \(\{0,1\}^\mu \), respectively, for some polynomials \({\ell _{\mathsf {}}}= {\ell _{\mathsf {}}}(\lambda )\) and \(\mu = \mu (\lambda )\) satisfying \(\mu = \varOmega (\ell \cdot \lambda )\), then for any polynomial \(\mu ' = \mu '(\lambda )\), there also exists a one-time \(\mathcal {P}\)-KDM secure SKE scheme that can encrypt messages of length \(\mu '\).
To see this, we observe that the KDM-CPA secure construction \(\mathsf {PKE}_{\mathsf {kdm}}^*\) that we described in Sect. 2.3, works also in the secret-key setting. Namely, if we replace the building block IND-CPA secure PKE schemes with IND-CPA secure SKE schemes, then the resulting SKE schemeFootnote 9 is (multi-time) \(\mathcal {B}_{\mathsf {size}}\)-KDM secure where \(\mathsf {size}=\mathsf {size}(\lambda )\) is some polynomial that depends on the size of a constant circuit (in which a message is hardwired). In fact, we can make the message space of this construction arbitrarily large since by setting \(\mathsf {size}\) appropriately, we can hardwire a message of arbitrary length into a circuit to be garbled without compromising the security. Moreover, we only need to assume that the underlying one-time \(\mathcal {P}\)-KDM secure SKE scheme can encrypt messages of length \(\mu = \varOmega ({\ell _{\mathsf {}}}\cdot \lambda )\) since it is only required to encrypt \({\ell _{\mathsf {}}}+ 1\) secret keys of IND-CPA secure SKE schemes, each of which can be assumed to be \(\lambda \)-bit without loss of generality. This means that, using this construction, we can extend the message space of a one-time \(\mathcal {P}\)-KDM secure SKE scheme as much as we want if the scheme can already encrypt a message of length \(\mu = \varOmega ({\ell _{\mathsf {}}}\cdot \lambda )\).
Next, we give a formalization of passive RKA-KDM security, which is a weaker variant of RKA-KDM security formalized by Applebaum [4]. Recall that the original RKA-KDM security of [4] is a slightly stronger form of standard KDM-CPA security (albeit in the presence of a single challenge key) where we consider an adversary that is allowed to ask encryptions of key-dependent messages, encrypted under “related” keys. In this paper, we only consider “XOR by a constant” as related-key deriving functions, and hence give a definition specialized to this setting. On the other hand, however, we only need a weaker “passive” variant of RKA-KDM security where the security game is changed as follows: (1) not the adversary but the challenger randomly chooses the related-key deriving functions (i.e. constants for XORing in our setting), and (2) an adversary has to make its RKA-KDM-encryption queries in one shot.
Definition 3 (Passive RKA-KDM Security)
Let \(\mathsf {SKE}\) be an SKE scheme whose key space is \(\{0,1\}^\ell \) for some polynomial \(\ell = \ell (\lambda )\) and whose message space is \(\mathcal {M}\). Let \(\mathcal {F}\) be a function family with domain \(\{0,1\}^{\ell }\) and range \(\mathcal {M}\). Let \(n \in \mathbb {N}\) be an a-priori bounded polynomial. Consider the following passive \(\mathcal {F}\text {-RKA-KDM}^{(n)}\) game between a challenger and an adversary \(\mathcal {A}\).
-
1.
First, the challenger chooses a challenge bit \(b \xleftarrow {\mathsf {r}}\{0,1\}\) and generates \(s \leftarrow \mathsf {K}(\lambda )\) and \(\varDelta ^i \xleftarrow {\mathsf {r}}\{0,1\}^\ell \) for every \(i \in [n]\). Then, the challenger sends \((\varDelta ^i)_{i \in [n]}\) to \(\mathcal {A}\).
-
2.
\(\mathcal {A}\) sends n functions \(f^1,\ldots ,f^n\in \mathcal {F}\) to the challenger. If \(b=1\), the challenger computes \(\mathsf {ct}^i \leftarrow \mathsf {E}(s \oplus \varDelta ^i, f^i(s))\) for every \(i\in [n]\). Otherwise, the challenger computes \(\mathsf {ct}^i \leftarrow \mathsf {E}(s \oplus \varDelta ^i, 0^{\left| f^i(\cdot )\right| })\) for every \(i\in [n]\). Finally, the challenger sends \(\left( \mathsf {ct}^i\right) _{i \in [n]}\) to \(\mathcal {A}\).
-
3.
\(\mathcal {A}\) outputs \(b' \in \{0,1\}\).
We say that \(\mathsf {SKE}\) is passively \(\mathcal {F}\text {-RKA-KDM}^{(n)}\) secure, if for all PPT adversaries \(\mathcal {A}\), we have \(\mathsf {Adv}_{\mathsf {SKE},\mathcal {F},\mathcal {A},n}^{\mathsf {prkakdm}}(\lambda ) := 2 \cdot \left| \Pr [b=b']-1/2\right| =\mathsf{negl}(\lambda )\).
3.4 Designated-Verifier Non-interactive Zero-Knowledge Arguments
Here, we review the definitions for (reusable) designated-verifier non-interactive zero-knowledge (DV-NIZK) argument systems.
Let L be an NP language associated with the corresponding NP relation R. A DV-NIZK argument system \(\mathsf {DVNIZK}\) for L is a three tuple \((\mathsf {DVKG}, \mathsf {P}, \mathsf {V})\) of PPT algorithms. \(\mathsf {DVKG}\) is the key generation algorithm that takes a security parameter \(1^\lambda \) as input, and outputs a public proving key \(\mathsf {pk}\) and a secret verification key \(\mathsf {sk}\). \(\mathsf {P}\) is the proving algorithm that takes a public proving key \(\mathsf {pk}\), a statement x, and a witness w as input, and outputs a proof \(\pi \). \(\mathsf {V}\) is the (deterministic) verification algorithm that takes a secret verification key \(\mathsf {sk}\), a statement x, and a proof \(\pi \) as input, outputs either \(\mathsf {accept}\) or \(\mathsf {reject}\).
We require that \(\mathsf {DVNIZK}\) satisfy the three requirements: Correctness, (adaptive) soundness, and zero-knowledge. In particular, we consider a version of soundness which holds against adversaries that make multiple verification queries, and a version of zero-knowledge which holds against adversaries that make multiple challenge proving queries. A DV-NIZK argument system that satisfies these versions of soundness and zero-knowledge is called reusable.
Formally, these requirements are defined as follows.
-
Correctness. We say that \(\mathsf {DVNIZK}\) is correct if we have \(\mathsf {V}(\mathsf {sk}, x, \mathsf {P}(\mathsf {pk}, x,w)) = \mathsf {accept}\) for all \(\lambda \in \mathbb {N}\), all key pairs \((\mathsf {pk}, \mathsf {sk})\) output by \(\mathsf {DVKG}(1^\lambda )\), and all valid statement/witness pairs \((x,w) \in R\).
-
Soundness. Consider the following soundness game between a challenger and an adversary \(\mathcal {A}\).
-
1.
First, the challenger generates \((\mathsf {pk},\mathsf {sk}) \leftarrow \mathsf {DVKG}(1^\lambda )\) and sends \(\mathsf {pk}\) to \(\mathcal {A}\).
-
2.
\(\mathcal {A}\) may adaptively make verification queries. When \(\mathcal {A}\) makes a verification query \((x, \pi )\), the challenger responds with \(\mathsf {V}(\mathsf {sk}, x, \pi )\).
-
3.
\(\mathcal {A}\) outputs \(({x^*},{\pi ^*})\).
We say that \(\mathsf {DVNIZK}\) is sound if for all PPT adversaries \(\mathcal {A}\), we have
$$ \mathsf {Adv}_{\mathsf {DVNIZK}, \mathcal {A}}^{\mathsf {sound}}(\lambda ) := \Pr [{x^*}\notin L \wedge \mathsf {V}(\mathsf {sk},{x^*},{\pi ^*})=\mathsf {accept}] = \mathsf{negl}(\lambda ). $$ -
1.
-
Zero-Knowledge. Let \(\mathsf {S}= (\mathsf {S}_1, \mathsf {S}_2)\) be a pair of PPT “simulator” algorithms whose syntax is as follows.
-
\(\mathsf {S}_1\) takes a security parameter \(1^\lambda \) as input, and outputs a fake public key \(\mathsf {pk}\), a fake secret key \(\mathsf {sk}\), and a trapdoor \(\mathsf {td}\).
-
\(\mathsf {S}_2\) takes a trapdoor \(\mathsf {td}\) and a statement x as input, and outputs a fake proof \(\pi \).
Consider the following zero-knowledge game between a challenger and an adversary \(\mathcal {A}\).
-
1.
First, the challenger chooses the challenge bit \(b\xleftarrow {\mathsf {r}}\{0,1\}\). If \(b=1\), then the challenger generates \((\mathsf {pk},\mathsf {sk})\leftarrow \mathsf {DVKG}(1^\lambda )\); Otherwise the challenger generates \((\mathsf {pk},\mathsf {sk},\mathsf {td})\leftarrow \mathsf {S}_1(1^\lambda )\). Then, the challenger sends \((\mathsf {pk},\mathsf {sk})\) to \(\mathcal {A}\).
-
2.
\(\mathcal {A}\) may adaptively make proving queries. When \(\mathcal {A}\) submits a proving query (x, w), if \((x, w) \notin R\), then the challenger returns \(\bot \) to \(\mathcal {A}\). Then, if \(b=1\), the challenger computes \(\pi \leftarrow \mathsf {P}(\mathsf {pk}, x, w)\); Otherwise, the challenger computes \(\pi \leftarrow \mathsf {S}_2(\mathsf {td}, x)\). Finally, the challenger returns \(\pi \) to \(\mathcal {A}\).
-
3.
\(\mathcal {A}\) outputs \(b'\in \{0,1\}\).
We say that \(\mathsf {DVNIZK}\) is zero-knowledge if there exists a PPT simulator \(\mathsf {S}= (\mathsf {S}_1, \mathsf {S}_2)\) such that for all PPT adversaries \(\mathcal {A}\), we have \(\mathsf {Adv}_{\mathsf {DVNIZK}, \mathcal {A},\mathsf {S}}^{\mathsf {zk}}(\lambda ) := 2 \cdot \left| \Pr [b=b'] - 1/2\right| = \mathsf{negl}(\lambda )\).
-
3.5 Garbled Circuits
Here, we recall the definitions of a garbling scheme in the form we use in this paper. We can realize a garbling scheme for all efficiently computable circuits based on one-way functions [40].
Let \(\{\mathcal {C}_n\}_{n \in \mathbb {N}}\) be a family of circuits where the input-length of each circuit in \(\mathcal {C}_n\) is n. A garbling scheme \(\mathsf{GC}\) is a three tuple \((\mathsf {Garble}, \mathsf {Eval},\mathsf {Sim})\) of PPT algorithms. \(\mathsf {Garble}\) is the garbling algorithm that takes as input a security parameter \(1^\lambda \) and a circuit \(C \in \mathcal {C}_n\), where \(n = n(\lambda )\) is a polynomial. Then, it outputs a garbled circuit \(\widetilde{C}\) and 2n labels \((\mathsf {lab}_{j,\alpha })_{j \in [n],\alpha \in \{0,1\}}\). For simplicity and without loss of generality, we assume that the length of each \(\mathsf {lab}_{j,\alpha }\) is \(\lambda \). \(\mathsf {Eval}\) is the evaluation algorithm that takes a garbled circuit \(\widetilde{C}\) and n labels \((\mathsf {lab}_j)_{j \in [n]}\) as input, and outputs an evaluation result y. \(\mathsf {Sim}\) is the simulator algorithm that takes a security parameter \(1^\lambda \), the size parameter \(\mathsf {size}\) (where \(\mathsf {size}= \mathsf {size}(\lambda )\) is a polynomial), and a string y as input, and outputs a simulated garbled circuit \(\widetilde{C}\) and n simulated labels \((\mathsf {lab}_j)_{j \in [n]}\).
For a garbling scheme, we require the following correctness and security properties.
-
Correctness. For all \(\lambda , n \in \mathbb {N}\), all \(x = (x_1,\dots ,x_n) \in \{0,1\}^n\), and all \(C \in \mathcal {C}_n\), we require that the following two equalities hold.Footnote 10
-
\(\mathsf {Eval}(\widetilde{C}, (\mathsf {lab}_{j,x_j})_{j \in [n]}) = C(x)\) for all \((\widetilde{C}, (\mathsf {lab}_{j,\alpha })_{j \in [n],\alpha \in \{0,1\}})\) output by \(\mathsf {Garble}(1^\lambda , C)\).
-
\(\mathsf {Eval}(\widetilde{C}, (\mathsf {lab}_{j})_{j \in [n]}) = C(x)\) for all \((\widetilde{C}, (\mathsf {lab}_{j})_{j \in [n]})\) output by \(\mathsf {Sim}(1^\lambda , |C|, C(x))\).
-
-
Security. Consider the following security game between a challenger and an adversary \(\mathcal {A}\).
-
1.
First, the challenger chooses a bit \(b \xleftarrow {\mathsf {r}}\{0,1\}\) and sends a security parameter \(1^\lambda \) to \(\mathcal {A}\).
-
2.
\(\mathcal {A}\) sends a circuit \(C \in \mathcal {C}_n\) and an input \(x = (x_1,\dots ,x_n) \in \{0,1\}^n\) to the challenger. Then, if \(b=1\), the challenger executes \((\widetilde{C}, (\mathsf {lab}_{j,\alpha })_{j \in [n],\alpha \in \{0,1\}}) \leftarrow \mathsf {Garble}(1^\lambda , C)\) and returns \((\widetilde{C}, (\mathsf {lab}_{j,x_j})_{j \in [n]})\) to \(\mathcal {A}\); Otherwise, the challenger returns \((\widetilde{C}, (\mathsf {lab}_j)_{j \in [n]}) \leftarrow \mathsf {Sim}(1^\lambda , \left| C\right| , C(x))\) to \(\mathcal {A}\).
-
3.
\(\mathcal {A}\) outputs \(b' \in \{0,1\}\).
We say that \(\mathsf{GC}\) is secure if for all PPT adversaries \(\mathcal {A}\), we have \(\mathsf {Adv}_{\mathsf{GC}, \mathcal {A}, \mathsf {Sim}}^{\mathsf {gc}}(\lambda ) := 2 \cdot \left| \Pr [b=b']-1/2\right| = \mathsf{negl}(\lambda )\).
-
1.
4 DV-NIZK via KDM Security
In this section, we explain how to construct a reusable DV-NIZK argument system from the combination of an IND-CPA secure PKE scheme and a one-time \(\mathcal {P}\)-KDM secure SKE scheme. Specifically, we explain how the following statement can be derived.
Theorem 2
Assume that there exist an IND-CPA secure PKE scheme and a one-time \(\mathcal {P}\)-KDM secure SKE scheme that can encrypt messages of length \(\varOmega (\ell \cdot \lambda )\), where \(\ell = \ell (\lambda )\) is the secret key length of the SKE scheme. Then, there exists a reusable DV-NIZK argument system for all NP languages.
As mentioned in the introduction, this almost immediately follows by combining the results and techniques from the recent works by Lombardi et al. [34] and by Kitagawa et al. [30]. To see this, we first briefly review Lombardi et al.’s work.
Lombardi et al. showed how to construct a reusable DV-NIZK argument system for all NP languages from the combination of an IND-CPA secure PKE scheme and a hinting PRG introduced by Koppula and Waters [33]. The main intermediate technical tool for their construction is what they call attribute-based secure function evaluation (AB-SFE), which can be seen as a generalization (and simplification) of a single-key attribute-based encryption (ABE) scheme (i.e., an ABE scheme secure in the presence of a single secret key). Lombardi et al. formalized two kinds of security notions for AB-SFE: key-hiding and message-hiding, each notion with strong and weak variants, resulting in total four security notions. Using the notion of AB-SFE, they achieved their result in a modular manner by showing the following steps:
-
(DV-NIZK-from-AB-SFE): A reusable DV-NIZK argument system can be constructed from an AB-SFE scheme satisfying strong key-hiding and weak message-hiding.
-
(Key-Hiding Enhancement): An AB-SFE scheme satisfying strong key-hiding and weak message-hiding can be constructed from an AB-SFE scheme satisfying weak key-hiding and weak message-hiding, by additionally assuming a hinting PRG. This step directly uses the CPA-to-CCA security transformation for ABE using a hinting PRG by Koppula and Waters [33].
-
(AB-SFE-from-PKE): An AB-SFE scheme satisfying weak key-hiding and weak message-hiding can be constructed from an IND-CPA secure PKE scheme.
On the other hand, Kitagawa et al. [30] showed that an IND-CCA secure PKE scheme can be constructed from the combination of an IND-CPA secure PKE scheme and a one-time \(\mathcal {P}\)-KDM secure SKE scheme which can encrypt messages of length \(\varOmega ({\ell _{\mathsf {}}}\cdot \lambda )\), where \({\ell _{\mathsf {}}}\) denotes the secret key length of the SKE scheme, based on the Koppula-Waters construction [33].
Kitagawa et al.’s result can be understood as showing a technique for replacing a hinting PRG in the Koppula-Waters construction (and its variants) with a one-time \(\mathcal {P}\)-KDM secure SKE scheme. Hence, we can apply Kitagawa et al.’s technique to the “key-hiding enhancement” step of Lombardi et al. to replace the hinting PRG with a one-time \(\mathcal {P}\)-KDM secure SKE scheme. This can be formally stated as follows.
Theorem 3 (Key-Hiding Enhancement via KDM Security)
Assume that there exists an AB-SFE scheme that satisfies weak key-hiding and weak message-hiding, and a one-time \(\mathcal {P}\)-KDM secure SKE scheme that can encrypt messages of length \(\varOmega ({\ell _{\mathsf {}}}\cdot \lambda )\), where \({\ell _{\mathsf {}}}= {\ell _{\mathsf {}}}(\lambda )\) is the secret key length of the SKE scheme. Then, there exists an AB-SFE scheme that satisfies strong key-hiding and weak message-hiding.
Then, Theorem 2 follows from the combination of the “DV-NIZK-from-AB-SFE” and “AB-SFE-from-PKE” steps of Lombardi et al. [34] and Theorem 3.
We give the formal proof of Theorem 3 in the full version.
5 Generic Construction of KDM-CCA Secure PKE
In this section, we show our main result: a CPA-to-CCA transformation for KDM security.
More specifically, we show how to construct a PKE scheme that is KDM-CCA secure with respect to circuits whose size is bounded by an a-priori determined polynomial \(\mathsf {size}= \mathsf {size}(\lambda )\) and in the single user setting (i.e. \({\mathcal {B}_{\mathsf {size}}}\text {-}\mathrm{{KDM}}^{(1)}\text {-}\mathrm{{CCA}}\)), from the combination of the five building block primitives: (1) an IND-CPA secure PKE scheme, (2) an IND-CCA secure PKE scheme, (3) a reusable DV-NIZK argument system for an NP language, (4) a garbling scheme, and (5) a one-time \(\mathcal {P}\)-KDM secure SKE scheme.
We have seen in Sect. 4 that a reusable DV-NIZK argument system can be constructed from the combination of an IND-CPA secure PKE scheme and a one-time \(\mathcal {P}\)-KDM secure SKE scheme. Furthermore, the recent work by Kitagawa et al. [30] showed that an IND-CCA secure PKE scheme can also be constructed from the same building blocks. Moreover, a garbling scheme can be constructed only from a one-way function [40], which is in turn implied by an IND-CPA secure PKE or a one-time \(\mathcal {P}\)-KDM secure SKE scheme. Hence, our result in this section implies that a \({\mathcal {B}_{\mathsf {size}}}\text {-}\mathrm{{KDM}}^{(1)}\text {-}\mathrm{{CCA}}\) secure PKE scheme can be constructed only from an IND-CPA secure PKE scheme and a one-time \(\mathcal {P}\)-KDM secure SKE scheme.
Looking ahead, in the next section, we will show that the same construction can be shown to be secure in the n-user setting (i.e. \({\mathcal {B}_{\mathsf {size}}}\text {-}\mathrm{{KDM}}^{(n)}\text {-}\mathrm{{CCA}}\) secure) if we additionally require the SKE scheme to be passively \(\mathcal {P}\text {-RKA-KDM}^{(n)}\) secure.
Construction. Let \({\ell _{\mathsf {m}}}= {\ell _{\mathsf {m}}}(\lambda )\) be a polynomial that denotes the length of messages to be encrypted by our constructed PKE scheme. Let \(\mathsf {size}= \mathsf {size}(\lambda )\) be a polynomial and let \(n \in \mathbb {N}\) be the number of users for which we wish to achieve \({\mathcal {B}_{\mathsf {size}}}\text {-}\mathrm{{KDM}}^{(n)}\text {-}\mathrm{{CCA}}\) security.Footnote 11
We use the following building blocks.
-
Let \(\mathsf {PKE}= (\mathsf {KG}, \mathsf {Enc}, \mathsf {Dec})\) be a PKE scheme whose message space is \(\{0,1\}^\lambda \). We denote the randomness space of \(\mathsf {Enc}\) by \(\mathcal {R}\), and the secret key length by \(\ell _{\mathsf {sk}}= \ell _{\mathsf {sk}}(\lambda )\).
-
Let \(\mathsf {PKE}'= (\mathsf {KG}_{\mathsf {cca}}, \mathsf {Enc}_{\mathsf {cca}}, \mathsf {Dec}_{\mathsf {cca}})\) be a PKE scheme whose message space is \(\{0,1\}^*\). We denote its secret key length by \(\ell '_{\mathsf {sk}}= \ell '_{\mathsf {sk}}(\lambda )\).
-
Let \(\mathsf {SKE}= (\mathsf {K}, \mathsf {E}, \mathsf {D})\) be an SKE scheme whose plaintext space is \(\{0,1\}^{\mu }\) for a polynomial \(\mu = \mu (\lambda )\) to be determined below and whose secret key space is \(\{0,1\}^{\ell _s}\) for some polynomial \(\ell _s= \ell _s(\lambda )\).
-
Let \(\mathsf{GC}= (\mathsf {Garble}, \mathsf {Eval}, \mathsf {Sim})\) be a garbling scheme.
-
Let \(\mathsf {DVNIZK}= (\mathsf {DVKG},\mathsf {P},\mathsf {V})\) be a DV-NIZK argument system for the following NP language

We denote the verification key length of \(\mathsf {DVNIZK}\) by \(\ell _{\mathsf {sk}_{\mathsf {dv}}}= \ell _{\mathsf {sk}_{\mathsf {dv}}}(\lambda )\).
We require the message length \(\mu \) of the underlying SKE scheme \(\mathsf {SKE}\) to satisfy \(\mu = \ell _s\cdot \ell _{\mathsf {sk}}+ \ell '_{\mathsf {sk}}+ \ell _{\mathsf {sk}_{\mathsf {dv}}}\). Finally, let \(\mathsf {pad}= \mathsf {pad}(\lambda , n) \ge \mathsf {size}\) be a polynomial that is used as the size parameter for the underlying garbling scheme, and is specified differently in Theorem 4 in this section and in Theorem 5 in Sect. 6.
Using these ingredients, we construct our proposed PKE scheme \(\mathsf {PKE}_{\mathsf {kdm}}= (\mathsf {KG}_{\mathsf {kdm}}, \mathsf {Enc}_{\mathsf {kdm}}, \mathsf {Dec}_{\mathsf {kdm}})\) whose message space is \(\{0,1\}^{{\ell _{\mathsf {m}}}}\), as described in Fig. 1.
The proposed PKE scheme \(\mathsf {PKE}_{\mathsf {kdm}}\). The notations like \((X_{j,\alpha })_{j,\alpha }\) and \((X_j)_{j}\) are abbreviations for \((X_{j,\alpha })_{j \in [\ell _s],\alpha \in \{0,1\}}\) and \((X_j)_{j \in [\ell _s]}\), respectively. \(^{(\star )}\) If \(\mathsf {D}\), \(\mathsf {Dec}\), or \(\mathsf {Dec}_{\mathsf {cca}}\) returns \(\bot \), then we make \(\mathsf {Dec}_{\mathsf {kdm}}\) return \(\bot \) and terminate. \(^{(\dag )}\) \(\mathsf {pad}= \mathsf {pad}(\lambda , n)\) denotes the size parameter that is specified differently in each of Theorems 4 and 5.
Correctness. The correctness of \(\mathsf {PKE}_{\mathsf {kdm}}\) follows from that of the building blocks. Specifically, let \((\mathsf {PK}, \mathsf {SK}) = (((\mathsf {pk}_{j,\alpha })_{j, \alpha }, \mathsf {pk}_{\mathsf {cca}}, \mathsf {pk}_{\mathsf {dv}}, \mathsf {ct}_{\mathsf {ske}}), s)\) be a key pair output by \(\mathsf {KG}_{\mathsf {kdm}}\), let \(m \in \{0,1\}^{{\ell _{\mathsf {m}}}}\) be any message, and let \(\mathsf {CT}\leftarrow \mathsf {Enc}_{\mathsf {kdm}}(\mathsf {PK}, m)\) be an honestly generated ciphertext. Due to the correctness of \(\mathsf {PKE}\), \(\mathsf {PKE}'\), \(\mathsf {SKE}\), and \(\mathsf {DVNIZK}\), each decryption/verification done in the execution of \(\mathsf {Dec}_{\mathsf {kdm}}(\mathsf {PK}, \mathsf {SK}, \mathsf {CT})\) never fails, and just before the final step of \(\mathsf {Dec}_{\mathsf {kdm}}\), the decryptor can recover a garbled circuit \(\widetilde{\mathsf {Q}}\) and the labels \((\mathsf {lab}_j)_{j}\), which must have been generated as \((\widetilde{\mathsf {Q}}, (\mathsf {lab}_j)_{j}) \leftarrow \mathsf {Sim}(1^\lambda , \mathsf {pad}, m)\). Hence, by the correctness of \(\mathsf{GC}\) (in particular, correctness of the evaluation of a simulated garbled circuit and labels), we have \(\mathsf {Eval}(\widetilde{\mathsf {Q}}, (\mathsf {lab}_j)_{j}) = m\).
Security. The following theorem guarantees the \({\mathcal {B}_{\mathsf {size}}}\text {-}\mathrm{{KDM}}^{(1)}\text {-}\mathrm{{CCA}}\) security of the PKE scheme \(\mathsf {PKE}_{\mathsf {kdm}}\).
Theorem 4
Let \({\ell _{\mathsf {m}}}= {\ell _{\mathsf {m}}}(\lambda )\) and \(\mathsf {size}= \mathsf {size}(\lambda ) \ge \max \{\ell _s,{\ell _{\mathsf {m}}}\}\) be any polynomials, and let \(\mathsf {pad}:= \mathsf {size}\). Assume that \(\mathsf {PKE}\) is IND-CPA secure, \(\mathsf {PKE}'\) is IND-CCA secure, \(\mathsf {SKE}\) is one-time \(\mathcal {P}\)-KDM secure, \(\mathsf{GC}\) is a secure garbling scheme, and \(\mathsf {DVNIZK}\) is a reusable DV-NIZK argument system for the NP language L. Then, \(\mathsf {PKE}_{\mathsf {kdm}}\) is \({\mathcal {B}_{\mathsf {size}}}\text {-}\mathrm{{KDM}}^{(1)}\text {-}\mathrm{{CCA}}\) secure.
One might wonder the necessity of IND-CCA security for the outer PKE scheme \(\mathsf {PKE}'\). Suppose the underlying garbling scheme \(\mathsf{GC}\) has the property that a circuit being garbled is hidden against adversaries that do not see the corresponding labels (which is satisfied by Yao’s garbling scheme). Then, among the components \((\widetilde{\mathsf {Q}},(\mathsf {ct}_{j,\alpha })_{j,\alpha },\pi )\), the only component that actually needs to be encrypted is the DV-NIZK proof \(\pi \), as long as all the components are “tied” together in a non-malleable manner (say, using a one-time signature scheme). Looking ahead, in a sequence of games argument in the security proof, we will consider a modified game in which the key pair \((\mathsf {pk}_{\mathsf {dv}}, \mathsf {sk}_{\mathsf {dv}})\) and proofs \(\pi \) in the challenge ciphertexts are generated by the zero-knowledge simulator of \(\mathsf {DVNIZK}\), and we have to bound the probability that an adversary makes a “bad” decryption query \(\mathsf {CT}\) such that the statement/proof pair \((x, \pi )\) corresponding to \(\mathsf {CT}\) is judged valid by \(\mathsf {V}\) while x is actually invalid (i.e. not in L). This could be done if \(\mathsf {DVNIZK}\) satisfies (unbounded) simulation soundness, which is not achieved by the DV-NIZK argument system in Sect. 4. By encrypting \(\pi \) with an IND-CCA secure scheme (and relying also on the security properties of the other building blocks), we can argue that the probability of the bad event that we would like to bound, is negligibly close to the probability of the bad event in another modified game in which the key pair \((\mathsf {pk}_{\mathsf {dv}},\mathsf {sk}_{\mathsf {dv}})\) is generated honestly by \(\mathsf {DVKG}\), and proofs \(\pi \) need not be generated for the challenge ciphertexts. The probability of the bad event in such a game can be bounded by the (ordinary) soundness of \(\mathsf {DVNIZK}\). For the details, see the proof below.
Proof of Theorem 4. Let \(\mathcal {A}\) be an arbitrary PPT adversary that attacks the \({\mathcal {B}_\mathsf {size}}\text {-}\mathrm{{KDM}}^{(1)}\text {-}\mathrm{{CCA}}\) security of \(\mathsf {PKE}_{\mathsf {kdm}}\). We proceed the proof via a sequence of games argument using eight games. For every \(t \in [7]\), let \(\mathtt{SUC}_{t}\) be the event that \(\mathcal {A}\) succeeds in guessing the challenge bit b in Game t. (Game 8 will be used only to bound the probability of a bad event introduced later.)
-
Game 1: This is the original \({\mathcal {B}_{\mathsf {size}}}\text {-}\mathrm{{KDM}}^{(1)}\text {-}\mathrm{{CCA}}\) game regarding \(\mathsf {PKE}_{\mathsf {kdm}}\). By definition, we have \(\mathsf {Adv}_{\mathsf {PKE}_{\mathsf {kdm}},\mathcal {B}_{\mathsf {size}},\mathcal {A},1}^{\mathsf {kdmcca}}(\lambda ) = 2 \cdot \left| \Pr [\mathtt{SUC}_{1}]-1/2\right| \).
-
Game 2: Same as Game 1, except that the challenger uses the simulator \(\mathsf {S}= (\mathsf {S}_1, \mathsf {S}_2)\) for the zero-knowledge property of \(\mathsf {DVNIZK}\) for generating \((\mathsf {pk}_{\mathsf {dv}}, \mathsf {sk}_{\mathsf {dv}})\) and a proof \(\pi \) in generating a ciphertext in response to KDM-encryption queries, instead of using \(\mathsf {DVKG}\) and \(\mathsf {P}\). Namely, when generating \(\mathsf {PK}\) and \(\mathsf {SK}\), the challenger generates \((\mathsf {pk}_{\mathsf {dv}}, \mathsf {sk}_{\mathsf {dv}}, \mathsf {td}) \leftarrow \mathsf {S}_1(1^\lambda )\) instead of \((\mathsf {pk}_{\mathsf {dv}}, \mathsf {sk}_{\mathsf {dv}}) \leftarrow \mathsf {DVKG}(1^\lambda )\). In addition, when \(\mathcal {A}\) makes a KDM-encryption query \((f_0,f_1)\), the challenger computes \(\pi \leftarrow \mathsf {S}_2(\mathsf {td}, x)\) instead of \(\pi \leftarrow \mathsf {P}(\mathsf {pk}_{\mathsf {dv}}, x, w)\), where \(x = (\mathsf {pk}_{j,\alpha }, \mathsf {ct}_{j,\alpha })_{j,\alpha }\) and \(w = (\mathsf {lab}_j, r_{j,0}, r_{j,1})_{j}\).
By the zero-knowledge property of \(\mathsf {DVNIZK}\), we have \(\left| \Pr [\mathtt{SUC}_{1}] - \Pr [\mathtt{SUC}_{2}]\right| = \mathsf{negl}(\lambda )\).
-
Game 3: Same as Game 2, except that when responding to a KDM-encryption query, the challenger generates a garbled circuit \(\widetilde{\mathsf {Q}}\) and labels \((\mathsf {lab}_j)_{j}\) by garbling \(f_b\). More precisely, when \(\mathcal {A}\) makes a KDM-encryption query \((f_0,f_1)\), the challenger computes \((\widetilde{\mathsf {Q}}, (\mathsf {lab}_{j,\alpha })_{j,\alpha }) \leftarrow \mathsf {Garble}(1^\lambda , f_b)\), instead of \((\widetilde{\mathsf {Q}}, (\mathsf {lab}_j)_{j}) \leftarrow \mathsf {Sim}(1^\lambda , \mathsf {pad}, f_b(s))\). Moreover, for every \(j \in [\ell _s]\) and \(\alpha \in \{0,1\}\), the challenger computes \(\mathsf {ct}_{j,\alpha } \leftarrow \mathsf {Enc}(\mathsf {pk}_{j,\alpha }, \mathsf {lab}_{j,s_j})\).Footnote 12
By definition, the circuit size of \(f_b\) is \(\mathsf {pad}= \mathsf {size}\). Hence, by the security of \(\mathsf{GC}\), we have \(\left| \Pr [\mathtt{SUC}_{2}] - \Pr [\mathtt{SUC}_{3}]\right| = \mathsf{negl}(\lambda )\).
-
Game 4: Same as Game 3, except that when responding to a KDM-encryption query \((f_0,f_1)\), the challenger computes \(\mathsf {ct}_{j,1 \oplus s_j} \leftarrow \mathsf {Enc}(\mathsf {pk}_{j,1 \oplus s_j}, \mathsf {lab}_{j, 1 \oplus s_j})\) for every \(j \in [\ell _s]\). Due to the change made in this game, the challenger now computes \(\mathsf {ct}_{j,\alpha } \leftarrow \mathsf {Enc}(\mathsf {pk}_{j,\alpha }, \mathsf {lab}_{j,\alpha })\) for every \(j \in [\ell _s]\) and \(\alpha \in \{0,1\}\).
In Games 3 and 4, we do not need the secret keys \((\mathsf {sk}_{j,1 \oplus s_j})_{j}\) of \(\mathsf {PKE}\) that do not correspond to \(s = (s_1, \dots , s_{\ell _s})\) (though we need \((\mathsf {sk}_{j,s_j})_{j}\) for computing \(\mathsf {ct}_{\mathsf {ske}}\) and responding to decryption queries). Therefore, by the \(\mathrm{{IND}}\text {-}\mathrm{{CPA}}\) security of \(\mathsf {PKE}\) under the keys \((\mathsf {pk}_{j, 1 \oplus s_j})_{j}\), we have \(\left| \Pr [\mathtt{SUC}_{3}]-\Pr [\mathtt{SUC}_{4}]\right| =\mathsf{negl}(\lambda )\).
At this point, the challenger need not use s to respond to KDM-encryption queries. In the next game, we will ensure that the challenger does not use s to respond to decryption queries.
-
Game 5: Same as Game 4, except that when responding to a decryption query, the challenger computes the labels \((\mathsf {lab}_j)_{j}\) of a garbled circuit by decrypting \(\mathsf {ct}_{j,0}\), instead of \(\mathsf {ct}_{j,s_j}\), for every \(j \in [\ell _s]\). More precisely, for a decryption query \(\mathsf {CT}\) from \(\mathcal {A}\), the challenger returns \(\bot \) to \(\mathcal {A}\) if \(\mathsf {CT}\in L_\mathsf {kdm}\), and otherwise responds as follows. (The change from the previous game is underlined.)
-
1.
Compute \((\widetilde{\mathsf {Q}},(\mathsf {ct}_{j,\alpha })_{j,\alpha },\pi ) \leftarrow \mathsf {Dec}_{\mathsf {cca}}(\mathsf {pk}_{\mathsf {cca}},\mathsf {sk}_{\mathsf {cca}},\mathsf {CT})\), and then set \(x := (\mathsf {pk}_{j, \alpha }, \mathsf {ct}_{j, \alpha })_{j,\alpha }\).
-
2.
If \(\mathsf {V}(\mathsf {sk}_{\mathsf {dv}}, x, \pi )=\mathsf {reject}\), then return \(\bot \) to \(\mathcal {A}\).
-
3.
For every \(j \in [\ell _s]\), compute
 .
. -
4.
Return \(m \leftarrow \mathsf {Eval}(\widetilde{\mathsf {Q}}, (\mathsf {lab}_j)_{j})\) to \(\mathcal {A}\).
-
1.
(By the change made in this game, s is not needed for responding to decryption queries.)
We define the following events in Game \(t \in \{4, \dots , 8\}\).
-
\(\mathtt{BDQ}_{t}\): In Game t, \(\mathcal {A}\) makes a decryption query \(\mathsf {CT}\notin L_\mathsf {kdm}\) that satisfies the following two conditions, where \((\widetilde{\mathsf {Q}},(\mathsf {ct}_{j,\alpha })_{j,\alpha },\pi ) \leftarrow \mathsf {Dec}_{\mathsf {cca}}(\mathsf {pk}_{\mathsf {cca}},\mathsf {sk}_{\mathsf {cca}},\mathsf {CT})\):
-
1.
\(\mathsf {V}(\mathsf {sk}_{\mathsf {dv}}, (\mathsf {pk}_{j, \alpha }, \mathsf {ct}_{j,\alpha })_{j,\alpha }, \pi )=\mathsf {accept}\).
-
2.
There exists \({j^*}\in [\ell _s]\) such that \(\mathsf {Dec}(\mathsf {pk}_{{j^*},0}, \mathsf {sk}_{{j^*},0}, \mathsf {ct}_{{j^*},0}) \ne \mathsf {Dec}(\mathsf {pk}_{{j^*},1}, \mathsf {sk}_{{j^*},1}, \mathsf {ct}_{{j^*},1})\).
We call such a decryption query a bad decryption query.
-
1.
Games 4 and 5 are identical unless \(\mathcal {A}\) makes a bad decryption query in the corresponding games. Therefore, we have \(\left| \Pr [\mathtt{SUC}_{4}] - \Pr [\mathtt{SUC}_{5}]\right| \le \Pr [\mathtt{BDQ}_{5}]\).
-
Game 6: Same as Game 5, except that when generating \(\mathsf {PK}\), the challenger generates \(\mathsf {ct}_{\mathsf {ske}}\leftarrow \mathsf {E}(s, 0^{\mu })\), instead of \(\mathsf {ct}_{\mathsf {ske}}\leftarrow \mathsf {E}(s, ((\mathsf {sk}_{j, s_j})_{j}, \mathsf {sk}_{\mathsf {cca}}, \mathsf {sk}_{\mathsf {dv}}))\).
In Games 5 and 6, when generating \(\mathsf {PK}\), the challenger does not need the secret key s of \(\mathsf {SKE}\) except for the step of computing \(\mathsf {ct}_{\mathsf {ske}}\). Furthermore, the “message” \(((\mathsf {sk}_{j, s_j})_{j}, \mathsf {sk}_{\mathsf {cca}}, \mathsf {sk}_{\mathsf {dv}})\) encrypted in \(\mathsf {ct}_{\mathsf {ske}}\) in Game 5 can be described by a projection function of s. Thus, by the one-time \(\mathcal {P}\)-KDM security of \(\mathsf {SKE}\), we have \(\left| \Pr [\mathtt{SUC}_{5}] - \Pr [\mathtt{SUC}_{6}]\right| = \mathsf{negl}(\lambda )\). In addition, whether \(\mathcal {A}\) has submitted a bad decryption query can be detected by using \(\mathsf {sk}_{\mathsf {cca}}\), \(\mathsf {sk}_{\mathsf {dv}}\), and \((\mathsf {sk}_{j,\alpha })_{j,\alpha }\), without using s. Thus, again by the one-time \(\mathcal {P}\)-KDM security of \(\mathsf {SKE}\), we have \(\left| \Pr [\mathtt{BDQ}_{5}] - \Pr [\mathtt{BDQ}_{6}]\right| = \mathsf{negl}(\lambda )\).
-
Game 7: Same as Game 6, except that when responding to a KDM-encryption query, the challenger computes \(\mathsf {CT}\leftarrow \mathsf {Enc}_{\mathsf {cca}}(\mathsf {pk}_{\mathsf {cca}}, 0^{{\ell _{\mathsf {}}}'})\), where \({\ell _{\mathsf {}}}' = |\widetilde{\mathsf {Q}}| + 2\ell _s\cdot |\mathsf {ct}_{j,\alpha }| + |\pi |\).
Recall that in the previous game, we have eliminated the information of \(\mathsf {sk}_{\mathsf {cca}}\) from \(\mathsf {ct}_{\mathsf {ske}}\). Thus, we can rely on the \(\mathrm{{IND}}\text {-}\mathrm{{CCA}}\) security of \(\mathsf {PKE}'\) at this point, and straightforwardly derive \(\left| \Pr [\mathtt{SUC}_{6}] - \Pr [\mathtt{SUC}_{7}]\right| = \mathsf{negl}(\lambda )\). Moreover, a reduction algorithm (attacking the IND-CCA security of \(\mathsf {PKE}'\)) can detect whether \(\mathcal {A}\)’s decryption query is bad by using \((\mathsf {sk}_{j,\alpha })_{j,\alpha }\), \(\mathsf {sk}_{\mathsf {dv}}\), and the reduction algorithm’s own decryption queries. Thus, again by the \(\mathrm{{IND}}\text {-}\mathrm{{CCA}}\) security of \(\mathsf {PKE}'\), we have \(\left| \Pr [\mathtt{BDQ}_{6}] - \Pr [\mathtt{BDQ}_{7}]\right| = \mathsf{negl}(\lambda )\).
We see that in Game 7, the challenge bit b is information-theoretically hidden from \(\mathcal {A}\)’s view. Thus, we have \(\Pr [\mathtt{SUC}_{7}] = 1/2\).
We need one more game to bound \(\Pr [\mathtt{BDQ}_{7}]\).
-
Game 8: Same as Game 7, except that when generating \(\mathsf {PK}\), the challenger uses \(\mathsf {DVKG}\) to generate \((\mathsf {pk}_{\mathsf {dv}}, \mathsf {sk}_{\mathsf {dv}})\), instead of using \(\mathsf {S}_1\). Namely, we undo the change made between Games 1 and 2 for generating \((\mathsf {pk}_{\mathsf {dv}}, \mathsf {sk}_{\mathsf {dv}})\).Footnote 13
By the zero-knowledge property of \(\mathsf {DVNIZK}\), we have \(\left| \Pr [\mathtt{BDQ}_{7}] - \Pr [\mathtt{BDQ}_{8}]\right| = \mathsf{negl}(\lambda )\).
Finally, we argue that the soundness of \(\mathsf {DVNIZK}\) implies \(\Pr [\mathtt{BDQ}_{8}] = \mathsf{negl}(\lambda )\). To see this, note that in Game 8, \((\mathsf {pk}_{\mathsf {dv}}, \mathsf {sk}_{\mathsf {dv}})\) is now generated by \(\mathsf {DVKG}\). Also, if \(\mathcal {A}\) submits a bad decryption query \(\mathsf {CT}\) such that (1) \(\mathsf {V}(\mathsf {sk}_{\mathsf {dv}}, (\mathsf {pk}_{j,\alpha }, \mathsf {ct}_{j,\alpha })_{j,\alpha }, \pi ) = \mathsf {accept}\) and (2) \(\mathsf {Dec}(\mathsf {pk}_{j^*, 0}, \mathsf {sk}_{j^*,0}, \mathsf {ct}_{j^*, 0}) \ne \mathsf {Dec}(\mathsf {pk}_{j^*,1}, \mathsf {sk}_{j^*,1}, \mathsf {ct}_{j^*,1})\) for some \(j^* \in [\ell _s]\), where \((\widetilde{\mathsf {Q}}, (\mathsf {ct}_{j,\alpha })_{j,\alpha }, \pi ) \leftarrow \mathsf {Dec}_{\mathsf {cca}}(\mathsf {pk}_{\mathsf {cca}}, \mathsf {sk}_{\mathsf {cca}}, \mathsf {CT})\), then the condition (2) in particular implies \((\mathsf {pk}_{j,\alpha },\mathsf {ct}_{j,\alpha })_{j, \alpha } \notin L\). Thus \(((\mathsf {pk}_{j,\alpha },\mathsf {ct}_{j,\alpha })_{j,\alpha }, \pi )\) satisfies the condition of violating the soundness of \(\mathsf {DVNIZK}\). Note that a reduction algorithm (attacking the soundness of \(\mathsf {DVNIZK}\)) is not directly given a secret verification key \(\mathsf {sk}_{\mathsf {dv}}\). However, the reduction algorithm is allowed to make verification queries, which is sufficient to perfectly simulate Game 8 for \(\mathcal {A}\). The reduction algorithm can also detect whether \(\mathcal {A}\) has made a bad decryption query by using \(\mathsf {sk}_{\mathsf {cca}}\) and \((\mathsf {sk}_{j,\alpha })_{j,\alpha }\), and verification queries. Hence, by the soundness of \(\mathsf {DVNIZK}\), we have \(\Pr [\mathtt{BDQ}_{8}] = \mathsf{negl}(\lambda )\).
From the above arguments, we see that \(\mathsf {Adv}_{\mathsf {PKE}_{\mathsf {kdm}}, \mathcal {B}_{\mathsf {size}}, \mathcal {A},1}^{\mathsf {kdmcca}}(\lambda )=\mathsf{negl}(\lambda )\). Since the choice of \(\mathcal {A}\) was arbitrary, we can conclude that \(\mathsf {PKE}_{\mathsf {kdm}}\) is \({\mathcal {B}_{\mathsf {size}}}\text {-}\mathrm{{KDM}}^{(1)}\text {-}\mathrm{{CCA}}\) secure. \(\Box \) (Theorem 4)
6 Multi-user KDM-CCA Security from RKA-KDM Security
In this section, we show that for any polynomial \(n = n(\lambda )\), our proposed PKE scheme \(\mathsf {PKE}_{\mathsf {kdm}}\) presented in Sect. 5 can be shown to be \({\mathcal {B}_{\mathsf {size}}}\text {-}\mathrm{{KDM}}^{(n)}\text {-}\mathrm{{CCA}}\) secure, by choosing a suitable parameter for \(\mathsf {pad}= \mathsf {pad}(\lambda , n)\) and additionally requiring the underlying SKE scheme \(\mathsf {SKE}\) satisfies \(\mathcal {P}\text {-RKA-KDM}^{(n)}\) security, and its key generation algorithm outputs a uniformly random string in the secret key space. Formally, our result for the multi-user setting is stated as follows.
Theorem 5
Let \(n = n(\lambda )\), \({\ell _{\mathsf {m}}}= {\ell _{\mathsf {m}}}(\lambda )\), and \(\mathsf {size}= \mathsf {size}(\lambda ) \ge \max \{\ell _s, {\ell _{\mathsf {m}}}\}\) be any polynomials, and let \(\mathsf {pad}:= \mathsf {size}+ O(\ell _s\cdot n)\). Assume that \(\mathsf {PKE}\) is IND-CPA secure, \(\mathsf {PKE}'\) is IND-CCA secure, \(\mathsf {SKE}\) is passively \(\mathcal {P}\text {-RKA-KDM}^{(n)}\) secure and its key generation algorithm outputs a string that is distributed uniformly over \(\{0,1\}^{\ell _s}\), \(\mathsf{GC}\) is a secure garbling scheme, and \(\mathsf {DVNIZK}\) is a reusable DV-NIZK argument system for the NP language L. Then, \(\mathsf {PKE}_{\mathsf {kdm}}\) is \({\mathcal {B}_{\mathsf {size}}}\text {-}\mathrm{{KDM}}^{(n)}\text {-}\mathrm{{CCA}}\) secure.
The formal proof is given in the full version. A high-level structure of the sequence of the games used in the proof of Theorem 5 is similar to that of Theorem 4. The main differences are as follows.
-
Before the game-hop for switching the simulator \(\mathsf {Sim}\) of the garbling scheme \(\mathsf{GC}\) to the ordinary algorithm \(\mathsf {Garble}\), we introduce a game in which every user’s secret key \(s^i\) is derived by using a randomly chosen single “main” key \(s \in \{0,1\}^{\ell _s}\) and a randomly chosen “shift” \(\varDelta ^i \in \{0,1\}^{\ell _s}\), so that \(s^i := s \oplus \varDelta ^i\). This does not at all change the distribution of the keys due to the requirement on \(\mathsf {SKE}\) that a secret key is distributed uniformly in the secret key space \(\{0,1\}^{{\ell _{\mathsf {s}}}}\). This enables us to conduct the remaining game-hops as if \(s \in \{0,1\}^{\ell _s}\) is the single “main” secret key such that we need to care only its leakage to an adversary via KDM-encryption and decryption queries.
-
In the game-hop for switching the simulator \(\mathsf {Sim}\) of \(\mathsf{GC}\) to the ordinary garbling algorithm \(\mathsf {Garble}\), instead of directly garbling a KDM-function \(f_b\) (which is a function of all users’ secret keys \(S:= s^1 \Vert \dots \Vert s^\ell _s\) in the n-user setting) appearing in an adversary’s KDM-encryption query \(({i^*}, f_0, f_1)\), we garble some appropriately designed circuit \(\mathsf {Q}\) with input length \(\ell _s\). More specifically, we garble a circuit \(\mathsf {Q}\) that has the index \(i^*\), the KDM-function \(f_b\), and the shifts \((\varDelta ^i)_{i \in [n]}\) hard-wired, and satisfies \(f_b(S) = \mathsf {Q}(s^{i^*})\).
-
In the game-hop for erasing the information of \(((\mathsf {sk}^i_{j,s_j})_{j}, \mathsf {sk}_{\mathsf {cca}}^i, \mathsf {sk}_{\mathsf {dv}}^i)\) from \(\mathsf {ct}_{\mathsf {ske}}^i\) for every \(i \in [n]\), we rely on the passive \(\mathcal {P}\text {-RKA-KDM}^{(n)}\) security of \(\mathsf {SKE}\) (as opposed to its one-time \(\mathcal {P}\)-KDM security). Intuitively, passive \(\mathcal {P}\text {-RKA-KDM}^{(n)}\) security suffices here because each user’s secret key \(s^i\) is computed as \(s^i = s \oplus \varDelta ^i\) where s and each \(\varDelta ^i\) are chosen randomly by the challenger, due to the change made in the first item above.
7 Putting It All Together
In this section, we summarize our results.
By combining Theorems 2 and 4, for any polynomial \(\mathsf {size}=\mathsf {size}(\lambda )\), a \({\mathcal {B}_{\mathsf {size}}}\text {-}\mathrm{{KDM}}^{(1)}\text {-}\mathrm{{CCA}}\) secure PKE scheme can be constructed from an IND-CPA secure PKE scheme, an IND-CCA secure PKE scheme, a one-time \(\mathcal {P}\)-KDM secure SKE scheme, and a garbling scheme. From the result by Kitagawa et al. [30], we can realize an IND-CCA secure PKE scheme from an IND-CPA secure PKE scheme and a one-time \(\mathcal {P}\)-KDM secure PKE scheme. Moreover, a garbling scheme is implied by one-way functions [40], which is in turn implied by an IND-CPA secure PKE scheme. From these, we obtain the following theorem.
Theorem 6
Assume that there exist an IND-CPA secure PKE scheme and a one-time \(\mathcal {P}\)-KDM secure SKE scheme that can encrypt messages of length \(\varOmega ({\ell _{\mathsf {}}}\cdot \lambda )\), where \({\ell _{\mathsf {}}}= {\ell _{\mathsf {}}}(\lambda )\) denotes the secret key length of the SKE scheme. Then, for any polynomial \(\mathsf {size}=\mathsf {size}(\lambda )\), there exists a \({\mathcal {B}_{\mathsf {size}}}\text {-}\mathrm{{KDM}}^{(1)}\text {-}\mathrm{{CCA}}\) secure PKE scheme.
Since both an IND-CPA secure PKE scheme and a one-time \(\mathcal {P}\)-KDM secure SKE scheme are implied by a \({\mathcal {P}}\text {-}\mathrm{{KDM}}^{(1)}\text {-}\mathrm{{CPA}}\) secure PKE scheme, we obtain the following main theorem.
Theorem 7
(CPA-to-CCA Transformation for KDM Security) Assume that there exists a \({\mathcal {P}}\text {-}\mathrm{{KDM}}^{(1)}\text {-}\mathrm{{CPA}}\) secure PKE scheme. Then, for any polynomial \(\mathsf {size}=\mathsf {size}(\lambda )\), there exists a \({\mathcal {B}_{\mathsf {size}}}\text {-}\mathrm{{KDM}}^{(1)}\text {-}\mathrm{{CCA}}\) secure PKE scheme.
Similarly to Theorem 6, by combining Theorems 2 and 5, and the previous results [30, 40], we also obtain the following theorem.
Theorem 8
Let \(n=n(\lambda )\) be a polynomial. Assume that there exist an IND-CPA secure PKE scheme, and a passively \(\mathcal {P}\text {-RKA-KDM}^{(n)}\) secure SKE scheme that can encrypt messages of length \(\varOmega ({\ell _{\mathsf {}}}\cdot \lambda )\), where \({\ell _{\mathsf {}}}= {\ell _{\mathsf {}}}(\lambda )\) denotes the secret key length of the SKE scheme, and whose secret key generation algorithm outputs a string that is distributed uniformly over \(\{0,1\}^{{\ell _{\mathsf {}}}}\). Then, for any polynomial \(\mathsf {size}=\mathsf {size}(\lambda )\), there exists a \({\mathcal {B}_{\mathsf {size}}}\text {-}\mathrm{{KDM}}^{(n)}\text {-}\mathrm{{CCA}}\) secure PKE scheme.
Note that a passively \(\mathcal {P}\text {-RKA-KDM}^{(n)}\) secure SKE scheme is also a one-time \(\mathcal {P}\)-KDM secure SKE scheme.
For any polynomials n and \(\mu \), we can construct a passively \(\mathcal {P}\text {-RKA-KDM}^{(n)}\) secure SKE scheme whose message space is \(\{0,1\}^{\mu }\) based on the LPN assumption [4]. In addition, as shown in the full version of this paper, for any polynomials n and \(\mu \), we can construct a \(\mathcal {P}\text {-RKA-KDM}^{(n)}\) secure SKE scheme whose message space is \(\{0,1\}^{\mu }\) based on the CDH assumption. The key generation algorithms of the LPN-/CDH-based constructions output a uniformly random string as a secret key. Since an IND-CPA secure PKE scheme can be constructed based on the LPN and CDH assumptions, we obtain the following corollary.
Corollary 1
Let \(n=n(\lambda )\) and \(\mathsf {size}=\mathsf {size}(\lambda )\) be any polynomials. There exists a \({\mathcal {B}_{\mathsf {size}}}\text {-}\mathrm{{KDM}}^{(n)}\text {-}\mathrm{{CCA}}\) secure PKE scheme under either the LPN or CDH assumption.
Notes
- 1.
In their actual construction, a one-time signature scheme is also used. We ignore it in this overview for simplicity, since the problem we explain below is unrelated to it.
- 2.
We note that in this construction, \(\mathsf {NIZK}\) need not satisfy the simulation soundness property [39], and we can complete the proof based on the ordinary soundness (and zero-knowledge) property of \(\mathsf {NIZK}\).
- 3.
The following explanations assume that the reader is familiar with a garbling scheme. See Sect. 3.5 for its formal definition.
- 4.
In the actual construction, we use a garbled circuit and labels that are generated by the simulator of the garbling scheme, instead of those generated by garbling a constant circuit. This makes the security proof simpler. We ignore this treatment here for the simplicity of the explanation.
- 5.
Usually, KDM security requires that an encryption of \(f(\mathsf {SK})\) be indistinguishable from that of some constant message such as \(0^{\left| f(\cdot )\right| }\) instead of requiring encryptions of \(f_0(\mathsf {SK})\) and \(f_1(\mathsf {SK})\) be indistinguishable, where f, \(f_0\), and \(f_1\) are functions chosen by adversaries. However, these definitions are equivalent if a function class with respect to which we consider KDM security contains constant functions, which is the case in this paper.
- 6.
Strictly speaking, we also use s to retrieve \((\mathsf {sk}',\mathsf {sk}_{\mathsf {dv}},(\mathsf {sk}_{j,s_j})_{j\in [{\ell _{\mathsf {s}}}]})\) from \(\mathsf {ct}_{\mathsf {ske}}\). However, we can omit this decryption process and use \((\mathsf {sk}',\mathsf {sk}_{\mathsf {dv}},(\mathsf {sk}_{j,s_j})_{j\in [{\ell _{\mathsf {s}}}]})\) directly without changing the view of an adversary, and thus we ignore this issue here.
- 7.
To make this change possible, in the formal proof, we need to pad a circuit garbled in the encryption algorithm to some appropriate size depending on n.
- 8.
These connections with the techniques by Barak et al. were pointed out by the anonymous reviewers.
- 9.
If we are only interested in one-time KDM security of the resulting scheme, the SKE-ciphertext \(\mathsf {ct}_{\mathsf {ske}}\) that is originally put in a public key of \(\mathsf {PKE}_{\mathsf {kdm}}^*\) can be sent as part of a ciphertext.
- 10.
Requiring correctness for the output of the simulator may be somewhat non-standard. However, it is satisfied by Yao’s garbling scheme based on an IND-CPA secure SKE scheme.
- 11.
As noted earlier, in this section we aim at achieving the security for \(n = 1\), and in the next section we will consider more general \(n \ge 1\).
- 12.
Note that in Game 3, the labels of the “opposite” positions, namely \((\mathsf {lab}_{j, 1 \oplus s_j})_{j}\), are not used. They will be used in the subsequent games.
- 13.
Note that in Games 7 and 8, \(\pi \) is not computed when generating \(\mathsf {CT}\), and thus we need not use \(\mathsf {S}_2\).
References
Adão, P., Bana, G., Herzog, J., Scedrov, A.: Soundness of formal encryption in the presence of key-cycles. In: di Vimercati, S.C., Syverson, P., Gollmann, D. (eds.) ESORICS 2005. LNCS, vol. 3679, pp. 374–396. Springer, Heidelberg (2005). https://doi.org/10.1007/11555827_22
Alekhnovich, M.: More on average case vs approximation complexity. In: 44th FOCS 2003, pp. 298–307 (2003)
Applebaum, B.: Key-dependent message security: generic amplification and completeness. In: Paterson, K.G. (ed.) EUROCRYPT 2011. LNCS, vol. 6632, pp. 527–546. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-20465-4_29
Applebaum, B.: Garbling XOR gates “For Free” in the standard model. In: Sahai, A. (ed.) TCC 2013. LNCS, vol. 7785, pp. 162–181. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36594-2_10
Applebaum, B., Cash, D., Peikert, C., Sahai, A.: Fast cryptographic primitives and circular-secure encryption based on hard learning problems. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 595–618. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03356-8_35
Barak, B., Haitner, I., Hofheinz, D., Ishai, Y.: Bounded key-dependent message security. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 423–444. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_22
Bellare, M., Desai, A., Pointcheval, D., Rogaway, P.: Relations among notions of security for public-key encryption schemes. In: Krawczyk, H. (ed.) CRYPTO 1998. LNCS, vol. 1462, pp. 26–45. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0055718
Black, J., Rogaway, P., Shrimpton, T.: Encryption-scheme security in the presence of key-dependent messages. In: Nyberg, K., Heys, H. (eds.) SAC 2002. LNCS, vol. 2595, pp. 62–75. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-36492-7_6
Bleichenbacher, D.: Chosen ciphertext attacks against protocols based on the RSA encryption standard PKCS #1. In: Krawczyk, H. (ed.) CRYPTO 1998. LNCS, vol. 1462, pp. 1–12. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0055716
Boneh, D., Halevi, S., Hamburg, M., Ostrovsky, R.: Circular-secure encryption from decision Diffie-Hellman. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 108–125. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85174-5_7
Boyle, E., Kohl, L., Scholl, P.: Homomorphic secret sharing from lattices without FHE. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019. LNCS, vol. 11477, pp. 3–33. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17656-3_1
Brakerski, Z., Goldwasser, S.: Circular and leakage resilient public-key encryption under subgroup indistinguishability. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 1–20. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14623-7_1
Brakerski, Z., Lombardi, A., Segev, G., Vaikuntanathan, V.: Anonymous IBE, leakage resilience and circular security from new assumptions. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10820, pp. 535–564. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78381-9_20
Camenisch, J., Chandran, N., Shoup, V.: A public key encryption scheme secure against key dependent chosen plaintext and adaptive chosen ciphertext attacks. In: Joux, A. (ed.) EUROCRYPT 2009. LNCS, vol. 5479, pp. 351–368. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-01001-9_20
Camenisch, J., Lysyanskaya, A.: Dynamic accumulators and application to efficient revocation of anonymous credentials. In: Yung, M. (ed.) CRYPTO 2002. LNCS, vol. 2442, pp. 61–76. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45708-9_5
Canetti, R., et al.: Fiat-Shamir: from practice to theory. In: 51st ACM STOC 2019, pp. 1082–1090 (2019)
Canetti, R., Chen, Y., Reyzin, L., Rothblum, R.D.: Fiat-Shamir and correlation intractability from strong KDM-secure encryption. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018, Part I. LNCS, vol. 10820, pp. 91–122. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78381-9_4
Canetti, R., Halevi, S., Katz, J.: Chosen-ciphertext security from identity-based encryption. In: Cachin, C., Camenisch, J.L. (eds.) EUROCRYPT 2004. LNCS, vol. 3027, pp. 207–222. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24676-3_13
Cramer, R., Shoup, V.: Universal hash proofs and a paradigm for adaptive chosen ciphertext secure public-key encryption. In: Knudsen, L.R. (ed.) EUROCRYPT 2002. LNCS, vol. 2332, pp. 45–64. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-46035-7_4
Dolev, D., Dwork, C., Naor, M.: Non-malleable cryptography (extended abstract). In: 23rd ACM STOC 1991, pp. 542–552 (1991)
Döttling, N.: Low noise LPN: KDM secure public key encryption and sample amplification. In: Katz, J. (ed.) PKC 2015. LNCS, vol. 9020, pp. 604–626. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46447-2_27
Döttling, N., Garg, S., Hajiabadi, M., Masny, D.: New constructions of identity-based and key-dependent message secure encryption schemes. In: Abdalla, M., Dahab, R. (eds.) PKC 2018, Part I. LNCS, vol. 10769, pp. 3–31. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-76578-5_1
Galindo, D., Herranz, J., Villar, J.: Identity-based encryption with master key-dependent message security and leakage-resilience. In: Foresti, S., Yung, M., Martinelli, F. (eds.) ESORICS 2012. LNCS, vol. 7459, pp. 627–642. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-33167-1_36
Gentry, C.: Fully homomorphic encryption using ideal lattices. In: 41st ACM STOC 2009, pp. 169–178 (2009)
Gertner, Y., Malkin, T., Myers, S.: Towards a separation of semantic and CCA security for public key encryption. In: Vadhan, S.P. (ed.) TCC 2007. LNCS, vol. 4392, pp. 434–455. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-70936-7_24
Goldwasser, S., Micali, S.: Probabilistic encryption and how to play mental poker keeping secret all partial information. In: 14th ACM STOC 1982, pp. 365–377 (1982)
Hajiabadi, M., Kapron, B.M.: Reproducible circularly-secure bit encryption: applications and realizations. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015, Part I. LNCS, vol. 9215, pp. 224–243. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-47989-6_11
Hohenberger, S., Lewko, A., Waters, B.: Detecting dangerous queries: a new approach for chosen ciphertext security. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 663–681. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_39
Kitagawa, F., Matsuda, T., Hanaoka, G., Tanaka, K.: Completeness of single-bit projection-KDM security for public key encryption. In: Nyberg, K. (ed.) CT-RSA 2015. LNCS, vol. 9048, pp. 201–219. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-16715-2_11
Kitagawa, F., Matsuda, T., Tanaka, K.: CCA security and trapdoor functions via key-dependent-message security. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019, Part III. LNCS, vol. 11694, pp. 33–64. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26954-8_2
Kitagawa, F., Tanaka, K.: A framework for achieving KDM-CCA secure public-key encryption. In: Peyrin, T., Galbraith, S. (eds.) ASIACRYPT 2018, Part II. LNCS, vol. 11273, pp. 127–157. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03329-3_5
Kitagawa, F., Tanaka, K.: Key dependent message security and receiver selective opening security for identity-based encryption. In: Abdalla, M., Dahab, R. (eds.) PKC 2018, Part I. LNCS, vol. 10769, pp. 32–61. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-76578-5_2
Koppula, V., Waters, B.: Realizing chosen ciphertext security generically in attribute-based encryption and predicate encryption. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019, Part II. LNCS, vol. 11693, pp. 671–700. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26951-7_23
Lombardi, A., Quach, W., Rothblum, R.D., Wichs, D., Wu, D.J.: New constructions of reusable designated-verifier NIZKs. IACR Cryptology ePrint Archive 242 (2019). Accessed 27 Feb 2019. A preliminary version of [35]
Lombardi, A., Quach, W., Rothblum, R.D., Wichs, D., Wu, D.J.: New constructions of reusable designated-verifier NIZKs. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019, Part III. LNCS, vol. 11694, pp. 670–700. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26954-8_22
Matsuda, T., Hanaoka, G.: Constructing and understanding chosen ciphertext security via puncturable key encapsulation mechanisms. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015, Part I. LNCS, vol. 9014, pp. 561–590. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46494-6_23
Naor, M., Yung, M.: Public-key cryptosystems provably secure against chosen ciphertext attacks. In: 22nd ACM STOC 1990, pp. 427–437 (1990)
Rackoff, C., Simon, D.R.: Non-interactive zero-knowledge proof of knowledge and chosen ciphertext attack. In: Feigenbaum, J. (ed.) CRYPTO 1991. LNCS, vol. 576, pp. 433–444. Springer, Heidelberg (1992). https://doi.org/10.1007/3-540-46766-1_35
Sahai, A.: Non-malleable non-interactive zero knowledge and adaptive chosen-ciphertext security. In: 40th FOCS 1999, pp. 543–553 (1999)
Yao, A.C.-C.: How to generate and exchange secrets (extended abstract). In: 27th FOCS 1986, pp. 162–167 (1986)
Yu, Y., Zhang, J.: Cryptography with auxiliary input and trapdoor from constant-noise LPN. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016, Part I. LNCS, vol. 9814, pp. 214–243. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53018-4_9
Acknowledgement
We thank the anonymous reviewers of TCC 2019 for helpful comments, in particular the connections of our techniques with those by Barak et al. [6]. A part of this work was supported by JST CREST Grant Number JPMJCR19F6.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 International Association for Cryptologic Research
About this paper
Cite this paper
Kitagawa, F., Matsuda, T. (2019). CPA-to-CCA Transformation for KDM Security. In: Hofheinz, D., Rosen, A. (eds) Theory of Cryptography. TCC 2019. Lecture Notes in Computer Science(), vol 11892. Springer, Cham. https://doi.org/10.1007/978-3-030-36033-7_5
Download citation
DOI: https://doi.org/10.1007/978-3-030-36033-7_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-36032-0
Online ISBN: 978-3-030-36033-7
eBook Packages: Computer ScienceComputer Science (R0)




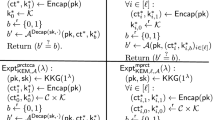
 ) security is equivalent to IND-CCA (resp. IND-CPA) security.
) security is equivalent to IND-CCA (resp. IND-CPA) security.

 .
.