Abstract
In syntax-guided synthesis (SyGuS), a synthesizer’s goal is to automatically generate a program belonging to a grammar of possible implementations that meets a logical specification. We investigate a common limitation across state-of-the-art SyGuS tools that perform counterexample-guided inductive synthesis (CEGIS). We empirically observe that as the expressiveness of the provided grammar increases, the performance of these tools degrades significantly.
We claim that this degradation is not only due to a larger search space, but also due to overfitting. We formally define this phenomenon and prove no-free-lunch theorems for SyGuS, which reveal a fundamental tradeoff between synthesizer performance and grammar expressiveness.
A standard approach to mitigate overfitting in machine learning is to run multiple learners with varying expressiveness in parallel. We demonstrate that this insight can immediately benefit existing SyGuS tools. We also propose a novel single-threaded technique called hybrid enumeration that interleaves different grammars and outperforms the winner of the 2018 SyGuS competition (Inv track), solving more problems and achieving a \(5\times \) mean speedup.
S. Padhi—Contributed during an internship at Microsoft Research, India.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
The syntax-guided synthesis (SyGuS) framework [3] provides a unified format to describe a program synthesis problem by supplying (1) a logical specification for the desired functionality, and (2) a grammar of allowed implementations. Given these two inputs, a SyGuS tool searches through the programs that are permitted by the grammar to generate one that meets the specification. Today, SyGuS is at the core of several state-of-the-art program synthesizers [5, 14, 23, 24, 29], many of which compete annually in the SyGuS competition [1, 4].
We demonstrate empirically that five state-of-the-art SyGuS tools are very sensitive to the choice of grammar. Increasing grammar expressiveness allows the tools to solve some problems that are unsolvable with less-expressive grammars. However, it also causes them to fail on many problems that the tools are able to solve with a less expressive grammar. We analyze the latter behavior both theoretically and empirically and present techniques that make existing tools much more robust in the face of increasing grammar expressiveness.
We restrict our investigation to a widely used approach [6] to SyGuS called counterexample-guided inductive synthesis (CEGIS) [37, §5]. In this approach, the synthesizer is composed of a learner and an oracle. The learner iteratively identifies a candidate program that is consistent with a given set of examples (initially empty) and queries the oracle to either prove that the program is correct, i.e., meets the given specification, or obtain a counterexample that demonstrates that the program does not meet the specification. The counterexample is added to the set of examples for the next iteration. The iterations continue until a correct program is found or resource/time budgets are exhausted.
Overfitting. To better understand the observed performance degradation, we instrumented one of these SyGuS tools (Sect. 2.2). We empirically observe that for a large number of problems, the performance degradation on increasing grammar expressiveness is often accompanied by a significant increase in the number of counterexamples required. Intuitively, as grammar expressiveness increases so does the number of spurious candidate programs, which satisfy a given set of examples but violate the specification. If the learner picks such a candidate, then the oracle generates a counterexample, the learner searches again, and so on.
In other words, increasing grammar expressiveness increases the chances for overfitting, a well-known phenomenon in machine learning (ML). Overfitting occurs when a learned function explains a given set of observations but does not generalize correctly beyond it. Since SyGuS is indeed a form of function learning, it is perhaps not surprising that it is prone to overfitting. However, we identify its specific source in the context of SyGuS—the spurious candidates induced by increasing grammar expressiveness—and show that it is a significant problem in practice. We formally define the potential for overfitting (\({\Omega } \)), in Definition 7, which captures the number of spurious candidates.
No Free Lunch. In the ML community, this tradeoff between expressiveness and overfitting has been formalized for various settings as no-free-lunch (NFL) theorems [34, §5.1]. Intuitively such a theorem says that for every learner there exists a function that cannot be efficiently learned, where efficiency is defined by the number of examples required. We have proven corresponding NFL theorems for the CEGIS-based SyGuS setting (Theorems 1 and 2).
A key difference between the ML and SyGuS settings is the notion of m-learnability. In the ML setting, the learned function may differ from the true function, as long as this difference (expressed as an error probability) is relatively small. However, because the learner is allowed to make errors, it is in turn required to learn given an arbitrary set of m examples (drawn from some distribution). In contrast, the SyGuS learning setting is all-or-nothing—either the tool synthesizes a program that meets the given specification or it fails. Therefore, it would be overly strong to require the learner to handle an arbitrary set of examples.
Instead, we define a much weaker notion of m-learnability for SyGuS, which only requires that there exist a set of m examples for which the learner succeeds. Yet, our NFL theorem shows that even this weak notion of learnability can always be thwarted: given an integer \(m \ge 0\) and an expressive enough (as a function of m) grammar, for every learner there exists a SyGuS problem that cannot be learned without access to more than m examples. We also prove that overfitting is inevitable with an expressive enough grammar (Theorems 3 and 4) and that the potential for overfitting increases with grammar expressiveness (Theorem 5).
Mitigating Overfitting. Inspired by ensemble methods [13] in ML, which aggregate results from multiple learners to combat overfitting (and underfitting), we propose PLearn—a black-box framework that runs multiple parallel instances of a SyGuS tool with different grammars. Although prior SyGuS tools run multiple instances of learners with different random seeds [7, 20], to our knowledge, this is the first proposal to explore multiple grammars as a means to improve the performance of SyGuS. Our experiments indicate that PLearn significantly improves the performance of five state-of-the-art SyGuS tools—CVC4 [7, 33], EUSolver [5], LoopInvGen [29], SketchAC [20, 37], and Stoch [3, III F].
However, running parallel instances of a synthesizer is computationally expensive. Hence, we also devise a white-box approach, called hybrid enumeration, that extends the enumerative synthesis technique [2] to efficiently interleave exploration of multiple grammars in a single SyGuS instance. We implement hybrid enumeration within LoopInvGenFootnote 1 and show that the resulting single-threaded learner, LoopInvGen +HE, has negligible overhead but achieves performance comparable to that of PLearn for LoopInvGen. Moreover, LoopInvGen +HE significantly outperforms the winner [28] of the invariant-synthesis (Inv) track of 2018 SyGuS competition [4]—a variant of LoopInvGen specifically tuned for the competition—including a \(5\times \) mean speedup and solving two SyGuS problems that no tool in the competition could solve.
Contributions. In summary, we present the following contributions:
-
(Section 2) We empirically observe that, in many cases, increasing grammar expressiveness degrades performance of existing SyGuS tools due to overfitting.
-
(Section 3) We formally define overfitting and prove no-free-lunch theorems for the SyGuS setting, which indicate that overfitting with increasing grammar expressiveness is a fundamental characteristic of SyGuS.
-
(Section 4) We propose two mitigation strategies – (1) a black-box technique that runs multiple parallel instances of a synthesizer, each with a different grammar, and (2) a single-threaded enumerative technique, called hybrid enumeration, that interleaves exploration of multiple grammars.
-
(Section 5) We show that incorporating these mitigating measures in existing tools significantly improves their performance.
2 Motivation
In this section, we first present empirical evidence that existing SyGuS tools are sensitive to changes in grammar expressiveness. Specifically, we demonstrate that as we increase the expressiveness of the provided grammar, every tool starts failing on some benchmarks that it was able to solve with less-expressive grammars. We then investigate one of these tools in detail.
2.1 Grammar Sensitivity of SyGuS Tools
We evaluated 5 state-of-the-art SyGuS tools that use very different techniques:
-
SketchAC [20] extends the Sketch synthesis system [37] by combining both explicit and symbolic search techniques.
-
Stoch [3, III F] performs a stochastic search for solutions.
-
EUSolver [5] combines enumeration with unification strategies.
-
Reynolds et al. [33] extend CVC4 [7] with a refutation-based approach.
-
LoopInvGen [29] combines enumeration and Boolean function learning.
We ran these five tools on 180 invariant-synthesis benchmarks, which we describe in Sect. 5. We ran the benchmarks with each of the six grammars of quantifier-free predicates, which are shown in Fig. 1. These grammars correspond to widely used abstract domains in the analysis of integer-manipulating programs— ,
,  [11],
[11],  [25],
[25],  [12], algebraic expressions (
[12], algebraic expressions ( ) and arbitrary integer arithmetic (
) and arbitrary integer arithmetic ( ) [30]. The
) [30]. The  operator denotes scalar multiplication, e.g.,
operator denotes scalar multiplication, e.g.,  , and
, and  denotes nonlinear multiplication, e.g.,
denotes nonlinear multiplication, e.g.,  .
.
In Fig. 2, we report our findings on running each benchmark on each tool with each grammar, with a 30-minute wall-clock timeout. For each \(\langle \)tool, grammar\(\rangle \) pair, the y-axis shows the number of failing benchmarks that the same tool is able to solve with a less-expressive grammar. We observe that, for each tool, the number of such failures increases with the grammar expressiveness. For instance, introducing the scalar multiplication operator ( ) causes CVC4 to fail on 21 benchmarks that it is able to solve with
) causes CVC4 to fail on 21 benchmarks that it is able to solve with  (
( ),
),  (
( ), or
), or  (
( ). Similarly, adding nonlinear multiplication causes LoopInvGen to fail on 10 benchmarks that it can solve with a less-expressive grammar.
). Similarly, adding nonlinear multiplication causes LoopInvGen to fail on 10 benchmarks that it can solve with a less-expressive grammar.
Observed correlation between synthesis time and number of rounds, upon increasing grammar expressiveness, with LoopInvGen [29] on 180 benchmarks
2.2 Evidence for Overfitting
To better understand this phenomenon, we instrumented LoopInvGen [29] to record the candidate expressions that it synthesizes and the number of CEGIS iterations (called rounds henceforth). We compare each pair of successful runs of each of our 180 benchmarks on distinct grammars.Footnote 2 In 65 % of such pairs, we observe performance degradation with the more expressive grammar. We also report the correlation between performance degradation and number of rounds for the more expressive grammar in each pair in Fig. 3.
In 67 % of the cases with degraded performance upon increased grammar expressiveness, the number of rounds remains unaffected—indicating that this slowdown is mainly due to a larger search space. However, there is significant evidence of performance degradation due to overfitting as well. We note an increase in the number of rounds for 27 % of the cases with degraded performance. Moreover, we notice performance degradation in 79 % of all cases that required more rounds on increasing grammar expressiveness.
Thus, a more expressive grammar not only increases the search space, but also makes it more likely for LoopInvGen to overfit—select a spurious expression, which the oracle rejects with a counterexample, hence requiring more rounds. In the remainder of this section, we demonstrate this overfitting phenomenon on the verification problem shown in Fig. 4, an example by Gulwani and Jojic [17], which is the fib_19 benchmark in the Inv track of SyGuS-Comp 2018 [4].
The fib_19 benchmark [17]
For Fig. 4, we require an inductive invariant that is strong enough to prove that the assertion on line 6 always holds. In the SyGuS setting, we need to synthesize a predicate \(\mathcal {I} :\mathbb {Z} ^{\,4} \rightarrow \mathbb {B} \) defined on a symbolic state \(\sigma = \langle m, n, x, y \rangle \), that satisfies \(\forall \sigma :\varphi (\mathcal {I}, \sigma )\) for the specification \(\varphi \):Footnote 3

where \(\sigma ' = \langle m', n', x', y' \rangle \) denotes the new state after one iteration, and T is a transition relation that describes the loop body:

In Fig. 5(a), we report the performance of LoopInvGen on fib_19 (Fig. 4) with our six grammars (Fig. 1). It succeeds with all but the least-expressive grammar. However, as grammar expressiveness increases, the number of rounds increase significantly—from 19 rounds with  to 88 rounds with
to 88 rounds with  .
.
LoopInvGen converges to the exact same invariant with both  and
and  but requires 30 more rounds in the latter case. In Figs. 5(b) and (c), we list some expressions synthesized with
but requires 30 more rounds in the latter case. In Figs. 5(b) and (c), we list some expressions synthesized with  and
and  respectively. These expressions are solutions to intermediate subproblems—the final loop invariant is a conjunction of a subset of these expressions [29, §3.2]. Observe that the expressions generated with the
respectively. These expressions are solutions to intermediate subproblems—the final loop invariant is a conjunction of a subset of these expressions [29, §3.2]. Observe that the expressions generated with the  grammar are quite complex and unlikely to generalize well.
grammar are quite complex and unlikely to generalize well.  ’s extra expressiveness leads to more spurious candidates, increasing the chances of overfitting and making the benchmark harder to solve.
’s extra expressiveness leads to more spurious candidates, increasing the chances of overfitting and making the benchmark harder to solve.
3 SyGuS Overfitting in Theory
In this section, first we formalize the counterexample-guided inductive synthesis (CEGIS) approach [37] to SyGuS, in which examples are iteratively provided by a verification oracle. We then state and prove no-free-lunch theorems, which show that there can be no optimal learner for this learning scheme. Finally, we formalize a natural notion of overfitting for SyGuS and prove that the potential for overfitting increases with grammar expressiveness.
3.1 Preliminaries
We borrow the formal definition of a SyGuS problem from prior work [3]:
Definition 1
(SyGuS Problem). Given a background theory \(\mathbb {T}\), a function symbol \(f :X \rightarrow Y\), and constraints on f: (1) a semantic constraint, also called a specification, \(\phi (f, x)\) over the vocabulary of \(\mathbb {T}\) along with f and a symbolic input x, and (2) a syntactic constraint, also called a grammar, given by a (possibly infinite) set \(\mathcal {E}\) of expressions over the vocabulary of the theory \(\mathbb {T}\); find an expression \(e \in \mathcal {E} \) such that the formula \(\forall x \in X :\phi (e, x)\) is valid modulo \(\mathbb {T}\).
We denote this SyGuS problem as  and say that it is satisfiable iff there exists such an expression e, i.e., \(\exists \, e \in \mathcal {E} :\forall x \in X :\phi (e, x)\). We call e a satisfying expression for this problem, denoted as
and say that it is satisfiable iff there exists such an expression e, i.e., \(\exists \, e \in \mathcal {E} :\forall x \in X :\phi (e, x)\). We call e a satisfying expression for this problem, denoted as  .
.
Recall, we focus on a common class of SyGuS learners, namely those that learn from examples. First we define the notion of input-output (IO) examples that are consistent with a SyGuS specification:
Definition 2
(Input-Output Example). Given a specification \(\phi \) defined on \(f :X \rightarrow Y\) over a background theory \(\mathbb {T}\), we call a pair  an input-output (IO) example for \(\phi \), denoted as
an input-output (IO) example for \(\phi \), denoted as  iff it is satisfied by some valid interpretation of f within \(\mathbb {T}\), i.e.,
iff it is satisfied by some valid interpretation of f within \(\mathbb {T}\), i.e.,

The next two definitions respectively formalize the two key components of a CEGIS-based SyGuS tool: the verification oracle and the learner.
Definition 3
(Verification Oracle). Given a specification \(\phi \) defined on a function \(f :X \rightarrow Y\) over theory \(\mathbb {T}\), a verification oracle  is a partial function that given an expression e, either returns \(\bot \) indicating \(\forall x \in X :\phi (e, x)\) holds, or gives a counterexample \(\langle x, y\rangle \) against e, denoted as
is a partial function that given an expression e, either returns \(\bot \) indicating \(\forall x \in X :\phi (e, x)\) holds, or gives a counterexample \(\langle x, y\rangle \) against e, denoted as  , such that
, such that

We omit \(\phi \) from the notations  and
and  when it is clear from the context.
when it is clear from the context.
Definition 4
(CEGIS-based Learner). A CEGIS-based learner  is a partial function that given an integer \(q \ge 0\), a set \(\mathcal {E}\) of expressions, and access to an oracle
is a partial function that given an integer \(q \ge 0\), a set \(\mathcal {E}\) of expressions, and access to an oracle  for a specification \(\phi \) defined on \(f :X \rightarrow Y\), queries
for a specification \(\phi \) defined on \(f :X \rightarrow Y\), queries  at most q times and either fails with \(\bot \) or generates an expression \(e \in \mathcal {E} \). The trace
at most q times and either fails with \(\bot \) or generates an expression \(e \in \mathcal {E} \). The trace

summarizes the interaction between the oracle and the learner. Each \(e_i\) denotes the \(i^\text {th}\) candidate for f and \(\langle x_i, y_i \rangle \) is a counterexample \(e_i\), i.e.,

Note that we have defined oracles and learners as (partial) functions, and hence as deterministic. In practice, many SyGuS tools are deterministic and this assumption simplifies the subsequent theorems. However, we expect that these theorems can be appropriately generalized to randomized oracles and learners.
3.2 Learnability and No Free Lunch
In the machine learning (ML) community, the limits of learning have been formalized for various settings as no-free-lunch theorems [34, §5.1]. Here, we provide a natural form of such theorems for CEGIS-based SyGuS learning.
In SyGuS, the learned function must conform to the given grammar, which may not be fully expressive. Therefore we first formalize grammar expressiveness:
Definition 5
(\(\varvec{k}\)-Expressiveness). Given a domain X and range Y, a grammar \(\mathcal {E}\) is said to be k-expressive iff \(\mathcal {E}\) can express exactly k distinct \(X \rightarrow Y\) functions.
A key difference from the ML setting is our notion of m-learnability, which formalizes the number of examples that a learner requires in order to learn a desired function. In the ML setting, a function is considered to m-learnable by a learner if it can be learned using an arbitrary set of m i.i.d. examples (drawn from some distribution). This makes sense in the ML setting since the learned function is allowed to make errors (up to some given bound on the error probability), but it is much too strong for the all-or-nothing SyGuS setting.
Instead, we define a much weaker notion of m-learnability for CEGIS-based SyGuS, which only requires that there exist a set of m examples that allows the learner to succeed. The following definition formalizes this notion.
Definition 6
(CEGIS-based \(\varvec{m}\)-Learnability). Given a SyGuS problem  and an integer \(m \ge 0\), we say that \(\textsf {S}\) is m-learnable by a CEGIS-based learner \(\mathcal {L}\) iff there exists a verification oracle
and an integer \(m \ge 0\), we say that \(\textsf {S}\) is m-learnable by a CEGIS-based learner \(\mathcal {L}\) iff there exists a verification oracle  under which \(\mathcal {L}\) can learn a satisfying expression for \(\textsf {S}\) with at most m queries to
under which \(\mathcal {L}\) can learn a satisfying expression for \(\textsf {S}\) with at most m queries to  , i.e.,
, i.e.,  .
.
Finally we state and prove the no-free-lunch (NFL) theorems, which make explicit the tradeoff between grammar expressiveness and learnability. Intuitively, given an integer m and an expressive enough (as a function of m) grammar, for every learner there exists a SyGuS problem that cannot be solved without access to at least \(m+1\) examples. This is true despite our weak notion of learnability.
Put another way, as grammar expressiveness increases, so does the number of examples required for learning. On one extreme, if the given grammar is 1-expressive, i.e., can express exactly one function, then all satisfiable SyGuS problems are 0-learnable—no examples are needed because there is only one function to learn—but there are many SyGuS problems that cannot be satisfied by this function. On the other extreme, if the grammar is \(|Y|^{|X|}\)-expressive, i.e., can express all functions from X to Y, then for every learner there exists a SyGuS problem that requires all |X| examples in order to be solved.
Below we first present the NFL theorem for the case when the domain X and range Y are finite. We then generalize to the case when these sets may be countably infinite. We provide the proofs of these theorems in the extended version of this paper [27, Appendix A.1].
Theorem 1
(NFL in CEGIS-based SyGuS on Finite Sets). Let X and Y be two arbitrary finite sets, \(\mathbb {T}\) be a theory that supports equality, \(\mathcal {E}\) be a grammar over \(\mathbb {T}\), and m be an integer such that \(0 \le m < |X|\). Then, either:
-
\(\mathcal {E}\) is not k-expressive for any \(k > \sum _{i \,=\, 0}^{m}\)
 , or
, or -
for every CEGIS-based learner \(\mathcal {L}\), there exists a satisfiable SyGuS problem
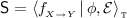 such that \(\textsf {S}\) is not m-learnable by \(\mathcal {L}\). Moreover, there exists a different CEGIS-based learner for which \(\textsf {S}\) is m-learnable.
such that \(\textsf {S}\) is not m-learnable by \(\mathcal {L}\). Moreover, there exists a different CEGIS-based learner for which \(\textsf {S}\) is m-learnable.
Theorem 2
(NFL in CEGIS-based SyGuS on Countably Infinite Sets). Let X be an arbitrary countably infinite set, Y be an arbitrary finite or countably infinite set, \(\mathbb {T}\) be a theory that supports equality, \(\mathcal {E}\) be a grammar over \(\mathbb {T}\), and m be an integer such that \(m \ge 0\). Then, either:
-
\(\mathcal {E}\) is not k-expressive for any \(k > \aleph _0\), where
 , or
, or -
for every CEGIS-based learner \(\mathcal {L}\), there exists a satisfiable SyGuS problem
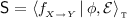 such that \(\textsf {S}\) is not m-learnable by \(\mathcal {L}\). Moreover, there exists a different CEGIS-based learner for which \(\textsf {S}\) is m-learnable.
such that \(\textsf {S}\) is not m-learnable by \(\mathcal {L}\). Moreover, there exists a different CEGIS-based learner for which \(\textsf {S}\) is m-learnable.
3.3 Overfitting
Last, we relate the above theory to the notion of overfitting from ML. In the context of SyGuS, overfitting can potentially occur whenever there are multiple candidate expressions that are consistent with a given set of examples. Some of these expressions may not generalize to satisfy the specification, but the learner has no way to distinguish among them (using just the given set of examples) and so can “guess” incorrectly. We formalize this idea through the following measure:
Definition 7
(Potential for Overfitting). Given a problem  and a set Z of IO examples for \(\phi \), we define the potential for overfitting \({\Omega } \) as the number of expressions in \(\mathcal {E}\) that are consistent with Z but do not satisfy \(\textsf {S}\), i.e.,
and a set Z of IO examples for \(\phi \), we define the potential for overfitting \({\Omega } \) as the number of expressions in \(\mathcal {E}\) that are consistent with Z but do not satisfy \(\textsf {S}\), i.e.,

Intuitively, a zero potential for overfitting means that overfitting is not possible on the given problem with respect to the given set of examples, because there is no spurious candidate. A positive potential for overfitting means that overfitting is possible, and higher values imply more spurious candidates and hence more potential for a learner to choose the “wrong” expression.
The following theorems connect our notion of overfitting to the earlier NFL theorems by showing that overfitting is inevitable with an expressive enough grammar. The proofs of these theorems can be found in the extended version of this paper [27, Appendix A.2].
Theorem 3
(Overfitting in SyGuS on Finite Sets). Let X and Y be two arbitrary finite sets, m be an integer such that \(0 \le m < |X|\), \(\mathbb {T}\) be a theory that supports equality, and \(\mathcal {E}\) be a k-expressive grammar over \(\mathbb {T}\) for some \(k>\)
 . Then, there exists a satisfiable SyGuS problem
. Then, there exists a satisfiable SyGuS problem  such that \({\Omega } (\textsf {S}, Z) > 0\), for every set Z of m IO examples for \(\phi \).
such that \({\Omega } (\textsf {S}, Z) > 0\), for every set Z of m IO examples for \(\phi \).
Theorem 4
(Overfitting in SyGuS on Countably Infinite Sets). Let X be an arbitrary countably infinite set, Y be an arbitrary finite or countably infinite set, \(\mathbb {T}\) be a theory that supports equality, and \(\mathcal {E}\) be a k-expressive grammar over \(\mathbb {T}\) for some \(k > \aleph _0\). Then, there exists a satisfiable SyGuS problem  such that \({\Omega } (\textsf {S}, Z) > 0\), for every set Z of m IO examples for \(\phi \).
such that \({\Omega } (\textsf {S}, Z) > 0\), for every set Z of m IO examples for \(\phi \).
Finally, it is straightforward to show that as the expressiveness of the grammar provided in a SyGuS problem increases, so does its potential for overfitting.
Theorem 5
(Overfitting Increases with Expressiveness). Let X and Y be two arbitrary sets, \(\mathbb {T}\) be an arbitrary theory, \(\mathcal {E} _1\) and \(\mathcal {E} _2\) be grammars over \(\mathbb {T}\) such that \(\mathcal {E} _1 \subseteq \mathcal {E} _2\), \(\phi \) be an arbitrary specification over \(\mathbb {T}\) and a function symbol \(f :X \rightarrow Y\), and Z be a set of IO examples for \(\phi \). Then, we have

4 Mitigating Overfitting
Ensemble methods [13] in machine learning (ML) are a standard approach to reduce overfitting. These methods aggregate predictions from several learners to make a more accurate prediction. In this section we propose two approaches, inspired by ensemble methods in ML, for mitigating overfitting in SyGuS. Both are based on the key insight from Sect. 3.3 that synthesis over a subgrammar has a smaller potential for overfitting as compared to that over the original grammar.

4.1 Parallel SyGuS on Multiple Grammars
Our first idea is to run multiple parallel instances of a synthesizer on the same SyGuS problem but with grammars of varying expressiveness. This framework, called PLearn, is outlined in Algorithm 1. It accepts a synthesis tool \(\mathcal {T}\), a SyGuS problem  , and subgrammars \(\mathcal {E} _{1\ldots p}\),Footnote 4 such that \(\mathcal {E} _i \subseteq \mathcal {E} \). The parallel for construct creates a new thread for each iteration. The loop in PLearn creates p copies of the SyGuS problem, each with a different grammar from \(\mathcal {E} _{1\ldots p}\), and dispatches each copy to a new instance of the tool \(\mathcal {T}\). PLearn returns the first solution found or \(\bot \) if none of the synthesizer instances succeed.
, and subgrammars \(\mathcal {E} _{1\ldots p}\),Footnote 4 such that \(\mathcal {E} _i \subseteq \mathcal {E} \). The parallel for construct creates a new thread for each iteration. The loop in PLearn creates p copies of the SyGuS problem, each with a different grammar from \(\mathcal {E} _{1\ldots p}\), and dispatches each copy to a new instance of the tool \(\mathcal {T}\). PLearn returns the first solution found or \(\bot \) if none of the synthesizer instances succeed.
Since each grammar in \(\mathcal {E} _{1\ldots p}\) is subsumed by the original grammar \(\mathcal {E}\), any expression found by PLearn is a solution to the original SyGuS problem. Moreover, from Theorem 5 it is immediate that PLearn indeed reduces overfitting.
Theorem 6
(PLearn Reduces Overfitting). Given a SyGuS problem  , if PLearn is instantiated with \(\textsf {S}\) and subgrammars \(\mathcal {E} _{1\ldots p}\) such that \(\forall \, \mathcal {E} _i \in \mathcal {E} _{1\ldots p} :\mathcal {E} _i \subseteq \mathcal {E} \), then for each
, if PLearn is instantiated with \(\textsf {S}\) and subgrammars \(\mathcal {E} _{1\ldots p}\) such that \(\forall \, \mathcal {E} _i \in \mathcal {E} _{1\ldots p} :\mathcal {E} _i \subseteq \mathcal {E} \), then for each  constructed by PLearn, we have that \({\Omega } (\textsf {S} _i, Z) \le {\Omega } (\textsf {S}, Z)\) on any set Z of IO examples for \(\phi \).
constructed by PLearn, we have that \({\Omega } (\textsf {S} _i, Z) \le {\Omega } (\textsf {S}, Z)\) on any set Z of IO examples for \(\phi \).
A key advantage of PLearn is that it is agnostic to the synthesizer’s implementation. Therefore, existing SyGuS learners can immediately benefit from PLearn, as we demonstrate in Sect. 5.1. However, running p parallel SyGuS instances can be prohibitively expensive, both computationally and memory-wise. The problem is worsened by the fact that many existing SyGuS tools already use multiple threads, e.g., the SketchAC [20] tool spawns 9 threads. This motivates our hybrid enumeration technique described next, which is a novel synthesis algorithm that interleaves exploration of multiple grammars in a single thread.
4.2 Hybrid Enumeration
Hybrid enumeration extends the enumerative synthesis technique, which enumerates expressions within a given grammar in order of size and returns the first candidate that satisfies the given examples [2]. Our goal is to simulate the behavior of PLearn with an enumerative synthesizer in a single thread. However, a straightforward interleaving of multiple PLearn threads would be highly inefficient because of redundancies – enumerating the same expression (which is contained in multiple grammars) multiple times. Instead, we propose a technique that (1) enumerates each expression at most once, and (2) reuses previously enumerated expressions to construct larger expressions.
To achieve this, we extend a widely used [2, 15, 31] synthesis strategy, called component-based synthesis [21], wherein the grammar of expressions is induced by a set of components, each of which is a typed operator with a fixed arity. For example, the grammars shown in Fig. 1 are induced by integer components (such as  ,
,  ,
,  ,
,  , etc.) and Boolean components (such as
, etc.) and Boolean components (such as  ,
,  ,
,  , etc.). Below, we first formalize the grammar that is implicit in this synthesis style.
, etc.). Below, we first formalize the grammar that is implicit in this synthesis style.
Definition 8
(Component-Based Grammar). Given a set \(\,\mathscr {C}\) of typed components, we define the component-based grammar \(\mathcal {E}\) as the set of all expressions formed by well-typed component application over \(\mathscr {C}\), i.e.,

where \(e : \tau \) denotes that the expression e has type \(\tau \).
We denote the set of all components appearing in a component-based grammar \(\mathcal {E}\) as \( \textsf {components} (\mathcal {E})\). Henceforth, we assume that \( \textsf {components} (\mathcal {E})\) is known (explicitly provided by the user) for each \(\mathcal {E}\). We also use \( \textsf {values} (\mathcal {E})\) to denote the subset of nullary components (variables and constants) in \( \textsf {components} (\mathcal {E})\), and \( \textsf {operators} (\mathcal {E})\) to denote the remaining components with positive arities.
The closure property of component-based grammars significantly reduces the overhead of tracking which subexpressions can be combined together to form larger expressions. Given a SyGuS problem over a grammar \(\mathcal {E}\), hybrid enumeration requires a sequence \(\mathcal {E} _{1\ldots p}\) of grammars such that each \(\mathcal {E} _i\) is a component-based grammar and that \(\mathcal {E} _1 \subset \cdots \subset \mathcal {E} _p \subseteq \mathcal {E} \). Next, we explain how the subset relationship between the grammars enables efficient enumeration of expressions.
Given grammars \(\mathcal {E} _1 \subset \cdots \subset \mathcal {E} _p\), observe that an expression of size k in \(\mathcal {E} _i\) may only contain subexpressions of size \(\{ 1, \ldots , (k-1) \}\) belonging to \(\mathcal {E} _{1\ldots i}\). This allows us to enumerate expressions in an order such that each subexpression e is synthesized (and cached) before any expressions that have e as a subexpression. We call an enumeration order that ensures this property a well order.
Definition 9
(Well Order). Given arbitrary grammars \(\mathcal {E} _{1\ldots p}\), we say that a strict partial order  on \(\mathcal {E} _{1\ldots p} \times \mathbb {N} \) is a well order iff
on \(\mathcal {E} _{1\ldots p} \times \mathbb {N} \) is a well order iff

Motivated by Theorem 5, our implementation of hybrid enumeration uses a particular well order that incrementally increases the expressiveness of the space of expressions. For a rough measure of the expressiveness (Definition 5) of a pair (\(\mathcal {E}\), k), i.e., the set of expressions of size k in a given grammar \(\mathcal {E}\), we simply overapproximate the number of syntactically distinct expressions:
Theorem 7
Let \(\mathcal {E} _{1\ldots p}\) be component-based grammars and \(\mathscr {C}_i = \textsf {components} (\mathcal {E} _i)\). Then, the following strict partial order  on \(\mathcal {E} _{1\ldots p} \times \mathbb {N} \) is a well order
on \(\mathcal {E} _{1\ldots p} \times \mathbb {N} \) is a well order

We now describe the main hybrid enumeration algorithm, which is listed in Algorithm 2. The HEnum function accepts a SyGuS problem  , a set \(\mathcal {E} _{1\ldots p}\) of component-based grammars such that \(\mathcal {E} _1 \subset \cdots \subset \mathcal {E} _p \subseteq \mathcal {E} \), a well order
, a set \(\mathcal {E} _{1\ldots p}\) of component-based grammars such that \(\mathcal {E} _1 \subset \cdots \subset \mathcal {E} _p \subseteq \mathcal {E} \), a well order  , and an upper bound \(q \ge 0\) on the size of expressions to enumerate. In lines 4–8, we first enumerate all values and cache them as expressions of size one. In general \(C[j, k][\tau ]\) contains expressions of type \(\tau \) and size k from \(\mathcal {E} _j \setminus \mathcal {E} _{j-1}\). In line 9 we sort (grammar, size) pairs in some total order consistent with
, and an upper bound \(q \ge 0\) on the size of expressions to enumerate. In lines 4–8, we first enumerate all values and cache them as expressions of size one. In general \(C[j, k][\tau ]\) contains expressions of type \(\tau \) and size k from \(\mathcal {E} _j \setminus \mathcal {E} _{j-1}\). In line 9 we sort (grammar, size) pairs in some total order consistent with  . Finally, in lines 10–20, we iterate over each pair \((\mathcal {E} _j, k)\) and each operator from \(\mathcal {E} _{1\ldots j}\) and invoke the Divide procedure (Algorithm 3) to carefully choose the operator’s argument subexpressions ensuring (1) correctness – their sizes sum up to \(k-1\), (2) efficiency – expressions are enumerated at most once, and (3) completeness – all expressions of size k in \(\mathcal {E} _j\) are enumerated.
. Finally, in lines 10–20, we iterate over each pair \((\mathcal {E} _j, k)\) and each operator from \(\mathcal {E} _{1\ldots j}\) and invoke the Divide procedure (Algorithm 3) to carefully choose the operator’s argument subexpressions ensuring (1) correctness – their sizes sum up to \(k-1\), (2) efficiency – expressions are enumerated at most once, and (3) completeness – all expressions of size k in \(\mathcal {E} _j\) are enumerated.
The Divide algorithm generates a set of locations for selecting arguments to an operator. Each location is a pair (x, y) indicating that any expression from \(C[x, y][\tau ]\) can be an argument, where \(\tau \) is the argument type required by the operator. Divide accepts an arity a for an operator o, a size budget q, the index l of the least-expressive grammar containing o, the index j of the least-expressive grammar that should contain the constructed expressions of the form \(o(e_1,\ldots ,e_a)\), and an accumulator \(\alpha \) that stores the list of argument locations. In lines 7–9, the size budget is recursively divided among \(a-1\) locations. In each recursive step, the upper bound \((q - a + 1)\) on v ensures that we have a size budget of at least \(q - (q - a + 1) = a - 1\) for the remaining \(a - 1\) locations. This results in a call tree such that the accumulator \(\alpha \) at each leaf node contains the locations from which to select the last \(a-1\) arguments, and we are left with some size budget \(q \ge 1\) for the first argument \(e_1\). Finally in lines 4–5, we carefully select the locations for \(e_1\) to ensure that \(o(e_1,\ldots ,e_a)\) has not been synthesized before—either \(o \in \textsf {components} (\mathcal {E} _j)\) or at least one argument belongs to \(\mathcal {E} _j \setminus \mathcal {E} _{j-1}\).Footnote 5


We conclude by stating some desirable properties satisfied by HEnum. Their proofs are provided in the extended version of this paper [27, Appendix A.3].
Theorem 8
(HEnum is Complete up to Size \(\varvec{q}\)). Given a SyGuS problem  , let \(\mathcal {E} _{1\ldots p}\) be component-based grammars over theory \(\mathbb {T}\) such that \(\mathcal {E} _1 \subset \cdots \subset \mathcal {E} _p = \mathcal {E} \),
, let \(\mathcal {E} _{1\ldots p}\) be component-based grammars over theory \(\mathbb {T}\) such that \(\mathcal {E} _1 \subset \cdots \subset \mathcal {E} _p = \mathcal {E} \),  be a well order on \(\mathcal {E} _{1\ldots p} \times \mathbb {N} \), and \(q \ge 0\) be an upper bound on size of expressions. Then, HEnum
be a well order on \(\mathcal {E} _{1\ldots p} \times \mathbb {N} \), and \(q \ge 0\) be an upper bound on size of expressions. Then, HEnum  will eventually find a satisfying expression if there exists one with size \(\le q\).
will eventually find a satisfying expression if there exists one with size \(\le q\).
Theorem 9
(HEnum is Efficient). Given a SyGuS problem  , let \(\mathcal {E} _{1\ldots p}\) be component-based grammars over theory \(\mathbb {T}\) such that \(\mathcal {E} _1 \subset \cdots \subset \mathcal {E} _p \subseteq \mathcal {E} \),
, let \(\mathcal {E} _{1\ldots p}\) be component-based grammars over theory \(\mathbb {T}\) such that \(\mathcal {E} _1 \subset \cdots \subset \mathcal {E} _p \subseteq \mathcal {E} \),  be a well order on \(\mathcal {E} _{1\ldots p} \times \mathbb {N} \), and \(q \ge 0\) be an upper bound on size of expressions. Then, HEnum
be a well order on \(\mathcal {E} _{1\ldots p} \times \mathbb {N} \), and \(q \ge 0\) be an upper bound on size of expressions. Then, HEnum  will enumerate each distinct expression at most once.
will enumerate each distinct expression at most once.
5 Experimental Evaluation
In this section we empirically evaluate PLearn and HEnum. Our evaluation uses a set of 180 synthesis benchmarks,Footnote 6 consisting of all 127 official benchmarks from the Inv track of 2018 SyGuS competition [4] augmented with benchmarks from the 2018 Software Verification competition (SV-Comp) [8] and challenging verification problems proposed in prior work [9, 10]. All these synthesis tasks are defined over integer and Boolean values, and we evaluate them with the six grammars described in Fig. 1. We have omitted benchmarks from other tracks of the SyGuS competition as they either require us to construct \(\mathcal {E} _{1\ldots p} \) (Sect. 4) by hand or lack verification oracles. All our experiments use an 8-core Intel ® Xeon ® E5 machine clocked at 2.30 GHz with 32 GB memory running Ubuntu ® 18.04.
5.1 Robustness of PLearn
For five state-of-the-art SyGuS solvers – (a) LoopInvGen [29], (b) CVC4 [7, 33], (c) Stoch [3, III F], (d) SketchAC [8, 20], and (e) EUSolver [5] – we have compared the performance across various grammars, with and without the PLearn framework (Algorithm 1). In this framework, to solve a SyGuS problem with the \(p^\text {th}\) expressiveness level from our six integer-arithmetic grammars (see Fig. 1), we run p independent parallel instances of a SyGuS tool, each with one of the first p grammars. For example, to solve a SyGuS problem with the  grammar, we run four instances of a solver with the
grammar, we run four instances of a solver with the  ,
,  ,
,  and
and  grammars. We evaluate these runs for each tool, for each of the 180 benchmarks and for each of the six expressiveness levels.
grammars. We evaluate these runs for each tool, for each of the 180 benchmarks and for each of the six expressiveness levels.
Figure 6 summarizes our findings. Without PLearn the number of failures initially decreases and then increases across all solvers, as grammar expressiveness increases. However, with PLearn the tools incur fewer failures at a given level of expressiveness, and there is a trend of decreased failures with increased expressiveness. Thus, we have demonstrated that PLearn is an effective measure to mitigate overfitting in SyGuS tools and significantly improve their performance.
5.2 Performance of Hybrid Enumeration
To evaluate the performance of hybrid enumeration, we augment an existing synthesis engine with HEnum (Algorithm 2). We modify our LoopInvGen tool [29], which is the best-performing SyGuS synthesizer from Fig. 6. Internally, LoopInvGen leverages Escher [2], an enumerative synthesizer, which we replace with HEnum. We make no other changes to LoopInvGen. We evaluate the performance and resource usage of this solver, LoopInvGen +HE, relative to the original LoopInvGen with and without PLearn (Algorithm 1).
Performance. In Fig. 7(a), we show the number of failures across our six grammars for LoopInvGen, LoopInvGen +HE and LoopInvGen with PLearn, over our 180 benchmarks. LoopInvGen +HE has a significantly lower failure rate than LoopInvGen, and the number of failures decreases with grammar expressiveness. Thus, hybrid enumeration is a good proxy for PLearn.
Resource Usage. To estimate how computationally expensive each solver is, we compare their total-time cost ( ). Since LoopInvGen and LoopInvGen +HE are single-threaded, for them we simply use the wall-clock time for synthesis as the total-time cost. However, for PLearn with p parallel instances of LoopInvGen, we consider the total-time cost as p times the wall-clock time for synthesis.
). Since LoopInvGen and LoopInvGen +HE are single-threaded, for them we simply use the wall-clock time for synthesis as the total-time cost. However, for PLearn with p parallel instances of LoopInvGen, we consider the total-time cost as p times the wall-clock time for synthesis.
In Fig. 7(b), we show the median overhead (ratio of \(\uptau \)) incurred by PLearn over LoopInvGen +HE and LoopInvGen +HE over LoopInvGen, at various expressiveness levels. As we move to grammars of increasing expressiveness, the total-time cost of PLearn increases significantly, while the total-time cost of LoopInvGen +HE essentially matches that of LoopInvGen.
5.3 Competition Performance
Finally, we evaluate the performance of LoopInvGen +HE on the benchmarks from the Inv track of the 2018 SyGuS competition [4], against the official winning solver, which we denote LIG [28]—a version of LoopInvGen [29] that has been extensively tuned for this track. In the competition, there are some invariant-synthesis problems where the postcondition itself is a satisfying expression. LIG starts with the postcondition as the first candidate and is extremely fast on such programs. For a fair comparison, we added this heuristic to LoopInvGen +HE as well. No other change was made to LoopInvGen +HE.
LoopInvGen solves 115 benchmarks in a total of 2191 seconds whereas LoopInvGen +HE solves 117 benchmarks in 429 seconds, for a mean speedup of over \(5 \times \). Moreover, no entrants to the competition could solve [4] the two additional benchmarks (gcnr_tacas08 and fib_20) that LoopInvGen +HE solves.
6 Related Work
The most closely related work to ours investigates overfitting for verification tools [36]. Our work differs from theirs in several respects. First, we address the problem of overfitting in CEGIS-based synthesis. Second, we formally define overfitting and prove that all synthesizers must suffer from it, whereas they only observe overfitting empirically. Third, while they use cross-validation to combat overfitting in tuning a specific hyperparameter of a verifier, our approach is to search for solutions at different expressiveness levels.
The general problem of efficiently searching a large space of programs for synthesis has been explored in prior work. Lee et al. [24] use a probabilistic model, learned from known solutions to synthesis problems, to enumerate programs in order of their likelihood. Other approaches employ type-based pruning of large search spaces [26, 32]. These techniques are orthogonal to, and may be combined with, our approach of exploring grammar subsets.
Our results are widely applicable to existing SyGuS tools, but some tools fall outside our purview. For instance, in programming-by-example (PBE) systems [18, §7], the specification consists of a set of input-output examples. Since any program that meets the given examples is a valid satisfying expression, our notion of overfitting does not apply to such tools. However in a recent work, Inala and Singh [19] show that incrementally increasing expressiveness can also aid PBE systems. They report that searching within increasingly expressive grammar subsets requires significantly fewer examples to find expressions that generalize better over unseen data. Other instances where the synthesizers can have a free lunch, i.e., always generate a solution with a small number of counterexamples, include systems that use grammars with limited expressiveness [16, 21, 35].
Our paper falls in the category of formal results about SyGuS. In one such result, Jha and Seshia [22] analyze the effects of different kinds of counterexamples and of providing bounded versus unbounded memory to learners. Notably, they do not consider variations in “concept classes” or “program templates,” which are precisely the focus of our study. Therefore, our results are complementary: we treat counterexamples and learners as opaque and instead focus on grammars.
7 Conclusion
Program synthesis is a vibrant research area; new and better synthesizers are being built each year. This paper investigates a general issue that affects all CEGIS-based SyGuS tools. We recognize the problem of overfitting, formalize it, and identify the conditions under which it must occur. Furthermore, we provide mitigating measures for overfitting that significantly improve the existing tools.
Notes
- 1.
Our implementation is available at https://github.com/SaswatPadhi/LoopInvGen.
- 2.
We ignore failing runs since they require an unknown number of rounds.
- 3.
We use \(\mathbb {B}\), \(\mathbb {N}\), and \(\mathbb {Z}\) to denote the sets of all Boolean values, all natural numbers (positive integers), and all integers respectively.
- 4.
We use the shorthand \( X _{1, \ldots , n}\) to denote the sequence \(\langle X _1, \ldots , X _n \rangle \).
- 5.
We use \(\diamond \) as the cons operator for sequences, e.g., \(x \diamond \langle y, z \rangle = \langle x, y, z \rangle \).
- 6.
All benchmarks are available at https://github.com/SaswatPadhi/LoopInvGen.
References
The SyGuS Competition (2019). http://sygus.org/comp/. Accessed 10 May 2019
Albarghouthi, A., Gulwani, S., Kincaid, Z.: Recursive program synthesis. In: Sharygina, N., Veith, H. (eds.) CAV 2013. LNCS, vol. 8044, pp. 934–950. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-39799-8_67
Alur, R., et al.: Syntax-guided synthesis. In: Formal Methods in Computer-Aided Design, FMCAD, pp. 1–8. IEEE (2013). http://ieeexplore.ieee.org/document/6679385/
Alur, R., Fisman, D., Padhi, S., Singh, R., Udupa, A.: SyGuS-Comp 2018: Results and Analysis. CoRR abs/1904.07146 (2019). http://arxiv.org/abs/1904.07146
Alur, R., Radhakrishna, A., Udupa, A.: Scaling enumerative program synthesis via divide and conquer. In: Legay, A., Margaria, T. (eds.) TACAS 2017. LNCS, vol. 10205, pp. 319–336. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54577-5_18
Alur, R., Singh, R., Fisman, D., Solar-Lezama, A.: Search-based program synthesis. Commun. ACM 61(12), 84–93 (2018). https://doi.org/10.1145/3208071
Barrett, C., et al.: CVC4. In: Gopalakrishnan, G., Qadeer, S. (eds.) CAV 2011. LNCS, vol. 6806, pp. 171–177. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22110-1_14
Beyer, D.: Software verification with validation of results. In: Legay, A., Margaria, T. (eds.) TACAS 2017. LNCS, vol. 10206, pp. 331–349. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54580-5_20
Bounov, D., DeRossi, A., Menarini, M., Griswold, W.G., Lerner, S.: Inferring loop invariants through gamification. In: Proceedings of the 2018 CHI Conference on Human Factors in Computing Systems, CHI, p. 231. ACM (2018). https://doi.org/10.1145/3173574.3173805
Bradley, A.R., Manna, Z., Sipma, H.B.: The polyranking principle. In: Caires, L., Italiano, G.F., Monteiro, L., Palamidessi, C., Yung, M. (eds.) ICALP 2005. LNCS, vol. 3580, pp. 1349–1361. Springer, Heidelberg (2005). https://doi.org/10.1007/11523468_109
Cousot, P., Cousot, R.: Static determination of dynamic properties of generalized type unions. In: Language Design for Reliable Software, pp. 77–94 (1977). https://doi.org/10.1145/800022.808314
Cousot, P., Halbwachs, N.: Automatic Discovery of Linear Restraints Among Variables of a Program. In: Conference Record of the Fifth Annual ACM Symposium on Principles of Programming Languages. pp. 84–96. ACM Press (1978), https://doi.org/10.1145/512760.512770
Dietterich, T.G.: Ensemble methods in machine learning. In: Kittler, J., Roli, F. (eds.) MCS 2000. LNCS, vol. 1857, pp. 1–15. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-45014-9_1
Ezudheen, P., Neider, D., D’Souza, D., Garg, P., Madhusudan, P.: Horn-ICE learning for synthesizing invariants and contracts. PACMPL 2(OOPSLA), 131:1–131:25 (2018). https://doi.org/10.1145/3276501
Feng, Y., Martins, R., Geffen, J.V., Dillig, I., Chaudhuri, S.: Component-based synthesis of table consolidation and transformation tasks from examples. In: Proceedings of the 38th ACM SIGPLAN Conference on Programming Language Design and Implementation, PLDI, pp. 422–436. ACM (2017). https://doi.org/10.1145/3062341.3062351
Godefroid, P., Taly, A.: Automated synthesis of symbolic instruction encodings from I/O samples. In: ACM SIGPLAN Conference on Programming Language Design and Implementation, PLDI, pp. 441–452. ACM (2012). https://doi.org/10.1145/2254064.2254116
Gulwani, S., Jojic, N.: Program verification as probabilistic inference. In: Proceedings of the 34th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL, pp. 277–289. ACM (2007). https://doi.org/10.1145/1190216.1190258
Gulwani, S., Polozov, O., Singh, R.: Program synthesis. Found. Trends Program. Lang. 4(1–2), 1–119 (2017). https://doi.org/10.1561/2500000010
Inala, J.P., Singh, R.: WebRelate: Integrating Web Data with Spreadsheets using Examples. PACMPL 2(POPL), 2:1–2:28 (2018). https://doi.org/10.1145/3158090
Jeon, J., Qiu, X., Solar-Lezama, A., Foster, J.S.: Adaptive concretization for parallel program synthesis. In: Kroening, D., Păsăreanu, C.S. (eds.) CAV 2015. LNCS, vol. 9207, pp. 377–394. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-21668-3_22
Jha, S., Gulwani, S., Seshia, S.A., Tiwari, A.: Oracle-guided component-based program synthesis. In: Proceedings of the 32nd ACM/IEEE International Conference on Software Engineering. ICSE, vol. 1, pp. 215–224. ACM (2010). https://doi.org/10.1145/1806799.1806833
Jha, S., Seshia, S.A.: A theory of formal synthesis via inductive learning. Acta Informatica 54(7), 693–726 (2017). https://doi.org/10.1007/s00236-017-0294-5
Le, X.D., Chu, D., Lo, D., Le Goues, C., Visser, W.: S3: syntax- and semantic-guided repair synthesis via programming by examples. In: Proceedings of the 11th Joint Meeting on Foundations of Software Engineering. ESEC/FSE, pp. 593–604. ACM (2017). https://doi.org/10.1145/3106237.3106309
Lee, W., Heo, K., Alur, R., Naik, M.: Accelerating search-based program synthesis using learned probabilistic models. In: Proceedings of the 39th ACM SIGPLAN Conference on Programming Language Design and Implementation, PLDI 2018, pp. 436–449. ACM (2018). https://doi.org/10.1145/3192366.3192410
Miné, A.: The octagon abstract domain. In: Proceedings of the Eighth Working Conference on Reverse Engineering, WCRE, p. 310. IEEE Computer Society (2001). https://doi.org/10.1109/WCRE.2001.957836
Osera, P., Zdancewic, S.: Type-and-example-directed program synthesis. In: Proceedings of the 36th ACM SIGPLAN Conference on Programming Language Design and Implementation, PLDI, pp. 619–630. ACM (2015). https://doi.org/10.1145/2737924.2738007
Padhi, S., Millstein, T., Nori, A., Sharma, R.: Overfitting in Synthesis: Theory and Practice. CoRR abs/1905.07457 (2019). https://arxiv.org/pdf/1905.07457
Padhi, S., Sharma, R., Millstein, T.: LoopInvGen: A Loop Invariant Generator based on Precondition Inference. CoRR abs/1707.02029 (2018). http://arxiv.org/abs/1707.02029
Padhi, S., Sharma, R., Millstein, T.D.: Data-driven precondition inference with learned features. In: Proceedings of the 37th ACM SIGPLAN Conference on Programming Language Design and Implementation, PLDI, pp. 42–56. ACM (2016). https://doi.org/10.1145/2908080.2908099
Peano, G.: Calcolo geometrico secondo l’Ausdehnungslehre di H. Grassmann: preceduto dalla operazioni della logica deduttiva, vol. 3. Fratelli Bocca (1888)
Perelman, D., Gulwani, S., Grossman, D., Provost, P.: Test-driven synthesis. In: ACM SIGPLAN Conference on Programming Language Design and Implementation, PLDI, pp. 408–418. ACM (2014). https://doi.org/10.1145/2594291.2594297
Polikarpova, N., Kuraj, I., Solar-Lezama, A.: Program synthesis from polymorphic refinement types. In: Proceedings of the 37th ACM SIGPLAN Conference on Programming Language Design and Implementation, PLDI, pp. 522–538. ACM (2016). https://doi.org/10.1145/2908080.2908093
Reynolds, A., Deters, M., Kuncak, V., Tinelli, C., Barrett, C.: Counterexample-guided quantifier instantiation for synthesis in SMT. In: Kroening, D., Păsăreanu, C.S. (eds.) CAV 2015. LNCS, vol. 9207, pp. 198–216. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-21668-3_12
Shalev-Shwartz, S., Ben-David, S.: Understanding Machine Learning: From Theory to Algorithms. Cambridge University Press, Cambridge (2014)
Sharma, R., Gupta, S., Hariharan, B., Aiken, A., Liang, P., Nori, A.V.: A data driven approach for algebraic loop invariants. In: Felleisen, M., Gardner, P. (eds.) ESOP 2013. LNCS, vol. 7792, pp. 574–592. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-37036-6_31
Sharma, R., Nori, A.V., Aiken, A.: Bias-variance tradeoffs in program analysis. In: The 41st Annual ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL, pp. 127–138. ACM (2014). https://doi.org/10.1145/2535838.2535853
Solar-Lezama, A.: Program sketching. STTT 15(5–6), 475–495 (2013)
Acknowledgement
We thank Guy Van den Broeck and the anonymous reviewers for helpful feedback for improving this work, and the organizers of the SyGuS competition for making the tools and benchmarks publicly available.
This work was supported in part by the National Science Foundation (NSF) under grants CCF-1527923 and CCF-1837129. The lead author was also supported by an internship and a PhD Fellowship from Microsoft Research.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this paper
Cite this paper
Padhi, S., Millstein, T., Nori, A., Sharma, R. (2019). Overfitting in Synthesis: Theory and Practice. In: Dillig, I., Tasiran, S. (eds) Computer Aided Verification. CAV 2019. Lecture Notes in Computer Science(), vol 11561. Springer, Cham. https://doi.org/10.1007/978-3-030-25540-4_17
Download citation
DOI: https://doi.org/10.1007/978-3-030-25540-4_17
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-25539-8
Online ISBN: 978-3-030-25540-4
eBook Packages: Computer ScienceComputer Science (R0)






 operator to append new rules to previously defined nonterminals.)
operator to append new rules to previously defined nonterminals.)



 , or
, or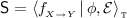 such that
such that  , or
, or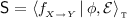 such that
such that 

 ) than P and a negligible overhead over L.
) than P and a negligible overhead over L.