A New Approach to Solve the Stokes-Darcy-Transport System Applying Stabilized Finite Element Methods

Abstract

In this work we propose a new combination of finite element methods to solve incompressible miscible displacements in heterogeneous media formed by the coupling of the free-fluid with the porous medium employing the stabilized hybrid mixed finite element method developed and analyzed by Igreja and Loula in [10] and the classical Streamline Upwind Petrov-Galerkin (SUPG) method presented and analyzed by Brooks and Hughes in [2]. The hydrodynamic problem is governed by the Stokes and Darcy systems coupled by Beavers-Joseph-Saffman interface conditions. To approximate the Stokes-Darcy coupled system we apply the stabilized hybrid mixed method, characterized by the introduction of the Lagrange multiplier associated with the velocity field in both domains. This choice naturally imposes the Beavers-Joseph-Saffman interface conditions on the interface between Stokes and Darcy domains. Thus, the global system is assembled involving only the degrees of freedom associated with the multipliers and the variables of interest can be solved at the element level. Considering the velocity fields given by the hybrid method we adopted the SUPG method combined with an implicit finite difference scheme to solve the transport equation associated with miscible displacements. Numerical studies are presented to illustrate the flexibility and robustness of the hybrid formulation. To verify the efficiency of the combination of hybrid and SUPG methods, computer simulations are also presented for the recovery hydrological flow problems in heterogeneous porous media, such as continuous injection.

1 Introduction

Numerical methods to simulate the incompressible viscous fluid flows coupling Stokes-Darcy problems has been widely developed due to various applications in physiological phenomena like the blood motion in vessels, hydrological systems in which surface water percolates through rocks and sand, petroleum engineering where are find fractured media containing vugs and caves as the naturally fractured carbonate karst reservoirs and industrial processes involving filtration [8, 14, 17, 21]. This coupled problem is characterized by the coexistence of the free fluid governed by the Stokes equations and the porous medium modeled by the Darcy problem connected by the interface conditions that guarantee continuity of mass and momentum across the interface [1, 18].

Numerically, among the several methods proposed for the coupled problem, we highlight the stable and stabilized methods introduced in [3,4,5, 13, 19]; using a Lagrange multiplier to impose the interface restrictions, we can cite [7, 11, 20]; and employing discontinuous Galerkin (DG) methods, we indicate [16] and [21]. Recently, hybridizations of DG methods have been successfully exploited to derive new finite element methods with improved stability and reduced computational cost but still preserving the robustness and flexibility of DG methods [6, 9, 10].

In this paper, in order to obtain efficiently the velocity field, we use the stabilized hybrid mixed method to solve the coupled Stokes-Darcy problem developed by [10]. This method is characterized by the introduction of a Lagrange multiplier associated with the velocity field to weakly impose continuity on each edge of the elements. Moreover, this approach naturally imposes the interface conditions between porous medium and free fluid through the Lagrange multiplier. This methodology allows the elimination of the local problems at each element level in favor of the Lagrange multiplier. Thus, the system involves only global degrees of freedom associated with the multiplier, reducing significantly the computational cost. The accuracy of this method is presented through convergence studies.

Once the hydrodynamic problem is calculated we supply the velocity field to the convection-dominated parabolic equation to obtain the concentration field in the coupled Stokes-Darcy domain. These results can, for example, characterize a reservoir through continuous or tracer injection processes, informing the preferred direction of flow [12, 14] or study the spread of pollution released in the water and assess the danger [21]. In order to illustrate the performance of the hybrid method applied to the coupled Stokes-Darcy-transport problem, where the Streamline Upwind Petrov-Galerkin (SUPG) method [2] combined with a backward finite difference scheme in time is employed to approximate the concentration equation, numerical simulations are demonstrated for the miscible transport problem using a five-spot pattern for different heterogeneous scenarios through continuous injection processes.

This paper is organized as follow. The Stokes-Darcy-transport model problem is introduced in Sect. 2. In Sect. 3, notations and definitions required to present the hybrid method are described. The stabilized mixed hybrid method for the coupled Stokes-Darcy problem is presented in Sect. 4. The Sect. 5 is devoted to convergence study and continuous injection simulations in a five-spot pattern for different heterogeneous scenarios. And finally, in Sect. 6, we present the concluding remarks of this work.

2 Model Problem

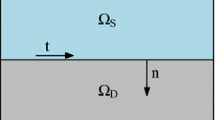
Let $\varOmega \subset \mathbb {R}^d$ ($d=2$ or 3) be the domain composed by two subdomains $\varOmega _S$ and $\varOmega _D$ related to free fluid and porous medium, respectively. In the subdomain $\varOmega _S$, with outward unit normal $\mathbf {n}_S$, the flow is governed by the Stokes problem and in porous medium $\varOmega _D$, with outward unit normal $\mathbf {n}_D$, the Darcy’s law holds. These subdomains are separated by a smooth interface $\varGamma _{SD} = \partial \varOmega _S \cap \partial \varOmega _D$, where $\mathbf {t}_j$ defines an orthonormal basis of tangent vectors on $\varGamma _{SD}$. Moreover, let $\varGamma = \varGamma _S \cup \varGamma _D$ with $\varGamma _i = \partial \varOmega _i \setminus \varGamma _{SD}$ ($i = S,D$). The Fig. 1 represents a sketch of the described domain.

Fig. 1.

A sketch of coupled Stokes-Darcy domain.

Denoting $\mathbf {u}^i=\mathbf {u}|_{\varOmega _i}$ and $p^i = p|_{\varOmega _i}$, with $i=S, D$, the free fluid domain $\varOmega _S$ is modeled by the Stokes problem that can be written as follows

Given the viscosity $\nu$ and the source $\mathbf {f}$, find the pressure $p^S:\varOmega _S\rightarrow \mathbb {R}$ and the velocity field $\mathbf {u}^S:\varOmega _S\rightarrow \mathbb {R}^d$, such that

$$\begin{aligned} -\nu \mathop {\text {div}}\nolimits \nabla \mathbf {u}^S + \nabla p^S&= \mathbf {f} \qquad \text {in} \quad \varOmega _S, \end{aligned}$$

(1)

$$\begin{aligned} \mathop {\text {div}}\nolimits \mathbf {u}_S&= 0 \qquad \text {in} \quad \varOmega _S, \end{aligned}$$

(2)

$$\begin{aligned} \mathbf {u}^S&= \mathbf {0} \quad \text {on} \quad \varGamma _S, \end{aligned}$$

(3)

where $\mathop {\text {div}}\nolimits$ and $\nabla$ denote, respectively, the divergent and gradient operators. On the other hand, in porous medium the flow is given by the Darcy problem

Given the hydraulic conductivity $\mathbf {K}$ and the source f, find the hydrostatic pressure $p_D:\varOmega _D\rightarrow \mathbb {R}$ and the Darcy velocity $\mathbf {u}_D:\varOmega _D\rightarrow \mathbb {R}^d$, such that

$$\begin{aligned} \mathbf {u}_D&=- \mathbf {K} \nabla p_D \qquad \text {in} \quad \varOmega _D, \end{aligned}$$

(4)

$$\begin{aligned} \mathop {\text {div}}\nolimits \mathbf {u}_D&= f \qquad \qquad \quad \text {in} \quad \varOmega _D, \end{aligned}$$

(5)

$$\begin{aligned} \mathbf {u}_D\cdot \mathbf {n}_D&= 0 \qquad \qquad \quad \text {on} \quad \varGamma _D, \end{aligned}$$

(6)

we define $\mathbf {K}=\mathbf {k}/\mu$ where $\mathbf {k}$ is the permeability of the porous medium. The solvability condition, which the source function f must satisfy

$$ \int _{\varOmega _D}f \, d\mathbf {x} = 0. $$

On the interface free fluid/porous medium $\varGamma _{SD}$ the following conditions are imposed

$$\begin{aligned} \mathbf {u}_S \cdot \mathbf {n}_S + \mathbf {u}_D \cdot \mathbf {n}_D = 0 \qquad \text {on} \quad \varGamma _{SD}, \end{aligned}$$

(7)

$$\begin{aligned} p_S - 2\mu \varvec{\varepsilon }(\mathbf {u}_S) \,\mathbf {n}_S \cdot \mathbf {n}_S = p_D \qquad \text {on} \quad \varGamma _{SD}, \end{aligned}$$

(8)

$$\begin{aligned} \mathbf {u}_S \cdot \mathbf {t}_j = - 2\dfrac{\sqrt{\mathbf {k}}}{\alpha } \varvec{\varepsilon }(\mathbf {u}_S) \,\mathbf {n}_S \cdot \mathbf {t}_j, \quad j=1,d-1, \qquad \text {on} \quad \varGamma _{SD}. \end{aligned}$$

(9)

The conditions (7) and (8) impose the continuity of flux and normal stress, respectively. The slip condition (9) is known as Beavers-Joseph-Saffman law [1, 18], where $\alpha >0$ is an experimentally determined dimensionless constant. The coupled problem, modeled by the Eqs. (1)–(9), is analyzed in detail by [11], where existence and uniqueness of the solution is demonstrated.

The Stokes-Darcy coupled problem provides the velocity field for the diffusive-convective-reactive transport equation defined on the domain $\varOmega = \varOmega _S \cup \varOmega _D$ whose problem is given by

Given the Stokes or Darcy velocity field $\mathbf {u}$, the porosity $\phi$, the diffusion-dispersion tensor $\mathbf {D}$, the sources $\hat{f}$ and g and the function $c_0$, find the concentration $c(\mathbf {x},t):\varOmega \times (0,T)\rightarrow \mathbb {R}^d$, such that

$$\begin{aligned} \phi \dfrac{\partial c}{\partial t} + \mathbf {u} \cdot \nabla c - \mathop {\text {div}}\nolimits (\mathbf {D} \nabla c) + \hat{f}c&= g \qquad \qquad \text {in} \quad \varOmega \times (0,T), \end{aligned}$$

(10)

$$\begin{aligned} c(\mathbf {x},0)&= c_0(\mathbf {x}) \qquad \, \, \text {in} \quad \varOmega , \end{aligned}$$

(11)

$$\begin{aligned} \mathbf {D}\nabla c \cdot \mathbf {n}&= 0 \qquad \qquad \text {on} \quad \varGamma \times (0,T). \end{aligned}$$

(12)

In the Stokes domain $\varOmega _S$

$$\begin{aligned} \phi = 1 \quad \text {and} \quad \mathbf {D}=\alpha _m\mathbf {I}, \end{aligned}$$

(13)

where $\alpha _m$ is a molecular diffusion coefficient and $\mathbf {I}$ the identity tensor. In the porous medium $\varOmega _D$, the tensor $\mathbf {D}$ can be defined as

$$\begin{aligned} \mathbf {D}=\mathbf {D}(\mathbf {u}_D)= \alpha _m\mathbf {I}+ \Vert \mathbf {u}_D\Vert \left[ \alpha _l \mathbf {E}(\mathbf {u}_D) + \alpha _t(\mathbf {I} - \mathbf {E}(\mathbf {u}_D))\right] , \quad \mathbf {E}(\mathbf {u}) = \dfrac{\mathbf {u} \otimes \mathbf {u}}{\Vert \mathbf {u}\Vert ^2}, \end{aligned}$$

with $\Vert \mathbf {u}\Vert ^2=\sum _{i=1}^d u_i^2$, $\otimes$ denoting the tensorial product, $\alpha _l$ being the longitudinal dispersion and $\alpha _t$ the transverse dispersion. In miscible displacement of a fluid through another in a reservoir, the dispersion is physically more important than the molecular diffusion [15]. Thus, we assume the following properties

$$ 0< \alpha _m \le \alpha _l, \quad \alpha _l\ge \alpha _t > 0 \quad \text {and} \quad 0< \phi \le 1 \quad \text {in} \quad \varOmega _D. $$

3 Notations and Definitions

To introduce the stabilized hybrid formulation we first recall some notations and definitions. Let $H^m(\varOmega )$ be the usual Sobolev space equipped with the usual norm $\parallel \cdot \parallel _{m,\varOmega }\,=\,\parallel \cdot \parallel _m$ and seminorm $\left| \cdot \right| _{m,\varOmega }=\left| \cdot \right| _{m}$, with $m\ge 0$. For $m=0$, we consider $L^2(\varOmega )=H^0(\varOmega )$ as the space of square integrable functions and $H^1_0(\varOmega )$ denotes the subspace of functions in $H^1(\varOmega )$ with zero trace on $\partial \varOmega$.

For a given function space $V(\varOmega )$, let $[V(\varOmega )]^d$ and $[V(\varOmega )]^{d\times d}$ be the spaces of all vectors and tensor fields whose components belong to $V(\varOmega )$, respectively. Without further specification, these spaces are furnished with the usual product norms (which, for simplicity, are denoted similarly as the norm in $V(\varOmega )$). For vectors $\mathbf {v},\mathbf {w} \in \mathbb {R}^d$ and matrices $\varvec{\sigma }, \varvec{\tau } \in \mathbb {R}^{d\times d}$ we use the standard notation.

Restricting to the two-dimensional case ($d=2$), we define a regular finite element partition $\mathcal {T}_h$ of the domain $\varOmega$:

$$\begin{aligned} \mathcal {T}_h = \{K\} := \mathrm{the\,\, union\,\, of\,\, all\,\, elements}\,\,K. \end{aligned}$$

In cases where $\varOmega$ is divided into subdomains $\varOmega _i$ with smooth boundary $\partial \varOmega _i$ and $\varGamma _i=\partial \varOmega \cap \partial \varOmega _i$, we have for each subdomain the following regular partition

$$\begin{aligned} \mathcal {T}_h^i = \{K \in \mathcal {T}_h \cap \varOmega _i\}, \end{aligned}$$

and the following set of edges

$$\begin{aligned} \mathcal {E}^i_h = \{e; e\,\,\mathrm{is\,\,an \,\,edge \,\,of}\,\,K,\,\,\mathrm{for\,\, at\,\, least\,\, one}\,\,K\in \mathcal {T}^i_h\}, \end{aligned}$$

$$\begin{aligned} \mathcal {E}^{\partial ,i}_h = \{e \in \mathcal {E}^i_h; e \subset \varGamma _i\} \end{aligned}$$

$$\begin{aligned} \mathcal {E}_h^{0,i} = \{e \in \mathcal {E}^i_h; e\,\mathrm{is\,\,an\,\,interior\,\,edge\,\,of}\,\,\varOmega _i \}, \end{aligned}$$

$$\begin{aligned} \mathcal {E}^{ij}_h = \mathcal {E}^{0,i}_h \cap \mathcal {E}^{0,j}_h. \end{aligned}$$

This last case denotes the edges that compose the interface between the subdomains, where $\varOmega _i$ and $\varOmega _j$ are two adjacent subdomains.

We assume that the domain $\varOmega$ is polygonal. Thus, there exists $c > 0$ such that $h\le c h_e$, where $h_e$ is the diameter of the edge $e \in \partial K$ and h, the mesh parameter, is the maximum element diameter. For each element K we associate a unit normal vector $\mathbf {n}_K$. Let $\mathbf {V}_h^l$ and $Q_h^m$ denote broken function spaces on $\mathcal {T}_h$ given by

$$\begin{aligned} \mathcal {V}_h^k= & {} \{\mathbf {v} \in \mathbf {L}^2(\varOmega ); \mathbf {v}_{h}|_{ K} \in [\mathbb {Q}_k({K})]^2, \ \forall K \in \mathcal {T}_h\},\end{aligned}$$

(14)

$$\begin{aligned} \mathcal {Q}_h^l= & {} \{q \in L^2(\varOmega );q_h|_{ K} \in \mathbb {Q}_l({ K}),\ \forall K \in \mathcal {T}_h \}, \end{aligned}$$

(15)

where $\mathbb {Q}_k(K)$ and $\mathbb {Q}_l(K)$ denote the space of polynomial functions of degree at most k and l, respectively, on each variable. To introduce the hybrid method, we define the following spaces associated with the Lagrange multiplier

$$\begin{aligned} \mathcal {M}^k_h= & {} \{\varvec{\mu } \in \mathbf {L}^2(\mathcal {E}_h) : \varvec{\mu }|_e = [p_k(e)]^2, \ \forall e \in \mathcal {E}^0_h,\, \varvec{\mu }|_e = \mathbf {0}, \ \forall e \in \mathcal {E}^{\partial }_h \}, \end{aligned}$$

(16)

$$\begin{aligned} \mathcal {W}^k_h= & {} \{\varvec{\mu } \in \mathbf {L}^2(\mathcal {E}_h) : \varvec{\mu }|_e = [p_k(e)]^2, \ \forall e \in \mathcal {E}^0_h,\, \varvec{\mu }|_e \cdot \mathbf {n}_e= {0}, \ \forall e \in \mathcal {E}^{\partial }_h \}, \end{aligned}$$

(17)

Similarly, $p_k(e)$ is the space of polynomial functions of degree at most k on an edge e.

Moreover, we consider the following finite element spaces

$$\begin{aligned} V_h^k(\mathcal {T}_h)&= \mathcal {V}^k_h(\mathcal {T}^S_h) \cup \mathcal {V}^k_h(\mathcal {T}^D_h) \end{aligned}$$

(18)

$$\begin{aligned} Q_h^l(\mathcal {T}_h)&= \mathcal {Q}^l_h(\mathcal {T}^S_h) \cup \mathcal {Q}^l_h(\mathcal {T}^D_h) \end{aligned}$$

(19)

for velocity and pressure fields, respectively,

$$\begin{aligned} M_h^k(\mathcal {E}_h) = \mathcal {M}^k_h(\mathcal {E}^S_h\setminus \mathcal {E}^{SD}_h) \cup \mathcal {W}^k_h(\mathcal {E}^D_h) \end{aligned}$$

(20)

for the multiplier in both Stokes and Darcy domains, the product space $\mathbf {V}_h = V_h^k(\mathcal {T}_h) \times Q_h^l(\mathcal {T}_h) \times M_h^k(\mathcal {E}_h)$ and set $\mathbf {X}_h=[\mathbf {u}_h,p_h,\varvec{\lambda }_{h}] \in \mathbf {V}_h$.

4 Stabilized Hybrid Mixed Method for Stokes-Darcy Flow

Unlike the numerical methods employing Lagrange multipliers only in the interface free fluid/porous medium to solve the coupled problem [7, 11], Igreja and Loula developed in [10] a stabilized hybrid mixed method, with Lagrange multipliers in all domain, where the interface conditions are naturally imposed, yielding a symmetric, robust and stable formulation. This formulation can be viewed below

Find $\mathbf {X}_h \in \mathbf {V}_h$ such that,

$$\begin{aligned} A_{SD}( \mathbf {X}_h, \mathbf {Y}_h) = F_{SD}(\mathbf {Y}_h), \quad \forall \mathbf {Y}_h \in \mathbf {V}_h, \end{aligned}$$

(21)

with

$$\begin{aligned} A_{SD}( \mathbf {X}_h, \mathbf {Y}_h)&=\sum _{K\in \mathcal {T}_h} A^K_{SD}([\mathbf {u}_h,p_h];[\mathbf {v}_h,q_h]) \\&+\sum _{K\in \mathcal {T}_h} \sum _{e\in \partial K } A^e_{SD}([\mathbf {u}_h,p_h,\varvec{\lambda }_h];[\mathbf {v}_h,q_h,\varvec{\mu }_h])\\ F_{SD}( \mathbf {Y}_h)&= \sum _{K\in \mathcal {T}_h} F_{SD}^K([\mathbf {v}_h,q_h]) \end{aligned}$$

where the local bilinear and linear forms are given in the Darcy domain by

$$\begin{aligned} A^K_{SD}([\mathbf {u}_h,p_h];[\mathbf {v}_h,q_h])&= A^K_{D}([\mathbf {u}^D_h,p^D_h];[\mathbf {v}_h,q_h]), \ \forall K\in \mathcal {T}^D_h, \\ F^K_{SD}([\mathbf {v}_h,q_h])&= F^K_{D}([\mathbf {v}_h,q_h]), \ \forall K\in \mathcal {T}^D_h, \nonumber \\ A^e_{SD}([\mathbf {u}_h,p_h,\varvec{\lambda }_h];[\mathbf {v}_h,q_h,\varvec{\mu }_h])&=A^e_{D}([\mathbf {u}^D_h,p^D_h,\varvec{\lambda }^D_h];[\mathbf {v}_h,q_h,\varvec{\mu }_h]), \forall e \not \in \mathcal {E}^{SD}_h \nonumber \end{aligned}$$

(22)

and in the Stokes domain by

$$\begin{aligned} A^K_{SD}([\mathbf {u}_h,p_h];[\mathbf {v}_h,q_h])&= A^K_{S}([\mathbf {u}^S_h,p^S_h];[\mathbf {v}_h,q_h]), \ \forall K\in \mathcal {T}^S_h, \\ F^K_{SD}([\mathbf {v}_h,q_h])&= F^K_{S}([\mathbf {v}_h,q_h]), \ \forall K\in \mathcal {T}^S_h, \nonumber \\ A^e_{SD}([\mathbf {u}_h,p_h,\varvec{\lambda }_h];[\mathbf {v}_h,q_h,\varvec{\mu }_h])&= A^e_{S}([\mathbf {u}^S_h,p^S_h,\varvec{\lambda }^S_h];[\mathbf {v}_h,q_h,\varvec{\mu }_h]), \ \forall e \not \in \mathcal {E}^{SD}_h. \nonumber \end{aligned}$$

(23)

plus the Beavers-Joseph-Saffman interface condition on $\varGamma _{SD}$

$$ A^e_{SD}([\mathbf {u}_h,p_h,\varvec{\lambda }_h];[\mathbf {v}_h,q_h,\varvec{\mu }_h]) = A^e_{BJS}([\mathbf {u}_h,p_h,\varvec{\lambda }_h];[\mathbf {v}_h,q_h,\varvec{\mu }_h]), \ \forall e \in \mathcal {E}^{SD}_h $$

Electing the Lagrange multiplier $\varvec{\lambda }_h^{SD} = \varvec{\lambda }^D_h = \mathbf {u}^D_h |_{\partial K} = \varvec{\lambda }^S_h = \mathbf {u}^S_h |_{\partial K}$ and the stabilization parameter $\beta _{SD}=\beta _S=\beta _D$ on the interface $\mathcal {E}_h^{SD}$, we have [10]

$$\begin{aligned} A_{BJS}^{e}&= \int _{e}\dfrac{\nu \alpha }{\sqrt{\mathbf {k}}} (\mathbf {u}^S_h \cdot \mathbf {t})(\mathbf {v}^S_h \cdot \mathbf {t}) \,ds -\int _{e} ( p_h^S-p_h^D - \nu \nabla \mathbf {u}^S_h \,\mathbf {n}_{S} \cdot \mathbf {n}_{S}) \varvec{\mu }_h \cdot \mathbf {n}_{S} \,ds \\&+\int _{e} \varvec{\lambda }^{SD}_h \cdot q^D_h \mathbf {n}_{S} \,ds + \beta _{SD} \int _{e} (\mathbf {u}^D_h-\varvec{\lambda }^{SD}_h) \cdot (\mathbf {v}^D_h - \varvec{\mu }_h) \, ds \\&+\int _{e} ( p_h^S- \nu \nabla \mathbf {u}^S_h \,\mathbf {n}_{S} \cdot \mathbf {n}_{S}) \mathbf {v}^S_h \cdot \mathbf {n}_{S} \,ds + \int _{e} q^S_h \, (\mathbf {u}^S_h-\varvec{\lambda }^{SD}_h) \cdot \mathbf {n}_{S} \,ds \\&-\int _{e} \nu \nabla \mathbf {v}^S_h \,\mathbf {n}_{S} \cdot \mathbf {n}_{S}(\mathbf {u}^S_h-\varvec{\lambda }^{SD}_h)\cdot \mathbf {n}_{S} \,ds \\&+\,\beta _{SD} \int _{e} (\mathbf {u}^S_h-\varvec{\lambda }^{SD}_h) \cdot \mathbf {n}_{S} (\mathbf {v}^S_h - \varvec{\mu }_h)\cdot \mathbf {n}_{S}\, ds. \end{aligned}$$

Moreover, the local bilinear and linear forms for the Darcy problem

$$\begin{aligned} A^K_{D}([\mathbf {u}^D_h,p^D_h];[\mathbf {v}_h,q_h])&= \int _K \mathbf {A} \mathbf {u}^D_h \cdot \mathbf {v}_h \,d\mathbf {x} + \,\int _K \nabla p_h^D \, \cdot \mathbf {v}_h \,d\mathbf {x}+ \int _K \mathbf {u}^D_h \cdot \nabla q_h \,d\mathbf {x} \nonumber \\&+\,\delta _1 \int _K \mathbf {K}(\mathbf {A}\mathbf {u}^D_h + \nabla p_h^D )\cdot (\mathbf {A}\mathbf {v}_h + \nabla q_h ) \,d\mathbf {x} \nonumber \\&+\,\delta _2 \int _K A\mathop {\text {div}}\nolimits \mathbf {u}^D_h\mathop {\text {div}}\nolimits \mathbf {v}_h\,d\mathbf {x} \nonumber \\&+\,\delta _3 \int _K \kappa \, \mathop {\text {rot}}\nolimits (\mathbf {A}\mathbf {u}^D_h) \mathop {\text {rot}}\nolimits (\mathbf {A}\mathbf {v}_h) \,d\mathbf {x}, \end{aligned}$$

(24)

$$\begin{aligned} A^e_{D}([\mathbf {u}^D_h,p_h^D,\varvec{\lambda }^D_h];[\mathbf {v}_h,q_h,\varvec{\mu }_h]) =&-\int _{e} \varvec{\lambda }^D_h \cdot q_h \mathbf {n}_K \,ds - \int _{e} \varvec{\mu }_h \cdot p_h^D \mathbf {n}_K \,ds \nonumber \\&+\, \beta _D \int _{e} (\mathbf {u}^D_h-\varvec{\lambda }^D_h) \cdot (\mathbf {v}_h - \varvec{\mu }_h) \, ds, \end{aligned}$$

(25)

$$\begin{aligned} F_{D}^K([\mathbf {v}_h,q_h]) =\,&\delta _2 \int _K A \, f \, \mathop {\text {div}}\nolimits \mathbf {v}_h\,d\mathbf {x} - \int _K f \, q_h \, d\mathbf {x}, \end{aligned}$$

(26)

For the Stokes problem, we have

$$\begin{aligned} A^K_{S}([\mathbf {u}_h^S,p_h^S];[\mathbf {v}_h,q_h])&= \int _K \nu \nabla \mathbf {u}_h^S : \nabla \mathbf {v}_h \,d\mathbf {x} \\&- \int _K \mathop {\text {div}}\nolimits \mathbf {u}_h^S \, q_h \,d\mathbf {x} - \int _K p_h^S\, \mathop {\text {div}}\nolimits \mathbf {v}_h \,d\mathbf {x} \\ F_{S}^K([\mathbf {v}_h,q_h])&= \int _K \mathbf {f} \cdot \mathbf {v}_h d\mathbf {x} \end{aligned}$$

and

$$\begin{aligned} A_{S}^{e}&([\mathbf {u}_h^S,p_h^S,\varvec{\lambda }_h^S];[\mathbf {v}_h,q_h,\varvec{\mu }_h])= -\int _{e} \nu \nabla \mathbf {u}_h^S \,\mathbf {n}_K \cdot (\mathbf {v}_h - \varvec{\mu }_h) ds \nonumber \\&-\int _{e} \nu \nabla \mathbf {v}_h \,\mathbf {n}_K \cdot (\mathbf {u}_h^S-\varvec{\lambda }_h^S) ds + \int _{e} p_h^S \, (\mathbf {v}_h - \varvec{\mu }_h) \cdot \mathbf {n}_K \,ds \nonumber \\&+ \int _{e} q_h \, (\mathbf {u}_h^S-\varvec{\lambda }_h^S) \cdot \mathbf {n}_K \,ds + \beta _S \int _{e} (\mathbf {u}_h^S-\varvec{\lambda }_h^S) \cdot (\mathbf {v}_h - \varvec{\mu }_h) ds. \end{aligned}$$

(27)

The stabilization parameters is given by

$$\begin{aligned} \beta _S=\nu \dfrac{\beta _0^S}{h}, \quad \text {with} \quad \beta _0^S>0 \quad \text {and} \quad \beta _D = A \dfrac{\beta _0^D}{h}. \end{aligned}$$

(28)

To solve this problem, the formulation (21) is splited in a set of local problems defined at the element level and a global problem associated with the multipliers. The degrees of freedom of the variables in the local problem are condensed, through the static condensation technique, and a global system is assembled in terms of the multipliers. Then, the global problem is solved leading to the approximate solution of the multipliers, which is plugged into the local problems to recover the discontinuous approximation of the velocity and pressure fields. For more details see [10].

4.1 Concentration Approximation

Given the velocity field calculated through the hybrid method (21), we can obtain the concentration field using the SUPG method [2] to approximate the transport equation (10)–(12). For this, let the time step $\varDelta t >0$, such that $N=T/\varDelta t$ and $t_n=n\varDelta t$ with $n = 1,2,...,N$ and let $I_h = \{ 0 = t_0< t_1< ... < t_N=T\}$ be a partition of the interval $I=[0,T]$. The term involving the time derivative of the concentration is approximated by backward Euler finite difference operator

$$ \dfrac{\partial c}{\partial t} (\mathbf {x},t_n) = \dfrac{\partial c^n}{\partial t} = \dfrac{c^{n+1}-c^n}{\varDelta t}. $$

Therefore, a semi-discrete approximation for the transport equation for each $n = 1, 2, ...N$, given $c^0(\mathbf {x}) = c_0(\mathbf {x})$, can be written as

$$\begin{aligned} \phi \dfrac{c^{n+1}-c^n}{\varDelta t} + \mathbf {u} \cdot \nabla c^{n+1} - \mathop {\text {div}}\nolimits (\mathbf {D}(\mathbf {u}) \nabla c^{n+1}) + \hat{f} c^{n+1} = g \quad \text {in} \quad \varOmega . \end{aligned}$$

(29)

Combining the semi-discrete approximation (29) with a stabilized finite element method in space (SUPG), we introduce the following fully discrete approximation for the concentration equation: for time levels $n = 1, 2, ...N$, find $c^{n+1}_h \in \mathcal {C}^k_h$, where $\mathcal {C}^k_h$ is a $C^0$ Lagrangean finite element space of degree at most k, such that

$$\begin{aligned} A_{SUPG}(c^{n+1}_h; \varphi _h) = F_{SUPG}(c^{n}_h; \varphi _h), \quad \forall \varphi _h \in \mathcal {C}^k_h, \end{aligned}$$

(30)

with

$$\begin{aligned} A_{SUPG}(c^{n+1}_h; \varphi _h)&= \phi \int _{\varOmega } c^{n+1}_h \varphi _h \, d\mathbf {x} +\varDelta t \int _{\varOmega } \mathbf {u}_h \cdot \nabla c^{n+1}_h \varphi _h \, d\mathbf {x} \nonumber \\&+ \varDelta t \int _{\varOmega } \mathbf {D}(\mathbf {u}_h) \nabla c^{n+1}_h \cdot \nabla \varphi _h\, d\mathbf {x} + \varDelta t \int _{\varOmega } \hat{f} c^{n+1}_h \varphi _h\, d\mathbf {x} \nonumber \\&+ \sum _{K\in \mathcal {T}_h}\int _{K} \left( \phi c^{n+1}_h + \varDelta t \mathbf {u}_h \cdot \nabla c^{n+1}_h + \varDelta t \hat{f} c^{n+1}_h \right) (\delta _K \mathbf {u}_h \cdot \nabla \varphi _h)\, ds \nonumber \\&+\sum _{K\in \mathcal {T}_h}\int _{K}\left( - \varDelta t \mathop {\text {div}}\nolimits (\mathbf {D}(\mathbf {u}_h) \nabla c^{n+1}_h)\right) (\delta _K \mathbf {u}_h \cdot \nabla \varphi _h)\, ds \end{aligned}$$

(31)

and

$$\begin{aligned} F_{SUPG}(c^{n}_h; \varphi _h)&= \phi \int _{\varOmega } c^{n}_h \, \varphi _h \, d\mathbf {x} +\,\varDelta t \int _{\varOmega } g \varphi _h \, d\mathbf {x} \nonumber \\&+ \sum _{K\in \mathcal {T}_h}\int _{K} \left( \phi c^{n}_h + \varDelta t \, g\right) (\delta _K \mathbf {u}_h \cdot \nabla \varphi _h)\, ds. \end{aligned}$$

(32)

In the system (30) the velocity field $\mathbf {u}_h$ is given by the solution of the hybrid formulation (21). The stabilization parameter $\delta _K$ is defined on each $K\in \mathcal {T}_h$ as described in [2, 14].

5 Numerical Results

In this section we present numerical experiments to evaluate the rates of convergence of the stabilized hybrid mixed formulation (21). Moreover, we use the approximate velocity field obtained by the hybrid method, which is responsible for the flow displacement, to find the concentration field calculated by a predominantly convective Eq. (10) that is numerically solved via SUPG method applied to continuous injection process in a quarter of a repeated five-spot pattern for different heterogenous scenarios [14].

5.1 Convergence Study

In this test problem, we solve a simple problem with $\mathbf {K}=\mathbf {I}$ and $\mu =1.0$ in a square domain $\varOmega = \varOmega _D \cup \varOmega _S = (0.0,1.0)^2$, with respective Stokes and Darcy sources

$$\begin{aligned} \mathbf {f} = \begin{bmatrix} \left( 1/2 + 1/(8\pi ^2)\right) \sin (\pi x) \exp (y/2) \\ \left( \pi - 3/(4\pi ) \right) \cos (\pi x) \exp (y/2) \end{bmatrix}, \qquad f = \left( \dfrac{1}{2\pi } -2\pi \right) \cos (\pi x) \exp (y/2), \end{aligned}$$

with the exact solution presented in [4, 10].

In the convergence study we adopt h-refinement strategy taking a sequence of $n\times n$ uniform meshes, with $n= 4,8,16,32,64$, using quadrilateral elements $\mathbb {Q}_k\mathbb {Q}_l-p_m$, where k, l and m denote, respectively, the degree of polynomial spaces for velocity, pressure and multiplier, considering equal order approximations for all fields $k=l=m=1$ and 2 with the respectives stabilization parameters for the Stokes and Darcy multipliers $\beta _0^S = 12.0$ and 24.0 and $\beta _0^D = 1.0$ and 15.0. For the least square stabilization parameters defined in the interior of the elements we adopt in all simulations

$$\begin{aligned} \delta _1 = -0.5, \quad \delta _2 = 0.5, \quad \delta _3 = 0.5. \end{aligned}$$

(33)

In Fig. 2 we can see the h-convergence study for the velocity and pressure in the $L^2(\varOmega )$ norm compared to the interpolant for $\mathbb {Q}_1\mathbb {Q}_1-p_1$ and $\mathbb {Q}_2\mathbb {Q}_2-p_2$ elements, respectively. The results demonstrate optimal convergence rates for all fields studied, except for the pressure field approximated by biquadratic elements (Fig. 2(d)), in which case the potential loses accuracy.

Fig. 2.

h-convergence study of the Stokes-Darcy approximations ($\mathbf {u}_h^{SD}$ and $p_h^{SD}$) comparing the hybrid method with the respective interpolant ($\mathbf {u}_I$ or $p_I$) in $L^2(\varOmega )$ norm for $\mathbb {Q}_1\mathbb {Q}_1-p_1$ and $\mathbb {Q}_2\mathbb {Q}_2-p_2$ elements.

5.2 Continuous Injection Simulation

Here we simulate a quarter of a repeated five-spot pattern in two dimension consisting of a square domain (unit thickness) with side $L=1000.0\,ft$. The injector well is located at the lower-left corner ($x = y = 0$) and the producer well at the upper-right corner ($x = y = L$). For this, we use the hybrid formulation (21) to approximate the hydrodynamic problem, then we supply the velocity field to the transport equation that is numerically solved by the SUPG method combined with an implicit finite difference scheme in three different scenarios described in Fig. 3.

Fig. 3.

Three coupled porous medium (shaded) free fluid (white) domains used to simulate the five-spot problem.

Fig. 4.

Scenario 1: front propagation of the concentration in five-spot problem.

Fig. 5.

Scenario 2: front propagation of the concentration in five-spot problem.

Fig. 6.

Scenario 3: front propagation of the concentration in five-spot problem.

These three cases are considered for a porous medium with homogeneous permeability $\kappa = 10.0 mD$, where $\mathbf {K}=(\kappa / \mu ) \mathbf {I}$, viscosity of the resident fluid is $\mu = 1.0 \, cP$, porosity $\phi = 0.1$, molecular diffusion $\alpha _m=0.0$, longitudinal dispersion $\alpha _l=10.0 \, ft^2/day$, transverse dispersion $\alpha _t=1.0 \, ft^2/day$ and the flow rate is 800 square feet per day. For the Stokes region the diffusion tensor is chosen to be $\mathbf {D}=\alpha _m \mathbf {I}$ with $\alpha _m=1.0\, ft^2/day$. We fix the same values of the numerical stabilization parameters presented in (33) and $\alpha =1.0$. Moreover, a time step of 5 days and uniform meshes of $40 \times 40$ bilinear quadrilateral elements are adopted employing equal order approximations for all fields (velocity, pressure, multiplier and concentration).

The Figs. 4, 5 and 6 show the concentration maps and concentration contours for the proposed scenarios. In these graphs we can clearly observe the effect of the barrier on the continuous injection transport generated by the low permeability of the porous medium. The continuous injection concentration in the scenario 3 (Fig. 6) takes longer time to reach the producer well due to the higher heterogeneity of the medium, because it presents more discontinuities generated by the free fluid/porous medium interfaces, which reduces the flow velocity.

6 Conclusions

In this work we recall the stabilized hybrid mixed formulation for the Stokes-Darcy problem to solve the hydrodynamic flow of the transport concentration approximated by SUPG method combined with a backward finite difference scheme in time to simulate the continuous injection in free fluid/porous medium domain. The hybrid method imposes naturally the interface conditions due to the choice of the Lagrange multipliers. Moreover, this formulation is able to recover stability of very convenient finite element approximations, such as equal order Lagrangian polynomial approximations for all fields which are unstable with standard dual mixed formulation for each region.

The convergence results for the hybrid method illustrate the flexibility and robustness of the hybrid finite element formulation and show optimal rates of convergence. With respect the concentration approximation, the combination of hybrid and SUPG methods gave stable and accurate results in heterogeneous media formed by free fluid and porous medium capturing precisely the phenomena arising of this interaction.