$\mathsf {StocHy}$: Automated Verification and Synthesis of Stochastic Processes

Abstract

$\mathsf {StocHy}$ is a software tool for the quantitative analysis of discrete-time stochastic hybrid systems (shs). $\mathsf {StocHy}$ accepts a high-level description of stochastic models and constructs an equivalent shs model. The tool allows to (i) simulate the shs evolution over a given time horizon; and to automatically construct formal abstractions of the shs. Abstractions are then employed for (ii) formal verification or (iii) control (policy, strategy) synthesis. $\mathsf {StocHy}$ allows for modular modelling, and has separate simulation, verification and synthesis engines, which are implemented as independent libraries. This allows for libraries to be easily used and for extensions to be easily built. The tool is implemented in c++ and employs manipulations based on vector calculus, the use of sparse matrices, the symbolic construction of probabilistic kernels, and multi-threading. Experiments show $\mathsf {StocHy}$’s markedly improved performance when compared to existing abstraction-based approaches: in particular, $\mathsf {StocHy}$ beats state-of-the-art tools in terms of precision (abstraction error) and computational effort, and finally attains scalability to large-sized models (12 continuous dimensions). $\mathsf {StocHy}$ is available at www.gitlab.com/natchi92/StocHy. Data or code related to this paper is available at: [31].

1 Introduction

Stochastic hybrid systems (shs) are a rich mathematical modelling framework capable of describing systems with complex dynamics, where uncertainty and hybrid (that is, both continuous and discrete) components are relevant. Whilst earlier instances of shs have a long history, shs proper have been thoroughly investigated only from the mid 2000s, and have been most recently applied to the study of complex systems, both engineered and natural. Amongst engineering case studies, shs have been used for modelling and analysis of micro grids [29], smart buildings [23], avionics [7], automation of medical devices [3]. A benchmark for shs is also described in [10]. However, a wider adoption of shs in real-world applications is stymied by a few factors: (i) the complexity associated with modelling shs; (ii) the generality of their mathematical framework, which requires an arsenal of advanced and diverse techniques to analyse them; and (iii) the undecidability of verification/synthesis problems over shs and the curse of dimensionality associated with their approximations.

This paper introduces a new software tool - $\mathsf {StocHy}$ - which is aimed at simplifying both the modelling of shs and their analysis, and which targets the wider adoption of shs, also by non-expert users. With focus on the three limiting factors above, $\mathsf {StocHy}$ allows to describe shs by parsing or extending well-known and -used state-space models and generates a standard shs model automatically and formats it to be analysed. $\mathsf {StocHy}$ can (i) perform verification tasks, e.g., compute the probability of staying within a certain region of the state space from a given set of initial conditions; (ii) automatically synthesise policies (strategies) maximising this probability, and (iii) simulate the shs evolution over time. $\mathsf {StocHy}$ is implemented in c++ and modular making it both extendible and portable.

Related work. There exist only a few tools that can handle (classes of) shs. Of much inspiration for this contribution, $\textsc {faust}^2$ [28] generates abstractions for uncountable-state discrete-time stochastic processes, natively supporting shs models with a single discrete mode and finite actions, and performs verification of reachability-like properties and corresponding synthesis of policies. $\textsc {faust}^2$ is naïvely implemented in matlab and lacks in scalability to large models. The modest toolset [18] allows to model and to analyse classes of continuous-time shs, particularly probabilistic hybrid automata (pha) that combine probabilistic discrete transitions with deterministic evolution of the continuous variables. The tool for stochastic and dynamically coloured petri nets (sdcpn) [13] supports compositional modelling of pha and focuses on simulation via Monte Carlo techniques. The existing tools highlight the need for a new software that allows for (i) straightforward and general shs modelling construction and (ii) scalable automated analysis.

Contributions. The $\mathsf {StocHy}$ tool newly enables

• formal verification of shs via either of two abstraction techniques:

  • for discrete-time, continuous-space models with additive disturbances, and possibly with multiple discrete modes, we employ formal abstractions as general Markov chains or Markov decision processes [28]; $\mathsf {StocHy}$ improves techniques in the $\textsc {faust}^2$ tool by simplifying the input model description, by employing sparse matrices to manipulate the transition probabilities and by reducing the computational time needed to generate the abstractions.

  • for models with a finite number of actions, we employ interval Markov decision processes and the model checking framework in [22]; $\mathsf {StocHy}$ provides a novel abstraction algorithm allowing for efficient computation of the abstract model, by means of an adaptive and sequential refining of the underlying abstraction. We show that we are able to generate significantly smaller abstraction errors and to verify models with up to 12 continuous variables.

• control (strategy, policy) synthesis via formal abstractions, employing:

  • stochastic dynamic programming; $\mathsf {StocHy}$ exploits the use of symbolic kernels.

  • robust synthesis using interval Markov decision processes; $\mathsf {StocHy}$ automates the synthesis algorithm with the abstraction procedure and the temporal property of interest, and exploits the use of sparse matrices;

• simulation of complex stochastic processes, such as shs, by means of Monte Carlo techniques; $\mathsf {StocHy}$ automatically generates statistics from the simulations in the form of histograms, visualising the evolution of both the continuous random variables and the discrete modes.

This contribution is structured as follows: Sect. 2 crisply presents the theoretical underpinnings (modelling and analysis) for the tool. We provide an overview of the implementation of $\mathsf {StocHy}$ in Sect. 3. We highlight features and use of $\mathsf {StocHy}$ by a set of experimental evaluations in Sect. 4: we provide four different case studies that highlight the applicability, ease of use, and scalability of $\mathsf {StocHy}$. Details on executing all the case studies are detailed in this paper and within a Wiki page that accompanies the $\mathsf {StocHy}$ distribution.

2 Theory: Models, Abstractions, Simulations

2.1 Models - Discrete-Time Stochastic Hybrid Systems

$\mathsf {StocHy}$ supports the modelling of the following general class of shs [1, 4].

Definition 1

A shs [4] is a discrete-time model defined as the tuple

$$\begin{aligned} \mathcal {H} =(\mathcal {Q},n,\mathcal {U}, T_{x}, T_{q}), \quad where \end{aligned}$$

(1)

• $\mathcal {Q} = \{q_{1},q_{2}, \dots ,q_{m}\}$, $m\in \mathbb {N},$ represents a finite set of modes (locations);

• $n\in \mathbb {N}$ is the dimension of the continuous space $\mathbb {R}^{n}$ of each mode; the hybrid state space is then given by $\mathcal {D}= \cup _{q\in \mathcal {Q}}\{q\} \times \mathbb {R}^{n}$;

• $\mathcal {U}$ is a continuous set of actions, e.g. $\mathbb {R}^{v}$;

• $T_{q}: \mathcal {Q} \times \mathcal {D}\times \mathcal {U} \rightarrow [0,1]$ is a discrete stochastic kernel on Q given $\mathcal {D}\times \mathcal {U}$, which assigns to each $s=(q,x) \in \mathcal {D}$ and $u \in \mathcal {U}$, a probability distribution over $\mathcal {Q}: T_{q}(\cdot |s,u)$;

• $T_{x}: \mathcal B(\mathbb {R}^{n}) \times \mathcal {D}\times \mathcal {U} \rightarrow [0,1]$ is a Borel-measurable stochastic kernel on $\mathbb {R}^{n}$ given $\mathcal {D}\times \mathcal {U}$, which assigns to each $s \in \mathcal {D}$ and $u \in \mathcal {U}$ a probability measure on the Borel space $(\mathbb {R}^{n}, \mathcal B(\mathbb {R}^{n})): T_{x}( \cdot |s,u)$.

In this model the discrete component takes values in a finite set $\mathcal {Q}$ of modes (a.k.a. locations), each endowed with a continuous domain (the Euclidean space $\mathbb {R}^{n}$). As such, a point s over the hybrid state space $\mathcal {D}$ is pair (q, x), where $q \in \mathcal {Q}$ and $x \in \mathbb {R}^{n}$. The semantics of transitions at any point over a discrete time domain, are as follows: given a point $s \in \mathcal {D}$, the discrete state is chosen from $T_{q}$, and depending on the selected mode $q \in \mathcal {Q}$ the continuous state is updated according to the probabilistic law $T_{x}$. Non-determinism in the form of actions can affect both discrete and continuous transitions.

Remark 1

A rigorous characterisation of shs can be found in [1], which introduces a general class of models with probabilistic resets and a hybrid actions space. Whilst we can deal with general shs models, in the case studies of this paper we focus on special instances, as described next.    $\square$

Remark 2

(Special instance). In Case Study 2 (see Sect. 4.2) we look at models where actions are associated to a deterministic selection of locations, namely $T_{q}: \mathcal {U} \rightarrow \mathcal {Q}$ and $\mathcal {U}$ is a finite set of actions.    $\square$

Remark 3

(Special instance). In Case Study 4 (Sect. 4.4) we consider non-linear dynamical models with bilinear terms, which are characterised for any $q \in \mathcal {Q}$ by $x_{k+1} = A_q x_{k}+ B_q u_k + x_k\sum _{i=1}^{v}N_{q,i}u_{i,k} + G_q w_k$, where $k \in \mathbb {N}$ represents the discrete time index, $A_q,\; B_q,\;G_q$ are appropriately sized matrices, $N_{q,i}$ represents the bilinear influence of the $i-$th input component $u_{i}$, and $w_k = w \sim \mathcal {N}(\cdot ;0,1)$ and $\mathcal {N}(\cdot ;\eta ,\nu )$ denotes a Gaussian density function with mean $\eta$ and covariance matrix ${\nu ^2}$. This expresses the continuous kernel $T_{x}: \mathcal B(\mathbb {R}^{n}) \times \mathcal {D}\times \mathcal {U} \rightarrow [0,1]$ as

$$\begin{aligned} \mathcal {N}(\cdot ; A_qx + B_qu + x\sum _{i=1}^{v}N_{q,i}u_{i} + F_q, G_q). \end{aligned}$$

(2)

In Case Study 1-2-3 (Sects. 4.1–4.3), we look at the special instance from [22], where the dynamics are autonomous (no actions) and linear: here $T_{x}$ is

$$\begin{aligned} \mathcal {N}(\cdot ; A_qx+ F_q, G_q), \end{aligned}$$

(3)

where in Case Studies 1, 3 $\mathcal {Q}$ is a single element.    $\square$

Definition 2

A Markov decision process (mdp) [5] is a discrete-time model defined as the tuple

$$\begin{aligned} \mathcal {H} =(\mathcal {Q},\mathcal {U},T_{q}), \quad where \end{aligned}$$

(4)

• $\mathcal {Q} = \{q_{1},q_{2}, \dots ,q_{m}\}$, $m\in \mathbb {N},$ represents a finite set of modes;

• $\mathcal {U}$ is a finite set of actions;

• $T_{q}: \mathcal {Q} \times \mathcal {Q} \times \mathcal {U} \rightarrow [0,1]$ is a discrete stochastic kernel that assigns, to each $q \in \mathcal {Q}$ and $u \in \mathcal {U}$, a probability distribution over $\mathcal {Q}: T_{q}(\cdot |q,u)$.

Whenever the set of actions is trivial or a policy is synthesised and used (cf. discussion in Sect. 2.2) the mdp reduces to a Markov chain (mc), and a kernel $T_{q}: \mathcal {Q} \times \mathcal {Q} \rightarrow [0,1]$ assigns to each $q \in \mathcal {Q}$ a distribution over $\mathcal {Q}$ as $T_q(\cdot |q)$.

Definition 3

An interval Markov decision process (imdp) [26] extends the syntax of an mdp by allowing for uncertain $T_{q}$, and is defined as the tuple

$$\begin{aligned} \mathcal {H} =(\mathcal {Q},\mathcal {U},\check{P},\hat{P}), \quad where \end{aligned}$$

(5)

• $\mathcal {Q}$ and $\mathcal {U}$ are as in Definition 2;

• $\check{P}$ and $\hat{P}: \mathcal {Q} \times \mathcal {U} \times \mathcal {Q} \rightarrow [0,1]$ is a function that assigns to each $q \in \mathcal {Q}$ a lower (upper) bound probability distribution over $\mathcal {Q}: \check{P}(\cdot |q,u)$ $(\hat{P}(\cdot |q,u)$ respectively).

For all $q, q' \in \mathcal {Q}$ and $u \in \mathcal {U}$, it holds that $\check{P}(q'|q,u) \le \hat{P}(q' |q,u)$ and,

$$ \sum _{q'\in \mathcal {Q}} \check{P}(q' |q,u) \le 1 \le \sum _{q'\in \mathcal {Q}} \hat{P}(q'|q,u).$$

Note that when $\check{P}(\cdot |q,u) = \hat{P}(\cdot |q,u)$, the imdp reduces to the mdp with $\check{P}(\cdot |q,u) = \hat{P}(\cdot |q,u)= T_q(\cdot |q,u)$.

2.2 Formal Verification and Strategy Synthesis via Abstractions

Formal verification and strategy synthesis over shs are in general not decidable [4, 30], and can be tackled via quantitative finite abstractions. These are precise approximations that come in two main different flavours: abstractions into mdp [4, 28] and into imdp [22]. Once the finite abstractions are obtained, and with focus on specifications expressed in (non-nested) pctl or fragments of ltl [5], formal verification or strategy synthesis can be performed via probabilistic model checking tools, such as prism [21], storm [12], iscasMc [17]. We overview next the two alternative abstractions, as implemented in $\mathsf {StocHy}$.

Abstractions into Markov decision processes. Following [27], mdp are generated by either (i) uniformly gridding the state space and computing an abstraction error, which depends on the continuity of the underlying continuous dynamics and on the chosen grid; or (ii) generating the grid adaptively and sequentially, by splitting the cells with the largest local abstraction error until a desired global abstraction error is achieved. The two approaches display an intuitive trade-off, where the first in general requires more memory but less time, whereas the second generates smaller abstractions. Either way, the probability to transit from each cell in the grid into any other cell characterises the mdp matrix $T_q$. Further details can be found in [28]. $\mathsf {StocHy}$ newly provides a c++ implementation and employs sparse matrix representation and manipulation, in order to attain faster generation of the abstraction and use in formal verification or strategy synthesis.

Verification via mdp (when the action set is trivial) is performed to check the abstraction against non-nested, bounded-until specifications in pctl [5] or co-safe linear temporal logic (csltl) [20].

Strategy synthesis via mdp is defined as follows. Consider, the class of deterministic and memoryless Markov strategies $\pi = (\mu _0, \mu _1, \dots )$ where $\mu _k: \mathcal {Q} \rightarrow \mathcal {U}$. We compute the strategy $\pi ^\star$ that maximises the probability of satisfying a formula, with algorithms discussed in [28].

Abstraction into Interval Markov decision processes (imdp) is based on a procedure in [11] performed using a uniform grid and with a finite set of actions $\mathcal {U}$ (see Remark 2). $\mathsf {StocHy}$ newly provides the option to generate a grid using adaptive/sequential refinements (similar to the case in the paragraph above) [27], which is performed as follows: (i) define a required minimal maximum abstraction error $\varepsilon _{max}$; (ii) generate a coarse abstraction using the Algorithm in [11] and compute the local error $\varepsilon _q$ that is associated to each abstract state q; (iii) split all cells where $\varepsilon _q > \varepsilon _{max}$ along the main axis of each dimension, and update the probability bounds (and errors); and (iv) repeat this process until $\forall q, \; \varepsilon _{q} < \varepsilon _{max}$.

Verification via imdp is run over properties in csltl or bounded-LTL (bltl) form using the imdp model checking algorithm in [22].

Synthesis via imdp [11] is carried out by extending the notions of strategies of mdp to depend on memory, that is on prefixes of paths.

2.3 Analysis via Monte Carlo Simulations

Monte Carlo techniques generate numerical sampled trajectories representing the evaluation of a stochastic process over a predetermined time horizon. Given a sufficient number of trajectories, one can approximate the statistical properties of the solution process with a required confidence level. This approach has been adopted for simulation of different types of shs. [19] applies sequential Monte Carlo simulation to shs to reason about rare-event probabilities. [13] performs Monte Carlo simulations of classes of shs described as Petri nets. [8] proposes a methodology for efficient Monte Carlo simulations of continuous-time shs. In this work, we analyse a shs model using Monte Carlo simulations following the approach in [4]. Additionally, we generate histogram plots at each time step, providing further insight on the evolution of the solution process.

3 Overview of $\mathsf {StocHy}$

Installation. $\mathsf {StocHy}$ is set up using the provided get_dep file found within the distribution package, which will automatically install all the required dependencies. The executable run.sh builds and runs $\mathsf {StocHy}$. This basic installation setup has been successfully tested on machines running Ubuntu 18.04.1 LTS GNU and Linux operating systems.

Input interface. The user interacts with $\mathsf {StocHy}$ via the main file and must specify (i) a high-level description of the model dynamics and (ii) the task to be performed. The description of model dynamics can take the form of a list of the transition probabilities between the discrete modes, and of the state-space models for the continuous variables in each mode; alternatively, a description can be obtained by specifying a path to a matlab file containing the model description in state-space form together with the transition probability matrix. Tasks can be of three kinds (each admitting specific parameters): simulation, verification, or synthesis. The general structure of the input interface is illustrated via an example in Listing 1.1: here the user is interested in simulating a shs with two discrete modes $\mathcal {Q} = \{q_0,q_1\}$ and two continuous variables evolve according to (3). The model is autonomous and has no control actions. The relationship between the discrete modes is defined by a fixed transition probability (line 1). The evolution of the continuous dynamics are defined in lines 2–14. The initial condition for both the discrete modes and the continuous variables are set in lines 16–21 (this is needed for simulation tasks). The equivalent shs model is then set up by instantiating an object of type (line 23). Next, the task is defined in line 27 (simulation with a time horizon $K= 32$, as specified in line 25 and using the simulator library, as set in line 26). We combine the model and task specification together in line 29. Finally, $\mathsf {StocHy}$ carries out the simulation using the function performTask (line 31).

Modularity. $\mathsf {StocHy}$ comprises independent libraries for different tasks, namely (i) $\textsc {faust}^2$, (ii) imdp, and (iii) simulator. Each of the libraries is separate and depends only on the model structure that has been entered. This allows for seamless extensions of individual sub-modules with new or existing tools and methods. The function performTask acts as multiplexer for calling any of the libraries depending on the input model and task specification.

Data structures. $\mathsf {StocHy}$ makes use of multiple techniques to minimise computational overhead. It employs vector algebra for efficient handling of linear operations, and whenever possible it stores and manipulates matrices as sparse structures. It uses the linear algebra library Armadillo [24, 25], which applies multi-threading and a sophisticated expression evaluator that has been shown to speed up matrix manipulations in c++ when compared to other libraries. $\textsc {faust}^2$ based abstractions define the underlying kernel functions symbolically using the library GiNaC [6], for easy evaluation of the stochastic kernels.

Output interface. We provide outputs as text files for all three libraries, which are stored within the results folder. We also provide additional python scripts for generating plots as needed. For abstractions based on $\textsc {faust}^2$, the user has the additional option to export the generated mdp or mc to prism format, to interface with the popular model checker [21] ($\mathsf {StocHy}$ prompts the user this option following the completion of the verification or synthesis task). As a future extension, we plan to export the generated abstraction models to the model checker storm [12] and to the modelling format jani [9].

4 $\mathsf {StocHy}$: Experimental Evaluation

We apply $\mathsf {StocHy}$ on four different case studies highlighting different models and tasks to be performed. All the experiments are run on a standard laptop, with an Intel Core i7-8550U CPU at 1.80 GHz $\times$ 8 and with 8 GB of RAM.

4.1 Case Study 1 - Formal Verification

We consider the shs model first presented in [2]. The model takes the form of (1), and has one discrete mode and two continuous variables representing the level of CO$_2$ ($x_1$) and the ambient temperature ($x_2$), respectively. The continuous variables evolve according to

$$\begin{aligned}&x_{1,k+1} = x_{1,k} + \frac{\varDelta }{V}(-\rho _mx_{1,k} + \varrho _{c}(C_{out} - x_{1,k})) + \sigma _{1} w_{k}, \\&x_{2,k+1} = x_{2,k} + \frac{\varDelta }{C_z}(\rho _mC_{pa} (T_{set} -x_{2,k}) + \frac{\varrho _{c}}{R}(T_{out} - x_{2,k})) + \sigma _{2} w_k, \nonumber \end{aligned}$$

(6)

where $\varDelta$ the sampling time [min], V is the volume of the zone [$m^3$], $\rho _m$ is the mass air flow pumped inside the room [$m^3/min$], $\varrho _{c}$ is the natural drift air flow [$m^3/min$], $C_{out}$ is the outside $CO_2$ level [ppm / min], $T_{set}$ is the desired temperature [$^oC$], $T_{out}$ is the outside temperature [${ ~^\circ C}/min$], $C_z$ is the zone capacitance [$Jm^3/{ ~^\circ C}$], $C_{pa}$ is the specific heat capacity of air [$J/{ ~^\circ C}$], R is the resistance to heat transfer [${ ~^\circ C}/J$], and $\sigma _{(\cdot )}$ is a variance term associated to the noise $w_k \sim \mathcal {N}(0,1)$.

We are interested in verifying whether the continuous variables remain within the safe set $X_{safe} =[405, 540] \times [18,24]$ over 45 min ($K = 3$). This property can be encoded as a bltl property, $\varphi _1 := \square ^{\le K} X_{safe},$ where $\square$ is the “always” temporal operator considered over a finite horizon. The semantics of bltl is defined over finite traces, denoted by $\zeta = \{\zeta _j\}_{j=0}^{K}$. A trace $\zeta$ satisfies $\varphi _1$ if $\forall j \le K, \zeta _j \in X_{safe}$, and we quantify the probability that traces generated by the shs satisfy $\varphi _1$.

When tackled with the method based on $\textsc {faust}^2$ that hinges on the computation of Lipschitz constants, this verification task is numerically tricky, in view of difference in dimensionality of the range of $x_1$ and $x_2$ within the safe set $X_{safe}$ and the variance associated with each dimension $G_{q_0}= [{\begin{matrix} \sigma _{1} &{} 0 \\ 0 &{} \sigma _{2} \\ \end{matrix}}] = [{\begin{matrix} 40.096 &{}0 \\ 0 &{} 0.511\\ \end{matrix}}]$. In order to mitigate this, $\mathsf {StocHy}$ automatically rescales the state space so all the dynamics evolve in a comparable range.

Implementation. $\mathsf {StocHy}$ provides two verification methods, one based on $\textsc {faust}^2$ and the second based on imdp. We parse the model from file cs1.mat (see line 2 of Listings 1.2(a) and 1.3(b), corresponding to the two methods). cs1.mat sets parameter values to (6) and uses a $\varDelta =$ 15 [min]. As anticipated, we employ both techniques over the same model description:

• for $\textsc {faust}^2$ we specify the safe set ($X_{safe}$), the maximum allowable error, the grid type (whether uniform or adaptive grid), the time horizon, together with the type of property of interest (safety or reach-avoid). This is carried out in lines 5–21 in Listing 1.2(a).

• for the imdp method, we define the safe set ($X_{safe}$), the grid size, the relative tolerance, the time horizon and the property type. This can be done by defining the task specification using lines 5–21 in Listing 1.3(b).

Finally, to run either of the methods on the defined input model, we combine the model and the task specification using , then run the command performTask(myInput). The verification results for both methods are stored in the results directory:

• for $\textsc {faust}^2$, $\mathsf {StocHy}$ generates four text files within the results folder: representative_points.txt contains the partitioned state space; transition_matrix.txt consists of the transition probabilities of the generated abstract mc; problem_solution.txt contains the sat probability for each state of the mc; and e.txt stores the global maximum abstraction error.

• for imdp, $\mathsf {StocHy}$ generates three text files in the same folder: stepsmin.txt stores $\check{P}$ of the abstract imdp; stepsmax.txt stores $\hat{P}$; and solution.txt contains the sat probability and the errors $\varepsilon _q$ for each abstract state q.

Table 1. Case study 1: Comparison of verification results for $\varphi _1$ when using $\textsc {faust}^2$ vs imdp.

Outcomes. We perform the verification task using both $\textsc {faust}^2$ and imdp, over different sizes of the abstraction grid. We employ uniform gridding for both methods. We further compare the outcomes of $\mathsf {StocHy}$ against those of the $\textsc {faust}^2$ tool, which is implemented in matlab [28]. Note that the imdp consists of $|\mathcal {Q}| + 1$ states, where the additional state is the sink state $q_u = \mathcal {D}\backslash X_{safe}$. The results are shown in Table 1. We saturate (conservative) errors output that are greater than 1 to this value. We show the probability of satisfying the formula obtained from imdp for a grid size of 3481 states in Fig. 1 – similar probabilities are obtained for the remaining grid sizes. As evident from Table 1, the new imdp method outperforms the approach using $\textsc {faust}^2$ in terms of the maximum error associated to the abstraction ($\textsc {faust}^2$ generates an abstraction error $< 1$ only with 4225 states). Comparing the $\textsc {faust}^2$ within $\mathsf {StocHy}$ and the original $\textsc {faust}^2$ implementation (running in matlab), $\mathsf {StocHy}$ offers computational speed-up for the same grid size. This is due to the faster computation of the transition probabilities, through $\mathsf {StocHy}$’s use of matrix manipulations. $\textsc {faust}^2$ within $\mathsf {StocHy}$ also simplifies the input of the dynamical model description: in the original $\textsc {faust}^2$ implementation, the user is asked to manually input the stochastic kernel in the form of symbolic equations in a matlab script. This is not required when using $\mathsf {StocHy}$, automatically generates the underlying symbolic kernels from the input state-space model descriptions.

Fig. 1.

Case study 1: Lower bound probability of satisfying $\varphi _1$ generated using imdp with 3481 states.

4.2 Case Study 2 - Strategy Synthesis

We consider a stochastic process with two modes $\mathcal {Q} = \{q_0, q_1\}$, which continuously evolves according to (3) with

$$\begin{aligned} A_{q_0} = \begin{bmatrix} 0.43&0.52\\ 0.65&0.12\\ \end{bmatrix}, G_{q_0}= \begin{bmatrix} 1&0.1\\ 0&0.1 \\ \end{bmatrix}, A_{q_0} = \begin{bmatrix} 0.65&0.12\\ 0.52&0.43\\ \end{bmatrix}, G_{q_1} = \begin{bmatrix} 0.2&0\\ 0&0.2\\ \end{bmatrix}, F_{q_{i}} = \begin{bmatrix} 0\\ 0\\ \end{bmatrix}, \end{aligned}$$

Fig. 2.

Case study 2: (a) Gridded domain together with a superimposed simulation of trajectory initialised at $(-0.5,-1)$ within $q_0$, under the synthesised optimal switching strategy $\pi ^*$. Lower probabilities of satisfying $\varphi _2$ for mode $q_0$ (b) and for mode $q_1$ (c), as computed by $\mathsf {StocHy}$.

and $i\in \{0,1\}$. Consider the continuous domain shown in Fig. 2a over both discrete locations. We plan to synthesise the optimal switching strategy $\pi ^\star$ that maximises the probability of reaching the green region, whilst avoiding the purple one, over an unbounded time horizon, given any initial condition within the domain. This can be expressed with the ltl formula, $\varphi _2 := (\lnot purple) \;\mathsf {U}\;green,$ where $\mathsf {U}$ is the “until” temporal operator, and the atomic propositions $\{purple, green\}$ denote regions within the set $X = [-1.5, 1.5]^2$ (see Fig. 2a).

Implementation. We define the model dynamics following lines 3–14 in Listing 1.1, while we use Listing 1.3 to specify the synthesis task and together with its associated parameters. The ltl property $\varphi _2$ is over an unbounded time horizon, which leads to employing the imdp method for synthesis (recall that the $\textsc {faust}^2$ implementation can only handle time-bounded properties, and its abstraction error monotonically increases with the time horizon of the formula). In order to encode the task we set the variable safe to correspond to X the grid size to 0.12 and the relative tolerance to 0.06 along both dimensions (cf. lines 5–10 in Listing 1.3). We set the time horizon K = -1 to represent an unbounded time horizon, let p = 4 to trigger the synthesis engine over the given specification and make lb = 3 to use imdp method (cf. lines 12–19 in Listing 1.3). This task specification partitions the set X into the underlying imdp via uniform gridding. Alternatively, the user has the option to make use of the adaptive-sequential algorithm by defining a new variable eps_max which characterise the maximum allowable abstraction error and then specify the task using taskSpec_t mySpec(lb,K,p,boundary,eps_max,grid,rtol);. Next, we define two files (phi1.txt and phi2.txt) containing the coordinates within the gridded domain (see Fig. 2a) associated with the atomic propositions purple and green, respectively. This allows for automatic labelling of the state-space over which synthesis is to be performed. Running the main file, $\mathsf {StocHy}$ generates a Solution.txt file within the results folder. This contains the synthesised $\pi ^\star$ policy, the lower bound for the probabilities of satisfying $\varphi _2$, and the local errors $\varepsilon _q$ for any region q.

Outcomes. The case study generates an abstraction with a total of 2410 states, a maximum probability of 1, a maximum abstraction error of 0.21, and it requires a total time of 1639.3 [s]. In this case, we witness a slightly larger abstraction error via the imdp method then in the previous case study. This is due the non-diagonal covariance matrix $G_{q_0}$ which introduces a rotation in X within mode $q_0$. When labelling the states associated with the regions purple and green, an additional error is introduced due to the over- and under-approximation of states associated with each of the two regions. We further show the simulation of a trajectory under $\pi ^\star$ with a starting point of $(-0.5,-1)$ in $q_0$, within Fig. 2a.

4.3 Case Study 3 - Scaling in Continuous Dimension of Model

We now focus on the continuous dynamics by considering a stochastic process with $\mathcal {Q} =\{q_0\}$ (single mode) and dynamics evolving according to (3), characterised by $A_{q_0} = 0.8\mathbf {I}_{d}$, $F_{q_0} = \mathbf 0 _d$ and $G_{q_0}= 0.2\mathbf {I}_{d}$, where d corresponds to the number of continuous variables. We are interested in checking the ltl specification $\varphi _3 := \square X_{safe}$, where $X_{safe}= [-1,1]^{d}$, as the continuous dimension d of the model varies. Here “$\square$” is the “always” temporal operator and a trace $\zeta$ satisfies $\varphi _3$ if $\forall k \ge 0,\; \zeta _k \in X_{safe}$. In view of the focus on scalability for this Case Study 3, we disregard discussing the computed probabilities, which we instead covered in Sect. 4.1.

Implementation. Similar to Case Study 2, we follow lines 3–14 in Listing 1.1 to define the model dynamics, while we use Listing 1.3 to specify the verification task using the imdp method. For this example, we employ a uniform grid having a grid size of 1 and relative tolerance of 1 for each dimension (cf. lines 5–10 in Listing 1.3). We set K = -1 to represent an unbounded time horizon, p = 1 to perform verification over a safety property and lb = 3 to use the imdp method (cf. lines 12–19 in Listing 1.3). In Table 2 we list the number of states required for each dimension, the total computational time, and the maximum error associated with each abstraction.

Table 2. Case study 3: Verification results of the imdp-based approach over $\varphi _3$, for varying dimension d of the stochastic process.

Outcomes. From Table 2 we can deduce that by employing the imdp method within $\mathsf {StocHy}$, the generated abstract models have manageable state spaces, thanks to the tight error bounds that is obtained. Notice that since the number of cells per dimension is increased with the dimension d of the model, the associated abstraction error $\varepsilon _{max}$ is decreased. The small error is also due to the underlying contractive dynamics of the process. This is a key fact leading to scalability over the continuous dimension d of the model: $\mathsf {StocHy}$ displays a significant improvement in scalability over the state of the art [28] and allows abstracting stochastic models with relevant dimensionality. Furthermore, $\mathsf {StocHy}$ is capable to handle specifications over infinite horizons (such as the considered until formula).

4.4 Case Study 4 - Simulations

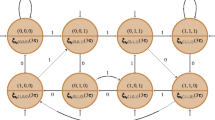
For this last case study, we refer to the $CO_2$ model described in Case Study 1 (Sect. 4.1). We extend the $CO_2$ model to capture (i) the effect of occupants leaving or entering the zone within a time step (ii) the opening or closing of the windows in the zone [2]. $\rho _m$ is now a control input and is an exogenous signal. This can be described as a shs comprising two-dimensional dynamics, over discrete modes in the set $\{q_0 = (E,C), q_1 = (F,C), q_2 = (F,O), q_3 =(E,O)\}$ describing possible configurations of the room (empty (E) or full (F), and with windows open (O) or closed (C)). A mc representing the discrete modes and their dynamics is in Fig. 3a. The continuous variables evolve according to Eq. (6), which now captures the effect of switching between discrete modes, as

$$\begin{aligned}&x_{1,k+1} = x_{1,k} + \frac{\varDelta }{V}(-\rho _mx_{1,k} + \varrho _{o,c}(C_{out} - x_{1,k})) + \mathbf {1}_{F}C_{occ,k} + \sigma _{1} w_{k}, \\&x_{2,k+1} = x_{2,k} + \frac{\varDelta }{C_z}(\rho _mC_{pa} (T_{set} -x_{2,k}) + \frac{\varrho _{o,c}}{R}(T_{out} - x_{2,k})) + \mathbf {1}_{F}T_{occ,k} + \sigma _{2} w_k, \nonumber \end{aligned}$$

(7)

where the additional terms are: $\varrho _{(\cdot )}$ is the natural drift air flow that changes depending whether the window is open ($\varrho _{o}$) or closed ($\varrho _{c}$) [$m^3/min$]; $C_{occ}$ is the generated $CO_2$ level when the zone is occupied (it is multiplied by the indicator function $\mathbf {1}_{F}$) [ppm / min]; $T_{occ}$ is the generated heat due to occupants [${ ~^\circ C}/min$], which couples the dynamics in (7) as $T_{occ,k} = vx_{1,k} + \hbar$.

Fig. 3.

Case study 4: (a) mc for the discrete modes of the $CO_2$ model and (b) input control signal.

Implementation. The provided file cs4.mat sets the values of the parameters in (7) and contains the transition probability matrix representing the relationships between discrete modes. We select a sampling time $\varDelta =$ 15 [min] and simulate the evolution of this dynamical model over a fixed time horizon $K = 8$ h (i.e. 32 steps) with an initial CO$_2$ level $x_1\sim \mathcal {N}(450,25)\; [ppm]$ and a temperature level of $x_2\sim \mathcal {N}(17,2) \;[{ ~^\circ C}]$. We define the initial conditions using Listing 1.4. Line 2 defines the number of Monte Carlo simulations using by the variable monte and sets this to 5000. We instantiate the initial values of the continuous variables using the term x_init, while we set the initial discrete mode using the variable q_init. This is done using lines 4–17 which defines independent normal distribution for each of the continuous variable from which we sample 5000 points for each of the continuous variables and defines the initial discrete mode to $q_0 = (E,C)$. We define the control signal $\rho _m$ in line 20, by parsing the u.txt which contains discrete values of $\rho _m$ for each time step (see Fig. 3b). Once the model is defined, we follow Listing 1.1 to perform the simulation. The simulation engine also generates a python script, simPlots.py, which gives the option to visualise the simulation outcomes offline.

Fig. 4.

Case study 4: Simulation single traces for continuous variables (a) $x_1$, (b) $x_2$ and discrete modes (c) q. Histogram plots with respect to time step for (d) $x_1$, (e) $x_2$ and discrete modes (f) q.

Outcomes. The generated simulation plots are shown in Fig. 4, which depicts: (i) a sample trace for each continuous variable (the evolution of $x_1$ is shown in Fig. 4a, $x_2$ in Fig. 4b) and for the discrete modes (see Fig. 4c); and (ii) histograms depicting the range of values the continuous variables can be in during each time step and the associated count (see Fig. 4c for $x_1$ and Fig. 4e for $x_2$); and a histogram showing the likelihood of being in a discrete mode within each time step (see Fig. 4f). The total time taken to generate the simulations is 48.6 [s].

5 Conclusions and Extensions

We have presented $\mathsf {StocHy}$, a new software tool for the quantitative analysis of stochastic hybrid systems. There is a plethora of enticing extensions that we are planning to explore. In the short term, we intend to: (i) interface with other model checking tools such as storm [12] and the modest toolset [16]; (ii) embed algorithms for policy refinement, so we can generate policies for models having numerous continuous input variables [15]; (iii) benchmarking the tool against a set of shs models [10]. In the longer term, we plan to extend $\mathsf {StocHy}$ such that (i) it can employ a graphical user-interface; (ii) it can allow analysis of continuous-time shs; and (iii) it can make use of data structures such as multi-terminal binary decision diagrams [14] to reduce the memory requirements during the construction of the abstract mdp or imdp.