Abstract
Graph repair, restoring consistency of a graph, plays a prominent role in several areas of computer science and beyond: For example, in model-driven engineering, the abstract syntax of models is usually encoded using graphs. Flexible edit operations temporarily create inconsistent graphs not representing a valid model, thus requiring graph repair. Similarly, in graph databases—managing the storage and manipulation of graph data—updates may cause that a given database does not satisfy some integrity constraints, requiring also graph repair.
We present a logic-based incremental approach to graph repair, generating a sound and complete (upon termination) overview of least-changing repairs. In our context, we formalize consistency by so-called graph conditions being equivalent to first-order logic on graphs. We present two kind of repair algorithms: State-based repair restores consistency independent of the graph update history, whereas delta-based (or incremental) repair takes this history explicitly into account. Technically, our algorithms rely on an existing model generation algorithm for graph conditions implemented in \(\textsc {AutoGraph}\). Moreover, the delta-based approach uses the new concept of satisfaction (ST) trees for encoding if and how a graph satisfies a graph condition. We then demonstrate how to manipulate these \(\mathrm {STs}\) incrementally with respect to a graph update.
F. Orejas has been supported by the Salvador de Madariaga grant PRX18/00308 and by funds from the Spanish Research Agency (AEI) and the European Union (FEDER funds) under grant GRAMM (ref. TIN2017-86727-C2-1-R).
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Graph repair, restoring consistency of a graph, plays a prominent role in several areas of computer science and beyond. For example, in model-driven engineering, models are typically represented using graphs and the use of flexible edit operations may temporarily create inconsistent graphs not representing a valid model, thus requiring graph repair. This includes the situation where different views of an artifact are represented by a different model, i.e., the artifact is described by a multi-model, see, e.g. [6], and updates in some models may cause a global inconsistency in the multimodel. Similarly, in graph databases—managing the storage and manipulation of graph data—updates may cause that a given database does not satisfy some integrity constraints [1], requiring also graph repair.
Numerous approaches on model inconsistency and repair (see [12] for an excellent recent survey) operate in varying frameworks with diverse assumptions. In our framework, we consider a typed directed graph (cf. [7]) to be inconsistent if it does not satisfy a given finite set of constraints, which are expressed by graph conditions [8], a formalism with the expressive power of first-order logic on graphs. A graph repair is, then, a description of an update that, if applied to the given graph, makes it consistent. Our algorithms do not just provide one repair, but a set of them from which the user must select the right repair to be applied. Moreover, we derive only least changing repairs, which do not include other smaller viable repairs. Our approach uses techniques (and the tool \(\textsc {AutoGraph}\)) [17] designed for model generation of graph conditions.
We consider two scenarios: In the first one, the aim is to repair a given graph (state-based repair). In the second one, a consistent graph is given together with an update that may make it inconsistent. In this case, the aim is to repair the graph in an incremental way (delta-based repair).
The main contributions of the paper are the following ones:
-
A precise definition of what an update is, together with the definition of some properties, like e.g. least changing, that a repair update may satisfy.
-
Two kind of graph repair algorithms: state-based and incremental (for the delta-based case). Moreover, we demonstrate for all algorithms soundness (the repair result provided by the algorithms is consistent) and completeness (upon termination, our algorithms will find all possible desired repairs)Footnote 1.
Summarizing, most repair techniques do not provide guarantees for the functional semantics of the repair and suffer from lack of information for the deployment of the techniques (see conclusion of the survey [12]). With our logic-based graph repair approach we aim at alleviating this weakness by presenting formally its functional semantics and describing the details of the underlying algorithms.
The paper is organized as follows: After introducing preliminaries in Sect. 2, we proceed in Sect. 3 with defining graph updates and repairs. In Sect. 4, we present the state-based scenario. We continue with introducing satisfaction trees in Sect. 5 that are needed for the delta-based scenario in Sect. 6. We close with a comparison with related work in Sect. 7 and conclusion with outlook in Sect. 8. For proofs of theorems and example details we refer to our technical report [18].
2 Preliminaries on Graph Conditions
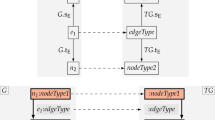
We recall graph conditions (\(\mathrm {GCs}\)), defined here over typed directed graphs, used for representing properties on such graphs. In our running exampleFootnote 2, we employ the type graph \( TG \) from Fig. 1 and we use nodes with names \(a_i\) and \(b_i\) to indicate that they are of type : A and : B, respectively.
\(\mathrm {GCs}\) state facts about the existence of graph patterns in a given graph, called a host graph. For example, in the syntax used in our running example, the GC \(\exists (a, true )\) means that the host graph must include a node of type : A. Also,  means that the host graph must include a node of type : A, another node of type : B, and an edge from the : A-node to the : B-node.
means that the host graph must include a node of type : A, another node of type : B, and an edge from the : A-node to the : B-node.
In general, in the syntax that we use in our running example, an atomic GC is of the form \(\exists (H, \phi )\) (or \(\lnot \exists (H, \phi )\)) where H is a graph that must be (or must not be) included in the host graph and where \(\phi \) is a condition expressing more restrictions on how this graph is found (or not found) in the host graph. For instance,  states that the host graph must include an : A-node such that it has no outgoing edge e to a : B-node. Moreover, we use the standard boolean operators to combine atomic GCs to form more complex ones. For instance,
states that the host graph must include an : A-node such that it has no outgoing edge e to a : B-node. Moreover, we use the standard boolean operators to combine atomic GCs to form more complex ones. For instance,  states that the host graph must include an : A-node, such that it does not hold that there is an outgoing edge e to a : B-node and node a has no loop. In addition, as an abbreviation for readability, we may use the universal quantifier with the meaning \(\forall (H,\phi ) = \lnot \exists (H, \lnot \phi )\). In this sense, the condition \(\phi \) from Fig. 1, used in our running example, states that every node of type : A must have an outgoing edge to a node of type : B and that such an : A-node must have no loop.
states that the host graph must include an : A-node, such that it does not hold that there is an outgoing edge e to a : B-node and node a has no loop. In addition, as an abbreviation for readability, we may use the universal quantifier with the meaning \(\forall (H,\phi ) = \lnot \exists (H, \lnot \phi )\). In this sense, the condition \(\phi \) from Fig. 1, used in our running example, states that every node of type : A must have an outgoing edge to a node of type : B and that such an : A-node must have no loop.
Formally, the syntax of \(\mathrm {GCs}\) [8], expressively equivalent to first-order logic on graphs [5], is given subsequently. This logic encodes properties of graph extensions, which must be explicitly mentioned as graph inclusions. For instance, the GC  in simplified notation is formally given in the syntax of \(\mathrm {GCs}\) as
in simplified notation is formally given in the syntax of \(\mathrm {GCs}\) as  , where \(\mathrm {i}_{H} \) denotes the inclusion
, where \(\mathrm {i}_{H} \) denotes the inclusion  with H the graph consisting of node a. This is because it expresses a property of the extension \(\mathrm {i}_{H} \). Moreover, therein the GC
with H the graph consisting of node a. This is because it expresses a property of the extension \(\mathrm {i}_{H} \). Moreover, therein the GC  is actually a property of the extension
is actually a property of the extension  .
.
Definition 1
(Graph Conditions (GCs) [8]). The class of graph conditions \(\varPhi ^{\mathrm {GC}} _H\) for the graph H is defined inductively:
-
\(\wedge S \in \varPhi ^{\mathrm {GC}} _H\) if \(S\subseteq _{{\text {fin}}}\varPhi ^{\mathrm {GC}} _H\).
-
\(\lnot \phi \in \varPhi ^{\mathrm {GC}} _H\) if \(\phi \in \varPhi ^{\mathrm {GC}} _H\).
-
 if \(\phi \in \varPhi ^{\mathrm {GC}} _{H'}\).
if \(\phi \in \varPhi ^{\mathrm {GC}} _{H'}\).
In addition \( true \), \( false \), \(\vee S\), \(\phi _1\Rightarrow \phi _2\), and \(\forall (a,\phi )\) can be used as abbreviations, with their obvious replacement.
A mono  satisfies a \(\mathrm {GC}\) \(\psi \in \varPhi ^{\mathrm {GC}} _{H}\), written \(m\models _{\mathrm {GC}} \psi \), if one of the following cases applies.
satisfies a \(\mathrm {GC}\) \(\psi \in \varPhi ^{\mathrm {GC}} _{H}\), written \(m\models _{\mathrm {GC}} \psi \), if one of the following cases applies.
-
\(\psi =\wedge S\) and \(m\models _{\mathrm {GC}} \phi \) for each \(\phi \in S\).
-
\(\psi =\lnot \phi \) and not \(m\models _{\mathrm {GC}} \phi \).
-
 and
and 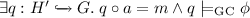 .
.
A graph G satisfies a \(\mathrm {GC}\) \(\psi \in \varPhi ^{\mathrm {GC}} _{\emptyset }\), written \(G\models _{\mathrm {GC}} \psi \) or \(G\in \llbracket \psi \rrbracket \), if \(\mathrm {i}_{G} \models _{\mathrm {GC}} \psi \).
3 Graph Updates and Repairs
In this section, we define graph updates to formalize arbitrary modifications of graphs, graph repairs as the desired graph updates resulting in repaired graphs, as well as further desireable properties of graph updates.
In particular, it is well known that a modification or update of \(G_1\) resulting in a graph \(G_2\) can be represented by two inclusions or, in general two monos, which we denote by  , where I represents the part of \(G_1\) that is preserved by this update. Intuitively,
, where I represents the part of \(G_1\) that is preserved by this update. Intuitively,  describes the deletion of elements from \(G_1\) (i.e., all elements in \(G_1 \setminus l(I)\) are deleted) and
describes the deletion of elements from \(G_1\) (i.e., all elements in \(G_1 \setminus l(I)\) are deleted) and  describes the addition of elements to I to obtain \(G_2\) (i.e., all elements in \(G_2\setminus r(I)\) are added).
describes the addition of elements to I to obtain \(G_2\) (i.e., all elements in \(G_2\setminus r(I)\) are added).
Definition 2
(Graph Update). A (graph) update u is a pair  of monos. The class of all updates is denoted by \(\mathcal {U} \).
of monos. The class of all updates is denoted by \(\mathcal {U} \).
Graph updates such as  where G is not the empty graph delete all the elements in G that are added by r afterwards. To rule out such updates, we define an update
where G is not the empty graph delete all the elements in G that are added by r afterwards. To rule out such updates, we define an update  to be canonical when the graph I is as large as possible, i.e. intuitively \(I = G_1\cap G_2\). Formally:
to be canonical when the graph I is as large as possible, i.e. intuitively \(I = G_1\cap G_2\). Formally:
Definition 3
(Canonical Graph Update). If  and every
and every  and mono
and mono  with \(l'\circ i=l\) and \(r'\circ i=r\) satisfies that i is an isomorphism then (l, r) is canonical, written \((l,r)\in \mathcal {U}_{\mathrm {can}} \).
with \(l'\circ i=l\) and \(r'\circ i=r\) satisfies that i is an isomorphism then (l, r) is canonical, written \((l,r)\in \mathcal {U}_{\mathrm {can}} \).

An update \(u_1\) is a sub-update (see [14]) of u whenever the modifications defined by \(u_1\) are fully contained in the modifications defined by u. Intuitively, this is the case when \(u_1\) can be composed with another update \(u_2\) such that (a) the resulting update has the same effect as u and (b) \(u_2\) does not delete any element that was added before by \(u_1\). This is stated, informally speaking, by requiring that I is the intersection (pullback) of \(I_1\) and \(I_2\) and that \(G_2\) is its union (pushout).
Definition 4
(Sub-update [14]). If  ,
,  ,
,  ,
,  is the pullback of \((r_1,l_2)\), and \((r_1,l_2)\) is the pushout of \((r_1',l_2')\) then \(u_1\) is a sub-update of u, written \(u_1 \le ^{u_2} u\) or simply \(u_1 \le u\).
is the pullback of \((r_1,l_2)\), and \((r_1,l_2)\) is the pushout of \((r_1',l_2')\) then \(u_1\) is a sub-update of u, written \(u_1 \le ^{u_2} u\) or simply \(u_1 \le u\).

Moreover, we write \(u_1 <^{u_2} u\) or \(u_1 < u\) when \(u_1 \le ^{u_2} u\) and not \(u \le u_1\).
We now define graph repairs as graph updates where the result graph satisfies the given consistency constraint \(\psi \).
Definition 5
(Graph Repair). If  , \(\psi \in \varPhi ^{\mathrm {GC}} _{\emptyset }\), and \(G_2\models _{\mathrm {GC}} \psi \) then u is a graph repair or simply repair of \(G_1\) with respect to \(\psi \), written
, \(\psi \in \varPhi ^{\mathrm {GC}} _{\emptyset }\), and \(G_2\models _{\mathrm {GC}} \psi \) then u is a graph repair or simply repair of \(G_1\) with respect to \(\psi \), written  .
.
To define a finite set of desirable repairs, we introduce the notion of least changing repairs that are repairs for which no sub-updates exist that are also repairs.
Definition 6
(Least Changing Graph Repair). If \(\psi \in \varPhi ^{\mathrm {GC}} _{\emptyset }\),  , and there is no
, and there is no  such that \(u'<u\) then u is a least changing graph repair of \(G_1\) with respect to \(\psi \), written
such that \(u'<u\) then u is a least changing graph repair of \(G_1\) with respect to \(\psi \), written  .
.
Note that every least changing repair is canonical according to this definition. Moreover, the notion of least changing repairs is unrelated to other notions of repairs such as the set of all repairs that require a smallest amount of atomic modifications of the graph at hand to result in a graph satisfying the consistency constraint. For instance, a repair \(u_1\) adding two nodes of type : A may be a least changing repair even if there is a repair \(u_2\) adding only one node of type : B.
A graph repair algorithm is stable [12], if the repair procedure returns the identity update  when graph G is already consistent. Obviously, a graph repair algorithm that only returns least changing repairs is stable, since the identity update is a sub-update of any other repair.
when graph G is already consistent. Obviously, a graph repair algorithm that only returns least changing repairs is stable, since the identity update is a sub-update of any other repair.
4 State-Based Repair
In this section, we introduce two state-based graph repair algorithms (see [18] for additional technical detail), which compute a set of graph repairs restoring consistency for a given graph.
Definition 7
(State-Based Graph Repair Algorithm). A state-based graph repair algorithm takes a graph G and a \(\mathrm {GC}\) \(\psi \in \varPhi ^{\mathrm {GC}} _{\emptyset }\) as inputs and returns a set of graph repairs in  .
.
Note that the tool \(\textsc {AutoGraph}\) [17] can be used to verify this condition as follows: It determines the operation  that constructs a finite set of all minimal graphs satisfying a given \(\mathrm {GC}\) \(\psi \). Formally,
that constructs a finite set of all minimal graphs satisfying a given \(\mathrm {GC}\) \(\psi \). Formally,  . While \(\textsc {AutoGraph}\) may not terminate when computing this operation due to the inherent expressiveness of \(\mathrm {GCs}\), it is known that \(\textsc {AutoGraph}\) terminates whenever \(\psi \) is not satisfied by any graph.
. While \(\textsc {AutoGraph}\) may not terminate when computing this operation due to the inherent expressiveness of \(\mathrm {GCs}\), it is known that \(\textsc {AutoGraph}\) terminates whenever \(\psi \) is not satisfied by any graph.
The state-based algorithm  uses
uses  to obtain repairs.
to obtain repairs.  computes the set
computes the set  that contains all minimal graphs that (a) satisfy \(\psi \) and (b) include a copy of G. All these extensions of G correspond to a graph repair. For our running example, we do not obtain any repair for graph \(\mathbf {G'_u} \) from Fig. 2 and \(\mathrm {GC}\) \(\varvec{\psi } \) from Fig. 1 because the loop on node \(a_2\) would invalidate any graph including \(\mathbf {G'_u} \). We state that
that contains all minimal graphs that (a) satisfy \(\psi \) and (b) include a copy of G. All these extensions of G correspond to a graph repair. For our running example, we do not obtain any repair for graph \(\mathbf {G'_u} \) from Fig. 2 and \(\mathrm {GC}\) \(\varvec{\psi } \) from Fig. 1 because the loop on node \(a_2\) would invalidate any graph including \(\mathbf {G'_u} \). We state that  indeed computes the non-deleting least changing graph repairs.
indeed computes the non-deleting least changing graph repairs.
Theorem 1
(Functional Semantics of  ).
). is sound, i.e.,
is sound, i.e.,  , and complete (upon termination) with respect to non-deleting repairs in
, and complete (upon termination) with respect to non-deleting repairs in  .
.
The second state-based algorithm  computes all least changing graph repairs. In this algorithm we use the approach of
computes all least changing graph repairs. In this algorithm we use the approach of  but compute
but compute  whenever an inclusion
whenever an inclusion  describes how G can be restricted to one of its subgraphs \(G_c\). Every graph \(G'\) obtained from the application of
describes how G can be restricted to one of its subgraphs \(G_c\). Every graph \(G'\) obtained from the application of  for one of these graphs \(G_c\) then results in one graph repair returned by
for one of these graphs \(G_c\) then results in one graph repair returned by  except for those that are not least changing.
except for those that are not least changing.
To this extent we introduce the notion of a restriction tree (see example in Fig. 2) having all subgraphs \(G_c\) of a given graph G as nodes as long as they include the graph \(G_{ min }\), which is the empty graph in the state-based algorithm  but not in the algorithm
but not in the algorithm  in Sect. 6, and where edges are given in this tree by inclusions that add precisely one node or edge.
in Sect. 6, and where edges are given in this tree by inclusions that add precisely one node or edge.
Definition 8
(Restriction Tree  ). If G and \(G_{ min }\) are graphs and
). If G and \(G_{ min }\) are graphs and  , \(S'\) is the least subset of S such that the closure of \(S'\) under \(\circ \) equals S then a restriction tree
, \(S'\) is the least subset of S such that the closure of \(S'\) under \(\circ \) equals S then a restriction tree  is a least subset of \(S'\) such that for all two inclusions
is a least subset of \(S'\) such that for all two inclusions  and
and  one of them is in
one of them is in  .
.
Considering our running example, the restriction tree in Fig. 2 is traversed entirely except for the four graphs without a border, which are not traversed as they have the supergraph marked 9 satisfying \(\varvec{\psi } \) and therefore traversing those would generate repairs that are not least changing. The resulting graph repairs for the condition \(\varvec{\psi } \) are given by the graphs marked by 3–6.
Our second state-based graph repair algorithm is indeed sound and complete whenever the calls to \(\textsc {AutoGraph}\) using  terminate.
terminate.
Theorem 2
(Functional Semantics of  ).
). is sound, i.e.,
is sound, i.e.,  , and complete, i.e.,
, and complete, i.e.,  , upon termination.
, upon termination.
5 Satisfaction Trees
The state-based algorithms introduced in the previous section are inefficient when used in a scenario where a graph needs repair after a sequence of updates that all need repair. We thus present in Sect. 6 an incremental algorithm reducing the computational cost for a repair when an update is provided. This algorithm uses an additional data structure, called satisfaction tree or \(\mathrm {ST}\), which stores information on if and how a graph G satisfies a \(\mathrm {GC}\) \(\psi \) (according to Definition 1). In this section, given \(\psi \) and G, we define how such an \(\mathrm {ST}\) \(\gamma \) is constructed and how it is updated once the graph G is updated.
If \(\psi \) is a conjunction of conditions, its associated \(\mathrm {ST}\) \(\gamma \) is a conjunction of \(\mathrm {STs}\) and if \(\psi \) is a negation of a conditions, its associated \(\gamma \) is a negation of an \(\mathrm {ST}\). In the case when \(\psi \) is a  , recall that a match
, recall that a match  satisfies \(\psi \) if there exists a
satisfies \(\psi \) if there exists a  such that \(m = q\circ a\) and \(q\models _{\mathrm {GC}} \phi \). For this case, we keep in \(\mathrm {ST}\) each q satisfying these two conditions and also each q that satisfies the first condition, but not the second. More precisely, for the case of existential quantification, the corresponding \(\mathrm {ST}\) is of the form
such that \(m = q\circ a\) and \(q\models _{\mathrm {GC}} \phi \). For this case, we keep in \(\mathrm {ST}\) each q satisfying these two conditions and also each q that satisfies the first condition, but not the second. More precisely, for the case of existential quantification, the corresponding \(\mathrm {ST}\) is of the form  , where \(m_t\) and \(m_f\) are partial mappings (we use
, where \(m_t\) and \(m_f\) are partial mappings (we use  to denoted the elements actually mapped by a partial map f) that map matches
to denoted the elements actually mapped by a partial map f) that map matches  that satisfy \(m=q\circ a\) (for a previously known
that satisfy \(m=q\circ a\) (for a previously known  ) to an \(\mathrm {ST}\) for the subcondition \(\phi \). The difference between both partial functions is that \(m_t\) maps matches q to \(\mathrm {STs}\) for which \(q\models _{\mathrm {GC}} \phi \) while \(m_f\) maps matches q to \(\mathrm {STs}\) for which \(q\not \models _{\mathrm {GC}} \phi \). Consider Fig. 3b for an example of an \(\mathrm {ST}\) \(\mathbf {\gamma }_{\mathbf{u}} \).
) to an \(\mathrm {ST}\) for the subcondition \(\phi \). The difference between both partial functions is that \(m_t\) maps matches q to \(\mathrm {STs}\) for which \(q\models _{\mathrm {GC}} \phi \) while \(m_f\) maps matches q to \(\mathrm {STs}\) for which \(q\not \models _{\mathrm {GC}} \phi \). Consider Fig. 3b for an example of an \(\mathrm {ST}\) \(\mathbf {\gamma }_{\mathbf{u}} \).
The following definition describes the syntax of \(\mathrm {STs}\). The \(\mathrm {STs}\) are defined over matches into a graph G to allow for the basic well-formedness condition that every mapped match q satisfies \(q\circ a=m\).
Definition 9
(Satisfaction Trees (STs)). The class of all Satisfaction Trees \(\Gamma ^{\mathrm {ST}} _{m}\) for a mono  contains \(\gamma \) if one of the following cases applies.
contains \(\gamma \) if one of the following cases applies.
-
\(\gamma =\wedge S\) and \(S\subseteq _{{\text {fin}}}\Gamma ^{\mathrm {ST}} _{m}\).
-
\(\gamma =\lnot \chi \) and \(\chi \in \Gamma ^{\mathrm {ST}} _{m}\).
-
\(\gamma =\exists (a,\phi ,m_t,m_f) \),
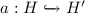 , \(\phi \in \varPhi ^{\mathrm {GC}} _{H'}\),
, \(\phi \in \varPhi ^{\mathrm {GC}} _{H'}\),  , and \(m_t,m_f\) are partial maps.
, and \(m_t,m_f\) are partial maps.
The following satisfaction predicate  for \(\mathrm {STs}\) defines when an \(\mathrm {ST}\) \(\gamma \) for a mono m states that the contained \(\mathrm {GC}\) \(\psi \) is satisfied by the morphism m.
for \(\mathrm {STs}\) defines when an \(\mathrm {ST}\) \(\gamma \) for a mono m states that the contained \(\mathrm {GC}\) \(\psi \) is satisfied by the morphism m.
Definition 10
(ST Satisfaction). An \(\mathrm {ST}\)  is satisfied, written \(\models _{\mathrm {ST}} \gamma \), if one of the following cases applies.
is satisfied, written \(\models _{\mathrm {ST}} \gamma \), if one of the following cases applies.
-
\(\gamma =\wedge S\) and \(\models _{\mathrm {ST}} \chi \) (for each \(\chi \in S\))
-
\(\gamma =\lnot \chi \) and \(\not \models _{\mathrm {ST}} \chi \).
-
\(\gamma =\exists (a,\phi ,m_t,m_f) \) and \(m_t\ne \emptyset \).
The following recursive operation constructs an \(\mathrm {ST}\) \(\gamma \) for a graph G and a condition \(\psi \) so that \(\gamma \) represents how G satisfies (or not satisfies) \(\psi \). Note that the match m in the definition of \(\mathrm {STs}\) above and the construction of an \(\mathrm {ST}\) below corresponds to the match  from Definition 1 that we operationalize in the following definition. For conjunction and negation, we construct the \(\mathrm {STs}\) from the \(\mathrm {STs}\) for the subconditions. For the case of existential quantification, we consider all morphisms
from Definition 1 that we operationalize in the following definition. For conjunction and negation, we construct the \(\mathrm {STs}\) from the \(\mathrm {STs}\) for the subconditions. For the case of existential quantification, we consider all morphisms  for which the triangle \(q\circ a=m\) commutes and construct the \(\mathrm {STs}\) for the subcondition \(\phi \) under this extended match q. The resulting \(\mathrm {STs}\) are inserted into \(m_t\) and \(m_f\) according to whether they are satisfied.
for which the triangle \(q\circ a=m\) commutes and construct the \(\mathrm {STs}\) for the subcondition \(\phi \) under this extended match q. The resulting \(\mathrm {STs}\) are inserted into \(m_t\) and \(m_f\) according to whether they are satisfied.
Definition 11
(Construct ST ( )). Given
)). Given  and \(\psi \in \varPhi ^{\mathrm {GC}} _H\), we define
and \(\psi \in \varPhi ^{\mathrm {GC}} _H\), we define  , with \(\gamma \in \Gamma ^{\mathrm {ST}} _{m}\) as follows.
, with \(\gamma \in \Gamma ^{\mathrm {ST}} _{m}\) as follows.
-
If \(\psi =\wedge S\) then
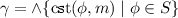 .
. -
If \(\psi =\lnot \phi \) then
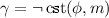 .
. -
If
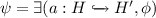 ,
,  , \(m_t=\{(q,\chi )\in m_{all} \mid \models _{\mathrm {ST}} \chi \}\), \(m_f= m_{all} \setminus m_t\), then \(\gamma =\exists (a,\phi ,m_t,m_f) \).
, \(m_t=\{(q,\chi )\in m_{all} \mid \models _{\mathrm {ST}} \chi \}\), \(m_f= m_{all} \setminus m_t\), then \(\gamma =\exists (a,\phi ,m_t,m_f) \).
If G is a graph and \(\psi \in \varPhi ^{\mathrm {GC}} _\emptyset \), then  .
.
This construction of \(\mathrm {STs}\) then ensures that \(\models _{\mathrm {ST}} \gamma \) if and only if \(G\models _{\mathrm {GC}} \psi \). Note that \(\models _{\mathrm {ST}} \mathbf {\gamma }_{\mathbf{u}} \) holds for the \(\mathrm {ST}\) \(\mathbf {\gamma }_{\mathbf{u}}\) from Fig. 3b, the \(\mathrm {GC}\) \(\varvec{\psi }\) from Fig. 1, and the graph \(\mathbf {G_u}\) from Fig. 3.
Theorem 3
(Sound Construction of STs). Given  , \(\psi \in \varPhi ^{\mathrm {GC}} _H\), and
, \(\psi \in \varPhi ^{\mathrm {GC}} _H\), and  then \(\models _{\mathrm {ST}} \gamma \) iff \(m\models _{\mathrm {GC}} \psi \).
then \(\models _{\mathrm {ST}} \gamma \) iff \(m\models _{\mathrm {GC}} \psi \).
Subsequently, we define a propagation operation  of an \(\mathrm {ST}\) \(\gamma \) for a graph update
of an \(\mathrm {ST}\) \(\gamma \) for a graph update  to obtain an \(\mathrm {ST}\) \(\gamma '\) such that
to obtain an \(\mathrm {ST}\) \(\gamma '\) such that  whenever
whenever  . This overall propagation is performed by a backward propagation of \(\gamma \) for l using the operation
. This overall propagation is performed by a backward propagation of \(\gamma \) for l using the operation  followed by a forward propagation of the resulting \(\mathrm {ST}\) for r using the operation
followed by a forward propagation of the resulting \(\mathrm {ST}\) for r using the operation  .
.
For backward propagation, we describe how the deletion of elements in G by \(l:I\hookrightarrow G\) affect its associated \(\mathrm {ST}\) \(\gamma \). To this end, we preserve those matches  for which no matched elements are deleted. This is formalized by requiring a mono
for which no matched elements are deleted. This is formalized by requiring a mono  such that \(l\circ q'=q\). The matches q with deleted matched elements can not be preserved and are therefore removed.
such that \(l\circ q'=q\). The matches q with deleted matched elements can not be preserved and are therefore removed.
Definition 12
(Propagate Match ( )). If
)). If  and
and  are monos, then
are monos, then  is the unique
is the unique  such that \(l\circ q'=q\) if it exists and \(\bot \) otherwise.
such that \(l\circ q'=q\) if it exists and \(\bot \) otherwise.
The following recursive backward propagation defines how deletions affect the maps \(m_t\) and \(m_f\) of the given \(\mathrm {ST}\). That is, when \(\gamma =\exists (a,\phi ,m_t,m_f) \), we (a) entirely remove a mapping \((m,\chi )\) from \(m_t\) or \(m_f\) if  and (b) construct for a mapping \((m,\chi )\) from \(m_t\) or \(m_f\) the pair
and (b) construct for a mapping \((m,\chi )\) from \(m_t\) or \(m_f\) the pair  where \(\chi '\) is obtained from recursively applying the backward propagation on \(\chi \) when
where \(\chi '\) is obtained from recursively applying the backward propagation on \(\chi \) when  . The updated pair
. The updated pair  must be rechecked to decide to which partial map this pair must be added to ensure that the resulting \(\mathrm {ST}\) corresponds to the \(\mathrm {ST}\) that would be constructed for \(G'\) directly.
must be rechecked to decide to which partial map this pair must be added to ensure that the resulting \(\mathrm {ST}\) corresponds to the \(\mathrm {ST}\) that would be constructed for \(G'\) directly.
Definition 13
(Backward Propagation ( )). If
)). If  , \(\gamma \in \Gamma ^{\mathrm {ST}} _{m}\),
, \(\gamma \in \Gamma ^{\mathrm {ST}} _{m}\),  ,
,  , and \(\gamma '\in \Gamma ^{\mathrm {ST}} _{m'}\) then
, and \(\gamma '\in \Gamma ^{\mathrm {ST}} _{m'}\) then  if one of the following cases applies.
if one of the following cases applies.
-
\(\gamma =\wedge S\) and
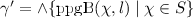 .
. -
\(\gamma =\lnot \chi \) and
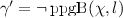 .
. -
\(\gamma =\exists (a,\phi ,m_t,m_f) \),
 ,
,  , \(m_f'= m_{all} \setminus m_t'\), and \(\gamma '=\exists (a,\phi ,m_t',m_f') \).
, \(m_f'= m_{all} \setminus m_t'\), and \(\gamma '=\exists (a,\phi ,m_t',m_f') \).
Note that  and, hence, the operation
and, hence, the operation  is applicable for all \(\mathrm {ST}\) \(\gamma \in \Gamma ^{\mathrm {ST}} _{\mathrm {i}_{G}}\), which is sufficient as we define consistency constraints using \(\mathrm {GCs}\) over the empty graph as well.
is applicable for all \(\mathrm {ST}\) \(\gamma \in \Gamma ^{\mathrm {ST}} _{\mathrm {i}_{G}}\), which is sufficient as we define consistency constraints using \(\mathrm {GCs}\) over the empty graph as well.
In the case of forward propagation where additions are given by  we can preserve all matches using an adaptation. But the addition of further elements may result in additional matches as well that may satisfy the conditions to be included in the corresponding \(m_t\) and \(m_f\) from the \(\mathrm {ST}\) at hand.
we can preserve all matches using an adaptation. But the addition of further elements may result in additional matches as well that may satisfy the conditions to be included in the corresponding \(m_t\) and \(m_f\) from the \(\mathrm {ST}\) at hand.
Definition 14
(Forward Propagation ( )). If
)). If  ,
,  , and \(\gamma '\in \Gamma ^{\mathrm {ST}} _{r\circ m}\) then
, and \(\gamma '\in \Gamma ^{\mathrm {ST}} _{r\circ m}\) then  if one of the following cases applies.
if one of the following cases applies.
-
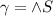 and
and 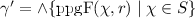 .
. -
\(\gamma =\lnot \chi \) and
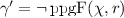 .
. -
\(\gamma =\exists (a,\phi ,m_t,m_f) \),
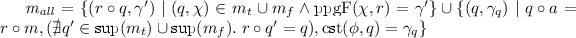 ,
, 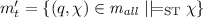 , \(m_f'= m_{all} \setminus m_t'\), and \(\gamma '=\exists (a,\phi ,m_t',m_f') \).
, \(m_f'= m_{all} \setminus m_t'\), and \(\gamma '=\exists (a,\phi ,m_t',m_f') \).
We now define the composition of both propagations to obtain the operation  that updates an \(\mathrm {ST}\) for an entire graph update.
that updates an \(\mathrm {ST}\) for an entire graph update.
Definition 15
(Update Propagation ( )). If
)). If  , \(\gamma \in \Gamma ^{\mathrm {ST}} _{m}\),
, \(\gamma \in \Gamma ^{\mathrm {ST}} _{m}\),  ,
,  , and
, and  then
then  .
.
The overall propagation given by this operation is incremental, in the sense that the operation  is only used in the forward propagation on parts of the graph \(G'\), where the addition of graph elements by r from the graph update results in additional matches q according to the satisfaction relation for \(\mathrm {GCs}\). Finally, we state that
is only used in the forward propagation on parts of the graph \(G'\), where the addition of graph elements by r from the graph update results in additional matches q according to the satisfaction relation for \(\mathrm {GCs}\). Finally, we state that  incrementally computes the \(\mathrm {ST}\) obtained using
incrementally computes the \(\mathrm {ST}\) obtained using  . The proof of this theorem relies on the fact that this property also holds for
. The proof of this theorem relies on the fact that this property also holds for  and
and  .
.
Theorem 4
(  is Compatible with
is Compatible with  ). If G is a graph, \(\psi \in \varPhi ^{\mathrm {GC}} _\emptyset \),
). If G is a graph, \(\psi \in \varPhi ^{\mathrm {GC}} _\emptyset \),  , and
, and  then
then  .
.
6 Delta-Based Repair
The local states of delta-based graph repair algorithms may contain, besides the current graph as in state-based graph repair algorithms, an additional value. In our delta-based graph repair algorithm this will be an \(\mathrm {ST}\).
Definition 16
(Delta-Based Graph Repair Algorithm). Delta-based graph repair algorithms take a graph G, a \(\mathrm {GC}\) \(\psi \in \varPhi ^{\mathrm {GC}} _{\emptyset }\), and a value q as inputs and return a set of pairs \((u,q')\) where  is a graph repair and \(q'\) is a value.
is a graph repair and \(q'\) is a value.
Our delta-based graph repair algorithm  will be based on the single step operation
will be based on the single step operation  . Given a graph G, a \(\mathrm {GC}\) \(\psi \in \varPhi ^{\mathrm {GC}} _\emptyset \), the \(\mathrm {ST}\) \(\gamma \) that equals
. Given a graph G, a \(\mathrm {GC}\) \(\psi \in \varPhi ^{\mathrm {GC}} _\emptyset \), the \(\mathrm {ST}\) \(\gamma \) that equals  , and a graph update
, and a graph update  , the single step operation
, the single step operation  first updates \(\gamma \) using
first updates \(\gamma \) using  for the graph update u and then determines using
for the graph update u and then determines using  , if necessary, graph repairs for the resulting \(\mathrm {ST}\) \(\gamma '\) according to the repair rules described in the following. The algorithm
, if necessary, graph repairs for the resulting \(\mathrm {ST}\) \(\gamma '\) according to the repair rules described in the following. The algorithm  then uses
then uses  in a breadth first manner to obtain multi-step repairs.
in a breadth first manner to obtain multi-step repairs.
For our example from Fig. 3a, such a multi-step repair of \(\mathbf {G'_u}\) is given in Fig. 4 where the graph updates are obtained resulting in the graphs marked 1–3, of which only the graph marked 1 satisfies \(\varvec{\psi }\). The algorithm  then computes further graph updates resulting in the graph marked 4 also satisfying \(\varvec{\psi }\).
then computes further graph updates resulting in the graph marked 4 also satisfying \(\varvec{\psi }\).
The operation  for deriving single-step repairs depends on two local modifications. Firstly, a \(\mathrm {GC}\)
for deriving single-step repairs depends on two local modifications. Firstly, a \(\mathrm {GC}\)  occurring as a subcondition in the consistency constraint \(\psi \) may be violated because, for the match
occurring as a subcondition in the consistency constraint \(\psi \) may be violated because, for the match  that locates a copy of H in the graph G under repair, no suitable match
that locates a copy of H in the graph G under repair, no suitable match  can be found for which \(q\circ a=m\) and \(q\models _{\mathrm {GC}} \phi \) are satisfied. The operation
can be found for which \(q\circ a=m\) and \(q\models _{\mathrm {GC}} \phi \) are satisfied. The operation  resolves this violation by (a) using \(\textsc {AutoGraph}\) to construct a suitable graph \(H_s\) and by (b) integrating this graph \(H_s\) into G resulting in \(G'\) such that a suitable match
resolves this violation by (a) using \(\textsc {AutoGraph}\) to construct a suitable graph \(H_s\) and by (b) integrating this graph \(H_s\) into G resulting in \(G'\) such that a suitable match  can be found.
can be found.
Definition 17
(Local Addition Operation  ). If
). If  ,
,  ,
,  ,
,  ,
,  , and
, and  is the pushout of (m, k) then
is the pushout of (m, k) then  .
.

In our running example,  determines a graph repair resulting in the graph marked 2 in Fig. 4. For this repair, we considered the sub-\(\mathrm {ST}\) marked by \((\mathsf {R2})\) in Fig. 3d, where the morphism m matches the node a from \(\varvec{\psi }\) to the node \(a_2\) in \(\mathbf {G'_u}\), but where no extension of m can also match a node : B and an edge between these two nodes. The repair performed then uses
determines a graph repair resulting in the graph marked 2 in Fig. 4. For this repair, we considered the sub-\(\mathrm {ST}\) marked by \((\mathsf {R2})\) in Fig. 3d, where the morphism m matches the node a from \(\varvec{\psi }\) to the node \(a_2\) in \(\mathbf {G'_u}\), but where no extension of m can also match a node : B and an edge between these two nodes. The repair performed then uses  for the graph \(H_s\), resulting in the addition of the node \(b_2\) and the edge from \(a_2\) to \(b_2\).
for the graph \(H_s\), resulting in the addition of the node \(b_2\) and the edge from \(a_2\) to \(b_2\).
Secondly, a \(\mathrm {GC}\)  occurring as a subcondition in the consistency constraint \(\psi \) may be satisfied even though it should not when occurring underneath some negation. Such a violation is determined, again for a given match
occurring as a subcondition in the consistency constraint \(\psi \) may be satisfied even though it should not when occurring underneath some negation. Such a violation is determined, again for a given match  , by some match
, by some match  satisfying \(q\circ a=m\) and \(q\models _{\mathrm {GC}} \phi \). The local repair operation
satisfying \(q\circ a=m\) and \(q\models _{\mathrm {GC}} \phi \). The local repair operation  repairs such an undesired satisfaction by selecting a graph \(H_p\) such that \(H\subseteq H_p\subset H'\) using a restriction tree (see Definition 8) and deleting \(G_{ del }=q(H')\setminus q(H_p)\) from G. Technically, we can not use the pushout complement of \(a'\) and q as it does not exists when edges from \(G\setminus G_{ del }\) are attached to nodes in \(G_{ del }\). Hence, we determine the pushout complement of \(a''\) and \(k'\), which must be constructed for this purpose suitably.
repairs such an undesired satisfaction by selecting a graph \(H_p\) such that \(H\subseteq H_p\subset H'\) using a restriction tree (see Definition 8) and deleting \(G_{ del }=q(H')\setminus q(H_p)\) from G. Technically, we can not use the pushout complement of \(a'\) and q as it does not exists when edges from \(G\setminus G_{ del }\) are attached to nodes in \(G_{ del }\). Hence, we determine the pushout complement of \(a''\) and \(k'\), which must be constructed for this purpose suitably.
Definition 18
(Local Deletion Operation  ). If
). If  ,
,  ,
,  ,
,  where \(X_2\) is obtained from \(q(H')\) by adding all edges (with their nodes) that are connected to nodes in \(q(H')\setminus q(a'(H_p))\),
where \(X_2\) is obtained from \(q(H')\) by adding all edges (with their nodes) that are connected to nodes in \(q(H')\setminus q(a'(H_p))\),  is obtained such that \(k'\circ m_1=q\),
is obtained such that \(k'\circ m_1=q\),  where \(X_1\) is obtained from \(H_p\) by adding all nodes in \(X_2\setminus q(H')\),
where \(X_1\) is obtained from \(H_p\) by adding all nodes in \(X_2\setminus q(H')\),  is obtained such that \(a''\circ m_2=m_1\circ a'\), and
is obtained such that \(a''\circ m_2=m_1\circ a'\), and  is the pushout complement of \((a'',k')\) then
is the pushout complement of \((a'',k')\) then  .
.

In our example,  determines a repair resulting in the graph marked 1 in Fig. 4. For this repair, we considered the sub-\(\mathrm {ST}\) marked by \((\mathsf {R1})\) in Fig. 3d where the mono m matches the node a from \(\varvec{\psi }\) to the node \(a_2\) in \(\mathbf {G'_u}\). The repair performed then uses \(H_p=\emptyset \) for the removal of the node \(a_2\) along with its adjacent loop (for which the technical handling in
determines a repair resulting in the graph marked 1 in Fig. 4. For this repair, we considered the sub-\(\mathrm {ST}\) marked by \((\mathsf {R1})\) in Fig. 3d where the mono m matches the node a from \(\varvec{\psi }\) to the node \(a_2\) in \(\mathbf {G'_u}\). The repair performed then uses \(H_p=\emptyset \) for the removal of the node \(a_2\) along with its adjacent loop (for which the technical handling in  is required).
is required).
The recursive operation  below derives updates from an \(\mathrm {ST}\) \(\gamma \) that corresponds to the current graph G (for our running example, these are \(\mathbf {\gamma '}_{\mathbf{u}} \) and \(\mathbf {G'_u} \) from Fig. 3d). In the algorithm
below derives updates from an \(\mathrm {ST}\) \(\gamma \) that corresponds to the current graph G (for our running example, these are \(\mathbf {\gamma '}_{\mathbf{u}} \) and \(\mathbf {G'_u} \) from Fig. 3d). In the algorithm  , we apply
, we apply  for the initial match \(\mathrm {i}_{G} \), \(\gamma \), and \( true \) where this boolean indicates that we want \(\gamma \) to be satisfied. This boolean is changed in Rule 3 whenever the recursion is applied to an \(\mathrm {ST}\) \(\lnot \gamma ' \) because we expect that \(\gamma '\) is not to be satisfied iff we expect that \(\lnot \gamma ' \) is to be satisfied. For conjunction, we either attempt to repair a sub-\(\mathrm {ST}\) for \(b= true \) in Rule 1 or we attempt to break one sub-\(\mathrm {ST}\) for \(b= false \). For existential quantification and \(b= true \), we use
for the initial match \(\mathrm {i}_{G} \), \(\gamma \), and \( true \) where this boolean indicates that we want \(\gamma \) to be satisfied. This boolean is changed in Rule 3 whenever the recursion is applied to an \(\mathrm {ST}\) \(\lnot \gamma ' \) because we expect that \(\gamma '\) is not to be satisfied iff we expect that \(\lnot \gamma ' \) is to be satisfied. For conjunction, we either attempt to repair a sub-\(\mathrm {ST}\) for \(b= true \) in Rule 1 or we attempt to break one sub-\(\mathrm {ST}\) for \(b= false \). For existential quantification and \(b= true \), we use  as discussed before in Rule 4 or we attempt to repair one existing match contained in \(m_f\) in Rule 5. Also, for existential quantification and \(b= false \), we use
as discussed before in Rule 4 or we attempt to repair one existing match contained in \(m_f\) in Rule 5. Also, for existential quantification and \(b= false \), we use  as discussed before in Rule 6 or we attempt to break one existing match contained in \(m_t\) in Rule 7.
as discussed before in Rule 6 or we attempt to break one existing match contained in \(m_t\) in Rule 7.
Definition 19
(Single-Step Delta-Based Repair Algorithm  ). If
). If  , \(\gamma \in \Gamma ^{\mathrm {ST}} _{m}\), and \(b\in \mathbf {B} \) then
, \(\gamma \in \Gamma ^{\mathrm {ST}} _{m}\), and \(b\in \mathbf {B} \) then  if one of the following cases applies.
if one of the following cases applies.
-
Rule 1 (repair one subcondition of a conjunction): \(b= true \),\(\gamma =\wedge S\), \(\chi \in S\), \(\not \models _{\mathrm {ST}} \chi \),
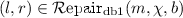 .
. -
Rule 2 (break one subcondition of a conjunction): \(b= false \),\(\gamma =\wedge S\), \(\chi \in S\), \(\models _{\mathrm {ST}} \chi \),
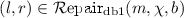 .
. -
Rule 3 (repair/break the subcondition of a negation): \(\gamma =\lnot \chi \),
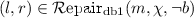 .
. -
Rule 4 (repair an existential quantification by local extension): \(b= true \),\(\gamma =\exists (a,\phi ,m_t,m_f) \), \(m_t=\emptyset \),
 , \(l=\mathrm {id}_{G} \).
, \(l=\mathrm {id}_{G} \). -
Rule 5 (repair an existential quantification recursively): \(b= true \),\(\gamma =\exists (a,\phi ,m_t,m_f) \), \(m_t=\emptyset \), \(m_f(k)=\chi \),
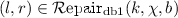 .
. -
Rule 6 (break an existential quantification by local removal): \(b= false \),\(\gamma =\exists (a,\phi ,m_t,m_f) \), \(m_t(k)\ne \bot \),
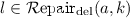 , \(r=\mathrm {id}_{G'} \).
, \(r=\mathrm {id}_{G'} \). -
Rule 7 (break an existential quantification recursively): \(b= false \),\(\gamma =\exists (a,\phi ,m_t,m_f) \), \(m_t(k)=\chi \),
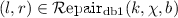 .
.
We define the recursive algorithm  to apply
to apply  to obtain repairs as iterated applications of single-step repairs computed by
to obtain repairs as iterated applications of single-step repairs computed by  .
.
Definition 20
(Delta-Based Repair Algorithm  ). If
). If  , \(\gamma \in \Gamma ^{\mathrm {ST}} _{\mathrm {i}_{G}}\), and
, \(\gamma \in \Gamma ^{\mathrm {ST}} _{\mathrm {i}_{G}}\), and  then
then  if one of the following cases applies.
if one of the following cases applies.
-
\(\models _{\mathrm {ST}} \gamma ' \) and \(S=\{((\mathrm {id}_{G'},\mathrm {id}_{G'}),\gamma ')\}\).
-
\(\not \models _{\mathrm {ST}} \gamma ' \),
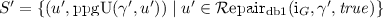 , and
, and  .Footnote 3
.Footnote 3
This computation does not terminate when repairs trigger each other ad infinitum. However, a breadth-first-computation of  gradually computes a set of sound repairs. Obviously, \(\mathrm {GCs}\) that trigger such nonterminating computations should be avoided but machinery for detecting such \(\mathrm {GCs}\) is called for.
gradually computes a set of sound repairs. Obviously, \(\mathrm {GCs}\) that trigger such nonterminating computations should be avoided but machinery for detecting such \(\mathrm {GCs}\) is called for.
Note that the algorithm  computes fewer graph repairs compared to
computes fewer graph repairs compared to  because repairs are applied locally in the scope defined by the \(\mathrm {GC}\) \(\psi \). For example, no repair would be constructed resulting in the graph marked 4 in Fig. 2. In general, explicitly also using bigger contexts in \(\psi \) results in the additional computation of less–local graph repairs. For example, the condition \(\varvec{\psi } \) may be rephrased into
because repairs are applied locally in the scope defined by the \(\mathrm {GC}\) \(\psi \). For example, no repair would be constructed resulting in the graph marked 4 in Fig. 2. In general, explicitly also using bigger contexts in \(\psi \) results in the additional computation of less–local graph repairs. For example, the condition \(\varvec{\psi } \) may be rephrased into  to also obtain the graph repair marked 4 in Fig. 2. We now define the updates, which we expect to be computed by
to also obtain the graph repair marked 4 in Fig. 2. We now define the updates, which we expect to be computed by  , as those that repair a single violation of the \(\mathrm {GC}\) \(\psi \) by defining a local update to be embeddable into the resulting update via a double pushout diagram as in the DPO approach to graph transformation [16].
, as those that repair a single violation of the \(\mathrm {GC}\) \(\psi \) by defining a local update to be embeddable into the resulting update via a double pushout diagram as in the DPO approach to graph transformation [16].
Definition 21
(Locally Least Changing Graph Update). If \(G_1\) is a graph, \(\psi \in \varPhi ^{\mathrm {GC}} _\emptyset \),  ,
,  , \(G_2\models _{\mathrm {GC}} \psi \), \(X_1\) is a minimal subgraph of \(G_1\) with a violation of \(\psi \) that is also a violation of \(\psi \) in G, and the diagram below exists and the right part of it is a DPO diagram then (l, r) is a locally least changing graph update.
, \(G_2\models _{\mathrm {GC}} \psi \), \(X_1\) is a minimal subgraph of \(G_1\) with a violation of \(\psi \) that is also a violation of \(\psi \) in G, and the diagram below exists and the right part of it is a DPO diagram then (l, r) is a locally least changing graph update.

 indeed generates such locally least changing graph updates because the graph \(X_1\) in this definition corresponds to the \(H_1\) and the \(H_2\) from an \(\mathrm {ST}\)
indeed generates such locally least changing graph updates because the graph \(X_1\) in this definition corresponds to the \(H_1\) and the \(H_2\) from an \(\mathrm {ST}\)  that is subject to
that is subject to  and
and  , respectively. For example, for
, respectively. For example, for  , the graph \(H_1\) in the \(\mathrm {ST}\) determines a subgraph in \(G_1\) that is a violation of the overall consistency condition given by a \(\mathrm {GC}\) \(\psi \) as its match can not be extended to the graph \(H_2\).
, the graph \(H_1\) in the \(\mathrm {ST}\) determines a subgraph in \(G_1\) that is a violation of the overall consistency condition given by a \(\mathrm {GC}\) \(\psi \) as its match can not be extended to the graph \(H_2\).
We now define the locally least changing graph repairs (which are to be computed by  such as for example the graphs marked 1 and 4 in Fig. 4) as the composition of a sequence of locally least changing updates where precisely the last graph update results in a graph satisfying the \(\mathrm {GC}\) \(\psi \).
such as for example the graphs marked 1 and 4 in Fig. 4) as the composition of a sequence of locally least changing updates where precisely the last graph update results in a graph satisfying the \(\mathrm {GC}\) \(\psi \).
Definition 22
(Locally Least Changing Graph Repair). If \(G_1\) is a graph, \(\psi \in \varPhi ^{\mathrm {GC}} _\emptyset \),  is a sequence of locally least changing graph updates, \(G_{1}\in \llbracket \psi \rrbracket \) implies \(n=0\) and \(l_1=r_1=\mathrm {id}_{G_1} \), \(G_{i}\notin \llbracket \psi \rrbracket \) (for each \(2\le i\le n\)), \(G_{n+1}\in \llbracket \psi \rrbracket \), (l, r) is the iterated composition of the updates in \(\pi \), and
is a sequence of locally least changing graph updates, \(G_{1}\in \llbracket \psi \rrbracket \) implies \(n=0\) and \(l_1=r_1=\mathrm {id}_{G_1} \), \(G_{i}\notin \llbracket \psi \rrbracket \) (for each \(2\le i\le n\)), \(G_{n+1}\in \llbracket \psi \rrbracket \), (l, r) is the iterated composition of the updates in \(\pi \), and  is a least changing graph repair then (l, r) is a locally least changing graph repair.
is a least changing graph repair then (l, r) is a locally least changing graph repair.
We now state that our delta-based graph repair algorithm  returns all desired locally least changing graph repairs upon termination.
returns all desired locally least changing graph repairs upon termination.
Theorem 5
(Functional Semantics of  ).
). is sound (i.e., it generates only locally least changing graph repairs) and complete (upon termination) with respect to locally least changing graph repairs.
is sound (i.e., it generates only locally least changing graph repairs) and complete (upon termination) with respect to locally least changing graph repairs.
The state-based algorithms  and
and  are inappropriate in environments where numerous updates that may invalidate consistency are applied to a large graph because the procedure of \(\textsc {AutoGraph}\) has exponential cost. The incremental delta-based algorithm
are inappropriate in environments where numerous updates that may invalidate consistency are applied to a large graph because the procedure of \(\textsc {AutoGraph}\) has exponential cost. The incremental delta-based algorithm  is a viable alternative when additional memory requirements for storing the \(\mathrm {ST}\) are acceptable. The \(\textsc {AutoGraph}\) applications for this algorithm have negligible costs because they may be performed a priori and must only be performed for subconditions of the consistency constraint, which can be assumed to feature reasonably small graphs only.
is a viable alternative when additional memory requirements for storing the \(\mathrm {ST}\) are acceptable. The \(\textsc {AutoGraph}\) applications for this algorithm have negligible costs because they may be performed a priori and must only be performed for subconditions of the consistency constraint, which can be assumed to feature reasonably small graphs only.
Finally, a classification of locally least changing repairs is useful for user-based repair selection. Delta preserving repairs defined below represent such a basic class, containing only those repairs that preserve the update resulting in a graph not satisfying \(\mathrm {GC}\) \(\psi \), i.e., it may be desirable to avoid repairs that revert additions or deletions of this update. In our example, the repair related to the graph marked 4 in Fig. 4 is not delta preserving w.r.t. \(\mathbf {u}\) from Fig. 3a.
Definition 23
(Delta Preserving Graph Repair). If \(\psi \in \varPhi ^{\mathrm {GC}} _\emptyset \),  is a graph repair,
is a graph repair,  is a graph update, and there exists a graph update u such that \(u_1 <^{u_2} u\) then \(u_2\) is a delta preserving graph repair with respect to \(u_1\).
is a graph update, and there exists a graph update u such that \(u_1 <^{u_2} u\) then \(u_2\) is a delta preserving graph repair with respect to \(u_1\).
7 Related Work
According to the recent survey on model repair [12], and the corresponding exhaustive classification of primary studies selected in the literature review, published online [11], we can see that the amount and wide variety of existing approaches makes a detailed comparison with all of them infeasible.
We consider our approach to be innovative, not only because of the proposed solutions, but because it addresses the issues of completeness and least changing for incremental graph repair in a precise and formal way. From the survey [11, 12] we can see that only two other approaches [10, 19] address completeness and least changing, relying also on constraint-solving technology. The main difference with our approach is that they are not incremental. In particular, the work of Schoenboeck et al. [19] proposes a logic programming approach allowing the exploration of model repair solutions ranked according to some quality criteria, re-establishing conformance of a model with its metamodel. Soundness and completeness of these repair actions is not formally proven. Moreover, the least changing bidirectional model transformation approach of Macedo et al. [10] has only a bounded search for repairs, relying on a bounded constraint solver.
Some recent work on rule-based graph repair [9] (not covered by the survey) addresses the least-changing principle by developing so-called maximally preserving (items are preserved whenever possible) repair programs. This state-based approach considers a subset of consistency constraints (up to nesting depth 2) handled by our approach, and is not complete, since it produces repairs including only a minimal amount of deletions. Some other recent rule-based graph repair approach [13, 20] (also not covered by the survey) proposes so-called change preserving repairs (similar to what we define as delta-preserving). The main difference with our work is that we do not require the user to specify consistency-preserving operations from which repairs are generated, since we derive repairs using constraint solving techniques directly from the consistency constraints.
Finally, there is a variety of work on incremental evaluation of graph queries (see e.g. [2, 4]), developed with the aim of efficiently re-evaluating a graph query after an update has been performed. Although not employed with the specific aim of complete and least changing graph repair, this work is related to our newly introduced concept of satisfaction trees, also using specific data structures to record with some detail the set of answers to a given query (as described for graph conditions, for example, also in [3]). It is part of ongoing work to evaluate how \(\mathrm {STs}\) can be employed similarly in this field of incremental query evaluation.
8 Conclusion and Future Work
We presented a logic-based incremental approach to graph repair. It is the first approach to graph repair returning a sound and complete overview of least changing repairs with respect to graph conditions equivalent to first-order logic on graphs. Technically, it relies on an existing model generation procedure for graph conditions together with the newly introduced concept of satisfaction trees, encoding if and how a graph satisfies a graph condition.
As future work, we aim at supporting partial consistency and gradually improving it. We are confident that we can extend our work to support attributes, since our underlying model generation procedure supports it. Ongoing work is the support of more expressive consistency constraints, allowing path-related properties. Moreover, we are in the process of implementing the algorithms presented here and evaluating them on a variety of case studies. The evaluation also pertains to the overall efficiency (for which we employ techniques for localized pattern matching) and includes a comparison with other approaches for graph repair. Finally, we aim at presenting new and refined properties distinguishing between all possible repairs supporting the implementation of interactive repair selection procedures.
Notes
- 1.
Note that completeness implies totality (if the given set of constraints is satisfiable by a finite graph, then the algorithms will find a repair for any inconsistent graph).
- 2.
We refer to Sect. 1 with pointers to related work including diverse use cases in Software Engineering for graph repair with more complex and motivating examples.
- 3.
If \(u_1\) and \(u_2\) are updates then \(u_1\circ u_2=u\) if \(u_1\le ^{u_2}u\) or \(u=\bot \) otherwise (see Definition 4).
References
Angles, R., Gutiérrez, C.: Survey of graph database models. ACM Comput. Surv. 40(1), 1:1–1:39 (2008). https://doi.org/10.1145/1322432.1322433
Bergmann, G., Ökrös, A., Ráth, I., Varró, D., Varró, G.: Incremental pattern matching in the viatra model transformation system. In: GRaMoT, pp. 25–32. ACM (2008). https://doi.org/10.1145/1402947.1402953
Beyhl, T., Blouin, D., Giese, H., Lambers, L.: On the operationalization of graph queries with generalized discrimination networks. In: Echahed, R., Minas, M. (eds.) ICGT 2016. LNCS, vol. 9761, pp. 170–186. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-40530-8_11
Beyhl, T., Giese, H.: Incremental view maintenance for deductive graph databases using generalized discrimination networks. In: GaM@ETAPS, EPTCS, vol. 231, pp. 57–71 (2016). https://doi.org/10.4204/EPTCS.231.5
Courcelle, B.: The expression of graph properties and graph transformations in monadic second-order logic. In: Rozenberg [16], pp. 313–400
Diskin, Z., König, H., Lawford, M.: Multiple model synchronization with multiary delta lenses. In: Russo, A., Schürr, A. (eds.) FASE 2018. LNCS, vol. 10802, pp. 21–37. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-89363-1_2
Ehrig, H., Ehrig, K., Prange, U., Taentzer, G.: Fundamentals of Algebraic Graph Transformation. Springer, Heidelberg (2006). https://doi.org/10.1007/3-540-31188-2
Habel, A., Pennemann, K.: Correctness of high-level transformation systems relative to nested conditions. MSCS 19(2), 245–296 (2009). https://doi.org/10.1017/S0960129508007202
Habel, A., Sandmann, C.: Graph repair by graph programs. In: Mazzara, M., Ober, I., Salaün, G. (eds.) STAF 2018. LNCS, vol. 11176, pp. 431–446. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-04771-9_31
Macedo, N., Cunha, A.: Least-change bidirectional model transformation with QVT-R and ATL. Softw. Syst. Model. 15(3), 783–810 (2016). https://doi.org/10.1007/s10270-014-0437-x
Macedo, N., Tiago, J., Cunha, A.: Systematic literature review of model repair approaches. http://tinyurl.com/hv7eh6h. Accessed 14 Nov 2018
Macedo, N., Tiago, J., Cunha, A.: A feature-based classification of model repair approaches. IEEE Trans. Softw. Eng. 43(7), 615–640 (2017). https://doi.org/10.1109/TSE.2016.2620145
Ohrndorf, M., Pietsch, C., Kelter, U., Kehrer, T.: Revision: a tool for history-based model repair recommendations. In: ICSE, pp. 105–108. ACM (2018). https://doi.org/10.1145/3183440.3183498
Orejas, F., Boronat, A., Ehrig, H., Hermann, F., Schölzel, H.: On propagation-based concurrent model synchronization. ECEASST 57 (2013). http://journal.ub.tu-berlin.de/eceasst/article/view/871
Rensink, A.: Representing first-order logic using graphs. In: Ehrig, H., Engels, G., Parisi-Presicce, F., Rozenberg, G. (eds.) ICGT 2004. LNCS, vol. 3256, pp. 319–335. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-30203-2_23
Rozenberg, G. (ed.): Handbook of Graph Grammars and Computing by Graph Transformations, Volume 1: Foundations. World Scientific (1997)
Schneider, S., Lambers, L., Orejas, F.: Automated reasoning for attributed graph properties. STTT 20(6), 705–737 (2018). https://doi.org/10.1007/s10009-018-0496-3
Schneider, S., Lambers, L., Orejas, F.: A logic-based incremental approach to graph repair. Technical report, 126, Hasso Plattner Institute at the University of Potsdam, Potsdam, Germany (2019)
Schoenboeck, J., et al.: CARE - A constraint-based approach for re-establishing conformance-relationships. In: APCCM 2014, vol. 154, pp. 19–28. Australian Computer Society (2014). http://crpit.com/abstracts/CRPITV154Schoenboeck.html
Taentzer, G., Ohrndorf, M., Lamo, Y., Rutle, A.: Change-preserving model repair. In: Huisman, M., Rubin, J. (eds.) FASE 2017. LNCS, vol. 10202, pp. 283–299. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54494-5_16
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this paper
Cite this paper
Schneider, S., Lambers, L., Orejas, F. (2019). A Logic-Based Incremental Approach to Graph Repair. In: Hähnle, R., van der Aalst, W. (eds) Fundamental Approaches to Software Engineering. FASE 2019. Lecture Notes in Computer Science(), vol 11424. Springer, Cham. https://doi.org/10.1007/978-3-030-16722-6_9
Download citation
DOI: https://doi.org/10.1007/978-3-030-16722-6_9
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-16721-9
Online ISBN: 978-3-030-16722-6
eBook Packages: Computer ScienceComputer Science (R0)





 if
if  and
and 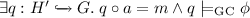 .
.
 (enclosed by the polygon) and four graph repairs (marked 3–6) generated using
(enclosed by the polygon) and four graph repairs (marked 3–6) generated using 
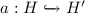 ,
,  , and
, and 
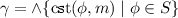 .
.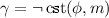 .
.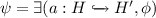 ,
,  ,
, 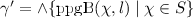 .
.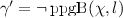 .
. ,
,  ,
, 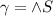 and
and 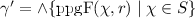 .
.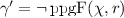 .
.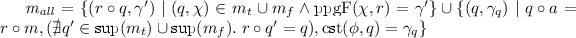 ,
, 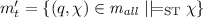 ,
, 

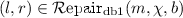 .
.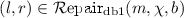 .
.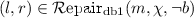 .
. ,
, 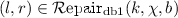 .
.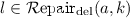 ,
, 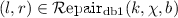 .
.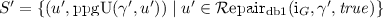 , and
, and  .
.