Keywords

1 Introduction

The cubic grid \(\mathbb {Z}^3\) is the most frequently used grid for three-dimensional images. Recently non standard, three-dimensional grids received a lot of interest with in particular applications to networks [18], image processing [6, 12, 19], computer vision [7] and many other fields. Among non standard grids we can cite face centered cubic (FCC), body centered cubic (BCC), honeycomb [3] and diamond grids [17]. Many works discussed coordinate system on the 3D grids such as [10] for cubic grids, [13, 14] for hexagonal and triangular grids and [4, 5, 20] for FCC grids.

Space filled entirely by rhombic dodecahedra may be sliced by specific planes to reveal patterns of hexagons. In [9], authors proposed a generation algorithm for discrete spheres on the FCC grid using layered discrete annuli on hexagonal grids; the general idea is to propose digital primitive generation algorithms that are compatible with additive manufacturing techniques.

The face centered cubic grid is the densest possible packing in three dimensions [20]. The shape of the cells in an FCC grid is rhombic dodecahedron, which is a space filling polyhedron described by 12 faces, 24 edges, and 14 vertices. The FCC grid can be seen as the union of four disjoint cubic grids [4, 8, 15, 16]. In such a rhombic dodecahedron grid system, sometimes distinction is made between the cells and not all the integer coordinates correspond to a cell. These make it difficult to use geometric transforms in those grid systems.

Our main contribution in this work is to propose a new non-orthogonal basis coordinate system that provides integer coordinates for rhombic dodecahedron centroids covering the whole set of integer points. The interest of such a system would be to facilitate work on such a grid. This will be highly beneficial considering the usage of this grid in image reconstruction and similar applications due to its correspondence with hexagonal grids in 2D, and also in additive manufacturing using spherical cells utilizing the emulation of densest sphere packing in space. The interest of the new coordinate system is illustrated in this paper with the (topological) characterization of various classes of digital planes and spheres in the FCC grid. The coordinate system offers a 48-symmetry which can be used to efficiently construct digital spheres and other symmetric objects.

Organization of the Paper. In Sect. 2, we present some preliminaries and basics as well as the Rhombic Dodecahedron Grid (RDG) and Nagy’s coordinate system [4]. In Sect. 3, we detail our coordinate system and we present some of its properties. In Sect. 4, we define the digital spheres and planes in this coordinate system and explore the required thickness for different models. We conclude and present perspectives in Sect. 5.

2 Preliminaries

In this section, we recall some of the basic terminologies and definitions relevant to our problem. We put forward the general definitions of a digital plane, a digital sphere, and the different topological models already established in literature for conventional cubic grid. We also talk about the formal notion of grids and coordinate systems and present the concept and importance of designing a rhombic dodecahedron grid.

We consider a 3D space. We call integer points the points that have integer coordinates on the three axes. Let us denote \(d_2\) as the Euclidean distance in the regular Cartesian space. The standard definitions of digital planes and digital spheres are as follows.

Definition 1

(Analytical Plane [1]). The digital plane P corresponding to the Euclidean plane \(ax+by+cz+d=0\), with \(\rho \) the thickness of the digital plane, is the set of integer coordinate points p(x, y, z) verifying the following inequalities:

$$-\frac{\rho }{2}\le ax+by+cz+d < \frac{\rho }{2}.$$

Definition 2

(Andres Analytical Sphere [2]). The digital sphere S centered in c, of radius r and thickness \(\rho \), is the set of integer coordinate points p verifying the following inequalities:

$$ (r -\frac{\rho }{2})\le d_2(c,p) < (r + \frac{\rho }{2}).$$

Different values of \(\rho \) in these definitions leads to different digitization models, e.g. 2-separating, 0-separating, etc. A digital object is l-separating if its inverse is not l-connected. Hence, a digital plane is 2-separating if the half-spaces specified by it are not 2-connected. Note that, 0-, 1-, and 2-connectivity here refer to the classical 26-, 18-, 6-connectivity respectively. Please consult [1, 2] for more details on digital hyperplanes and hyperspheres in cubic grid.

We consider a grid based on rhombic dodecahedrons (which are space-filling). A rhombic dodecahedron has 12 face-connected neighbors and 6 strictly vertex-connected neighbors. A consistent coordinate system for the RDG will help us to utilize this grid in 3D with similar advantages as hexagonal grid gives over square grid in 2D, specially in the domain of imaging, tomography, etc. As rhombic dodecahedron space filling arrangement emulates the close sphere packing in space, RDG can be used for additive manufacturing using spherical material particle powder.

Fig. 1.
figure 1

(a) Unit dodecahedron in the Cartesian coordinate system, where \(t=\frac{1}{\sqrt{3}}\). (b) Combinatorial coordinates for vertices in the face centered cubic grid [4]. (c) Vertex coordinates in the proposed non-orthogonal coordinate system, where \(u=\frac{1}{4}\).

Full size image

The main problem of the unit dodecahedron (see Fig. 1) is that neither its vertices nor its centroids form an integer coordinate grid. It is however simple to get integer coordinates for either centroids or vertices or both using a scale and a rotation as presented in [4]. In this paper [4], a combinatorial 3-coordinate system for cells in the face centered cubic grid is presented and some of its properties are detailed; authors made a rescaling with factor 2, in order to assign to each cell the Cartesian coordinates of its center and to have only integer coordinates for faces and edges. However, the main drawback of this system, which we want to address here, is that this coordinate system leads to two different and intricate grids, and any integer point in this space may either represent a centroid or a vertex. This will be a major cause of anomaly while doing transformation operations such as rotation, shear etc. and construction of different digital objects in this grid.

3 Rhombic Dodecahedron Grid

In this section, we propose a non-orthogonal coordinate system for the rhombic dodecahedron grid (RDG). The grid is formed on the rhombic dodecahedron close packing such that each integer point corresponds to centroid of a rhombic dodecahedron and vice versa. We talk about the conversion of this new coordinate system to and from the Cartesian coordinate system and define the corresponding distance metric. We also show that there exists a 48-symmetry in RDG using this new coordinate system which can be utilized further to propose efficient algorithm for geometric object construction in this type of grid.

Fig. 2.
figure 2

Coordinate system transformation: (a) Initial arrangement of axes in Cartesian coordinate system, (b) After 45\(^\circ \) rotation along Z-axis, (c) After required transformation to get non-orthogonal coordinate system.

Full size image

3.1 Non-orthogonal Coordinate System

We propose a non-orthogonal coordinate system to represent the RDG where each grid point represents the centroid of a rhombic dodecahedron cell. We transform the well-known Cartesian space to obtain non-orthogonal grid vectors. Figure 2(a) shows the initial positioning of the rhombic dodecahedron centered at the origin with respect to the coordinate axes. All three axes are orthogonal to each other and pass through vertices of the rhombic dodecahedron.

First, we give a clockwise rotation of 45\(^\circ \) with respect to the positive Z-axis. This gives us the arrangement as shown in Fig. 2(b). Notice that, to simplify the visualization, we have kept the rhombic dodecahedron fixed while transforming the coordinate axes. In this state, X- and Y-axes passes through the center of faces of the rhombic dodecahedron and Z-axis still passes through the same vertex.

Next, we keep the X- and Y-axis same while bending the Z-axis away from the positive X- and Y-axes to make it pass through the center of the face of the rhombic dodecahedron. At the third step, a scaling may be required to make the rhombic dodecahedron cells unit in size; we consider our cells to have unit distance between opposite faces and do not show any explicit scaling step to obtain the same.

The following two lemmas states the transformation needed for a point in the new coordinate system to and from the Cartesian coordinate system. The steps for rotation and transformation of Z-axis is described in the corresponding proofs.

Lemma 1

(Cartesian to New). The transformation of a point p(x, y, z) from the Cartesian coordinate system to the new coordinate system is given by,

$$\begin{aligned} \mathcal {N}(p) = \left( \frac{-\sqrt{2}y+z}{2}, \frac{\sqrt{2}x+z}{2}, z\right) . \end{aligned}$$

Proof

As explained using Fig. 2, the steps to get the new coordinate values for a point p(x, y, z) in the Cartesian space are a clockwise rotation of 45\(^\circ \) along positive Z-axis followed by a transformation to make the Z-axis non-orthogonal with respect to the XY-plane. The final transformation can be calculated as follows.

   \(\square \)

Lemma 2

(New to Cartesian). The transformation of a point p(x, y, z) from the new coordinate system to the Cartesian coordinate system is given by,

$$\begin{aligned} \mathcal {C}(p) = \left( \frac{2y - z}{\sqrt{2}}, \frac{-2x + z}{\sqrt{2}}, z\right) . \end{aligned}$$

Proof

To get the Cartesian coordinate values for a point p(x, y, z) in the new coordinate space, we need to do the reverse transformation as given in Lemma 1. Therefore, the first step is to make the Z-axis orthogonal to the XY-plane and then doing a anticlockwise rotation of 45\(^\circ \) with respect to the positive Z-axis. Following calculation can be used to obtain the same.

   \(\square \)

Lemma 3

(Euclidean Distance). Let p(x, y, z) and \(p'(x', y',z')\) be two points in the new coordinate system. The Euclidean distance between p and \(p'\) is given by,

$$\begin{aligned} d_2(p,p') = \sqrt{2((x - x')^2 + (y - y')^2 + (z - z')^2 - (x - x') (z - z') - (y - y') (z - z'))}. \end{aligned}$$

Proof

The proof follows directly from Lemma 2.

   \(\square \)

We simplify the distance calculation by dropping the constant factor from the Euclidean distance as calculated in Lemma 3, and define our new distance which is to be used for further calculations.

Definition 3

(New Distance). Let p(x, y, z) and \(p'(x', y',z')\) be two points in the new coordinate system. The new distance between p and \(p'\) is defined as,

$$\begin{aligned} d(p,p')&= \tfrac{1}{\sqrt{2}}d_2(p,p')\\&= \sqrt{(x - x')^2 + (y - y')^2 + (z - z')^2 - (x - x') (z - z') - (y - y') (z - z')}. \end{aligned}$$
Fig. 3.
figure 3

The twelve face-connected neighbors and the six strictly vertex-connected neighbors in the proposed non-orthogonal coordinate system.

Full size image

A rhombic dodecahedron has 12 face-connected neighbors and 6 strictly vertex-connected neighbor as shown in Fig. 3. We make the following observations regarding the neighborhood of each rhombic dodecahedron cell.

Observation 1

(Neighbors). Rhombic dodecahedron cell p and \(p'\) are face (respectively strictly vertex) connected neighbors iff the new distance between p and \(p'\) i.e. \(d(p,p')\) is equal to 1 (respectively \(\sqrt{2}\)).

Proof

From the positioning of the rhombic dodecahedron cell with respect to the non-orthogonal coordinate axes, as shown in Fig. 2(c), following are the face-connected neighbors of a cell (x, y, z): \((x+1, y, z)\), \((x-1, y, z)\), \((x, y+1, z)\), \((x, y-1, z)\), \((x, y, z+1)\), \((x, y, z-1)\), \( (x+1, y+1, z+1)\), \((x-1, y-1, z-1)\), \((x, y+1, z+1)\), \((x+1, y, z+1)\), \((x-1, y, z-1)\), \((x, y-1, z-1)\). By using the definition of \(d(p,p')\), we can see that the distance between p and \(p'\) is always 1 when they are face-connected neighbors.

Similarly, we can have the strictly vertex-connected neighbors of (x, y, z), which are \((x+1, y+1, z)\), \((x+1, y-1, z)\), \((x-1, y+1, z)\), \((x-1, y-1, z)\), \((x+1, y+1, z+2)\), \((x-1, y-1, z-2)\), and the distance between two strictly vertex-connected neighbors comes out to be \(\sqrt{2}\).   \(\square \)

3.2 48-Symmetry

The rhombic dodecahedron belongs to the octahedral symmetry group. It therefore has 24 rotational symmetries and 48 symmetries when considering transformations that combine a reflection and a rotation. Table 1 shows the 48 symmetric points corresponding to a point (x, y, z) in the non-orthogonal coordinate system. This symmetry can be utilized while constructing symmetrical geometric objects, e.g. spheres, cones, cylinders, etc., in this digital space.

Table 1. 48-symmetry in RDG using proposed non-orthogonal coordinate system.
Full size table

4 Digital Objects: Definition and Topological Analysis

In this section, we define digital models of two primitive geometric objects, namely, digital sphere and digital plane. We define these using the proposed non-orthogonal coordinate space and use the defined distance to control the thickness of the objects resulting in different topological models.

Fig. 4.
figure 4

Digital sphere of radius 8 (a) and radius 23 (b) in the rhombic dodecahedron grid, with one of the \(48^{th}\) parts shown in blue, computed using the proposed non-orthogonal coordinate system.

Full size image

4.1 Digital Sphere

We define a digital sphere in the proposed orthogonal coordinate space using the same thickness notion as used while defining Andres Analytical Sphere (recollected in Definition 2). However, we use our new distance measure as defined in Definition 3.

Definition 4

(Digital Sphere). The set of Dodecahedron centroids belonging to the digitization of a Sphere centered on c of radius r and thickness \(\rho \) is given by: \(S_{(c,r)}=\{p \in \mathbb {Z}^3 | r-\frac{\rho }{2}\le d(c,p)<r+\frac{\rho }{2} \}\)

To control the topology of the resulting sphere, we use one of the two following values for the thickness.

Proposition 1

(Topology and Separation). The thickness \(\rho = 1\) provides a 2-separating sphere. The thickness \(\rho = \sqrt{2}\) provides a 0-separating sphere.

Proof

The proof for the 2-separating value comes directly from the distance between a dodecahedron and its face neighbors which is 1 (leading to a thickness 1). The distance \(\sqrt{2}\) between the dodecahedron and its vertex neighbors leads to the 0-separating thickness of \(\sqrt{2}\).   \(\square \)

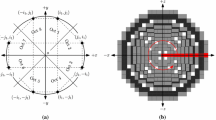
The spheres presented in Fig. 4 are obtained using a brute force algorithm implemented in Mathematica that tests every integer coordinate point (i.e. dodecahedron centroid) in the bounding box with the sphere inequality using the 2-separating thickness 1. An optimization of this algorithm could be implemented using a \(48^{th}\) of the bounding box (see Fig. 4(a)) and build the rest of the sphere using the symmetries we have previously defined in Sect. 3.2.

4.2 Digital Plane

Similar to digital sphere, we define digital plane in the new coordinate system using the classical definition. However, note that, the real plane in consideration here is given in the new coordinate system and not in the Cartesian coordinate system.

Definition 5

(Digital Plane). Let \(ax+by+cz+d=0\) be a plane equation in the new coordinate system. Let \(\rho \) be the thickness of the digital plane. The digitization of the plane in the dodecahedron grid is the set of dodecahedron (x, y, z) satisfying the following inequality.

$$\begin{aligned} -\rho /2 \le ax+by+cz+d < \rho /2. \end{aligned}$$
(1)

Following we give the formulas for converting between plane equations from the new coordinate system to the Cartesian coordinate system and reverse.

Proposition 2

(New to Cartesian Plane Equation). Let \(ax_n+by_n+cz_n+d=0\) be a plane equation in the new coordinate system. The equation of the same plane in the Cartesian coordinate system is given by:

$$\begin{aligned} b \sqrt{2} x_c - a\sqrt{2} y_c + (a + b + 2 c) z_c + 2 d = 0 \end{aligned}$$
(2)

Proposition 3

(Cartesian to New Plane Equation). Let \(ax_c+by_c+cz_c+d=0\) be a plane equation in the Cartesian coordinate system. The equation of the same plane in the new coordinate system is given by:

$$\begin{aligned} -\frac{2 b}{\sqrt{2}} x_n +a \sqrt{2} y_n + (b /\sqrt{2} + c - a /\sqrt{2}) z_n+d = 0 \end{aligned}$$
(3)

We can control the topology of the digital plane by changing the value of \(\rho \) as mentioned in Proposition 4 below.

Proposition 4

(Topology and Separation). The Supercover plane is obtained using:

$$\begin{aligned} \rho _{Sup}=\max \left( |a + b|, |b - a|, |a + b + 2c|, \frac{1}{2} (|a + b|+ |b - a| + |a + b + 2c|)\right) . \end{aligned}$$
(4)

The 0-separating (thinner than the supercover) plane is obtained using:

$$\begin{aligned} \rho _{Std}=\max \left( |a|,|b|, |c|,|a + b + c|, |a + c|,|b + c|, |a + b|, |a - b|,|a + b + 2c|\right) . \end{aligned}$$
(5)

The 2-separating digital plane in the dodecahedron grid is obtained for

$$\begin{aligned} \rho _{N}=\max \left( |a|, |b|, |c|, |a + b + c|,|a + c|, |b + c|\right) . \end{aligned}$$
(6)

Proof

The proof for the supercover is the same as in [11] using the following plane equation in Nagy’s coordinate system:

$$Ax+By+Cz+D=0$$

where \(A=\frac{a+b}{2}, B=\frac{b-a}{2}, C=\frac{a+b+2c}{2}, D=d\). It can also be proven by considering the thickness of the thickest directions we can have in the dodecahedron, i.e. the distance between opposite vertices or opposite faces as necessary.

Figure 5 presents the three different digitizations for the plane \(x+11y+z+20=0\) in the dodecahedron non-orthogonal grid. Figure 5(a) shows the thickest plane, i.e. the supercover plane which uses Eq. 4 for the thickness. On Fig. 5(b), we can see the standard 0-separating plane obtained with Eq. 5 and on Fig. 5(c) we present the Naive 2-separating plane for the thickness defined by Eq. 6.

Fig. 5.
figure 5

Dodecahedron Digitizations for the plane \(x+11y+z+20=0\) in the new coordinate system.

Full size image

5 Conclusion

In this paper, we have defined a new coordinate system. The novelty of this system is that unlike the previous coordinate system, every single one of the integer coordinate points is the centroid of a dodecahedron. Using this system we have defined spheres (together with their 48 symmetries) and planes. Both can be topologically controlled, i.e. both are proposed with a 0- and a 2-separating forms. In future works, we want to explore the possibilities of defining lines in this coordinate system and to study the graphical transforms such as the rotation.