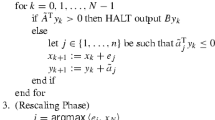Skip to main content
SpringerLink
Log in

The Duality Between the Perceptron Algorithm and the von Neumann Algorithm

  • Conference paper
  • First Online:
Modeling and Optimization: Theory and Applications

Part of the book series: Springer Proceedings in Mathematics & Statistics ((PROMS,volume 62))

Abstract

The perceptron and the von Neumann algorithms were developed to solve linear feasibility problems. In this paper, we investigate and reveal the duality relationship between these two algorithms. The specific forms of linear feasibility problems solved by the perceptron and the von Neumann algorithms are a pair of alternative systems by the Farkas Lemma. A solution of one problem serves as an infeasibility certificate of its alternative system. Further, we adapt an Approximate Farkas Lemma to interpret the meaning of an approximate solution from its alternative perspective. The Approximate Farkas Lemma also enables us to derive bounds for the distance to feasibility or infeasibility from approximate solutions of the alternative systems. Based on these observations, we interpret variants of the perceptron algorithm as variants of the von Neumann algorithm and vice versa, as well as transit the complexity results from one family to the other.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution
Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
USD 39.99
Price excludes VAT (USA)
  • Available as EPUB and PDF
  • Read on any device
  • Instant download
  • Own it forever
Softcover Book
USD 54.99
Price excludes VAT (USA)
  • Compact, lightweight edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info
Hardcover Book
USD 54.99
Price excludes VAT (USA)
  • Durable hardcover edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Similar content being viewed by others

References

  1. Bárány, I., Onn, S.: Colourful linear programming and its relatives. Mathe. Oper. Res. 22(3), 550–567 (1997)

    Article  MATH  Google Scholar 

  2. Beck, A., Teboulle, M.: A conditional gradient method with linear rate of convergence for solving convex linear systems. Math. Methods Oper. Res. 59, 235–247 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  3. Bertsimas, D., Tsitsiklis, J.N.: Introduction to Linear Optimization. Nashua, NH, (1997)

    Google Scholar 

  4. Blum, A., Dunagan, J.: Smoothed analysis of the perceptron algorithm for linear programming. In: Proceedings of the 13th Annual ACM-SIAM Symposium on Discrete Algorithms, publisher: SIAM, Philadalphia, PA, pp. 905–914 (2002)

    Google Scholar 

  5. Blum, A., Frieze, A., Kannan, R., Vempala, S.: A polynomial-time algorithm for learning noisy linear threshold functions. Algorithmica 22(1), (1998)

    Google Scholar 

  6. Cheung, D., Cucker, F.: A new condition number for linear programming. Math. Program. 91, 163–174 (2001)

    MathSciNet  MATH  Google Scholar 

  7. Dantzig, G.B.: Converting a converging algorithm into a polynomially bounded algorithm. Technical Report SOL 91-5, Stanford University, (1991)

    Google Scholar 

  8. Dantzig, G.B.: Bracketing to speed convergence illustrated on the von Neumann algorithm for finding a feasible solution to a linear program with a convexity constraint. Technical Report SOL 92-6, Stanford University, (1992)

    Google Scholar 

  9. Dantzig, G.B.: An ε-precise feasible solution to a linear program with a convexity constraint in 1∕ε 2 iterations independent of problem size. Technical Report SOL 92-5, Stanford University, (1992)

    Google Scholar 

  10. Dunagan, J., Vempala, S.: A simple polynomial-time rescaling algorithm for solving linear programs. In: Proceedings of STOC’04, pp. 315–320. ACM Press, New York, NY, (2004)

    Google Scholar 

  11. Epelman, M.A., Freund, R.M.: Condition number complexity of an elementary algorithm for resolving a conic linear system. Operations Research Center, Massachusetts Institute of Technology. Working paper, 319–97 (1997)

    Google Scholar 

  12. Epelman, M.A., Freund, R.M.: Condition number complexity of an elementary algorithm for computing a reliable solution of a conic linear system. Math. Program. 88, 451–485 (2000)

    MathSciNet  MATH  Google Scholar 

  13. Frank, M., Wolfe, P.: An algorithm for quadratic programming. Naval Res. Logist. Q. 3, 95–110 (1956)

    Article  MathSciNet  Google Scholar 

  14. Freund, R.M.: Dual gauge programs, with applications to quadratic programming and the minimum-norm problem. Math. Program. 38, 47–67 (1987)

    Article  MathSciNet  MATH  Google Scholar 

  15. Freund, R.M., Vera, J.R.: Some characterizations and properties of the “distance to ill-posedness” and the condition measure of a conic linear system. Math. Program. 86(2), 225–260 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  16. Freund, R.M., Vera, J.R.: Equivalence of convex problem geometry and computational complexity in the separation oracle model. Math. Oper. Res. 34, 869–879 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  17. Gonçalves, J.P.M.: A family of linear programming algorithms based on the von Neumann algorithm. PhD Thesis, Department of Industrial and Systems Engineering, Lehigh University, Bethlehem (2004)

    Google Scholar 

  18. Khachian, L.G.: A polynomial algorithm for linear programming. Sov. Math. Dokl. 20, 191–194 (1979)

    Google Scholar 

  19. Klafszky, E., Terlaky, T.: On the ellipsoid method. Rad. Math. 8, 269–280 (1992)

    MathSciNet  Google Scholar 

  20. Li, D.: On rescaling algorithms for linear optimization, PhD Proposal, Revised. Department of Industrial and Systems Engineering, Lehigh University, Bethlehem, (2011)

    Google Scholar 

  21. Minsky, M., Papert, S.A.: Perceptrons: An Introduction To Computational Geometry. MIT Press, Cambridge, MA, (1969)

    MATH  Google Scholar 

  22. Renegar, J.: Linear programming, complexity theory and elementary functional analysis. Technical Report 1090, School of Operations Research and Industrial Engineering College of Engineering, Cornell University, Ithaca, NY, USA, (1994)

    Google Scholar 

  23. Renegar, J.: Some perturbation theory for linear programming. Math. Program. 65, 73–91 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  24. Roos, C., Terlaky, T., Vial, J.-P.: Interior Point Methods for Linear Optimization. Springer, New York, NY, (2006)

    MATH  Google Scholar 

  25. Rosenblatt, F.: The perceptron – a perceiving and recognizing automaton. Technical Report 85-460-1, Cornell Aeronautical Laboratory, Ithaca, NY, USA, (1957)

    Google Scholar 

  26. Schrijver, A.: Theory of Linear and Integer Programming. Wiley, Hoboken, NJ, (1998)

    MATH  Google Scholar 

  27. Shawe-Taylor, J., Cristianini, N.: Support Vector Machines and Other Kernel-Based Learning Methods. Cambridge University Press Cambridge, England, (2000)

    Google Scholar 

  28. Soheili, N., Peña, J.: A primal-dual smooth perceptron-von Neumann algorithm. In: Discrete Geometry and Optimization Fields Institute Communications 69, 303–320 (2013)

    Article  Google Scholar 

  29. Soheili, N., Peña, J.: A smooth perceptron algorithm. SIAM J. Optim. 22(2), 728–737 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  30. Todd, M.J., Ye, Y.: Approximate Farkas Lemmas and stopping rules for iterative infeasible-point algorithms for linear programming. Math. Program. 81, 1–21 (1998)

    MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Industrial and Systems Engineering, Lehigh University, Bethlehem, PA, USA

    Dan Li & Tamás Terlaky

Authors
  1. Dan Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Tamás Terlaky
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Tamás Terlaky .

Editor information

Editors and Affiliations

  1. Department of Industrial and Systems Engineering, Lehigh University, Bethlehem, Pennsylvania, USA

    Luis F. Zuluaga

  2. Dept. Industrial & Systems Engineering, Lehigh University, Bethlehem, Pennsylvania, USA

    Tamás Terlaky

Rights and permissions

Reprints and permissions

Copyright information

© 2013 Springer Science+Business Media New York

About this paper

Cite this paper

Li, D., Terlaky, T. (2013). The Duality Between the Perceptron Algorithm and the von Neumann Algorithm. In: Zuluaga, L., Terlaky, T. (eds) Modeling and Optimization: Theory and Applications. Springer Proceedings in Mathematics & Statistics, vol 62. Springer, New York, NY. https://doi.org/10.1007/978-1-4614-8987-0_5

Download citation

Publish with us

Policies and ethics

Search

Navigation