Abstract
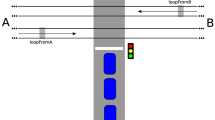
Consider a two-lane road which is intersected on one side by a single-lane secondary road. A single car waiting on the secondary road may merge into either the nearest or the farthest lane. It is assumed that the traffic in each lane is independent of the other lanes and that the inter-arrival times of cars at the intersection in their respective lanes is exponential. The main purpose of this paper is to study the queue size on the secondary road when the secondary road has a special right-turn lane (or left-turn lane in some countries) which allows some cars to merge into the nearest lane of the main road even when other cars waiting to enter the far lane are present. The problem is approached by first setting up a four-state Markov Renewal process to describe the traffic on the main road. Next the merging process on the secondary road is described as a Markov Renewed process with a random environment. The event that the queue is empty is studied, and conditions are stated under which this event is recurrent or transient. Finally, the quantities which occur in the conditions for recurrence of an empty queue are derived explicitly for a one-car right turn lane.
This is a preview of subscription content, log in via an institution to check access.
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Adams, W. F., Road Traffic Considered as a Random Series, J. Inst. Civil. Engrs. London, 4 (1936), 121 - 130.
Frechet, N., Recherches Theoriques Modernes Sur Les Calcul des Probabilities, Second Livre, Gauthier-Villars, Paris, 1938.
Garwood, F., The Application of the Theory of Probability to the Operation of Vehicular Controlled Traffic Signals, J. Roy. Statist. Soc. Suppl., 7 (1940), 65 - 77.
Gaver, D. P., Accommodation of Second Class Traffic, Technical Re-port No. 74, Applied Math, and Stat. Lab., Stanford University, California.
Haight, F. A., Mathematical Theories of Traffic Flow, Mathematics in Science and Eng., Vol. 7, Academic Press, New York, 1963.
Jewell, W. S., Waiting for a Gap in Traffic, Research Report No. 6, Operations Center, University of California-Berkeley (June 1961).
Newell, G. F., The Effect of Left Turns on the Capacity of Traffic Intersection, Quart. Appl. Math., 17, No. 1 (1959), 67 - 76.
Newell, G. F., Queues for a Fixed-cycle Traffic Light, Ann. Math. Stat., 31 No. 3 (1960), 589 - 597.
Oliver, R. M., Distribution of Gaps and Blocks in a Traffic Stream, Operations Research, 10 No. 2 (1962), 197 - 217.
Pyke, R., Markov Renewal Processes: Definitions and Preliminary Properties, Ann. Math. Stat., 32 (1961), 1231 - 1242.
Pyke, R., Markov Renewal Processes with Finitely Many States, Ann. Math. Stat., 32 (1961), 1243 - 1259.
Pyke, R. and Schaufele, R., Limit Theorems for Markov Renewal Processes, Technical Report No. 6, University of Washington, June 1963.
Raff, M. S., The Distribution of Blocks in an Uncongested Stream of Traffic, J. Am. Stat. Assoc., 46 (1951), 114 - 123.
Tanner, J.C., The Delay to Pedestrians Crossing a Road, Biometrika, 38 (1951), 383–392.
Weiss, G. H. and Maradudin, A. A., Some Problems in Traffic Delay, Operations Research, 10 (1962), 74–104, No. 1.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 1999 Kluwer Academic Publishers
About this chapter
Cite this chapter
Gideon, R., Pyke, R. (1999). Markov Renewal Modelling of Poisson Traffic at Intersections having Separate Turn Lanes. In: Janssen, J., Limnios, N. (eds) Semi-Markov Models and Applications. Springer, Boston, MA. https://doi.org/10.1007/978-1-4613-3288-6_18
Download citation
DOI: https://doi.org/10.1007/978-1-4613-3288-6_18
Publisher Name: Springer, Boston, MA
Print ISBN: 978-1-4613-3290-9
Online ISBN: 978-1-4613-3288-6
eBook Packages: Springer Book Archive